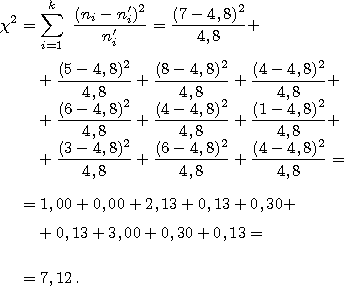Пусть из генеральной совокупности извлечена выборка объема П, в которой значение X1 некоторого исследуемого признака Х наблюдалось П1 раз, значение X2 — п2 раз, …, значение XK — Nk раз. Значения Xi называются Вариантами, а их последовательность, записанная в возрастающем порядке,— Вариационным рядом. Числа Ni называются Частотами, а их отношения к объему выборки
— Относительными частотами. При этом Ni = П. Модой Мo называется варианта, имеющая наибольшую частоту. Медианой те называется варианта, которая делит вариационный ряд на две части с одинаковым числом вариант в каждой. Если число вариант нечетно, т. е. K = 2L + 1, то Me = Xl+1; если же число вариант четно (k = 2L), То те = (Xl + Xl+1)/2. Размахом варьирования называется разность между максимальной и минимальной вариантами или длина интервала, которому принадлежат все варианты выборки:
Перечень вариант и соответствующих им частот называется Статистическим распределением выборки. Здесь имеется аналогия с законом распределения случайной величины: в теории вероятностей — это соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике — это соответствие между наблюдаемыми вариантами и их частотами (относительными частотами). Нетрудно видеть, что сумма относительных частот равна единице: Wi = 1.
Пример 2. Выборка задана в виде распределения частот:
Найти распределение относительных частот и основные характеристики вариационного ряда.
Решение. Найдем объем выборки: П = 2 + 4 + 5 + 6 + 3 = 20. Относительные частоты соответственно равны W1 = 2/20 = 0,1; W2 = 4/20 = 0,2; W3 = 5/20 = 0,25; W4 = 6/20 = 0,3; W5 = 3/20 = 0,15. Контроль: 0,1 + 0,2 + 0,25 + 0,3 + 0,15 = 1. Искомое распределение относительных частот имеет вид
Мода этого вариационного ряда равна 12. Число вариант в данном случае нечетно: K = 2 ∙ 2 + 1, поэтому медиана Me = X3 = 8. Размах варьирования, согласно формуле (18.48), R = 17 – 4 = 13.
| < Предыдущая | Следующая > |
|---|
Методика вычисления теоретических частот равномерного распределения
Если проверяется
гипотеза о равномерном распределении
выборочной совокупности, теоретические
частоты определяются очень легко.
Действительно, в этом случае на каждый
разряд наблюдаемых значений должно
приходиться одинаковое число наблюдений.
Поэтому для равномерного распределения
где
—
общее число наблюдений, то есть, объем
выборки, а—
число разрядов наблюдаемых значений.
Методика вычисления теоретических частот нормального распределения
Значительно сложнее
обстоит дело в случае нормального
распределения. Один из способов нахождения
теоретических частот нормального
распределения состоит в следующем.
-
Весь интервал
наблюдаемых значений величины
делят на
частичных
интерваловодинаковой длины. Затем — находят
середины этих интервалов
и строят статистическое
распределение равноотстоящих значений
из получившегося набора значений.
-
Вычисляют выборочное
среднее значение
и выборочное
среднее квадратичное отклонение
.
-
Нормируют случайную
величину
,
то есть — переходят к случайной величине,
следующим образом:
после чего —
вычисляют границы частичных интервалов,
в пределах которых изменяются значения
:
-
Вычисляют
теоретические вероятности
попадания величины
в интервалы
по следующим формулам:
где
—
функция Лапласа, значения которой
табулированы.
-
Наконец, теоретические
частоты
находят, исходя из найденных теоретических
вероятностей:
Заметим, что теоретические частоты, в
отличие от эмпирических, могут быть
дробными. Однако их сумма должна, как
и в случае эмпирических частот, давать,
то есть, объем выборки. Этот факт можно
использовать для проверки собственных
вычислений.
Пример применения статистического критерия согласия распределений (Пирсона)
Рассмотрим пример
с распределением выборов испытуемых
из акцентированного и контрольного
списков.
В информатике
важна проблема поиска или выбора
информации. Идея примера состоит в том,
что заголовки HTML-документов можно
акцентировать, исходя из предполагаемой
поисковой фразы, таким образом, что при
прочих равных акцентированный заголовок
будет выбираться пользователями чаще,
чем неакцентированный.
Здесь мы рассмотрим
частоты выборов в двух списках:
контрольном, который состоял из десяти
неакцентированных заголовков, и
экспериментальном, содержащем десять
заголовков, акцентированных пятью
способами. После этого мы установим,
что распределение в акцентированном
случае отличается от равномерного
(тогда как в контрольном случае оно
равномерно).
Частота выборов
в контрольном списке (статистическое
распределение выборов) представлена в
следующей таблице:
|
Позиция |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Частота |
7 |
5 |
8 |
4 |
6 |
4 |
1 |
3 |
6 |
4 |
Распределение
данного ряда выборов мы подвергаем
анализу при помощи
-критерия,
для чего выдвигаем следующие статистические
гипотезы:
распределение
выборов в контрольном списке подчинено
равномерному закону;
распределение
выборов в контрольном списке отличается
от равномерного.
В целом пользователи
совершили 48 выборов (число, равное сумме
всех наблюдаемых частот). Следовательно,
если бы предпочтения пользователей
были распределены равномерно, то каждая
позиция получила бы 4,8 выбора. Это и есть
теоретическая частота
.
Вычислим эмпирическое
значение
-критерия
Пирсона:
Равномерное
распределение характеризуется двумя
параметрами — границами возможных
значений — следовательно, вычисляя
число степеней свободы, имеем:
Зададимся уровнем
значимости
и по таблице критических значений
определим.
Итак:
следовательно, на
уровне значимости
,
мы принимаем основную гипотезу:
распределение выборов в контрольном
списке подчинено равномерному закону.
Поступим так же
со второй выборкой, где испытуемые
совершали выбор из акцентированных
заголовков. Частоты этих выборов
представлены в следующей таблице:
|
Акцент |
A |
B |
C |
D |
E |
|
Частота |
4 |
4 |
7 |
11 |
22 |
Данный ряд
распределения выборов мы также подвергаем
анализу при помощи
-критерия,
для этого — выдвигаем статистические
гипотезы:
распределение
выборов в акцентированном списке
подчинено равномерному закону;
распределение
выборов в акцентированном списке
отличается от равномерного.
В данном случае
речь идет о выборе не между позициями
списка, а между различными степенями
акцентированности заголовков: от вообще
не акцентированных (акцент A)
до наиболее акцентированных (акцент
E).
В целом пользователи совершили те же
48 выборов, что и в контрольном случае.
Но на этот раз их предпочтения
распределялись не между десятью позициями
списка, а между пятью способами
акцентированности. Поэтому, если бы
предпочтения распределялись равномерно,
то каждый способ акцента получил бы 9,6
выборов. Это число — теоретическая
частота распределения выборов:
.
Снова вычисляем
эмпирическое значение критерия:
Так же как и в
предыдущем случае, учитывая, что
равномерное распределение характеризуется
двумя параметрами, вычисляем число
степеней свободы:
На уровне значимости
найдем то таблице критических значений
-критерия
Пирсона критическое значение:.
Получаем следующее неравенство:
следовательно,
основная гипотеза отвергается и
принимается альтернативная: распределение
выборов в акцентированном списке
отличается от равномерного.
Основной целью
анализа вариационных рядов является
выявление закономерности распределения,
исключая при этом влияние случайных
для данного распределения факторов.
Этого можно достичь, если увеличивать
объем исследуемой совокупности и
одновременно уменьшать интервал ряда.
При попытке изображения этих данных
графически мы получим некоторую плавную
кривую линию, которая для полигона
частот будет являться некоторым пределом.
Эту линию называют кривой распределения.
Иными словами,
кривая
распределения
есть графическое изображение в виде
непрерывной линии изменения частот в
вариационном ряду, которое функционально
связано с изменением вариант. Кривая
распределения отражает закономерность
изменения частот при отсутствии случайных
факторов. Графическое изображение
облегчает анализ рядов распределения.
Известно достаточно
много форм кривых распределения, по
которым может выравниваться вариационный
ряд, но в практике статистических
исследований наиболее часто используются
такие формы, как нормальное распределение
и распределение Пуассона.
Нормальное
распределение зависит от двух параметров:
средней арифметической
и
среднего квадратического отклонения.
Его кривая выражается уравнением

где у – ордината
кривой нормального распределения;
–
стандартизованные отклонения; е и π –
математические постоянные; x – варианты
вариационного ряда;–
их средняя величина;–
cреднее квадратическое отклонение.
Если нужно получить
теоретические частоты f’ при выравнивании
вариационного ряда по кривой нормального
распределения, то можно воспользоваться
формулой

где
–
сумма всех эмпирических частот
вариационного ряда; h – величина интервала
в группах;–
cреднее квадратическое отклонение;–
нормированное отклонение вариантов от
средней арифметической; все остальные
величины легко вычисляются по специальным
таблицам.
При помощи этой
формулы мы получаем теоретическое
(вероятностное)
распределение,
заменяя им эмпирическое
(фактическое)
распределение,
по характеру они не должны отличаться
друг от друга.
Тем не менее в ряде
случаев, если вариационный ряд представляет
собой распределение по дискретному
признаку, где при увеличении значений
признака х частоты начинают резко
уменьшаться, а средняя арифметическая,
в свою очередь, равна или близка по
значению к дисперсии (),
такой ряд выравнивается по кривой
Пуассона.
Кривую
Пуассона можно
выразить отношением
(7.8)
где Px
– вероятность наступления отдельных
значений х;
–
средняя арифметическая ряда.
При выравнивании
эмпирических данных теоретические
частоты можно определить по формуле
(7.9)
где f’ – теоретические
частоты; N – общее число единиц ряда.
Сравнивая полученные
величины теоретических частот f’ c
эмпирическими (фактическими) частотами
f, убеждаемся, что их расхождения могут
быть весьма невелики.
Объективная
характеристика соответствия теоретических
и эмпирических частот может быть получена
при помощи специальных статистических
показателей, которые называют критериями
согласия.
Для оценки близости
эмпирических и теоретических частот
применяются критерий согласия Пирсона,
критерий согласия Романовского, критерий
согласия Колмогорова.
Закон равномерного
распределения случайной величины
Закон
распределения непрерывной случайной
величины называется равномерным,
если на интервале, которому принадлежат
все возможные значения случайной
величины, плотность распределения
сохраняет постоянное значение (
f(x)
= const
при a
≤ x
≤ b,
f(x)
= 0 при x
< a,
x
> b.
Найдем
значение, которое принимает f(x)
при
Из
условия нормировки следует, что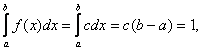
.
Вероятность
попадания равномерно распределенной
случайной величины на интервал
равна
при этом
Вид
функции распределения для нормального
закона:
Пример.
Автобусы некоторого маршрута идут с
интервалом 5 минут. Найти вероятность
того, что пришедшему на остановку
пассажиру придется ожидать автобуса
не более 2 минут.
Решение.
Время ожидания является случайной
величиной, равномерно распределенной
в интервале [0, 5]. Тогда
Соседние файлы в папке Лекции
- #
- #
- #
- #
- #
- #
- #
- #
- #
Проверка гипотезы о нормальном распределении генеральной совокупности
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Проверка дискретного распределения на нормальность
Пусть
эмпирическое распределение задано в виде последовательности равноотстоящих
вариант и соответствующих им частот:
|
|
|
|
… |
|
|
|
|
|
… |
|
Требуется, используя критерий Пирсона, проверить
гипотезу о том, что генеральная совокупность
распределена нормально.
Для того,
чтобы при заданном уровне значимости
проверить гипотезу о нормальном распределении
генеральной совокупности, надо:
1. Вычислить
выборочную среднюю
и выборочное среднее квадратическое отклонение
.
2.
Вычислить теоретические частоты
где
– объем выборки,
– шаг (разность между двумя соседними
вариантами)
3. Сравнить эмпирические и теоретические частоты
с помощью критерия Пирсона. Для этого:
а)
составляют расчетную таблицу (см. пример), по которой находят наблюдаемое
значение критерия
б) по
таблице критических точек распределения
, по заданному уровню
значимости
и числу степеней свободы
(
– число групп выборки) находят критическую
точку
правосторонней критической области.
Если
– нет оснований отвергнуть гипотезу о
нормальном распределении генеральной совокупности. Если
– гипотезу отвергают.
Проверка интервального распределения на нормальность
Пусть
эмпирическое распределение задано в виде последовательности интервалов
и соответствующих им частот
.
Требуется,
используя критерий Пирсона, проверить гипотезу о том, что генеральная
совокупность
распределена нормально.
Для того,
чтобы при уровне значимости
проверить гипотезу о нормальном распределении
генеральной совокупности, надо:
1.
Вычислить выборочную среднюю
и выборочное среднее квадратическое отклонение
, причем в качестве вариант
принимают среднее арифметическое концов
интервала:
2.
Пронормировать
, то есть перейти к
случайной величине
и
вычислить концы интервалов:
причем
наименьшее значение
, то есть
полагают равным
, а наибольшее, то есть
полагают равным
.
3. Вычислить теоретические
частоты:
где
– объем выборки
– вероятности попадания
в интервалы
– функция Лапласа.
4. Сравнить эмпирические и
теоретические частоты с помощью критерия Пирсона. Для этого:
а)
составляют расчетную таблицу (см. пример), по которой находят наблюдаемое
значение критерия
б) по
таблице критических точек распределения
, по заданному уровню
значимости
и числу степеней свободы
(
– число групп выборки) находят критическую
точку
правосторонней критической области.
Если
– нет оснований отвергнуть гипотезу о
нормальном распределении генеральной совокупности. Если
– гипотезу отвергают.
Замечание.
Малочисленные частоты
следует объединить, в этом случае и
соответствующие им теоретические частоты также надо сложить. Если производилось
объединение частот, то при определении числа степеней свободы по формуле
следует в качестве
принять число групп выборки, оставшихся после
объединения частот.
Примеры решения задач
Пример 1
Используя
критерий Пирсона при уровне значимости 0,05, проверить, согласуется ли гипотеза
с нормальным распределением генеральной совокупности X с заданным эмпирическим
распределением:
| xi | -4.5 | -3.5 | -2.5 | -1.5 | -0.5 | 0.5 | 1.5 | 2.5 | 3.5 | 4.5 |
| ni | 1 | 4 | 21 | 30 | 63 | 59 | 34 | 18 | 5 | 2 |
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Вычислим
характеристики распределения. Для этого составим расчетную таблицу.
Выборочная средняя:
Средняя
квадратов:
Выборочная
дисперсия:
Среднее квадратическое
отклонение:
Вычислим
теоретические частоты.
Вероятность
попадания в соответствующий интервал:
Теоретические
частоты:
где
-объем выборки
Составим
расчетную таблицу:
Проверим
степень согласия эмпирического и теоретического распределения по критерию
Пирсона. Объединяем малочисленные частоты (
).
Из
расчетной таблицы
Уровень
значимости
Число
степеней свободы
По
таблице критических точек распределения:
Нет
оснований отвергнуть гипотезу о нормальном распределении генеральной
совокупности.
Пример 2
Из большой партии по схеме случайной
повторной выборки было проверено 150 изделий с целью определения процента
влажности древесины, из которой изготовлены эти изделия. Получены следующие
результаты:
|
Процент влажности, xi |
11-13 |
13-15 |
15-17 |
17-19 |
19-21 |
|
Число изделий, ni |
8 |
42 |
51 |
37 |
12 |
На уровне значимости 0,05 проверить
гипотезу о нормальном законе распределения признака (случайной величины) X, используя критерий χ2 – Пирсона.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Составим расчетную таблицу
Средняя:
Средняя квадратов:
Дисперсия:
Исправленная дисперсия:
Исправленное среднее квадратическое
отклонение:
Вычислим теоретические частоты.
Составим расчетную таблицу:
Вероятность попадания в
соответствующий интервал:
, где
– функция Лапласа
Теоретические частоты:
, где
-объем выборки
Составим расчетную таблицу:
Проверим степень согласия
эмпирического и теоретического распределения по критерию Пирсона:
Из расчетной таблицы
Уровень значимости
Число степеней свободы
По таблице критических точек
распределения:
Нет оснований отвергать гипотезу о
распределении случайной величины по нормальному закону.
Задачи контрольных и самостоятельных работ
Задача 1
Выборка X
объемом n=100 задана таблицей:
|
|
0.8 | 1.1 | 1.4 | 1.7 | 2 | 2.3 | 2.6 |
|
|
5 | 13 | 25 | 25 | 19 | 10 | 3 |
1) Построить
полигон относительных частот
.
2) Вычислить
среднее выборочное
, выборочную дисперсию
и среднее квадратическое отклонение
.
3) Вычислить
теоретические частоты
. Построить график
на одном рисунке с полигоном.
4) С помощью
критерия χ2 проверить гипотезу о нормальном распределении
генеральной совокупности при уровне значимости α=0.05.
Задача 2
Построить
нормальную кривую по опытным данным. Рассчитать теоретические (выравнивающие) частоты
и сравнить с опытным распределением.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 3
Выборка X
объемом N=100 измерений задана таблицей:
|
|
0.6 | 1.5 | 2.4 | 3.3 | 4.2 | 5.1 | 6 |
|
|
5 | 13 | 26 | 24 | 19 | 10 | 3 |
а)
Построить полигон относительных частот
б)
вычислить среднее выборочное
, выборочную дисперсию
и среднее квадратическое отклонение
;
в) по
критерию χ2 проверить гипотезу о
нормальном распределении генеральной совокупности при уровне значимости α=0.05.
Задача 4
Для
изучения количественного признака
из генеральной совокупности извлечена выборка
объема n, имеющая данное
статистическое распределение.
а)
Построить полигон частот по данному распределению выборки.
б) Найти
выборочное среднее
, выборочное среднее
квадратическое отклонение
и исправленное среднее квадратическое
отклонение
.
в) При
данном уровне значимости
проверить по критерию Пирсона гипотезу о
нормальном распределении генеральной совокупности.
г) В
случае принятия гипотезы о нормальном распределении генеральной совокупности
найти доверительные интервалы для математического ожидания
и среднего квадратического отклонения σ при
данном уровне надежности γ=1-α; α=0.05
|
|
4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 |
|
|
5 | 9 | 15 | 19 | 20 | 16 | 10 | 6 |
Задача 5
Для выборки
объема N=100, представленной вариационным рядом
|
|
-1 | 0 | 1 | 2 | 3 | 4 | 5 |
|
|
3 | 8 | 11 | 19 | 37 | 17 | 5 |
построить
полигон относительных частот и гистограмму накопленных частот. Найти выборочное
среднее
и выборочное среднее квадратичное отклонение
. Определить доверительный интервал с
доверительной вероятностью β=0,95 для оценки математического ожидания
генеральной совокупности в предположении, что среднее квадратическое отклонение
генеральной совокупности σ равно исправленному выборочному среднему s. Проверить
гипотезу о нормальности закона распределения генеральной совокупности,
используя критерий Пирсона с уровнем значимости α=0,05.
Задача 6
Для случайной величины X составить интервальный
вариационный ряд, вычислить выборочные средние характеристики, подобрать
теоретический закон распределения, проверить его согласование с теоретическим
критерием Пирсона при α=0,05.
| 7 | 4 | 4 | 15 | 1 | 1 | 7 | 15 | 19 | 4 |
| 0 | 4 | 8 | 14 | 10 | 0 | 1 | 11 | 8 | 2 |
| 6 | 2 | 5 | 3 | 12 | 2 | 9 | 6 | 2 | 5 |
| 13 | 5 | 7 | 3 | 3 | 10 | 0 | 11 | 17 | 11 |
| 9 | 6 | 11 | 7 | 20 | 1 | 14 | 6 | 7 | 4 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 7
Данные о
продолжительности телефонных разговоров, отобранные по схеме
собственно-случайной бесповторной выборки, приведены в таблице:
| Время, мин | 1.5-2.5 | 2.5-3.5 | 3.5-4.5 | 4.5-5.5 | 5.5-6.5 | 6.5-7.5 | 7.5-8.5 | 8.5-9.5 | 9.5-10.5 | Итого |
| Число разговоров | 3 | 4 | 9 | 14 | 37 | 12 | 8 | 8 | 5 | 100 |
Используя χ2-критерий Пирсона при уровне
значимости α=0.05 проверить гипотезу о том, что случайная величина X –
продолжительность телефонных разговоров – распределена по нормальному закону.
Построить на одном чертеже гистограмму и соответствующую нормальную кривую.
Задача 8
Распределение
случайной величины X – заработной платы сотрудников на фирме (в у.е.) –
задано в виде интервального ряда:
Найти:
. Построить теоретическое
нормальное распределение и сравнить его с эмпирическим с помощью критерия
согласия Пирсона χ2 при α=0,05.
Задача 9
Записать для выборки интервальное
распределение, построить гистограмму относительных частот. По критерию Пирсона
проверить гипотезу нормальном распределении.
| 7.81 | 3.15 | 2.27 | 32.64 | 4.72 | 5.33 | 8.51 | 7.72 | 30.23 | 20.12 |
| 9.83 | 8.33 | 9.61 | 31.83 | 8.52 | 27.22 | 27.22 | 8.43 | 15.91 | 25.46 |
| 24.82 | 26.54 | 46.73 | 17.31 | 13.05 | 53.24 | 5.23 | 18.28 | 40.93 | 17.44 |
| 32.34 | 28.26 | 9.75 | 3.72 | 8.16 | 22.91 | 0.74 | 12.97 | 12.05 | 1.53 |
| 43.15 | 45.57 | 2.02 | 32.23 | 8.67 | 4.83 | 9.12 | 6.77 | 6.48 | 19.22 |
| 36.42 | 47.81 | 40.64 | 5.45 | 0.21 | 26.51 | 17.36 | 3.62 | 15.57 | 23.21 |
| 58.73 | 62.52 | 10.15 | 38.36 | 35.55 | 6.10 | 3.04 | 4.54 | 1.95 | 5.24 |
| 64.71 | 67.63 | 1.21 | 0.81 | 2.03 | 10.17 | 5.51 | 8.35 | 43.76 | 8.74 |
| 4.72 | 17.54 | 17.32 | 29.43 | 5.91 | 6.92 | 4.72 | 16.04 | 57.54 | 15.46 |
| 13.31 | 36.45 | 3.45 | 16.15 | 15.77 | 2.43 | 14.24 | 2.25 | 15.63 | 23.72 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 10
Результаты наблюдений над случайной
величиной
оказались
лежащими на отрезке
и были
сгруппированы в 10 равновеликих интервалов. Значения
и частоты
попадания в интервалы приведены в таблице. Построить: гистограмму частот,
эмпирическую функцию распределения, найти медиану. Найти выборочное среднее
и исправленное
среднеквадратическое отклонение
. Указать 95-процентные доверительные интервалы для
. С помощью критерия Пирсона проверить гипотезу о
нормальном (с параметрами
) законе распределения (уровень значимости α=0.02
.
Задача 11
В таблице приведены результаты
измерения роста (см.) случайно отобранных 100 студентов:
|
Интервалы роста |
154-158 | 158-162 | 162-166 | 166-170 | 170-174 | 174-178 | 178-182 |
|
Число студентов, |
10 | 14 | 26 | 28 | 12 | 8 | 2 |
С помощью критерия Пирсона при
уровне значимости α=0.05 проверить правдоподобие гипотезы о нормальном
распределении роста студентов.
Задача 12
При массовых стрельбах из пушек для
одинаковых общих условий были зафиксированы продольные ошибки (м) попадания
снарядов в цель:
На уровне значимости 0,05 проверить
гипотезу о нормальном законе распределения признака (случайной величины) L, используя критерий χ2– Пирсона.
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Что такое относительное частотное распределение?
17 авг. 2022 г.
читать 2 мин
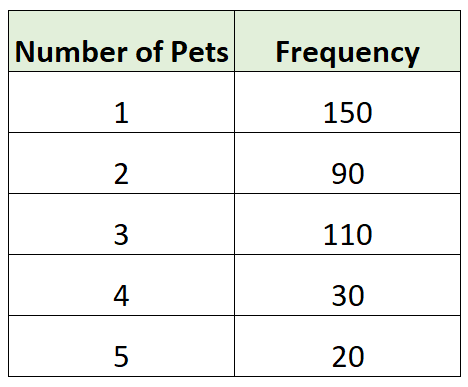
Распределение частоты описывает, как часто разные значения встречаются в наборе данных.
Например, предположим, что мы собираем простую случайную выборку из 400 домохозяйств в городе и записываем количество домашних животных в каждом домохозяйстве. В следующей таблице показаны результаты:
В этой таблице представлено частотное распределение.
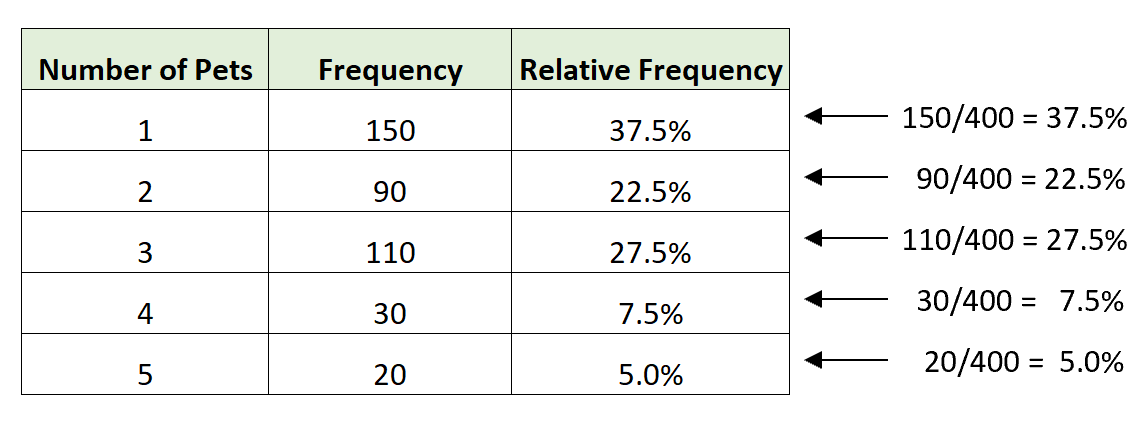
Связанное распределение известно как распределение относительной частоты , которое показывает относительную частоту каждого значения в наборе данных в процентах от всех частот.
Например, в предыдущей таблице мы видели, что всего было 400 домохозяйств. Чтобы найти относительную частоту каждого значения в распределении, мы просто делим каждую отдельную частоту на 400:
Обратите внимание, что распределения относительной частоты обладают следующими свойствами:
- Каждая отдельная относительная частота находится в диапазоне от 0% до 100%.
- Сумма всех отдельных относительных частот составляет 100%.
Если эти условия не выполняются, то относительное частотное распределение недействительно.
Почему относительные частотные распределения полезны
Распределения относительной частоты полезны, потому что они позволяют нам понять, насколько распространено значение в наборе данных по отношению ко всем другим значениям.
В предыдущем примере мы видели, что у 150 домохозяйств было только одно домашнее животное. Но это число само по себе не особенно полезно.
Напротив, полезнее знать, что 37,5% всех домохозяйств в выборке имели только одно домашнее животное. Это помогает нам понять, что чуть более чем в 1 из 3 домохозяйств было только одно домашнее животное, что дает нам некоторое представление о том, насколько «обычно» иметь только одного домашнего животного.
Визуализация относительного частотного распределения
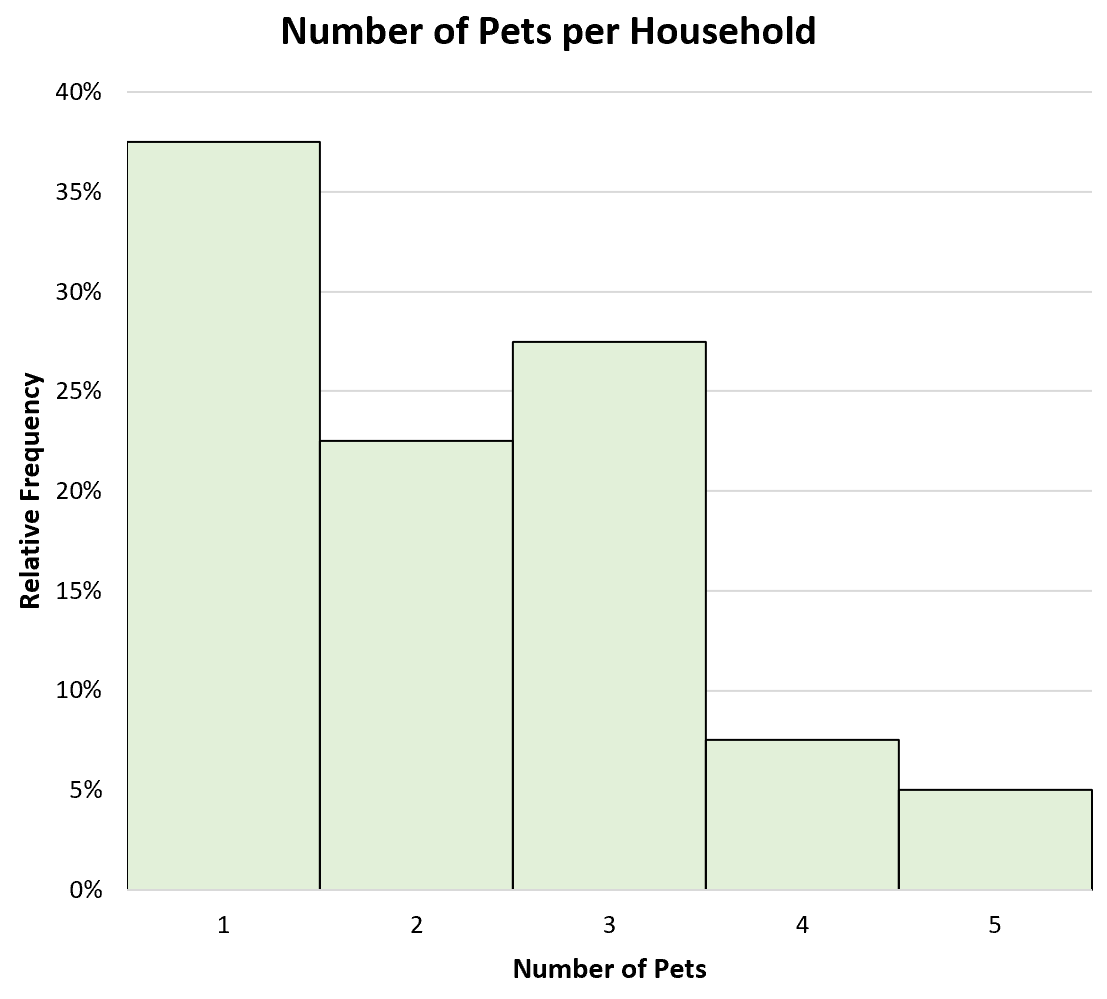
Самый распространенный способ визуализировать распределение относительной частоты — создать гистограмму относительной частоты , которая отображает отдельные значения данных по оси x графика и использует столбцы для представления относительной частоты каждого класса по оси y.
Например, вот как будет выглядеть гистограмма относительной частоты для данных из нашего предыдущего примера:
По оси X отображается количество домашних животных в домашнем хозяйстве, а по оси Y — относительная частота домашних хозяйств, в которых есть такое количество домашних животных.
Эта гистограмма помогает нам визуализировать распределение относительных частот.
Дополнительные ресурсы
Калькулятор относительной частоты
Как рассчитать относительную частоту в Excel
Как рассчитать относительную частоту в Python
Как создать гистограмму относительной частоты в R
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость
Статистическое распределение выборки
Содержание:
- Примеры использования формул и таблиц для решения практических задач
- Статистический интервальный ряд распределения
Предположим случай, когда из генеральной совокупности извлекается некоторая выборка, при этом каждому значению соответствует некоторый параметр, означающий количество раз, когда появлялось данное значение. Здесь $x_1$ было зафиксировано $n_1$ раз, $x_2$ было обнаружено $n_2$$x_k$ выявлено $n_k$. При этом
$sum_{i=1}^{k}n_i=n$
Где n — объём рассматриваемой выборки.
Определение 1
Используется следующая терминология: $x_k$ носят наименование вариантов, а последовательность таких вариантов, зафиксированный по возрастанию именуется вариационным рядом. Количество наблюдений каждого из вариантов носят название частот. При этом частное частот и выборки называют относительными частотами.
Определение 2
Статистическое распределение —это название всего набора вариантов и частот, которые с ними соотносятся. Чаще всего задаётся с помощью специальной таблицы, где представлены частоты, а также интервалы им соответствующие.
| $x_1$ | $x_2$ | … | $x_k$ |
| $n_1$ | $n_2$ | … | $n_k$ |
| $frac{n_1}{n}$ | $frac{n_2}{n}$ | $frac{n_k}{n}$ |
Здесь в первой строке представлены варианты, во второй частоты, в третьеq взяты относительные частоты.
Для определения размера интервала используется следующее выражение:
$d=frac{x_{max}- x_{min}}{1+3,332cdot lg n}$
Здесь $x_{max}$, $x_{min}$ наибольшее и наименьшее значения ряда вариантов, а n характеризуем объём выборки.
Примеры использования формул и таблиц для решения практических задач
Пример 1
В ходе проведения измерений в однородных группах, были определены следующие значения выборки: 71, 72, 74, 70, 70, 72, 71, 74, 71, 72, 71, 73, 72, 72, 72, 74, 72, 73, 72, 74. Необходимо использовать данные значения, что определить ряд распределения частот и ряд распределения относительных частот.
Решение.
1) Составим статистический ряд распределения частот:
| xi | 70 | 71 | 72 | 73 | 74 |
| ni | 2 | 4 | 8 | 2 | 4 |
2) Рассчитаем суммарный размер выборки: n=2+4+8+2+4=20. Определим относительные частоты, для этого используем формулы: ni/n=wi: wi=2/20=0.1; w2=4/20=0.2; w3=0.4; w4=4/20=0.1; w5=2/20=0.2. Теперь зафиксируем в таблице распределение относительных частот:
| xi | 70 | 71 | 72 | 73 | 74 |
| wi | 0.1 | 0.2 | 0.4 | 0.1 | 0.2 |
Контрольная сумма должна равняться единице: 0,1+0,2+0,4+0,1+0,2=1.
Полигон частот
Название «полигоном частот» применяют для обозначения ломаной линии, каждый отрезок, которой соединяют точки $(х_1,n_1),(х_2,n_2),…,(х_k,n_k)$. Для построения на графике полигона частот по оси абсцисс отмечают варианты $х_2$, при этом на оси ординат отсчитывают– соответствующие частоты $n_i$. Когда полученные точки $(х_i,n_i)$ соединяются с помощью отрезков, то автоматически получают полигон частот.
Статистический интервальный ряд распределения.
Статистическим дискретным рядом (или эмпирической функцией распределения) обычно пользуются, если число различающихся вариант в полученной выборке не слишком большое. Также применение возможно, когда дискретность имеет важное значение для экспериментатора. В тех случаях, когда важный для задачи признак генеральной совокупности Х распределяется непрерывным образом, либо его дискретность нет возможности учесть, то варианты предпочтительнее всего группировать, чтобы получить интервалы.
Статистическое распределение допустимо задавать в том числе в качестве последовательности интервалов и частот, соответствующих этим интервалам. При это за частоту какого-либо интервала принимается сумма всех частот, вошедших в данный интервал.
Особенно следует отметить ,что $h_i-h_{i-1}=h$ при всех i, т.е. группировка проводится с равным шагом h. Также в вопросе группировки можно ориентироваться на ряд полученных опытным путём рекомендацийу, касающихся таких параметров, как а, k и $h_i$:
1. $Rраз_{мах}=X_{max}-X_{min}$
2. $h=R/k$; k-число групп
3.$ kgeq 1+3.321lgn$ (формула Стерджеса)
4. $a=x_{min}, b=x_{max}$
5.$ h=a+h_i, i=0,1…k$
Определённую в ходе решения задачи группировку удобнее всего скомпоновать и перевести в вид специальной таблицы, которая также может именоваться — «статистический интервальный ряд распределения»:
| Интервалы группировки | [h0;h1) | [h1;h2) | … | [hk-2;hk-1) | [hk-1;hk) |
| Частоты | n1 | n2 | … | nk-1 | nk |
Таблицу подобного вида можно сделать, поменяв частоты $n_i$ на относительные частоты:
| Интервалы группировки | [h0;h1) | [h1;h2) | … | [hk-2;hk-1) | [hk-1;hk) |
| Отн. частоты | w1 | w2 | … | wk-1 | wk |

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример 2
На склад пришла крупная партия деталей. Из них методом случайного отбора взято 50 экземпляров. Рассматривая изделия по одному, особенно интересующему признаку — размеру, определённому с точностью до 1 см, получим следующий вариационный ряд: 22, 47, 26, 26, 30, 28, 28, 31, 31, 31, 32, 32, 33, 33, 33, 33, 34, 34, 34, 34, 34, 35, 35, 36, 36, 36, 36, 36, 37, 37, 37, 37, 37, 37, 38, 38, 40, 40, 40, 40, 40, 41, 41, 43, 44, 44, 45, 45, 47, 50. Требуется произвести расчёт и определить статистический интервальный ряд распределения.
Решение
Найдём параметры выборки используя сведения из условия задачи.
$k geq1+3,321cdot lg50=1+3.32lg(5cdot10)=1+3.32(lg5+lg10)=6.6$
Получили a=22, k=7, h=(50-22)/7=4, hi=22+4i, i=0,1,…,7.
| Интервалы группировки | 22-26 | 26-30 | 30-34 | 34-38 | 38-42 | 42-46 | 46-50 |
| Частоты | 1 | 4 | 10 | 18 | 9 | 5 | 3 |
| Отн. частоты | 0.02 | 0.08 | 0.2 | 0.36 | 0.18 | 0.1 | 0.06 |
Десятичные логарифмы от 1 до 10
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| lnn≈ | 0 | 0.3 | 0.48 | 0.6 | 0.7 | 0.78 | 0.85 | 0.9 | 0.95 | 1 |
Не получается написать работу самому?
Доверь это кандидату наук!