Как найти частоту появления простых чисел - Сайт, где вы сможете решить свои вопросы

Частота события. Статистическое определение вероятности

содержание учебника

Классическое определение вероятности предполагает, что все элементарные исходы равновозможны. О равновозможности исходов опыта заключают в силу соображений симметрии (как в случае монеты или игрального кубика). Задачи, в которых можно исходить из соображений симметрии, на практике встречаются редко. Во многих случаях трудно указать основания, позволяющие считать, что все элементарные исходы равновозможны. В связи с этим появилась необходимость введения еще одного определения вероятности, называемого статистическим. Чтобы дать это определение, предварительно вводят понятие относительной частоты события.

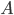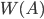Относительной частотой события, или частотой, называется отношение числа опытов, в которых появилось это событие, к числу всех произведенных опытов. Обозначим частоту события через W(A) , тогда по определению

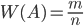$W(A)=displaystylefrac{m}{n}$ (1.4.1)
где – число опытов, в которых появилось событие 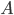и – число всех произведенных опытов.

Частота события обладает следующими свойствами.

Частота случайного события есть число, заключенное между нулем и единицей:
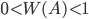. (1.4.2)
Частота достоверного события 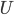равна единице:
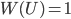(1.4.3)
Частота невозможного события 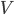равна нулю:
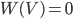(1.4.4)
Частота суммы двух несовместных событи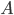й и равна сумме частот этих событий:
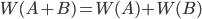(1.4.5)

Наблюдения позволили установить, что относительная частота обладает свойствами статистической устойчивости: в различных сериях многочленных испытаний (в каждом из которых может появиться или не появиться это событие) она принимает значения, достаточно близкие к некоторой постоянной. Эту постоянную, являющуюся объективной числовой характеристикой явления, считают вероятностью данного события.

Вероятностью события называется число, около которого группируются значения,частоты данного события в различных сериях большого числа испытаний.

Это определение вероятности называется статистическим.

В случае статистического определения вероятность обладает следующими свойствами:
1) вероятность достоверного события равна единице;
2) вероятность невозможного события равна нулю;
3) вероятность случайного события заключена между нулем и единицей;
4) вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.

Пример 1. Из 500 взятых наудачу деталей оказалось 8 бракованных. Найти частоту бракованных деталей.

Решение. Так как в данном случае = 8, = 500, то в соответствии с формулой (1.4.1) находим

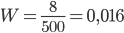
$W=displaystylefrac{8}{500}=0,016$

Пример 2. Игральный кубик подброшен 60 раз, при этом шестерка появилась 10 раз. Какова частота появления шестерки?

Решение. Из условия задачи следует, что = 60, = 10, поэтому

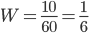
$W=displaystylefrac{10}{60}=frac{1}{6}$

Пример 3. Среди 1000 новорожденных оказалось 515 мальчиков.Чему равна частота рождения мальчиков?
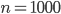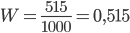Решение. Поскольку в данном случае n=1000 , m=515 , то $W=displaystylefrac{515}{1000}=0,515$ .

Пример 4. В результате 20 выстрелов по мишени получено 15 попаданий. Какова частота попаданий?

Решение. Так как = 20, = 15, то

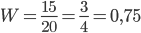
$W=displaystylefrac{15}{20}=frac{3}{4}=0,75$

Пример 5. При стрельбе по мишени частота попаданий 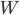= 0,75. Найти число попаданий при 40 выстрелах.

Решение. Из формулы (1.4.1) следует, что 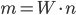. Так как 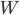= 0,75, = 40, то 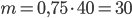. Таким образом, было получено 30 попаданий.

Пример 6. www.itmathrepetitor.ru Частота нормального всхода семян W = 0,97. Из высеянных семян взошло 970. Сколько семян было высеяно?

Решение. Из формулы (1.4.1) следует, что 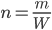$n=displaystylefrac{m}{W}$ . Поскольку 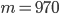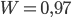m = 970 , W=0,97 , то . Итак, было высеяно 1000 семян.

Пример 7. На отрезке натурального ряда от 1 до 20 найти частоту простых чисел.

Решение. На указанном отрезке натурального ряда чисел находятся следующие простые числа: 2, 3, 5, 7, 11, 13, 17, 19; всего их 8. Так как = 20, = 8, то искомая частота

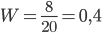$W=displaystylefrac{8}{20}=0,4$ .

Пример 8. Проведены три серии многократных подбрасываний симметричной монеты, подсчитаны числа появлений герба: 1) 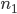n_1 = 4040, 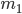m_1 =2048, 2) 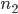n_2 = 12000, 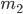m_2 = 6019; 3) 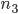n_3 = 24000, 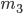m_3 = 12012. Найти частоту появления герба в каждой серии испытаний.

Решение. В соответствии с формулой (1.4.1) находим:

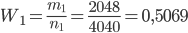
$W_1=displaystylefrac{m_1}{n_1}=frac{2048}{4040}=0,5069$

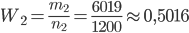
$W_2=displaystylefrac{m_2}{n_2}=frac{6019}{1200}approx0,5016$

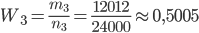$W_3=displaystylefrac{m_3}{n_3}=frac{12012}{24000}approx0,5005$ .

Замечание. Эти примеры свидетельствуют о том, что при многократных испытаниях частота события незначительно отличается от его вероятности. Вероятность появления герба при подбрасывании монеты р = 1/2 = 0,5 , так как в этом случае n = 2, m = 1.

Пример 9. Среди 300 деталей, изготовленных на автоматическом станке, оказалось 15, не отвечающих стандарту. Найти частоту появления нестандартных деталей.

Решение. В данном случае n = 300, m = 15, поэтому

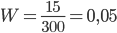
$W=displaystylefrac{15}{300}=0,05$

Пример 10. Контролер, проверяя качество 400 изделий установил, что 20 из них относятся ко второму сорту, а остальные – к первому. Найти частоту изделий первого сорта, частоту изделий второго сорта.

Решение. Прежде всего, найдем число изделий первого сорта: 400 – 20 = 380. Поскольку n = 400, 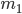m_1 = 380, то частота изделий первого сорта

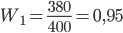
$W_1=displaystylefrac{380}{400}=0,95$

Аналогично находим частоту изделий второго сорта:

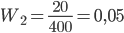
$W_2=displaystylefrac{20}{400}=0,05$

Задачи

Отдел технического контроля обнаружил 10 нестандартных изделий в партии из 1000 изделий. Найдите частоту изготовления бракованных изделий.
Для выяснения качества семян было отобрано и высеяно в лабораторных условиях 100 штук. 95 семян дали нормальный всход. Какова частота нормального всхода семян?
Найдите частоту появления простых чисел в следующих отрезках натурального ряда: а) от 21 до 40; б) от 41 до 50; в) от 51 до 70.
Найдите частоту появления цифры при 100 подбрасываниях симметричной монеты. (Опыт проводите самостоятельно).
Найдите частоту появления шестерки при 90 подбрасываниях игрального кубика.
Путем опроса всех студентов Вашего курса определите частоту дней рождения, попадающих на каждый месяц года.
Найдите частоту пятибуквенных слов в любом газетном тексте.

Ответы

0,01. 2. 0,95; 0,05. 3. а) 0,2; б) 0,3; в) 0,2.

Вопросы

Что такое частота события?
Чему равна частота достоверного события?
Чему равна частота невозможного события?
В каких пределах заключена частота случайного события?
Чему равна частота суммы двух несовместных событий?
Какое определение вероятности называют статистическим?
Какими свойствами обладает статистическая вероятность?

содержание учебника

Источник

Относительная частота.
Статистическая вероятность

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Краткая теория

Относительная
частота наряду с вероятностью принадлежит к основным понятиям теории
вероятностей. Относительной частотой события называют отношение числа
испытаний, в которых событие появилось, к общему числу фактически произведенных
испытаний.

Таким
образом, относительная частота события

определяется формулой:

где

– число появления события

– общее число испытаний

Сопоставляя
определения вероятности и относительной частоты, заключаем: определение
вероятности не требует, чтобы испытания производились в действительности;
определение же относительной частоты предполагает, что испытания были
произведены фактически. Другими словами, вероятность вычисляют до опыта, а относительную
частоту – после опыта.

Длительные
наблюдения показали, что если в одинаковых условиях производят опыты, в каждом
из которых число испытаний достаточно велико, то относительная частота
обнаруживает свойство устойчивости. Это свойство состоит в том, что в различных
опытах относительная частота изменяется мало (тем меньше, чем больше
произведено испытаний), колеблясь около некоторого постоянного числа.
Оказалось, что это постоянное число есть вероятность появления события.

Таким
образом, если опытным путем установлена относительная частота, то полученное
число можно принять за приближенное значение вероятности.

Классическое
определение вероятности предполагает, что число элементарных исходов испытания
конечно. На практике же весьма часто встречаются испытания, число возможных
исходов которых бесконечно. В таких случаях классическое определение
неприменимо.

По этой
причине наряду с классическим определением вероятности используют и другие
определения, в частности статистическое определение: в качестве статистической
вероятности события принимают относительную частоту или число, близкое к ней.
Например, если в результате достаточно большого числа испытаний оказалось, что
относительная частота весьма близка числу 0,4, то это число можно принять за
статистическую вероятность события.

Для
существования статистической вероятности события

требуется:

а)
возможность, хотя бы принципиально, производить неограниченное число испытаний,
в каждом из которых событие А наступает или не наступает;

б)
устойчивость относительных частот появления

в различных сериях достаточно большого числа
испытаний.

Смежные темы решебника:

Классическое определение вероятности
Геометрическое определение вероятности

Примеры решения задач

Пример 1

Игральный
кубик подброшен 60 раз, при этом шестерка появилась 10 раз. Какова относительная
частота появления шестерки?

Решение

Из
условия задачи следует, что

, поэтому

Ответ:

Пример 2

При
стрельбе по мишени относительная частота попаданий

. Найти число попаданий при
40 выстрелах.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Из
формулы

следует,
что

Так как

, то искомое число
попаданий:

Ответ:

Пример 3

Контролер, проверяя качество 400 изделий
установил, что 20 из них относятся ко второму сорту, а остальные – к первому.
Найти относительная частоту изделий первого сорта, относительную частоту
изделий второго сорта.

Решение

Прежде
всего, найдем число изделий первого сорта:

Относительная
частота изделий 1-го сорта:

Аналогично
находим относительную частоту изделий второго сорта:

Ответ:

Задачи контрольных и самостоятельных работ

Задача 1

Найдите частоту появления простых
чисел в следующих отрезках натурального ряда: а) от 21 до 40; б) от 41 до 50;
в) от 51 до 70.

Задача 2

Отдел технического контроля
обнаружил 10 нестандартных изделий в партии из 1000 изделий. Найдите частоту
изготовления бракованных изделий.

Задача 3

Многолетними
наблюдениями установлено, что в некоторой области ежегодно в среднем в тридцати
хозяйствах из каждых ста среднегодовой удой молока от одной коровы составляет
4100-4300 кг. Какова вероятность того, что в текущем году в одном из хозяйств
этой области, отобранном случайным образом, будет получен такой среднегодовой
удой?

Задача 4

Для выяснения качества семян было
отобрано и высеяно в лабораторных условиях 100 штук. 95 семян дали нормальный
всход. Какова частота нормального всхода семян?

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 5

Для
проведения исследований на некотором поле взяли случайную выборку из 200
колосьев пшеницы. Относительная частота колосьев, имеющих по 12 колосков в
колосе, оказалось равной 0,123, а по 18 колосков – 0,05. Найти для этой выборки
количество колосьев, имеющих по 12 и 18 колосков.

Задача 6

Найдите частоту появления цифры при
100 подбрасываниях симметричной монеты. (Опыт проводите самостоятельно).

Задача 7

Найдите частоту пятибуквенных слов в
любом газетном тексте.

Задача 8

Путем опроса всех студентов Вашего
курса определите частоту дней рождения, попадающих на каждый месяц года.

Задача 9

За лето на Черноморском побережье
было 67 солнечных дней. Какова частота солнечных дней на побережье за лето?
Частота пасмурных дней?

Задача 10

Найдите частоту появления шестерки
при 90 подбрасываниях игрального кубика.

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Источник

Статистическая вероятность

План урока

Статистическая вероятность

Цели урока

Знать определения абсолютной частоты, относительной частоты и статистической вероятности
Уметь вычислять относительную частоту события на основе статистических данных

Разминка

Какое событие называют случайным?
Как называется событие, вероятность которого равна 1?
Как называется событие, вероятность которого равна 0?
Вероятность появления события A при некотором испытании равна 0,3. Чему равна вероятность того, что при этом испытании событие A не произойдёт?

Статистическая вероятность

Вам уже знакомо классическое определение вероятности. Однако, оно применимо лишь в тех случаях, когда можно теоретически выявить все равновозможные исходы испытания. На практике часто встречаются такие испытания (явления), в которых число исходов необозримо велико. Кроме того, не все исходы могут быть равновозможными или установить их равновозможность проблематично. Поэтому существует другой подход к определению понятия вероятности. Весь наш жизненный опыт подсказывает, что любое событие считается более вероятным, чем чаще оно происходит. Значит, вероятность события должна быть каким-то образом связана с частотой появления этого события.

Абсолютной частотой случайного события A в серии из N случайных опытов называется число M, которое показывает, сколько раз в этой серии произошло событие A.

Абсолютная частота всегда выражается целым числом 0≤𝑀≤𝑁. При этом:

для невозможного события 𝑀=0;
для достоверного события 𝑀=𝑁.

Относительной частотой случайного события A в серии из N случайных опытов называется число WA, которое показывает, какая доля опытов в этой серии завершилась наступлением события A:

𝑊(𝐴)=𝑀N.

Относительная частота выражается числом от 0 до 1. При этом:

для невозможного события 𝑊(𝐴)=0;
для достоверного события 𝑊(𝐴)=1.

При стократном бросании монеты «орёл» выпал 48 раз. Какова относительная частота выпадения «орла» в данной серии бросания монеты?

Решение

Событие A – выпадение «орла», произошло в 48 случаях, т.е. M=48. Общее число испытаний (бросаний монеты) N=100. Следовательно, относительная частота выпадения «орла» в данной серии равна 𝑊(𝐴) =48100=0,48.

Ответ: 0,48.

Контролер, проверяя качество 400 изделий установил, что 20 из них относятся ко второму сорту, а остальные – к первому. Найти относительную частоту изделий первого сорта, относительную частоту изделий второго сорта.

Решение

Прежде всего, найдем число изделий первого сорта: 400-20=380. Поскольку N=400, M1=380, то частота изделий первого сорта:

W1=380400=0,95.

Аналогично, находим частоту изделий второго сорта:

W2=20400=0,05.

Ответ: 0,95; 0,05.

Если проводить реальные испытания с подбрасыванием монеты и фиксировать количество появлений «орла» в разных сериях испытаний, то можно заметить: чем больше проводится испытаний, тем меньше относительная частота появления «орла» отличается от значения 0,5. То есть можно сказать, что относительная частота появления орла стремится к вероятности этого события в классическом понимании. Такие эксперименты проводили различные учёные прошлого. Так французский математик и естествоиспытатель XVIII века Жорж-Луи Леклерк де Бюффон, выполнив 4040 подбрасываний монеты, наблюдал появление «орла» 2048 раз и, следовательно, получил относительную частоту появления «орла», равную 20484040≈0,5069. Английский учёный Карл Пирсон со своими учениками выполнил 24000 подбрасываний монеты. «Орёл» выпал в 12012 случаях. Таким образом, у Пирсона частота появления «орла» оказалась равной 1201224000≈0,5005.

Статистической вероятностью случайного события A называется число P(A), к которому приближается относительная частота W(A) в длинной серии экспериментов.

С математической точки зрения данную формулировку нельзя назвать определением. Во-первых, где гарантия, что относительная частота вообще будет к чему-то «приближаться»? Во-вторых, насколько длинной должна быть сама серия, чтобы полученная в ней частота достаточно хорошо приближала вероятность? И так далее. Получается, что точно найти вероятность с помощью этого определения нельзя. Тем не менее оно даёт возможность приближённо оценить вероятность по частоте – причём тем точнее, чем длиннее серия проведённых экспериментов.

Из 1000 произвольно выбранных деталей примерно 4 бракуются. Сколько примерно бракованных окажется среди 2400 деталей?

Решение

Обозначим событие A – наугад выбранная деталь бракованная. Тогда статистическая вероятность примерно равна 𝑃(𝐴)≈𝑊(𝐴)=0,004.

Пусть среди 2400 деталей x бракованных. Тогда

𝑥2400≈0,004⇒𝑥≈10.

Ответ: ≈10.

При стрельбе по мишени относительная частота попаданий W=0,75. Найти примерное число попаданий при 40 выстрелах.

Решение

𝑃(𝐴)≈𝑊(𝐴)=0,75. Пусть при 40 выстрелах x попаданий. Тогда

𝑥40≈ 0,75⇒𝑥≈30.

Ответ: 30.

Отдел технического контроля обнаружил 10 нестандартных изделий в партии из 1000 изделий. Найдите относительную частоту изготовления бракованных изделий.
Для выяснения качества семян было отобрано и высеяно в лабораторных условиях 100 штук. 95 семян дали нормальный всход. Какова относительная частота нормального всхода семян?
Найдите относительную частоту появления простых чисел в следующих отрезках натурального ряда: а) от 21 до 40; б) от 41 до 50; в) от 51 до 70.
Чтобы определить, какой цвет волос встречается в городе чаще, а какой реже, студенты за полчаса провели следующий эксперимент. Каждый выбрал свой маршрут и записывал по пути следования цвет волос каждого пятого встречного. Результаты были занесены в следующую таблицу:

Цвет волос	Брюнеты	Шатены	Рыжие	Блондины	Всего
Число людей	198	372	83	212	865

Оцените вероятность того, что выбранный наугад житель этого города будет:

а) шатеном;

б) рыжим;

в) не рыжим.

Контрольные вопросы

Что такое абсолютная частота события?
Что такое относительная частота события?
В каких пределах заключена относительная частота случайного события?
Сформулируйте статистическое определение вероятности.

Ответы

Упражнение 1

0,01;
0,95 и 0,05;
а) 0,2; б) 0,3; в) 0,2;
а) ≈0,43; б) ≈0,096; в) ≈0,904.

Источник

В математике функция распределения простых чисел, или пи-функция pi (x) , — это функция, равная числу простых чисел, меньших либо равных действительному числу x.^[1]^[2] Она обозначается pi (x) (это никак не связано с числом пи).

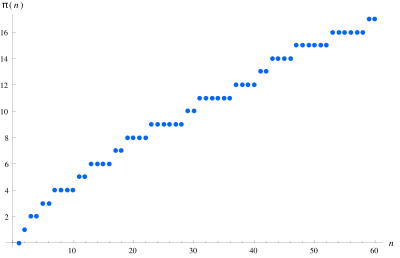
Значения пи-функции для первых 60 натуральных чисел

История[править | править код]

Большой интерес в теории чисел представляет скорость роста пи-функции.^[3]^[4] В конце XVIII столетия Гауссом и Лежандром было выдвинуто предположение, что пи-функция оценивается как

${frac {x}{ln x}}$

в смысле, что

$lim limits _{{xto +infty }}{frac {pi (x)}{x/ln x}}=1.$

Это утверждение — теорема о распределении простых чисел. Оно эквивалентно утверждению

$lim limits _{{xto +infty }}{frac {pi (x)}{operatorname {li}(x)}}=1$

где — это интегральный логарифм. Теорема о простых числах впервые была доказана в 1896 Жаком Адамаром и независимо Валле-Пуссеном, используя дзета-функцию Римана введенную Риманом в 1859.

Точнее рост pi (x) сейчас описывается как

${displaystyle pi (x)=operatorname {li} (x)+O{bigl (}xe^{-{sqrt {ln x}}/15}{bigr )}}$

где обозначает O большое. Когда x не сильно велико больше, чем pi (x) , однако разность меняет свой знак бесконечное число раз, наименьшее натуральное число, для которого происходит смена знака называется числом Скьюза.

Доказательства теоремы о простых числах, не использующие дзета-функцию или комплексный анализ, были найдены в 1948 году Атле Сельбергом и Паулем Эрдёшом (большей частью независимо).^[5]

Таблицы для пи-функции, x / ln x и li(x)[править | править код]

В следующей таблице показан рост функций ${displaystyle pi (x),{frac {x}{ln x}},operatorname {li} (x)}$ по степеням 10^[3]^[6]^[7]^[8].

x	π(x)	π(x) − x / ln x	li(x) − π(x)	x / π(x)	π(x)/x (доля простых чисел)
10	4	−0,3	2,2	2,500	40 %
10²	25	3,3	5,1	4,000	25 %
10³	168	23	10	5,952	16,8 %
10⁴	1 229	143	17	8,137	12,3 %
10⁵	9 592	906	38	10,425	9,59 %
10⁶	78 498	6 116	130	12,740	7,85 %
10⁷	664 579	44 158	339	15,047	6,65 %
10⁸	5 761 455	332 774	754	17,357	5,76 %
10⁹	50 847 534	2 592 592	1 701	19,667	5,08 %
10¹⁰	455 052 511	20 758 029	3 104	21,975	4,55 %
10¹¹	4 118 054 813	169 923 159	11 588	24,283	4,12 %
10¹²	37 607 912 018	1 416 705 193	38 263	26,590	3,76 %
10¹³	346 065 536 839	11 992 858 452	108 971	28,896	3,46 %
10¹⁴	3 204 941 750 802	102 838 308 636	314 890	31,202	3,20 %
10¹⁵	29 844 570 422 669	891 604 962 452	1 052 619	33,507	2,98 %
10¹⁶	279 238 341 033 925	7 804 289 844 393	3 214 632	35,812	2,79 %
10¹⁷	2 623 557 157 654 233	68 883 734 693 281	7 956 589	38,116	2,62 %
10¹⁸	24 739 954 287 740 860	612 483 070 893 536	21 949 555	40,420	2,47 %
10¹⁹	234 057 667 276 344 607	5 481 624 169 369 960	99 877 775	42,725	2,34 %
10²⁰	2 220 819 602 560 918 840	49 347 193 044 659 701	222 744 644	45,028	2,22 %
10²¹	21 127 269 486 018 731 928	446 579 871 578 168 707	597 394 254	47,332	2,11 %
10²²	201 467 286 689 315 906 290	4 060 704 006 019 620 994	1 932 355 208	49,636	2,01 %
10²³	1 925 320 391 606 803 968 923	37 083 513 766 578 631 309	7 250 186 216	51,939	1,92 %
10²⁴	18 435 599 767 349 200 867 866	339 996 354 713 708 049 069	17 146 907 278	54,243	1,84 %
10²⁵	176 846 309 399 143 769 411 680	3 128 516 637 843 038 351 228	55 160 980 939	56,546	1,77 %
10²⁶	1 699 246 750 872 437 141 327 603	28 883 358 936 853 188 823 261	155 891 678 121	58,850	1,70 %
10²⁷	16 352 460 426 841 680 446 427 399	267 479 615 610 131 274 163 365	508 666 658 006	61,153	1,64 %

В OEIS первая колонка значений pi (x) — это последовательность A006880, $pi (x)-leftlfloor {frac {x}{ln x}}+0{,}5rightrfloor$ — это последовательность A057835, а — это последовательность A057752.

Алгоритмы вычисления пи-функции[править | править код]

Простой способ найти pi (x) , если не очень велико, — это использование решета Эратосфена выдающего простые, не превосходящие и подсчитать их.

Более продуманный способ вычисления pi (x) был дан Лежандром: дан , если $p_{1},p_{2},ldots ,p_{k}$ — различные простые числа, то число целых чисел, не превосходящих и не делящихся на все $p_{i}$ равно

$lfloor xrfloor -sum _{{i}}leftlfloor {frac {x}{p_{i}}}rightrfloor +sum _{{i<j}}leftlfloor {frac {x}{p_{i}p_{j}}}rightrfloor -sum _{{i<j<k}}leftlfloor {frac {x}{p_{i}p_{j}p_{k}}}rightrfloor +cdots$

(где обозначает целую часть). Следовательно, полученное число равно

если числа $p_{1},p_{2},ldots ,p_{k}$ — это все простые числа, не превосходящие sqrt{x} .

В 1870—1885 годах в серии статей Эрнст Майссель описал (и использовал) практический комбинаторный способ вычисления pi (x) . Пусть $p_{1},p_{2},ldots ,p_{n}$ — первые простых, обозначим число натуральных чисел, не превосходящих , которые не делятся ни на одно $p_{i}$ . Тогда

$Phi (m,n)=Phi (m,n-1)-Phi left(left[{frac {m}{p_{n}}}right],n-1right)$

Возьмем натуральное , если и если , то

$pi (m)=Phi (m,n)+n(mu +1)+{frac {mu ^{2}-mu }{2}}-1-sum _{{k=1}}^{mu }pi left({frac {m}{p_{{n+k}}}}right)$

Используя этот подход, Майссель вычислил pi (x) для $x=5cdot 10^{5};10^{6};10^{7};10^{8}$ .

В 1959 году Деррик Генри Лемер расширил и упростил метод Майсселя. Определим, для действительного и для натуральных n,k величину $P_{k}(m,n)$ как число чисел, не превосходящих m имеющих ровно k простых множителей, причем все они превосходят p_n . Кроме того, положим $P_{0}(m,n)=1$ . Тогда

$Phi (m,n)=sum _{{k=0}}^{{+infty }}P_{k}(m,n)$

где сумма явно всегда имеет конечное число ненулевых слагаемых. Пусть — целое, такое, что , и положим . Тогда $P_{1}(m,n)=pi (m)-n$ и $P_{k}(m,n)=0$ при . Следовательно

$pi (m)=Phi (m,n)+n-1-P_{2}(m,n)$

Вычисление $P_{2}(m,n)$ может быть получено следующим способом:

$P_{2}(m,n)=sum _{{y<pleqslant {sqrt {m}}}}left(pi left({frac mp}right)-pi (p)+1right)$

С другой стороны, вычисление может быть выполнено с помощью следующих правил:

$Phi (m,b)=Phi (m,b-1)-Phi left({frac m{p_{b}}},b-1right)$

Используя этот метод и IBM 701, Лемер смог вычислить $pi left(10^{{10}}right)$ .

Дальнейшие усовершенствования этого метода были сделаны Lagarias, Miller, Odlyzko, Deleglise и Rivat.^[9]

Китайский математик Hwang Cheng использовал следующие тождества:^[10]

$e^{{(a-1)Theta }}f(x)=f(ax),$

$J(x)=sum _{{n=1}}^{{infty }}{frac {pi (x^{{1/n}})}{n}}$

и, полагая $x=e^{t}$ , выполняя преобразование Лапласа обеих частей и применяя сумму геометрической прогрессии с $e^{{nTheta }}$ , получил выражение:

${frac {1}{2{pi }i}}int _{{c-iinfty }}^{{c+iinfty }}g(s)t^{{s}},ds=pi (t)$

${frac {ln zeta (s)}{s}}=(1-e^{{Theta (s)}})^{{-1}}g(s)$

$Theta (s)=s{frac {d}{ds}}$

Другие функции, подсчитывающие простые числа[править | править код]

Другие функции, подсчитывающие простые числа, также используются, поскольку с ними удобнее работать. Одна из них — функция Римана, часто обозначаемая как $Pi _{0}(x)$ или $J_{0}(x)$ . Она испытывает прыжок на 1/n для степеней простых $p^{n}$ , причем в точке прыжка её значение равно полусумме значений на обеих сторонах от . Эти дополнительные детали нужны для того, чтобы она могла быть определена обратным преобразованием Меллина. Формально, мы определим $Pi _{0}(x)$ как

$Pi _{0}(x)={frac 12}{bigg (}sum _{{p^{n}<x}}{frac 1n} +sum _{{p^{n}leq x}}{frac 1n}{bigg )}$

где p простое.

Мы также можем записать

$Pi _{0}(x)=sum limits _{{n=2}}^{x}{frac {Lambda (n)}{ln n}}-{frac 12}{frac {Lambda (x)}{ln x}}=sum _{{n=1}}^{infty }{frac 1n}pi _{0}({sqrt[ {n}]{x}})$

где — функция Мангольдта и

$pi _{0}(x)=lim _{{varepsilon rightarrow 0}}{frac {pi (x-varepsilon )+pi (x+varepsilon )}2}.$

Формула обращения Мёбиуса дает

$pi _{{0}}(x)=sum _{{n=1}}^{infty }{frac {mu (n)}n}Pi _{0}({sqrt[ {n}]{x}})$

Используя известное соотношение между логарифмом дзета-функции Римана и функцией Мангольдта Lambda , и используя формулу Перрона мы получим

$ln zeta (s)=sint _{0}^{infty }Pi _{0}(x)x^{{-s-1}},dx$

Функция Римана имеет производящую функцию

${displaystyle sum _{n=1}^{infty }Pi _{0}(n)x^{n}=sum _{a=2}^{infty }{frac {x^{a}}{1-x}}-{frac {1}{2}}sum _{a=2}^{infty }sum _{b=2}^{infty }{frac {x^{ab}}{1-x}}+{frac {1}{3}}sum _{a=2}^{infty }sum _{b=2}^{infty }sum _{c=2}^{infty }{frac {x^{abc}}{1-x}}-{frac {1}{4}}sum _{a=2}^{infty }sum _{b=2}^{infty }sum _{c=2}^{infty }sum _{d=2}^{infty }{frac {x^{abcd}}{1-x}}+cdots }$

Функции Чебышёва — это функции, подсчитывающие степени простых чисел $p^{n}$ с весом ln p :

$theta (x)=sum _{{pleqslant x}}ln p$

$psi (x)=sum _{{p^{n}leqslant x}}ln p=sum _{{n=1}}^{infty }theta ({sqrt[ {n}]{x}})=sum _{{nleqslant x}}Lambda (n).$

Формулы для функций, подсчитывающих простые числа[править | править код]

Формулы для функций, подсчитывающих простые числа, бывают двух видов: арифметические формулы и аналитические формулы. Аналитические формулы для таких функций были впервые использованы для доказательства теоремы о простых числах. Они происходят от работ Римана и Мангольдта и в общем известны как явные формулы.^[11]

Существует следующее выражение для psi -функции Чебышёва:

$psi _{0}(x)=x-sum _{rho }{frac {x^{rho }}{rho }}-ln 2pi -{frac 12}ln(1-x^{{-2}})$

где

$psi _{0}(x)=lim _{{varepsilon rightarrow 0}}{frac {psi (x-varepsilon )+psi (x+varepsilon )}2}.$

Здесь rho пробегает нули дзета-функции в критической полосе, где действительная часть rho лежит между нулем и единицей. Формула верна для всех x>1 . Ряд по корням сходится условно, и может быть взят в порядке абсолютного значения возрастания мнимой части корней. Заметим, что аналогичная сумма по тривиальным корням дает последнее слагаемое в формуле.

Для $scriptstyle Pi _{0}(x)$ мы имеем следующую сложную формулу

$Pi _{0}(x)=operatorname {li}(x)-sum _{{rho }}operatorname {li}(x^{{rho }})-ln 2+int _{x}^{infty }{frac {dt}{t(t^{2}-1)ln t}}.$

Опять же, формула верна для всех x>1 , где rho — нетривиальные нули зета-функции, упорядоченные по их абсолютному значению, и, снова, последний интеграл берется со знаком «минус» и является такой же суммой, но по тривиальным нулям. Выражение $operatorname {li}(x^{{rho }})$ во втором члене может быть рассмотренно как , где — это аналитическое продолжение интегральной показательной функции на комплексную плоскость с ветвью, вырезанной вдоль прямой x<0 .

Таким образом, формула обращения Мёбиуса дает нам^[12]

$pi _{{0}}(x)=operatorname {R}(x)-sum _{{rho }}operatorname {R}(x^{{rho }})-{frac {1}{ln x}}+{frac {1}{pi }}{mathop {{mathrm {arctg}}}}{frac {pi }{ln x}}$

верное для x>1 , где

$operatorname {R}(x)=sum _{{n=1}}^{{infty }}{frac {mu (n)}{n}}operatorname {li}(x^{{1/n}})=1+sum _{{k=1}}^{infty }{frac {(ln x)^{k}}{k!kzeta (k+1)}}$

называется R-функцией также в честь Римана.^[13] Последний ряд в ней известен как ряд Грама^[14] и сходится для всех x>0 .

Сумма по нетривиальным нулям дзета-функции в формуле для $pi _{0}(x)$ описывает флуктуации $pi _{0}(x)$ , в то время как остальные слагаемые дают гладкую часть пи-функции,^[15] поэтому мы можем использовать

$operatorname {R}(x)-{frac {1}{ln x}}+{frac {1}{pi }}{mathop {{mathrm {arctg}}}}{frac {pi }{ln x}}$

как наилучшее приближение для pi (x) для x>1 .

Амплитуда «шумной» части эвристически оценивается как , поэтому флуктуации в распределении простых могут быть явно представлены Delta -функцией:

$Delta (x)=left(pi _{0}(x)-operatorname {R}(x)+{frac {1}{ln x}}-{frac {1}{pi }}{mathop {{mathrm {arctg}}}}{frac {pi }{ln x}}right){frac {ln x}{{sqrt x}}}.$

Обширные таблицы значений доступны здесь.^[7]

Неравенства[править | править код]

Здесь выписаны некоторые неравенства для pi (x) .

${displaystyle {frac {x}{ln x}}<pi (x)<1{,}25506cdot {frac {x}{ln x}}qquad xgeqslant 17.}$

Левое неравенство выполняется при , а правое — при ^[16]

Неравенства для -го простого числа p_n :

${displaystyle nln n+nln ln n-3/2cdot n<p_{n}<nln n+nln ln n, ngeqslant 6.}$

Левое неравенство верно при , а правое — при .

Имеет место следующая асимптотика для -го простого числа p_n :

${displaystyle p_{n}=nln nleft(1+{frac {ln ln n-1}{ln n}}+{frac {ln ln n-2}{ln ^{2}n}}+{frac {-1/2ln ^{2}ln n+3ln ln n-11/2}{ln ^{3}n}}+Oleft({frac {ln ^{3}ln n}{ln ^{4}n}}right)right)}$

Гипотеза Римана[править | править код]

Гипотеза Римана эквивалентна более точной границе ошибки приближения pi (x) интегральным логарифмом, а отсюда и более регулярному распределению простых чисел

pi (x)=operatorname {li}(x)+O({sqrt {x}}ln x).

В частности,^[17]

$|pi (x)-operatorname {li}(x)|<{frac {1}{8pi }}{sqrt {x}},ln x,qquad xgeqslant 2657.$

См. также[править | править код]

Теорема о распределении простых чисел
Постулат Бертрана
Число Скьюза

Примечания[править | править код]

↑ Bach, Eric; Shallit, Jeffrey. Section 8.8 // Algorithmic Number Theory (неопр.). — MIT Press, 1996. — Т. 1. — С. 234. — ISBN 0-262-02405-5.
↑ Weisstein, Eric W. Prime Counting Function (англ.) на сайте Wolfram MathWorld.
↑ ¹ ² How many primes are there? Chris K. Caldwell. Дата обращения: 2 декабря 2008. Архивировано 20 сентября 2012 года.
↑ Dickson, Leonard Eugene (англ.) (рус.. History of the Theory of Numbers I: Divisibility and Primality (англ.). — Dover Publications, 2005. — ISBN 0-486-44232-2.
↑ K. Ireland, M. Rosen. A Classical Introduction to Modern Number Theory (англ.). — Second. — Springer, 1998. — ISBN 0-387-97329-X.
↑ Tables of values of pi(x) and of pi2(x). Tomas Oliveira e Silva. Дата обращения: 14 сентября 2008. Архивировано 20 сентября 2012 года.
↑ ¹ ² Values of π(x) and Δ(x) for various x’s. Andrey V. Kulsha. Дата обращения: 14 сентября 2008. Архивировано 20 сентября 2012 года.
↑ A table of values of pi(x). Xavier Gourdon, Pascal Sebah, Patrick Demichel. Дата обращения: 14 сентября 2008. Архивировано 20 сентября 2012 года.
↑ Computing ?(x): The Meissel, Lehmer, Lagarias, Miller, Odlyzko method. Marc Deleglise and Joel Rivat, Mathematics of Computation, vol. 65, number 33, January 1996, pages 235–245. Дата обращения: 14 сентября 2008. Архивировано 20 сентября 2012 года.
↑ Hwang H., Cheng. Demarches de la Geometrie et des Nombres de l’Universite du Bordeaux, Prime Magic conference.
↑ Titchmarsh, E.C. The Theory of Functions, 2nd ed (англ.). — Oxford University Press, 1960.
↑ Riesel, Hans (англ.) (рус.; Gohl, Gunnar. Some calculations related to Riemann’s prime number formula (англ.) // Mathematics of Computation (англ.) (рус. : journal. — American Mathematical Society, 1970. — Vol. 24, no. 112. — P. 969—983. — ISSN 0025-5718. — doi:10.2307/2004630. — JSTOR 2004630.
↑ Weisstein, Eric W. Riemann Prime Counting Function (англ.) на сайте Wolfram MathWorld.
↑ Weisstein, Eric W. Gram Series (англ.) на сайте Wolfram MathWorld.
↑ The encoding of the prime distribution by the zeta zeros. Matthew Watkins. Дата обращения: 14 сентября 2008. Архивировано 20 сентября 2012 года.
↑ Rosser, J. Barkley (англ.) (рус.; Schoenfeld, Lowell. Approximate formulas for some functions of prime numbers (англ.) // Illinois J. Math. : journal. — 1962. — Vol. 6. — P. 64—94. — ISSN 0019-2082. Архивировано 28 февраля 2019 года.
↑ Lowell Schoenfeld. Sharper bounds for the Chebyshev functions θ(x) and ψ(x). II (англ.) // Mathematics of Computation (англ.) (рус. : journal. — American Mathematical Society, 1976. — Vol. 30, no. 134. — P. 337—360. — ISSN 0025-5718. — doi:10.2307/2005976. — JSTOR 2005976.

Литература[править | править код]

К. Прахар. Распределение простых чисел. — Мир, 1967.
В. И. Зенкин. Распределение простых чисел. Элементарные методы. Калининград, 2008.

Ссылки[править | править код]

Chris Caldwell, The Nth Prime Page at The Prime Pages.

Источник

Очевидно,
не всякий опыт может быть сведен к схеме
случаев, и поэтому
существуют события, вероятности которых
невозможно вычислить
по формуле (1.1), например, вероятность
сбить самолет одним выстрелом, вероятность
выпадения герба, если монета не имеет
правильной
формы, вероятность появления той или
иной игральной карты, если
игра нечестная, и т. д. Для таких событий
применяют другие способы
определения вероятностей. Все эти
способы связаны с опытом (экспериментом)
и понятием относительной частоты
(частоты) события.

Относительной
частотой
события
называют
отношение
числа появлений этого события т
к
числу всех произведенных
опытов п, т.
е.

(1.2)

При
неограниченном числе опытов с вероятностью,
сколь угодно близкой
к единице, можно ожидать, что относительная
частота события
приближается к его вероятности (теорема
Бернулли), т. е.

вер

(1.3)

Вероятный предел
(вер
)
отличается от математического предела
и понимается как тенденция стремления
к пределу. Выражение (1.3) пишут также в
виде
{|Q–р|
< ε} = 1-δ,
где ε и δ — сколь угодно малые положительные
величины.

Относительную
частоту называют также статистической
вероятностью
события.

1.47. Из 5000 взятых
наудачу деталей оказалось 32 бракованных.
Найти
частость бракованных Деталей
в данной партии.

Решение. В этой
задаче нас интересует событие А —
появление бракованной детали.
Произведено п. = 5000 испытаний, причем
событие А наступило от = 32 раза.
Поэтому искомая частость

Q₅₀₀₀ (А)
= 32/5000 = 0,0064.

Французский естествоиспытатель XVIII
в. Бюффон при экспериментальной
проверке закона больших чисел бросил
монету,4040 раз, в результате чего герб
выпал 2048 раз. Найти частость выпадения
герба.
Произведя 100 выстрелов, стрелок попал
в цель 89 раз. Чему равна частость его
попадания в цель?
Среди 1000 новорожденных оказалось 517
мальчиков. Найти частость рождения
мальчиков и девочек.
Среди 4000 первых чисел натурального
ряда имеется 551 простое число. Найти
частость появления простого числа.
Из таблицы прил. I выбрать
100 чисел. Найти частость и вероятность
появления последней цифры, кратной
двум, кратной трем.
Произведено 5000 измерений. Число
положительных ошибок оказалось
равным 1000. Можно ли сделать предварительное
заключение о наличии систематических
ошибок?
При некоторых измерениях оказалось,
что относительная частота положительных
ошибок Q = 0,40. Сколько было
произведено всего измерений п, если
отрицательных ошибок оказалось 15.

О т в е т: 25.

§ 4. Теоремы сложения и умножения вероятностей

Как
уже отмечалось, события подразделяют
на два класса — простые
(элементарные) и сложные. Такое разделение
условно и целиком определяется
условиями эксперимента. Например, при
многократном бросании
монеты сложным следует считать число
выпадений гербов, а
простым выпадение герба при одном
бросании монеты. При опыте с несколькими
монетами число выпадений герба на одной
монете можно рассматривать
как событие простое.

Сложные
события различают двух видов: сумма и
произведение событий.

Суммой
двух или нескольких событий A_i(i
= 1, 2, …, п)
называется
сложное событие, которое заключается
в появлении хотя бы одного
из событий A_i.
Другими словами, это означает В
= или A₁,
или A₂,
… или A_n,
или A₁
и A₂,
или A₁
и A₃,
… или все
A_i.

В этом выражении
союз и, очевидно, имеет смысл, если
события совместны. Пишут также
условно В =
A₁
+ A₂
+ … + A_n
=

Произведением
С двух или нескольких событий A_i
(i
= 1, 2, …, п)
называется
сложное событие, которое заключается
в совместном появлении всех событий
A_i.
Пишут также
С =
.

Для
двух событий понятие «сумма» и
«произведение» событий легко
иллюстрировать геометрически (рис.
1).

На рис. 1 пунктиром
обведен контур, заключающий событие В
= или A₁или A₂,
или A₁
и A₂,
а перекрывающийся контур — событие С
= A₁
и A₂.

Рисунок 1

Пусть событие А₁ —
появление карты бубновой масти, А₂
– появление туза из колоды карт. В чем
заключается сумма и произведение этих
событий?
Взятая наудачу деталь может оказаться
либо первого (событие А), либо второго
(событие В),
либо третьего
(событие С) сорта. Что представляют
собой следующие события:
;;;?

Решение.
—
это событие, которое состоится при
наступлении хотя бы одного из событий
А и В. Следовательно, А + B
в нашем случае — деталь первого
или второго сорта. Так как, А + С –
деталь первого или третьего сорта,
то противоположное этому событие
–
деталь второго сорта.

– невозможное событие, поскольку
деталь одновременно не может быть и
первого и третьего сорта,
как
сумма невозможного события и события
C равна C,
т.e.
–
деталь третьего сорта.

1.57. Доказать,
что
=

.

Доказательство.
Если произошло событие
,
то это означает, что ни одно из событий
А и В не наступило, т. е. произошло
событие
.
Отсюда
=

.

Докажите более общее соотношение:

=
.

В урне 5 красных, 2 синих и 3 белых шара.
Все они пронумерованы цифрами 1, 2, …,
10. Из урны берется наудачу 1 шар. Событие
– шар с четным номером – обозначим через
А, с номером, кратным 3 – через В,
шар красного цвета – через С, синего
– через D и, наконец,
белого – через Е. Что представляют
собой следующие события:
,,,?
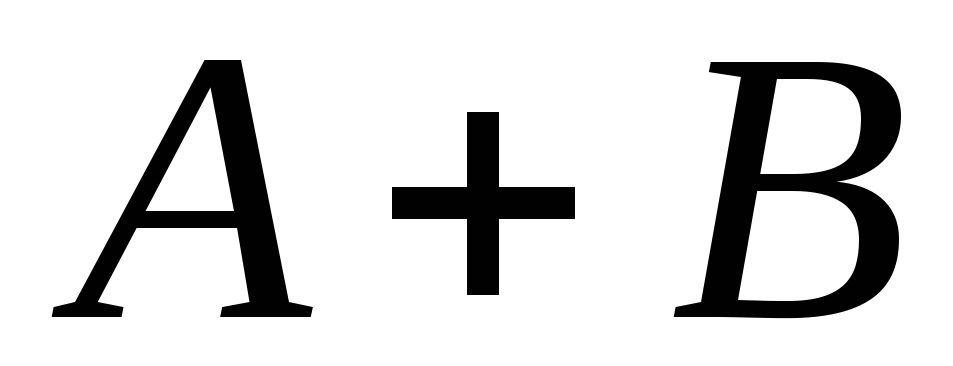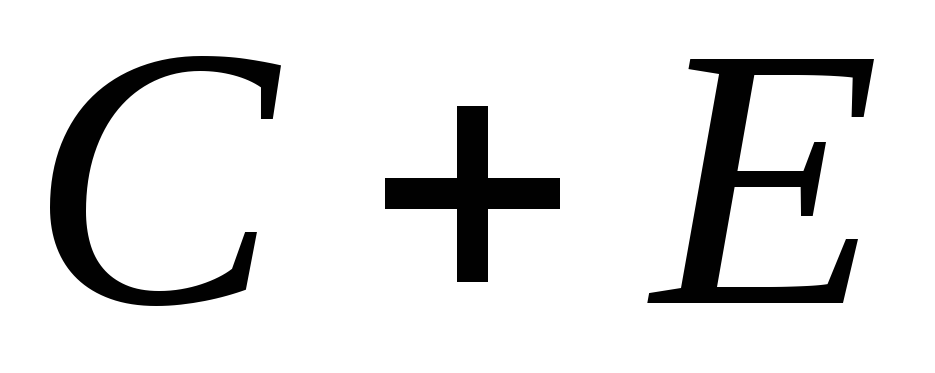Доказать равенства:

1)
; 3)

;

2)
; 4)

1.60. При каких
условиях справедливы следующие
соотношения:

1)
; 2)

;
3)
?

Теоремы теории
вероятностей позволяют определять
вероятности сложных событий, зная
вероятности простых событий.

Теорема сложения
для несовместных событий

Вероятность суммы
двух или нескольких несовместных событий
равна сумме вероятностей этих событий,
т. е.

,
(1.4)

где
.

1.61. Бросают
игральную кость. Какова вероятность
того, что выпадет
грань с четной цифрой?

Решение. Искомое
событие наступает, когда выпадают грани
с цифрами: или 2, или 4, или 6. Вероятность
выпадения любой грани p(A_i)
= 1/6. Искомая вероятность

р(В) =р (четная цифра) = 1/6+ 1/6+1/6= 1/2.

Следствия
теоремы
сложения

Следствие
1. Если события A_i образуют
полную группу, то

(1.5)

Следствие
2.
Сумма вероятностей двух противоположных
событий
равна 1:

и

(1.6)

1.62. В группе 24
студента, из них отлично успевающих 4,
хорошо – 12, удовлетворительно — 6 и слабо
— 2 человека. Подсчитать вероятность
того, что вызванный наугад студент
окажется отлично, хорошо или
удовлетворительно успевающим.

Решение. 1-й
способ. Применяя теорему сложения
вероятностей, находим

p = 4/24 + 12/24 + 6/24 = 22/24 =
11/12 =92%.

2-й способ. Обозначим вероятность вызова
одного из успевающих студентов через
р, а вероятность противоположного
события, т. е. вызова одного из слабых
студентов, — через q.
Тогда р = 1 — q
= 1 — 2/24-22/24 = 92 %.

В урну положено 10 белых шаров, 6 синих
и 4 красных. Шары перемешивают и
наугад вынимают один. Вычислить: а)
вероятности появления белого, синего,
красного и цветного шаров; б) сумму
первых трех вероятностей.
Для производственной практики на 30
студентов предоставлено 15 мест в Минске,
8 — в Гомеле и 7 — в Витебске. Какова
вероятность того, что два определенных
студента попадут на практику в один
город?

От в е т : 0,331.

1.65. Пассажир
ждет трамвая маршрута № 2 или № 12 на
остановке, через которую проходят
трамваи № 2, 6, 12 и 18. Предполагая, что
трамваи всех маршрутов появляются
одинаково часто, найти вероятность
того, что первый подошедший к остановке
трамвай будет нужного пассажиру маршрута.

Ответ: 1/2.

1.66. На 100 лотерейных
билетов приходится: 1 выигрыш в 500 руб.,
2 – по 250 руб., 5 – по 100 руб., 10 – по 50 руб., и
20 – по 10 руб. Какова вероятность
выиграть не менее 100 руб. на 1 билет?

Ответ: 0,08.

1.67. По условиям
задачи 1.66 вычислить вероятность выиграть
не более 100 руб.

Ответ: 0,35.

1.68. Найти
вероятность того, что при одном бросании
игральной кости выпадет грань с
двойкой или цифрой, кратной трем.

Ответ: 3/6.

1.69. Определить
вероятность появление девятки или
десятки при взятии наугад одной карты
из колоды в 36 листов.

Ответ: 2/9.

1.70. Мастер
обслуживает 5 станков. 20% рабочего времени
он проводит у первого станка, 10% – у
второго, 15% – у третьего, 25% – у четвертого
и, наконец, 30% – у пятого. Найти вероятность
того, что в наудачу выбранный момент
времени он находится у первого или
третьего станка.

Ответ: 0,35.

1.71. В ящике
находятся шары четырех цветов: белых –
50%, красных – 20%, зеленых – 20%, синих – 10%.
Какова вероятность того, что взятый на
удачу шар окажется зеленым или синим?

Теорема умножения
для независимых событий

Вероятность
произведения независимых событий равна
произведению их вероятностей, т. е. если

то

(1.7)

Вероятности
независимых событий называют безусловными.
3ависимые
события
имеют так называемые условные вероятности,
которые записываются в виде р(A₂/A₁)
– условная вероятность
события A₂,
вычисленная в предположении, что
произошло событие
A₁;
p(A_i/A₁,
А₂,
… A_i_-1)
–
условная вероятность события A_iвычисленная
в предположении, что произошли события
А₁,
A₂,
A_i_-1.

Теорема умножения
для зависимых событий

Вероятность
произведения зависимых событий

p(C)=p(A_l)p(A₂/A₁)…p(A_n/A₁,
A₂,…
A_n_-1). (1.8)

Ясно, что теорема
(1.7) является частным случаем теоремы
(1.8), когда события независимы.

Условием
независимости A_i
событий
является равенство

P(A_i)
= p(A_i/A₁,A₂,
… , A_i-1).

1.72. Опыт состоит
в бросании двух монет. Рассматриваются
следующие события:

А — появление герба на первой монете;

В — появление цифры на первой монете;

С — появление герба на второй монете;

D — появление
цифры на второй монете;

Е — появление хотя бы одного герба;

F — появление хотя
бы одной цифры;

G — появление
одного герба и одной цифры;

Н — непоявление ни одного герба;

К — появление двух гербов.

Определить, каким событиям этого списка
равносильны следующие события; А +
С, AC ,EF,
G + Е, GE,
BD, Е + К.

О т в е т: А + С = Е, АС = К, EF
= G, G
+ Е = Е, GE = G,
BD = Н, Е+К = Е.

1.73.
Зависимы или независимы:

несовместные события;
события, образующие полную группу;
равновозможные события?

Ответ: 1) Зависимы,
так как появление любого из них обращает
в нуль вероятности всех остальных;
2) зависимы, так как непоявление всех,
кроме одного, обращает в единицу
вероятность последнего; 3) могут быть,
как зависимы, так и независимы.

1.74. Опыт состоит
в последовательном бросании двух монет.
Рассматриваются события:

А — выпадение герба на первой
монете; D — выпадение
хотя бы одного герба;

Е — выпадение хотя бы одной цифры;
F — выпадение
герба на второй монете. Определить,
зависимы или независимы пары событий:
А и Е, А и F,
D и Е, D
и F. Определить
условные и безусловные вероятности
событий в каждой паре. Ответ:

р(Е) = 3/4; р(Е/А) = 1/2 – события
зависимы;
р(А) = 1/2; p(A/F)
= 1/2 – события независимы;
p(D)
= 3/4; p(D/E)
= 2/3 – события зависимы;
p(D)
= 3/4; p(D/F)
= 1 – события зависимы.

1.75. По мишени
производится три выстрела. Рассматриваются
события А_i
— попадание при i-м
выстреле (i = 1, 2, 3).

Представить
в виде сумм, произведений или сумм
произведений событий A_i и A_i следующие события:

А — все три попадания;
Е — не меньше двух попаданий;

В — все три промаха;
F — не больше
одного попадания;

С — хотя бы одно попадание;
G — попадание в мишень
не раньше, чем при третьем выстреле.

D — хотя бы один
промах;

0
т в е т: А = А₁ А₂
А₃; В = А₁ А₂
А₃; С=А₁+А₂+А₃;
С = А₁ + A₁A₂
+ А₁ А₂ А₃
и т. д.

1.76. В урне а
белых и Ь черных шаров. Из урны
вынимают (одновременно или последовательно)
два шара. Найти вероятность того, что
оба шара будут белыми.

Ответ: по теореме
умножения вероятностей:

1.77. В урне а
белых и Ь черных шаров. Из урны
вынимается один шар, отмечается его
цвет, и шар возвращается в урну. После
этого из урны берется еще один
шар.
Найти вероятность того, что оба вынутых
шара будут белыми.

Ответ: (a/(a+b))².

1.78. В урне а
белых и Ь черных шаров. Из урны
вынимаются сразу два шара. Найти
вероятность того, что эти шары будут
разных цветов.

Решение. Событие
может появиться в двух несовместных
вариантах «б, ч» или «ч, б»; по теоремам
сложения и умножения:

Решить, применяя теорему умножения,
задачи 1.19 – 1.21, 1.24 – 1.33.
Из полной колоды карт вынимают сразу
четыре карты. Найти вероятность
того, что все они будут разных мастей.

Ответ: 1*39/51*26/50*13/49
= 0,106.

1.81. Перемножаются
два наугад взятых числа. Найти вероятность
того, что они будут оканчиваться на
цифру 1.

Ответ: 0,04.

1.82. Найти
вероятность того, что первая положительная
ошибка появится в пятом измерении.

Ответ: p
= 1/32.

1.83. Деталь
испытывается на трех контрольных
стендах. Вероятности обнаружения
бракованной детали на каждом стенде
соответственно равны: р₁
= 0,5; р₂ = 0,7; р₃
= 0,9. Найти вероятность того, что
бракованная деталь будет обнаружена.

Решение. Так как
искомое событие есть сложное событие,
заключающееся в том, что бракованная
деталь будет обнаружена или на первом
стенде (событие А₁), или
на втором стенде (событие А₂),
или на третьем стенде (событие А₃),
а события A_i
несовместны, то искомая вероятность
р(В) = р(А₁) + р(А₂)
+ + р(А₃), при этом p(A_i)
= 0,5.

Для того чтобы произошло событие А₂,
необходимо, чтобы деталь прошла первый
стенд и была задержана на втором, поэтому
по теореме умножения p(A₂)
= (1 — 0,5)*0,7 = 0,35. Легко понять, что р(А₃)
= (1 — 0,5)(1 — 0,7)0,9 = 0,135.

Поэтому, р(В) = 0,500 + 0,350 + 0,135 = 0,985.

1.84. Найти вероятность того, что в июле
первый дождливый день будет 10-числа,
если вероятность дождливого дня в этом
месяце равна 0,3.

Ответ: (0,7)⁹*0,3.

Теорема сложения
для совместных событий

Вероятность суммы
совместных событий определяется формулой

(1.9)

Формула (1.9) легко
получается из следующих соображений.

Рассмотрим
событие В =
хотя бы одно
A_i
= ни одного
А_i
= все A_i.
Тогда,
применяя теорему умножения, получим

Но
так как р(В)
+ р(В) = 1, то
отсюда сразу следует выражение (1.9).

Если события A_i
независимы,
то

(1.10)

Для двух таких
событий р(В)
— p(A_t)
+ р(А₂)—p(Ai)p(A₂).
Когда все
p(A_t)
равны между
собой, то

p(B)
= 1 – (p(A))ⁿ
(1.11)

1.85. На испытательном
стенде размещено 50 приборов. Вероятность
отказа в работе одного прибора за время
t равна р(А) =
0,1. Найти вероятность того, что за время
t откажет хотя бы
один прибор, если приборы работают
независимо друг от друга.

Решение.
На основании формулы (1.11) имеем p(B)
= 1 – (p(A))⁵⁰
= 1 — 0,9⁵⁰. Логарифмируя р(А) =
0,9⁵⁰, получим

Lg
(р (А)) = 50*1g0,9
= 50 * (1,954) = 50 • 0,046= -2,30;

Lg
(р (А)) = 3,70,

откуда
р(А) = 0,0051; р(В) = 0,995.

1.86. Два стрелка
делают по одному выстрелу в мишень с
вероятностью попадания, соответственно
равной p_t
= 0,7 и р₂ — 0,9. Найти
вероятность хотя бы одного попадания.

Решение. Так как
попадание в мишень обоими стрелками —
события независимые, но совместные, то,
применяя формулу (1.11), имеем р(В) = 1
– 0,3 * 0,1 = 0,97.

1.87. Электрическая
цепь составлена по схеме (рис. 2). Выход
из строя за время t
различных элементов цепи — независимые
события, имеющие следующие вероятности:

Элемент Кг K₁ Л₁ JI₂ Л₃

Вероятность 0,10 0,10 0,05 0,02 0,04

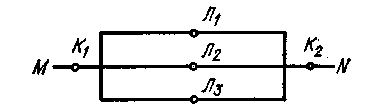
Рисунок 2

Определить вероятность разрыва цепи
за указанный промежуток времени.

Решение. Цепь
выйдет из строя (событие В), когда
откажут в работе следующие элементы:
или K₁ (событие
А₁), или все Лj
(событие A₃), или
К₂ (событие A₂),
или все K_i
и Лj вместе.
Так как эти события совместны, то имеем
на основании формулы (1.10)

р
(В) = 1 – p(A₁)*
р (A₂)*р
(A₃)

Вероятности:
p(A₁)
= 0,90, р(A₂)
= 0,90.

Событие
A₃ заключается
в том, что хотя бы один из элементов Лj
не откажет. Поэтому p(A₃)
находим также по теореме сложения
для совместных событий

p(А₃)
=1 – 0.05*0.02*0.04=1.

Поэтому р(В) = 1 — 0,9 * 0,9 * 1 = 0,19.

1.88. Вычислительная
машина состоит из п блоков. Надежность
(вероятность безотказной работы) в
течение времени Т первого блока
равна р₁ второго – р₂
и т. д. Блоки отказывают независимо друг
от друга. При отказе любого блока
отказывает машина. Найти вероятность
того, что машина откажет за время Т.

Ответ:

1.89. В аудитории находятся 100 студентов.
Найти вероятность того, что хотя бы у
одного из них данный день является днем
рождения, если год не високосный.

Ответ: 0,240.

1.90. Найти, какое число человек должно
быть вместе, чтобы с вероятностью р =
0,95 хотя бы у одного из них данный день
был днем рождения.

Ответ: 1100.

1.91. Завод изготовляет определенного
типа изделия; каждое изделие имеет
дефект с вероятностью р. Изделие
осматривается одним контролером; он
обнаруживает имеющийся дефект с
вероятностью p_i,
а если дефект не обнаружен, пропускает
изделие в готовую продукцию. Кроме того,
контролер может по ошибке забраковать
изделие, не имеющее дефекта; вероятность
этого равна α. Найти вероятности следующих
событий:

А — изделие будет забраковано; В
— изделие будет забраковано, но
ошибочно; С — изделие будет
пропущено в готовую продукцию с дефектом.

Ответ: р(А) =
pp₁ +
(1 — р)*α; р(В) =
(1 – р) *α; р(С)
= р*(1 – р₁).

1.92. Происходит «дуэль» между участниками
A и В. По условиям
«дуэли» A начинает
первым и поражает В с вероятностью
р₁. Если В уцелеет, то
он поражает A с
вероятностью р₂. В свою
очередь, A поражает B
с вероятностью р₃. На этом «дуэль»
прекращается. Найти вероятности: а)
гибели А, б) гибели В,
а) гибели
или A, или В.

Ответ: р_a = (1 – р₁)*р₂; р_б = р₁
+ (1 — р₁)*(1 — р₂)*р₃; р_в = p₁
+ р₂.

1.93. Бросают две монеты. Рассматриваются
события:

A – выпадение герба на
первой монете; В – выпадение герба
на второй монете. Найти вероятность
события С = А + В.

Р е ш е н и е. р{С) = р(А) + р(В) — р(АВ)
= 1/2 + 1/2 -1/4 =3/4 или (через противоположное
событие) р(С) =1 – 1/4 = 3/4.

1.94. При одном цикле обзора радиолокационной
станции, следящей за космическим
объектом, объект обнаруживается с
вероятностью р. Обнаружение объекта
в каждом цикле происходит независимо
от других. Найти вероятность того, что
при n циклах объект
будет обнаружен.

1.95. Найти вероятность того, что наудачу
взятое двузначное число окажется
кратным либо 2, либо 5, либо тому и другому
одновременно.

Решение. Пусть
A₁ –
событие, которое состоится, если наудачу
взятое двузначное число кратно 2, а A₂
– событие, которое состоится, если это
число кратно 5. Надо найти р(А₁
+ A₂). Так
как А₁ и A₂
– события совместимые, то р(A₁
+ А₂) = p(A₁)
+ р(А₂) – р(A_1*А₂).

Двузначные числа — это 10, 11 98, 99. Всех их
90. Очевидно, 45 из них кратны 2 (благоприятствуют
наступлению A₁),
18 кратны 5 (благоприятствуют наступлению
A₂) и, наконец,
9 кратны и 2 и 5 одновременно (благоприятствуют
наступлению А₁А₂).
Поэтому

p (A₁)
= 45/90 = 0.5; p (A₂)
= 18/90 = 0.2; p (A₁
*A₂) = 9/90 = 0.1

и, следовательно, р(А₁ +
A₂) = 0,5 + 0,2 –
0,1 = 0,6.

1.96. Рабочий
обслуживает 3 станка. Вероятность того,
что в течение часа станок не потребует
внимания рабочего, равна для первого
станка 0,9, для второго – 0,8 и для третьего
– 0,85. Найти вероятность того, что: 1) в
течение некоторого часа ни один из
станков не потребует внимания рабочего;
2) все станки потребуют внимания рабочего.

Ответ: 1) 0,997; 2)
0,003.

1.97. Чему равна
вероятность того, что при п подбрасываниях
игральной кости выпадет хотя бы один
раз единица?

Ответ: 1
– (1/6)ⁿ

1.98. Вероятность
того, что неопытный наблюдатель измерение
превышений на станции выполнит с
соблюдением всех допусков инструкции,
равна 0,4. Сколько раз он должен
повторить измерения, чтобы с вероятностью,
не меньшей 0,9, он получил хотя бы один
правильный результат.

Решение. Применим
формулу (1.11) или р(В) = 1 — qⁿ.
По условию задачи 1 — 0,6″ ≥ 0,9,
откуда 0,6″ ≤ 0,1.

N ≤ lg0,1/
lg0,6 = -1/-0.2218 = 4.5.

Ответ: 5 раз.

1.99. Вероятность
того, что событие А появится хотя
бы один раз при двух независимых
испытаниях, равна 0,75. Найти вероятность
появления события в одном испытании,
если вероятность появления события в
каждом испытании одинакова.

Ответ: 0,5.

1.100. Вероятности
появления положительной и отрицательной
ошибок равны между собой. Определить,
сколько нужно произвести измерений,
чтобы с вероятностью р = 0,98 появилась
хотя бы одна положительная ошибка.

Ответ: п = 6.

1.101. Определить
вероятность того, что при двух измерениях
появится хотя бы одна положительная
ошибка; две положительные ошибки.

Ответ: 0,75; 0 25.

1.102. Вероятность
поражения цели одним стрелком р =
0,004. Определить количество стрелков,
необходимое для поражения цели хотя бы
одним выстрелом с вероятностью 0,98.

Ответ: п =
976.

1.103. При печатании
карт на офсетных машинах вероятность
появления брака за несовмещение красок
р₁ = 0,20 и за деформацию
бумаги p₂ =
0,015. Какова вероятность получить
бракованный оттиск и по совмещению, и
по деформации бумаги?

Ответ: 0,0003.

1.104. При печатании
карт на офсетных машинах вероятность
выхода тиражных оттисков первой
категории р_х = 0,85, а
второй —р₂ = 0,10. Какова вероятность
выпуска карт по качеству не ниже второй
категории?

Ответ: 0,95.

1.105. Вероятность
получить аэрофотоснимок бракованным
из-за покрытия облаком р₁
= 0,020; из-за неприжатия пленки р₂
= 0,009. Какова вероятность получения
снимка бракованным?

Ответ: 0,0288.

Источник

Частота события. Статистическое определение вероятности

Относительная частота. Статистическая вероятность

Краткая теория

Примеры решения задач

Пример 1

Пример 2

Пример 3

Задачи контрольных и самостоятельных работ

Статистическая вероятность

История[править | править код]

Таблицы для пи-функции, x / ln x и li(x)[править | править код]

Алгоритмы вычисления пи-функции[править | править код]

Другие функции, подсчитывающие простые числа[править | править код]

Формулы для функций, подсчитывающих простые числа[править | править код]

Неравенства[править | править код]

Гипотеза Римана[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

§ 4. Теоремы сложения и умножения вероятностей

Вам также может понравиться

Как найти консоль в виндовс 10

Как найти потерянную почту gmail

Ошибка е6 кондиционер балу как исправить

Добавить комментарий Отменить ответ

Относительная частота.
Статистическая вероятность