Как найти частоту следования импульсов

The pulse repetition frequency (PRF) is the number of pulses of a repeating signal in a specific time unit. The term is used within a number of technical disciplines, notably radar.

In radar, a radio signal of a particular carrier frequency is turned on and off; the term “frequency” refers to the carrier, while the PRF refers to the number of switches. Both are measured in terms of cycle per second, or hertz. The PRF is normally much lower than the frequency. For instance, a typical World War II radar like the Type 7 GCI radar had a basic carrier frequency of 209 MHz (209 million cycles per second) and a PRF of 300 or 500 pulses per second. A related measure is the pulse width, the amount of time the transmitter is turned on during each pulse.

After producing a brief pulse of radio signal, the transmitter is turned off in order for the receiver units to hear the reflections of that signal off distant targets. Since the radio signal has to travel out to the target and back again, the required inter-pulse quiet period is a function of the radar’s desired range. Longer periods are required for longer range signals, requiring lower PRFs. Conversely, higher PRFs produce shorter maximum ranges, but broadcast more pulses, and thus radio energy, in a given time. This creates stronger reflections that make detection easier. Radar systems must balance these two competing requirements.

Using older electronics, PRFs were generally fixed to a specific value, or might be switched among a limited set of possible values. This gives each radar system a characteristic PRF, which can be used in electronic warfare to identify the type or class of a particular platform such as a ship or aircraft, or in some cases, a particular unit. Radar warning receivers in aircraft include a library of common PRFs which can identify not only the type of radar, but in some cases the mode of operation. This allowed pilots to be warned when an SA-2 SAM battery had “locked on”, for instance. Modern radar systems are generally able to smoothly change their PRF, pulse width and carrier frequency, making identification much more difficult.

Sonar and lidar systems also have PRFs, as does any pulsed system. In the case of sonar, the term pulse repetition rate (PRR) is more common, although it refers to the same concept.

Introduction[edit]

Electromagnetic (e.g. radio or light) waves are conceptually pure single frequency phenomena while pulses may be mathematically thought of as composed of a number of pure frequencies that sum and nullify in interactions that create a pulse train of the specific amplitudes, PRRs, base frequencies, phase characteristics, et cetera (See Fourier Analysis). The first term (PRF) is more common in device technical literature (Electrical Engineering and some sciences), and the latter (PRR) more commonly used in military-aerospace terminology (especially United States armed forces terminologies) and equipment specifications such as training and technical manuals for radar and sonar systems.

The reciprocal of PRF (or PRR) is called the pulse repetition time (PRT), pulse repetition interval (PRI), or inter-pulse period (IPP), which is the elapsed time from the beginning of one pulse to the beginning of the next pulse. The IPP term is normally used when referring to the quantity of PRT periods to be processed digitally. Each PRT having a fixed number of range gates, but not all of them being used. For example, the APY-1 radar used 128 IPP’s with a fixed 50 range gates, producing 128 Doppler filters using an FFT. The different number of range gates on each of the five PRF’s all being less than 50.

Within radar technology PRF is important since it determines the maximum target range (R_max) and maximum Doppler velocity (V_max) that can be accurately determined by the radar.^[1] Conversely, a high PRR/PRF can enhance target discrimination of nearer objects, such as a periscope or fast moving missile. This leads to use of low PRRs for search radar, and very high PRFs for fire control radars. Many dual-purpose and navigation radars—especially naval designs with variable PRRs—allow a skilled operator to adjust PRR to enhance and clarify the radar picture—for example in bad sea states where wave action generates false returns, and in general for less clutter, or perhaps a better return signal off a prominent landscape feature (e.g., a cliff).

Definition[edit]

Pulse repetition frequency (PRF) is the number of times a pulsed activity occurs every second.

This is similar to cycle per second used to describe other types of waveforms.

PRF is inversely proportional to time period which is the property of a pulsed wave.

$mathrm{T} ={frac {1}{{text{PRF}}}}$

PRF is usually associated with pulse spacing, which is the distance that the pulse travels before the next pulse occurs.

${text{Pulse Spacing}}={frac {{text{Propagation Speed}}}{{text{PRF}}}}$

Physics[edit]

PRF is crucial to perform measurements for certain physics phenomenon.

For example, a tachometer may use a strobe light with an adjustable PRF to measure rotational velocity. The PRF for the strobe light is adjusted upward from a low value until the rotating object appears to stand still. The PRF of the tachometer would then match the speed of the rotating object.

Other types of measurements involve distance using the delay time for reflected echo pulses from light, microwaves, and sound transmissions.

Measurement[edit]

PRF is crucial for systems and devices that measure distance.

Radar
Laser range finder
Sonar

Different PRF allow systems to perform very different functions.

A radar system uses a radio frequency electromagnetic signal reflected from a target to determine information about that target.

PRF is required for radar operation. This is the rate at which transmitter pulses are sent into air or space.

Range ambiguity[edit]

A real target in 100 km or a second-sweep echo in a distance of 400 km

A radar system determines range through the time delay between pulse transmission and reception by the relation:

${text{Range}}={frac {ctau }{2}}$

For accurate range determination a pulse must be transmitted and reflected before the next pulse is transmitted. This gives rise to the maximum unambiguous range limit:

${text{Max Range}}={frac {ctau _{{text{PRT}}}}{2}}={frac {c}{2,{text{PRF}}}}qquad {begin{cases}tau _{{text{PRT}}}={frac {1}{{text{PRF}}}}end{cases}}$

The maximum range also defines a range ambiguity for all detected targets. Because of the periodic nature of pulsed radar systems, it is impossible for some radar system to determine the difference between targets separated by integer multiples of the maximum range using a single PRF. More sophisticated radar systems avoid this problem through the use of multiple PRFs either simultaneously on different frequencies or on a single frequency with a changing PRT.

The range ambiguity resolution process is used to identify true range when PRF is above this limit.

Low PRF[edit]

Systems using PRF below 3 kHz are considered low PRF because direct range can be measured to a distance of at least 50 km. Radar systems using low PRF typically produce unambiguous range.

Unambiguous Doppler processing becomes an increasing challenge due to coherency limitations as PRF falls below 3 kHz.

For example, an L-Band radar with 500 Hz pulse rate produces ambiguous velocity above 75 m/s (170 mile/hour), while detecting true range up to 300 km. This combination is appropriate for civilian aircraft radar and weather radar.

${text{300 km range}}={frac {C}{2times 500}}$

${text{75 m/s velocity}}={frac {500times C}{2times 10^{9}}}$

Low PRF radar have reduced sensitivity in the presence of low-velocity clutter that interfere with aircraft detection near terrain. Moving target indicator is generally required for acceptable performance near terrain, but this introduces radar scalloping issues that complicate the receiver. Low PRF radar intended for aircraft and spacecraft detection are heavily degraded by weather phenomenon, which cannot be compensated using moving target indicator.

Medium PRF[edit]

Range and velocity can both be identified using medium PRF, but neither one can be identified directly. Medium PRF is from 3 kHz to 30 kHz, which corresponds with radar range from 5 km to 50 km. This is the ambiguous range, which is much smaller than the maximum range. Range ambiguity resolution is used to determine true range in medium PRF radar.

Medium PRF is used with Pulse-Doppler radar, which is required for look-down/shoot-down capability in military systems. Doppler radar return is generally not ambiguous until velocity exceeds the speed of sound.

A technique called ambiguity resolution is required to identify true range and speed. Doppler signals fall between 1.5 kHz, and 15 kHz, which is audible, so audio signals from medium-PRF radar systems can be used for passive target classification.

For example, an L band radar system using a PRF of 10 kHz with a duty cycle of 3.3% can identify true range to a distance of 450 km (30 * C / 10,000 km/s). This is the instrumented range. Unambiguous velocity is 1,500 m/s (3,300 mile/hour).

${text{450 km}}={frac {C}{0.033times 2times 10,000}}$

${text{1,500 m/s}}={frac {10,000times C}{2times 10^{9}}}$

The unambiguous velocity of an L-Band radar using a PRF of 10 kHz would be 1,500 m/s (3,300 mile/hour) (10,000 x C / (2 x 10^9)). True velocity can be found for objects moving under 45,000 m/s if the band pass filter admits the signal (1,500/0.033).

Medium PRF has unique radar scalloping issues that require redundant detection schemes.

High PRF[edit]

Systems using PRF above 30 kHz function better known as interrupted continuous-wave (ICW) radar because direct velocity can be measured up to 4.5 km/s at L band, but range resolution becomes more difficult.

High PRF is limited to systems that require close-in performance, like proximity fuses and law enforcement radar.

For example, if 30 samples are taken during the quiescent phase between transmit pulses using a 30 kHz PRF, then true range can be determined to a maximum of 150 km using 1 microsecond samples (30 x C / 30,000 km/s). Reflectors beyond this range might be detectable, but the true range cannot be identified.

${text{150 km}}={frac {30times C}{2times 30,000}}$

${text{4,500 m/s}}={frac {30,000times C}{2times 10^{9}}}$

It becomes increasingly difficult to take multiple samples between transmit pulses at these pulse frequencies, so range measurements are limited to short distances.^[2]

Sonar[edit]

Sonar systems operate much like radar, except that the medium is liquid or air, and the frequency of the signal is either audio or ultra-sonic. Like radar, lower frequencies propagate relatively higher energies longer distances with less resolving ability. Higher frequencies, which damp out faster, provide increased resolution of nearby objects.

Signals propagate at the speed of sound in the medium (almost always water), and maximum PRF depends upon the size of the object being examined. For example, the speed of sound in water is 1,497 m/s, and the human body is about 0.5 m thick, so the PRF for ultrasound images of the human body should be less than about 2 kHz (1,497/0.5).

As another example, ocean depth is approximately 2 km, so sound takes over a second to return from the sea floor. Sonar is a very slow technology with very low PRF for this reason.

Laser[edit]

Light waves can be used as radar frequencies, in which case the system is known as lidar. This is short for “LIght Detection And Ranging,” similar to the original meaning of the initialism “RADAR,” which was RAdio Detection And Ranging. Both have since become commonly-used english words, and are therefore acronyms rather than initialisms.

Laser range or other light signal frequency range finders operate just like radar at much higher frequencies. Non-laser light detection is utilized extensively in automated machine control systems (e.g. electric eyes controlling a garage door, conveyor sorting gates, etc.), and those that use pulse rate detection and ranging are at heart, the same type of system as a radar—without the bells and whistles of the human interface.

Unlike lower radio signal frequencies, light does not bend around the curve of the earth or reflect off the ionosphere like C-band search radar signals, and so lidar is useful only in line of sight applications like higher frequency radar systems.

References[edit]

^ “Pulse Repetition Frequency”. Radartutorial.
^ Piper, Samuel; Wiltse, James (2007). “Continuous Wave Radar”. RF and Microwave Applications and Systems. Electrical Engineering Handbook. Vol. 20071745. doi:10.1201/9781420006711.ch14. ISBN 978-0-8493-7219-3. Retrieved January 29, 2011.^{[permanent dead link]}

Источник

Добавил:

Upload

Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Предмет:

Файл:

Скачиваний:

345

Добавлен:

10.02.2015

Размер:

395.79 Кб

Скачать

Наибольшее
применение получили прямоугольные и
экспоненциальные видеоимпульсы.
На практике в
импульсной технике наиболее широко
используются видеоимпульсы. Поэтому
более подробно рассмотрим вид и параметры
таких импульсов.
Вид импульсов и характерные участки импульсов.
Реальные
видеоимпульсы имеют вид представленный
ниже на рисунке.
Видеоимпульс
имеет следующие основные составные
части:
Участок AB – фронт,
т.е. отклонение напряжения от исходного
уровня.
Участок BC –
вершина
импульса.
Участок CD-
срез (задний фронт),
т.е. возврат напряжения к исходному
уровню.
Участок AD –основание
импульса.
Такое подробное
рассмотрение параметров импульсов
необходимо в связи с их влиянием на
срабатывание (отпирание и запирание)
импульсных устройств. При этом, моменты
срабатывания определяются фронтом и
срезом импульса. Вершина импульса
соответствует рабочей части импульса,
которая определяет, например, время
открытого состояния импульсного
устройства.
Основные параметры импульсов.
Параметры
импульса:

Амплитуда
импульса
U_m
– наибольшее отклонение импульса от
исходного уровня.
Длительность
импульса
t_и.
Измеряется на различных уровнях U_m.
Длительность бывает

полная,
на уровне 0,1U_m
(t_ио);
активная,
при которой обычно срабатывает импульсное
устройство – на уровне 0,5U_m
(t_иа).

Длительность
фронта (t_ф)
– время нарастания напряжения от 0,1U_m
до 0,9U_m(может
быть полной и активной).

Длительность
среза (t_c)
– время возвращения напряжения к
исходному уровню от 0,9U_m
до 0,1U_m.
Спад вершины
импульса
(U_m).
Описывается коэффициентом спада

К_с=U_m/U_m
Величина коэффициента
спада колеблется в диапазоне от 0,01 до
0,1.
В качестве
дополнительного можно отметить такой
параметр как крутизна
– скорость нарастания (спада) импульса.
Крутизна фронта
определяется как
S_ф=U_m./t_ф
Крутизна среза
определяется как
S_с=U_m./t_с
Определяется
крутизна в [В/с].
Прямоугольный
импульс обладает бесконечно большой
крутизной.
Параметры последовательности импульсов.
Понятно, что на
практике используются не единичные
импульсы, а их последовательность.
Рассмотрим
параметры последовательности импульсов.

Период следования
(повторения) – Т.

T=t_и+t_п

Частота следования
(повторения) – F. Это есть число импульсов
в cекунду.

Выражение для
определения частоты имеет вид:
F=1/T

Скважность
-отношение интервала между импульсами
(периода) (скважины) к длительности
самого импульса (Q).

Q=T/t_и
Как правило,
скважность всегда
должна быть больше 1 (Q>1).

Коэффициент
заполнения
– величина, обратная скважности ()

=1/Q
Таким образом:

Основными
параметрами импульсов являются
амплитуда, длительность импульса,
длительность фронта, длительность
среза, спад вершины импульса.
Параметрами
последовательности импульсов являются
период следования импульсов, частота
следования импульсов, скважность,
коэффициент заполнения.

2. Переходные процессы в линейных цепях.

В импульсной
технике широко применяются устройства
формирующие напряжение одной формы из
напряжения другой формы. В качестве
входного сигнала могут использоваться
сигналы гармонической или скачкообразной
формы.
Устройства,
предназначенные для решения задач
формирования импульсов называются
формирующими.
Формирующие
устройства строятся с использованием
линейных и нелинейных элементов. При
этом, различие между получаемыми
устройствами заключается в характере
изменения ВАХ используемых приборов.
Рассмотрим
линейные формирующие цепи.
Линейная цепь
состоит из элементов R, L, C параметры
которых не зависят от значения и
направления протекающего тока и
приложенного напряжения.
Процессы в цепях,
содержащих конденсаторы (и катушки
индуктивности), могут быть как
установившиеся, так и переходные.
В установившихся
режимах напряжения на элементах и токи
в ветвях остаются неизменными (в цепях
переменного тока остаются неизменными
амплитудные значения напряжений и
токов).
Процесс перехода
цепи от одного энергетического
установившегося режима к другому
называют переходным. Переходные процессы
возникают как вследствие коммутаций
(включения или выключения источников
питания, подключение или отключение
элементов цепей), так и при возникновении
аварийных режимов (обрыве или коротком
замыкании какой-либо части электрических
цепей).
Назначение
линейных цепей.
В импульсной
технике линейные цепи используются
для формирования и преобразования
импульсов, для получения желаемого
изменения формы передаваемого напряжения.
Классификация
линейных цепей
Основными линейными
цепями являются:

дифференцирующие
цепи;
интегрирующие
цепи;
линии задержки;
формирующие цепи
(формирующие линии) и т.д.

Как основополагающие,
рассмотрим дифференцирующие и
интегрирующие цепи.
В связи с
необходимостью микроминиатюризации
в импульсной технике преимущественно
используются дифференцирующие
интегрирующие цепи на базе R и C. (R и L не
используются).
Поэтому рассмотрим
именно такие дифференцирующие и
интегрирующие цепи на базе R и C.
Принцип
действия.
Возникновение
переходных процессов связано с
особенностями изменения энергии
электрического поля конденсаторов
(изменение энергии не может происходить
мгновенно, скачком, т.е. напряжение на
конденсаторе мгновенно не изменяются:
u_C(о^–)=u_C(о⁺)
.
В цепях, содержащих
только резистивные элементы, энергия
не запасается и переходные процессы
не возникают.
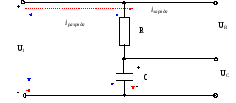
Схема
включения.
Линейная RC имеет
вид:
Функционирование
схемы.
Физическая
интерпретация процессов происходящих
в RC- цепях такова: в момент скачкообразного
увеличения напряжения, напряжение на
незаряженном конденсаторе сохранит
свое первоначальное значение равное
нулю (конденсатор не может зарядиться
мгновенно); напряжение резистора примет
значение входного сигнала; ток в цепи
максимален. С течением времени, по мере
зарядки конденсатора, напряжение на
конденсаторе будет возрастать, ток в
цепи и напряжение на резисторе уменьшатся.
Если длительность входного импульса
напряжения не меньше времени переходного
процесса, то напряжение на конденсаторе
к моменту окончания импульса станет
равным входному напряжению, напряжение
на резисторе – нулю.
При скачкообразном
уменьшении входного напряжения резистор
и конденсатор оказываются соединенными
параллельно. Следовательно, напряжение
на резисторе принимает значение, равное
напряжению на конденсаторе, но с
полярностью, противоположной полярности
напряжения на конденсаторе в момент
включения импульса. С течением времени,
по мере разряда конденсатора, напряжение
на элементах будет уменьшатся до нуля.
Рассмотрим
работу RC схемы более подробно.
При подаче на вход
прямоугольного импульса длительностью
t_и
и амплитудой U_m
происходит заряд конденсатора C. После
окончания действия импульса конденсатор
разряжается по цепи через сопротивление
R, плюс источника питания, минус источника
питания. Известно, что RC цепь обладает
постоянной времени t_ц
которая определяется как
t_ц=RC.
Поэтому возможны
случаи, когда t_и>>t_ци, наоборот,
t_и<<t_ц.
При этом, форма сигнала зависит еще и
от того, какой сигнал является выходным
(т.е. с какого элемента снимается выходное
напряжение).
Рассмотрим работу
схемы и формы напряжений на элементах
как указано на рисунках.
Рассмотрим цепь
при воздействии прямоугольного импульса
(скачка напряжения на входе цепи). На
основании 2 закона Кирхгоффа уравнение
цепи для t0
интегро-дифференциальное уравнение
имеет вид:
U_r+U_c=U_m
где

U_r
– падение напряжения на сопротивлении;
U_c
– падение напряжения на конденсаторе;
U_m
– амплитудное значение напряжения
входного прямоугольного импульса.

В исходном состоянии
до подачи входного сигнала ток в цепи
не протекает, и конденсатор разряжен.
В рабочий период
в момент подачи t=0 на вход подается
напряжения с амплитудой U_m.
В соответствии со 2-м законом коммутации
(закона непрерывного изменения
электрического заряда, который звучит
следующим образом: величина электрического
заряда конденсатора не может изменяться
скачком) напряжение на C скачком
измениться не может, U_c(0)=0.
Все напряжение приложено к резистору,
т.е. U_r(0)=U_m.
Ток в цепи имеет
максимальное значение
i=U_m/R
Далее конденсатор
С заряжается, напряжение на нем растет,
соответственно, напряжение на
сопротивлении R уменьшается, ток в цепи
также падает. В итоге при t=бесконечности
U_c()=U_m
и U_r()
=0.
Так как,
U_r=iR,
i=CdU_c/dt,
то
RCdU_c/dt+U_c=U_m.
Решая относительно
U_c,
получаем:
Здесь через t_ц=RC
обозначается постоянная времени цепи.
Процесс получения
напряжения, отвечающий данному закону
называется интегрированием. Решая
относительно U_r,
получаем:
Процесс получения
напряжения, отвечающий данному закону
называется дифференцированием.
Таким образом,
видно, что напряжение на R уменьшается
от максимального значения до 0 по
экспоненциальному закону. Соответственно,
напряжение на C увеличивается от 0 до
максимального значения так же по
экспоненте. (См. рис.)
Ток в цепи
пропорционален напряжению U_r(t),
следовательно, ток в цепи так же убывает
по экспоненте.
Постоянная времени
цепи t_ц
характеризует крутизну экспоненты.
Чем меньше t_ц,
тем быстрее напряжение на сопротивлении
стремится к нулю. И, наоборот, чем больше
t_ц,
тем медленнее убывает напряжение U_r.
Соответственно,
для напряжения на конденсаторе C, чем
меньше t_ц,
тем быстрее стремится напряжение на
конденсаторе к максимальному значению
(амплитуде подаваемого импульса) U_m.
А чем больше t_ц,
тем медленнее стремится напряжение на
конденсаторе к U_m.
Таким образом:

Постоянная времени
цепи t_ц
характеризует крутизну экспоненты:
чем меньше t_ц
тем больше скорость изменения экспоненты.
Считается, что
переходный процесс заканчивается,
когда напряжение на конденсаторе U_c(t)
достигает 90% от величины амплитуды
подаваемого импульса, т.е. U_c(t)=0,9U_m
(или U_r(t)=0,1U_m),
т.е.

Тогда,

t_пер=t₁=t_цln10=2.3t_ц.

Таким образом,
меняя R и C (т.е. t_ц),
можно регулировать длительность
переходного процесса. При этом в случае,
если

t_пер=t_ц,
то U_c=0,63U_m;
t_пер=3t_ц,
то U_c=0,95U_m;
t_пер=5t_ц,
то U_c=U_m.

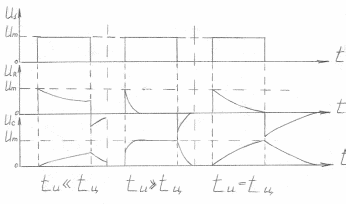
Для различных
соотношений длительности импульса t_и
и постоянной времени цепи t_ц
построена диаграмма на рисунке ниже.
В зависимости от
соотношения t_ц/t_и
напряжение на элементах цепи меняется
по разному.
При

t_ц<<t_и
конденсатор заряжается до величины
амплитуды подаваемого импульса, т.е.
U_c=U_m
за время 2,3t_ц,
а напряжение на сопротивлении убывает
за это же время до нуля. С момента t₁
(см. рис.) конденсатор разряжается с той
же постоянной времени цепи t_ц
от амплитудного значения импульса до
нуля, т.е. от U_c=U_m
до U_c=0.
Таким образом в цепи меняется знак
напряжения на противоположный. При
этом на R возникает два остроконечных
импульса длительностью 2,3t_ц,
начала которых совпадают по времени с
перепадами входного напряжения и имеют
полярность этих перепадов;
t_ц>>t_и
конденсатор на успевает зарядиться до
U_c=U_m,
а лишь до U_с=U<U_m.
Следовательно, напряжение на сопротивлении
U_r
уменьшится до величины U_m-U,
а не до нуля. В момент окончания импульса
t₁
конденсатор C разряжается от U,
ток в цепи будет меньше, амплитуда
напряжения отрицательного импульса,
снимаемого с резистора, будет меньше.
В этом случае напряжение на резисторе,
по существу, представляет собой
искаженный входной сигнал. Искажения
проявляются в виде спада вершины и
обратного выброса напряжения. Как видно
из рисунка, с увеличением отношения
t_ц/t_и
форма напряжения на резисторе приближается
к прямоугольной.

Соседние файлы в папке Импульсные

Источник

радиоликбез

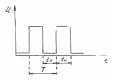
Для периодической последовательности импульсов (рис, 151, а) свойственно следование импульсов через равные промежутки времени. Ее характеризуют следующие параметры.

Период следованияТ_и — интервал времени от момента появления одного импульса до момента появления следующего импульса той же полярности.

Частота следования F_и, являющаяся величиной, обратной периоду следования, т. е.

Длительность паузы Т_и — время между моментом окончания одного импульса и началом другого:

Скважность импульсов Q, определяемая как отношение периода следования Т_и к длительности t_и

Среднее значение импульсного тока (напряжения) получается, если ток (напряжение) импульса равномерно распределить на весь период так, чтобы площадь прямоугольника I_срT_и (рис. 151,б) была равновелика площади импульса S_и

Коэффициент заполнения — величина, обратная скважности, показывающая, какую часть периода занимает импульс:

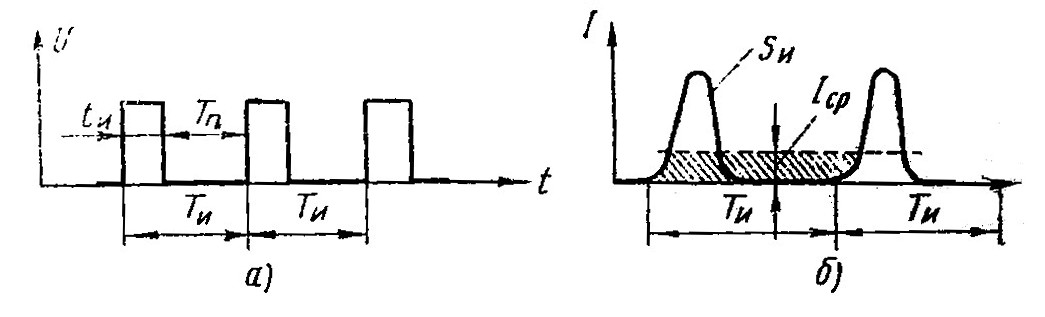Параметры периодической последовательности импульсного сигнала

Рис. 151. Периодическая последовательность импульсов:

а — прямоугольных, б — колоколообразных

Средняя мощность P_Ср определяется отношением энергии W, выделенной в цепи за период следования импульса T_и, к длительности этого периода:

Очевидно, Р_срТ_и=P_иt_и, откуда

Электронные приборы для импульсных схем очень часто выбирают по средней мощности.

Читайте также: Общая характеристика импульсного сигнала
Прохождение импульсов через линейные цепи

Источник

Определение частоты следования импульсов

Страницы работы

Содержание работы

Глава № 15

1. Определить частоту следования
импульсов. Если известно разрядное напряжение = 50 В ,начальное напряжение = 60
В, зарядное напряжение = 90 В, допустимый ток выпрямителя 25 А. Расстояние
между обкладками конденсатора 3 мм, длина 30 мм, ширина 20 мм.

Решение:

;

;
;

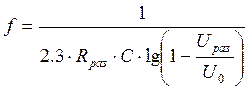
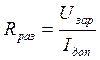
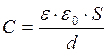
где: U_зар– зарядное напряжение, В;

I_доп– допустимый ток выпрямителя, А;

R_зар– зарядное сопротивление, Ом;

С – ёмкость конденсатора, Ф;

U₀–
начальное напряжение, В;

d –
расстояние между обкладками конденсатора, мм;

мм²

Ом

Гн =
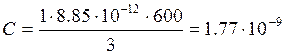
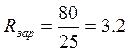
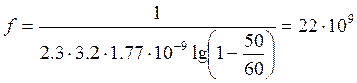
22 МГц

2. С какой частотой происходит
переключение конденсатора? Конденсатор емкостью С = 10 мкФ периодически
заряжается от батареи с ЭДС Е = 120 В и разряжается через соленоид длиной l = 10 см. Соленоид имеет N = 200
витков. Среднее значение напряженности магнитного поля внутри соленоида H = 200 А/м.

3. Определить электромагнитную
мощность P_эм, передаваемую от статора к
жидкому металлу, в магнито-импульсной установке обработки металлов. Если
известны: радиус полого ротора R = 0,6 м, толщина слоя металла в радиальном направлении 0,2 м, длина внутренней полости трубы,
заполненной жидким металлом в осевом направлении 0,9 м, полюсное деление 3, число фаз 3, частота 50 Гц, число витков обмотки статора 20, обмоточный
коэффициент 0,95, скорость ротора 2340 об/мин.

4. Определить время деформации
заготовки τ_деф и энергию используемую на нагрев W_н
материала заготовки (трубчатая алюминиевая) при магнитоимпульсной обработке.
Толщина стенки заготовки 0,3 см. Плотность материала γ = 7,8 г/ см².
Давление на заготовку 0,04 кг/ см², ξ = 200 см.

5. Определить время деформации
заготовки и электромагнитную энергию W_н, используемую на нагрев материала
заготовки. Если перемещение стенки трубчатой заготовки в направлении обжатия , удельное сопротивление заготовки, железо,
, плотность железо ,
толщина стенки заготовки , ее поперечное сечение S = 0,3м², индукция магнитного поля В =
50Тл.

6. Определить силу, которая
действует на жидкий металл, если известно число фаз m =
3, частота f = 50 Гц, число витков ω₁= 5,
коэффициент обмотки статора К₀₁= 0,5, длина внутренней полости l = 2м, линейная скорость перемещения поля υ₁= 1
м/сек, линейная скорость перемещения жидкости υ = 0,5 м/сек, приведённое
сопротивление жидкого металла = 30 Ом, полюсное
деление τ = 1

7. Вычислить количество тепла, отведенного от индуктора с
концентратором магнитного поля водой и скорость воды в канале. Допустимый цикл
работы концентратора , , , потери в рабочей обмотке , потери в
поверхности пазов, прилегающих к рабочей обмотке , потери в рабочей поверхности концентратора , , , .

8. Определите частоту следования
импульсов, если известно зарядное сопротивление , , ,
допустимый ток выпрямителя , начальное напряжение , расстояние между обкладками , длина , ширина
.

9. Определить время и скорость
деформации трубчатой алюминиевой заготовки а так же энергию используемую на
нагрев. Известна плотность материала г/ см²,
давление на заготовку кг/ см², толщина
стенки заготовки см.

10. Внутрь соленоида помещают
проводник, с какой силой магнитное поле будет действовать на проводник с током
1А, если длина соленоида 50см, имеющий 1000 витков, по которым протекает ток в
5 А ? Считать, что проводник находится на оси соленоида и его длина равна длине
соленоида. Краевым эффектом пренебречь.

11.
Сколько ампер-витков потребуется для того чтобы внутри соленоида малого
диаметра и длиной 30см, объёмная плотность энергии магнитного поля была равна
1,75Дж/м³ ?

12. Длина железного сердечника
тороида 1м, длина воздушного зазора Змм. Число витков в обмотки тороида N=2000
. Найти напряжённость магитного поля в воздушном зазоре при силе тока7А в
обмотке тороида.

13. Незамкнутый магнитопровод катушки состоит из двух различных по
сечению участков 1 и 2 . Определить ток в обмотке катушки, если магнитная
индукция в зазоре 1Тл, длина участка с сечением 1см² – 4см, длина
участка с сечением 0.5см^А2 – 7см, воздушный зазор 0.01мм. Число
витков обмотки – 100. Материалы магнитопровода – сталь 1512 . При расчёте рассеянием пренебречь и магнитное поле
в зазоре считать равномерным.

14.Для охлаждения
теплоносителя атомного реактора применяется жидкий металл. К зазору между
полюсами электромагнита N – S подводятся медные шины А
и Б , концы которых подключены к источнику напряжения . В направлении ,
перпендикулярном направлениям магнитного поля электромагнита и шины ,
пропускается струя жидкого металла . В результате взаимодействия магнитного
поля с током создаёт усилие , под влиянием которого движется струя жидкого
металла . Определить силу . действующую на струю , если ток I=10000А
, активная длина струи L=10cm и магнитная индукция В=1Тл.

15.
Определить энергию магнитного поля , развиваемую
соленоидами магнитно-импульсных установок, энергию магнитного поля, расходуемую
на импульс в соленоидом W₀, энергию,
расходуемую на намагничивание стальной детали , а
так же определить время выдержки инструмента из быстрорежущей стали после
магнитно-импульсной обработки, если известно: – коэффициент,
учитывающий потери энергии при магнитно-импульсной обработке МИО, – магнитная индукция в соленоиде, – напряженность магнитного поля, – объем пространства, где
концентрируется магнитное поле, – коэффициент не
учетных потерь энергии, – энергия, расходуемая
на локальный нагрев детали, – коэффициент
пропорциональности, зависящий от свойств металла –
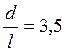
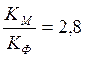
коэффициент, зависящий от свойств материала инструмента. – напряженность поля установки, отношение диаметра инструмента к ее длине,
– отношение магнитной проницаемости
материала инструмента к магнитной проницаемости феррита, т = 25 кг – масса инструмента, – объем металла
инструмента.