Как найти частоту слов в газетном тексте

Частота события. Статистическое определение вероятности

содержание учебника

Классическое определение вероятности предполагает, что все эле­ментарные исходы равновозможны. О равновозможности исходов опы­та заключают в силу соображений симметрии (как в случае монеты или игрального кубика). Задачи, в которых можно исходить из соображений симметрии, на практике встречаются редко. Во многих случаях трудно указать основания, позволяющие считать, что все элементарные исходы равновозможны. В связи с этим появилась необходимость введения еще одного определения вероятности, называемого статистическим. Чтобы дать это определение, предварительно вводят понятие относительной частоты события.

Относительной частотой события, или частотой, называется от­ношение числа опытов, в которых появилось это событие, к числу всех произведенных опытов. Обозначим частоту события 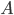через 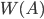, тогда по определению

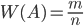    (1.4.1)
где – число опытов, в которых появилось событие 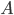и – число всех произведенных опытов.

Частота события обладает следующими свойствами.

1. Частота случайного события есть число, заключенное между ну­лем и единицей:
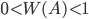   .    (1.4.2)
2. Частота достоверного события 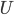 равна единице:
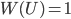      (1.4.3)
3. Частота невозможного события 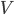 равна нулю:
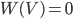      (1.4.4)
4. Частота суммы двух несовместных событи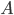й  и равна сумме частот этих событий:
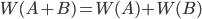      (1.4.5)

Наблюдения позволили установить, что относительная частота об­ладает свойствами статистической устойчивости: в различных сериях многочленных испытаний (в каждом из которых может появиться или не появиться это событие) она принимает значения, достаточно близкие к некоторой постоянной. Эту постоянную, являющуюся объективной числовой характеристикой явления, считают вероятностью данного со­бытия.

Вероятностью события называется число, около которого группи­руются значения,частоты данного события в различных сериях большо­го числа испытаний.

Это определение вероятности называется статистическим.

В случае статистического определения вероятность обладает сле­дующими свойствами:
1) вероятность достоверного события равна еди­нице;
2) вероятность невозможного события равна нулю;
3) вероятность случайного события заключена между нулем и единицей;
4) вероятность суммы двух несовместных событий равна сумме вероятностей этих со­бытий.

Пример 1. Из 500 взятых наудачу деталей оказалось 8 бракован­ных. Найти частоту бракованных деталей.

Решение. Так как в данном случае  = 8,  = 500, то в соответствии с формулой (1.4.1) находим

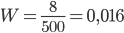
Пример 2. Игральный кубик подброшен 60 раз, при этом шестерка появилась 10 раз. Какова частота появления шестерки?

Решение. Из условия задачи следует, что  = 60,  = 10, поэтому

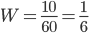
Пример 3. Среди 1000 новорожденных оказалось 515 мальчиков.Чему равна частота рождения мальчиков?
Решение. Поскольку в данном случае 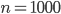, , то .

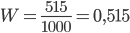Пример 4. В результате 20 выстрелов по мишени получено 15 попаданий. Какова частота попаданий?

Решение. Так как  = 20,  = 15, то

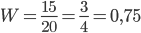
Пример 5. При стрельбе по мишени частота попаданий 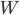= 0,75. Найти число попаданий при 40 выстрелах.

Решение. Из формулы (1.4.1) следует, что 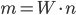. Так как  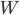= 0,75,  = 40, то 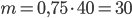 . Таким образом, было получено 30 попаданий.

Пример 6. www.itmathrepetitor.ru Частота нормального всхода семян W = 0,97. Из высе­янных семян взошло 970. Сколько семян было высеяно?

Решение. Из формулы (1.4.1) следует, что 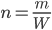. Поскольку 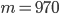, , 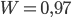то . Итак, было высеяно 1000 семян.

Пример 7. На отрезке натурального ряда от 1 до 20 найти частоту простых чисел.

Решение. На указанном отрезке натурального ряда чисел находятся следующие простые числа: 2, 3, 5, 7, 11, 13, 17, 19; всего их 8. Так как = 20,  = 8, то искомая частота

.

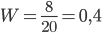Пример 8. Проведены три серии многократных подбрасываний симметричной монеты, подсчитаны числа появлений герба: 1) 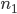 = 4040,  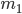=2048, 2)  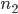= 12000,  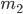= 6019; 3)  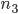= 24000,  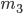= 12012. Найти частоту появления герба в каждой серии испытаний.

Решение. В соответствии с формулой (1.4.1) находим:

                                                                .

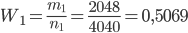
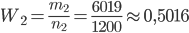
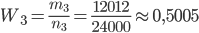Замечание. Эти примеры свидетельствуют о том, что при многократ­ных испытаниях частота события незначительно отличается от его вероятности. Вероятность появления герба при подбрасывании монеты р = 1/2 = 0,5 , так как в этом случае n = 2, m = 1.

Пример 9. Среди 300 деталей, изготовленных на автоматическом станке, оказалось 15, не отвечающих стандарту. Найти частоту появле­ния нестандартных деталей.

Решение. В данном случае n = 300, m = 15, поэтому

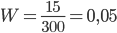
Пример 10. Контролер, проверяя качество 400 изделий установил, что 20 из них относятся ко второму сорту, а остальные – к первому. Най­ти частоту изделий первого сорта, частоту изделий второго сорта.

Решение. Прежде всего, найдем число изделий первого сорта: 400 – 20 = 380. Поскольку n = 400, 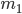= 380, то частота изделий перво­го сорта

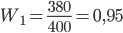
Аналогично находим частоту изделий второго сорта:

Задачи

1. Отдел технического контроля обнаружил 10 нестандартных изде­лий в партии из 1000 изделий. Найдите частоту изготовления бракован­ных изделий.
2. Для выяснения качества семян было отобрано и высеяно в лабо­раторных условиях 100 штук. 95 семян дали нормальный всход. Какова частота нормального всхода семян?
3. Найдите частоту появления простых чисел в следующих отрезках натурального ряда: а) от 21 до 40; б) от 41 до 50; в) от 51 до 70.
4. Найдите частоту появления цифры при 100 подбрасываниях сим­метричной монеты. (Опыт проводите самостоятельно).
5. Найдите частоту появления шестерки при 90 подбрасываниях иг­рального кубика.
6. Путем опроса всех студентов Вашего курса определите частоту дней рождения, попадающих на каждый месяц года.
7. Найдите частоту пятибуквенных слов в любом газетном тексте.

Ответы

1. 0,01. 2. 0,95; 0,05. 3. а) 0,2; б) 0,3; в) 0,2.

Вопросы

1. Что такое частота события?
2. Чему равна частота достоверного события?
3. Чему равна частота невозможного события?
4. В каких пределах заключена частота случайного события?
5. Чему равна частота суммы двух несовместных событий?
6. Какое определение вероятности называют статистическим?
7. Какими свойствами обладает статистическая вероятность?

содержание учебника

Последние комментарии

Частотный анализ текста онлайн

Частотный анализ – это один из методов криптоанализа, основывающийся на предположении о существовании нетривиального статистического распределения отдельных символов и их последовательностей как в открытом тексте, так и шифрованном тексте, которое с точностью до замены символов будет сохраняться в процессе шифрования и дешифрования.

Кратко говоря, частотный анализ предполагает, что частота появления заданной буквы алфавита в достаточно длинных текстах одна и та же для разных текстов одного языка. При этом в случае моно алфавитного шифрования, если в шифрованном тексте будет символ с аналогичной вероятностью появления, то можно предположить, что он и является указанной зашифрованной буквой. Аналогичные рассуждения применяются к биграммам (двухбуквенным последовательностям), триграммам в случае поли алфавитных шифров.

Метод частотного анализа известен с еще IX-го века и связан и именем Ал-Кинди. Но наиболее известным случаем применения такого анализа является дешифровка египетских иероглифов Ж.-Ф. Шампольоном в 1822 году.

Данный вид анализа основывается на том, что текст состоит из слов, а слова из букв. Количество различных букв в каждом языке ограничено и буквы могут быть просто перечислены. Важными характеристиками текста являются повторяемость букв, пар букв (биграмм) и вообще m-ок (m-грамм), сочетаемость букв друг с другом, чередование гласных и согласных и некоторые другие.

Если – число появлений m-граммы ai1ai2. aim в тексте T, а L – общее число подсчитанных m-грамм, то опыт показывает, что при достаточно больших L частоты

для данной m-граммы мало отличаются друг от друга.

В силу этого, относительную частоту считают приближением вероятности P (ai1ai2. aim) появления данной m-граммы в случайно выбранном месте текста (такой подход принят при статистическом определении вероятности).

В представленной ниже таблице приводятся частоты встречаемости букв в русском языке (в процентах):

Буква алфавита	Показатель частоты встречаемости	Буква алфавита	Показатель частоты встречаемости
А	0,062	Р	0,04
В	0,038	Т	0,053
Д	0,025	Ф	0,002
Ж	0,007	Ц	0,004
И	0,062	Ш	0,006
К	0,028	Ъ, Ь	0,014
М	0,026	Э	0,003
О	0,09	Я	0,018

Имеется мнемоническое правило запоминания десяти наиболее частых букв русского алфавита. Эти буквы составляют слово СЕНОВАЛИТР.

Устойчивыми являются также частотные характеристики биграмм, триграмм и четырехграмм осмысленных текстов. Существуют специальные таблицы с указанием частоты биграмм некоторых алфавитов. По результатам исследований с помощью таких таблиц ученые определили наиболее часто встречаемые биграммы и триграммы для русского алфавита:

СТ, НО, ЕН, ТО, НА, ОВ, НИ, РА, ВО, КО, СТО, ЕНО, НОВ, ТОВ, ОВО, ОВА.

Из таблиц биграмм можно также легко извлечь информацию о сочетаемости букв, т.е. о предпочтительных связях букв друг с другом.

Результатом таких исследований является таблица, в которой слева и справа от каждой буквы расположены наиболее предпочтительные «соседи» (в порядке убывания частоты соответствующих биграмм). В таких таблицах обычно указывается также доля гласных и согласных букв (в процентах), предшествующих (или следующих за) данной букве.

Г	С	Слева	Справа	Г	С
3	97	л, д, к, т, в, р, н	А	л, н, с, т, р, в, к, м	12	88
80	20	я, е, у, и, а, о	Б	о, ы, е, а, р, у	81	19
68	32	я, т, а, е, и, о	В	о, а, и, ы, с, н, л, р	60	40
78	22	р, у, а, и, е, о	Г	о, а, р, л, и, в	69	31
72	28	р, я, у, а, и, е, о	Д	е, а, и, о, н, у, р, в	68	32
19	81	м, и, л, д, т, р, н	Е	н, т, р, с, л, в, м, и	12	88
83	17	р, е, и, а, у, о	Ж	е, и, д, а, н	71	29
89	11	о, е, а, и	З	а, н, в, о, м, д	51	49
27	73	р, т, м, и, о, л, н	И	с, н, в, и, е, м, к, з	25	75
55	45	ь, в, е, о, а, и, с	К	о, а, и, р, у, т, л, е	73	27
77	23	г, в, ы, и, е, о, а	Л	и, е, о, а, ь, я, ю, у	75	25
80	20	я, ы, а, и, е, о	М	и, е, о, у, а, н, п, ы	73	27
55	45	д, ь, н, о	Н	о, а, и, е, ы, н, у	80	20
11	89	р, п, к, в, т, н	О	в, с, т, р, и, д, н, м	15	85
65	35	в, с, у, а, и, е, о	П	о, р, е, а, у, и, л	68	32
55	45	и, к, т, а, п, о, е	Р	а, е, о, и, у, я, ы, н	80	20
69	31	с, т, в, а, е, и, о	С	т, к, о, я, е, ь, с, н	32	68
57	43	ч, у, и, а, е, о, с	Т	о, а, е, и, ь, в, р, с	63	37
15	85	п, т, к, д, н, м, р	У	т, п, с, д, н, ю, ж	16	84
70	30	н, а, е, о, и	Ф	и, е, о, а, е, о, а	81	19
90	10	у, е, о, а, ы, и	Х	о, и, с, н, в, п, р	43	57
69	31	е, ю, н, а, и	Ц	и, е, а, ы	93	7
82	18	е, а, у, и, о	Ч	е, и, т, н	66	34
67	33	ь, у, ы, е, о, а, и, в	Ш	е, и, н, а, о, л	68	32
84	16	е, б, а, я, ю	Щ	е, и, а	97	3
0	100	м, р, т, с, б, в, н	Ы	л, х, е, м, и, в, с, н	56	44
0	100	н, с, т, л	Ь	н, к, в, п, с, е, о, и	24	76
14	86	с, ы, м, л, д, т,, р, н	Э	н, т, р, с, к	0	100
58	42	ь, о, а, и, л, у	Ю	д, т, щ, ц, н, п	11	89
43	57	о, н, р, л, а, и, с	Я	в, с, т, п, д, к, м, л	16	84

Пример: Проведем анализ текста следующего содержания

«СОКРАТ из Афин (469–399 до н.э.) – знаменитый античный философ, учитель Платона, воплощенный идеал истинного мудреца в исторической памяти человечества. С именем Сократа связано первое фундаментальное деление истории античной философии на до- и после-Сократовскую («Досократики»), отражающее интерес ранних философов VI–V вв. к натурфилософии, а последующего поколения софистов V в. – к этико-политическим темам, главная из которых – воспитание добродетельного человека и гражданина. Сократу был близок софистическому движению. Учение Сократа было устным; все свободное время он проводил в беседах с приезжими софистами и местными гражданами, политиками и обывателями, друзьями и незнакомыми на темы, ставшими традиционными для софистической практики: что есть добро и что – зло, что прекрасно, а что безобразно, что добродетель и что порок, можно ли научиться быть хорошим и как приобретается знание. Об этих беседах мы знаем в основном благодаря ученикам Сократа – Ксенофонту и Платону. Кроме их сочинений, имеются также фрагменты и свидетельства о содержании «сократических диалогов» других сократиков, пародийное изображение Сократа в комедии Аристофана Облака и ряд замечаний о Сократе у Аристотеля. Проблема достоверности изображения личности Сократа в сохранившихся произведениях – ключевой вопрос всех исследований о нем.»

Источник

Частотный анализ текста на С++. Быстро и просто

Хочу рассказать о быстром частотном анализе текста на С++, практически без применения головы и алгоритмов.
Иногда такое задание часто дают на контрольной по программированию в каком-нибудь МИРЭА, или МИФИ.

Суть задачи такова. На входе текстовый файл TextForAnalyze.txt(довольно большой ≈ 400кб). Необходимо получить порядок встречаемости слов файле(в порядке убывания частоты). При сравнении слов регистр не учитывать. Необходимо игнорировать предлоги и союзы (список слов в стоп-словаре составить самостоятельно, стоп-словарь хранить в файле). Разделителями слов являются пробел, табуляция, символы перевода строки, знаки, «слеши» и тд.

Названия функций я делал понятными и не нуждающихся в объяснении.

Для начала нужно быстро получить текст.

Обратим внимание на tolowerStr! Я написал его сам так как мы все знаем какая прожорливая функция, поэтому забудем про нее и реализуем более быструю «функцию»:

В итоге наша «tolowerStr» будет выглядеть так:

Теперь мы будем извращаться по полной и создавать свою локаль. Точнее новый «объект локали» т.к нам не нужны всякие скобки, звездочки, проценты и так далее.

Эта битовая маска наследуется от класса ctype. всего до 256 символов. Да, выглядит ужасно, но зато это очень удобно на практике.

Ну теперь практически все сделано. Записываем в текстовый файл с руки все предлоги, которые не хотим видеть в списке, и пишем такой вот код.

Ну вот и все дело сделано, научный текст весом в 400кб был пройден за 21ms.
Что я считаю довольно хорошим результатом.
Для тестирования я пользуюсь GTEST`ами это удобно.

Источник

Дешифровка текста методом частотного анализа

Привет, Хабр! В этой статье я покажу как сделать частотный анализ современного русского интернет-языка и воспользуюсь им для расшифровки текста. Кому интересно, добро пожаловать под кат!

Частотный анализ русского интернет-языка

В качестве источника, откуда можно взять много текста с современным интернет-языком, была взята социальная сеть Вконтакте, а если быть точнее, то это комментарии к публикациям в различных сообществах данной сети. В качестве сообщества я выбрал реальный футбол. Для парсинга комментариев я воспользовался API Вконтакте:

В результате было получено около 200MB текста. Теперь считаем, какой символ сколько раз встречается:

Полученные результаты можно сравнить с результатами из Википедии и отобразить в виде:

1) сравнительной диаграммы

2) таблицы(слева — данные википедии, справа — мои данные)

Проанализировав данные, можно сделать вывод, что частота встречаемости символов в процентном соотношении в двух источниках практически одинакова, за исключением таких букв как «а» и «о».

Шифрование и дешифрование текста

Далее я выбрал из того же сообщества более развёрнутый комментарий, который найти было не так уж и легко, так как в основном комментарии состоят из 2-4 слов:

дружа слово почти не считается, вар извинилась за неправильное решение, и этого достаточно чтобы сделать вывод и усомниться во многих их решениях, вар вместо того чтобы исключать ошибки делает их, это абсолютно не нормально, народ не такой уже и тупой, не по радио же слушаем транслы а в живую смотрим, по этому я больше чем уверен если бы не было столько пенок для мю они бы подавно в топ не попали, аналогично касается ман с, хотя играют местами захватывающе и красиво

После этого необходимо зашифровать полученный текст с помощью какого-нибудь симметричного алгоритма шифрования. Первое, что приходит на ум — это шифр цезаря, сущность которого заключается в том, чтобы изменить символ на другой с определенным шагом:

жуцйг фосес тсъхл рз фълхгзхфв егу лкелрлогфя кг рзтугелоярсз узызрлз л ахсёс жсфхгхсърс ъхсдю фжзогхя еюесж л цфспрлхяфв ес прсёлш лш узызрлвш егу епзфхс хсёс ъхсдю лфнобъгхя сылднл жзогзх лш ахс гдфсобхрс рз рсупгоярс ргусж рз хгнсм цйз л хцтсм рз тс угжлс йз фоцыгзп хугрфою г е йлецб фпсхулп тс ахспц в дсояыз ъзп цезузр зфол дю рз дюос фхсоянс тзрсн жов пб срл дю тсжгерс е хст рз тстгол гргосёлърс нгфгзхфв пгр ф шсхв лёугбх пзфхгпл кгшегхюегбьз л нугфлес

Затем осталось расшифровать текст с помощью частотного анализа:

двужа лросо мопти не лпитаетлб сав ишсиниралг ша немвасиргное вейение и ютохо долтатопно птоыч лдератг счсод и улокнитглб со кнохиз из вейенибз сав скелто тохо птоыч ильряпатг ойиыьи дерает из юто аылорятно не новкаргно навод не таьоф уже и тумоф не мо вадио же лруйаек тванлрч а с жисуя лкотвик мо ютоку б ыоргйе пек усевен елри ыч не ычро лторгьо меноь дрб кя они ыч модасно с том не момари анарохипно ьалаетлб кан л зотб ихваят келтаки шазсатчсаяэе и ьвалисо

Заключение

Источник

Частотный анализ текста. Пример написания калькулятора

Немного о частотном анализе текста и рассказ о создании калькулятора.

В общем, есть такая тема — частотный анализ текста. Утверждается, что для данного языка частота встречаемости отдельных букв в осмысленном тексте есть устойчивая величина. Устойчивыми также являются комбинации двух, трех (биграммы, триграммы) и четырех букв.
Этот факт, в частности, использовался в криптографии для вскрытия шифров.

Я в криптографии не очень, и единственное, что приходит на ум, это вскрытие шифра прямой замены. Надо сказать, наиболее примитивного шифра, когда символы исходного алфавита, используемого в сообщении, преобразуются в другие символы по определенному правилу. Такие шифры, кстати сказать, можно было вскрывать и без применения статистического анализа (где для уменьшения погрешности, очевидно, требуется наличие довольно больших кусков текста), а просто догадываясь о некоторых словах — см. рассказ «Пляшущие человечки».

Вот тут, впрочем, интересная статья про историю криптографии.

На самом деле частота встречаемости букв также зависит от типа текста. Калькулятор ниже рассчитывает частоты букв для введенного пользователем текста и выводит для сравнения теоретические частоты букв для художественного русского текста. В качестве значения по умолчанию взят научный текст (начало определения дифференциального уравнения из Википедии), и сразу видно, как, например, различается частота встречаемости буквы Ф в художественном и научном текстах.

Частоты букв для художественного текста я взял отсюда, ну а по указанному адресу утверждают, что взяли их из книги «Яглом А. М., Яглом И. М., Вероятость и информация, М.: Наука, 1973».

Этот калькулятор был создан как пример, для того чтобы продолжить рассказ о том, как создавать калькуляторы на этом сайте, начатый здесь — Площадь четырехугольника. Пример написания калькулятора. В данном случае на примере этого калькулятора я расскажу о том, как писать калькуляторы, выводящие таблицы и строящие графики. Как обычно, все что нужно от автора — некоторое знание Javascript, ну или вообще любого алгоритмического языка программирования. Интересующиеся смотрят текст после самого калькулятора.

Источник

Частота слов в тексте

Частота встречаемости слов в тексте
Здравствуйте, потихоньку осваиваю С# нашел задачу : Дан небольшой текст на английском языке.

Частота встречаемости символов в тексте
Привет. Помогите, пожалуйста. Нужно, чтобы программа брала текст из txt файла и подсчитывала.

Частота повторения слов в тексте
Привет всем Помогите пожалуйста с Си: Разработать программу, подсчитывающую частоту повторения.

Решение

Решение

Частота повторения букв в тексте
Доброго дня. Помогите пожалуйста разобраться. Простенькая программка по подсчеты количества букв в.

Частота встречи различных букв в тексте
Ребят, помогите пожалуйста решить вот такую задачку- Задан текст, содержащий не более 255.

В заданном тексте вычислить количество слов в тексте и распечатать их по одному в строку
Всем доброго вечера, заканчиваю практику в университете и осталась последняя задачка, которую надо.

В данном тексте подсчитать количество слов. Слова в тексте отделены пробелами
В данном тексте подсчитать количество слов. Слова в тексте отделены пробелами.

Частота повторений для всех символов в тексте
У меня есть текст, допустим: фывфыв ывфваавв ( на практике тут будет 200 символов ). Мне нужно.

Частота повторений для всех символов в тексте
У меня есть текст, допустим: фывфыв ывфваавв ( на практике тут будет 200 символов ). Мне нужно.

Источник

Мы уже анализировали самые частые слова в тексте, но делали это быстро, на коленке и с помощью Экселя. Теперь подойдём к этому серьёзно и используем дата-сайенс и Python — с ним такой анализ будет проще, быстрее и эффективнее. Заодно научимся делать такое красивое облако самых частых слов — это из первого тома «Войны и мира»:

Что делаем

Сегодня мы проанализируем текст всех томов «Войны и мира» и посмотрим, изменятся ли самые частые слова, как это будет выглядеть в облаке. Интересно, можно ли по таким облакам хотя бы примерно понять общее настроение или содержание текста.

Логика будет простая:

Вместо художественного текста анализировать так можно что угодно: статьи «Кода», записи в дневнике или инструкцию от пылесоса.

Загружаем текст

Мы всё будем делать в редакторе VS Code — он бесплатный, есть окно вывода сообщений и ошибок, а ещё он умеет сразу показывать сгенерированные картинки в отдельном окне.

Также нам понадобятся все тома «Войны и мира»:

Их нужно положить в ту же папку, где будет скрипт.

Создаём новый python-файл, указываем в нём путь к файлу, потом загружаем в переменную и сразу проверяем, получилось или нет. Для этого выводим первые 300 символов текста:

# открываем текстовый файл
f = open('tom1.txt', "r", encoding="utf-8")
# закидываем его содержимое в переменную
text = f.read()
# выводим начало, чтобы убедиться, что всё считалось правильно
print(text[:300])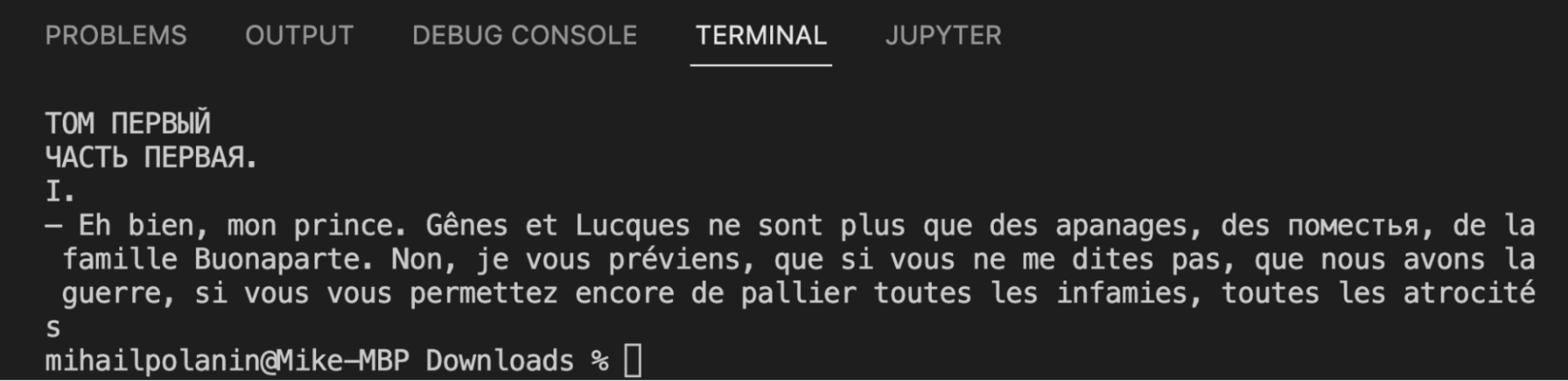

Видно, что файл считался нормально, всё на месте. Ещё сразу становится понятно, что в тексте будет много французского языка — это тоже мы учтём при анализе.

Убираем лишнее

Сейчас в тексте много лишнего, что будет мешать анализу:

Исправим это с помощью встроенного модуля String — в нём уже есть почти вся пунктуация, которую мы дополним несколькими символами:

# переводим символы в нижний регистр, чтобы всё было одинаково
text = text.lower()
# подключаем встроенный модуль работы со строками
import string
# добавляем к стандартным знакам пунктуации кавычки и многоточие
spec_chars = string.punctuation + '«»t—…’'
# очищаем текст от знаков препинания
text = "".join([ch for ch in text if ch not in spec_chars])
# подключаем регулярные выражения
import re
# меняем переносы строк на пробелы
text = re.sub('n', ' ', text)
# убираем из текста цифры
text = "".join([ch for ch in text if ch not in string.digits])
# смотрим на результат
print(text[:300])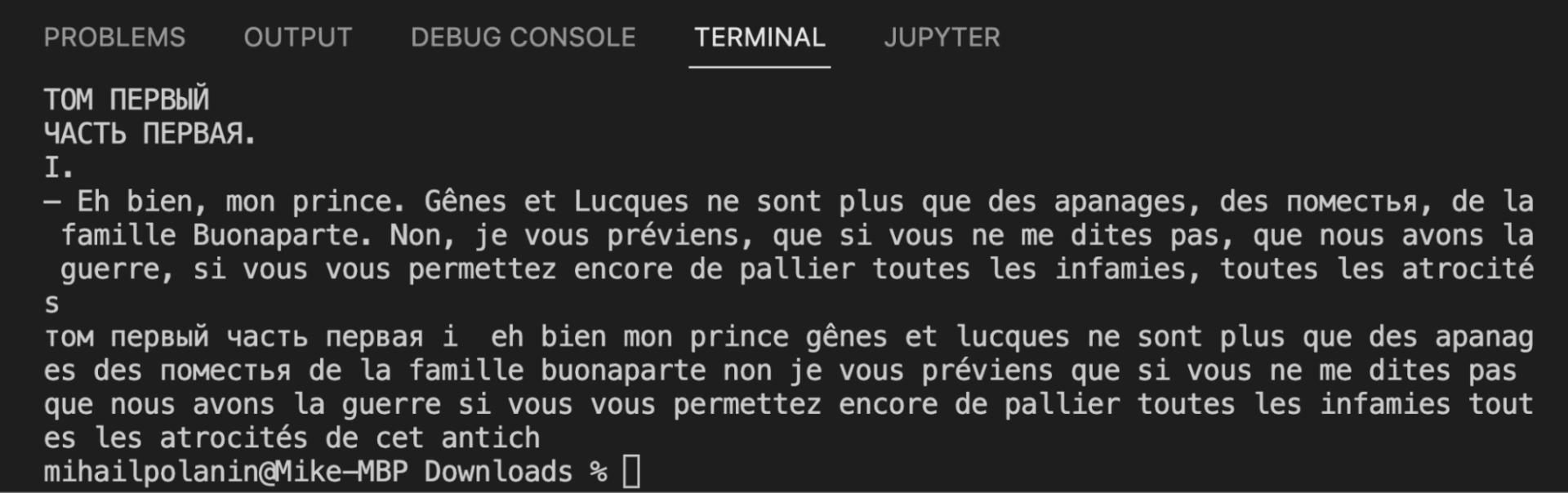

Текст стал однородным: его теперь сложно читать, зато компьютеру будет легко распознать каждое слово. 

Библиотека NLTK и токенизация

Дальше нам понадобится NLTK — мощная библиотека для обработки текста. Технически это даже не одна библиотека, а набор модулей, внутри которых тоже может быть разное, но для простоты назовём это так.

Токенизация — это сегментация, или разделение текста на отдельные компоненты, а токены — это и есть те самые компоненты. Так как мы ищем самые популярные слова, то нам нужно токенизировать на уровне слов. Например, если токенизировать по словам предложение «и швец, и жнец, и на дуде игрец», то токены будут такие: «и», «швец», «жнец», «на», «дуде», «игрец».

Для установки библиотеки используем команду:

pip install nltk

Для установки отдельных модулей, например, word_tokenize, нам понадобится сделать такое:

Теперь найдём первые 5 самых популярных слов в тексте:

# из библиотеки обработки текста подключаем модуль для токенизации слов
from nltk import word_tokenize
# токенизируем текст
text_tokens = word_tokenize(text)
# подключаем библиотеку для работы с текстом
import nltk
# переводим токены в текстовый формат
text = nltk.Text(text_tokens)
# подключаем статистику 
from nltk.probability import FreqDist
# и считаем слова в тексте по популярности
fdist = FreqDist(text)
# выводим первые 5 популярных слов
print(fdist.most_common(5))

Чистим текст от стоп-слов

Стоп-слова в NLTK — это те слова, которые мешают правильно оценить весь текст. К ним относятся:

Чтобы избавиться от них, используем специальный модуль, в котором уже собраны все стоп-слова из разных языков. Сразу добавим туда стоп-слова из французского языка, так как герои романа часто общаются друг с другом по-французски:

# подключаем модуль со стоп-словами
from nltk.corpus import stopwords
# добавляем русские и французские стоп-слова
russian_stopwords = stopwords.words("russian")
russian_stopwords += stopwords.words("french")
# перестраиваем токены, не учитывая стоп-слова
text_tokens = [token.strip() for token in text_tokens if token not in russian_stopwords]
# снова приводим токены к текстовому виду
text = nltk.Text(text_tokens)
# считаем заново частоту слов
fdist_sw = FreqDist(text)
# показываем самые популярные
print(fdist_sw.most_common(10))

Стало лучше, но появилась новая проблема: судя по первой десятке, герои слишком много говорят — «cказал», «сказала», «говорил». Для чистоты эксперимента их тоже можно убрать из текста, поместив их в список стоп-слов. Туда же отнесём «это» и «что»:

# добавляем свои слова в этот список
russian_stopwords.extend(['это', 'чтò','всё','сказал', 'сказала','говорил','говорила'])
# перестраиваем токены, не учитывая стоп-слова
text_tokens = [token.strip() for token in text_tokens if token not in russian_stopwords]
# снова приводим токены к текстовому виду
text = nltk.Text(text_tokens)
# считаем заново частоту слов
fdist_sw = FreqDist(text)
# показываем самые популярные

Рисуем облако слов

У нас всё готово, чтобы вывести слова в виде красивой картинки: чем чаще встречается слово, тем большим шрифтом оно будет написано. Сделаем это с помощью библиотеки wordcloud, которую нужно будет установить отдельно:

pip install wordcloud

# подключаем библиотеку для создания облака слов
from wordcloud import WordCloud
# и графический модуль, с помощью которого нарисуем это облако
import matplotlib.pyplot as plt
# переводим всё в текстовый формат
text_raw = " ".join(text)
# готовим размер картинки
wordcloud = WordCloud(width=1600, height=800).generate(text_raw)
plt.figure( figsize=(20,10), facecolor='k')
# добавляем туда облако слов
plt.imshow(wordcloud)
# выключаем оси и подписи
plt.axis("off")
# убираем рамку вокруг
plt.tight_layout(pad=0)
# выводим картинку на экран
plt.show()

Точно так же получаем картинки для второго, третьего и четвёртого тома — просто меняем название файла в первой команде скрипта и запускаем код:

Что с этим можно сделать

Вот несколько идей:

Что-то из этого мы сделаем в будущем. Или это вы сделаете сами, потому что пойдёте заниматься дата-сайенсом впереди нас.

Относительная частота.
Статистическая вероятность

• Краткая теория
• Примеры решения задач
• Задачи контрольных и самостоятельных работ

Краткая теория

---

Относительная
частота наряду с вероятностью принадлежит к основным понятиям теории
вероятностей. Относительной частотой события называют отношение числа
испытаний, в которых событие появилось, к общему числу фактически произведенных
испытаний.

Таким
образом, относительная частота события

 определяется формулой:

где

 – число появления события

 – общее число испытаний

Сопоставляя
определения вероятности и относительной частоты, заключаем: определение
вероятности не требует, чтобы испытания производились в действительности;
определение же относительной частоты предполагает, что испытания были
произведены фактически. Другими словами, вероятность вычисляют до опыта, а относительную
частоту – после опыта.

Длительные
наблюдения показали, что если в одинаковых условиях производят опыты, в каждом
из которых число испытаний достаточно велико, то относительная частота
обнаруживает свойство устойчивости. Это свойство состоит в том, что в различных
опытах относительная частота изменяется мало (тем меньше, чем больше
произведено испытаний), колеблясь около некоторого постоянного числа.
Оказалось, что это постоянное число есть вероятность появления события.

Таким
образом, если опытным путем установлена относительная частота, то полученное
число можно принять за приближенное значение вероятности.

Классическое
определение вероятности предполагает, что число элементарных исходов испытания
конечно. На практике же весьма часто встречаются испытания, число возможных
исходов которых бесконечно. В таких случаях классическое определение
неприменимо.

По этой
причине наряду с классическим определением вероятности используют и другие
определения, в частности статистическое определение: в качестве статистической
вероятности события принимают относительную частоту или число, близкое к ней.
Например, если в результате достаточно большого числа испытаний оказалось, что
относительная частота весьма близка числу 0,4, то это число можно принять за
статистическую вероятность события.

Для
существования статистической вероятности события

 требуется:

а)
возможность, хотя бы принципиально, производить неограниченное число испытаний,
в каждом из которых событие А наступает или не наступает;

б)
устойчивость относительных частот появления

 в различных сериях достаточно большого числа
испытаний.

Смежные темы решебника:

• Классическое определение вероятности
• Геометрическое определение вероятности

Примеры решения задач

---

Пример 1

Игральный
кубик подброшен 60 раз, при этом шестерка появилась 10 раз. Какова относительная
частота появления шестерки?

Решение

Из
условия задачи следует, что

,

, поэтому

Ответ: 

---

Пример 2

При
стрельбе по мишени относительная частота попаданий

. Найти число попаданий при
40 выстрелах.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Из
формулы

следует,
что

.

Так как

,

, то искомое число
попаданий:

Ответ:

---

Пример 3

 Контролер, проверяя качество 400 изделий
установил, что 20 из них относятся ко второму сорту, а остальные – к первому.
Найти относительная частоту изделий первого сорта, относительную частоту
изделий второго сорта.

Решение

Прежде
всего, найдем число изделий первого сорта:

Относительная
частота изделий 1-го сорта:

Аналогично
находим относительную частоту изделий второго сорта:

Ответ:

Задачи контрольных и самостоятельных работ

---

Задача 1

Найдите частоту появления простых
чисел в следующих отрезках натурального ряда: а) от 21 до 40; б) от 41 до 50;
в) от 51 до 70.

---

Задача 2

Отдел технического контроля
обнаружил 10 нестандартных изделий в партии из 1000 изделий. Найдите частоту
изготовления бракованных изделий.

---

Задача 3

Многолетними
наблюдениями установлено, что в некоторой области ежегодно в среднем в тридцати
хозяйствах из каждых ста среднегодовой удой молока от одной коровы составляет
4100-4300 кг. Какова вероятность того, что в текущем году в одном из хозяйств
этой области, отобранном случайным образом, будет получен такой среднегодовой
удой?

---

Задача 4

Для выяснения качества семян было
отобрано и высеяно в лабораторных условиях 100 штук. 95 семян дали нормальный
всход. Какова частота нормального всхода семян?

---

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 5

Для
проведения исследований на некотором поле взяли случайную выборку из 200
колосьев пшеницы. Относительная частота колосьев, имеющих по 12 колосков в
колосе, оказалось равной 0,123, а по 18 колосков – 0,05. Найти для этой выборки
количество колосьев, имеющих по 12 и 18 колосков.

---

Задача 6

Найдите частоту появления цифры при
100 подбрасываниях симметричной монеты. (Опыт проводите самостоятельно).

---

Задача 7

Найдите частоту пятибуквенных слов в
любом газетном тексте.

---

Задача 8

Путем опроса всех студентов Вашего
курса определите частоту дней рождения, попадающих на каждый месяц года.

---

Задача 9

За лето на Черноморском побережье
было 67 солнечных дней. Какова частота солнечных дней на побережье за лето?
Частота пасмурных дней?

---

Задача 10

Найдите частоту появления шестерки
при 90 подбрасываниях игрального кубика.

• Краткая теория
• Примеры решения задач
• Задачи контрольных и самостоятельных работ