Построение полигона, гистограммы, кумуляты, огивы
Для наглядности строят различные графики статистического
распределения, и, в частности, полигон и гистограмму.
- Полигон
- Гистограмма
- Кумулята и огива
Полигон
Полигоном частот называют
ломаную, отрезки которой соединяют точки
. Для построения полигона частот на оси
абсцисс откладывают варианты
, а на оси ординат – соответствующие им
частоты
. Такие точки
соединяют
отрезками прямых и получают полигон частот.
Полигоном относительных
частот называют ломаную, отрезки которой соединяют
точки
. Для построения полигона относительных
частот на оси абсцисс откладывают варианты
, а на оси ординат – соответствующие им
относительные частоты (частости)
. Такие точки
соединяют
отрезками прямых и получают полигон частот.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Пример 1
Построить полигон частот и
полигон относительных частот (частостей):
Решение
Вычислим относительные
частоты (частости):
Полигон частот
Полигон относительных частот
В случае интервального ряда для
построения полигона в качестве
берутся середины интервалов.
Гистограмма
В случае интервального
статистического распределения целесообразно построить гистограмму.
Гистограммой частот
называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых
служат частичные интервалы длиною
, а высоты (в случае равных интервалов) должны
быть пропорциональны частотам. При построении гистограммы с неравными
интервалами по оси ординат наносят не частоты, а плотность частоты
. Это необходимо сделать для устранения
влияния величины интервала на распределение и иметь возможность сравнивать
частоты.
В случае построения
гистограммы относительных частот (гистограммы частостей)
высоты в случае равных интегралов должны быть пропорциональны относительной
частоте
, а в случае неравных интервалов высота
равна плотности относительной частоты
.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Пример 2
Построить гистограмму
частот и относительных частот (частостей)
Гистограмма частот
Гистограмма относительных частот
Пример 3
Построить гистограмму
частот (случай неравных интервалов).
Решение
Вычислим плотности
частоты:
Гистограмма частот
Кроме этой задачи на другой странице сайта есть
пример построения полигона и гистограммы на одном графике для интервального вариационного ряда
Кумулята и огива
При помощи кумуляты (кривой сумм) изображается ряд накопленных частот.
Накопленные частоты определяются путём последовательного суммирования частот по
группам и показывают, сколько единиц совокупности имеют значения признака не больше,
чем рассматриваемое значение. При построении кумуляты
интервального вариационного ряда по оси абсцисс откладываются варианты ряда, а
по оси ординат накопленные частоты, которые наносят на поле в виде
перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти
перпендикуляры соединяют и получают ломаную линию, т.е. кумуляту.
Если при графическом
изображении вариационного ряда в виде кумуляты оси
поменять местами, то получим огиву. То есть огива строится аналогично кумуляте с той
лишь разницей, что накопленные частоты помещают на оси абсцисс, а значения
признака — на оси ординат.
Пример 4
Построить кумулятивную
кривую:
Решение
Вычислим накопленные
частоты:
Кумулятивная кривая
Загрузить PDF
Загрузить PDF
С абсолютной частотой все довольно просто: она определяет, сколько раз конкретное число содержится в имеющемся наборе данных (объектов или значений). А вот относительная частота характеризует отношение количества конкретного числа в наборе данных. Другими словами, относительная частота – это отношение количества определенного числа к общему количеству чисел в наборе данных. Имейте в виду, что вычислить относительную частоту достаточно легко.
-

1
Соберите данные. Если вы решаете математическую задачу, в ее условии должен быть дан набор данных (чисел). В противном случае проведите эксперимент или исследование и соберите необходимые данные. Подумайте, в какой форме записать исходные данные.
- Например, нужно собрать данные о возрасте людей, которые посмотрели определенный фильм. Конечно, можно записать точный возраст каждого человека, но в этом случае вы получите довольно большой набор данных с 60-70 числами в пределах от 10 до 70 или 80. Поэтому лучше сгруппировать данные по категориям, таким как «Моложе 20», «20-29», «30-39» «40-49», «50-59» и «Старше 60». Получится упорядоченный набор данных с шестью группами чисел.
- Другой пример: врач собирает данные о температуре пациентов в определенный день. Если записать округленные числа, например, 37, 38, 39, то результат будет не слишком точным, поэтому здесь данные нужно представить в виде десятичных дробей.
-

2
Упорядочьте данные. Когда вы соберете данные, у вас, скорее всего, получится хаотичный набор чисел, например, такой: 1, 2, 5, 4, 6, 4, 3, 7, 1, 5, 6, 5, 3, 4, 5, 1. Такая запись кажется практически бессмысленной и с ней сложно работать. Поэтому упорядочьте числа по возрастанию (от меньшего к большему), например, так: 1,1,1,2,3,3,4,4,4,5,5,5,5,6,6,7.[1]
- Упорядочивая данные, будьте внимательны, чтобы не пропустить ни одного числа. Посчитайте общее количество чисел в наборе данных, чтобы убедиться, что вы записали все числа.
-

3
Создайте таблицу с данными. Собранные данные можно организовать в виде таблицы. Такая таблица будет включать три столбца и использоваться для вычисления относительной частоты. Столбцы обозначьте следующим образом:[2]
Реклама
-

1
Найдите количество чисел в наборе данных. Относительная частота характеризует, сколько раз конкретное число содержится в имеющемся наборе данных по отношению к общему количеству чисел. Чтобы найти относительную частоту, нужно посчитать общее количество чисел в наборе данных. Общее количество чисел станет знаменателем дроби, с помощью которой будет вычислена относительная частота.[3]
- В нашем примере набор данных содержит 16 чисел.
-

2
Найдите количество определенного числа. То есть посчитайте, сколько раз конкретное число встречается в наборе данных. Это можно сделать как для одного числа, так и для всех чисел из набора данных.[4]
- Например, в нашем примере число
встречается в наборе данных три раза.
- Например, в нашем примере число
-

3
Разделите количество конкретного числа на общее количество чисел. Так вы найдете относительную частоту для определенного числа. Вычисление можно представить в виде дроби или воспользоваться калькулятором или электронной таблицей, чтобы разделить два числа.[5]
Реклама
-

1
Результаты вычислений запишите в созданную ранее таблицу. Она позволит представить результаты в наглядной форме. По мере вычисления относительной частоты результаты записывайте в таблицу напротив соответствующего числа. Как правило, значение относительной частоты можно округлить до второго знака после десятичной запятой, но это на ваше усмотрение (в зависимости от требований задачи или исследования). Помните, что округленный результат не равен точному ответу.[6]
- В нашем примере таблица относительных частот будет выглядеть следующим образом:
- x : n(x) : P(x)
- 1 : 3 : 0,19
- 2 : 1 : 0,06
- 3 : 2 : 0,13
- 4 : 3 : 0,19
- 5 : 4 : 0,25
- 6 : 2 : 0,13
- 7 : 1 : 0,06
- Итого : 16 : 1,01
-

2
Представьте числа (элементы), которых нет в наборе данных. Иногда представление чисел с нулевой частотой так же важно, как и представление чисел с ненулевой частотой. Обратите внимание на собранные данные; если между данными имеются пробелы, их нужно заполнить нулями.
- В нашем примере набор данных включает все числа от 1 до 7. Но предположим, что числа 3 нет в наборе. Возможно, это немаловажный факт, поэтому нужно записать, что относительная частота числа 3 равна 0.
-

3
Выразите результаты в процентах. Иногда результаты вычислений нужно преобразовать из десятичных дробей в проценты. Это общепринятая практика, потому что относительная частота характеризует процент случаев появления определенного числа в наборе данных. Чтобы преобразовать десятичную дробь в проценты, нужно десятичную запятую передвинуть на две позиции вправо и приписать символ процента.
- Например, десятичная дробь 0,13 равна 13%.
- Десятичная дробь 0,06 равна 6% (обратите внимание, что перед 6 стоит 0).
Реклама
Советы
- Относительная частота характеризует наличие или возникновение определенного события в наборе событий.
- Если сложить относительные частоты всех чисел из набора данных, вы получите единицу. Помните, что при сложении округленных результатов сумма не будет равна 1,0.
- Если набор данных слишком большой, чтобы обработать его вручную, воспользуйтесь программой MS Excel или MATLAB; это позволит избежать ошибок в процессе вычисления.
Реклама
Источники
Об этой статье
Эту страницу просматривали 144 126 раз.
Была ли эта статья полезной?
§ 2. Введение в визуализацию данных
Как правило, использование списков данных – не самый лучший способ
представить данные в вашей работе потому что мы не можем получить много
информации о них просто взглянув на список. Есть и более удобные способы
и в этой статье мы рассмотрим 3 из них на примере следующей выборки:
30 студентов СПбГАУ набрали на интернет-тестировании следующее
количество баллов:
86
80
25
77
73
76
100
90
69
93
90
83
70
73
73
70
90
83
71
95
40
58
68
69
100
78
87
97
92
74
Листостебельная диаграмма
Одним из простейших способов как-то визуализировать данные являются
листостебельные диаграммы (stem and leaf diagrams). Для нашего
примера мы можем построить такую диаграмму:
2
5
3
4
0
5
8
6
9
8
9
7
7
3
6
0
3
3
0
1
8
4
8
6
0
3
3
7
9
0
3
0
0
5
7
2
10
0
0
Эта диаграмма состоит из стебля – чисел, стоящих слева от
вертикальной линии, которые представляют собой десятки и
листьев – соответствующих чисел справа от линии, которые являются
единицами. В общем случае, стебель строят из редко меняющихся разрядов
(десятков в нашем случае), а листья – из тех разрядов, которые меняются
часто (в нашем случае это единицы). Из такой диаграммы мы сможем быстро
получить некую информацию, например, мы видим что 2 студента набрали
максимальное количество баллов, а 3 написали тест меньше, чем на 60
баллов.
Мы также можем построить
сортированную листостебельную диаграмму (sorted stem and leaf diagram)
– она строится точно так же как и обычная, но её листья отсортированны в
проядке возрастания. Для нашего примера:
2
5
3
4
0
5
8
6
8
9
9
7
0
0
1
3
3
3
4
6
7
8
8
0
3
3
6
7
9
0
0
0
2
3
5
7
10
0
0
Такие диаграммы могут быть довольно гибкими: например мы можем разбить
элементы стебля на более мелкие диапазоны. Так, разобьём значение 80 на
два (80-84 и 85-89):
8
0
3
3
8
6
7
Как построить листостебельную диаграмму по шагам:
- Определите часто и редко меняющиеся разряды в ваших данных
- Выпишите редко меняющиеся разряды слева от линии
- Выпишите часто меняющиеся разряды справа от линии
Гистограмма частот
Листостебельная диаграмма непрактична для большой выборки, поэтому можно
использовать
гистограмму частот (frequency histogram). Сначала мы выделяем
группы каких-либо значений, например значения из примера выше мы можем
сгруппировать так:
группа
0
10
20
30
40
50
60
70
80
90
100
значения
0-9
10-19
20-29
30-39
40-49
50-59
60-69
70-79
80-89
90-99
100
Затем подсчитываем частоту для каждой группы (то есть строим таблицу
частот для групп):
x
0
10
20
30
40
50
60
70
80
90
100
f
0
0
1
0
1
1
3
10
5
7
2
И строим диаграмму частот, отмечая группы по оси
x
, а их частоты – по оси
y
:
Этот способ может быть применён к любому количественному набору данных.
Вы можете создавать группы на своё усмотрение, например, разделить
группу 80 на две: 80 и 85.
Как построить гистограмму частот по шагам:
- Сгруппируйте данные
- Постройте таблицу частот для групп
-
Постройте гистограмму, отметив по оси
x
группы, а по оси
y
частоты
Гистограмма относительных частот
До этого момента мы работали с
абсолютными частотами (absolute frequency) то есть количеством
вхождений элемента в набор данных (в случае с частотами группы –
количеством значений, входящих в группу), но мы также можем работать и с
относительными частотами.
Относительная частота (relative frequency),
ω
– отношение частоты элемента к размеру выборки или генеральной
совокупности
Мы можем построить таблицу относительных частот для нашего примера:
x
0
10
20
30
40
50
60
70
80
90
100
ω
0
0
0.033
0
0.033
0.033
0.01
0.333
0.167
0.233
0.067
И строим гистограмму, на этот раз отмечая по оси y уже относительные
частоты:
Как вы можете заметить, пропорции столбиков и общий вид гистограммы не
отличается от гистограммы абсолютных частот – изменяются лишь числа на
оси
y
.
Тем не менее, гистограмма относительных частот позволяет нам
моментально оценить какую часть данных занимает та или иная группа.
Также как и при построении гистограммы частот, при построении
гистограммы относительных частот выбор количества групп обычно зависит
от размера выборки или генеральной совокупности. Чем больше размер, тем
больше групп мы можем выделить.
Как построить гистограмму относительных частот по шагам:
- Сгруппируйте данные
- Постройте таблицу частот для групп
- Постройте таблицу относительных частот для групп
-
Постройте гистограмму, отметив по оси
x
группы, а по оси
y
– относительные частоты
Нормальное распределение: понимание гистограмм и вероятностей
Добавлено 14 августа 2020 в 19:41
В данной статье мы продолжаем исследование нормального распределения, рассматривая концепцию гистограмм и вводя функцию массы вероятности.
Данная статья является частью серии статей о статистике в электротехнике, которую мы начали с обсуждения статистического анализа и описательной статистики. Затем мы исследовали три описательных статистических показателя с точки зрения применения в обработке сигналов.
Затем мы коснулись стандартного отклонения (в частности, определения компенсации размера выборки при вычислении стандартного отклонения и понимания взаимосвязи между стандартным отклонением и среднеквадратичным значением).
В прошлой статье мы представили нормальное распределение в электротехнике, заложив основу для нашего текущего обсуждения: понимание вероятностей в измеренных данных.
Понимание гистограмм
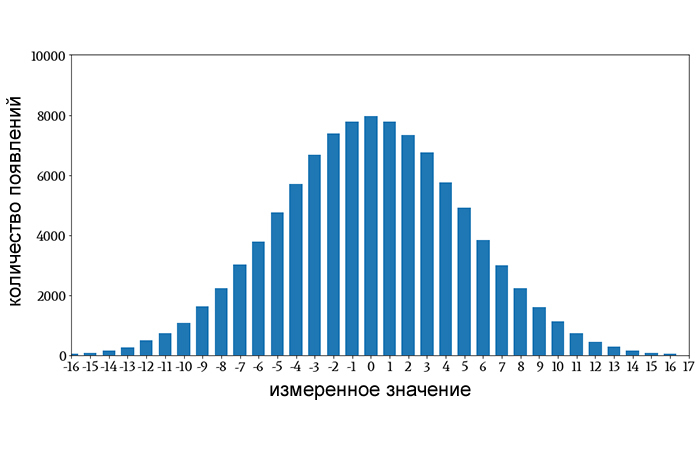
В предыдущей статье мы начали обсуждение нормального распределения, обратившись к форме этой гистограммы:
Я думаю, что большинство людей, работающих в области науки или техники, хотя бы смутно знакомы с гистограммами, но давайте сделаем шаг назад.
Что такое гистограмма?
Гистограммы – это визуальные представления 1) значений, присутствующих в наборе данных, и 2) частоты появления этих значений. Показанная выше гистограмма может представлять множество различных типов информации.
Представим, что она представляет собой распределение значений, полученных нами при измерении разницы, округленной до ближайшего милливольта, между номинальным и фактическим выходным напряжением линейного стабилизатора, который подвергался различным температурам и условиям эксплуатации. Так, например, примерно 8000 измерений показали разницу в 0 мВ между номинальным и фактическим выходными напряжениями, а примерно 1000 измерений показали разницу в 10 мВ.
Гистограммы – чрезвычайно эффективный способ обобщения больших объемов данных. Взглянув на гистограмму выше, мы можем быстро найти частоту отдельных значений в наборе данных и определить тенденции или закономерности, которые помогут нам понять взаимосвязь между измеренным значением и частотой.
Гистограммы с интервалами
Когда набор данных содержит так много разных значений, что мы не можем удобно связать их с отдельными столбцами гистограммы, мы используем объединение в интервалы (биннинг). То есть мы определяем диапазон значений как интервал, группируем результаты измерений в эти интервалы и создаем по одному столбцу для каждого интервала.
Следующая гистограмма, которая была сгенерирована из нормально распределенных данных со средним значением 0 и стандартным отклонением 0,6, использует интервалы вместо отдельных значений:
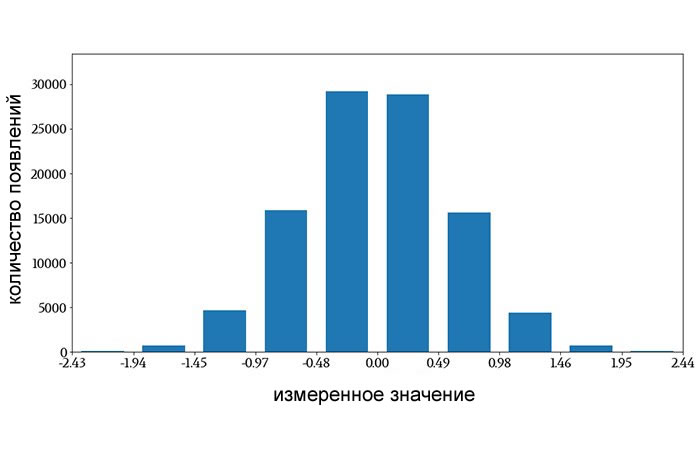
Горизонтальная ось разделена на десять интервалов одинаковой ширины, и каждому интервалу назначен один столбец. Все результаты измерений, попадающие в числовой интервал, влияют на высоту соответствующего столбца (метки на горизонтальной оси показывают, что интервалы не одинаковой ширины, но это просто потому, что значения меток округлены).
Гистограммы и вероятность
В некоторых ситуациях гистограмма не дает нужной нам информации. Мы можем посмотреть на гистограмму и легко определить частоту измеренного значения, но не можем легко определить вероятность измеренного значения.
Например, если я посмотрю на первую гистограмму, я знаю, что примерно 8000 измерений показали разницу в 0 В между номинальным и фактическим напряжениями стабилизатора, но я не знаю, какова вероятность того, что результат случайно выбранного измерения или нового измерения сообщит о разнице в 0 В.
Это серьезное ограничение, потому что вероятность отвечает на чрезвычайно распространенный вопрос: каковы шансы, что…?
Каковы шансы, что у моего линейного стабилизатора погрешность выходного напряжения будет менее 2 мВ? Какова вероятность того, что частота битовых ошибок моего канала передачи данных будет выше 10-3? Какова вероятность того, что из-за шума мой входной сигнал превысит порог срабатывания? И так далее.
Причина этого ограничения заключается в том, что гистограмма просто четко не передает размер выборки, то есть общее количество измерений (теоретически общее количество измерений можно определить, сложив значения всех столбцов гистограммы, но это было бы утомительно и неточно).
Если мы знаем размер выборки, мы можем разделить количество появлений на размер выборки и таким образом определить вероятность. Давайте рассмотрим пример.
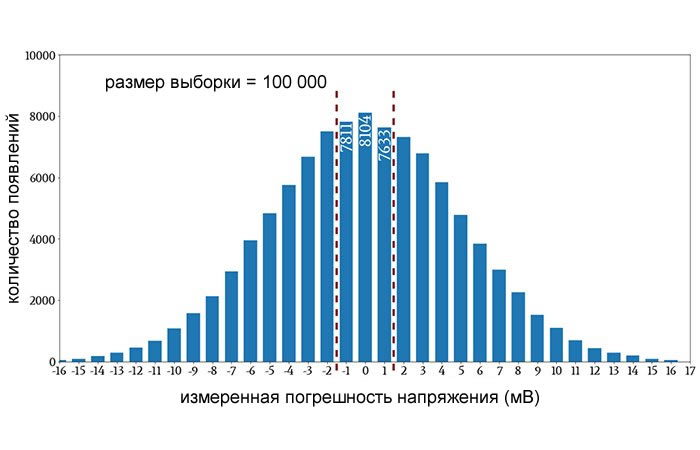
Красные пунктирные линии заключают в себя столбцы, которые указывают на погрешности напряжения менее 2 мВ, а числа, написанные внутри столбцов, указывают точное количество появлений этих трех значений погрешности напряжения. Сумма этих трех чисел составляет 23 548. Таким образом, на основе этого примера по сбору данных вероятность получения погрешности менее 2 мВ составляет 23 548/100 000 ≈ 23,5%.
Функция массы вероятности
Если наша основная цель при создании гистограммы – передать информацию о вероятности, мы можем изменить всю гистограмму, разделив все счетчики вхождений на размер выборки.
Полученный график является аппроксимацией функции массы вероятности. Например:
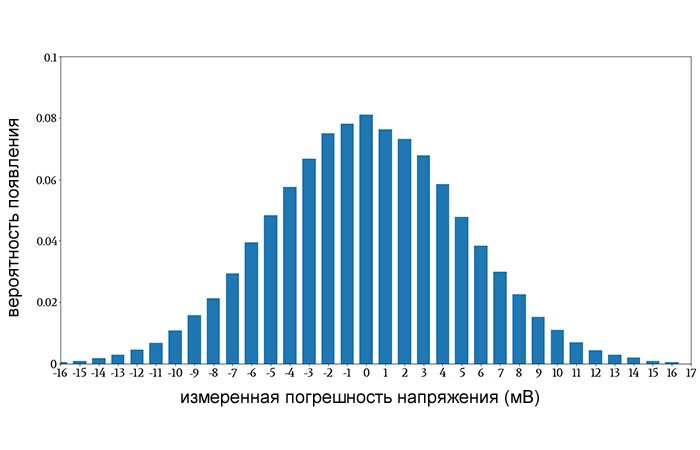
Всё, что мы на самом деле выполнили, это изменили числа на вертикальной оси. Тем не менее, теперь мы можем посмотреть на отдельное значение или на группу значений и легко определить вероятность появления.
Хочу прояснить следующую деталь: я сказал, что мы аппроксимируем функцию массы вероятности, когда берем гистограмму и делим значения на размер выборки. Истинная функция массы вероятности представляет собой идеализированное распределение вероятностей, что означает, что для этого потребуется бесконечное количество измерений.
Таким образом, когда мы работаем с реалистичными размерами выборки, гистограмма, созданная на основе измеренных данных, дает нам только приближение функции массы вероятности.
Масса вероятности против плотности вероятности
Стоит подчеркнуть, что функция массы вероятности является дискретным эквивалентом функции плотности вероятности (о которой мы говорили в предыдущей статье).
В то время как функция плотности вероятности является непрерывной и предоставляет значения вероятности, когда мы интегрируем функцию в указанном диапазоне, функция массы вероятности дискретизируется и дает нам вероятность, связанную с конкретным значением или интервалом.
Эти две функции передают одну и ту же общую статистическую информацию о переменной или о сигнале, но делают это по-разному.
Обратите внимание на разницу между двумя названиями: вертикальная ось функции массы вероятности указывает массу вероятности, как количественное значение. Вертикальная ось функции плотности вероятности указывает плотность вероятности относительно горизонтальной оси; чтобы определить количественное значение вероятности, мы должны интегрировать эту плотность по горизонтальной оси.
Заключение
Мы рассмотрели функции массы и плотности вероятности, и теперь мы готовы изучить кумулятивную функцию распределения и исследовать вероятности нормального распределения с точки зрения стандартного отклонения. Об этом мы поговорим в следующей статье.
Теги
ГистограммаМасса вероятностиНормальное распределение / Гауссово распределениеПлотность вероятностиСтатистикаФункция массы вероятностиФункция плотности вероятности
Гистограмма
Гистограмма – это способ представления статистических данных в графическом виде – в виде столбчатой диаграммы. Она отображает распределение отдельных измерений параметров изделия или процесса. Иногда ее называют частотным распределением, так как гистограмма показывает частоту появления измеренных значений параметров объекта.
Высота каждого столбца указывает на частоту появления значений параметров в выбранном диапазоне, а количество столбцов – на число выбранных диапазонов.
Важное преимущество гистограммы заключается в том, что она позволяет наглядно представить тенденции изменения измеряемых параметров качества объекта и зрительно оценить закон их распределения. Кроме того, гистограмма дает возможность быстро определить центр, разброс и форму распределения случайной величины. Строится гистограмма, как правило, для интервального изменения значений измеряемого параметра.
Порядок построения гистограммы следующий:
1. Собираются статистические данные – результаты измерений параметра объекта. Для того, чтобы гистограмма позволяла оценить вид распределения случайной величины предпочтительно иметь не менее тридцати результатов измерений.
2. Выявляется наибольшее и наименьшее значение показателя среди полученных результатов измерений.
3. Определяется ширина диапазона значений показателя – из наибольшего значения показателя вычитается наименьшее значение.
4. Выбирается надлежащее число интервалов, в пределах которых необходимо сгруппировать результаты измерений.
5. Устанавливаются границы интервалов. Границы интервалов необходимо установить так, чтобы значения данных не попадали ни на одну из границ интервала. Например, если были выбраны интервалы с границами от 0,5 до 5,5 от 5,5 до 10,5 и т.д. то значение данных 5,5 будет попадать как в первый, так и во второй интервал. Чтобы избежать этой проблемы можно изменить интервалы от 0,51 до 5,50 от 5,51 до 10,50 и так далее, таким образом ни одно значение данных не попадет на границу интервала.
6. Подсчитывается число попаданий значений результатов измерений в каждый из интервалов.
7. Строится гистограмма – на оси абсцисс (горизонтальной оси) отмечаются интервалы, а на оси ординат (вертикальной оси) отмечается частота попаданий результатов измерений в каждый интервал. Интервалы можно устанавливать в натуральных единицах (если позволяет масштаб), т.е. в тех единицах, в которых проводились измерения, либо каждому интервалу можно присвоить порядковый номер и отмечать на оси абсцисс номера интервалов
1. Анализ продаж, выручки или поставок по различным срезам:
● по периодам времени;
● по регионам;
● по филиалам/подразделениям;
● по товарам/услугам.
2. Маркетинговый анализ:
● эффективность коммуникативных акций по каналам;
● аналитика затрат на рекламу;
● количество проведенных активностей и их полезность.
3. Финансовый анализ:
● планы и динамика по выручке и прибыли;
● учет приходов и расходов денежных средств;
● количество денег на счетах.
4. Анализ производственных процессов:
● отслеживание складских запасов;
● эффективность использования мощностей;
● учет отгрузок и поставок.
5. Статистический и социодемографический анализ, а также многое другое.
Интервальные ряды данных изображают с помощью гистограммы.
Гистограмма представляет собой ступенчатую фигуру, составленную из сомкнутых прямоугольников. Основание каждого прямоугольника равно длине интервала, а высота – частоте или относительной частоте.
Таким образом, в гистограмме, в отличие от обычной столбчатой диаграммы, основания прямоугольника выбираются не произвольно, а строго определены длиной интервала.
Вот, к примеру, у нас есть следующие данные о росте игроков, вызванных в сборную:
|
Рост |
175-180 |
181-185 |
186-195 |
196-200 |
|
Количество |
14 |
9 |
7 |
1 |
Итак, нам дана частота (количество игроков с соответствующим ростом). Мы можем дополнить табличку, рассчитав относительную частоту:
|
Рост |
175-180 |
181-185 |
186-195 |
196-200 |
|
Количество |
14 |
9 |
7 |
1 |
|
Относительная частота |
45,2% |
29,0% |
22,6% |
3,2% |
Ну вот, теперь можем строить гистограммы. Сначала построим на основании частоты.
Вот, что получилось: ( строим столбчатую диаграмму)

А теперь на основании данных об относительной частоте:
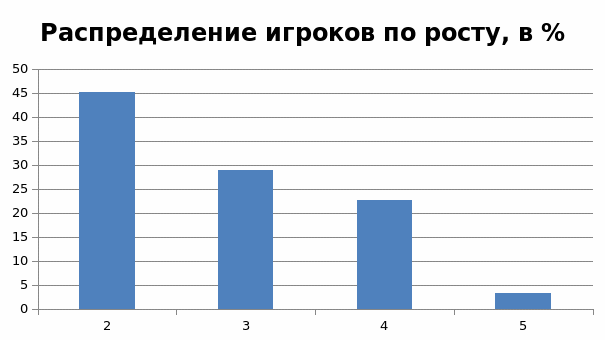
Пример. На выставку по инновационным технологиям приехали представители 50 компаний. На диаграмме показано распределение этих компаний по количеству персонала.
По горизонтали представлено количество сотрудников в компании, по вертикали – количество компаний, имеющих данное число сотрудников.

Какой процент составляют компании с общим числом сотрудников больше 50 человек?
Ответ: 68%.
Этапы построения
Создание любой диаграммы — это не просто дизайнерская работа. Здесь важно не только сделать красиво и аккуратно, но и облегчить восприятие данных. Чтобы результат получился именно таким, весь процесс работы можно разделить на несколько этапов.
Постановка цели
Чтобы решить, как создать и построить гистограмму, надо в первую очередь определить, для чего она строится и что показывает. Если хочется сравнить показатели между собой, то барчарт подойдет лучше остальных, так как можно сразу выделить лидеров и отстающих. Если цель — понять, как показатель изменился за небольшое количество периодов, например, 3-5 дней, месяцев или лет, он также будет наиболее наглядным.
Подготовка данных
Для построения нам нужна таблица с параметрами и значениями, которые будут отражены на графике. К форме и структуре этого документа есть определенные требования, так как цифры будут подвергаться машинной обработке, а система работает по строгому алгоритму.
Поэтому любые диаграммы строятся на так называемых «плоских» таблицах, где в каждой ячейке располагается уникальное значение и отсутствуют любые формы объединения столбцов, строк или ячеек. Иногда аналитики тратят до 80% рабочего времени на подготовку тех данных, что относятся к гистограмме.
Построение графика
Большинство программ имеют опцию автоматического создания визуализации, пошагово мы рассмотрим это ниже. Как правило, для этого необходимо выделить таблицу и выбрать из меню с вариантами визуализаций нужный элемент.
Редактирование результата
Изображение, которое автоматически создает для нас программа, практически всегда требует корректировки. Это тоже достаточно трудозатратный этап, так как необходимо поработать со всеми элементами диаграммы: цветом, подписями, шрифтами, оформлением, легендой и так далее. Подробнее об этом этапе — ниже, в разделе «Редактирование и настройка».
Построение гистограмм с примерами в различных сервисах
Столбчатую диаграмму можно сделать во многих программах, включая простые графические редакторы. Серьезные аналитики обычно используют специализированные платформы вроде Power BI или Tableau, которые позволяют не только строить графики, но и проводить глубинную расширенную аналитику. Мы рассмотрим этапы работы в самых распространенных программах для неспециалистов.
