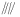Загрузить PDF
Загрузить PDF
С абсолютной частотой все довольно просто: она определяет, сколько раз конкретное число содержится в имеющемся наборе данных (объектов или значений). А вот относительная частота характеризует отношение количества конкретного числа в наборе данных. Другими словами, относительная частота – это отношение количества определенного числа к общему количеству чисел в наборе данных. Имейте в виду, что вычислить относительную частоту достаточно легко.
-

1
Соберите данные. Если вы решаете математическую задачу, в ее условии должен быть дан набор данных (чисел). В противном случае проведите эксперимент или исследование и соберите необходимые данные. Подумайте, в какой форме записать исходные данные.
- Например, нужно собрать данные о возрасте людей, которые посмотрели определенный фильм. Конечно, можно записать точный возраст каждого человека, но в этом случае вы получите довольно большой набор данных с 60-70 числами в пределах от 10 до 70 или 80. Поэтому лучше сгруппировать данные по категориям, таким как «Моложе 20», «20-29», «30-39» «40-49», «50-59» и «Старше 60». Получится упорядоченный набор данных с шестью группами чисел.
- Другой пример: врач собирает данные о температуре пациентов в определенный день. Если записать округленные числа, например, 37, 38, 39, то результат будет не слишком точным, поэтому здесь данные нужно представить в виде десятичных дробей.
-

2
Упорядочьте данные. Когда вы соберете данные, у вас, скорее всего, получится хаотичный набор чисел, например, такой: 1, 2, 5, 4, 6, 4, 3, 7, 1, 5, 6, 5, 3, 4, 5, 1. Такая запись кажется практически бессмысленной и с ней сложно работать. Поэтому упорядочьте числа по возрастанию (от меньшего к большему), например, так: 1,1,1,2,3,3,4,4,4,5,5,5,5,6,6,7.[1]
- Упорядочивая данные, будьте внимательны, чтобы не пропустить ни одного числа. Посчитайте общее количество чисел в наборе данных, чтобы убедиться, что вы записали все числа.
-

3
Создайте таблицу с данными. Собранные данные можно организовать в виде таблицы. Такая таблица будет включать три столбца и использоваться для вычисления относительной частоты. Столбцы обозначьте следующим образом:[2]
Реклама
-

1
Найдите количество чисел в наборе данных. Относительная частота характеризует, сколько раз конкретное число содержится в имеющемся наборе данных по отношению к общему количеству чисел. Чтобы найти относительную частоту, нужно посчитать общее количество чисел в наборе данных. Общее количество чисел станет знаменателем дроби, с помощью которой будет вычислена относительная частота.[3]
- В нашем примере набор данных содержит 16 чисел.
-

2
Найдите количество определенного числа. То есть посчитайте, сколько раз конкретное число встречается в наборе данных. Это можно сделать как для одного числа, так и для всех чисел из набора данных.[4]
- Например, в нашем примере число
встречается в наборе данных три раза.
- Например, в нашем примере число
-

3
Разделите количество конкретного числа на общее количество чисел. Так вы найдете относительную частоту для определенного числа. Вычисление можно представить в виде дроби или воспользоваться калькулятором или электронной таблицей, чтобы разделить два числа.[5]
Реклама
-

1
Результаты вычислений запишите в созданную ранее таблицу. Она позволит представить результаты в наглядной форме. По мере вычисления относительной частоты результаты записывайте в таблицу напротив соответствующего числа. Как правило, значение относительной частоты можно округлить до второго знака после десятичной запятой, но это на ваше усмотрение (в зависимости от требований задачи или исследования). Помните, что округленный результат не равен точному ответу.[6]
- В нашем примере таблица относительных частот будет выглядеть следующим образом:
- x : n(x) : P(x)
- 1 : 3 : 0,19
- 2 : 1 : 0,06
- 3 : 2 : 0,13
- 4 : 3 : 0,19
- 5 : 4 : 0,25
- 6 : 2 : 0,13
- 7 : 1 : 0,06
- Итого : 16 : 1,01
-

2
Представьте числа (элементы), которых нет в наборе данных. Иногда представление чисел с нулевой частотой так же важно, как и представление чисел с ненулевой частотой. Обратите внимание на собранные данные; если между данными имеются пробелы, их нужно заполнить нулями.
- В нашем примере набор данных включает все числа от 1 до 7. Но предположим, что числа 3 нет в наборе. Возможно, это немаловажный факт, поэтому нужно записать, что относительная частота числа 3 равна 0.
-

3
Выразите результаты в процентах. Иногда результаты вычислений нужно преобразовать из десятичных дробей в проценты. Это общепринятая практика, потому что относительная частота характеризует процент случаев появления определенного числа в наборе данных. Чтобы преобразовать десятичную дробь в проценты, нужно десятичную запятую передвинуть на две позиции вправо и приписать символ процента.
- Например, десятичная дробь 0,13 равна 13%.
- Десятичная дробь 0,06 равна 6% (обратите внимание, что перед 6 стоит 0).
Реклама
Советы
- Относительная частота характеризует наличие или возникновение определенного события в наборе событий.
- Если сложить относительные частоты всех чисел из набора данных, вы получите единицу. Помните, что при сложении округленных результатов сумма не будет равна 1,0.
- Если набор данных слишком большой, чтобы обработать его вручную, воспользуйтесь программой MS Excel или MATLAB; это позволит избежать ошибок в процессе вычисления.
Реклама
Источники
Об этой статье
Эту страницу просматривали 144 126 раз.
Была ли эта статья полезной?
Содержание
- Как рассчитать относительную частоту в Excel
- Пример: относительные частоты в Excel
- Функция ЧАСТОТА() — Подсчет ЧИСЛОвых значений в EXCEL
- Синтаксис функции
- Пример
- Функция ЧАСТОТА
- Пример
- Дополнительные сведения
- Частотный анализ по интервалам функцией ЧАСТОТА (FREQUENCY)
- Примеры функции ЧАСТОТА в Excel для расчета частоты повторений
- Пример использования функции ЧАСТОТА в Excel
- Пример определения вероятности используя функцию ЧАСТОТА в Excel
- Как посчитать неповторяющиеся значения в Excel?
- Функция ЧАСТОТА в Excel и особенности ее синтаксиса
Как рассчитать относительную частоту в Excel
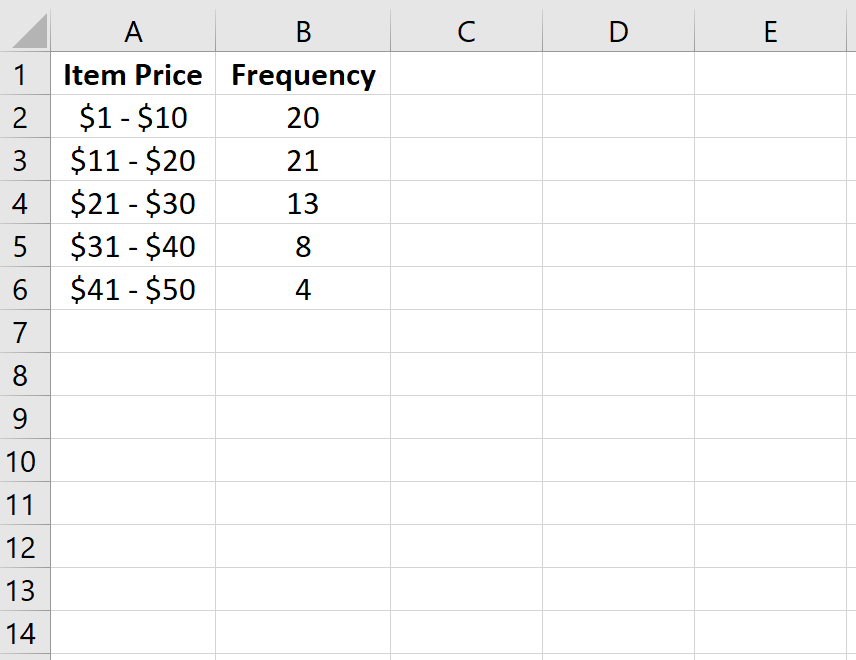
Таблица частот — это таблица, в которой отображается информация о частотах. Частоты просто говорят нам, сколько раз произошло определенное событие.
Например , в следующей таблице показано, сколько товаров было продано магазином в разных ценовых диапазонах за данную неделю:
| Цена товара | Частота | | — | — | | $1 – $10 | 20 | | $11 – $20 | 21 | | 21 – 30 долларов США | 13 | | $31 – $40 | 8 | | $41 — $50 | 4 |
В первом столбце отображается ценовой класс, а во втором столбце — частота этого класса.
Также можно рассчитать относительную частоту для каждого класса, которая представляет собой просто частоту каждого класса в процентах от целого.
| Цена товара | Частота | Относительная частота | | — | — | — | | $1 – $10 | 20 | 0,303 | | $11 – $20 | 21 | 0,318 | | 21 – 30 долларов США | 13 | 0,197 | | $31 – $40 | 8 | 0,121 | | $41 — $50 | 4 | 0,061 |
Всего было продано 66 штук. Таким образом, мы нашли относительную частоту каждого класса, взяв частоту каждого класса и разделив ее на общее количество проданных товаров.
Например, было продано 20 товаров по цене от 1 до 10 долларов. Таким образом, относительная частота класса $1 – $10 составляет 20/66 = 0,303 .
Затем был продан 21 предмет в ценовом диапазоне от 11 до 20 долларов. Таким образом, относительная частота класса $11 – $20 составляет 21/66 = 0,318 .
В следующем примере показано, как найти относительные частоты в Excel.
Пример: относительные частоты в Excel
Сначала мы введем класс и частоту в столбцах A и B:
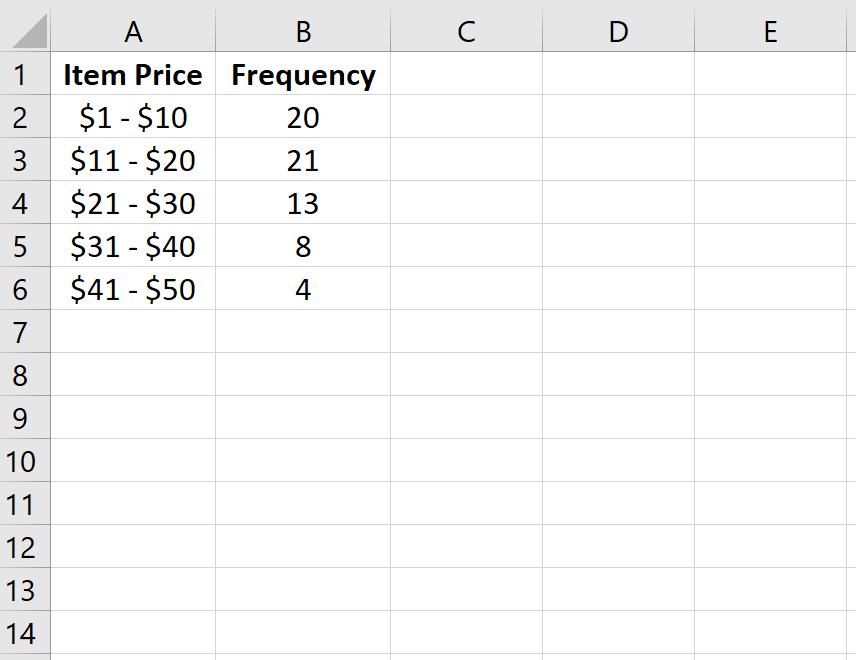
Далее мы рассчитаем относительную частоту каждого класса в столбце C. В столбце D показаны формулы, которые мы использовали:
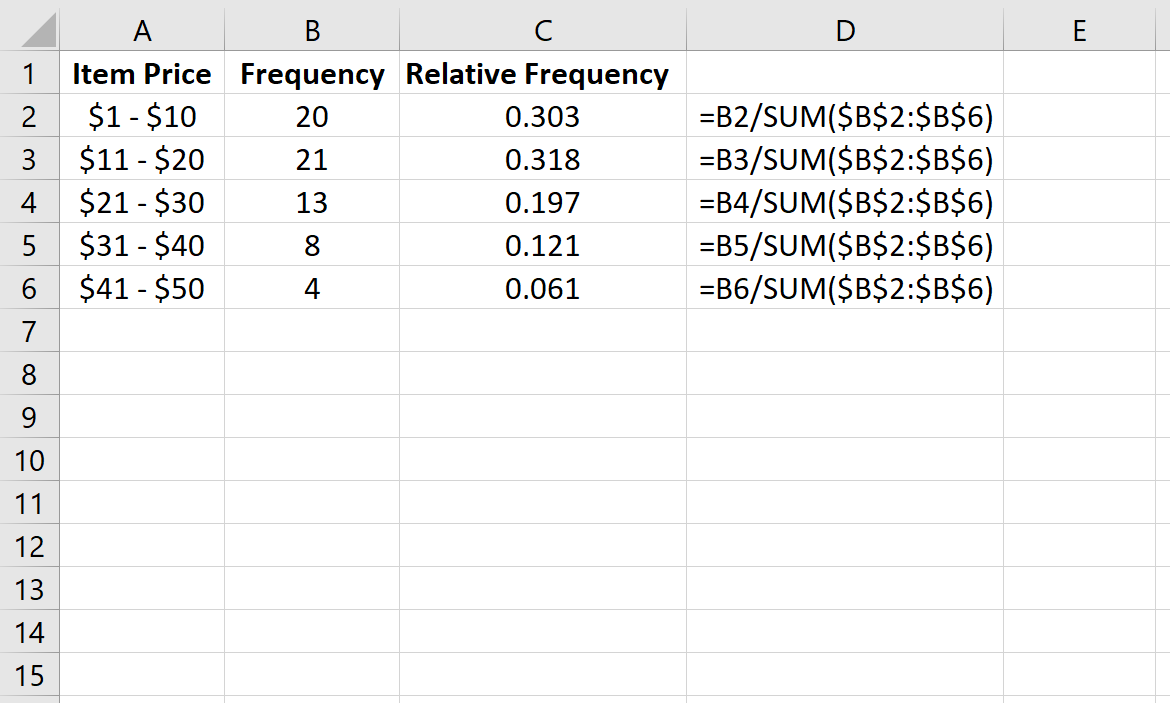
Мы можем проверить правильность наших расчетов, убедившись, что сумма относительных частот равна 1:
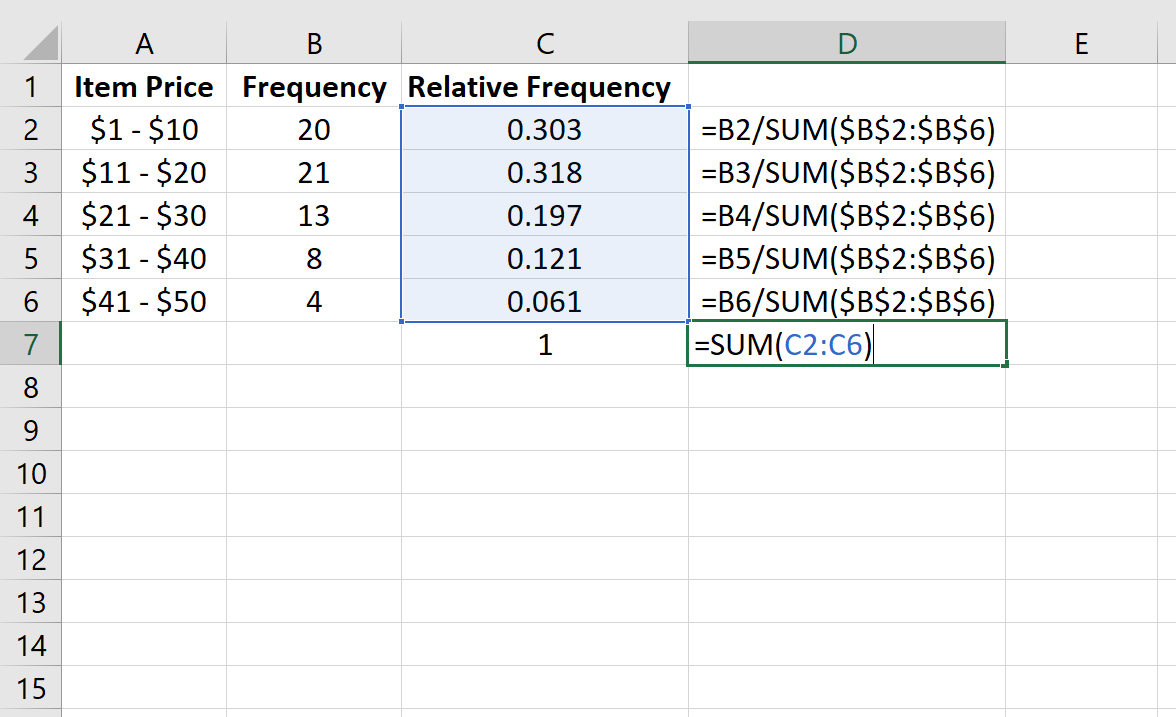
Мы также можем создать гистограмму относительной частоты для визуализации относительных частот.
Просто выделите относительные частоты:

Затем перейдите в группу « Диаграммы » на вкладке « Вставка » и щелкните первый тип диаграммы в « Вставить столбец» или «Гистограмма» :
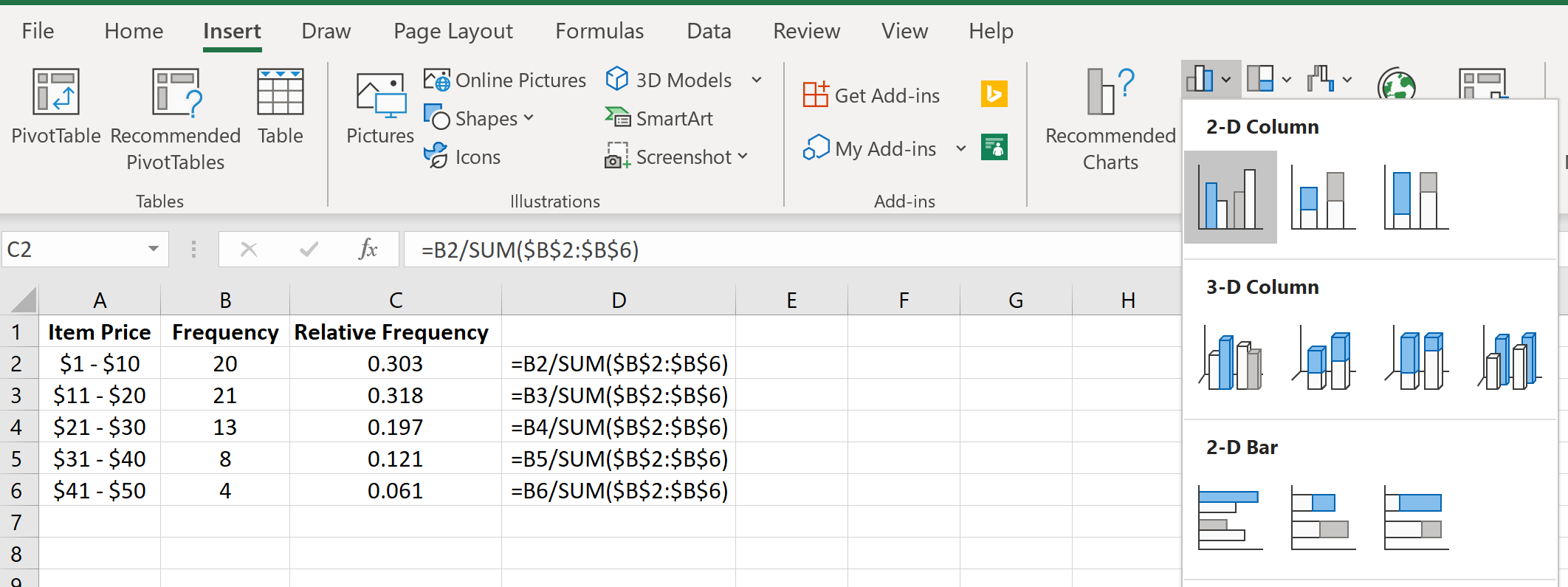
Автоматически появится гистограмма относительной частоты:
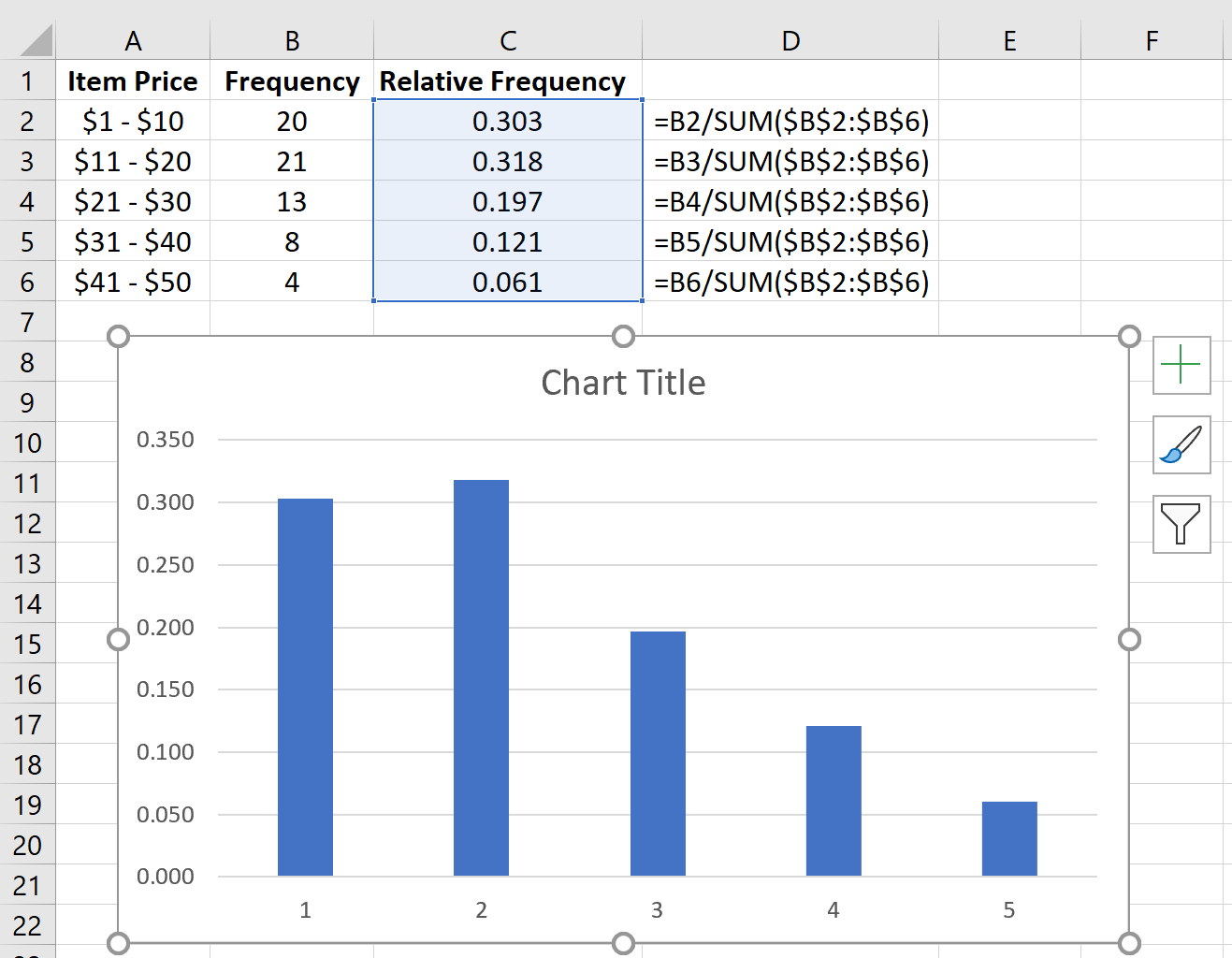
Измените метки оси X, щелкнув правой кнопкой мыши диаграмму и выбрав Выбрать данные.В разделе « Ярлыки горизонтальной (категории) оси » нажмите « Изменить » и введите диапазон ячеек, содержащий цены на товары. Нажмите OK , и новые метки осей появятся автоматически:
Источник
Функция ЧАСТОТА() — Подсчет ЧИСЛОвых значений в EXCEL
history 9 апреля 2013 г.
Функция ЧАСТОТА( ) , английская версия FREQUENCY() , вычисляет частоту попадания значений в заданные пользователем интервалы и возвращает соответствующий массив чисел.
Функцией ЧАСТОТА() можно воспользоваться, например, для подсчета количества результатов тестирования, попадающих в определенные интервалы (См. Файл примера )
Синтаксис функции
ЧАСТОТА ( массив_данных ; массив_интервалов )
Массив_данных — массив или ссылка на множество ЧИСЛОвых данных, для которых вычисляются частоты.
Массив_интервалов — массив или ссылка на множество интервалов, в которые группируются значения аргумента «массив_данных».
Функция ЧАСТОТА() вводится как формула массива после выделения диапазона смежных ячеек, в которые требуется вернуть полученный массив распределения (частот). Т.е. после ввода формулы необходимо вместо нажатия клавиши ENTER нажать сочетание клавиш CTRL+SHIFT+ENTER .
Количество элементов в возвращаемом массиве на единицу больше числа элементов в массиве « массив_интервалов ». Дополнительный элемент в возвращаемом массиве содержит количество значений, превышающих верхнюю границу интервала, содержащего наибольшие значения (см. пример ниже).
Пример
Пусть в диапазоне А2:А101 имеется исходный массив чисел от 1 до 100.
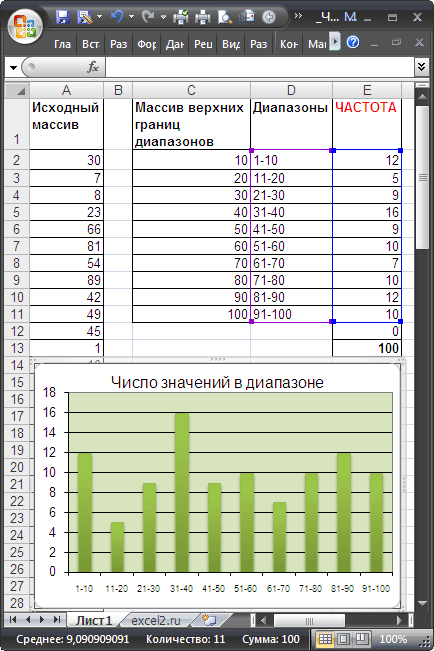
Подсчитаем количество чисел, попадающих в интервалы 1-10; 11-20; . 91-100.
Сформируем столбце С массив верхних границ диапазонов (интервалов). Для наглядности в столбце D сформируем текстовые значения соответствующие границам интервалов (1-10; 11-20; . 91-100).
Для ввода формулы выделим диапазон Е2:Е12 , состоящий из 11 ячеек (на 1 больше, чем число верхних границ интервалов). В Строке формул введем =ЧАСТОТА($A$2:$A$101;$C$2:$C$11) . После ввода формулы необходимо нажать сочетание клавиш CTRL+SHIFT+ENTER . Диапазон Е2:Е12 заполнится значениями:
- в Е2 — будет содержаться количество значений из А2:А101 , которые меньше или равны 10;
- в Е3 — количество значений из А2:А101 , которые меньше или равны 20, но больше 10;
- в Е11 — количество значений из А2:А101 , которые меньше или равны 100, но больше 90;
- в Е12 — количество значений из А2:А101 , которые больше 100 (таких нет, т.к. исходный массив содержит числа от 1 до 100).
Примечание . Функцию ЧАСТОТА() можно заменить формулой = СУММПРОИЗВ(($A$5:$A$104>C5)*($A$5:$A$104 (См. Файл примера )
Источник
Функция ЧАСТОТА
Функция ЧАСТОТА вычисляет частоту ветвей значений в диапазоне значений и возвращает вертикальный массив чисел. Функцией ЧАСТОТА можно воспользоваться, например, для подсчета количества результатов тестирования, попадающих в интервалы результатов. Поскольку данная функция возвращает массив, ее необходимо вводить как формулу массива.
Аргументы функции ЧАСТОТА описаны ниже.
data_array — обязательный аргумент. Массив или ссылка на множество значений, для которых вычисляются частоты. Если аргумент «массив_данных» не содержит значений, функция ЧАСТОТА возвращает массив нулей.
bins_array — обязательный аргумент. Массив или ссылка на множество интервалов, в которые группируются значения аргумента «массив_данных». Если аргумент «массив_интервалов» не содержит значений, функция ЧАСТОТА возвращает количество элементов в аргументе «массив_данных».
Примечание: Если у вас установлена текущая версия Microsoft 365, можно просто ввести формулу в верхней левой ячейке диапазона вывода и нажать клавишу ВВОД, чтобы подтвердить использование формулы динамического массива. Иначе формулу необходимо вводить с использованием прежней версии массива, выбрав диапазон вывода, введя формулу в левой верхней ячейке диапазона и нажав клавиши CTRL+SHIFT+ВВОД для подтверждения. Excel автоматически вставляет фигурные скобки в начале и конце формулы. Дополнительные сведения о формулах массива см. в статье Использование формул массива: рекомендации и примеры.
Количество элементов в возвращаемом массиве на единицу больше числа элементов в массиве «массив_интервалов». Дополнительный элемент в возвращаемом массиве содержит количество значений, превышающих верхнюю границу интервала, содержащего наибольшие значения. Например, при подсчете трех диапазонов значений (интервалов), введенных в три ячейки, убедитесь в том, что функция ЧАСТОТА возвращает значения в четырех ячейках. Дополнительная ячейка возвращает число значений в аргументе «массив_данных», превышающих значение верхней границы третьего интервала.
Функция ЧАСТОТА пропускает пустые ячейки и текст.
Пример
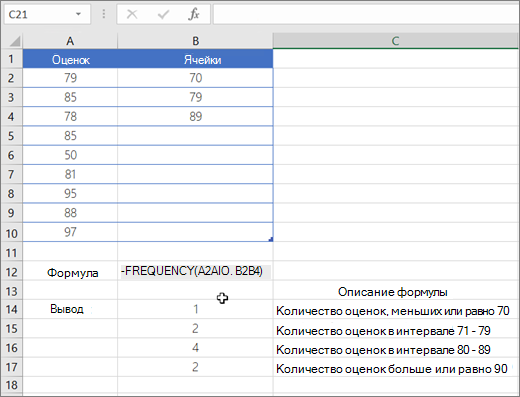
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Источник
Частотный анализ по интервалам функцией ЧАСТОТА (FREQUENCY)
При анализе данных периодически возникает задача подсчитать количество значений, попадающих в заданные интервалы «от и до» (в статистике их называют «карманы»). Например, подсчитать количество звонков определенной длительности при разборе статистики по мобильной связи, чтобы понимать какой тариф для нас выгоднее:
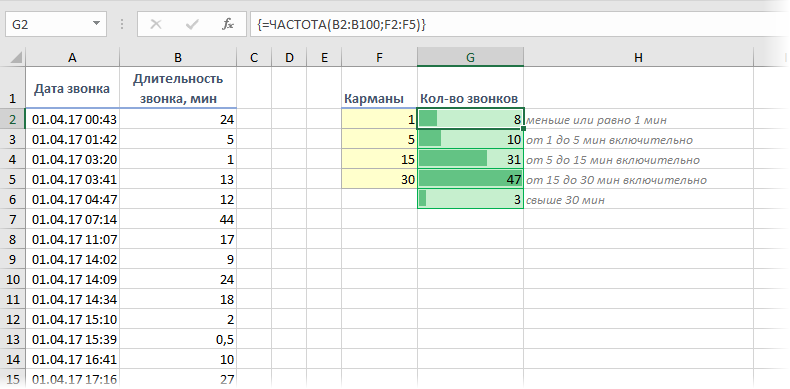
Для решения подобной задачи можно воспользоваться функцией ЧАСТОТА (FREQUENCY) . Ее синтаксис прост:
=ЧАСТОТА( Данные ; Карманы )
- Карманы — диапазон с границами интервалов, попадание в которые нас интересует
- Данные — диапазон с исходными числовыми значениями, которые мы анализируем
Обратите внимание, что эта функция игнорирует пустые ячейки и ячейки с текстом, т.е. работает только с числами.
Для использования функции ЧАСТОТА нужно:
- заранее подготовить ячейки с интересующими нас интервалами-карманами (желтые F2:F5 в нашем примере)
- выделить пустой диапазон ячеек (G2:G6) по размеру на одну ячейку больший, чем диапазон карманов (F2:F5)
- ввести функцию ЧАСТОТА и нажать в конце сочетание Ctrl+Shift+Enter, т.е. ввести ее как формулу массива
Во всех предварительно выделенных ячейках посчитается количество попаданий в заданные интервалы. Само-собой, для реализации подобной задачи можно использовать и другие способы (функцию СЧЁТЕСЛИ, сводные таблицы и т.д.), но этот вариант весьма хорош.
Кроме того, с помощью функции ЧАСТОТА можно легко подсчитывать количество уникальных чисел в наборе с помощью простой формулы массива:
Источник
Примеры функции ЧАСТОТА в Excel для расчета частоты повторений
Функция ЧАСТОТА используется для определения количества вхождения определенных величин в заданный интервал и возвращает данные в виде массива значений. Используя функцию ЧАСТОТА, мы узнаем, как посчитать частоту в Excel.
Пример использования функции ЧАСТОТА в Excel
Пример 1. Студенты одной из групп в университете сдали экзамен по физике. При оценке качества сдачи экзамена используется 100-бальная система. Для определения окончательной оценки по 5-бальной системе используют следующие критерии:
- От 0 до 50 баллов – экзамен не сдан.
- От 51 до 65 баллов – оценка 3.
- От 66 до 85 баллов – оценка 4.
- Свыше 86 баллов – оценка 5.
Для статистики необходимо определить, сколько студентов получили 5, 4, 3 баллов и количество тех, кому не удалось сдать экзамен.
Внесем данные в таблицу:
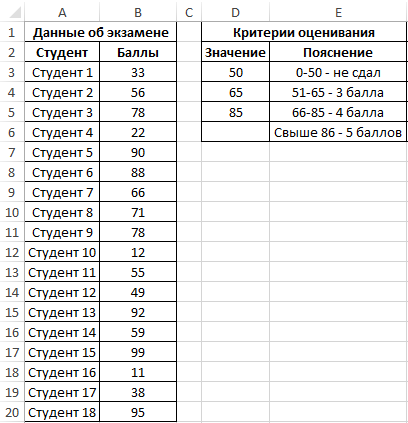
Для решения выделим области из 4 ячеек и введем следующую функцию:
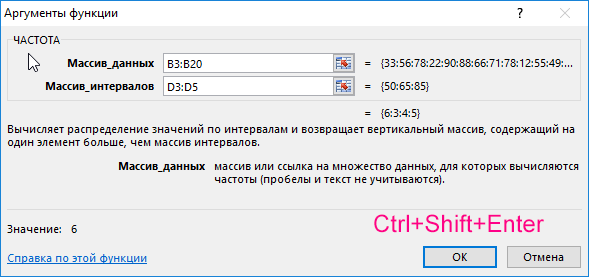
- B3:B20 – массив данных об оценках студентов;
- D3:D5 – массив критериев нахождения частоты вхождений в массиве данных об оценках.
Выделяем диапазон F3:F6 жмем сначала клавишу F2, а потом комбинацию клавиш Ctrl+Shift+Enter, чтобы функция ЧАСТОТА была выполнена в массиве. Подтверждением того что все сделано правильно будут служить фигурные скобки <> в строке формул по краям. Это значит, что формула выполняется в массиве. В результате получим:
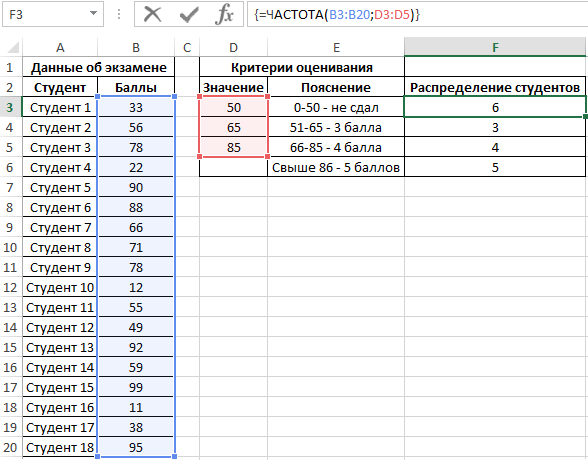
То есть, 6 студентов не сдали экзамен, оценки 3, 4 и 5 получили 3, 4 и 5 студентов соответственно.
Пример определения вероятности используя функцию ЧАСТОТА в Excel
Пример 2. Известно то, что если существует только два возможных варианта развития событий, вероятности первого и второго равны 0,5 соответственно. Например, вероятности выпадения «орла» или «решки» у подброшенной монетки равны ½ и ½ (если пренебречь возможностью падения монетки на ребро). Аналогичное расчетное распределение вероятностей характерно для следующей функции СЛУЧМЕЖДУ(1;2), которая возвращает случайное число в интервале от 1 до 2. Было проведено 20 вычислений с использованием данной функции. Определить фактические вероятности появления чисел 1 и 2 соответственно на основании полученных результатов.
Заполним исходную таблицу случайными значениями от 1-го до 2-ух:
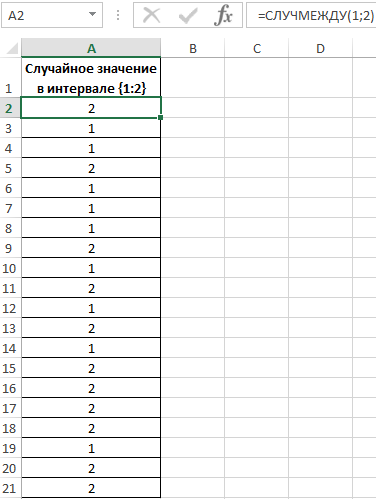
Для определения случайных значений в исходной таблице была использована специальная функция:
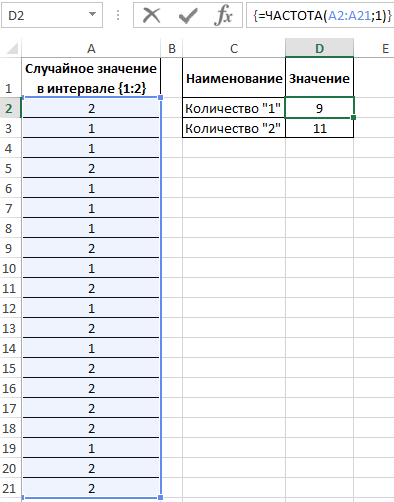
Для определения количества сгенерированных 1 и 2 используем функцию:
- A2:A21 – массив сгенерированных функцией =СЛУЧМЕЖДУ(1;2) значений;
- 1 – критерий поиска (функция ЧАСТОТА ищет значения от 0 до 1 включительно и значения >1).
В результате получим:
Вычислим вероятности, разделив количество событий каждого типа на общее их число:
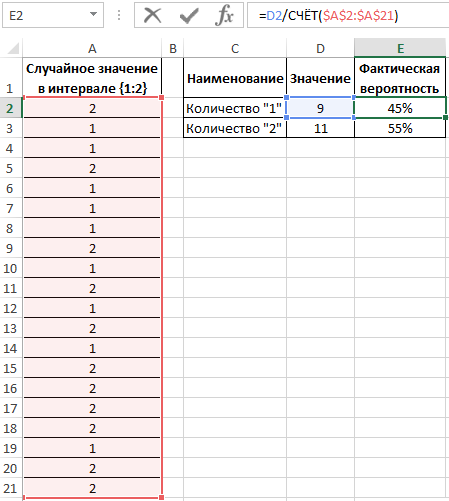
Для подсчета количества событий используем функцию =СЧЁТ($A$2:$A$21). Или можно просто разделить на значение 20. Если заранее не известно количество событий и размер диапазона со случайными значениями, тогда можно использовать в аргументах функции СЧЁТ ссылку на целый столбец: =СЧЁТ(A:A). Таким образом будет автоматически подсчитывается количество чисел в столбце A.
Вероятности выпадения «1» и «2» — 0,45 и 0,55 соответственно. Не забудьте присвоить ячейкам E2:E3 процентный формат для отображения их значений в процентах: 45% и 55%.
Теперь воспользуемся более сложной формулой для вычисления максимальной частоты повторов:
1)*СТРОКА($A$2:$A$21)))-1′ > 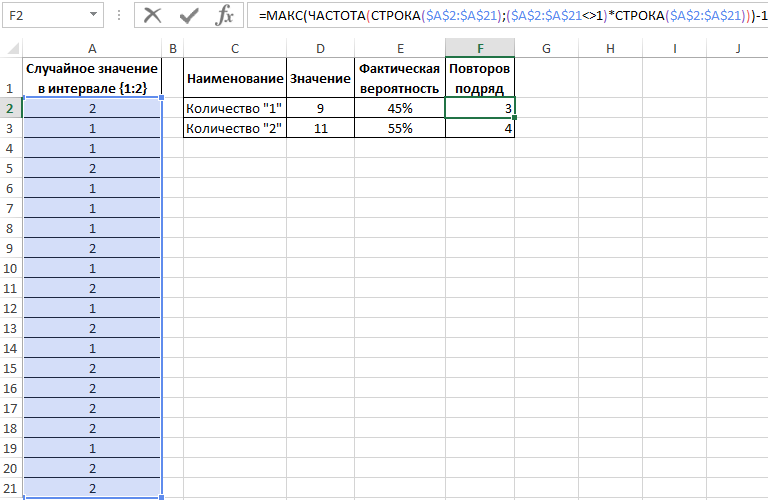
Формулы в ячейках F2 и F3 отличаются только одним лишь числом после оператора сравнения «не равно»: <>1 и <>2.
Интересный факт! С помощью данной формулы можно легко проверить почему не работает стратегия удвоения ставок в рулетке казино. Данную стратегию управления ставками в азартных играх называют еще Мартингейл. Дело в том, что количество случайных повторов подряд может достигать 18-ти раз и более, то есть восемнадцать раз подряд красные или черные. Например, если ставку в 2 доллара 18 раз удваивать – это уже более пол миллиона долларов «просадки». Это уже провал по любым техникам планирования рисков. Так же следует учитывать, что кроме «черные» и «красные» иногда выпадает еще и «зеро», что окончательно уничтожает все шансы. Так же интересно, что сумма всех чисел в рулетке от 0 до 36 равна 666.
Как посчитать неповторяющиеся значения в Excel?
Пример 3. Определить количество уникальных вхождений в массив числовых данных, то есть не повторяющихся значений.
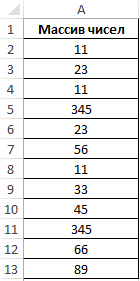
Определим искомую величину с помощью формулы:
В данном случае функция ЧАСТОТА выполняет проверку наличия каждого из элементов массива данных в этом же массиве данных (оба аргумента совпадают). С помощью функции ЕСЛИ задано условие, которое имеет следующий смысл:
- Если искомый элемент содержится в диапазоне значений, вместо фактического количества вхождений будет возвращено 1;
- Если искомого элемента нет – будет возвращен 0 (нуль).
Полученное значение (количество единиц) суммируется.
В результате получим:
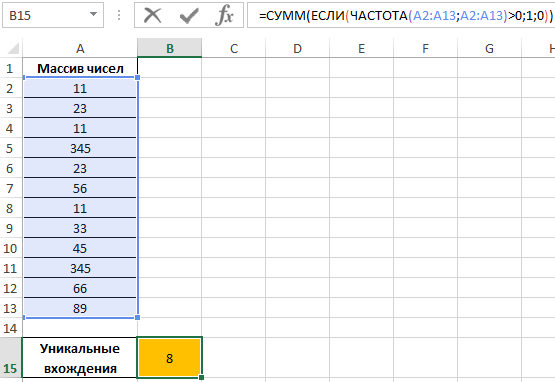
То есть, в указанном массиве содержится 8 уникальных значений.
Функция ЧАСТОТА в Excel и особенности ее синтаксиса
Данная функция имеет следующую синтаксическую запись:
Описание аргументов функции (оба являются обязательными для заполнения):
- массив_данных – данные в форме массива либо ссылка на диапазон значений, для которых необходимо определить частоты.
- массив_интервалов — данные в формате массива либо ссылка не множество значений, в которые группируются значения первого аргумента данной функции.
- Если в качестве аргумента массив_интервалов был передан пустой массив или ссылка на диапазон пустых значений, результатом выполнения функции ЧАСТОТА будет являться число элементов, входящих диапазон данных, которые были переданы в качестве первого аргумента.
- При использовании функции ЧАСТОТА в качестве обычной функции Excel будет возвращено единственное значение, соответствующее первому вхождению в массив_интервалов (то есть, первому критерию поиска частоты вхождения).
- Массив возвращаемых данной функцией элементов содержит на один элемент больше, чем количество элементов, содержащихся в массив_интервалов. Это происходит потому, что функция ЧАСТОТА вычисляет также количество вхождений величин, значения которых превышают верхнюю границу интервалов. Например, в наборе данных 2,7, 10, 13, 18, 4, 33, 26 необходимо найти количество вхождений величин из диапазонов от 1 до 10, от 11 до 20, от 21 до 30 и более 30. Массив интервалов должен содержать только их граничные значения, то есть 10, 20 и 30. Функция может быть записана в следующем виде: =ЧАСТОТА(<2;7;10;13;18;4;33;26>;<10;20;30>), а результатом ее выполнения будет столбец из четырех ячеек, которые содержат следующие значения: 4,2, 1, 1. Последнее значение соответствует количеству вхождений чисел > 30 в массив_данных. Такое число действительно является единственным – это 33.
- Если в состав массив_данных входят ячейки, содержащие пустые значения или текст, они будут пропущены функцией ЧАСТОТА в процессе вычислений.
- Функция может использоваться для выполнения статистического анализа, например, с целью определения наиболее востребованных для покупателей наименований продукции.
Источник
Цели урока:
- Сформировать
понятия эксперимента со случайными исходами, абсолютной и относительной
частоты. - Формировать
основы исследовательской деятельности, повышать интерес к учению, развивать
умение анализировать, обобщать и систематизировать знания. - Воспитывать
ответственное отношение к учебному труду, дисциплинированность и собранность,
коммуникативные качества личности.
Оборудование: компьютер, проектор,
экран.
Ход
урока
I. Самоопределение к
учебной деятельности
Цель этапа:
- включить учащихся в
учебную деятельность: «Что такое теория вероятностей»; - определить
содержательные рамки урока: начинаем работать над темой «Частота и
вероятность».
– Здравствуйте ребята!
– На прошлом уроке вы
получили задание подготовить сообщение по теме «Что такое теория вероятностей».
Давайте заслушаем сообщение.
Сообщение ученика
«Что такое теория
вероятностей»
В повседневной жизни в
разговоре часто используется слово «вероятность», например: «это невероятный
случай», «вероятнее всего он опоздает» и т.д. Здесь интуитивно оценивается
возможность того или иного события, исходя из здравого смысла, интуиции.
Например, мы заранее знаем, что на детский сеанс пойдет больше школьников, чем
взрослых, или, что при выполнении многих видов работ вредна торопливость, т.к.
в спешке можно сделать брак.
В задачах, которые мы
решаем на уроках математики у всех получается один и тот же ответ. И этот ответ
не зависит от способа решения задачи, а зависит только от правильности
выполнения вычислений. В реальной же жизни не все так просто. Многие события
нельзя предсказать заранее. Мы не можем знать, какая погода будет в первый день
весны, когда будет первая гроза. Нельзя наверняка сказать, сколько человек
решат позвонить по телефону в ближайший час. Кто может гарантировать, что если
я сейчас пойду в магазин, то обязательно встречу там свою одноклассницу. Все
эти события могут произойти, а могут не и не произойти. Поэтому эти события
называются случайными.
Оказывается, что
случайные события тоже имеют свои закономерности, которые изучает раздел
математики – Теория вероятностей.
Теория вероятностей
неразрывно связана с нашей повседневной жизнью. Она помогает оценить свои шансы
на успех, принимать оптимальные решения.
– Сегодня мы начинаем
знакомство с очень интересным разделом математики – теорией вероятностей.
II. Повторение
Цель этапа:
- актуализировать учебное
содержание, необходимое и достаточное для восприятия нового материала:
отношение двух чисел; - зафиксировать
индивидуальное затруднение в деятельности, демонстрирующее на личностно
значимом уровне недостаточность имеющихся знаний: определение частоты.
1. Устная работа (задания проецируются на
экран)
1. Что
называется отношением двух чисел? (Отношением двух чисел называется их
частное).
2. Найдите
отношение чисел:
а) 4 к 8; б) 2 к  ; в) 0,5 к 0,125.
; в) 0,5 к 0,125.
Ответ: а) 0,5; б) 3; в) 4.
3. Из
25 студентов группы 7 отличников. Какой процент всех студентов группы
составляют отличники?
Ответ: 28%.
4. Из
2000 зерен гороха 1800 оказались всхожими. Определите процент всхожести зерен.
Ответ: 90%.
5. Определите
процент содержания соли в растворе, если в 300 г раствора содержится 15 г соли.
Ответ: 5%.
2. Индивидуальное
задание:
За четверть домашнее
задание по алгебре было задано 16 раз.
а) Света два раза не
сделала домашнее задание. Какова частота невыполнения домашнего задания у Светы
за четверть?
б) Женя не сделал
домашнее задание девять раз. Какова частота выполнения домашнего задания у Жени
за четверть?
III. Выявление причины
затруднения и постановка цели деятельности
Цель этапа:
- организовать коммуникативное
взаимодействие, в ходе которого выявляется и фиксируется отличительное свойство
задания, вызвавшего затруднение в учебной деятельности; - согласовать цель и тему
урока.
– В чем причина
затруднения? (Не знаем, как определить частоту события).
– Какова цель урока?
(Научиться находить частоту события).
– Запишите тему урока:
«Относительная частота случайного события».
IV. Изучение нового материала
Цель этапа:
- организовать работу в
малых группах для определения абсолютной и относительной частот случайного
события. - актуализировать
мыслительные операции, необходимые и достаточные для восприятия нового
материала: сравнение, анализ, обобщение; - зафиксировать новый
способ действия в знаковой, вербальной форме и с помощью эталона.
1. Теоретический
материал.
Частота случайного
события
Теория вероятностей
имеет дело с экспериментами, исходы которых непредсказуемы: они зависят от
случая. Чтобы выяснить, насколько вероятно то или иное случайное событие, нужно
вычислить, как часто оно происходит. Для этого используют важные величины:
абсолютную и относительную частоту.
Абсолютная частота показывает, сколько раз
в серии экспериментов наблюдалось данное событие.

Относительная частота показывает, какая доля
экспериментов завершилась наступлением данного исхода.

Определение. Относительной частотой
события А называют отношение абсолютной частоты  к общему числу
к общему числу
n фактически проведенных
испытаний, т.е.

Поскольку 0 ≤  ≤ n, то относительная
≤ n, то относительная
частота выражается числом от 0 до 1. Относительную частоту принято выражать в
процентах.
При определении
относительной частоты случайного события результаты удобно сводить в таблицу.
2. Практическая часть
1) Проведем лабораторную
работу (работа в группах по 2 человека.)
Цель работы: определить
абсолютную и относительную частоту каждого исхода; выяснить, чему равна сумма
абсолютных частот и сумма относительных частот.
Оборудование: игральные кубики,
пластмассовые стаканчики.
Ход работы:
1. Провести
50 экспериментов по выбрасыванию игрального кубика из закрытого сосуда –
стаканчика.
2. Полученные
результаты оформить в виде таблицы.
3. Найдите
абсолютную и относительную частоты для каждого исхода.
4. Подсчитайте,
чему равна сумма абсолютных частот и чему равна сумма относительных частот.
5. Сделайте
вывод.
Протокол
экспериментального исследования частоты выпадения различных очков игрального
кубика.
|
События |
Подсчеты |
Абсолютная частота |
|---|---|---|
|
А 1 |
||
|
В 2 |
||
|
С 3 |
||
|
D 4 |
||
|
E 5 |
||
|
F 6 |
||
|
n = |
Дата_________ Подпись____________
2) Сведите все
результаты, полученные в классе, в одну общую таблицу.
3) Двое учеников
обрабатывают протокол и представляют информацию в виде сводной таблицы:

Сводная таблица
подготовлена в формате Excel, что позволяет быстро подвести итоги и вывести
результат на экран.
4) Проанализируйте, чему
равна сумма абсолютных частот и сумма относительных частот, в случае большого
числа экспериментов.
5) Сделайте вывод.
6) Как вы считаете,
справедливо ли использование кубика в настольных играх?
V. Самостоятельная работа
с последующей проверкой
Цель этапа: проверить своё умение применять новое учебное содержание в
типовых условиях на основе сопоставления своего решения с эталоном для
самопроверки.
– Вернемся к заданию,
которое вызвало затруднение в начале урока.
За четверть домашнее
задание по алгебре было задано 16 раз.
а) Света два раза не
сделала домашнее задание. Какова частота невыполнения домашнего задания у Светы
за четверть?
б) Женя не сделал
домашнее задание девять раз. Какова частота выполнения домашнего задания у Жени
за четверть?
– После выполнения
задания, выполняется проверка. Правильное решение проецируется на экран.
А = {невыполненное
задание};
 = {выполненное задание}.
= {выполненное задание}.
а) Найдем частоту
невыполнения домашнего задания Светой.


б) Найдем частоту
выполнения домашнего задания Женей.

 0,4375
0,4375
VI. Включение в систему
знаний и повторение.
Цель этапа:
- тренировать навыки
использования нового содержания совместно с ранее изученным: решение задач на
определение среднего арифметического, размаха и моды ряда; - повторить учебное
содержание, которое потребуется на следующих уроках: графики зависимостей.
– Вероятность тесно
связана со статистикой. Давайте вспомним основные статистические
характеристики.
– Найдите среднее
арифметическое ряда чисел, его моду и размах:
13; 15; 13; 12; 12; 12;
13;14; 13; 15; 13.
– Найдите абсолютную и
относительную частоту для значений, входящих в этот ряд.
– Чем являются графики
зависимостей? (Выражением на геометрическом языке различных зависимостей).
– Можно ли представить
величины, с которыми мы познакомились на уроке, графически? (Можно представит
графически зависимость частоты появления какого-либо события от числа
проведенных экспериментов).
– Вот этим мы и займемся
на следующем уроке.
VII. Рефлексия деятельности
на уроке.
Цель этапа:
- зафиксировать новое
содержание, изученное на уроке; - оценить собственную
деятельность на уроке; - обсудить и записать
домашнее задание.
– Что мы сегодня узнали?
– Что мы использовали
для определения частоты события?
– Это понятие
используется в практической деятельности человека? Где?
– Оцените свою работу на
уроке.
Домашнее задание: п 9.1, № 943.
Творческое задание: «Вероятность вокруг
нас» – подобрать задачи, содержащие сведения из повседневной жизни.
17 авг. 2022 г.
читать 2 мин
Таблица частот — это таблица, в которой отображается информация о частотах. Частоты просто говорят нам, сколько раз произошло определенное событие.
Например , в следующей таблице показано, сколько товаров было продано магазином в разных ценовых диапазонах за данную неделю:
| Цена товара | Частота | | — | — | | $1 – $10 | 20 | | $11 – $20 | 21 | | 21 – 30 долларов США | 13 | | $31 – $40 | 8 | | $41 — $50 | 4 |
В первом столбце отображается ценовой класс, а во втором столбце — частота этого класса.
Также можно рассчитать относительную частоту для каждого класса, которая представляет собой просто частоту каждого класса в процентах от целого.
| Цена товара | Частота | Относительная частота | | — | — | — | | $1 – $10 | 20 | 0,303 | | $11 – $20 | 21 | 0,318 | | 21 – 30 долларов США | 13 | 0,197 | | $31 – $40 | 8 | 0,121 | | $41 — $50 | 4 | 0,061 |
Всего было продано 66 штук. Таким образом, мы нашли относительную частоту каждого класса, взяв частоту каждого класса и разделив ее на общее количество проданных товаров.
Например, было продано 20 товаров по цене от 1 до 10 долларов. Таким образом, относительная частота класса $1 – $10 составляет 20/66 = 0,303 .
Затем был продан 21 предмет в ценовом диапазоне от 11 до 20 долларов. Таким образом, относительная частота класса $11 – $20 составляет 21/66 = 0,318 .
В следующем примере показано, как найти относительные частоты в Excel.
Пример: относительные частоты в Excel
Сначала мы введем класс и частоту в столбцах A и B:

Далее мы рассчитаем относительную частоту каждого класса в столбце C. В столбце D показаны формулы, которые мы использовали:

Мы можем проверить правильность наших расчетов, убедившись, что сумма относительных частот равна 1:

Мы также можем создать гистограмму относительной частоты для визуализации относительных частот.
Просто выделите относительные частоты:

Затем перейдите в группу « Диаграммы » на вкладке « Вставка » и щелкните первый тип диаграммы в « Вставить столбец» или «Гистограмма» :

Автоматически появится гистограмма относительной частоты:

Измените метки оси X, щелкнув правой кнопкой мыши диаграмму и выбрав Выбрать данные.В разделе « Ярлыки горизонтальной (категории) оси » нажмите « Изменить » и введите диапазон ячеек, содержащий цены на товары. Нажмите OK , и новые метки осей появятся автоматически:
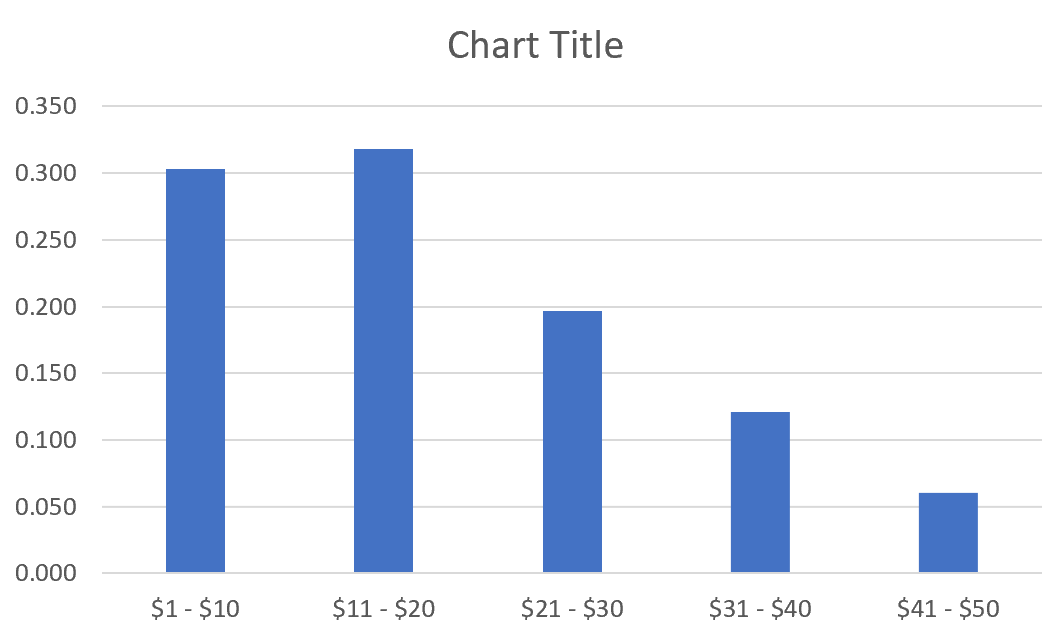
Дополнительные ресурсы
Калькулятор относительной частоты
Гистограмма относительной частоты: определение + пример
Частота случайного события
1. Когда перед началом игры игроки хотят договориться, кто из них делает первый ход, то обычно подбрасывают монету. Так поступают потому, что выпадание орла или решки считается равновероятным и заинтересованные стороны имеют равные шансы.
Результат подбрасывания монеты, кнопки, игрального кубика, раскрытие книги наугад заранее предсказать нельзя, в каждом таком эксперименте результат зависит от случая, поэтому их называют экспериментами со случайными исходами или просто случайными экспериментами. Важно, что такие случайные эксперименты можно повторить многократно, причём в одних и тех же условиях.
Обычно многократные случайные эксперименты проводят, чтобы определить, насколько часто появляется интересующий нас результат. Например, как часто при подбрасывании монеты выпадает орёл или при одновременном подбрасывании двух кубиков выпадает двенадцать очков. Для этого по результатам серии экспериментов вычисляется частота наблюдаемого события.
Частотой случайного события в серии экспериментов называют отношение числа экспериментов, в которых это событие произошло, к общему числу экспериментов.
Частота показывает, какую часть от общего числа проведённых экспериментов составляют эксперименты, завершившиеся интересующим нас результатом.
Пусть в серии из N экспериментов интересующее нас событие произошло n раз, тогда его частота равна 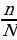 . Поскольку 0 ≤ n ≤ N, то частота выражается числом от 0 до 1. Если событие не произошло ни разу, т.е. n=0, то его частота в серии экспериментов равна 0. Если оно происходило каждый раз, то его частота равна 1.Частот у принято выражать также и в процентах.
. Поскольку 0 ≤ n ≤ N, то частота выражается числом от 0 до 1. Если событие не произошло ни разу, т.е. n=0, то его частота в серии экспериментов равна 0. Если оно происходило каждый раз, то его частота равна 1.Частот у принято выражать также и в процентах.
2. Представим, что монеты у наших игроков не оказалось, и один из них предложил подбросить кнопку. Можно ли считать такую замену справедливой, т.е. останутся ли шансы сторон равными? Давайте разберёмся.
Кнопка может упасть либо остриём вверх, либо остриём вниз. Чтобы ответить на вопрос, равны ли шансы этих исходов, надо много раз подбросить кнопку и собрать информацию о результатах. Если окажется, что при многократном подбрасывании кнопки частота падения кнопки остриём вниз и частота падения кнопки остриём вверх будут примерно равными, то это означает, что эти два исхода практически равновероятны и замена монеты на кнопку справедлива. Если же результаты будут отличаться, то эти два исхода равновероятными считать нельзя.
Проведем серию экспериментов по подбрасыванию кнопки с целью выявления закономерности падение кнопки остриём вниз и остриём вверх. Для этого работаем в парах, каждая из которых 100 раз побрасывает кнопку. Результаты заносим в таблицу. (Для экономии времени таблицу готовим заранее). Количество участников эксперимента определяем количеством учащихся в классе. Результаты всех испытаний заносим в общую таблицу. В первый столбец таблицы вносим результаты экспериментов, полученных одной парой. Далее каждый раз, заполняя следующий столбец таблицы, к результатам предыдущего столбца прибавляем результаты, полученные следующей парой учеников, и подсчитываем соответствующие частоты.
Возможные результаты. Перед вами таблица результатов, полученных одной из пар.
Таблица 1.
|
Событие |
Подсчёты |
Всего событий |
|
Остриём вниз |
|
44 |
|
Остриём вверх |
|
56 |
|
Итого |
100 |
Из таблицы 1 видно, что частота падения кнопки остриём вниз в этой серии экспериментов равна 0,44, а частота падения кнопки остриём вверх равна 0,56.
Такие серии по 100 экспериментов в классе провели 10 пар учеников. Каждая пара получила свою таблицу результатов. Поскольку все кнопки из одной коробки можно считать одинаковыми, они свели результаты в одну таблицу.
Таблица 2.
|
Число экспериментов |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
900 |
1000 |
|
|
Остриём вниз |
Всего событий |
44 |
94 |
130 |
173 |
221 |
265 |
310 |
356 |
403 |
448 |
|
Частота |
0,44 |
0,47 |
0,43 |
0,43 |
0,44 |
0,44 |
0,44 |
0,45 |
0,45 |
0,45 |
|
|
Остриём вверх |
Всего событий |
56 |
106 |
170 |
227 |
279 |
235 |
390 |
444 |
497 |
552 |
|
Частота |
0,56 |
0,53 |
0,57 |
0,57 |
0,56 |
0,56 |
0,56 |
0,55 |
0,55 |
0,55 |
Из таблицы 2 видно, что при увеличении числа экспериментов частота каждого события выравнивается, ил, как говорят, стабилизируется. Частота события «остриём вверх» стабилизируется около числа 0,45, а частота события «остриём вверх» – около числа 0,55. Значит, шансы падения кнопки остриём вниз несколько меньше, чем остриём вверх.
Стабилизация частоты будет нагляднее, если данные представить графически. Для этого каждая пара чисел таблицы ( число экспериментов – частота) отмечена точкой на координатной плоскости. Полученные точки соединены ломаной , которая при увеличении числа экспериментов становится практически горизонтальной прямой.
График зависимости частоты результата «остриём вниз» от числа экспериментов.
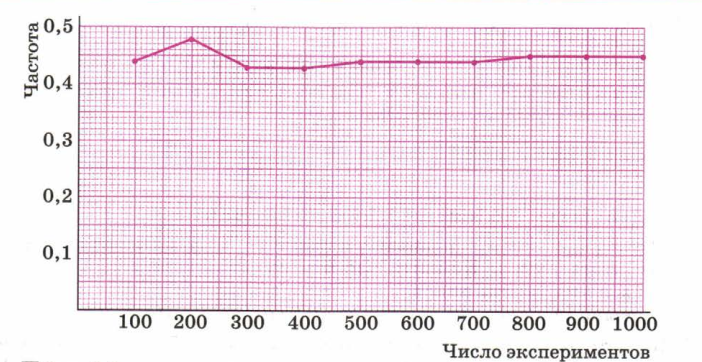
3. К экспериментам со случайными исходами относятся не только эксперименты, которые мы проводим сами. К ним относятся и самые разные опыты, испытания, наблюдения, измерения, проведённые кем-то другим, а также наблюдения за явлениями природы. Важно здесь то, что их результаты завияст от случая, но происходят каждый раз примерно в одних и тех же условиях. Надо лишь зафиксировать эти результаты. Случайными исходами таких испытаний являются, например, количество петухов и количество кур, вылупляющихся из каждой сотни яиц, температура воздуха в оин и тот же день в одном и том же месте, итоги еженедельной лотереи, результаты стрельбы по мишени, уровень весеннего разлива реки. В экспериментах со случыайными исходами уди вительно то, что, хотя проведении большого числа таких испытаний выявляются отчётливые закономерности. Частота соответствующих событий позволяет строить обоснованные прогнозы для решения задач, возникающих в жизни.
Ответьте на вопросы :
-
Что называют частотой случайного события?
-
Назовите два свойства случайного экспреимента
-
Монету подбросили 1000 раз, при этом 495 раз выпал орёл. Чему равна частота события « выпал орёл» в этой1 серии экспериментов?
Ответьте на вопросы по таблице 2:
-
Чему равна частота события «остриём вниз» после 300 испытаний? События «остриём вверх» после 500 испытаний?
-
После какого числа испытаний частота события «остриём вниз» стала равна 0,45?
-
Сколько раз кнопка упала остриём вверх у 6-й пары?
-
За лето на Черноморское побережье было 67 солнечных дней. Какова частота солнечных дней на побережье за лето? пасмурных дней? ( Используйте калькулятор)
Приведите примеры природных явлений, которые можно считать экспериментами со случайными исходами.
Примерное домашнее задание
1.В марте в городе родилось 2348 мальчиков и 2027 девочек. Найдите частоту рождения мальчиков и частоту рождения девочек в этом месяце. ( Используйте калькулятор)
2. Многолетняя проверка показала, что всхожесть семян огурцов определённого сорта составляет 90%. Посеяли 200 семян. Какое число проросших семян следует ожидать?
3. Готовясь к участию в теллеигре «Поле чудес», где по буквам отгадываются слова, олег задумался: «А какую букву стоит назвать первой, когда в слове ещё не угадано ни одной буквы?»
Понятно, что в такой ситуации выигрышная стратегия – начать игру с самой распространённой в русском языке буквы. Но как её определить? Чтобы помочь Олегу, 33 его одноклассника распределили между собой все буквы алфавита, взяли один и тот же текст и каждый посчитал, сколько раз в нём встречается его буква. Так они экспериментально определили самую распространённую букву русского языка.
Как вы думаете, что это за буква? Чтобы проверить свою догадку, проведите в классе такой же эксперимент, выбрав случайным образом текст из книги, которая есть у всех, например из учебника.