Содержание:
Свободные и вынужденные колебания:
Работа силы вычисляется по формуле А = 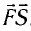
Как Вам уже известно, механическая энергия гармонического осциллятора пропорциональна квадрату амплитуды его колебаний. Колебания, происходящие с постоянной во времени амплитудой, называются незатухающими колебаниями.
Незатухающие колебания, вызванные кратковременным внешним воздействием, называются свободными или собственными. Они происходят под действием внутренних сил, возникающих в самой системе. Свободные колебания — это колебания, происходящие в отсутствие внешних воздействий на систему, со строго определенной частотой, называемой частотой собственных колебаний системы. Эта частота зависит только от параметров системы. Примерами таких колебаний могут служить колебания математического и пружинного маятников, происходящие в отсутствие сил трения.
В любой реальной системе всегда присутствуют силы трения (сопротивления), поэтому механическая энергия системы с течением времени уменьшается, переходя во внутреннюю энергию. Вместе с тем убыль механической энергии означает и уменьшение амплитуды колебаний.
Колебания, амплитуда которых уменьшается с течением времени вследствие потери энергии колебательной системой, называются затухающими колебаниями (рис. 10, а, б).
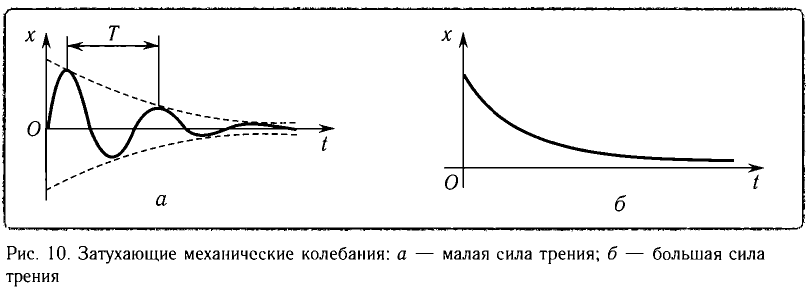
Уменьшение механической энергии системы (превращение ее во внутреннюю энергию) происходит вследствие трения и сопротивления окружающей среды. Такие системы называют диссипативными (от латинского слова dissipation — рассеяние).
При малых потерях энергии колебания можно считать периодическими и пользоваться такими понятиями, как период и частота колебаний. Так, например, период — промежуток времени между двумя последовательными максимумами колеблющейся физической величины (см. рис. 10, а).
Любые собственные колебания в реальной системе рано или поздно затухают. Чтобы колебания не затухали, необходимо воздействие внешней силы. Однако не всякая внешняя сила заставляет систему двигаться периодически. Например, невозможно раскачать качели, если действовать на них с постоянной по модулю и направлению силой. Внешняя сила тоже должна быть периодической.
Колебания тел под действием внешней периодической силы называются вынужденными, а сила — вынуждающей. В случае гармонической силы 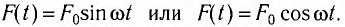 . Частота установившихся вынужденных колебаний всегда равна частоте вынуждающей силы.
. Частота установившихся вынужденных колебаний всегда равна частоте вынуждающей силы.
Амплитуда колебаний и энергия, передаваемая системе за период вынужденных колебаний, зависят от того, насколько различаются частота вынуждающей силы 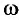 и частота собственных колебаний
и частота собственных колебаний 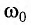 , а также от величины трения в системе.
, а также от величины трения в системе.
При вынужденных колебаниях возможно явление, называемое резонансом (от латинского слова resono — откликаюсь, звучу в ответ).
Резонанс — это явление резкого возрастания амплитуды вынужденных колебаний при действии на колебательную систему внешней силы с частотой 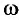 , совпадающей с собственной частотой
, совпадающей с собственной частотой 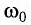 системы ((
системы ((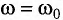 ) (рис. 11).
) (рис. 11).
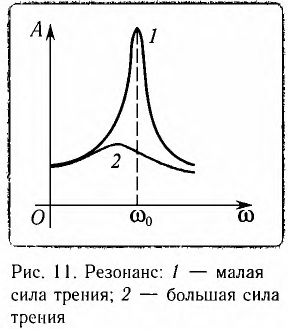
При резонансе создаются оптимальные условия для передачи системе энергии от внешнего источника, так как в течение всего периода работа внешней силы над системой положительна. Вспомните процесс раскачивания на качелях — если качели толкать с большой частотой или с малой, то их практически невозможно раскачать. Если же подобрать частоту толчков, близкую к частоте собственных колебаний качелей, то раскачивание будет эффективным.
Пример №1
Определите модуль скорости v движения поезда, при которой маятник длиной l=11 см, подвешенный в вагоне, особенно сильно раскачивается. Длина рельса L = 12,5 м.
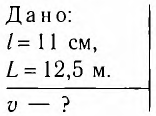
Решение
Маятник начинает сильно раскачиваться, когда частота его собственных колебаний совпадает с частотой вынуждающей
Частотой вынуждающей силы является частота ударов колес вагона о стыки рельс. Промежуток времени между двумя последовательными ударами (период)
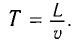 (1)
(1)
Поскольку частота — величина, обратная периоду, то можно записать частоту вынуждающей силы
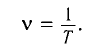
Частота собственных колебаний математического маятника
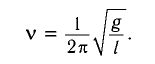 (2)
(2)
Приравняв формулы (I) и (2), получим
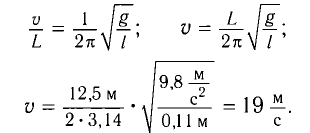
Ответ: о = 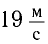 .
.
Распространение колебаний в упругой среде. Продольные и поперечные волны
Опыт показывает, что колебания, возбужденные в какой-либо точке упругой среды, с течением времени передаются в ее другие точки. Так от камня, брошенного в спокойную воду озера, кругами расходятся волны, которые со временем достигают берега. Колебания сердца, расположенного внутри грудной клетки, можно ощутить на запястье, что используется для определения пульса.
Перечисленные примеры связаны с явлением распространения механических колебаний в среде.
Механической волной называется процесс распространения колебаний в упругой среде, который сопровождается передачей энергии от одной точки среды к другой.
Механические волны не могут распространяться в вакууме.
Источником механических волн является колеблющееся тело. Если источник колеблется синусоидально, то и волна в упругой среде будет иметь форму синусоиды. Колебания, вызванные в каком-либо месте упругой среды, распространяются в ней с определенной скоростью, зависящей от плотности и упругих свойств среды.
Подчеркнем, что при распространении волны отсутствует перенос вещества, т. е. частицы колеблются вблизи положений равновесия. Среднее смещение частиц относительно положения равновесия за большой промежуток времени равно нулю.
Механизм образования волны можно представить следующим образом. Источник волны — колеблющееся тело — воздействует на частицы упругой среды, соприкасающиеся с ними, и заставляет их совершать вынужденные колебания. Среда вблизи источника деформируется, и в ней возникают силы упругости, препятствующие деформации. Если частицы среды сближаются, то возникают силы отталкивания, а если они удаляются друг от друга, то — силы притяжения. Постепенно эти силы будут действовать на все более удаленные от источника частицы среды, приводя их в колебательное движение, которое будет распространяться в виде волны.
Рассмотрим основные характеристики волны.
Волновой фронт — это воображаемая поверхность, до которой дошло волновое возмущение в данный момент времени.
Линия, проведенная перпендикулярно волновому фронту в направлении распространения волны, называется лучом. Луч указывает направление распространения волны.
Основные характеристики волны:
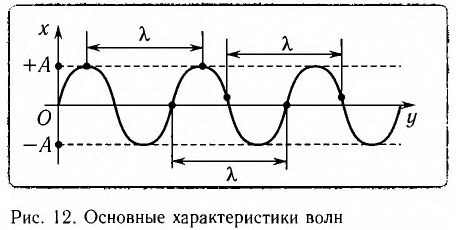
Амплитуда (А) — модуль максимального смещения точек среды из положений равновесия при колебаниях (рис. 12).
Период (Т) — время полного колебания (период колебаний точек среды равен периоду колебаний источника волны):
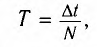
где 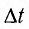 — промежуток времени, в течение которого совершаются N колебаний.
— промежуток времени, в течение которого совершаются N колебаний.
Частота (v) — число полных колебаний, совершаемых в данной точке в единицу времени:
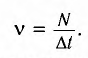
Частота волны определяется частотой колебаний источника.
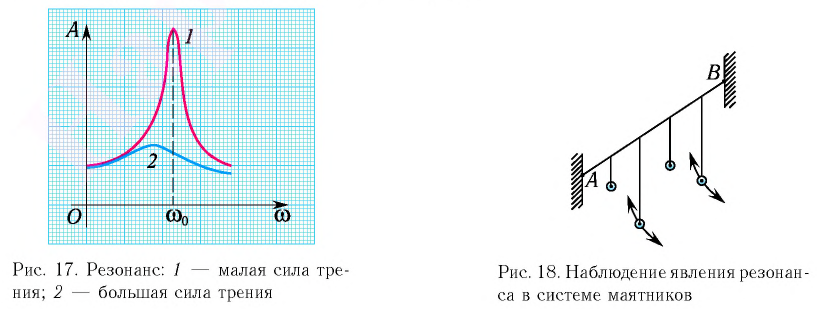
Скорость (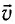 ) — скорость перемещения гребня волны (это не скорость частиц! ).
) — скорость перемещения гребня волны (это не скорость частиц! ).
Длина волны (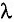 ) — наименьшее расстояние между двумя точками, колебания в которых происходят в одинаковой фазе, т. е. это расстояние, на которое волна распространяется за промежуток времени, равный периоду колебаний источника (см. рис. 12):
) — наименьшее расстояние между двумя точками, колебания в которых происходят в одинаковой фазе, т. е. это расстояние, на которое волна распространяется за промежуток времени, равный периоду колебаний источника (см. рис. 12):
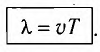
Рассмотрим колебания источника волны, происходящие с циклической частотой 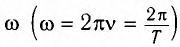 и амплитудой А:
и амплитудой А:
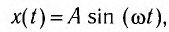
где x(t) — смещение источника от положения равновесия.
В некоторую точку среды колебания придут не мгновенно, а через промежуток времени, определяемый скоростью волны и расстоянием от источника до точки наблюдения. Если скорость волны в данной среде равна у, то зависимость от времени t координаты (смещения) х колеблющейся точки, находящейся на расстоянии г от источника, описывается уравнением
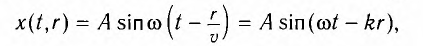 (1)
(1)
где k — волновое число 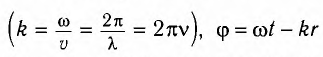 — фаза волны.
— фаза волны.
Выражение (1) называется уравнением распространяющейся (бегущей) волны.
Бегущую волну можно наблюдать при следующем эксперименте: если один конец резинового шнура, лежащего на гладком горизонтальном столе, закрепить и, слегка натянув шнур рукой, привести его второй конец в колебательное движение в направлении, перпендикулярном шнуру, то по нему побежит волна.
Волна называется продольной, если колебания частиц среды происходят вдоль направления распространения волн. Продольную волну легко получить с помощью длинной пружины, которая лежит на гладкой горизонтальной поверхности и один конец ее закреплен. Упругие волны в газах и жидкостях возникают только при сжатии или разрежении среды. Поэтому в таких средах возможно распространение только продольных волн.
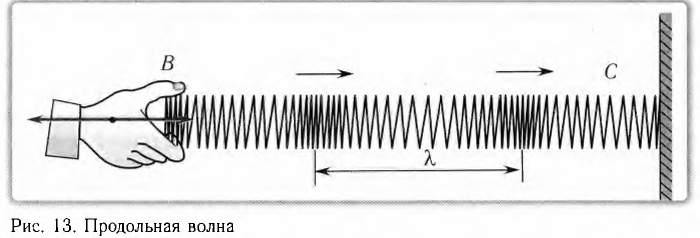
Легким ударом по свободному концу В пружины мы вызовем появление волны (рис. 13). При этом каждый виток пружины будет колебаться вдоль направления распространения волны ВС. Примерами продольных волн являются звуковые волны в газе и жидкости.
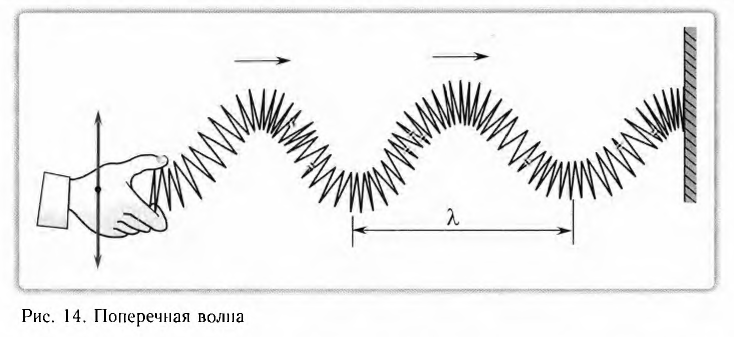
Волна называется поперечной, если частицы среды колеблются в плоскости, перпендикулярной направлению распространения волны. Используя длинную пружину, можно продемонстрировать распространение поперечных волн, если совершать колебания незакрепленного конца перпендикулярно продольной оси пружины (рис. 14). В твердых телах упругие волны могут возникать также и при смещении или сдвиге одних слоев среды относительно других. Поэтому в отличие от жидкостей и газов в твердых телах возможно распространение и поперечных волн.
Поперечные волны вызывают звучание струн музыкальных инструментов при их возбуждении.
Для характеристики энергии, переносимой волнами, используется понятие интенсивности волны (l), определяемое как энергия (W), переносимая волной в единицу времени (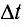 = 1с) через поверхность площадью S= I м2, расположенную перпендикулярно к направлению распространения волны:
= 1с) через поверхность площадью S= I м2, расположенную перпендикулярно к направлению распространения волны:
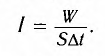
Другими словами, интенсивность представляет собой мощность, переносимую волнами через поверхность единичной площади, перпендикулярно к направлению распространения волны. Единицей интенсивности в СИ является
ватт на метр в квадрате (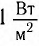 ).
).
Волны могут распространяться не только в среде, но и вдоль границы раздела двух сред. Такие волны получили название поверхностных волн. Примером данного типа волн служат хорошо знакомые всем волны на поверхности воды.
Пример №2
Определите длину X волны, излучаемой источником колебаний с частотой v = 200 Гц, если модуль скорости распространения волны v = 1450 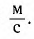
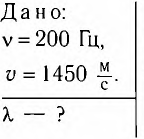
Решение
Модуль скорости распространения волны можно вычислить по формуле
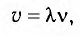
где 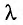 — длина волны, v — частота колебаний. Откуда находим
— длина волны, v — частота колебаний. Откуда находим
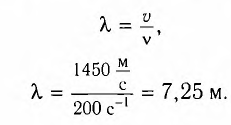
Ответ: 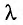 = 7,25 м.
= 7,25 м.
Пример №3
Поперечная волна распространяется вдоль упругого шнура со скоростью, модуль которой v = 5,0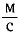 / Период колебания точек шнура Т= 1,2 с, амплитуда колебаний A = 20 мм. Определите длину волны
/ Период колебания точек шнура Т= 1,2 с, амплитуда колебаний A = 20 мм. Определите длину волны 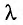 , фазу колебаний
, фазу колебаний 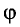 и смещение х точки, находящейся на расстоянии г= 15 м от источника колебаний, через промежуток времени
и смещение х точки, находящейся на расстоянии г= 15 м от источника колебаний, через промежуток времени 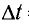 = 4,0 с.
= 4,0 с.
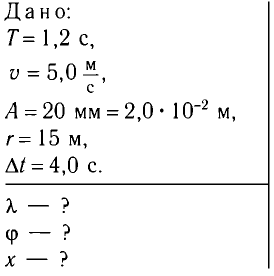
Решение
Длина волны находится из выражения
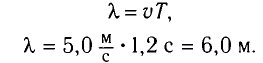
Волна пройдет расстояние г за время 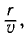 следовательно, фаза колебаний определится по формуле
следовательно, фаза колебаний определится по формуле
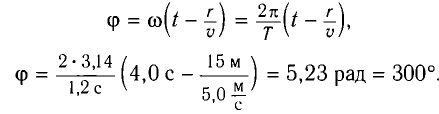
Подставив вычисленное значение фазы в уравнение колебаний, получим:
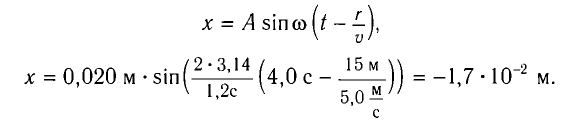
Ответ: 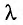 = 6,0 м,
= 6,0 м, 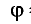 = 300°, х = -1,7 см.
= 300°, х = -1,7 см.
Определение свободных и вынужденных колебаний
Силы взаимодействия тел системы называют внутренними. Тела, не входящие в систему, называют внешними телами. Силы, которые действуют на тела системы со стороны внешних тел, называют внешними силами.
Как вам уже известно, механическая энергия гармонического осциллятора (например, груза на пружине) пропорциональна квадрату амплитуды его колебаний. Колебания, происходящие с постоянной во времени амплитудой, называются незатухающими колебаниями.
Колебания, которые совершает система около положения устойчивого равновесия под действием внутренних сил после того, как она была выведена из состояния равновесия и предоставлена самой себе, называются свободными (собственными) колебаниями.
Свободные колебания происходят со строго определенной частотой 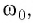 называемой частотой свободных (собственных) колебаний системы. Эта частота зависит только от параметров системы. Примерами таких колебаний могут служить колебания математического и пружинного маятников, происходящие в отсутствие сил трения. Амплитуда свободных колебаний определяется начальными условиями, т. е. тем начальным отклонением или толчком, которым маятник или груз на пружине приведен в движение. Свободные колебания являются самым простым видом колебаний.
называемой частотой свободных (собственных) колебаний системы. Эта частота зависит только от параметров системы. Примерами таких колебаний могут служить колебания математического и пружинного маятников, происходящие в отсутствие сил трения. Амплитуда свободных колебаний определяется начальными условиями, т. е. тем начальным отклонением или толчком, которым маятник или груз на пружине приведен в движение. Свободные колебания являются самым простым видом колебаний.
В любой реальной колебательной системе всегда присутствуют силы трения (сопротивления), поэтому механическая энергия системы с течением времени уменьшается, переходя во внутреннюю энергию. Вместе с тем убыль механической энергии означает и уменьшение амплитуды колебаний.
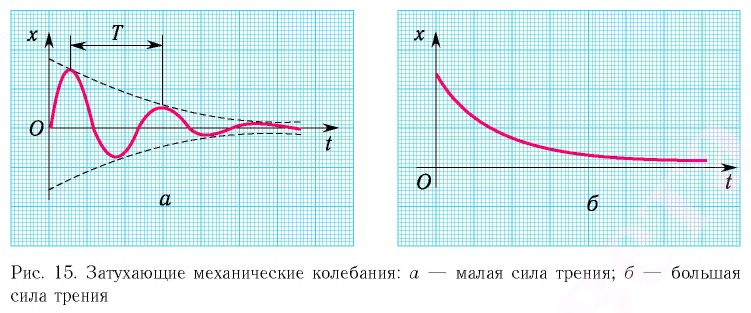
Колебания, амплитуда которых уменьшается с течением времени вследствие потери энергии колебательной системой, называются затухающими колебаниями (рис. 15). Уменьшение механической энергии системы (превращение ее во внутреннюю энергию) происходит вследствие трения и сопротивления окружающей среды.
Систему называют диссипативной (от лат. dissipation — рассеяние), если ее механическая энергия с течением времени уменьшается за счет превращения ее во внутреннюю энергию.
При малых потерях энергии колебания можно считать периодическими и пользоваться такими понятиями, как период и частота колебаний. Так, например, период — промежуток времени между двумя последовательными максимумами колеблющейся физической величины (см. рис. 15, а).
Колебания в любой реальной системе рано или поздно затухают. Чтобы колебания не затухали, необходимо воздействие внешней силы. Однако не всякая внешняя сила заставляет систему двигаться периодически. Например, невозможно раскачать качели, если действовать на них постоянной силой. Внешняя сила тоже должна быть периодической.
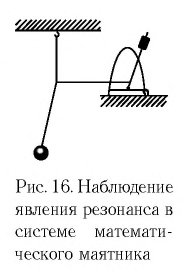
Проведем следующий эксперимент. Соединим математический маятник с метрономом (рис. 16). Изменяя частоту колебаний маятника метронома, добиваемся увеличения амплитуды колебаний математического маятника. Оказывается, что его амплитуда будет максимальной при совпадении собственной частота колебаний маятника и маятника метронома.
Колебания тел под действием внешней периодической силы называются вынужденными, а сила — вынуждающей. В случае гармонической силы: 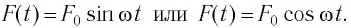 Вначале действия внешней силы наблюдается достаточно сложное движение тела. Спустя некоторое время после начала действия внешней силы колебания приобретают стационарный характер и не зависят от начальных условий. Таким образом, при вынужденных колебаниях система полностью «забывает» свое начальное состояние. Частота установившихся вынужденных колебаний всегда равна частоте вынуждающей силы.
Вначале действия внешней силы наблюдается достаточно сложное движение тела. Спустя некоторое время после начала действия внешней силы колебания приобретают стационарный характер и не зависят от начальных условий. Таким образом, при вынужденных колебаниях система полностью «забывает» свое начальное состояние. Частота установившихся вынужденных колебаний всегда равна частоте вынуждающей силы.
Амплитуда колебаний и энергия, передаваемая системе за период вынужденных колебаний, зависят от того, насколько различаются частота 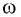 вынуждающей силы и частота
вынуждающей силы и частота 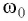 собственных колебаний, а также от величины трения в системе.
собственных колебаний, а также от величины трения в системе.
При вынужденных колебаниях возможно явление, называемое резонансом (от лат. resono — откликаюсь, звучу в ответ).
Резонанс — это явление резкого возрастания амплитуды вынужденных колебаний при действии на колебательную систему внешней силы с частотой со, совпадающей с собственной частотой 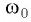 системы
системы 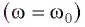 (рис. 17).
(рис. 17).
Подвесим на упругой нити 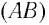 четыре математических маятника с одинаковыми грузами, три из которых имеют различную длину, а длина четвертого равна длине второго (рис. 18). Сначала посмотрим, что будет с маятниками, если раскачать первый или третий маятник. Наблюдения показывают, что через некоторое время начнут качаться и остальные маятники. Но амплитуда их колебаний мала, и вскоре колебания затухают. А вот если раскачать второй маятник, то амплитуда колебаний четвертого будет непрерывно возрастать, пока не достигнет наибольшего значения.
четыре математических маятника с одинаковыми грузами, три из которых имеют различную длину, а длина четвертого равна длине второго (рис. 18). Сначала посмотрим, что будет с маятниками, если раскачать первый или третий маятник. Наблюдения показывают, что через некоторое время начнут качаться и остальные маятники. Но амплитуда их колебаний мала, и вскоре колебания затухают. А вот если раскачать второй маятник, то амплитуда колебаний четвертого будет непрерывно возрастать, пока не достигнет наибольшего значения.
Это происходит потому, что частота собственных колебаний четвертого маятника совпадает с частотой колебаний внешней силы (частотой колебаний второго маятника), так как их длины равны. А колебания первого и третьего маятников, как и в первом эксперименте, быстро затухают.
При резонансе создаются оптимальные условия для передачи системе энергии от внешнего источника, так как в течение всего периода работа внешней силы над системой положительна. Вспомните процесс раскачивания на качелях: если качели толкать очень быстро или очень медленно, их практически невозможно будет раскачать. Если же подбирать частоту толчков, близкую к частоте собственных колебаний качелей, то раскачивание будет эффективным.
Большинство сооружений и машин, обладая определенной упругостью, способны совершать свободные колебания. Поэтому при внешних периодических воздействиях в них вследствие явления резонанса могут возбуждаться колебания большой амплитуды, которые могут привести к разрушительным последствиям. Например, для исключения разрушения мостов вследствие явления резонанса при прохождении по ним войсковых частей приказывают идти вольным шагом (не в ногу). Поезда переезжают мосты либо очень медленно, либо с максимальной скоростью.
В 1750 г. цепной мост вблизи г. Анжер (Франция) был разрушен в результате резонанса, во время прохождения по нему отряда солдат, так как частота их шага совпала с частотой свободных колебаний моста.
В 1906 г. в г. Петербурге (Россия) обрушился Египетский мост, по которому проходил кавалерийский эскадрон.
7 ноября 1940 г. сильный порыв ветра вызвал резонансные колебания Такомского моста (США), что привело к его разрушению.
Пример №4
Определите модуль скорости 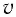 движения поезда, при которой математический маятник, подвешенный в вагоне, особенно сильно раскачивается. Длина маятника
движения поезда, при которой математический маятник, подвешенный в вагоне, особенно сильно раскачивается. Длина маятника 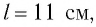 длина рельса
длина рельса 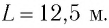
Дано:
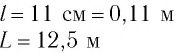

Решение
Маятник начинает сильно раскачиваться, когда частота его собственных колебаний
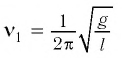
совпадает с частотой вынуждающей силы
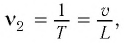
которая совпадает с частотой ударов колес вагона о стыки рельсов: 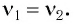
Отсюда
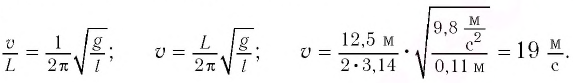
Ответ: 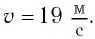
- Вынужденные электромагнитные колебания
- Резонанс в физике
- Распространение механических волн в средах
- Электромагнитное поле
- Механические колебания и волны в физике
- Гармонические колебания в физике
- Вынужденные колебания в физике
- Электромагнитные колебания
Рассмотрим величины, с помощью которых можно охарактеризовать колебания.

Рис. (1). Движение пустых качелей и качелей с мальчиком
Сравним колебания двух качелей на рисунке (1) — пустых качелей и качелей с мальчиком. Качели с мальчиком колеблются с большим размахом, то есть их крайние положения находятся дальше от положения равновесия, чем у пустых качелей.
Амплитудой колебаний (A) называется максимальное отклонение колеблющегося тела от положения равновесия.
([A]=1~м)
Полным колебанием называют движение, за которое тело возвращается в исходную точку (из которой началось колебание).
За одно полное колебание тело дважды максимально отклоняется от положения равновесия, поэтому один полный путь одного полного колебания равен четырём амплитудам: (s=4A).
Период колебаний — это промежуток времени, за который тело совершает одно полное колебание.
([T]=1~с)
Пример:
ударим по столу двумя линейками — металлической и деревянной (рис. (2)) Линейки после этого начнут колебаться, но за один и тот же промежуток времени металлическая линейка (B) сделает больше колебаний, чем деревянная (A).

Рис. (2). Колебания металлической (B) и деревянной (A) линеек
Число колебаний в единицу времени называется частотой колебаний.
Обрати внимание!
Обозначается частота греческой буквой
ν
(«ню»). За единицу частоты принято одно колебание в секунду. Эта единица в честь немецкого учёного Генриха Герца названа герцем (Гц).
Период колебания (T) и частота колебаний
ν
связаны следующей зависимостью:
Свободные колебания в отсутствие трения и сопротивления воздуха называются собственными колебаниями, а их частота — собственной частотой колебательной системы.
Для описания закономерностей колебательной системы необходимо учитывать зависимость параметров колебания от параметров системы. Например, период колебаний и их частота зависят от массы груза и жёсткости пружины для физического маятника.

Рис. (3). Движение пустых качелей и качелей с мальчиком
Рассмотрим колебания двух одинаковых пустых качелей на рисунке (3). В один и тот же момент времени красные качели из положения равновесия начинают движение вперед, а зелёные качели из положения равновесия движутся назад. Движение качелей таково, что их амплитуды и периоды колебаний одинаковы. А если одинаковы периоды, то и частота колебаний совпадает. Однако, направлений движения качелей противоположно. О таких движениях говорят, что они движутся в противофазах.
Красные пустые качели и качели с мальчиком тоже колеблются с одинаковыми частотами. Направление скоростей этих качелей тоже совпадает. Это означает, что колебания происходят в одинаковых фазах, т.е. совпадают по фазе.
Фаза — физическая величина. Её используют для описания колебания тела.
Исходя из выше сказанного следует, что характеристиками колебательного движения являются:
- амплитуда,
- частота (можно использовать период),
- фаза.
Источники:
Рис. 1, 3. Движение пустых качелей и качелей с мальчиком.
Рис. 2. Колебания металлической и деревянной линеек.
Частота в физике, теория и онлайн калькуляторы
Частота
Определение частоты
Определение
Частотой называют физическую величину, характеризующую периодический процесс.
Она равна числу повторений или реализации событий за единицу времени. Обозначают частоту $nu ,$ могут встречаться другие варианты обозначений частоты, например $f$ или $F$.
Частота (наряду со временем) – это наиболее точно измеряемая величина.
Частота колебаний
Частота служит одним из основных параметров, характеризующих колебания.
Определение
Частота – это физическая величина обратная периоду колебаний (T). Частота – это число полных колебаний, которые совершаются за
единицу времени.
[nu =frac{1}{T}left(1right).]
В Международной системе единиц (СИ) частота измеряется в герцах или обратных секундах:
[left[nu right]=с^{-1}=Гц.]
Герц – единица измерения частоты периодического процесса, при которой за время в одну секунду протекает один цикл процесса. Единица измерения частоты периодического процесса получила свое наименование в честь немецкого ученого Г. Герца.
Частота биений, которые возникают при сложении двух колебаний, происходящих по одной прямой с разными, о близкими по величине частотами (${nu }_1 и {nu }_2$) равна:
[{nu =nu }_1- {nu }_2left(2right).]
Другой характеристикой колебаний является циклическая частота, которая равна:
[{omega }_0=2pi nu left(3right).]
Циклическая частота измеряется в радианах, деленных на секунду:
[left[{omega }_0right]=frac{рад}{с}.]
Частота колебаний тела, массой$ m,$ подвешенного на пружине с жесткостью $k$ равна:
[nu =frac{1}{2pi sqrt{{m}/{k}}}left(4right).]
Выражение (4) выполняется для упругих, малых колебаний. Масса пружины должна быть мала в сравнении с массой тела.
Частота колебаний математического маятника, длина нити которого $l$:
[nu =frac{1}{2pi sqrt{{l}/{g}}}left(5right),]
где $g$ – ускорение свободного падения.
Частота колебаний физического маятника:
[nu =frac{1}{2pi sqrt{{J}/{mgd}}}left(6right),]
где $J$ – момент инерции тела, совершающего колебания относительно оси; $d$ – расстояние от центра масс маятника до оси колебаний.
Формулы (4) – (6) приближенные. Чем меньше амплитуда колебаний, тем точнее результаты дают эти формулы.
Частота дискретных событий, частота вращения
Определение
Частотой дискретных колебаний ($n$) – называют физическую величину, которая равна количеству действий (событий) в единицу времени.
Если время, которое занимает одно событие обозначить как $tau $, то частота дискретных событий равна:
[n=frac{1}{tau }left(7right).]
Единицей измерения частоты дискретных событий является обратная секунда:
[left[nright]=frac{1}{с}.]
Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.
Частотой вращения ($n$) – называют величину, равную количеству полных оборотов, которое совершает тело в единицу времени. Если $tau $ – время, затрачиваемое на один полный оборот, то:
[n=frac{1}{tau }left(8right).]
Примеры задач с решением
Пример 1
Задание. Частица совершает гармонические колебания, которые описывает следующий закон: $x=6{sin left(frac{pi }{4}t+frac{pi }{3}right) }(м)$. Какова частота этих колебаний?
Решение. Рассмотрим уравнение движения частицы:
[x=6{sin left(frac{pi }{4}t+frac{pi }{3}right)left(1.1right). }]
Из этого уравнения мы видим, что амплитуда колебаний точки равна: $x_m=6 left(мright);;$ циклическая частота колебаний равна ${omega }_0=frac{pi }{4}(frac{рад}{с})$; начальная фаза колебаний: ${varphi }_0=frac{pi }{3}(рад)$. Частоту найдем, используя формулу:
[{omega }_0=2pi nu left(1.2right),]
из которой имеем:
[nu =frac{{omega }_0}{2pi }left(1.3right).]
Подставим значение циклической частоты, полученное из уравнения (1.1) в формулу (1.3), получаем:
[nu =frac{frac{pi }{4}}{2pi }=frac{1}{8} left(Гцright).]
Ответ. $nu =frac{1}{8}Гц$
Пример 2
Задание. К упругой пружине прикрепили маленький груз, при этом она растянулась на $Delta x$ (м). Какой будет частота колебаний грузика, если он будет совершать свободные колебания? Затуханием колебаний пренебречь.
Решение. Сделаем рисунок.
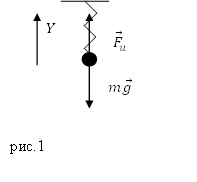
В нашей задаче мы имеем колебания пружинного маятника, частоту которого можно найти как:
[nu =frac{1}{2pi sqrt{{m}/{k}}}left(2.1right).]
Рассмотрим состояние равновесия тела, которое прикреплено к пружине (рис.1). Запишем второй закон Ньютона для сил, действующих на это тело в состоянии равновесия:
[moverline{g}+{overline{F}}_u=0 left(2.2right).]
Запишем проекцию уравнения (2.2) на ось Y:
[F_u=mgleft(2.3right).]
Так как колебания груза на пружине малые, то выполняется закон Гука и мы можем считать, что:
[F_u=kDelta x left(2.4right).]
Из (2.3) и (2.4) найдем отношение ${m}/{k}:$
[mg=kDelta x to {m}/{k}={Delta x}/{g}left(2.5right).]
Подставим полученный в (2.5) результат в (1.1), частота колебаний тела на пружине равна:
[nu =frac{1}{2pi sqrt{{Delta x}/{g}}}.]
Ответ. $nu =frac{1}{2pi sqrt{{Delta x}/{g}}}$
Читать дальше: эффект Доплера.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
