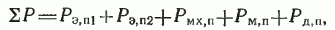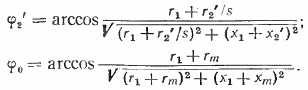Как найти частоту тока в обмотке ротора

Эдс, частота тока ротора, скольжение

Из выражения
(10.11) следует, что частота тока статора
пропорциональна частоте вращения
магнитного поля, созданного током
статора:

f₁ = n₀p/60.
(10.20)

Так как ротор
вращается в сторону поля (рис. 10.14),
частота пересечения его обмотки магнитным
полем будет определяться разностью
частот вращения магнитного поля и
ротора. По аналогии с (10.20) частота тока
ротора

f₂ =
(n₀ – n)р/60.
(10.21)

Из отношения
(10.20) к (10.21)

f₁/f₂ =
n/(n₀ – n)

получаем выражение
частоты тока ротора

f₂ =
f₁ (n₀ – n)/n₀ =
f₁s,
(10.22)

где s
— скольжение:

s =
(n₀ – n)/n₀.
(10.23)

Скольжение
— величина безразмерная, представляющая
собой частоту вращения ротора относительно
поля статора, выраженную в долях частоты
вращения поля статора. Когда ротор
неподвижен (n =
0),

Рис.  
10.14.   К  пояснению  скольжения
и частоты тока ротора

s =
(n₀ –
0)/n₀ =
1; f₂ = f₁s = f₁ •
1 = f₁.

Если ротор вращается
с частотой поля, то

s =
(n₀ – n₀)/n₀ =
0;    f₂ = f₁s = f2
• 0 = 0.

При неподвижном
роторе его обмотка относительно поля
находится в тех же условиях, что и обмотка
статора. Поэтому ЭДС обмотки ротора
может быть определена по аналогичной
формуле, что и ЭДС обмотки статора:

E_2к =
4,44f₁w₂Фk₀₂,
(10.24)

где w₂ —
число витков фазы обмотки ротора k₀₂ —
обмоточный коэффициент обмотки ротора.
Когда ротор вращается,

Е₂ =
4,44f₂w₂Фk₀₂.
(10.25)

Из отношения
(10.24) и (10.25) вытекает, что

E₂ = E_2к = f₂/f₁.
(10.26)

Подставив
в (10.26) вместо f₂ его
значение из (10.22), получим

E₂ = E_2k = f₁s/f₁ = E_2ks.
(10.27)

Таким образом, ЭДС
обмотки ротора пропорциональна
скольжению.

При n =
0 s =
1, E₂ = E_2к;
при n
= n₀ s
= 0, E₂ =
0.

Индуктивные сопротивления обмоток статора и ротора

Ток
обмотки статора создает вращающийся
магнитный поток, основная часть которого
Ф (см. рис. 10.13, б)
сцеплена с обмоткой статора и ротора,
а небольшая часть Ф_р1 —
только с обмоткой статора. Этот магнитный
поток называется потоком рассеяния.
Поток рассеяния Ф_р1 наводит
в обмотке статоpa ЭДС E_p1,
которую можно определить с помощью
выражения

Е_р1 =
4,44f₁Ψ_p1k₀₁.

Для облегчения
анализа работы двигателя и упрощения
расчетов ЭДС выражают обычно через
индуктивное сопротивление и ток обмотки:

Е_р1 =
– U_р1 =
– Ix₁,

где x₁ =
2πf₁L₁, L₁ =
Ψ_p1/I₁ —
индуктивное сопротивление и индуктивность
обмотки статора, обусловленные потоком
рассеяния.

Аналогичная
картина имеет место и в обмотке ротора.
Индуктивное сопротивление обмотки
ротора, обусловленное потоком рассеяния
Ф_р2,
равно

x_2s =
2πf₂L₂,
(10.28)

где L₂ =
Ψ_p2/I₂.

Подставив
в (10.28) вместо f₂ его
значение из (10.22), получим

x_2s =
2πf₁sL₂,

или

x_2s = x₂s,
(10.28a)

где
х₂ —
индуктивное сопротивление рассеяния
фазы обмотки неподвижного ротора.

Следовательно,
индуктивное сопротивление обмотки
ротора прямо пропорционально скольжению.

Ток и эквивалентная схема фазы обмотки ротора

Ток фазы обмотки
ротора

I2 =	E2	.
√r22 + (x2s)2

Подставив
вместо Е₂ и x_2s их
значения из (10.27) и (10.28, а),
получим

I2 =	E2ks	.
√r22 + (x2s)2

(10.29)

Рис.
10.15. Реальная (а)
и эквивалентная (б)
схемы фазы обмотки ротора (б)

а
затем,  разделив  числитель  и 
знаменатель  на s, 
получим

I2 =	E2k	.
√(r2/s)2 + x22

(10.30)

где E_2к и х₂ –
ЭДС и индуктивное сопротивление рассеяния
обмотки неподвижного ротора, когда
частота f₂ = f₁.
В (10.30) r₂/s можно
выразить следующим образом:

r2/s = r2 + r2	1 – s	.
s

Тогда

I2 =	E2k	.
√	(r2 + r2	1 – s	)2 + x22
	s

(10.31)

Сравнивая
(10.31) с выражением тока вторичной обмотки
трансформатора (8.11а), легко установить,
что величину r₂(1-s)/s можно
рассматривать как активное сопротивление
потребителя, подключенное ко вторичной
обмотке трансформатора. Таким образом,
эквивалентная схема фазы обмотки ротора
будет иметь тот же вид, что и схема
замещения вторичной обмотки трансформатора,
в которой вместо r_п включено
сопротивление r₂ (1
– s)/s.

На
рис. 10.15, а изображена
реальная, а на рис. 10.15, б —
эквивалентная схемы фазы обмотки ротора
асинхронного двигателя.

В
эквивалентной схеме
значения E_2к, х₂ и I₂ соответствуют
неподвижному ротору, хотя в действительности
ротор вращается, что учитывается
включением в цепь эквивалентного
сопротивления r₂(1
– s)/s.

Отношение E₁/E_2к = k называется
по аналогии с трансформатором коэффициентом
трансформации асинхронного двигателя.

Соседние файлы в папке Архив ZIP – WinRAR

• #
• #

Из (3.3) следует, что частота тока  обмотки  ротора  пропорциональна n₁ – n, т.е.

Если числитель и знаменатель (3.4) умножить на n₁, тогда

(3.5)

Для f₁ = 50 Гц и s =2÷8%, частота тока обмотки ротора будет  f2 =1÷4Гц.

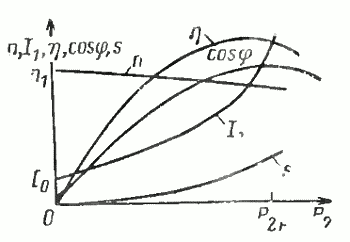
 Рабочие характеристики асинхронного двигателя – зависимости потребляемого тока I₁ и мощности Р₁, КПД, cos φ и скольжения s от полезной механической мощности P₂. Эти характеристики определяются при постоянном напряжении U₁ и частоте f₁ сети.

Рабочие характеристики асинхронного двигателя могут быть получены экспериментально (опытным путем) и рассчитаны с помощью схемы замещения.

Ниже приводится расчет рабочих характеристик асинхронного двигателя по схеме замещения.

По обмотке статора асинхронной машины протекает многофазная система токов, обычно трехфазная, которая создает в воздушном зазоре машины вращающееся магнитное поле (магнитный поток Ф).

 Вращающееся магнитное поле в свою очередь индуктирует (наводит) в проводниках обмотки ротора ЭДС, под действием которой в замкнутой накоротко обмотке ротора протекает ток I₂. Этот ток, взаимодействуя с магнитным потоком Ф, создает механическую силу, стремящуюся привести ротор во вращение в сторону вращения магнитного поля.

Определим, с какой частотой вращения магнитное поле машины пересекает проводники ротора. Эта частота равна, об/мин:

             (9)

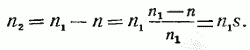
Определим частоту ЭДС f₂, которая наводится магнитным полем асинхронной машины в проводниках ротора, Гц:

f₂=р n₂/60.            (10)

Если учесть, что n₂=n₁s [см. формулу (9)], то можно записать

       (11)

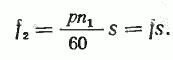
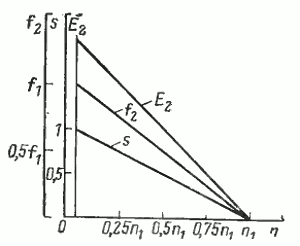
Из формулы (11) видно, что если ротор машины неподвижен (n=0, s=l), то частота ЭДС, наводимой в роторе, равна частоте сети. По мере увеличения частоты вращения ротора ЭДС понижается и при синхронной частоте будет равна нулю. На рис. 13 показаны изменения скольжения, частоты и ЭДС в роторе в зависимости от частоты вращения ротора.

Рис. 13. Зависимость скольжения s, частоты f₂ и ЭДС, наводимой в роторе, E2 от частоты вращения асинхронного двигателя n

Из закона электромагнитной индукции следует, что при гармоническом изменении магнитного поля наводимая в обмотке ЭДС равна:

E=4,44fwk_обФ_max,             (12)

где f — электрическая частота, Гц; w — число последовательно соединенных витков фазы; k_об — обмоточный коэффициент; Ф_max — максимальное значение рабочего потока, сцепленного с обмоткой, Вб.

Знание частоты f₂ в роторе дает возможность определить ЭДС ротора Е₂ при произвольной частоте вращения (скольжении), В, в виде

E₂=4,44f₂w2k_об2Ф_max,           (13)

где w₂ — число последовательно  соединенных витков обмотки ротора; k_об2 — обмоточный   коэффициент   ротора.

Подстановка f₂  из формулы (11) дает, В,

E_2s=4,44f s w₂k_об2Ф_max=sE₂,     (   14)

где Е₂ — ЭДС, наводимая в неподвижной обмотке ротора потоком Ф_max, В.

Осветим теперь важный для анализа работы асинхронных двигателей вопрос о зависимости вращающегося магнитного потока двигателя от режима работы машины. Для этого, чтобы представить себе эту зависимость, определим вначале, какую ЭДС Е₁ наводит этот поток в каждой фазе обмотки статора, В:

E₁=4,44fw₁k_об1Ф_max,     (15)

где w₁ — число витков одной фазы статора; k_об1 —обмоточный коэффициент обмотки статора.

Напряжение U₁, приложенное к статору, уравновешивается ЭДС E₁ и падением напряжения I₁z₁ на внутреннем сопротивлении z₁=r₁+jx₁ обмотки статора (х₁— индуктивное сопротивление обмотки, определяемое потоком рассеяния) . При изменении нагрузки двигателя от нуля (холостой ход) до номинальной падение напряжения составляет 5—10 % приложенного. Таким образом, с достаточной для качественного анализа точностью можно полагать, что напряжение U₁ полностью компенсируется ЭДС Е1 т. е. .

U₁≈E₁         (16)

Учитывая формулу (15), нетрудно заключить, что ЭДС и вращающийся магнитный поток двигателя зависят от приложенного к двигателю напряжения. При постоянном напряжении поток Фmах остается приблизительно постоянным независимо от изменения нагрузки двигателя.

Рассмотрим вначале явления, происходящие в машине с заторможенным ротором и замкнутой накоротко обмоткой ротора. Асинхронный двигатель в этом режиме подобен трансформатору с короткозамкнутой вторичной обмоткой. Отличие состоит в том, что вторичная магнитная цепь отделена от первичной воздушным зазором, первичная обмотка (статора) и вторичная обмотка (ротора) равномерно распределены по окружности, а магнитное поле вращающееся.

Как видно из формулы (14) и рис. 13, ЭДС, наводимая в обмотке ротора, когда он неподвижен, является максимальной. В силу этого и ток, проходящий по обмоткам статора и ротора, также будет наибольшим. Этот режим называется режимом короткого замыкания (КЗ). Ток статора в этом режиме называется током короткого замыкания и превышает его номинальный ток в 4—7 раз. Асинхронный двигатель в таких условиях нельзя длительно оставлять под полным напряжением из-за перегрева обмоток, который может привести к аварии.

Для определения тока короткого замыкания двигателя делают опыт КЗ. Этот опыт заключается в том, что к двигателю с заторможенным (неподвижным) ротором подводят пониженное напряжение, регулируя которое, устанавливают номинальный ток. Напряжение, подводимое к двигателю в опыте КЗ, оказывается малым (15— 20%) по сравнению с номинальным. На базе этого опыта можно в безопасных для двигателя условиях определить величину тока короткого замыкания /к при номинальном напряжении, А:

       (17)

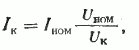
где U_ном — номинальное напряжение, В; U_к — напряжение в опыте КЗ при номинальном токе, В; I_ном — номинальный ток, А.

Замеряя в этом опыте по ваттметру мощность короткого замыкания Р_к, подводимую к одной фазе двигателя,  находят также  коэффициент  мощности в режиме  КЗ

      (18)

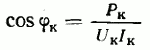
и эквивалентное активное сопротивление статора и ротора двигателя гк в режиме КЗ на одну фазу, Ом,

r_к=P_к/I_ном2              (19) 

Это эквивалентное активное сопротивление равно сумме активного сопротивления статора и приведенного активного сопротивления ротора. Понятие о приведенном активном и реактивном сопротивлении ротора будет дано ниже.

Определив угол φк по значению cosφк из формулы (18), легко найти и эквивалентное реактивное сопротивление двигателя в режиме короткого замыкания, Ом:

х_к=r_кctgφ_к (20)

Индуктивное сопротивление хк равно сумме индуктивного сопротивления статора и приведенного индуктивного сопротивления ротора.

Поскольку частота вращения ротора двигателя в этом режиме равна нулю, его механическая мощность также равна нулю. Потери в стали во время опыта короткого замыкания очень малы, так как мал вращающийся магнитный поток. Поэтому мощность Р_к, которая подводится к машине, почти вся идет на нагрев проводников обмоток статора и ротора. То же самое можно сказать о режиме КЗ при полном напряжении.

Теперь представим себе, что обмотка ротора разомкнута, а обмотка статора включена в сеть. Ток по роторной обмотке при этом не проходит и асинхронный двигатель подобен трансформатору, но уже в режиме холостого хода (XX). Так как ток в проводниках ротора отсутствует, то механическая сила не возникает и ротор остается неподвижным.

По обмотке статора при этом проходит ток холостого хода I₀, который создает магнитодвижущую силу (МДС), необходимую для создания магнитного потока Ф_max. Поскольку в магнитной цепи асинхронного двигателя имеется зазор, то для создания магнитного потока требуется относительно больший ток, чем в трансформаторе. В двигателях большой и средней мощности ток XX составляет 25—35, а в двигателях малой мощности — 35—60% номинального тока.

Наводимая в неподвижном роторе ЭДС может быть определена по формуле (14), если учесть, что скольжение в этом режиме равно 1. Отношение ЭДС в обмотке статора к ЭДС в обмотке ротора называется коэффициентом трансформации ЭДС и может быть определено по формуле

           (21)

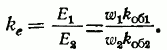
Мощность, потребляемая двигателем в режиме XX при неподвижном роторе, расходуется на потери в проводниках статора двигателя, потери на перемагничивание и вихревые токи в стали статора и в стали ротора.

Важно заметить, что режим XX при неподвижном роторе очень близок к режиму, который возникает, когда  асинхронный двигатель не выполняет полезной работы и вращается на холостом ходу. В этом случае частота вращения ротора двигателя почти равна синхронной, а  скольжение примерно равно нулю [см. формулы (4), (9) и рис. 13]. Электродвижущая сила в роторе будет близкой к нулю, и, следовательно, подобно режиму XX при неподвижном роторе практически равен  нулю ток в роторе. При холостом ходе вращающегося двигателя ток в обмотке статора, как и в случае холостого хода неподвижного двигателя, определяется в основном МДС, необходимой для создания магнитного потока Ф_max.

При вращении ротора в двигателе появляются потери, которых нет в случае неподвижного ротора; это механические потери на трение и вентиляционные. Однако когда частота вращения ротора примерно равна синхронной, исчезают потери в стали ротора двигателя, поскольку магнитное поле теперь очень медленно перемещается относительно ротора и его сталь почти не перемагничивается. Таким образом, потери и, следовательно, мощность в двух режимах холостого хода оказываются близкими.

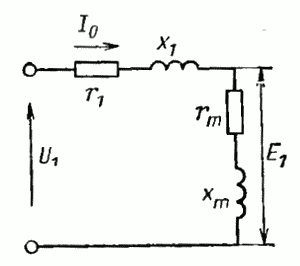
Асинхронная машина в режиме холостого хода может быть представлена схемой замещения, показанной на рис. 14. Для определения параметров и характеристик двигателя помимо опыта КЗ выполняют опыт XX, во время которого замеряют ток обмотки статора I₀ (А) и потребляемую мощность Р₀ (Вт). Это позволяет определить сопротивления в схеме замещения двигателя на холостом ходу, а также коэффициент мощности XX:

cosφ₀=P₀/(UI₀).            (22)

Рис. 14. Схема замещения первичной цепи (статора)   асинхронного  двигателя,  работающего  в режиме холостого хода

Перейдем теперь к рассмотрению общего случая режима нагрузки, когда ротор вращается с частотой, меньшей частоты XX. Определим, какой ток будет проходить по обмотке ротора во всем диапазоне рабочих режимов. Наводимая вращающимся магнитным потоком ЭДС в обмотке ротора зависит при постоянном напряжении только от скольжения и может быть найдена по (14). Ток ротора будет, очевидно, зависеть от ЭДС, наводимой в роторе, и сопротивления обмотки ротора, при этом полное сопротивление цепи в случае переменного тока определяется не только активным сопротивлением проводников обмотки, но и ее индуктивным сопротивлением. Индуктивное сопротивление обмотки ротора изменяется так же, как и ЭДС ротора E_2s, Ом:

x_2s=2πf₂L₂=s2πf₁L₂ =sx₂,      (23)

где L₂ — индуктивность обмотки ротора, Гн; х₂— индуктивное сопротивление рассеяния обмотки неподвижного ротора при s=l, Ом.

Теперь, используя закон Ома для цепей переменного тока, найдем ток ротора, А:

      (24)

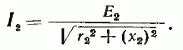
Учитывая (14) и (23), формулу (24) можно записать иначе:

           (25)

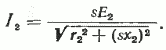
Таким образом, можно видеть, что при скольжении, равном нулю или близком к нему (это соответствует синхронной или близкой к синхронной частоте вращения ротора), ток ротора равен нулю или очень мал. Это совпадает с тем, что было сказано выше относительно режима XX при вращающемся роторе. По мере уменьшения частоты вращения двигателя, т. е. при увеличении скольжения, ток возрастает за счет увеличения ЭДС ротора, однако рост тока ограничивается увеличением индуктивного сопротивления ротора.

Если разделить числитель и знаменатель выражения (25) для тока ротора I₂ на s, то получим следующую формулу:

           (26)

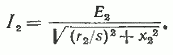
Из этого следует, что если мы примем, что ротор неподвижен, а его активное сопротивление меняется обратно пропорционально скольжению, то по его обмотке будет проходить точно такой же ток, как и при вращающемся роторе. Удобство такого преобразования состоит в том, что оно позволяет вместо вращающегося ротора (вращающаяся вторичная электрическая цепь) рассматривать неподвижный ротор (неподвижная вторичная цепь).

Однако изучение процессов, происходящих в асинхронной машине, и расчет ее характеристик можно сделать более удобными, если заменить реальную обмотку ротора эквивалентной с числом витков в фазе и числом фаз, равным им у первичной обмотки (обмотки статора), т. е. вместо обмотки ротора с числом фаз m₂, числом витков в фазе w₂ и обмоточным коэффициентом k_об2 будем полагать, что обмотка ротора имеет число фаз ти число витков в фазе w₁ и обмоточный коэффициент k_об1. Эта замена называется приведением обмотки ротора к обмотке статора. Нетрудно видеть, что магнитный поток Ф в этом случае будет наводить в эквивалентной (приведенной) обмотке ротора ЭДС, равную ЭДС обмотки статора E₂‘=E₁ (штрихом будем обозначать приведенные величины).

Замена обмотки ротора не должна привести к изменению потребляемой мощности, потерь, магнитодвижущей силы и фазы тока обмотки. Из этого условия определяются приведенные величины тока, активного и индуктивного сопротивлений обмотки ротора .

В соответствии с (13) имеем, В

           (27)

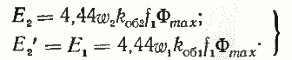
Из формул (27) вытекает отношение между ЭДС приведенной и реальной обмоток заторможенного ротора, которое называется коэффициентом трансформации ЭДС или напряжений. Он равен:

          (28)

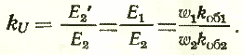
Из условия неизменности магнитодвижущих сил F₂‘ =F₂ следует, что

   

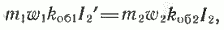
откуда вытекает отношение между токами, которое называется коэффициентом трансформации токов. Он равен:

          (29)

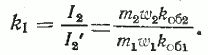
Из условия неизменности потерь в обмотке ротора при приведении следует, что

   

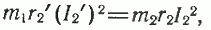
откуда

           (30)

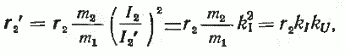
или r₂‘=k_rr₂,

где k_r=k_Ik_U — коэффициент приведения сопротивлений.

Из условия неизменности фазы тока обмотки ротора следует

           (31)

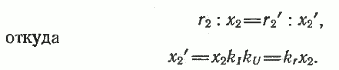
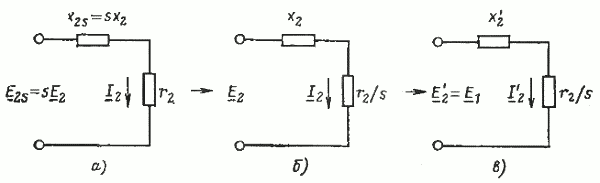
Процесс приведения цепи ротора показан на рис. 15. От схемы замещения обмотки вращающегося ротора (рис. 15,а) переходим к схеме замещения неподвижного ротора (рис. 15,б), а затем приводим обмотку ротора к обмотке статора (рис. 15, в).

Рис. 15. Схемы замещения: а — обмотки вращающегося ротора; б — неподвижного ротора; в — обмотки ротора, приведенной к обмотке статора

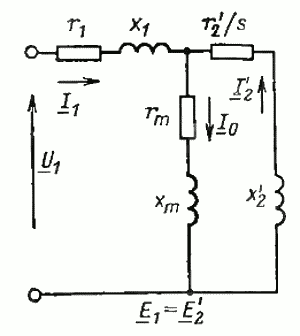
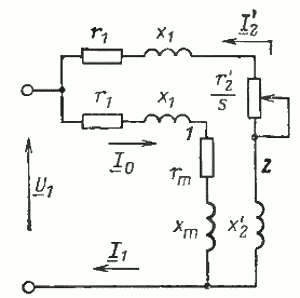
Поскольку теперь ЭДС Е₁ первичной обмотки равна ЭДС Е₂‘ вторичной обмотки, мы можем соединить электрически соответствующие точки схемы замещения обмотки статора и ротора. В результате получим схему замещения асинхронного двигателя, показанную на рис. 16. Здесь активное сопротивление r_m отражает наличие потерь в стали двигателя. Для двигателей средней и большой мощности удобнее пользоваться упрощенной схемой замещения, приведенной на рис. 17.

Рис. 16. Т-образная схема замещения  асинхронного двигателя

Рис. 17. Упрощенная Г-образная схема замещения  асинхронного двигателя

Используя последнюю схему, легко найти токи и ЭДС в обмотках, подводимую и полезную мощность, а также мощность потерь при любой частоте вращения двигателя. Для этого следует лишь найти скольжение, соответствующее заданной частоте n, по формуле (4)
и вычислить сопротивление r₂‘/s в схеме по рис. 17. После этого нетрудно найти ток намагничивания I₀ и приведенный ток I₂‘ в роторной цепи, А:

              (32)

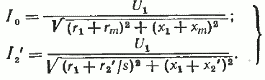
Это дает возможность вычислить электрические потери в обмотке статора трехфазного двигателя (m₁=3), Вт:

               (33)

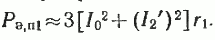
Электрические потери в обмотке ротора (Вт) можно найти, предварительно рассчитав по (30) приведенное сопротивление ротора r₂‘  (Ом):

              (34)

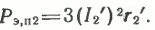
Суммарная активная мощность, передаваемая со статора на ротор, как видно из схемы (рис. 17), будет равна, Вт:

               (35)

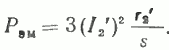
Эта мощность передается на ротор электромагнитным путем и поэтому называется электромагнитной мощностью.

Если из электромагнитной мощности вычесть мощность электрических потерь в обмотке ротора, то получим полную механическую мощность двигателя, Вт:

               (36)

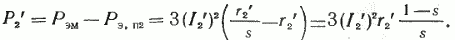
Полная механическая мощность расходуется на вращение приводного механизма (полезная механическая мощность) и на покрытие механических Р_мх.п и добавочных Р_д.п потерь самого двигателя. Поэтому полезная механическая мощность Р₂ будет равна, Вт:

               (37)

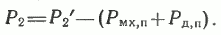
Коэффициент полезного действия двигателя по определению равен отношению отдаваемой (полезной механической) мощности к потребляемой (активной электрической) мощности. Разность между этими мощностями составляют потери в двигателе, равные, Вт:

 

где P_м.п=m₁I₀2r_m — магнитные потери или потери в стали. Таким образом, КПД двигателя равен:

              (38)

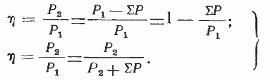
Использование первого или второго выражения для КПД определяется тем, какая из мощностей — P₁ или Р₂— известна. На практике наиболее часто применяется первое выражение (38).

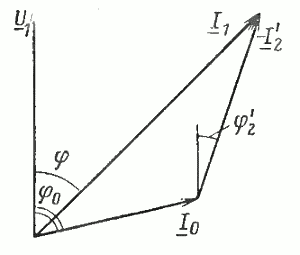
Используя схему замещения, можно определить также ток, потребляемый двигателем из сети, т. е. ток статора, который равен сумме двух токов. Первый из них — это ток XX, который протекает по цепи 1 (рис. 17) и не изменяется при изменении частоты вращения ротора, второй — ток ротора I₂‘, который определяется по (32). Складывая геометрически эти два тока, можно получить ток статорной обмотки. Такое геометрическое сложение показано на рис. 18. Углы φ₂‘, φ₀, необходимые для построения, можно найти с помощью схемы замещения (см. рис. 17):

Таким образом, знание параметров схемы замещения (r₁, x₁, r₂‘, х₂‘, rm, хm) и приложенного напряжения U₁ (напряжение сети) позволяет с помощью приведенных выше формул определить полезную мощность, токи, потери, КПД, коэффициент мощности двигателя при различных скольжениях (частоте вращения).

Рис. 18. Диаграмма токов асинхронного двигателя  

Зависимости потребляемого тока I₁ и мощности Р₁, КПД, cosφ и скольжения s от полезной механической мощности P₂ носят название рабочих характеристик двигателя. Эти характеристики определяются при постоянном напряжении U₁ и частоте f₁ сети. Пример рабочих характеристик приведен на рис. 19.

Рис. 19. Рабочие характеристики асинхронного двигателя 

Рассмотрим рабочие характеристики асинхронного двигателя. При холостом ходе (полезная мощность Р₂—0) скольжение s также равно нулю (частота вращения ротора n практически равна синхронной), сопротивление r₂/’s равно бесконечности (см. рис. 17) и ток I₂‘==0. По обмотке статора протекает ток холостого хода I₀. Коэффициент полезного действия η равен нулю, так как равна нулю полезная мощность Р₂, а коэффициент мощности равен коэффициенту мощности для тока холостого хода (cosφ₁=cosφ₀).

При увеличении нагрузки частота вращения ротора уменьшается и увеличивается скольжение s. За счет увеличения s уменьшается сопротивление цепи 2 (см. рис. 17) и увеличивается ток ротора, а следовательно, и ток статоpa. Поскольку увеличивается полезная мощность, растет, КПД двигателя, а также коэффициент мощности.

Обычно номинальная мощность на валу двигателя достигается уже при небольшом понижении частоты вращения ротора и вся область рабочих режимов находится в диапазоне скольжений от 0 до 2—5%.

Поэтому скоростная характеристика n=f(P₂) у асинхронного двигателя имеет небольшой наклон к оси абсцисс. Характеристики такого вида принято называть жесткими. Соответственно характеристика s=f(P₂) имеет слабый подъем при возрастании нагрузки. В асинхронном двигателе частота вращения ротора меньше частоты вращения поля, за счет чего обеспечивается наведение ЭДС, а также создание тока 1% в обмотке ротора и вращающего электромагнитного момента, под действием которого ротор приходит во вращение.

Характеристика cosφ=f(P₂) лежит в области значений, меньших 1, так как асинхронный двигатель всегда потребляет ток I₀, почти не зависящий от нагрузки в диапазоне мощностей от Р₀ до Р₂≈Р_ном. При XX обычно  φ₀<0,2, т. е. он содержит большую реактивную составляющую. При увеличении нагрузки cosφ быстро возрастает и достигает максимального значения при мощности Р₂≈Р_2ном. При увеличении нагрузки выше номинальной cosφ  несколько снижается.

Коэффициент полезного действия достигает своего максимального значения при Р₂≈ (0,6÷0,8)Р_2ном и снижается при дальнейшем росте нагрузки. Поскольку двигатель обычно работает при переменной нагрузке, изменяющейся в пределах (0,6—1)Р_2ном, то КПД в этом диапазоне изменения нагрузки должен быть достаточно высок.

При рассмотрении вопроса о получении переменного тока указывают, что за один оборот ротора индуктированная в проводниках обмотки генератора электродвижущая сила (ЭДС) имела один период. Если ротор генератора делает, например 5 об/сек, то ЭДС будет иметь 5 пер/сек или частота тока генератора будет равна 5 Гц. Следовательно, число оборотов в секунду ротора генератора численно равно частоте тока.

Частота тока f выражается следующим соотношением:

где n – число оборотов ротора в минуту.

Для получения от генератора стандартной частоты тока – 50 Гц ротор должен делать 3000 об/мин, то есть

Однако наши рассуждения были справедливы только для двухполюсного генератора, то есть для машины с одной парой полюсов p.

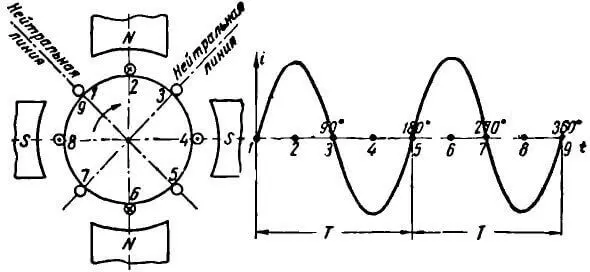
Если машина четырехполюсная, то есть число пар полюсов равно двум: p = 2 (рисунок 1), то один полный период изменения тока будет иметь место за пол-оборота ротора (1 – 5 положения проводника на чертеже). За второй полуоборот ротора ток будет иметь еще один период. Следовательно, за один оборот ротора четырехполюсной машины ток в проводнике имеет два периода. В шестиполюсной машине (p = 3) ток в проводнике за один оборот ротора будет иметь три периода.

Рисунок 1. Изменение переменного тока в проводнике ротора четырехполюсного генератора

Таким образом, для машин, имеющих p пар полюсов, частота тока при об/сек будет в p раз больше, чем для двухполюсной машины, то есть

Отсюда формула зависимости скорости вращения от частоты и числа пар полюсов будет иметь следующий вид:

Пример 1. Определить частоту переменного тока, получаемого от генератора с восемью полюсами (p = 4), скорость вращения ротора которого n = 750 об/мин. Подставляя в формулу для определения частоты тока значение p и n получим:

Пример 2. Определить скорость вращения ротора двадцатиполюсного генератора (p = 10), если частотомер показал частоту тока f = 25 Гц. Подставляя в формулу для определения числа оборотов ротора n значения p и f, получим:

Пример 3. Скорость вращения ротора асинхронного двигателя, составляет 250 об/мин. Определить число пар полюсов асинхронного двигателя, если частота тока питающей сети равна 50 Гц:

Следовательно, двигатель имеет 24 полюса.

Источник: Кузнецов М. И., “Основы электротехники” – 9-е издание, исправленное – Москва: Высшая школа, 1964 – 560 с.

ПРАКТИЧЕСКАЯ РАБОТА №6

«Расчет ЭДС и токов асинхронных
двигателей»

ЦЕЛЬ РАБОТЫ: рассчитать значение скольжения, ЭДС асинхронного двигателя
и величину протекающих в нем  токов.   

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ:

В соответствии с принципом обратимости элек­трических
машин асинхронные машины могут работать как в двигательном, так и в генератор­ном
режимах. Кроме того, возможен еще и режим электромагнитного торможения
противовключением. 

Двигательный режим. При включении обмотки статора в сеть трех­фазного тока возникает
вращающееся магнитное поле, которое, сцепляясь с короткозамкнутой обмот­кой
ротора, наводит в ней ЭДС. При этом в стерж­нях обмотки ротора появляются токи.
В результате взаимодействия этих токов с вращаю­щимся магнитным полем на роторе
возникают элек­тромагнитные силы. Совокупность этих сил создает
электромагнитный вращающий момент, под дейст­вием которого ротор асинхронного
двигателя при­ходит во вращение с частотой n₂ < n₁ в сторону вра­щения поля статора. Если вал асинхронного
двигателя механически соединить с валом какого-либо исполнительного механизма
ИМ (станка, подъ­емного крана и т. п.), то вращающий момент двига­теля М,
преодолев противодействующий (нагрузоч­ный) момент М_нагр,
исполнительного механизма, приведет механизм во вращение. Следовательно,
электрическая мощность Р₁, поступающая в двига­тель из сети, в
основной своей части преобразуется в механическую мощность Р₁ и передается исполни­тельному
механизму ИМ.

   Весьма важным параметром асинхронной ма­шины
является скольжение — величина, характери­зующая разность частот вращения
ротора и вра­щающегося поля статора:

S = (n₁ – n₂)/ n₁                   (формула 6.1)

Скольжение выражают в долях единицы либо в
процентах. В последнем случае величину, получен­ную по (6.1), следует умножить
на 100.

С увеличением нагрузочного момента на валу
асинхронного двигателя частота вращения ротора n₂ умень­шается. Следовательно, скольжение асинхронного двигателя зави­сит
от механической нагрузки на валу двигателя и может изме­няться в диапазоне 0
< s ≤ 1.

Скольжение, соответствующее номинальной
нагрузке двигателя, называют номинальным скольжением s_hom. Для асинхронных
дви­гателей общего назначения s_hom
= 18%,
при этом для двигателей большой мощности s_ном = 1%, а для двигателей малой мощности s_ном = 8%.

Формула для опре­деления асинхронной частоты вращения
(об/мин):

n₂ = n₁(1-s).                           (формула 
6.2)

Пример 6.1. Трехфазный
асинхронный двигатель с числом полюсов 2р = 4 работает от сети с
частотой тока f₁ = 50 Гц.
Определить частоту вращения двигателя при номинальной нагрузке, если скольжение
при этом составляет 6%.

Решение.
Синхронная частота вращения по (6.9) n₁ = f₁ 60/ р = 50 • 60/4 = 1500 об/мин.

Номинальная частота вращения по (6.2): n_ном = n₁(1 – s_ном ) = 1500(1 – 0,06) = 1412 об/мин.

Генераторный режим. Если обмотку статора включить в сеть, а ротор асинхронной машины
посредством приводного дви­гателя ПД (двигатель внутреннего сгорания, турбина и
т. п.),  яв­ляющегося источником механической энергии, вращать в направ­лении
вращения магнитного поля статора с частотой n₂ > n₁, то направление движения ротора относительно поля
статора изме­нится на обратное (по сравнению с двигательным режимом работы пой
машины), так как ротор будет обгонять поле статора. При этом скольжение станет
отрицательным, а ЭДС, наведенная в обмотке ротора, изменит свое направление.
Электромагнитный момент на роторе М также изменит свое направление, т. е. будет
направлен встречно вращающемуся магнитному полю статора и станет тормозящим по
отношению к вращающемуся моменту приводного двигателя М₁. В этом
случае механическая мощность приводного двигателя в основной своей части будет
преобразована в электрическую активную мощность Р₂ перемен­ного
тока. Особенность работы асинхронного генератора состоит в том, что вращающееся
магнитное поле в нем создается реактивной мощностью Q
трехфазной сети, в которую включен генератор и да он отдает вырабатываемую
активную мощность Р₂. Следовательно,
для работы асинхронного генератора необходим источник переменного тока, при
подключении к которому происходит возбуждение генератора.

Скольжение асинхронной машины в генераторном
режиме может изменяться в диапазоне       – ∞ < s <
0, т. е. оно может прини­мать любые отрицательные значения.

Наибольшее практическое применение получил
двигательный режим асинхронной машины, т. е. чаще используют асинхронные
двигатели, которые составля­ют основу современного электропривода, выгодно
отличаясь от других электродвигателей простотой конструкции и высокой на­дежностью.

Магнитодвижущая сила обмотки статора созда­ет магнитный поток, который замыкается через эле­менты магнитной
системы машины. Магнитную систему асинхронной машины называют неявнополюсной,
так как она не имеет явно выра­женных магнитных полюсов. Количество магнитных
полюсов в неявнополюсной магнитной системе определяется числом полюсов в
обмотке, возбуждающей магнитное поле, в данном случае в обмотке статора.
Магнитная система маши­ны, состоящая из сердечников статора и ротора, представляет
собой разветвленную симметричную магнитную цепь.

Значение МДС на пару полюсов позволяет определить
намагничиваю­щий ток (основную гармонику) обмотки статора:

I_1μ =                                    (формула
6.3)

Исходным параметром при расчете магнитной
цепи асин­хронного двигателя является максимальная магнитная индукция в
воздушном зазоре В_δ. Величину В_δ  принимают по
рекомендуемым значениям в зависимости от наружного диаметра сердечника статора D_1нар и числа полюсов 2р.

Магнитная индукция В_δ определяет
магнитную нагрузку двигателя: при слишком малом В_δ магнитная система
двигателя недогружена, а поэтому габаритные размеры двигателя получаются
неоправданно большими; если же задаться чрезмерно большим течением В_δ,
то резко возрастут магнитные напряжения на участ­ках магнитной системы,
особенно в зубцовых слоях статора и ротopa, в результате
возрастет намагничивающий ток статора I_1μ  снизится КПД двигателя.

Расчет магнитной цепи асинхронного
двигателя. Расчет магнитной цепи электрической машины
состоит в ос­новном в определении магнитных напряжений для всех ее участ­ков.
Магнитное напряжение F_x для любого участка
магнитной це­пи равно произведению напряженности поля на этом участке Н_х
на его длину l_Х.

Участки магнитной цепи различаются
конфигурацией, разме­рами и материалом. Наибольшее магнитное напряжение в
воздуш­ном зазоре δ. Напряженность магнитного поля в воздушном зазоре

H_δ = B_δ/
μ₀, где μ₀ = 4π/ 10^-7  Гн/м. Расчетная длина
зазора l_δ = δk_δ
, где k_δ, — коэффициент воздушного зазора,
учитывающий увеличение магнитного сопротивления зазора, вызванное зубчато­стью
поверхностей статора и ротора, ограничивающих воздушный зазор в асинхронном
двигателе (k_δ > 1). Учитывая это, получим вы­ражение
магнитного напряжения воздушного зазора (А):

F_δ
= 0,8 B_δ δ k_δ 10³.                    (формула
6.4)

где δ — значение
одностороннего воздушного зазора, мм.

Обычно магнитное напряжение двух воздушных
зазоров, вхо­дящих в расчетную часть магнитной цепи асинхронного двигателя,
составляет — 85% от суммарной МДС на пару полю­сов . Из
этого следует, насколько значительно влияние вели­чины воздушного зазора  δ на свойства двигателя. С увеличением δ МДС  значительно возрастает, что ведет к
увеличению намаг­ничивающего тока статора I_1μ, а, следовательно, ведет к росту потерь и снижению КПД двигателя. И
наоборот, с уменьше­нием δ  уменьшается , что ведет к росту КПД, т. е. двигатель
становится более экономичным в эксплуатации. Однако при слишком малых зазорах δ усложняется изготовление двигателя (он становится менее
технологичным), так как требует более высокой точности при обработке деталей и
сборке двигателя. При этом снижается надежность двигателя – возрастает
вероятность возникновения не­равномерности зазора и, как следствие, вероятность
задевания ро­тора о статор.

Пример 6.2. Воздушный зазор трехфазного асинхронного двигателя δ = 0,5 мм, максимальное
значение магнитной индукции В_δ  = 0,9 Тл. Обмотка
статора              четырехполюсная, число последовательно соединенных витков
в обмотке одной фазы ω₁ = 130, обмоточный коэффициент k_об1 = 0,91. Определить значение намагничивающего
тока обмотки статора I_1μ, если коэффициент
воздушного зазора      k_δ = 1,38, а коэффициент
магнитного насыщения k_μ = 1,4.

Решение.

Магнитное напряжение воздушного зазора по (6
.4)

F_δ = 0,8 В_δ
δ k_δ • 10³ = 0,8 • 0,9 • 0,5 • 1,38 •
10³ = 497 A.

Так как коэффициент магнитного насыщения k_μ = _ном / (2F_δ), то МДС обмотки статора в режиме х.х. на пару полюсов _ном = 2F_δ  k_μ =2 • 497 • 1,4 = 1392 А.

Намагничивающий ток статора по (6.3)

I_1μ = p _ном
/ (0,9 m₁ ω₁ k_об1) = 2 • 1392 / (0,9 • 3 • 130 • 0,91) = 8,7 A

Если воздушный зазор данного двигателя
увеличить на 20%, т. е. принять δ = 0,6 мм (при прочих
неизменных условиях), то намагничивающий ток статора станет равным  I_1μ = 10,4 А, т. е. он возрастет
пропорционально увеличению воз­душного зазора.

Электродвижущие силы, наводимые в обмотке
ротора. Асинхронный двигатель аналогичен трансформатору,
у которо­го вторичная обмотка (обмотка ротора) вращается. При этом вра­щающийся
магнитный поток сцепляется не только с обмоткой ста­тора, где индуцирует ЭДС Е_и но и с обмоткой вращающегося рото­ра, где индуцирует ЭДС.  В
процессе работы асинхронного двигателя ротор вращается в сто­рону вращения поля
статора с частотой n₂.
Поэтому частота вра­щения поля статора относительно ротора равна разности
частот вращения (n₁ – n₂). Основной магнитный поток Ф, обгоняя
ротор с частотой вращения  n_s = (n₁ – n₂), индуцирует в обмотке ротора ЭДС

Е₂
= 4,44 f₂ Ф ω₂ к_об2                         (формула
6.5)

где f₂— частота ЭДС Е_2s в роторе,
Гц; ω₂ — число последовательно соединенных витков одной фазы обмотки
ротора; k_o62 —
обмоточный коэффициент обмотки ротора.

Частота ЭДС (тока) в обмотке вращающегося
ротора пропор­циональна частоте вращения магнитного поля относительно ротора n_s = n₁ – n₂, называемой частотой скольжения:

f₂ = pn_s
/ 60 = p(n₁ – n₂) / 60,

или

f₂ = =  =
f₁s       (формула 6.6)

т. е. частота ЭДС (тока) ротора
пропорциональна скольжению. Для асинхронных двигателей общепромышленного
назначения эта частота обычно невелика и при f₁ = 50 Гц не превышает нескольких герц, так при s =
5%  частота f₂ = 50 0,05 = 2,5 Гц.  

E_2s =
4,44 f₁ s Ф ω₂ k_об2
= E₂ s.         (формула 6.7)

Здесь Е₂ –  ЭДС, наведенная в
обмотке ротора при скольжении s = 1, т. е. при неподвижном
роторе, В.

Уравнения МДС и токов асинхронного
двигателя. МДС обмоток статора и ротора на один полюс
в режиме на­груженного двигателя

                                            
F₁ = 0,45 m₁ I₁ ω₁ k_об1/ P

       F₂
= 0,45 m₂ I₂ ω₂ k_об2/
P            (формула 6.8)

где m₂ — число фаз в обмотке
ротора; k_o62 —
обмоточный коэффи­циент обмотки ротора.

С подключением нагрузки в фазах обмотки
статора появляются токи I_А,
I_B, I_C.  При этом
трехфазная обмотка ста­тора создает вращаю­щееся магнитное поле. Частота вращения
этого поля равна частоте вра­щения ротора генерато­ра (об/мин):

n₁ = f₁60/p.         
(формула 6.9)

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:

1.   
Решить задачу №1. В табл. 6.1 приведены данные
следующих параметров трехфазного асинхронного двигателя с короткозамкнутым
ротором: основной магнитный поток ф, число последовательно соединенных витков  в обмотке статора,
номинальное скольжение , ЭДС, индуцируемая в
обмотке ротора при его неподвижном состоянии , и ЭДС ротора при его
вращении с номинальным скольжением E_2s, частота этой ЭДС f₂ при частоте вращения ротора n_ном. Частота тока в питающей сети 50 Гц. Требуется определить значения
параметров, не указанные в таблице в каждом из вариантов.

Таблица 6.1.

Параметр	Варианты
1	2	3	4	5	6	7	8	9	10
Ф, Вб	0,028	0,032	0,048	−	0,025	−	−	0,028	0,028	−
Kоб1	0,95	0,96	0,96	0,98	0,98	0,96	0,95	0,95	0,98	0,98
1, витков	18	−	24	16	−	24	18	−	36	18
Sном	0,04	−	0,05	0,04	−	0,05	−	−	−	−
2p	4	6	2	4	−	8	4	8	−	4
E1ф, В	−	210	−	98	110	200	−	120	−	100
E2,В	−	−	−	−	−	−	−	−	−	−
E2s,В	−	−	−	−	−	−	0,13	−	−	−
f2, Гц	−	−	−	−	−	−	2,5	3,2	−	2,5
nном, об/мин	−	970	−	−	2920	−	−	−	1470	−

2.   
Решить задачу №2. В табл.6.2. приведены значения
следующих параметров трехфазного асинхронного двигателя: односторонний
воздушный зазор между статором и ротором δ, число полюсов 2Ƥ, число
пазов , максимальное значение
магнитной индукции в воздушном зазоре , число витков в одной
катушке обмотки статора (все катушки фазной обмотки
соединены последовательно), обмоточный коэффициент обмотки
статора для основной гармоники , коэффициент магнитного
насыщения , коэффициент воздушного
зазора , Необходимо определить
величину намагничивающего тока статора при заданном воздушном
зазоре.

                                                                                                                                              
Таблица 6.2.

Параметры	Варианты
1	2	3	4	5	6	7	8	9	10
δ,мм	0,6	0,4	0,8	0,5	0,7	0,3	0,4	0,7	0,5	0,6
2Ƥ	6	4	8	6	6	2	4	6	4	8
Число пазов	24	24	48	36	60	18	36	48	32	54
,Тл	0,9	0,8	0,9	1,0	0,7	0,8	0,8	1,0	0,7	0,9
Число витков	8	7	6	8	5	4	5	5	6	4
	0,91	0,95	0,92	0,94	0,96	0,92	0,92	0,94	0,93	0,92
	1,37	1,35	1,38	1,40	1,35	1,40	1,34	1,37	1,35	1,38
	1,30	1,35	1,36	1,38	1,34	1,37	1,35	1,36	1,34	1,38

       
Решение:

–         
Определить величину магнитного напряжения
воздушного зазора.

–         
Определить значение МДС обмотки статора на пару
полюсов в режиме холостого хода номинальном подведении напряжении.

–         
Определить число последовательно соединенных витков
фазной обмотки статора.

–           
Определить величину намагничивающего тока статора.                   

3. Решить задачу №3. Трехфазный
асинхронный двигатель с фазным ро­тором имеет данные, приведенные в табл. 6.3.
максимальное значе­ние магнитной индукции в воздушном зазоре В_δ,
диаметр расточки статора D_1, длина
сердечника статора l₁,
равная 0,81D₁,
число полю­сов в обмотках статора и ротора 2р,
число последовательно соеди­ненных витков в фазных обмотках статора ω₁
и ротора ω₂,
обмоточные коэффициенты для основной гармоники статора к_об1
и ротора к_об2
принять равными к_об1
= к_иб2
= 0,93. Требуется определить фаз­ные значения ЭДС в обмотке статора Е₁
 и в обмотке фазного ротора при неподвижном его состоянии Е₂
и вращающемся со скольжени­ем s,
частоту тока в неподвижном и вращающемся роторе.
Частота тока в питающей сети f
= 50 Гц.

Таблица 6.3.

Параметр	Варианты
1	2	3	4	5	6	7	8	9	10
Вδ , Тл	1,5	1,35	1,50	1,40	1,45	1,50	1,38	1,45	1,50	1,38
D1, мм	180	160	228	235	160	300	280	320	360	290
l1, мм	141	130	180	190	130	250	250	270	300	250
2 р	4	4	4	6	4	4	6	4	8	6
ω1	48	18	24	32	48	36	32	36	12	24
ω2	8	4	6	10	16	12	16	18	8	12
s, %	8	12	10	6	5	12	8	10	6	8

Решение:

–         
Определить полюсное деление.

–         
Определить величину основного магнитного
потока.

–         
Определить ЭДС фазной обмотки статора.

–         
Определить ЭДС в обмотке неподвижного
ротора.

–         
Определить ЭДС во вращающемся роторе при
скольжении 8 %.

–         
Определить частоту тока во вращающемся
роторе при скольжении 8
%.

–         
 

4.
Решить задачу №4. Трехфазный асинхронный двигатель с
короткозамкнутым ротором серии 4А имеет технические данные, приведенные в табл.
6.4. Определить высоту оси вращения h, число полюсов 2p, скольжение при номинальной нагрузке s_ном, момент на валу М_ном, начальный пусковой М_n и максимальный  момент, потребляемую
двигателем из сети активную мощность Р_1ном,
суммарные потери при номинальной нагрузки ∑Р, номинальный и пусковой токи I_1ном и I_n в
питающей сети при соединении обмоток статора «звездой» и «треугольником».

 Таблица 6.4.

№ В	Тип двигателя	Pном, кВт	n2ном, об/мин	nном, %					U1,В
1	4A100S2У3	4,0	2880	86,5	0,89	7,5	2,0	2,5	220/380
2	4A160S2У3	15,0	2945	88,0	0,91	7,0	1,4	2,2	220/380
3	4A200М2У3	37,0	2945	90,0	0,89	7,5	1,4	2,5	380/660
4	4A112М2У3	5,5	1445	85,5	0,85	7,0	2,0	2,2	220/380
5	4A132М2У3	11,0	1460	87,5	0,87	7,5	2,2	3,0	220/380
6	4A180М2У3	30,0	1470	91,0	0,89	6,5	1,4	2,3	380/660
7	4A200М6У3	22,0	475	90,0	0,90	6,5	1,3	2,4	220/380
8	4A280М6У3	90,0	985	92,5	0,89	5,5	1,4	2,2	380/660
9	4A315М8У3	110	740	93,0	0,85	6,5	1,2	2,3	380/660
10	4A355М10У3	110	590	93,0	0,83	6,0	1,0	1,8	380/660

Решение:

–         
В обозначении типоразмера двигателя цифры, стоящие
после обозначения серии  4А, указывают на высоту оси вращения (мм).

–         
Следующая далее цифра указывает на число плюсов 2p.

–         
Определить синхронную частоту вращения  при частоте переменного
тока 50 Гц.

–         
Определить скольжение при номинальной нагрузке  =/.

–         
Определить момент на валу двигателя (полезный
момент двигателя) при номинальной нагрузке  = 9,55/.

–         
Определить начальный пусковой момент. =().

–         
Определить максимальный (критический)момент
двигателя по его перегрузочной способности..

–    
Определить номинальный ток в фазной обмотке
статора.

–         
Определить потребляемую двигателем из сети активную
мощность в режиме номинальной нагрузки..

–         
Определить суммарные потери двигателя при номинальной
нагрузке

–    
=

–         
Определить линейный ток статора: при соединении
обмоток статора «звездой» =.

–         
При соединении обмоток статора «треугольником» .

5.       
Решить задачу №5. Трехфазный асинхронный
двигатель с фазным ро­тором имеет эффективное число витков в фазных обмотках
статора  и ротора , ЭДС фазной обмотки статора
= 0,95, ЭДС фазной обмотки
неподвижного ротора  , а вращающегося со
скольжением s, равно . Используя приведенные в
табл. 6.5. значения параметров, определить неуказанные значения, если
напряжение питания двигателя = 220/380 B.

Таблица 6.5. 

Параметр	Варианты
1	2	3	4	5	6	7	8	9	10
	18	24	—	32	—	36	—	24	—	48
	12	—	18	—	12	—	18	—	16	—
, B	—	—	—	—	—	—	—	—	—	—
, B	—	93	—	105	—	104	—	98	—	110
, B	—	5,58	6,5	5,25	5,8	—	4,0	5,8	4,6	—
s	0,05	—	0,04	—	0,07	0,05	0,03	—	0,05	0,04

6.     
Оформить отчет по практической работе.

7.     
Ответить на контрольные вопросы.

8.     
Сделать вывод о проделанной работе.

КОНТРОЛЬНЫЕ
ВОПРОСЫ:

1.     
Что такое скольжение асинхронной машины?

2.       
Какие режимы работы синхронной машины
существуют?

3.       
Каков диапазон изменения скольжения
асинхронной машины в различных режимах ее работы?

4.       
Что такое номинальное скольжение?

5.       
С какой целью обмотку статора асинхронного
генератора подключают к сети трехфазного тока?

6.       
Какова цель расчета магнитной цепи
асинхронной машины?

7.       
Как влияет выбор значения магнитной индукции
в воздушном зазоре на свойства асинхронного двигателя?

8.       
В чем сходство трансформатора и асинхронного
двигателя?