поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,658 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,962 -
разное
16,905
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Задачи на Механические волны с решениями
Формулы, используемые на уроках «Задачи на Механические волны».
Название величины |
Обозначение |
Единица измерения |
Формула |
Длина волны |
λ |
м |
λ = vT ;λ = v / v |
Скорость волны |
v |
м/с |
v = λ / T ;v = λv |
Период колебаний |
T |
с |
T = λ / v ;T = t / N |
Частота колебаний |
v |
Гц |
v = v / λ ;v = N / t |
Число колебаний |
N |
N = t / T ;N = vt |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Лодка качается на волнах, распространяющихся со скоростью 4 м/с, и за 10 с совершает 20 колебаний. Каково расстояние между соседними гребнями волн?

Задача № 2.
Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.

Задача № 3.
Скорость звука в эбоните 2400 м/с, а в кирпиче — 3600 м/с. В каком веществе звуковому сигналу требуется большее время для распространения? Во сколько раз?

Задача № 4.
Расстояние между ближайшими гребнями волн в море 6 м. Лодка качается на волнах, распространяющихся со скоростью 2 м/с. Какова частота ударов волн о корпус лодки?

Задача № 5.
Наблюдатель, находящийся на расстоянии 2 км 150 м от источника звука, слышит звук, пришедший по воздуху, на 4,8 с позднее, чем звук от того же источника, пришедший по воде. Определите скорость звука в воде, если скорость звука в воздухе равна 345 м/с.

Задача № 6.
Охотник выстрелил, находясь на расстоянии 170 м от лесного массива. Через сколько времени после выстрела охотник услышит эхо?

Задача № 7.
Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.

Задача № 8.
Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?

Задача № 9.
Длина волны в воздухе 17 см (при скорости 340 м/с). Найти скорость распространения звука в теле, в котором при той же частоте колебаний длина волны равна 1,02 м.

Задача № 10.
ОГЭ
Расстояние между гребнями волн в море λ = 5 м. При встречном движении катера волна за t = 1 с ударяет о корпус катера N1 = 4 раза, а при попутном — N2 = 2 раза. Найти скорость катера и волны.

Задача № 11.
ОГЭ
Звуковые колебания, имеющие частоту v = 500 Гц и амплитуду А = 0,25 мм, распространяются в воздухе. Длина волны λ = 70 см. Найти скорость распространения колебаний v и максимальную скорость частиц среды.

Краткая теория для решения Задачи на Механические волны.
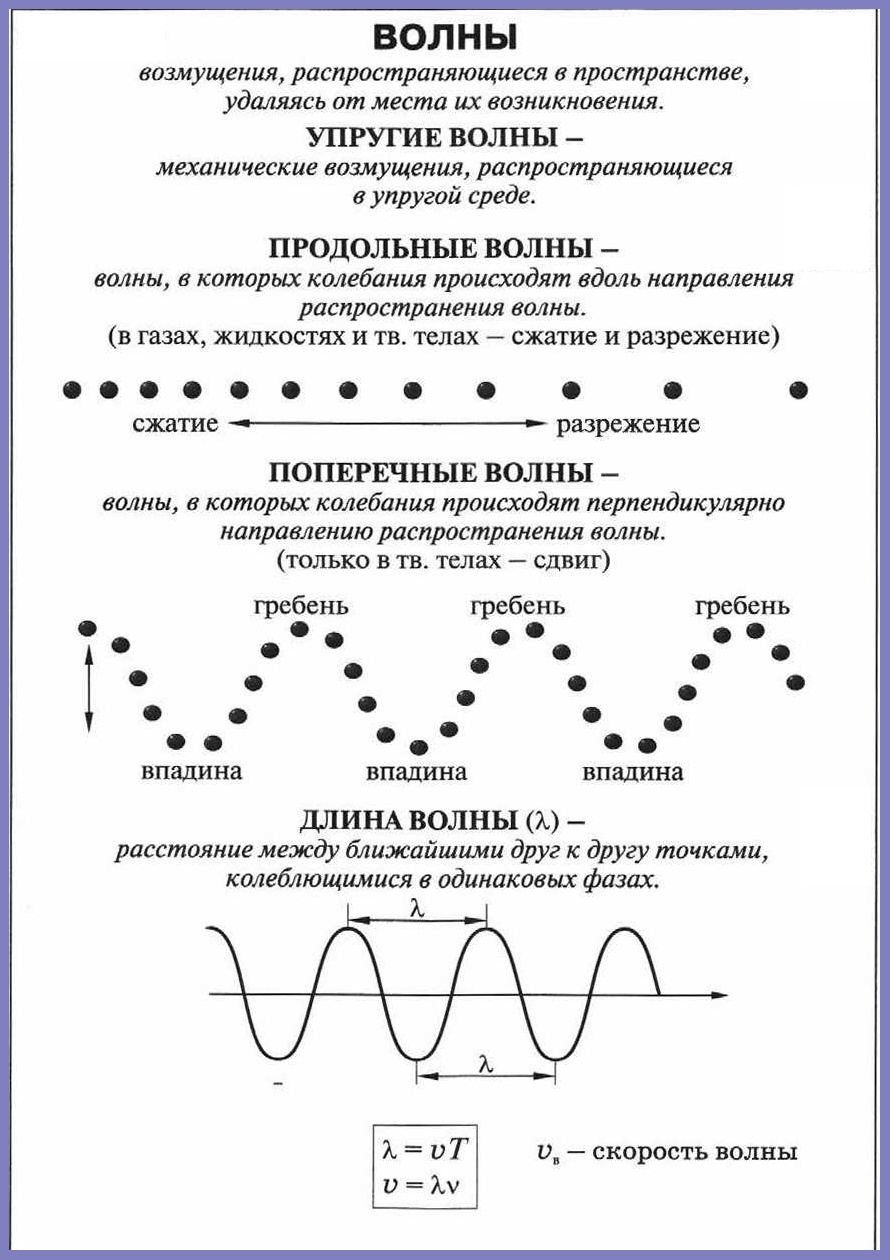

Это конспект по теме «ЗАДАЧИ на Механические волны». Выберите дальнейшие действия:
- Перейти к теме: ЗАДАЧИ на
- Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
Как найти частоту волны? Процесс прост; количество оборотов, которое требуется для завершения конкретной вещи, называется частотой.
Когда объект движется, мы обычно определяем движение, силу и многие другие факторы. Но нам также нужно знать, с какой частотой он будет двигаться в данный момент времени. Таким образом, обратное время дается как частота в стандартных терминах.
В подробном случае мы также могли бы определить частоту данной волны, частицы в краткосрочной перспективе, а также более широкий контекст. частота является широко используемым фактором с точки зрения волны. Скажем, например, волна распространяется с определенной скоростью, и мы должны найти частоту волны.
Обычно мы погружаемся в математическую часть решения, но, говоря простым языком, мы также можем быстро определить волны. То частота сколько циклов он делает за одну секунду. Таким образом, если волна завершает один цикл, частота составляет половину от него.
Частота — это то, что появляется постоянно или в определенный момент времени. Подобно соленоиду, он имеет несколько витков при намотке на проводник и производит электричество. Точно так же частота — это количество циклов, которые волна совершает за одну секунду, и она обычно равна 2 герцам.
Компания количество циклов световой волны сделанное за одну секунду, также оценивается с точки зрения длины волны и скорость световой волны. Звуковая волна является наиболее распространенной областью, где часто рассматривается частотный термин.
Существует также научная вещь: собаки и птицы слышат звук за пределами определенного уровня, который даже люди не способны слышать. Мы созданы таким образом, что только определенное количество частота звука мы могли вынести услышать.
Частота волновой формулы
Частота имеет общую формулу, которую можно применять во всех контекстах. Период времени является основной причиной, которая помогает в формуле частоты.
Количество циклов, которые волна делает за один, рассматривается как частота этой конкретной волны. Следовательно, формула частоты в повседневном исчислении такова: f=1/T. Здесь Т — период времени, за который волны совершают число циклов.
Чтобы рассчитать частоту, нам нужно знать характеристики волны. Волна — это совокупность вибраций, называемых энергиями. Они достигли пика на обоих концах. Верхний узел называется впадина, а нижний узел называется гребень.
Высота волны обычно считается амплитудой волны. Высота волны будет определять, будет ли амплитуда больше или меньше. Поэтому, когда они изменяются, циклы, сделанные в секунду, также будут изменены.
Таким образом, когда волна завершает один цикл, то есть если волна имеет и гребень, и впадину в одной и той же фазе, тогда получаемая частота равна половине.
Волна совершает определенное количество циклов за одну секунду, что в основном известно как частота волны. И это дается формулой f=1/Т. Тип волны может зависеть от среды, через которую она проходит.
Как найти частоту волны по графику?
Теперь давайте посмотрим, как найти частоту волны на графике. Во-первых, частота — это количество циклов, которые волна пытается совершить, чтобы совершить один полный круг в данный конкретный момент времени.
Когда волна сделает один цикл, на это потребуется некоторое время. На графике мы называем это единицами. По сути, на графике есть несколько единиц, по которым мы можем быстро определить, как найти частоту волны в данном конкретном случае.
Скажем, например, волна движется с определенной скоростью, и мы также должны знать, сколько секунд это занимает. Скажи, что есть 12 секунд отмечены на графике, поэтому этой волне требуется 4 секунды, чтобы завершить один полный цикл. Итак, по формуле f=1/Т, частота волны 0.25Гц.
Давайте рассмотрим несколько задач по расчету частоты.
Проблема:
Типичная волна совершает два цикла за 30 секунд, и какова будет частота волны, если она будет распространяться в той же среде?
Решение:
f=1/Т
f=2/30
f=0.0667 Гц
Всегда возникает путаница между частота волны и скорость волны. Есть амплитуда волны, которая в основном является высотой волны. Таким образом, скорость рассчитывается, чтобы найти скалярную часть скорости, которая является скоростью.
Когда мы обнаруживаем, что волна является световой, звуковой или электромагнитной волной, нам нужно найти частоту волна, завершающая циклы. Период времени между циклами, совершаемыми волной, обычно определяется формулой как обратную частоту.
Как найти частоту волны по длине и амплитуде?
Как найти частоту волны по длине и амплитуде? Когда мы рассматриваем волну как свет, мы должны знать все факторы, влияющие на частоту волны.
Во-первых, необходимо учитывать длину волны. Как найти частоту волны с длиной волны? Формула очень проста, и нам нужно найти формулу скорости света.
Будет формула, называемая скоростью света, с = fλ. Здесь c — скорость света, f — определяемая частота, λ — длина волны света. Из этой формулы мы можем найти частоту волны через длину волны, переставив члены, данные в формуле.
Если говорят, что волна движется с определенной скоростью и временем, нам также нужно найти частота с которым распространяется световая волна. Таким образом, формула, упомянутая выше, будет использоваться для расчета частоты в заданный период времени.
Найдем частоту волны и посмотрим, как частота определяется по формуле.
Проблема:
Световая волна распространяется со скоростью 3×108 РС. Данную длину волны световой волны называют равной 2000 Å. Какова частота?
Решение:
с = fλ
f = с / λ
ф = 3×108 / 2000 Å
f= 1.5 х 1018 герц
Итак, из вышеприведенной задачи видно, что частоту можно найти, используя длину волны.
Теперь нам нужно знать, как найти частоту волны через амплитуду. Для этого рассмотрим теперь общую формулу частоты, т. е. f=1/Т. Здесь f также можно записать как f = ω / 2 π.
Здесь формула для T дается как 2 π/ω. Отсюда легко найти значение амплитуды, если упомянут период времени. А частоту можно найти по приведенной выше формуле, если в конкретной задаче задана амплитуда.
Как найти частоту волны, зная только длину волны?
Нам нужно знать, как длина волны влияет на волну, когда она распространяется с определенной скоростью и в заданном направлении. Это то, как далеко волна сможет пройти в среде.
Мы все знаем, что скорость света является стандартом для большинства формул, и мы также знаем, как переставить детали данной формулы, чтобы найти частоту данной волны. Как правило, когда световая волна распространяется в определенном направлении со скоростью 3×108, он также будет собирать информацию о частоте волны.
Формула скорости света является основой для определения длины волны или частоты распространяющейся световой волны. Скорость формулы света определяется выражением с = fλ. Отсюда мы получаем частоту волны через длину волны, соответствующим образом изменяя формулу.
Окончательная формула f = с / λ. Давайте посмотрим на проблему, как работает формула для электромагнитной волны.
Проблема:
Вычислите частоту электромагнитной волны, которая распространяется со скоростью 2×106м/с с длиной волны 1000 Å. С заданными деталями используйте формулу частота по длине волны.
Решение:
с = fλ
f = с / λ
f = 0.002 х 106 герц
f = 2 х 106/ 1000 Å
Таким образом, мы можем быстро определить частоту волны, используя значение скорости и, главным образом, значение длины волны.
Длина волны волны — это в основном пространство между гребнями или впадинами волны, которые следуют друг за другом. В основном концы одной и той же волны, которая была передана с точки зрения звука или электромагнитная волна.
Когда гребни и впадины волны, находящиеся в одной и той же фазе, встречаются в одном и том же месте, обычно считается, что это длина волны.
Как найти частоту волны по заданному периоду?
Как найти частоту волны через период времени? Ответ на этот вопрос прост, так как это общая формула для определения частоты волны.
Мы должны знать, что период времени в волне — это расстояние между гребнем и впадиной в одной и той же фазе. Поэтому, когда волна в основном распространяется с определенной частотой в заданный промежуток времени, нам нужна формула для расчета частоты.
Вот формула для частота с точки зрения периода времени, f=1/Т. Период времени обычно является еще одним термином для амплитуды волны. Т можно также записать как 2 π/ω, Где ω является мерой амплитуды.
Компания амплитуда – это в основном высота волны в зависимости от чего нам нужно сделать вывод, что амплитуда большая или малая. Если высота волны велика, то амплитуда называется значительной, а если высота волны мала, то говорят, что амплитуда волны мала.
Амплитуда имеет два конца, называемые гребень и впадина. Впадина — это верхний узел амплитуды, а гребень — нижний узел амплитуды.
Когда расстояние между двумя волнами называется длиной волны, а количество циклов, которое совершает одна волна, называется частота, когда период времени равен единице единица на графике, что в стандартном выражении составляет одну секунду.
Как найти частоту волны без скорости?
Из формулы скорости света мы могли бы заметить, что длина волны обратно пропорциональна частоте волны, то есть циклам, совершаемым волной за период времени.
Мы также знаем, что частота не прямо пропорциональна периоду времени; следовательно, длина волны и период времени пропорциональны друг другу. Длина волны связана с энергией, поэтому, когда длина волны увеличивается, энергия уменьшается. Формула основана на энергии фотона.
Мы предполагаем, что длина волны и период времени пропорциональны, а частота и энергия быть пропорциональным. Частота волны без скорости была бы формулой энергии, где E=hf, где E — энергия, h — постоянная Планка, f — частота.
Итак, зная конкретную базовую формулу света и энергии, мы можем соответствующим образом переставить термины и узнать, как найти частоту волны во всех возможных терминах. Кроме того, все эти факторы влияют на волну и ее количество, способствуя ее собственному распространению.
-
Физика
Предыдущий вопрос
Следующий вопрос
vikagarkuscha
3 года назад
Ответ
Ответ дан
crdd
λ = 10м – расстояние между ближайшими гребнями
v = 3м/с – скорость волн
ν – ? – частота
λ = v*T, Т – период
Т = 1/ν
значит, λ = v/ν
отсюда частота:
ν = v/λ = 3м/с/10м = 0,3 с^-1
Ответ: 0,3 с^-1
Ответы и объяснения
- vikagarkuscha
Не тот ответ, который тебе нужен?
Найди нужный
Захар Яшин
30 ноября, 02:38
0
Начальные данные: λ (расстояние между ближайшими гребнями волн) = 6 м; υ (скорость распространения волн) = 2 м/с;.
Частоту ударов волн о берег определим из формулы для вычисления скорости распространения волн: υ = λ * ν; ν = υ / λ.
Выполним расчет частоты ударов: ν = 2 / 6 ≈ 0,33 Гц.
Ответ: Частота ударов волн о берег составляет 0,33 Гц.
- Комментировать
- Жалоба
- Ссылка
