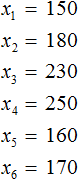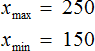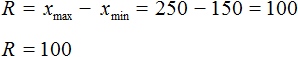Загрузить PDF
Загрузить PDF
С абсолютной частотой все довольно просто: она определяет, сколько раз конкретное число содержится в имеющемся наборе данных (объектов или значений). А вот относительная частота характеризует отношение количества конкретного числа в наборе данных. Другими словами, относительная частота – это отношение количества определенного числа к общему количеству чисел в наборе данных. Имейте в виду, что вычислить относительную частоту достаточно легко.
-
1
Соберите данные. Если вы решаете математическую задачу, в ее условии должен быть дан набор данных (чисел). В противном случае проведите эксперимент или исследование и соберите необходимые данные. Подумайте, в какой форме записать исходные данные.
- Например, нужно собрать данные о возрасте людей, которые посмотрели определенный фильм. Конечно, можно записать точный возраст каждого человека, но в этом случае вы получите довольно большой набор данных с 60-70 числами в пределах от 10 до 70 или 80. Поэтому лучше сгруппировать данные по категориям, таким как «Моложе 20», «20-29», «30-39» «40-49», «50-59» и «Старше 60». Получится упорядоченный набор данных с шестью группами чисел.
- Другой пример: врач собирает данные о температуре пациентов в определенный день. Если записать округленные числа, например, 37, 38, 39, то результат будет не слишком точным, поэтому здесь данные нужно представить в виде десятичных дробей.
-
2
Упорядочьте данные. Когда вы соберете данные, у вас, скорее всего, получится хаотичный набор чисел, например, такой: 1, 2, 5, 4, 6, 4, 3, 7, 1, 5, 6, 5, 3, 4, 5, 1. Такая запись кажется практически бессмысленной и с ней сложно работать. Поэтому упорядочьте числа по возрастанию (от меньшего к большему), например, так: 1,1,1,2,3,3,4,4,4,5,5,5,5,6,6,7.[1]
- Упорядочивая данные, будьте внимательны, чтобы не пропустить ни одного числа. Посчитайте общее количество чисел в наборе данных, чтобы убедиться, что вы записали все числа.
-
3
Создайте таблицу с данными. Собранные данные можно организовать в виде таблицы. Такая таблица будет включать три столбца и использоваться для вычисления относительной частоты. Столбцы обозначьте следующим образом:[2]
Реклама
-
1
Найдите количество чисел в наборе данных. Относительная частота характеризует, сколько раз конкретное число содержится в имеющемся наборе данных по отношению к общему количеству чисел. Чтобы найти относительную частоту, нужно посчитать общее количество чисел в наборе данных. Общее количество чисел станет знаменателем дроби, с помощью которой будет вычислена относительная частота.[3]
- В нашем примере набор данных содержит 16 чисел.
-
2
Найдите количество определенного числа. То есть посчитайте, сколько раз конкретное число встречается в наборе данных. Это можно сделать как для одного числа, так и для всех чисел из набора данных.[4]
- Например, в нашем примере число встречается в наборе данных три раза.
- Например, в нашем примере число
-
3
Разделите количество конкретного числа на общее количество чисел. Так вы найдете относительную частоту для определенного числа. Вычисление можно представить в виде дроби или воспользоваться калькулятором или электронной таблицей, чтобы разделить два числа.[5]
Реклама
-
1
Результаты вычислений запишите в созданную ранее таблицу. Она позволит представить результаты в наглядной форме. По мере вычисления относительной частоты результаты записывайте в таблицу напротив соответствующего числа. Как правило, значение относительной частоты можно округлить до второго знака после десятичной запятой, но это на ваше усмотрение (в зависимости от требований задачи или исследования). Помните, что округленный результат не равен точному ответу.[6]
- В нашем примере таблица относительных частот будет выглядеть следующим образом:
- x : n(x) : P(x)
- 1 : 3 : 0,19
- 2 : 1 : 0,06
- 3 : 2 : 0,13
- 4 : 3 : 0,19
- 5 : 4 : 0,25
- 6 : 2 : 0,13
- 7 : 1 : 0,06
- Итого : 16 : 1,01
-
2
Представьте числа (элементы), которых нет в наборе данных. Иногда представление чисел с нулевой частотой так же важно, как и представление чисел с ненулевой частотой. Обратите внимание на собранные данные; если между данными имеются пробелы, их нужно заполнить нулями.
- В нашем примере набор данных включает все числа от 1 до 7. Но предположим, что числа 3 нет в наборе. Возможно, это немаловажный факт, поэтому нужно записать, что относительная частота числа 3 равна 0.
-
3
Выразите результаты в процентах. Иногда результаты вычислений нужно преобразовать из десятичных дробей в проценты. Это общепринятая практика, потому что относительная частота характеризует процент случаев появления определенного числа в наборе данных. Чтобы преобразовать десятичную дробь в проценты, нужно десятичную запятую передвинуть на две позиции вправо и приписать символ процента.
- Например, десятичная дробь 0,13 равна 13%.
- Десятичная дробь 0,06 равна 6% (обратите внимание, что перед 6 стоит 0).
Реклама
Советы
- Относительная частота характеризует наличие или возникновение определенного события в наборе событий.
- Если сложить относительные частоты всех чисел из набора данных, вы получите единицу. Помните, что при сложении округленных результатов сумма не будет равна 1,0.
- Если набор данных слишком большой, чтобы обработать его вручную, воспользуйтесь программой MS Excel или MATLAB; это позволит избежать ошибок в процессе вычисления.
Реклама
Источники
Об этой статье
Эту страницу просматривали 145 557 раз.
Была ли эта статья полезной?
Продолжаем изучать элементарные задачи по математике. Сегодня мы поговорим о статистике.
Статистика — это раздел математики в котором изучаются вопросы сбора, измерения и анализа информации, представленной в числовой форме. Происходит слово статистика от латинского слова status (состояние или положение дел).
Так, с помощью статистики мы можем узнать свое положение дел, касающихся финансов. С начала месяца можно вести дневник расходов и по окончании месяца, воспользовавшись статистикой, узнать сколько денег в среднем мы тратили каждый день или какая потраченная сумма была наибольшей в этом месяце либо узнать какую сумму мы тратили наиболее часто.
На основе этой информации можно провести анализ и сделать определенные выводы: следует ли в следующем месяце немного сбавить аппетит, чтобы тратить меньше денег, либо наоборот позволить себе не только хлеб с водой, но и колбасу.
Выборка. Объем. Размах
Что такое выборка? Если говорить простым языком, то это отобранная нами информация для исследования. Например, мы можем сформировать следующую выборку — суммы денег, потраченных в каждый из шести дней. Давайте нарисуем таблицу в которую занесем расходы за шесть дней
Выборка состоит из n-элементов. Вместо переменной n может стоять любое число. У нас имеется шесть элементов, поэтому переменная n равна 6
n = 6
Элементы выборки обозначаются с помощью переменных с индексами 
. Последний 
элемент является шестым элементом выборки, поэтому вместо n будет стоять число 6.
Обозначим элементы нашей выборки через переменные
Количество элементов выборки называют объемом выборки. В нашем случае объем равен шести.
Размахом выборки называют разницу между самым большим и маленьким элементом выборки.
В нашем случае, самым большим элементом выборки является элемент 250, а самым маленьким — элемент 150. Разница между ними равна 100
Среднее арифметическое
Понятие среднего значения часто используется в повседневной жизни.
Примеры:
- средняя зарплата жителей страны;
- средний балл учащихся;
- средняя скорость движения;
- средняя производительность труда.
Речь идет о среднем арифметическом — результате деления суммы элементов выборки на их количество.
Среднее арифметическое — это результат деления суммы элементов выборки на их количество.
Вернемся к нашему примеру
Узнаем сколько в среднем мы тратили в каждом из шести дней:
Средняя скорость движения
При изучении задач на движение мы определяли скорость движения следующим образом: делили пройденное расстояние на время. Но тогда подразумевалось, что тело движется с постоянной скоростью, которая не менялась на протяжении всего пути.
В реальности, это происходит довольно редко или не происходит совсем. Тело, как правило, движется с различной скоростью.
Когда мы ездим на автомобиле или велосипеде, наша скорость часто меняется. Когда впереди нас помехи, нам приходиться сбавлять скорость. Когда же трасса свободна, мы ускоряемся. При этом за время нашего ускорения скорость изменяется несколько раз.
Речь идет о средней скорости движения. Чтобы её определить нужно сложить скорости движения, которые были в каждом часе/минуте/секунде и результат разделить на время движения.
Задача 1. Автомобиль первые 3 часа двигался со скоростью 66,2 км/ч, а следующие 2 часа — со скоростью 78,4 км/ч. С какой средней скоростью он ехал?
Сложим скорости, которые были у автомобиля в каждом часе и разделим на время движения (5ч)
Значит автомобиль ехал со средней скоростью 71,08 км/ч.
Определять среднюю скорость можно и по другому — сначала найти расстояния, пройденные с одной скоростью, затем сложить эти расстояния и результат разделить на время. На рисунке видно, что первые три часа скорость у автомобиля не менялась. Тогда можно найти расстояние, пройденное за три часа:
66,2 × 3 = 198,6 км.
Аналогично можно определить расстояние, которое было пройдено со скоростью 78,4 км/ч. В задаче сказано, что с такой скоростью автомобиль двигался 2 часа:
78,4 × 2 = 156,8 км.
Сложим эти расстояния и результат разделим на 5
Задача 2. Велосипедист за первый час проехал 12,6 км, а в следующие 2 часа он ехал со скоростью 13,5 км/ч. Определить среднюю скорость велосипедиста.
Скорость велосипедиста в первый час составляла 12,6 км/ч. Во второй и третий час он ехал со скоростью 13,5. Определим среднюю скорость движения велосипедиста:
Мода и медиана
Модой называют элемент, который встречается в выборке чаще других.
Рассмотрим следующую выборку: шестеро спортсменов, а также время в секундах за которое они пробегают 100 метров
Элемент 14 встречается в выборке чаще других, поэтому элемент 14 назовем модой.
Рассмотрим еще одну выборку. Тех же спортсменов, а также смартфоны, которые им принадлежат
Элемент iphone встречается в выборке чаще других, значит элемент iphone является модой. Говоря простым языком, носить iphone модно.
Конечно элементы выборки в этот раз выражены не числами, а другими объектами (смартфонами), но для общего представления о моде этот пример вполне приемлем.
Рассмотрим следующую выборку: семеро спортсменов, а также их рост в сантиметрах:
Упорядочим данные в таблице так, чтобы рост спортсменов шел по возрастанию. Другими словами, построим спортсменов по росту:
Выпишем рост спортсменов отдельно:
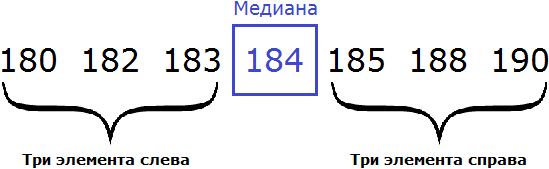
180, 182, 183, 184, 185, 188, 190
В получившейся выборке 7 элементов. Посередине этой выборки располагается элемент 184. Слева и справа от него по три элемента. Такой элемент как 184 называют медианой упорядоченной выборки.
Медианой упорядоченной выборки называют элемент, располагающийся посередине.
Отметим, что данное определение справедливо в случае, если количество элементов упорядоченной выборки является нечётным.
В рассмотренном выше примере, количество элементов упорядоченной выборки было нечётным. Это позволило нам быстро указать медиану
Но возможны случаи, когда количество элементов выборки чётно.
К примеру, рассмотрим выборку в которой не семеро спортсменов, а шестеро:
Построим этих шестерых спортсменов по росту:
Выпишем рост спортсменов отдельно:
180, 182, 184, 186, 188, 190
В данной выборке не получается указать элемент, который находился бы посередине. Если указать элемент 184 как медиану, то слева от этого элемента будут располагаться два элемента, а справа — три. Если как медиану указать элемент 186, то слева от этого элемента будут располагаться три элемента, а справа — два.
В таких случаях для определения медианы выборки, нужно взять два элемента выборки, находящихся посередине и найти их среднее арифметическое. Полученный результат будет являться медианой.
Вернемся к нашим спортсменам. В упорядоченной выборке 180, 182, 184, 186, 188, 190 посередине располагаются элементы 184 и 186
Найдем среднее арифметическое элементов 184 и 186
Элемент 185 является медианой выборки, несмотря на то, что этот элемент не является членом исходной и упорядоченной выборки. Спортсмена с ростом 185 нет среди остальных спортсменов. Рост в 185 см используется в данном случае для статистики, чтобы можно было сказать о том, что срединный рост спортсменов составляет 185 см.
Поэтому более точное определение медианы зависит от количества элементов в выборке.
Если количество элементов упорядоченной выборки нечётно, то медианой выборки называют элемент, располагающийся посередине.
Если количество элементов упорядоченной выборки чётно, то медианой выборки называют среднее арифметическое двух чисел, располагающихся посередине этой выборки.
Медиана и среднее арифметическое по сути являются «близкими родственниками», поскольку и то и другое используют для определения среднего значения. Например, для предыдущей упорядоченной выборки 180, 182, 184, 186, 188, 190 мы определили медиану, равную 185. Этот же результат можно получить путем определения среднего арифметического элементов 180, 182, 184, 186, 188, 190
Но медиана в некоторых случаях отражает более реальную ситуацию. Например, рассмотрим следующий пример:
Было подсчитано количество имеющихся очков у каждого спортсмена. В результате получилась следующая выборка:
0, 1, 1, 1, 2, 1, 2, 3, 5, 4, 5, 0, 1, 6, 1
Определим среднее арифметическое для данной выборки — получим значение 2,2
По данному значению можно сказать, что в среднем у спортсменов 2,2 очка
Теперь определим медиану для этой же выборки. Упорядочим элементы выборки и укажем элемент, находящийся посередине:
0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 3, 4, 5, 5, 6
В данном примере медиана лучше отражает реальную ситуацию, поскольку половина спортсменов имеет не более одного очка.
Частота
Частота это число, которое показывает сколько раз в выборке встречается тот или иной элемент.
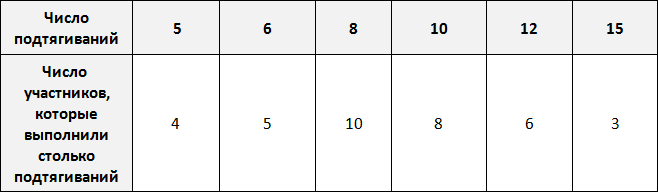
Предположим, что в школе проходят соревнования по подтягиваниям. В соревнованиях участвует 36 школьников. Составим таблицу в которую будем заносить число подтягиваний, а также число участников, которые выполнили столько подтягиваний.
По таблице можно узнать сколько человек выполнило 5, 10 или 15 подтягиваний. Так, 5 подтягиваний выполнили четыре человека, 10 подтягиваний выполнили восемь человек, 15 подтягиваний выполнили три человека.
Количество человек, повторяющих одно и то же число подтягиваний в данном случае являются частотой. Поэтому вторую строку таблицы переименуем в название «частота»:
Такие таблицы называют таблицами частот.
Частота обладает следующим свойством: сумма частот равна общему числу данных в выборке.
Это означает, что сумма частот равна общему числу школьников, участвующих в соревнованиях, то есть тридцати шести. Проверим так ли это. Сложим частоты, приведенные в таблице:
4 + 5 + 10 + 8 + 6 + 3 = 36
Относительная частота
Относительная частота это в принципе та же самая частота, которая была рассмотрена ранее, но только выраженная в процентах.
Относительная частота равна отношению частоты на общее число элементов выборки.
Вернемся к нашей таблице:
Пять подтягиваний выполнили 4 человека из 36. Шесть подтягиваний выполнили 5 человек из 36. Восемь подтягиваний выполнили 10 человек из 36 и так далее. Давайте заполним таблицу с помощью таких отношений:
Выполним деление в этих дробях:
Выразим эти частоты в процентах. Для этого умножим их на 100. Умножение на 100 удобно выполнить передвижением запятой на две цифры вправо:
Теперь можно сказать, что пять подтягиваний выполнили 11% участников, 6 подтягиваний выполнили 14% участников, 8 подтягиваний выполнили 28% участников и так далее.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Теория вероятностей – это раздел математики, который
изучает закономерности случайных событий.
События
можно считать случайными – это те, которые могут произойти, а могут и не
произойти.
Примерами
таких событий являются: выпадение орла или решки при подбрасывании монеты;
поражение мишени или промах при стрельбе; выпадение того или иного количества
очков при бросании игрального кубика.
Пример.
Провели
испытания. 100 раз бросали игральный кубик и подсчитали, что 6 очков выпало 17
раз – частота рассматриваемого события, то есть выпадения очков.
Отношение
частоты к общему числу испытаний называют относительной частотой этого
события.
Пусть
некоторое испытание проводилось многократно в одних и тех же условиях. При этом
фиксировалось, произошло или нет некоторое интересующее нас событие А.
Если
общее число испытаний – n,
а число испытаний, при которых произошло событие А, – m. То m называют
частотой события А, частное m и n –
относительной
частотой.
Определение:
Относительной
частотой случайного события в серии испытаний называется
отношение числа испытаний, в которых это событие наступило, к числу всех
испытаний.
В
ходе исследований выяснилось, что относительная частота появления ожидаемого
события при повторении опытов в одних и тех же условиях, может оставаться
примерно одинаковой, незначительно отличаясь от некоторого числа р.
Пример.
При
подбрасывании монеты отмечают те случаи, когда выпадает орёл.
Если
монета однородна и имеет правильную геометрическую форму, то шансы выпадения
орла или решки будут примерно одинаковы. Но при
небольшом количестве бросков такой результат может не получиться.
А
вот если испытание проводиться большое количество раз, то относительная частота
выпадения орла близка к относительной частоте выпадения решки.
Многие
учёные проводили такой эксперимент.
Так,
например, английский математик Карл Пирсон бросал монету 24 тысячи раз, и
относительная частота выпадения орла оказалось равной 0,5005.
А
наш соотечественник, Всеволод Иванович Романовский, подбрасывая монету 80 тысяч
640 раз, нашёл, что относительная частота выпадения орла в его испытании была
равна 0,4923.
Заметим,
что в обоих случаях относительная частота выпадения орла очень близка к .
Говорят,
что вероятность выпадения орла при подбрасывании монеты правильной
геометрической формы равна .
Пример.
В
непрозрачном мешке лежит 7 зелёных и 12 синих кубиков. За раз можно доставать
только 1 из них. Какова вероятность того, что из мешка достанут синий кубик?
Всего
в мешке 19 кубиков. Значит, n=19.
Синий
кубик мы можем достать 12 раз. Получаем, что m=12.
Относительная
частота равна:
Вероятность
того, что из мешка достанут синий кубик, равна .
Пример.
Определить
относительную частоту появления буквы «о» в слове «достопримечательность».
Общее
число букв, то есть n=21.
А количество букв «о», то есть m=3.
Значит
относительная частота:
Пример.
Отмечая
число попаданий в корзину в каждой серии из 40 бросков, которые совершал
баскетболист, получили такие данные:
Какова
относительная вероятность попадания мяча в корзину для данного баскетболиста?
Определим
общее число бросков. Было 5 серий по 40 бросков, то есть n=200.
Сосчитаем
число попаданий в корзину:
Получили,
что m=184.
Относительная
вероятность попадания в корзину будет:
Пример.
Стрелок
совершил 50 выстрелов. Относительная частота попадания в цель оказалась равной
0,88. Сколько раз он промахнулся?
Зная
общее число выстрелов n=50
и относительную вероятность попадания p=0,88.
Найдем число попаданий в цель:
Стрелок
попал в цель 44 раза.
Найдём
число промахов
Стрелок
промахнулся 6 раз.
Мода и медиана
Модой ряда чисел называется число, наиболее часто встречающееся в данном ряду.
Обратимся снова к нашему примеру со сборной по футболу:
Чему в данном примере равна мода? Какое число наиболее часто встречается в этой выборке?
Все верно, это число ( displaystyle 181), так как два игрока имеют рост ( displaystyle 181) см; рост же остальных игроков не повторяется.
Тут все должно быть ясно и понятно, да и слово знакомое, правда?
Перейдем к медиане, ты ее должен знать из курса геометрии. Но мне не сложно напомнить, что в геометрии медиана (в переводе с латинского- «средняя») — отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны.
Ключевое слово – СЕРЕДИНА. Если ты знал это определение, то тебе легко будет запомнить, что такое медиана в статистике.
Медианой ряда чисел с нечетным числом членов называется число, которое окажется посередине, если этот ряд упорядочить (проранжировать, т.е. расположить значения в порядке убывания или возрастания).
Медианой ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине, если этот ряд упорядочить.
Ну что, вернемся к нашей выборке футболистов?
Ты заметил в определении медианы важный момент, который нам еще здесь не встречался? Конечно, «если этот ряд упорядочить»!
Для того, чтобы в ряду чисел был порядок, можно расположить значения роста футболистов как в порядке убывания, так и в порядке возрастания. Мне удобней выстроить этот ряд в порядке возрастания (от самого маленького к самому большому).
Вот, что у меня получилось:
Так, ряд упорядочили, какой еще есть важный момент в определении медианы? Правильно, четное и нечетное количество членов в выборке.
Заметил, что для четного и нечетного количества даже определения отличаются? Да, ты прав, не заметить – сложно. А раз так, то нам надо определиться, четное у нас количество игроков в нашей выборке или нечетное?
Все верно – игроков ( displaystyle 11), значит, количество нечетное! Теперь можем применять к нашей выборке менее заковыристое определение медианы для нечетного количества членов в выборке.
Ищем число, которое оказалось посередине в нашем упорядоченном ряду:
Ну вот, чисел у нас ( displaystyle 11), значит, по краям остается по пять чисел, а рост ( displaystyle 183) см будет медианой в нашей выборке.
Не так уж и сложно, правда?
Частота и относительная частота
Частота представляет собой число повторений, сколько раз за какой-то период происходило некоторое событие, проявлялось определенное свойство объекта либо наблюдаемый параметр достигал данной величины.
То есть частота определяет то, как часто повторяется та или иная величина в выборке.
Разберемся на нашем примере с футболистами. Перед нами вот такой вот упорядоченный ряд:
Частота – это число повторений какой-либо величины параметра. В нашем случае, это можно считать вот так. Сколько игроков имеет рост ( 176)?
Все верно, один игрок. Таким образом, частота встречи игрока с ростом ( 176) в нашей выборке равна ( 1).
Сколько игроков имеет рост ( 178)? Да, опять же один игрок. Частота встречи игрока с ростом ( 178) в нашей выборке равна ( 1).
Задавая такие вопросы и отвечая на них, можно составить вот такую табличку:
Ну вот, все довольно просто. Помни, что сумма частот должна равняться количеству элементов в выборке (объему выборки).
То есть в нашем примере: ( 1+1+1+2+1+1+1+1+1+1=11)
Перейдем к следующей характеристике – относительная частота.
Относительная частота – это отношение частоты к общему числу данных в ряду. Как правило, относительная частота выражается в процентах.
Обратимся опять к нашему примеру с футболистами. Частоты для каждого значения мы рассчитали, общее количество данных в ряду мы тоже знаем ( left( n=11 right)) .
Рассчитываем относительную частоту для каждого значения роста и получаем вот такую табличку:
А теперь сам составь таблицы частот и относительных частот для примера с 9-классниками, решающими задачи.
Скачать материал
Скачать материал
- Сейчас обучается 964 человека из 80 регионов
- Сейчас обучается 97 человек из 37 регионов
Описание презентации по отдельным слайдам:
-
1 слайд
Элементы Статистики
Сбор и группировка статистических данных -
2 слайд
2
Статистические характеристики
Среднее арифметическое
ряда чисел – частное от деления суммы этих чисел на число слагаемыхЗадача: сколько минут тратят на домашнее задание по алгебре?
23, 30, 25, 20, 34, 25, 30, 34, 35, 14
23+30+25+20+34+25+30+34+35+14 = 24
10 -
3 слайд
3
Статистические характеристики
Размах ряда чисел – разность между наибольшим и наименьшим из этих чисел
Пример: дан упорядоченный ряд чисел
35, 35, 36, 36, 36, 36, 37, 37, 38, 39, 39
39 – 34 = 4 – размах ряда -
4 слайд
4
Статистические характеристики
Модой ряда чисел – число наиболее часто встречающееся в данном рядуРяд чисел может иметь более одной моды или не иметь моды совсем
35, 35, 36, 36, 36, 36, 37, 37, 38, 39, 39
36 –мода ряда, так как встречается чаще всего в этом ряду -
5 слайд
5
Статистические характеристики (4)
Медианой упорядоченного ряда чисел с нечётным числом членов называется среднее в ряду число;
с чётным числом членов среднее арифметическое чисел, записанных посередине1) 64, 72, 72, 75, 78, 82, 85, 91, 93
2) 64, 72, 72, 75, 78, 82, 85, 88, 91, 93
78+82 = 80
2 -
6 слайд
Общие замечания
Для обобщения и систематизации данных, полученных в результате статистического наблюдения, их по какому-либо признаку разбивают на группы и результаты группировки сводят в таблицы. -
7 слайд
Пример №1
Администрация школы решила проверить математическую подготовку восьмиклассников. С этой целью был составлен тест, содержащий 9 заданий. Работу выполняли 40 учащихся школы. При проверке каждой работы учитель отмечал число верно выполненных заданий. В результате был составлен такой ряд чисел:
6, 5, 4, 0, 4, 5, 7, 9, 1, 6, 8, 7, 9, 5, 8, 6, 7, 2, 5, 7,
6, 3, 4, 4, 5, 6, 8, 6, 7, 7, 4, 3, 5, 9, 6, 7, 8, 6, 9, 8. -
8 слайд
Пример 1
6, 5, 4, 0, 4, 5, 7, 9, 1, 6, 8, 7, 9, 5, 8, 6, 7, 2, 5, 7,
6, 3, 4, 4, 5, 6, 8, 6, 7, 7, 4, 3, 5, 9, 6, 7, 8, 6, 9, 8Для того чтобы удобно было анализировать полученные данные, упорядочим этот ряд:
0, 1, 2, 3, 3, 4, 4, 4, 4, 4,
5, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6, б, 6,
7, 7, 7, 7, 7, 7, 7, 8, 8, 8, 8, 8, 9, 9, 9, 9. -
9 слайд
Представим полученные данные в виде таблицы, в которой для каждого числа верно выполненных заданий, записанного в верхней строке, укажем в нижней строке количество появлений этого числа в ряду, т. е. частоту.
0, 1, 2, 3, 3, 4, 4, 4, 4, 4,
5, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6, б, 6,
7, 7, 7, 7, 7, 7, 7, 8, 8, 8, 8, 8, 9, 9, 9, 9.
Такую таблицу называют таблицей частот.
Пример 1 -
10 слайд
В рассмотренном примере сумма частот равна общему числу проверяемых работ, т. е. 40.
Вообще, если результат исследования представлен в виде таблицы частот, то сумма частот равна общему числу данных в ряду. -
11 слайд
Анализ статистических данных
При проведении статистического исследования после сбора и группировки данных переходят к их анализу, используя для этого различные обобщающие показатели. Простейшими из них являются такие известные вам статистические характеристики, как среднее арифметическое, мода, медиана, размах. -
12 слайд
Таблица частот по результатам тестирования восьмиклассников по математике
среднее арифметическое
Чтобы найти среднее арифметическое, надо общее число верно выполненных заданий разделить на число учащихся, т. е. 40. Получаем
(0*1+1*1+2*1+3*2+4*5+5*6 + 6*8+7*7 + 8*5 + 9*4)= 232 : 40 = 5,8Значит, в среднем учащиеся выполнили по 5,8 заданий, т. е. примерно две трети общего объема работы.
-
13 слайд
Таблица частот по результатам тестирования восьмиклассников по математике
размах рассматриваемого ряда данных
Наибольшее число верно выполненных учащимися заданий равно 9, а наименьшее равно 0. Значит, размах рассматриваемого ряда данных равен 9-0=9, т. е. различие в числе верно выполненных заданий достаточно велико. -
14 слайд
Таблица частот по результатам тестирования восьмиклассников по математике
Из таблицы видно, что чаще всего встречаются работы, в которых верно выполнено 6 заданий, т. е. мода ряда равна 6
мода -
15 слайд
Таблица частот по результатам тестирования восьмиклассников по математике
Так как в ряду всего 40 чисел, то медиана равна среднему арифметическому 20-го и 21-го членов соответствующего упорядоченного ряда. Значит, медиана ряда равна (6 + 6): 2 = 6.0, 1, 2, 3, 3, 4, 4, 4, 4, 4,
5, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6, б, 6,
7, 7, 7, 7, 7, 7, 7, 8, 8, 8, 8, 8, 9, 9, 9, 9. -
16 слайд
Таблица частот по результатам тестирования восьмиклассников по математике
Таблица относительных частот ряда
Иногда составляют таблицу, в которой для каждого данного указывается не частота, а отношение частоты к общему числу данных в ряду. Это отношение, выраженное в процентах, называют относительной частотой, а саму таблицу — таблицей относительных частот.
В нашем примере общая численность данных — это число учащихся, писавших работу, т. е. 40.
Например, относительная частота данного в ряду, характеризующая количество учащихся, набравших 9 баллов, будет вычисляться
4 : 40*100=0,1*100=10 (Смотри следующий слайд) -
17 слайд
Таблица относительных частот ряда
Нетрудно убедиться, что сумма относительных частот составляет 100%.
Вообще,
если по результатам исследования составлена таблица относительных частот, то сумма относительных частот равна 100%. -
18 слайд
Интервальный ряд
Заметим, что если в ряду имеется большое число данных и одинаковые значения встречаются редко, то таблицы частот или относительных частот теряют наглядность и становятся излишне громоздкими. В таких случаях для анализа данных строят интервальный ряд. Для этого разность между наибольшим и наименьшим значениями делят на несколько равных частей (примерно 5—10) и, округляя полученный результат, определяют длину интервала. За начало первого интервала часто выбирают наименьшее данное или ближайшее к нему целое число, его не превосходящее. Для каждого интервала указывают число данных, попадающих в этот интервал, или выраженное в процентах отношение этого числа к общей численности данных. При этом граничное число обычно считают относящимся к последующему интервалу -
19 слайд
Пример интервального ряда
Пусть, например, на партии из 50 электроламп изучали продолжительность их горения (в часах). По результатам составили такую таблицу: -
20 слайд
Пример интервального ряда
Пользуясь составленной таблицей, найдем среднюю продолжительность горения. Для этого составим новую таблицу частот, заменив каждый интервал числом, которое является его серединой -
21 слайд
средняя продолжительность горения
(100 • 1 + 300 • 3 + 500 • 5 + 700 • 9 + 900 • 16 + 1100 • 9 + 1300 • 5 + 1500*2): 50 ~ 870 (с точностью до десятков). Значит, средняя продолжительность горения электроламп приближенно равна 870 ч -
22 слайд
В рассмотренном в начале пункта примере были проанализированы результаты выполнения теста восьмиклассниками одной школы. Тот же тест можно было бы использовать для более широкой проверки математической подготовки учащихся, например предложить его восьмиклассникам всех школ города или региона. Заметим, что организация такой проверки связана с серьезными трудностями по пересылке текстов заданий в школы, сбору и проверке работ учащихся, обработке полученных результатов. Вообще проведение любого массового исследования требует больших организационных усилий и финансовых затрат. Например, перепись населения страны связана с подготовкой разнообразной документации, выделением и инструктажем переписчиков, сбором информации, обработкой собранных сведений
Выборочное исследование
-
23 слайд
Выборочное исследование
В тех случаях, когда бывает сложно или даже невозможно провести сплошное исследование, его заменяют выборочным. При выборочном исследовании из всей изучаемой совокупности данных, называемой генеральной совокупностью, выбирается определенная ее часть, т. е. составляется выборочная совокупность (выборка), которая подвергается исследованию. При этом выборка должна быть представительной, или, как говорят, репрезентативной, т. е. достаточной по объему и отражающей характерные особенности исследуемой генеральной совокупности. -
24 слайд
Выборочное исследование
Пусть, например, в ходе кампании по выборам мэра в городе со стотысячным населением хотят узнать, кто из кандидатов имеет наибольшие шансы на успех. Для этого проводят опрос, например, полутора тысяч избирателей, в ходе которого выясняется, за кого они собираются голосовать. При этом нельзя опрашивать только молодых избирателей или только пенсионеров, так как это может привести к неправильным выводам. Необходимо, чтобы среди опрашиваемых было примерно одинаковое число мужчин и женщин. Кроме того, должны быть представлены люди с разным социальным положением и образованием. -
25 слайд
Выборочное исследование
Выборочное исследование проводят также и тогда, когда проведение сплошного исследования связано с порчей или уничтожением продукции. Например, при исследовании продолжительности горения партии электроламп, выпущенных заводом, невозможно проверить всю партию, так как это привело бы просто к ее уничтожению -
26 слайд
Решение упражнений по теме: «Сбор и группировка данных»
-
27 слайд
Практические задачи
Задача №1
На выборах мэра города будут баллотироваться три кандидата: Алексеев, Иванов, Карпов (обозначим их буквами А, И, К). Проводя опрос 50 избирателей, выяснили, за кого из кандидатов они собираются голосовать. Получили следующие данные:
И, А, И, И, К, К, И, И, И, А, К, А, А, А, К, К, И, К, А, А, И, К, И, И, К, И, К, А, И, И, И, А, И, И, К, И, А, И, К, К, И, К, А, И, И, И, А, А, К, И.
Представьте эти данные в виде таблицы частот. Достаточно ли этих данных, чтобы сделать вывод о предстоящих результатах голосования? -
28 слайд
Практические задачи
Задача №1
На выборах мэра города будут баллотироваться три кандидата: Алексеев, Иванов, Карпов (обозначим их буквами А, И, К). Проводя опрос 50 избирателей, выяснили, за кого из кандидатов они собираются голосовать. Получили следующие данные:Упорядоченный ряд
А, А, А, А, А, А, А, А, А, А, А, А, А,
И, И, И, И, И, И, И, И, И, И, И, И, И, И, И, И, И, И, И, И, И, И, И,
К, К, К, К, К, К, К, К, К, К, К, К, К, К. -
29 слайд
Практические задачи
Задача №1
На выборах мэра города будут баллотироваться три кандидата: Алексеев, Иванов, Карпов (обозначим их буквами А, И, К). Проводя опрос 50 избирателей, выяснили, за кого из кандидатов они собираются голосовать. Получили следующие данные:
Упорядоченный ряд
А, А, А, А, А, А, А, А, А, А, А, А, А,
И, И, И, И, И, И, И, И, И, И, И, И, И, И, И, И, И, И, И, И, И, И, И,
К, К, К, К, К, К, К, К, К, К, К, К, К, К.
Таблица частот -
30 слайд
Практические задачи
Задача №1
Мода статистического ряда равна 23.
Это значит, что больше всего голосов при опросе отдано за кандидата по фамилии Иванов.
Но этих данных недостаточно, чтобы сделать вывод о результатах предстоящего голосования на выборах мэра города, т.к. выборка из 50 человек не является представительной, т. е. достаточной по объему, чтобы сделать правильный вывод. -
31 слайд
Упражнения
№ 1030В ходе опроса 40 учащихся школы было выяснено, сколько времени (с точностью до 0,5 ч) в неделю они затрачивают на занятия в кружках и спортивных секциях. Получили следующие данные:
5, 1,5, 0, 2,5, 1, 0, 0, 2, 2,5, 3,5,
4, 5, 3,5, 2,5, 0, 1,5, 4,5, 3, 3, 5,
3,5, 4, 3,5, 3, 2,5, 2, 1, 2, 2, 4,5,
4, 3,5, 2, 5, 4, 2, 2,5, 0, 0, 3.
Представьте этот ряд данных в виде таблицы частот. -
32 слайд
№ 1030
5, 1,5, 0, 2,5, 1, 0, 0, 2, 2,5, 3,5,
4, 5, 3,5, 2,5, 0, 1,5, 4,5, 3, 3, 5,
3,5, 4, 3,5, 3, 2,5, 2, 1, 2, 2, 4,5,
4, 3,5, 2, 5, 4, 2, 2,5, 0, 0, 3.
Представьте этот ряд данных в виде таблицы частот.
Решение.
Упорядоченный ряд
0, 0, 0, 0, 0, 0, 1, 1, 1.5, 1.5,
2, 2, 2, 2, 2, 2, 2.5, 2.5, 2.5, 2.5,
2.5, 3, 3, 3, 3, 3.5, 3.5, 3.5, 3.5, 3.5,
4, 4, 4, 4, 4.5, 4.5, 5, 5, 5, 5 -
33 слайд
№ 1030 Решение(Продолжение)
Представьте этот ряд данных в виде таблицы частот. Найдите среднее арифметическое, размах, моду и медиану ряда.
0, 0, 0, 0, 0, 0, 1, 1, 1.5, 1.5,
2, 2, 2, 2, 2, 2, 2.5, 2.5, 2.5, 2.5,
2.5, 3, 3, 3, 3, 3.5, 3.5, 3.5, 3.5, 3.5,
4, 4, 4, 4, 4.5, 4.5, 5, 5, 5, 5
Таблица частот1) Среднее арифметическое.
(0*6+1*2+1.5*2+2*6+2.5*5+3*4+3.5*5+4*4+4.5*2+5*4):40=(0+2+3+12+12.5+12+17.5+16+9+20):40=104:40=2.6 -
34 слайд
№ 1030 Решение (продолжение 1)
Представьте этот ряд данных в виде таблицы частот.
0, 0, 0, 0, 0, 0, 1, 1, 1.5, 1.5,
2, 2, 2, 2, 2, 2, 2.5, 2.5, 2.5, 2.5,
2.5, 3, 3, 3, 3, 3.5, 3.5, 3.5, 3.5, 3.5,
4, 4, 4, 4, 4.5, 4.5, 5, 5, 5, 5.Таблица частот
2) Размах. 5-0=5
-
35 слайд
№ 1030 Решение (продолжение 2)
Представьте этот ряд данных в виде таблицы частот.
0, 0, 0, 0, 0, 0, 1, 1, 1.5, 1.5,
2, 2, 2, 2, 2, 2, 2.5, 2.5, 2.5, 2.5,
2.5, 3, 3, 3, 3, 3.5, 3.5, 3.5, 3.5, 3.5,
4, 4, 4, 4, 4.5, 4.5, 5, 5, 5, 5Таблица частот
3) Мода. Моды две: 0 и 2
-
36 слайд
№ 1030 Решение (Продолжение 3)
Представьте этот ряд данных в виде таблицы частот.
0, 0, 0, 0, 0, 0, 1, 1, 1.5, 1.5,
2, 2, 2, 2, 2, 2, 2.5, 2.5, 2.5, 2.5,
2.5, 3, 3, 3, 3, 3.5, 3.5, 3.5, 3.5, 3.5,
4, 4, 4, 4, 4.5, 4.5, 5, 5, 5, 5Таблица частот
4) Медиана. (2.5+2.5):2=2.5
-
37 слайд
№ 1030 Решение (Образец записи решения в тетради ученика)
Представьте этот ряд данных в виде таблицы частот.
Упорядоченный ряд
0, 0, 0, 0, 0, 0, 1, 1, 1.5, 1.5,
2, 2, 2, 2, 2, 2, 2.5, 2.5, 2.5, 2.5,
2.5, 3, 3, 3, 3, 3.5, 3.5, 3.5, 3.5, 3.5,
4, 4, 4, 4, 4.5, 4.5, 5, 5, 5, 5
Таблица частот1) Среднее арифметическое.
(0*6+1*2+1.5*2+2*6+2.5*5+3*4+3.5*5+4*4+4.5*2+5*4):40=(0+2+3+12+12.5+12+17.5+16+9+20):40=104:40=2.6
2) Размах. 5-0=5
3) Мода. Моды две: 0 и 2
4) Медиана. (2.5+2.5):2=2.5
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 262 826 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
Другие материалы
Памятка по алгебре 7 класс.
- Учебник: «Алгебра», Макарычев Ю.Н., Миндюк Н.Г. и др.
- Тема: 42. Системы линейных уравнений с двумя переменными
- 20.11.2021
- 409
- 5
Карточки для коррекции знаний учащегося
- Учебник: «Алгебра», Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. / Под ред. Теляковского С.А.
- Тема: § 7. Уравнения с двумя переменными и их системы
- 20.11.2021
- 204
- 5
- 20.11.2021
- 244
- 0
- 20.11.2021
- 205
- 6
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Организация научно-исследовательской работы студентов в соответствии с требованиями ФГОС»
-
Курс повышения квалификации «История и философия науки в условиях реализации ФГОС ВО»
-
Курс повышения квалификации «Разработка бизнес-плана и анализ инвестиционных проектов»
-
Курс повышения квалификации «Финансы: управление структурой капитала»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Управление ресурсами информационных технологий»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Организация деятельности секретаря руководителя со знанием английского языка»
-
Курс профессиональной переподготовки «Организация системы менеджмента транспортных услуг в туризме»
-
Курс профессиональной переподготовки «Гражданско-правовые дисциплины: теория и методика преподавания в образовательной организации»
