Загрузить PDF
Загрузить PDF
С абсолютной частотой все довольно просто: она определяет, сколько раз конкретное число содержится в имеющемся наборе данных (объектов или значений). А вот относительная частота характеризует отношение количества конкретного числа в наборе данных. Другими словами, относительная частота – это отношение количества определенного числа к общему количеству чисел в наборе данных. Имейте в виду, что вычислить относительную частоту достаточно легко.
-

1
Соберите данные. Если вы решаете математическую задачу, в ее условии должен быть дан набор данных (чисел). В противном случае проведите эксперимент или исследование и соберите необходимые данные. Подумайте, в какой форме записать исходные данные.
- Например, нужно собрать данные о возрасте людей, которые посмотрели определенный фильм. Конечно, можно записать точный возраст каждого человека, но в этом случае вы получите довольно большой набор данных с 60-70 числами в пределах от 10 до 70 или 80. Поэтому лучше сгруппировать данные по категориям, таким как «Моложе 20», «20-29», «30-39» «40-49», «50-59» и «Старше 60». Получится упорядоченный набор данных с шестью группами чисел.
- Другой пример: врач собирает данные о температуре пациентов в определенный день. Если записать округленные числа, например, 37, 38, 39, то результат будет не слишком точным, поэтому здесь данные нужно представить в виде десятичных дробей.
-

2
Упорядочьте данные. Когда вы соберете данные, у вас, скорее всего, получится хаотичный набор чисел, например, такой: 1, 2, 5, 4, 6, 4, 3, 7, 1, 5, 6, 5, 3, 4, 5, 1. Такая запись кажется практически бессмысленной и с ней сложно работать. Поэтому упорядочьте числа по возрастанию (от меньшего к большему), например, так: 1,1,1,2,3,3,4,4,4,5,5,5,5,6,6,7.[1]
- Упорядочивая данные, будьте внимательны, чтобы не пропустить ни одного числа. Посчитайте общее количество чисел в наборе данных, чтобы убедиться, что вы записали все числа.
-

3
Создайте таблицу с данными. Собранные данные можно организовать в виде таблицы. Такая таблица будет включать три столбца и использоваться для вычисления относительной частоты. Столбцы обозначьте следующим образом:[2]
Реклама
-

1
Найдите количество чисел в наборе данных. Относительная частота характеризует, сколько раз конкретное число содержится в имеющемся наборе данных по отношению к общему количеству чисел. Чтобы найти относительную частоту, нужно посчитать общее количество чисел в наборе данных. Общее количество чисел станет знаменателем дроби, с помощью которой будет вычислена относительная частота.[3]
- В нашем примере набор данных содержит 16 чисел.
-

2
Найдите количество определенного числа. То есть посчитайте, сколько раз конкретное число встречается в наборе данных. Это можно сделать как для одного числа, так и для всех чисел из набора данных.[4]
- Например, в нашем примере число
встречается в наборе данных три раза.
- Например, в нашем примере число
-

3
Разделите количество конкретного числа на общее количество чисел. Так вы найдете относительную частоту для определенного числа. Вычисление можно представить в виде дроби или воспользоваться калькулятором или электронной таблицей, чтобы разделить два числа.[5]
Реклама
-

1
Результаты вычислений запишите в созданную ранее таблицу. Она позволит представить результаты в наглядной форме. По мере вычисления относительной частоты результаты записывайте в таблицу напротив соответствующего числа. Как правило, значение относительной частоты можно округлить до второго знака после десятичной запятой, но это на ваше усмотрение (в зависимости от требований задачи или исследования). Помните, что округленный результат не равен точному ответу.[6]
- В нашем примере таблица относительных частот будет выглядеть следующим образом:
- x : n(x) : P(x)
- 1 : 3 : 0,19
- 2 : 1 : 0,06
- 3 : 2 : 0,13
- 4 : 3 : 0,19
- 5 : 4 : 0,25
- 6 : 2 : 0,13
- 7 : 1 : 0,06
- Итого : 16 : 1,01
-

2
Представьте числа (элементы), которых нет в наборе данных. Иногда представление чисел с нулевой частотой так же важно, как и представление чисел с ненулевой частотой. Обратите внимание на собранные данные; если между данными имеются пробелы, их нужно заполнить нулями.
- В нашем примере набор данных включает все числа от 1 до 7. Но предположим, что числа 3 нет в наборе. Возможно, это немаловажный факт, поэтому нужно записать, что относительная частота числа 3 равна 0.
-

3
Выразите результаты в процентах. Иногда результаты вычислений нужно преобразовать из десятичных дробей в проценты. Это общепринятая практика, потому что относительная частота характеризует процент случаев появления определенного числа в наборе данных. Чтобы преобразовать десятичную дробь в проценты, нужно десятичную запятую передвинуть на две позиции вправо и приписать символ процента.
- Например, десятичная дробь 0,13 равна 13%.
- Десятичная дробь 0,06 равна 6% (обратите внимание, что перед 6 стоит 0).
Реклама
Советы
- Относительная частота характеризует наличие или возникновение определенного события в наборе событий.
- Если сложить относительные частоты всех чисел из набора данных, вы получите единицу. Помните, что при сложении округленных результатов сумма не будет равна 1,0.
- Если набор данных слишком большой, чтобы обработать его вручную, воспользуйтесь программой MS Excel или MATLAB; это позволит избежать ошибок в процессе вычисления.
Реклама
Источники
Об этой статье
Эту страницу просматривали 144 126 раз.
Была ли эта статья полезной?
Пусть
требуется изучить статистическую
совокупность относительно некоторого
количественного признака X.
Числовые значения признака будем
обозначать через хi.
Из
генеральной совокупности извлекается
выборка объёма п.
-
Количественный
признак Х
– дискретная
случайная величина.
Наблюдаемые
значения хi
называют вариантами,
а последовательность вариантов,
записанных в возрастающем
порядке, –
вариационным
рядом.
Пусть
x1
наблюдалось n1
раз,
x2
наблюдалось n2
раз,
xk
наблюдалось nk
раз,
причем
![]()
.
Числа ni
называют
частотами,
а их отношение к объёму выборки, т.е.
![]()
,
–
относительными
частотами (или
частостями), причем
![]()
.
Значение
вариант и соответствующие им частоты
или относительные
частоты можно записать в виде таблиц 1
и 2.
Таблица
1
|
Варианта |
x1 |
x2 |
… |
xk |
|
Частота |
n1 |
n2 |
… |
nk |
Таблицу
1 называют дискретным
статистическим
рядом распределения (ДСР) частот, или
таблицей частот.
Таблица
2
|
Варианта |
x1 |
x2 |
… |
xk |
|
Относительная |
w1 |
w2 |
… |
wk |
Таблица
2
ДСР
относительных частот, или
таблица относительных частот.
Определение.
Модой
называется наиболее часто встречающийся
вариант, т.е. вариант с наибольшей
частотой. Обозначается xмод.
Определение.
Медианой
называется
такое значение признака, которое делит
всю статистическую совокупность,
представленную в виде вариационного
ряда, на две равных по числу части.
Обозначается
![]()
.
Если
n
нечетно, т.е. n
= 2m
+ 1,
то
=
xm+1.
Если
n
четно, т.е. n
= 2m,
то
![]()
.
Пример
3.
По результатам наблюдений: 1, 7, 7, 2, 3, 2,
5, 5, 4, 6, 3, 4, 3, 5, 6, 6, 5, 5, 4, 4 построить ДСР
относительных частот. Найти моду и
медиану.
Решение.
Объем выборки n
= 20. Составим ранжированный ряд элементов
выборки: 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5, 6, 6, 6,
7, 7. Выделим варианты и подсчитаем их
частоты (в скобках): 1 (1), 2 (2), 3 (3),
4 (4),
5 (5), 6 (3), 7 (2). Строим таблицу:
|
xi |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
wi |
1/20 |
2/20 |
3/20 |
4/20 |
5/20 |
3/20 |
2/20 |
Наиболее
часто встречающийся вариант xi
=
5. Следовательно, xмод
=
5. Так
как объем выборки n
– четное число, то
![]()
Если
на плоскости нанести точки
![]()
и соединить их отрезками прямых, то
получим полигон
частот.
Если
на плоскости нанести точки
![]()
,
то получим полигон
относительных частот.
Пример 4.
Построить полигон частот и полигон
относительных частот по данному
распределению выборки:
|
xi |
4 |
7 |
8 |
12 |
17 |
|
ni |
2 |
4 |
5 |
6 |
3 |
|
wi |
2/20 |
4/20 |
5/20 |
6/20 |
3/20 |
Решение.
На рисунке 2 показан полигон частот и
на рисунке 3 – полигон относительных
частот.


Рис.
2 Рис.
3
Замечание.
Чем круче полигон, тем равномернее
процесс.
-
Пусть
количественный признак X
– непрерывная
случайная величина,
принимающая значения из интервала
(а,b).
Весь диапазон наблюдаемых данных делят
на частичные
интервалы
[хi;
xi+1),
которые берут обычно одинаковыми по
длине:

=
xi+1
–
xi
(i
= 0, 1, …, k).
Для определения величины интерваламожно использовать формулу
Стерджеса:
![]()
где
(xmax
–
xmin)
разность между наибольшим и наименьшим
значениями признака, k
= 1 + log2
n
число интервалов (log2
n
3,322
lg
n).
Если окажется, что h
дробное число, то за длину частичного
интервала следует брать либо ближайшее
целое число, либо ближайшую простую
дробь. За начало первого интервала
рекомендуется брать величину xнач
=
xmin
–
![]()
.
В каждом
из частичных интервалов подсчитывают
число наблюдаемых значений, т.е. частоту
ni.
По частотам находят относительные
частоты
![]()
.
Полученные интервалы и соответствующие
им частоты (или относительные частоты)
записывают в виде таблицы 3. При этом
правая граница последнего интервала
тоже включается.
Таблица
3
|
Частичный |
[x0, |
[x1, |
… |
[xk-1, |
|
Относительная |
w1 |
w2 |
… |
wk |
Таблица
3 называется интервальным
статистическим рядом распределения
(ИСР) относительных частот,
который задаёт распределение
выборки. Аналогично
составляется ИСР
частот.
Пример
5.
Измерили рост (с точностью до см) 30
наудачу отобранных студентов. Результаты
измерений таковы:
178,
160, 154, 183, 155, 153, 167, 186, 163, 155, 157, 175, 170, 166, 159,
173,
182, 167, 171, 169, 179, 165, 156, 179, 158, 171, 175, 173, 164, 172.
Построить
интервальный статистический ряд
относительных частот.
Решение.
Для
удобства проранжируем полученные
данные:
153,
154, 155, 155, 156, 157, 158, 159, 160, 163, 164, 165, 166, 167, 167,
169,
170, 171, 171, 172, 173, 173, 175, 175, 178, 179, 179, 182, 183, 186.
Отметим,
что Х
рост студента
непрерывная случайная величина. Как
видим, xmin
=
153, хmax
=
186; по формуле Стерджеса, при n
= 30, находим длину частичного интервала
![]()
Примем
![]()
= 6. Тогда хнач
= 153 –
![]()
=150.
Исходные данные разбиваем на шесть (k
=
1 + log230
= 5,907
6) интервалов:
[150,
156), [156, 162), [162, 168), [168, 174), [174, 180), [180, 186].
Подсчитав
число студентов ni,
попавших в каждый из полученных
промежутков, получим ИСР:
|
[xi,xi+1) |
[150, |
[156, |
[162, |
[168, |
[174,180) |
[180,186] |
|
ni |
4 |
5 |
6 |
7 |
5 |
3 |
|
wi |
4/30 |
5/30 |
6/30 |
7/30 |
5/30 |
3/30 |
Первая
и третья строчка таблицы образует ИСР
относительных частот.
Замечание.
При
решении учебных задач на построение
ИСР можно пользоваться следующими
правилами.
-
Назначаются нижняя
граница а
и верхняя граница b
для вариант так, чтобы отрезок [a;
b]
вместил всю выборку; часто полагают
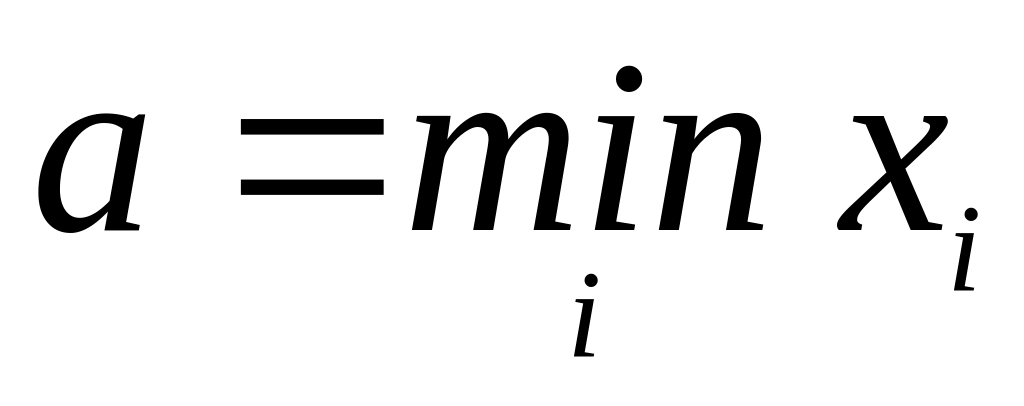
,

,
но иногда a
и b
назначают из соображений удобства, но
не слишком далеко от

и

. -
Находится число
k
равных по длине частичных интервалов
варьирования, которое зависит от объема
выборки и обычно 6
k
20;
рассчитывается длина интервалов
группирования

.
Интервальный
статистический ряд распределения,
представленный графически, называется
гистограммой.
Гистограмма
относительных частот
строится следующим образом: по оси
абсцисс откладываются
интервалы (хi;
хi+1)
и на каждом из них строится прямоугольник
высотой
![]()
где
![]()
;
![]()
.
Площадь
i–го
прямоугольника
![]()
.
Площадь
всей гистограммы
![]()
.
З
амечание:
гистограмма на рисунке 4 – гистограмма
относительных частот.
x3
Рис.
4
Можно
построить гистограмму
частот,
высоты прямоугольников которых равны
![]()
.
Пример 6.
Построить гистограмму частот по данному
ИСР частот:
|
[xi; |
[100; |
[120; |
[140; |
[160; |
[180; |
|
ni |
20 |
50 |
80 |
40 |
10 |
Решение.
По ИСР частот находим длину частичных
интервалов
![]()
= 20 и высоты прямоугольников hi
=
![]()
.
Результаты занесем в таблицу:
|
[xi; |
[100; |
[120; |
[140; |
[160; |
[180; |
|
ni |
20 |
50 |
80 |
40 |
10 |
|
hi |
1 |
2,5 |
4 |
2 |
0,5 |
Искомая
гистограмма частот изображена на рис.
5.

hi
xi
xi
Рис.
5
В
теории вероятностей гистограмме
относительных частот соответствует
график плотности распределения
вероятностей. Распределение выборки,
задаваемое интервальным статистическим
рядом (табл. 3) или таблицей относительных
частот (табл. 2), называется эмпирическим
распределением случайной величины.
По
теореме Бернулли относительная частота
wi,
появление события в п
независимых
испытаниях
сходится
по вероятности к вероятности рi
этого события
![]()
.
Значит во второй строке таблицы 3 и
таблицы 2 стоят
приближённые значения вероятностей рi
следующих событий
![]()
и
![]()
,
поэтому
распределение выборки называют
эмпирическим распределением случайной
величины X.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость
Статистическое распределение выборки
Содержание:
- Примеры использования формул и таблиц для решения практических задач
- Статистический интервальный ряд распределения
Предположим случай, когда из генеральной совокупности извлекается некоторая выборка, при этом каждому значению соответствует некоторый параметр, означающий количество раз, когда появлялось данное значение. Здесь $x_1$ было зафиксировано $n_1$ раз, $x_2$ было обнаружено $n_2$$x_k$ выявлено $n_k$. При этом
$sum_{i=1}^{k}n_i=n$
Где n — объём рассматриваемой выборки.
Определение 1
Используется следующая терминология: $x_k$ носят наименование вариантов, а последовательность таких вариантов, зафиксированный по возрастанию именуется вариационным рядом. Количество наблюдений каждого из вариантов носят название частот. При этом частное частот и выборки называют относительными частотами.
Определение 2
Статистическое распределение —это название всего набора вариантов и частот, которые с ними соотносятся. Чаще всего задаётся с помощью специальной таблицы, где представлены частоты, а также интервалы им соответствующие.
| $x_1$ | $x_2$ | … | $x_k$ |
| $n_1$ | $n_2$ | … | $n_k$ |
| $frac{n_1}{n}$ | $frac{n_2}{n}$ | $frac{n_k}{n}$ |
Здесь в первой строке представлены варианты, во второй частоты, в третьеq взяты относительные частоты.
Для определения размера интервала используется следующее выражение:
$d=frac{x_{max}- x_{min}}{1+3,332cdot lg n}$
Здесь $x_{max}$, $x_{min}$ наибольшее и наименьшее значения ряда вариантов, а n характеризуем объём выборки.
Примеры использования формул и таблиц для решения практических задач
Пример 1
В ходе проведения измерений в однородных группах, были определены следующие значения выборки: 71, 72, 74, 70, 70, 72, 71, 74, 71, 72, 71, 73, 72, 72, 72, 74, 72, 73, 72, 74. Необходимо использовать данные значения, что определить ряд распределения частот и ряд распределения относительных частот.
Решение.
1) Составим статистический ряд распределения частот:
| xi | 70 | 71 | 72 | 73 | 74 |
| ni | 2 | 4 | 8 | 2 | 4 |
2) Рассчитаем суммарный размер выборки: n=2+4+8+2+4=20. Определим относительные частоты, для этого используем формулы: ni/n=wi: wi=2/20=0.1; w2=4/20=0.2; w3=0.4; w4=4/20=0.1; w5=2/20=0.2. Теперь зафиксируем в таблице распределение относительных частот:
| xi | 70 | 71 | 72 | 73 | 74 |
| wi | 0.1 | 0.2 | 0.4 | 0.1 | 0.2 |
Контрольная сумма должна равняться единице: 0,1+0,2+0,4+0,1+0,2=1.
Полигон частот
Название «полигоном частот» применяют для обозначения ломаной линии, каждый отрезок, которой соединяют точки $(х_1,n_1),(х_2,n_2),…,(х_k,n_k)$. Для построения на графике полигона частот по оси абсцисс отмечают варианты $х_2$, при этом на оси ординат отсчитывают– соответствующие частоты $n_i$. Когда полученные точки $(х_i,n_i)$ соединяются с помощью отрезков, то автоматически получают полигон частот.
Статистический интервальный ряд распределения.
Статистическим дискретным рядом (или эмпирической функцией распределения) обычно пользуются, если число различающихся вариант в полученной выборке не слишком большое. Также применение возможно, когда дискретность имеет важное значение для экспериментатора. В тех случаях, когда важный для задачи признак генеральной совокупности Х распределяется непрерывным образом, либо его дискретность нет возможности учесть, то варианты предпочтительнее всего группировать, чтобы получить интервалы.
Статистическое распределение допустимо задавать в том числе в качестве последовательности интервалов и частот, соответствующих этим интервалам. При это за частоту какого-либо интервала принимается сумма всех частот, вошедших в данный интервал.
Особенно следует отметить ,что $h_i-h_{i-1}=h$ при всех i, т.е. группировка проводится с равным шагом h. Также в вопросе группировки можно ориентироваться на ряд полученных опытным путём рекомендацийу, касающихся таких параметров, как а, k и $h_i$:
1. $Rраз_{мах}=X_{max}-X_{min}$
2. $h=R/k$; k-число групп
3.$ kgeq 1+3.321lgn$ (формула Стерджеса)
4. $a=x_{min}, b=x_{max}$
5.$ h=a+h_i, i=0,1…k$
Определённую в ходе решения задачи группировку удобнее всего скомпоновать и перевести в вид специальной таблицы, которая также может именоваться — «статистический интервальный ряд распределения»:
| Интервалы группировки | [h0;h1) | [h1;h2) | … | [hk-2;hk-1) | [hk-1;hk) |
| Частоты | n1 | n2 | … | nk-1 | nk |
Таблицу подобного вида можно сделать, поменяв частоты $n_i$ на относительные частоты:
| Интервалы группировки | [h0;h1) | [h1;h2) | … | [hk-2;hk-1) | [hk-1;hk) |
| Отн. частоты | w1 | w2 | … | wk-1 | wk |

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример 2
На склад пришла крупная партия деталей. Из них методом случайного отбора взято 50 экземпляров. Рассматривая изделия по одному, особенно интересующему признаку — размеру, определённому с точностью до 1 см, получим следующий вариационный ряд: 22, 47, 26, 26, 30, 28, 28, 31, 31, 31, 32, 32, 33, 33, 33, 33, 34, 34, 34, 34, 34, 35, 35, 36, 36, 36, 36, 36, 37, 37, 37, 37, 37, 37, 38, 38, 40, 40, 40, 40, 40, 41, 41, 43, 44, 44, 45, 45, 47, 50. Требуется произвести расчёт и определить статистический интервальный ряд распределения.
Решение
Найдём параметры выборки используя сведения из условия задачи.
$k geq1+3,321cdot lg50=1+3.32lg(5cdot10)=1+3.32(lg5+lg10)=6.6$
Получили a=22, k=7, h=(50-22)/7=4, hi=22+4i, i=0,1,…,7.
| Интервалы группировки | 22-26 | 26-30 | 30-34 | 34-38 | 38-42 | 42-46 | 46-50 |
| Частоты | 1 | 4 | 10 | 18 | 9 | 5 | 3 |
| Отн. частоты | 0.02 | 0.08 | 0.2 | 0.36 | 0.18 | 0.1 | 0.06 |
Десятичные логарифмы от 1 до 10
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| lnn≈ | 0 | 0.3 | 0.48 | 0.6 | 0.7 | 0.78 | 0.85 | 0.9 | 0.95 | 1 |
Не получается написать работу самому?
Доверь это кандидату наук!
17 авг. 2022 г.
читать 2 мин
Таблица частот — это таблица, в которой отображается информация о частотах. Частоты просто говорят нам, сколько раз произошло определенное событие.
Например , в следующей таблице показано, сколько товаров было продано магазином в разных ценовых диапазонах за данную неделю:
| Цена товара | Частота | | — | — | | $1 – $10 | 20 | | $11 – $20 | 21 | | 21 – 30 долларов США | 13 | | $31 – $40 | 8 | | $41 — $50 | 4 |
В первом столбце отображается ценовой класс, а во втором столбце — частота этого класса.
Также можно рассчитать относительную частоту для каждого класса, которая представляет собой просто частоту каждого класса в процентах от целого.
| Цена товара | Частота | Относительная частота | | — | — | — | | $1 – $10 | 20 | 0,303 | | $11 – $20 | 21 | 0,318 | | 21 – 30 долларов США | 13 | 0,197 | | $31 – $40 | 8 | 0,121 | | $41 — $50 | 4 | 0,061 |
Всего было продано 66 штук. Таким образом, мы нашли относительную частоту каждого класса, взяв частоту каждого класса и разделив ее на общее количество проданных товаров.
Например, было продано 20 товаров по цене от 1 до 10 долларов. Таким образом, относительная частота класса $1 – $10 составляет 20/66 = 0,303 .
Затем был продан 21 предмет в ценовом диапазоне от 11 до 20 долларов. Таким образом, относительная частота класса $11 – $20 составляет 21/66 = 0,318 .
В следующем примере показано, как найти относительные частоты в Excel.
Пример: относительные частоты в Excel
Сначала мы введем класс и частоту в столбцах A и B:
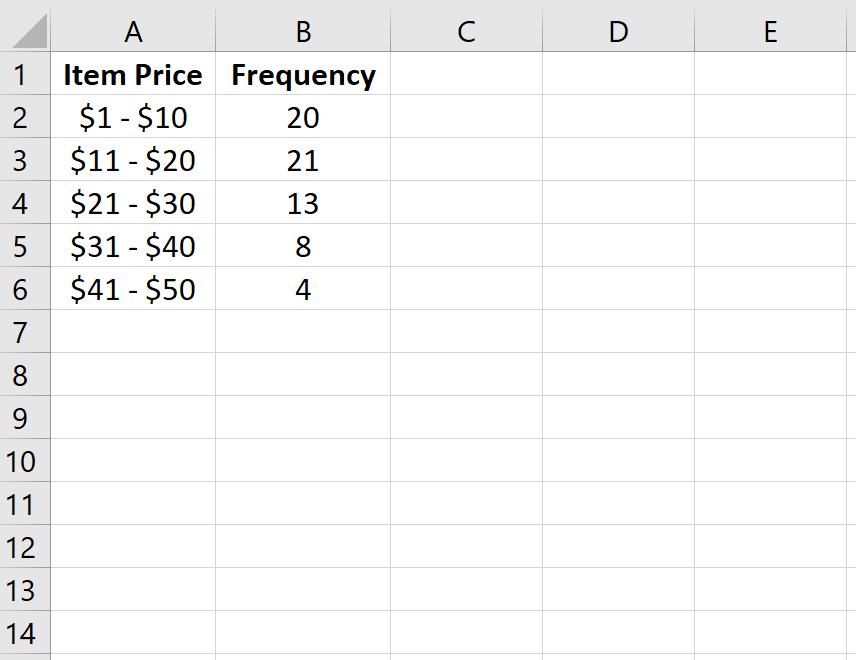
Далее мы рассчитаем относительную частоту каждого класса в столбце C. В столбце D показаны формулы, которые мы использовали:
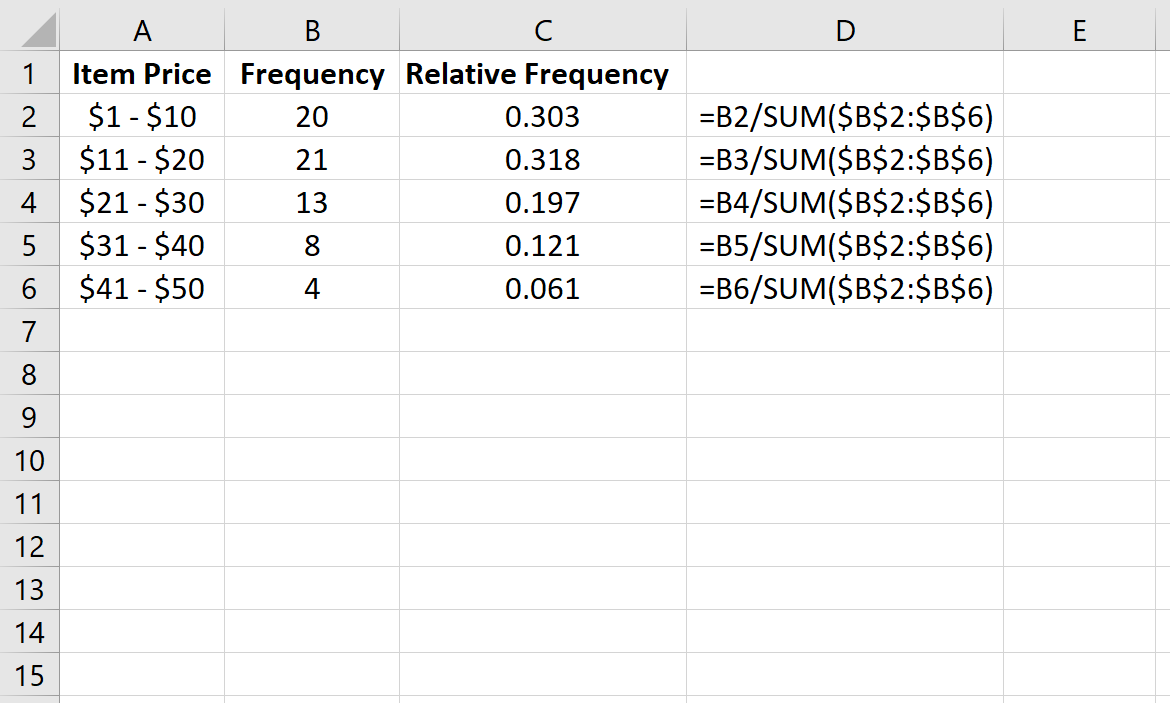
Мы можем проверить правильность наших расчетов, убедившись, что сумма относительных частот равна 1:
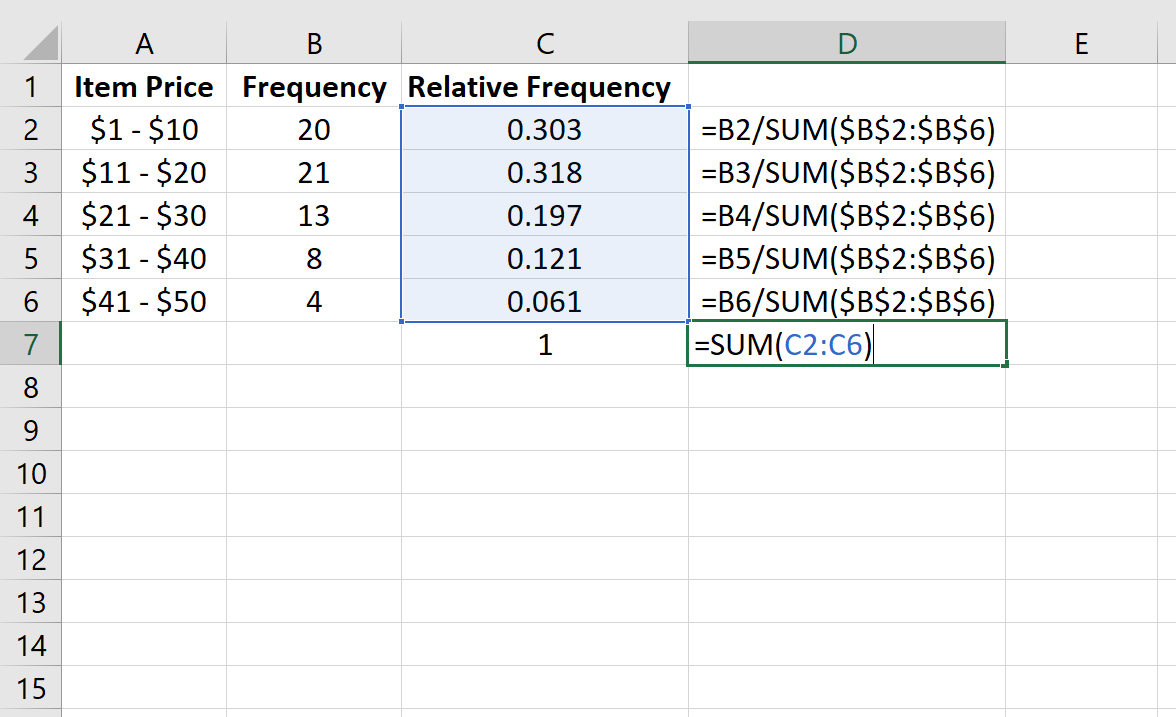
Мы также можем создать гистограмму относительной частоты для визуализации относительных частот.
Просто выделите относительные частоты:

Затем перейдите в группу « Диаграммы » на вкладке « Вставка » и щелкните первый тип диаграммы в « Вставить столбец» или «Гистограмма» :
Автоматически появится гистограмма относительной частоты:
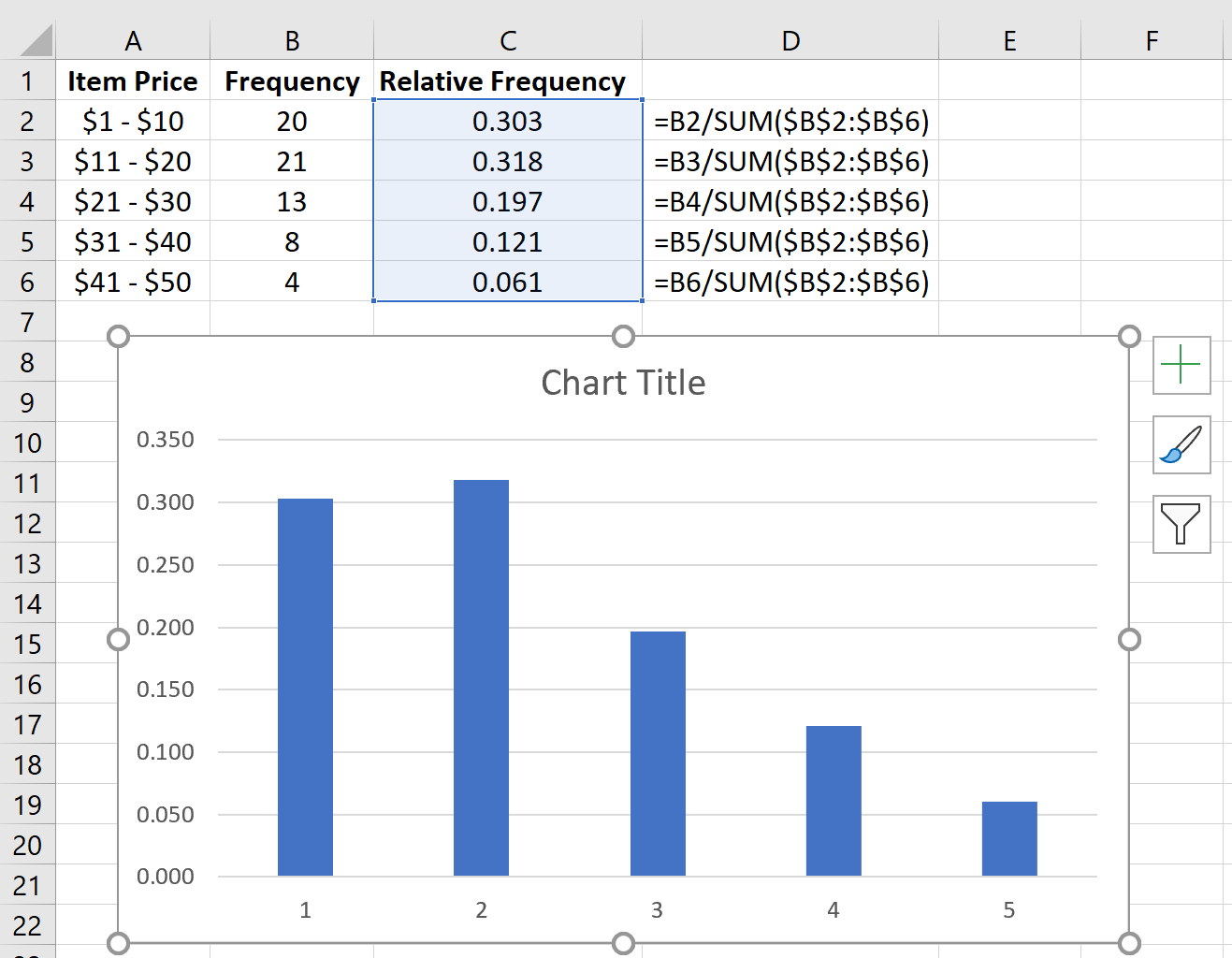
Измените метки оси X, щелкнув правой кнопкой мыши диаграмму и выбрав Выбрать данные.В разделе « Ярлыки горизонтальной (категории) оси » нажмите « Изменить » и введите диапазон ячеек, содержащий цены на товары. Нажмите OK , и новые метки осей появятся автоматически:
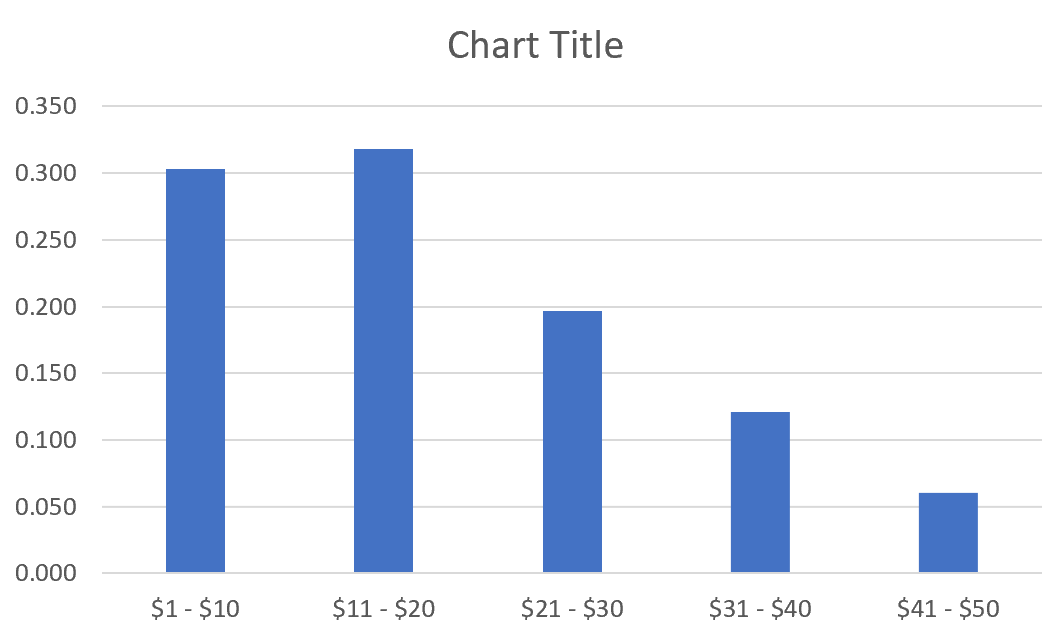
Дополнительные ресурсы
Калькулятор относительной частоты
Гистограмма относительной частоты: определение + пример
Мода и медиана
Модой ряда чисел называется число, наиболее часто встречающееся в данном ряду.
Обратимся снова к нашему примеру со сборной по футболу:
Чему в данном примере равна мода? Какое число наиболее часто встречается в этой выборке?
Все верно, это число ( displaystyle 181), так как два игрока имеют рост ( displaystyle 181) см; рост же остальных игроков не повторяется.
Тут все должно быть ясно и понятно, да и слово знакомое, правда?
Перейдем к медиане, ты ее должен знать из курса геометрии. Но мне не сложно напомнить, что в геометрии медиана (в переводе с латинского- «средняя») — отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны.
Ключевое слово – СЕРЕДИНА. Если ты знал это определение, то тебе легко будет запомнить, что такое медиана в статистике.
Медианой ряда чисел с нечетным числом членов называется число, которое окажется посередине, если этот ряд упорядочить (проранжировать, т.е. расположить значения в порядке убывания или возрастания).
Медианой ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине, если этот ряд упорядочить.
Ну что, вернемся к нашей выборке футболистов?
Ты заметил в определении медианы важный момент, который нам еще здесь не встречался? Конечно, «если этот ряд упорядочить»!
Для того, чтобы в ряду чисел был порядок, можно расположить значения роста футболистов как в порядке убывания, так и в порядке возрастания. Мне удобней выстроить этот ряд в порядке возрастания (от самого маленького к самому большому).
Вот, что у меня получилось:
Так, ряд упорядочили, какой еще есть важный момент в определении медианы? Правильно, четное и нечетное количество членов в выборке.
Заметил, что для четного и нечетного количества даже определения отличаются? Да, ты прав, не заметить – сложно. А раз так, то нам надо определиться, четное у нас количество игроков в нашей выборке или нечетное?
Все верно – игроков ( displaystyle 11), значит, количество нечетное! Теперь можем применять к нашей выборке менее заковыристое определение медианы для нечетного количества членов в выборке.
Ищем число, которое оказалось посередине в нашем упорядоченном ряду:
Ну вот, чисел у нас ( displaystyle 11), значит, по краям остается по пять чисел, а рост ( displaystyle 183) см будет медианой в нашей выборке.
Не так уж и сложно, правда?
Частота и относительная частота
Частота представляет собой число повторений, сколько раз за какой-то период происходило некоторое событие, проявлялось определенное свойство объекта либо наблюдаемый параметр достигал данной величины.
То есть частота определяет то, как часто повторяется та или иная величина в выборке.
Разберемся на нашем примере с футболистами. Перед нами вот такой вот упорядоченный ряд:
![]()
Частота – это число повторений какой-либо величины параметра. В нашем случае, это можно считать вот так. Сколько игроков имеет рост ( 176)?
Все верно, один игрок. Таким образом, частота встречи игрока с ростом ( 176) в нашей выборке равна ( 1).
Сколько игроков имеет рост ( 178)? Да, опять же один игрок. Частота встречи игрока с ростом ( 178) в нашей выборке равна ( 1).
Задавая такие вопросы и отвечая на них, можно составить вот такую табличку:
Ну вот, все довольно просто. Помни, что сумма частот должна равняться количеству элементов в выборке (объему выборки).
То есть в нашем примере: ( 1+1+1+2+1+1+1+1+1+1=11)
Перейдем к следующей характеристике – относительная частота.
Относительная частота – это отношение частоты к общему числу данных в ряду. Как правило, относительная частота выражается в процентах.
Обратимся опять к нашему примеру с футболистами. Частоты для каждого значения мы рассчитали, общее количество данных в ряду мы тоже знаем ( left( n=11 right)) .
Рассчитываем относительную частоту для каждого значения роста и получаем вот такую табличку:
А теперь сам составь таблицы частот и относительных частот для примера с 9-классниками, решающими задачи.

