Как найти частоту волны в физике формула

Была ли эта статья полезной?

---

Сайт «Все формулы» работает на WordPress

Содержание:

Волны:

Стоя на берегу озера или пруда, вы могли наблюдать, как кольцами разбегаются волны от места, куда был брошен камень, как волны раскачивают лодку или катер. Ветер нарушает равновесие морской поверхности, кажется, что море надвигается на берег, но это не так. Не перемещаются по полю колосья, когда «волнуется» нива, они только наклоняются и опять выпрямляются. Вслед за кораблем или лодкой всегда возникает типичная картина волн.

Волновые процессы широко распространены в природе. Физические основы волновых движений различны, но все они объясняются одинаковыми законами.

Что же такое волна и каковы причины возникновения волн

Вам известно, что твердые, жидкие и газообразные тела состоят из частей, взаимодействующих между собой. Если частица тела начинает совершать колебания, то в результате взаимодействия ее с другими частицами тела это движение распространяется с определенной скоростью во всех направлениях.

Волна — процесс распространения колебаний в любой среде. Волна — это изменение состояния среды, распространяющееся в пространстве и переносящее энергию.

Наблюдения. Рассмотрим особенности распространения волн. Если рассматривать волны на поверхности воды (рис. 204), то они кажутся валами, движущимися в определенном направлении, причем расстояния между валами, или гребнями, одинаковы.

Если бросить в воду поплавок, его не будет относить волной, а он начнет совершать колебания вверх-вниз, оставаясь почти на одном месте.

При распространении волны изменяется состояние колеблющейся среды, но не перенос вещества. От брошенного камня начинает колебаться определенный участок воды, эти колебания передаются соседним участкам и постепенно распространяются во все стороны. Течение воды не возникает, перемещается только форма ее поверхности.

Опыт 1. Закрепим один конец длинного резинового шнура и легонько заставим шнур колебаться. По шнуру побежит волна (рис. 205). Чем сильнее колеблется шнур, тем больше скорость распространения волны. Волна добежит до точки крепежа, отразится и побежит в обратном направлении.

При распространении волны изменяется только форма шнура, а каждый его участок колеблется относительно своего положения равновесия, причем колебания происходят в направлении, перпендикулярном направлению распространения волны (рис. 206). Такие волны называют поперечными волнами.

Поперечные волны

Поперечные волны — это волны, в которых частицы совершают колебания в направлении, перпендикулярном направлению распространения волны.

Опыт 2. Если ударить по одному из концов длинной мягкой пружины большого диаметра, то по пружине «побежит» сжатие. Повторяя удары, можно возбудить в пружине волну, представляющую собой последовательные сжатия и растяжения пружины, «бегущие» друг за другом (рис. 207). Любой виток пружины совершает колебания вдоль направления распространения волны. Такую волну называют продольной волной.

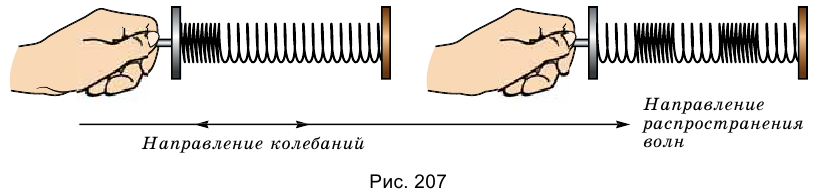
Продольные волны

Продольные волны — это волны, в которых частицы совершают колебания вдоль направления распространения волны.

При распространении волны движение передается от одного участка тела к другому. С передачей движения связана передача энергии. Передача энергии без передачи вещества – основное свойство всех волн.

Любые волны характеризуются длиной и скоростью их распространения.

Длина волны — это расстояние между ближайшими друг к другу точками волны, колеблющимися в одинаковых фазах (рис. 208).

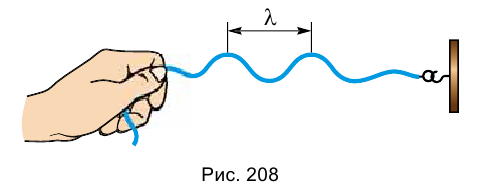
Длину волны обозначают греческой буквой А. (лямбда). Ее единицей является один метр (1 м).

Волны любого происхождения распространяются в пространстве не мгновенно, а с определенной скоростью. Например, можно увидеть, как чайка летит над морем будто все время над одним гребнем волны. В этом случае скорость полета чайки равна скорости распространения волны.

А как можно определить скорость распространения волны?

Вы уже знаете, что любое колебание характеризуется периодом колебаний, то есть временем, после которого колебания повторяются. Тогда можно сказать, что за один период волна распространяется на расстояние 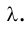. Поэтому скорость ее распространения можно найти по формуле:

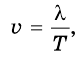
где v – скорость распространения волны (м/с); 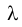– длина волны (м); Т – период колебаний (с).

Так как период и частота связаны соотношением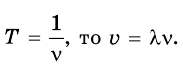

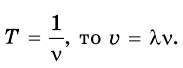
Пример №1

Определите скорость распространения волны на воде, если ее длина равна 180 м, а период колебаний – 15 с.

Дано:

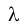= 180 м

Т = 15 с

v – ?

Решение
По формуле 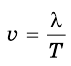определяем скорость распространения волны на воде.

v = 180 м : 15 с = 12 м/с.
Ответ: 12 м/с.

Пример №2

Каково основное свойство механической волны?

Ответ: переносить энергию.

Интерференция волн

Для волн не очень больших амплитуд справедлив принцип суперпозиции: если в точку пространства приходят волны от нескольких источников, то эти волны накладываются друг на друга. В результате такого наложения в некоторых точках пространства может наблюдаться постоянное усиление колебаний, а в некоторых — ослабление. Выясним, почему и когда это происходит. Пусть в некоторую точку M поступают две когерентные волны — волны от двух источников 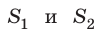, колеблющихся синхронно, то есть в одинаковых фазах и с одинаковой частотой (рис. 22.6, а).

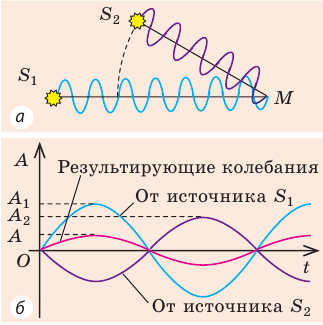
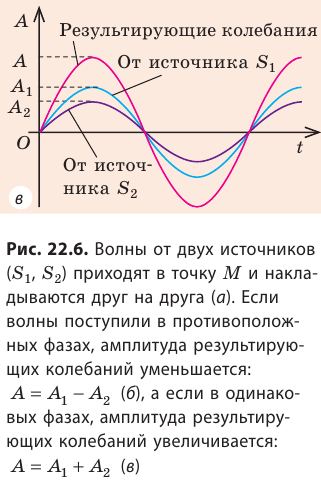
Если волны приходят в точку М в противоположных фазах (в один и тот же момент времени одна волна «толкает» точку М вверх, а вторая «толкает» ее вниз), то волны будут постоянно гасить друг друга (рис. 22.6, б). Если же волны приходят в точку М в одинаковых фазах, то в точке M будут все время наблюдаться колебания с увеличенной амплитудой (рис. 22.6, в). явление наложения волн, вследствие которого в некоторых точках пространства наблюдается устойчивое во времени усиление или ослабление результирующих колебаний, называют интерференцией.

Дифракция волн

Судно, плывущее по морю, образует на поверхности воды волну. Если на своем пути волна встретит скалу или торчащую из воды ветку, то за скалой образуется тень (то есть непосредственно за скалу волна не проникает), а за веткой тень не образуется (волна ветку огибает).

Явление огибания волнами препятствий называют дифракцией (от лат. difractus — разломанный) (рис. 22.8).

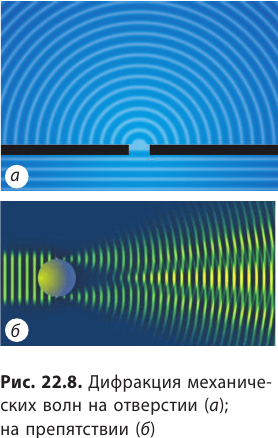
В приведенном примере дифракция волны происходит на ветке, но не происходит на скале. Но это не всегда так. Если скала достаточно удалена от берега, то на некотором расстоянии от скалы тень исчезнет — волна обогнет и скалу. Дело в том, что дифракция наблюдается в двух случаях: 1) когда линейные размеры препятствий, на которые находит волна (или размеры отверстий, сквозь которые проходит волна), сопоставимы с длиной волны; 2) когда расстояние от препятствия до места наблюдения намного больше размера препятствия.

Выводы:

• Распространение в пространстве колебаний вещества или поля называют волной. Механической волной называют распространение колебаний в упругой среде.
• Волна распространяется в пространстве не мгновенно, а с конечной скоростью. При распространении волны происходит перенос энергии без переноса вещества. В некоторых точках пространства вследствие наложения волн друг на друга может наблюдаться устойчивое во времени усиление или ослабление результирующих колебаний — это явление называют интерференцией. Волны могут огибать препятствия — это явление называют дифракцией.
• Волну, в которой частицы среды колеблются перпендикулярно направлению распространения волны, называют поперечной. Волну, в которой частицы среды колеблются вдоль направления распространения волны, называют продольной.
• Волна периодична во времени и пространстве. Периодичность волны во времени характеризуется периодом колебаний каждой отдельной точки волны. Периодичность волны в пространстве характеризуется длиной волны. Длина волны — это расстояние, на которое распространяется волна за время, равное периоду колебаний. Длина λ, частота ν и скорость v распространения волны связаны формулой волны: v = λν .

Звуковые волны

Звучание флейты, шум мегаполиса, шорох травы, грохот водопада, человеческая речь, музыкальный звук, шум, акустический резонанс… Все это связано с распространением в пространстве определенных механических волн, которые называют звуковыми волнами. Их изучает акустика — наука о звуке. С элементами акустики вы начали знакомиться в курсе физики 9 класса. Итак, вспоминаем и узнаем новое.

Звуковые (акустические) волны — это механические волны с частотами от 20 Гц до 20 кГц. Звуковые волны обычно доходят до уха через воздух — в виде последовательных сгущений и разрежений (то есть в воздухе звуковые волны являются продольными). В зонах сгущений (разрежений) давление воздуха незначительно больше (меньше) атмосферного (рис. 23.1).

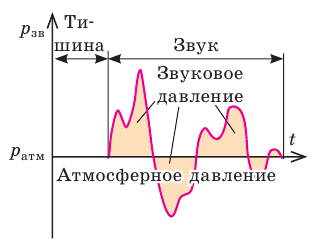
Рис. 23.1. Человеческое ухо воспринимает звуковые волны с избыточным (звуковым) давлением примерно от 20 мкПа (0 децибелов — порог слышимости) до 20 Па (120 децибелов — болевой порог). Для сравнения 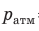=100 000 Па

Звук — механическая волна, потому все свойства волнового движения касаются и звука.

• Звук распространяется в среде с конечной скоростью, зависящей от температуры, плотности, состава и других характеристик среды. Так, в жидкостях звук распространяется быстрее, чем в газах, и медленнее, чем в твердых телах. Скорость распространения звука обычно увеличивается с увеличением температуры среды (в воздухе при температуре 0 °С скорость распространения звука составляет около 330 м/с, а при 20 °С — 340 м/с). Кроме того, чем меньше масса молекул среды, тем быстрее распространяется звук.
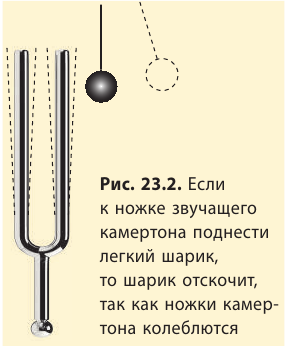
• Источником звука является колеблющееся тело (рис. 23.2). Такие колебания могут быть вынужденными (диффузор громкоговорителя), свободными (струна гитары), автоколебаниями (струны смычковых инструментов).
• Звук не распространяется в вакууме.
• При распространении звука не происходит переноса вещества, но происходит перенос энергии.
• Звуковые волны могут накладываться друг на друга (явление интерференции); могут огибать препятствия (явление дифракции).

Как связаны субъективные и объективные характеристики звука

Все физические величины, характеризующие механические волны (амплитуда, частота, длина, энергия), являются и характеристиками звука. Эти величины не зависят от особенностей восприятия звука человеком, поэтому их называют объективными, или физическими, характеристиками звука. Субъективные характеристики звука (громкость, высота, тембр) обусловлены особенностями слуха человека, поэтому их называют физиологическими. Понятно, что физические и физиологические характеристики звука связаны (см. таблицу).

• Заказать решение задач по физике

Субъективные (физиологические) характеристики звука
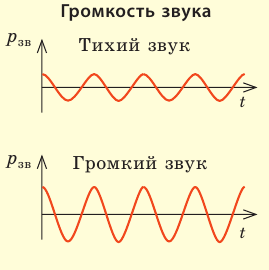	Громкость звука определяется прежде всего амплитудой звуковой волны (звуковым давлением), однако зависит и от частоты звуковой волны. Человеческое ухо плохо воспринимает звуки низких (около 20 Гц) и высоких (около 20 кГц) частот, лучше всего — средних частот (1–3 кГц). Громкость звука измеряют в децибелах (дБ). Так, при частоте звука 1 кГц и звуковом давлении 20 Па громкость звука составляет 120 дБ — это болевой порог звука — наиболее громкий звук, который может воспринимать человек, не чувствуя боли (звук такой громкости издает двигатель реактивного самолета).
Обратите внимание! Громкий звук может привести к ухудшению слуха и даже к глухоте, особенно это касается прослушивания громкой музыки в наушниках. Слушать музыку в наушниках следует при минимальной громкости!
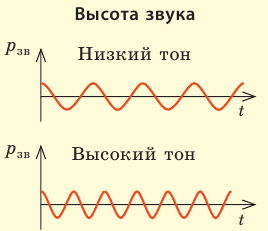	Высота звука определяется в основном частотой звуковой волны: чем больше ее частота, тем выше тон звука. Например, ноте «ля» первой октавы соответствует частота 440 Гц; ноте «ля» второй октавы — частота 880 Гц. Свойство человеческого уха различать звуки по их частоте также зависит от интенсивности звуков. При увеличении интенсивности звука его высота кажется более низкой.
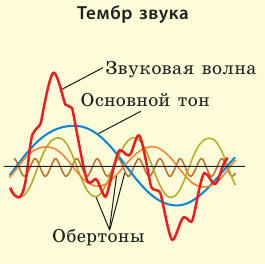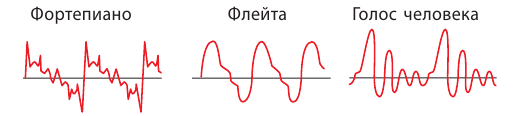
	Тембр звука определяется составом звуковой волны: кроме основной частоты (по которой мы и оцениваем высоту звука) любой звук содержит несколько более слабых и более высоких дополнительных частот — обертонов. Именно благодаря тембру мы узнаем человека по голосу, отличаем звуки фортепиано от звуков флейты и т. д. Каждый музыкальный инструмент, каждый человек или животное имеют свой тембр.

Что такое акустический резонанс

На любое тело, расположенное в пределах распространения звуковой волны, действует периодическая сила, частота которой равна частоте волны. Под действием этой силы тело начинает совершать вынужденные колебания. Если частота собственных колебаний тела сов падает с частотой звуковой волны, то амплитуда колебаний тела увеличивается и оно начинает издавать звук — наблюдается акустический резонанс.

Акустический резонанс — это явление резкого возрастания амплитуды звукового сигнала при приближении частоты сигнала-возбудителя к частоте собственных колебаний системы.

Наблюдать акустический резонанс можно с помощью опыта с двумя камертонами, имеющими одинаковую частоту (рис. 23.3).

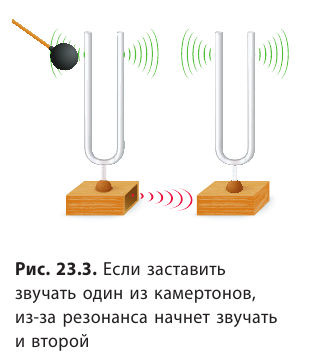
Акустический резонанс используют для увеличения интенсивности звука, созданного некоторым источником (струной, ножками камертона, голосовыми связками и т. д.). Например, для увеличения громкости камертона его присоединяют к деревянному ящику (резонатору), собственная частота колебаний воздуха в котором равна частоте колебаний камертона. Камертон, присоединенный к резонатору, звучит гораздо громче, чем тот, который держат в руке.

Акустический резонанс используют во многих музыкальных инструментах. Воздух в трубах органа, корпусах арф, бандур, гитар и т. д. резонирует с тонами и обертонами звуков, издаваемых колеблющимися телами, и усиливает их. Полость рта — резонатор для звуковых волн, которые создаются благодаря колебаниям голосовых связок. Рис. 23.3. Если заставить звучать один из камертонов, из-за резонанса начнет звучать и второй

Звуковая волна, достигнув уха, испытывает ряд преобразований. Сначала она действует на барабанную перепонку, заставляя ее вибрировать. Чем громче звук, тем сильнее вибрирует перепонка, передавая звуковые колебания в среднее ухо, где они усиливаются.

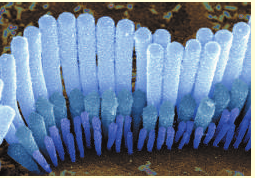
Усиленный звук попадает во внутреннее ухо с заполненной жидкостью улиткой. Поверхность улитки покрыта волосковыми клетками, количество которых достигает 15 000. Каждая клетка резонирует с определенным диапазоном частот. Обнаружив «собственную» частоту, клетка начинает колебаться, возбуждая нервные окончания, и в мозг идет нервный импульс — человек слышит звук.

С возрастом количество волосковых клеток уменьшается (от 15 000 у ребенка до 4 тысяч у пожилого человека). Первыми погибают клетки, «отвечающие» за высокую частоту, поэтому взрослый человек не слышит высоких звуков (подросток слышит звуки до 22 кГц, пожилой человек — до 12 кГц).

Вспоминаем инфра- и ультразвук

Инфразвук (от лат. infra — ниже, под) — это механические волны, частота которых меньше 20 Гц. Инфразвуковые волны возникают во время штормов, землетрясений, цунами, извержений вулканов, вследствие ударов о берег морских волн. Некоторые существа способны воспринимать инфразвуковые волны (рис. 23.4). Источником инфразвука могут быть и объекты, созданные человеком: турбины, двигатели внутреннего сгорания и т. д. В городах наибольший уровень инфразвука около автомагистралей.

Инфразвук очень опасен для животных и человека: он может вызывать симптомы морской болезни, головокружение, потерю зрения, стать причиной повышенной агрессивности. При длительном воздействии интенсивное инфразвуковое излучение может привести к остановке сердца. При этом человек даже не понимает, что происходит, ведь он не слышит инфразвука. Механические волны, частота которых превышает 20 кГц, называют ультразвуковыми волнами (от лат. ultra — сверх, за пределами).

Ультразвук есть в шуме ветра и водопада, в звуках, которые издают некоторые живые существа. Установлено, что ультразвук до 100 кГц воспринимают многие насекомые и грызуны; улавливают его и собаки.

Слабый ультразвук — основа ультразвуковой локации — определения расположения и характера движения объекта с помощью ультразвука. Так, летучие мыши и дельфины, излучая ультразвук и воспринимая его эхо, могут даже в полной темноте найти дорогу или поймать добычу. Ультразвуковое исследование позволяет «увидеть» еще не родившегося младенца, исследовать состояние внутренних органов, выявить инородные тела в тканях. Ультразвуковую локацию применяют также на морских судах — для выявления объектов в воде (сонары) и исследования рельефа морского дна (эхолоты); в металлургии — для выявления и установления размеров дефектов в изделиях (дефектоскопы).

Мощный ультразвук применяют в технике (обработка прочных материалов, сварка, очистка поверхностей от загрязнений); медицине (измельчение камней в организме, что позволяет избежать хирургических операций); пищевой промышленности (изготовление сыров, соусов); косметологии (изготовление кремов, зубной пасты).

Выводы:

• Механические волны с частотами 20 Гц — 20 кГц называют звуковыми волнами (звуком). Субъективные характеристики звука: высота звука (определяется частотой звуковой волны); громкость звука (определяется амплитудой и частотой звуковой волны); тембр звука (определяется спектром звуковой волны).
• Явление резкого возрастания амплитуды звукового сигнала в случае приближения частоты сигнала-возбудителя к частоте собственных колебаний системы называют акустическим резонансом. Акустические резонаторы имеют почти все музыкальные инструменты.
• Механические волны, частота которых меньше 20 Гц, называют инфразвуковыми волнами (инфразвук). Механические волны, частота которых превышает 20 кГц, называют ультразвуковыми волнами (ультразвук).