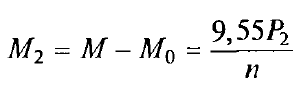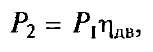Основные уравнения двигателя постоянного тока (ДПТ)
В этой статье описаны основные формулы, величины и их обозначения которые относятся ко всем двигателям постоянного тока.
В результате взаимодействия Iя тока якоря в проводнике L обмотки якоря с внешним магнитным полем возникает электромагнитная сила создающая электромагнитный момент М который приводит якорь во вращение с частотой n.
Противо ЭДС двигателя Eя
При вращении якоря пазовый проводник пресекает линии поля возбуждения с магнитной индукцией B и в соответствии с явлением электромагнитной индукции в проводнике наводится ЭДС Eя направленная навстречу Iя. Поэтому эта ЭДС называется противо ЭДС и она прямо пропорциональна Ф магнитному потоку и частоте вращения n.
Ce — постоянный коэффициент определяемой конструкцией двигателя.
Применив второй закон Кирхгофа получаем уравнение напряжения двигателя.
где ∑R — суммарное сопротивления обмотки якоря включающая сопротивление :
- обмотки якоря
- добавочных полюсов
- обмотки возбуждения (для двигателей с последовательным возбуждением)
Ток якоря Iя
Выразим из формулы 2 ток якоря.
Частота вращения якоря
Из формул 1 и 2 выведем формулу для частоты вращения якоря.
Электромагнитная мощность двигателя
Электромагнитный момент
где: ω = 2*π*f — угловая скорость вращения якоря, Cм — постоянный коэффициент двигателя (включает в себя конструктивные особенности данного двигателя)
Момент на валу двигателя, т.е. полезный момент, где М0 момент холостого хода;
Электродвигатель постоянного тока
Основные параметры электродвигателя постоянного тока
Постоянная момента

- где M – момент электродвигателя, Нм,
– постоянная момента, Н∙м/А,
- I – сила тока, А
Постоянная ЭДС
Направление ЭДС определяется по правилу правой руки. Направление наводимой ЭДС противоположно направлению протекающего в проводнике тока.
Наведенная ЭДС последовательно изменяется по направлению из-за перемещения проводников в магнитном поле. Суммарная ЭДС, равная сумме ЭДС в каждой катушке, прикладывается к внешним выводам двигателя. Это и есть противо-ЭДС. Направление противо-ЭДС противоположно приложенному к двигателю напряжению. Значение противо-ЭДС пропорционально частоте вращения и определяется из следующего выражения: [1]

- где
– электродвижущая сила, В,
– постоянная ЭДС, В∙с/рад,
– угловая частота, рад/с
Постоянные момента и ЭДС в точности равны между собой KT = KE. Постоянные KT и KE равны друг другу, если они определены в единой системе едениц.
Постоянная электродвигателя
Одним из основных параметров электродвигателя постоянного тока является постоянная электродвигателя Kм. Постоянная электродвигателя определяет способность электродвигателя преобразовывать электрическую энергию в механическую.

Постоянная электродвигателя не зависит от соединения обмоток, при условии, что используется один и тот же материал проводника. Например, обмотка двигателя с 6 ветками и 2 параллельными проводами вместо 12 одиночных проводов удвоят постоянную ЭДС, при этом постоянная электродвигателя останется не изменой.
Жесткость механической характеристики двигателя

- где
– жесткость механической характеристики электродвигателя постоянного тока
Напряжение электродвигателя
Уравнение баланса напряжений на зажимах двигателя постоянного тока имеет вид (в случае коллекторного двигателя не учитывается падение напряжения в щеточно-коллекторном узле):

Уравнение напряжения выраженное через момент двигателя будет выглядеть следующим образом:
Соотношение между моментом и частотой вращения при двух различных напряжениях питания двигателя постоянного тока неизменно. При увеличении частоты вращения момент линейно уменьшается. Наклон этой функции KTKE/R постоянный и не зависит от значения напряжения питания и частоты вращения двигателя.
Благодаря таким характеристикам упрощается управление частотой вращения и углом поворота двигателей постоянного тока. Это характерно для коллекторных и вентильных двигателей постоянного тока, что нельзя сказать о двигателях переменного тока и шаговых двигателях [1].
Мощность электродвигателя постоянного тока
Упрощенная модель электродвигателя выглядит следующим образом:
- где I – сила тока, А
- U – напряжение, В,
- M – момент электродвигателя, Н∙м
- R – сопротивление токопроводящих элементов, Ом,
- L – индуктивность, Гн,
- Pэл – электрическая мощность (подведенная), Вт
- Pмех – механическая мощность (полезная), Вт
- Pтеп – тепловые потери, Вт
- Pинд – мощность затрачиваемая на заряд катушки индуктивности, Вт
- Pтр – потери на трение, Вт
Механическая постоянная времени
Механическая постоянная времени – это время, отсчитываемое с момента подачи постоянного напряжения на электродвигатель, за которое частота вращения ненагруженного электродвигателя достигает уровня в 63,21% (1-1/e) от своего конечного значения.

- где
– механическая постоянная времени, с
Электроника для всех
Блог о электронике
Двигатель постоянного тока. Характеристики и регулирование
После предыдущего поста о мотор-редукторе мне пришло несколько вопросов по регулированию двигателя постоянного тока. Так что пора написать очередной пост 🙂
Двигатель постоянного тока (ДПТ) это один из самых привычных и понятных электродвигателей, он изучается даже в школе, на физике. Он используется практически везде, где нужен малогабаритный моторчик, а также не спешит сдавать своих позиций и там, где мощность измеряется десятками киловатт. О нем и поговорим.
▌Конструктив и базовый принцип
Не буду тут особо распинаться, покажу картинку из википедии и укажу ряд основных узлов. Все остальное вы и так знаете и трогали своими руками.
1. Статор состоит из источника магнитного поля. Далеко не всегда это постоянный магнит, более того, постоянный магнит это скорей исключение, чем правило. Обычно все же это обмотка возбуждения. По крайней мере на всем, что больше кулака по размерам.
Работает все очень и очень просто. Обмотка якоря отталкивается от магнитного поля статора силой Ампера и совершает пол оборота, стремясь вывести эту силу на ноль и таки вывела бы если бы не коллектор, который ловко всех обламывает переключает полярность катушки и сила вновь становится максимальной. И так по кругу. Т.е. коллектор служит механическим инвертором напряжения в якоре. Запомните этот момент, он нам еще пригодится 🙂
Обычно в мелких моторчиках всего два полюса обмотки возбуждения (одна пара) и трехзубцовый якорь. Три зуба это минимум для запуска из любого положения, но чем больше зубцов тем более эффективно используется обмотка, меньше токи и более плавный момент, т.к сила является проекцией на угол, а активный участок обмотки проворачивается на меньший угол
▌Происходящие в двигателе процессы
Думаю многие из вас кто баловался с движками могли заметить, что у них есть ярко выраженный пусковой ток, когда мотор на старте может рвануть стрелку амперметра, например, до ампера, а после разгона ток падает до каких-нибудь 200мА.
Почему это происходит? Это работает противоэдс. Когда двигатель стоит, то ток который через него может пройти зависит только лишь от двух параметров — напряжения питания и сопротивления якорной обмотки. Так что предельный ток который может развить движок и на который следует рассчитывать схему узнать несложно. Достаточно замерить сопротивление обмотки двигателя и поделить на это значение напряжение питания. Просто по закону Ома. Это и будет максимальный ток, пусковой.
Но по мере разгона начинается забавная вещь, обмотка якоря движется поперек магнитного поля статора и в ней наводится ЭДС, как в генераторе, но направлена она встречно той, что вращает двигатель. И в результате, ток через якорь резко снижается, тем больше, чем выше скорость.
А если движок дополнительно еще подкручивать по ходу, то противоэдс будет выше питания и движок начнет вкачивать энергию в систему, став генератором.
▌Немного формул
Не буду грузить никого выводами, их найдете сами если захотите. Чтобы было поменьше матана рекомендую найти учебник по электроприводу для средних учебных заведений и годом выпуска подревней. От 50х-60х годов самое то 🙂 Там и картинки винтажные и расписано для вчерашнего выпускника сельской семилетки. Много букв и никакого грузилова, все четко и по делу.
Самая главная формула коллекторного двигателя постоянного тока:
- U — напряжение подаваемое на якорь
- Rя — сопротивление якорной цепи. Обычно за этот символ считают только сопротивление обмотки, хотя можно снаружи навесить резистор какой и он к ней приплюсуется. Тогда пишут как (Rя+Rд)
- Iя — ток в якорной цепи. Тот самый который замеряется амперметром при попытке измерять потребление движка 🙂
- Е — это противоэдс или ЭДС генератора, в генераторном режиме. Она зависит от конструкции двигателя, оборотов и описывается вот такой вот простой формулой
- Ce — одна из конструктивных констант. Они зависят от конструкции двигателя, числа полюсов, количества витков, толщин зазоров между якорем и статором. Нам она не особо нужна, при желании ее можно вычислить экспериментально. Главное, что она константа и на форму кривых не влияет 🙂
- Ф — поток возбуждения. Т.е. сила магнитного поля статора. В мелких моторчиках, где оно задается постоянным магнитом это тоже константа. Но бывает под возбуждение выведена отдельная обмотка и тогда мы можем ее менять.
- n — обороты якоря.
Ну и зависимость момента от тока и потока:
См — конструктивная констатнта.
Вот тут стоит обратить внимание, что зависимость момента от тока совершенно прямая. Т.е. просто замеряя ток, при неизменном потоке возбуждения, мы можем совершенно точно узнать величину момента. Это может быть важно, например, чтобы не сломать привод, когда двигло может развить такое усилие, что легко поломает то, что оно там вращает. Особенно с редуктором.
Ну и из этого же следует, что момент у машины постоянного тока зависит только от способности источника снабжать его током. Так что идеальный нерушимый сверхпроводящий движок вам на раз лом в узел завяжет, пусть даже он сам с ноготок будет. Только энергию подавай.
А теперь смешаем все это в кучу и получим зависимость оборотов от момента — механическую характеристику двигателя.
Если ее построить, то будет нечто следующее:
n0 — это обороты идеального холостого хода сферического двигателя в вакууме. Т.е. когда наш движок ну ваще халявит, момент равен нулю. Ток потребления тоже, естественно, ноль. Т.к. противоэдс равна напряжению. Чисто теоретический вариант. А вторая точка строится уже с каким-либо моментом на валу. Получается прямая зависимость оборотов от момента. А наклон характеристики определяется сопротивлением якорной цепи. Если никаких добавочных резисторов там нет, то это зовут естественной характеристикой.
Обороты идеального холостого хода зависят от напряжения и потока. Больше ни от чего. А если поток константа (постоянный магнит), то только от напряжения. Снижая напряжение вся наша характеристика параллельно смещается вниз. Уменьшили напряжение в два раза — скорость упала в два раза.
Если есть возможность менять поток возбуждения, то можно поднимать скорость выше номинальной. Тут зависимость обратная. Ослабляем поток — двигатель разгоняется, но либо падает момент, либо ему надо жрать больше тока.
Иной двигатель со снятием возбуждения может и в разнос пойти. Помнится сдавал я затянувшийся курсач по электроприводу, уже хрен знает спустя сколько времени после сессии. Вломы мне его делать было, ага 🙂 Ну и сидел в лаборатории, ждал препода. А там какие то балбесы, на курс ниже, лабу делали. Крутили движок вхолостую, а возбуждение к стенду приверчено было на соплях и слетело с клеммы. Движок в разнос пошел. У нас в лаборатории ЭПА ЮУРГУ все серьезно было, машины стояли нешуточные, по десятку киловатт и под сотню другую кг каждый. Все на суровом напряжении в 380 вольт.
В общем, когда эта дура взревела как монстр и стала рваться с креплений, я только и успел крикнуть, что все нахер от машины, вырубай к черту. Не успели, двигло сорвало с креплений, обмотка повылетала с пазов и движку пришел кирдык. Ладно никого не покалечило.
Впрочем, лабы привода это то еще развлечение было. У нас там и горело и взрывалось. Там я приобрел замечательные навыки чинить что угодно, чем угодно в сжатые сроки. В среднем, каждый успел по разу убить стенд наглухо, а лаба часто начиналась с починки паяльника, которым чинили осциллограф с помощью которого реанимировали убитый стенд.
Добавляя резисторы в якорную цепь мы можем увеличить наклон, т.е. чем больше грузим тем больше падает скорость.
Метод плох тем, что резисторы в цепи якоря должны быть расчитаны на ток двигателя, т.е. быть мощными и будут греться зря. Ну и момент резко падает, что плохо.
Есть еще двигатели не независимого, а последовательного возбуждения. Это когда обмотка статора включена последовательно якорю. Не каждый двигатель так можно включить, обмотка возбуждения должна выдерживать ток якоря. Но у них возникает одно интересное свойство. При пуске возникает большой пусковой ток и этот пусковой ток является же током возбуждения, обеспечивая огромный пусковой момент. Механическая характеристика напоминает гиперболу с максимумом в районе нулевых оборотов.
А дальше, по мере разгона, момент падает, а обороты наоборот растут. И если нагрузку убрать с вала, то движок сразу же уходит в разнос. Такие движки ставят на тягловый привод в основном. По крайней мере ставили раньше, до развития силовой электроники. С места эта хрень рвет так, что все стритсракеры нервно закуривают.
▌Режимы работы двигателя постоянного тока
Направление вращения движка зависит от направления тока якоря или направления потока возбуждения. Так что если взять коллекторный двигатель и подключить обмотку возбуждения параллельно якорю, то он будет прекрасно вращаться и на переменном токе (универсальные двигатели, их в кухонную технику часто ставят). Т.к. ток будет одновременно меняться и в якоре и в возбуждении. Момент правда будет пульсирующим, но это мелочи. А для реверса там надо будет поменять полярность включения якоря или возбуждения.
Если нарисовать механическую характеристику в четырех квадрантах, то у нас будет нечто похожее на это:
Вот, например, характеристика 1 на I участке у нас машина работает как двигатель. Нагрузка растет и в определенный момент двигатель останавливается и начинает вращаться в обратную сторону, т.е. нагрузка обращает его вспять. Это тормозной режим, противовключение. Режим очень тяжелый, двигло греется просто зверски, но для торможения очень эффективный. Если же момент на валу сменит направление и пойдет вращать навстречу движку, то мотор сразу же выйдет на генерацию (IV участок).
Характеристика 2 это то же самое, только с обратной полярностью питающего напряжения двигателя.
А характеристика 3 это динамическое торможение. Оно же реостатное. Т.е. когда мы берем и просто коротим наш двигатель на резистор или сам на себя. Можете сами проверить, возьмите любой моторчик и покрутите его, а потом закоротите ему якорь и покрутите снова. На валу будет ощутимое усилие, тем больше, чем качественнее движок.
Кстати, драйвера двигателей вроде L293 или L297 имеют возможность включить реостатное торможение, подачей обоих ключей вверх или вниз. При этом якорь коротится через драйвер на шину земли или питания.
▌Бесколлекторные двигатели постоянного тока
Коллекторный движок он очень хорош. Он чертовски легко и гибко регулируется. Можно повышать обороты, понижать, механическая характеристика жесткая, момент он держит на ура. Зависимость прямая. Ну сказка, а не мотор. Если бы не одна ложка говна во всей этой вкусняшке — коллектор.
Это сложный, дорогой и очень ненадежный узел. Он искрит, создает помехи, забивается проводящей пылью от щеток. А при большой нагрузке может полыхнуть, образовав круговой огонь и тогда все, капец движку. Закоротит все дугой наглухо.
Но что такое коллектор вообще? Нафига он нужен? Выше я говорил, что коллектор это механический инвертор. Его задача переключать напряжение якоря туда сюда, подставляя обмотку под поток.
А на дворе то уже 21 век и дешевые и мощные полупроводники сейчас на каждом шагу. Так зачем нам нужен механический инвертор если мы можем сделать его электронным? Правильно, незачем! Так что берем и заменяем коллектор силовыми ключами, а еще добавляем датчики положения ротора, чтобы знать в какой момент переключать обмотки.
А для пущего удобства выворачиваем двигатель наизнанку — гораздо проще вращать магнит или простенькую обмотку возбуждения, чем якорь со всей этой тряхомудией на борту. В качестве ротора тут выступает либо мощный постоянный магнит, либо обмотка питаемая с контактных колец. Что хоть и смахивает на коллектор, но не в пример надежней его.
И получаем что? Правильно! Бесщеточный двигатель постоянного тока aka BLDC. Все те же няшные и удобные характеристики ДПТ, но без этого мерзкого коллектора. И не надо путать BLDC с синхронными двигателями. Это совсем разные машины и разным принципом действия и управления, хотя конструктивно они ОЧЕНЬ схожи и тот же синхронник вполне может работать как BLDC, добавить ему только датчиков да систему управления. Но это уже совсем другая история.
Спасибо. Вы потрясающие! Всего за месяц мы собрали нужную сумму в 500000 на хоккейную коробку для детского дома Аистенок. Из которых 125000+ было от вас, читателей EasyElectronics. Были даже переводы на 25000+ и просто поток платежей на 251 рубль. Это невероятно круто. Сейчас идет заключение договора и подготовка к строительству!
А я встрял на три года, как минимум, ежемесячной пахоты над статьями :)))))))))))) Спасибо вам за такой мощный пинок.
106 thoughts on “Двигатель постоянного тока. Характеристики и регулирование”
Я очень ждал статей про двигатели. Специалист по электроприводу научил нас как работать с AVR, а про моторчики нифига не написал. Еще будут статьи на эту тему?
Мне порвала шаблон обратная зависимость между магнитным потоком возбуждения и скоростью вращения. По формуле я вижу, что это так, но понять не могу. Особенно удивил уход вразнос при отключении обмотки возбуждения. Если нет магнитного потока статора, то от чего «отталкивается» ротор? Как двигатель может вообще работать в таком режиме?
Отталкивается от остаточного возбуждения. Намагниченности полюсов. Но ты обрати внимание, что момент там тоже уходит в ноль. Так что либо отталкиваться бешеным током, либо снижать момент до нуля.
Да, про момент я заметил. Понятно, что разгон будет происходить только без нагрузки и только, если источник питания способен выдать нужный ток.
Статьи может быть будут еще, не скажу. Я, на самом деле, за 7 лет изрядно эту тему подзабыл за неиспользованием. Особенно касаемо всякого продвинутого регулирования и динамики привода. Так что не такой я уж специалист по приводу 🙂
Можно и без продвинутого регулирования для начала. Меня совсем базовые вещи интересуют. Типа, какие бывают способы управления и, соответственно, какие драйверы их реализуют, чем отличаются, плюсы, минусы, подводные камни. Для коллекторных и бесколлекторных двигателей постоянного тока. На что следует обратить внимание при разработке схем с электродвигателями, чтобы не сжечь все нафиг. В общем, такая статья в раздел «Начинающим». Но и более емкие статьи я бы с удовольствием прочитал.
Ну базовые вещи я уже описал 🙂 А дальше додумываешь сам. Напряжение можно рулить ШИМом. Можно обратную связь по току-моменту замутить. Обращаться с ними также как с любой индуктивностью, о чем я тоже уже писал. Не расписывал только H-мосты самодельные. Но тут тема такая, на всех не угодишь, слишком они разные бывают.
Он используется практически везде, где нужен малогабаритный моторчик
То-то все авиамодели, квадкоптеры и прочая летучая нечисть — на бесколлекторниках, кроме совсем позорного Китая за $100.
Я БУДУ ЧИТАТЬ ДО КОНЦА, ПРЕЖДЕ ЧЕМ КОММЕНТИРОВАТЬ. Я БУДУ ЧИТАТЬ ДО КОНЦА, ПРЕЖДЕ ЧЕМ КОММЕНТИРОВАТЬ. Я БУДУ ЧИТАТЬ ДО КОНЦА, ПРЕЖДЕ ЧЕМ КОММЕНТИРОВАТЬ. Я БУДУ ЧИТАТЬ ДО КОНЦА, ПРЕЖДЕ ЧЕМ КОММЕНТИРОВАТЬ. Я БУДУ ЧИТАТЬ ДО КОНЦА, ПРЕЖДЕ ЧЕМ КОММЕНТИРОВАТЬ.
Модели — не игрушки. Совсем другие требования, и другие цены.
А в дешевых игрушках, — как правило, дешевые коллекторные движки с проволочными щетками. Да и в самых дешевых моделях вертолета с соосными винтами (по сути, те же игрушки) — тоже коллекторные.
Имеется двигатель постоянного тока мощностью 60Вт, напряжение питания 48В. Как его можно переделать чтобы питать от 12В не потеряв в мощности?
[spoiler title=”источники:”]
http://engineering-solutions.ru/motorcontrol/dcmotor/
[/spoiler]
Работа электропривода характеризуется в первую очередь механической характеристикой двигателя ? = f (М) или n = f (М).
Для двигателя постоянного тока также часто используют электромеханические характеристики ? = f (Iя) или n = f (Iя), где ?, n, Iя, М — соответственно угловая скорость, частота вращения, сила тока якоря и вращающий момент двигателя. Механические характеристики можно рассчитывать как в абсолютных, так и в относительных единицах. Для двигателей постоянного тока наибольшее распространение получил расчет характеристик в относительных единицах.
При расчетах в относительных единицах за базисные величины принимают номинальные данные двигателя Iя, Мном, Uном, nном. Иногда в качестве базисных принимают величины, отличающиеся от номинальных (например, момент статической нагрузки). Величины, выражаемые в относительных единицах, в дальнейшем будут обозначены знаком.
Сопротивления главной цепи в относительных единицах определяют в долях номинального сопротивления.. Под номинальным понимают такое сопротивление цепи якоря, которое при неподвижном якоре и номинальном расчетном напряжении Uном обусловливает номинальную силу тока в якоре:
Сопротивление цепи якоря складывается из внутреннего и внешнего сопротивлений. Значения внутреннего сопротивления обмоток двигателей серий ДП и Д в долях номинального при ПВ = 25 % приведены в табл. 2.23. В графе rя* указано сопротивление якоря и дополнительных полюсов двигателей, а в графе r’n* — сопротивление обмотки двигателей последовательного возбуждения. Сопротивление стабилизирующих обмоток двигателей параллельного возбуждения настолько мало, что им можно пренебречь. При расчете типовых характеристик для группы двигателей сопротивление обмоток следует определять как среднее арифметическое значений, приведенных в соответствующих строках табл. 2.23.
Расчет механических характеристик двигателей в относительных единицах приведен ниже и является универсальным. Этот метод расчета пригоден для различных способов возбуждения и соединения обмоток.
Схема включения двигателя изображена на рис. 2.12, на котором показаны три варианта (1, 2, 3) включения обмоток последовательного возбуждения. Сила тока в этих обмотках обозначена через Iп1, Iп2, Iп3. Обмотка параллельного возбуждения в общем случае получает питание от независимого источника с напряжением Uв.
При расчете механических характеристик, как правило, используют известные схему включения обмотки последовательного возбуждения, сопротивления последовательной и шунтирующей цепей Rп и Rш, напряжение источника питания цепи якоря (главной цепи) Uг, МДС обмотки параллельного возбуждения и соотношение между МДС обмоток последовательного и параллельного возбуждения при номинальной нагрузке. Напряжение Uг может иметь независимое от нагрузки значение Uг — const (сеть постоянного тока). При применении вращающихся или статических преобразователей энергии задают внешнюю характеристику этих преобразователей Uг = f (I) (I — сила тока нагрузки).
МДС главных полюсов двигателя обусловлена суммарным действием электрического тока в обмотках возбуждения, расположенных на этих полюсах. Поскольку номинальная МДС, принятая за базисную, складывается из МДС обмотки параллельного возбуждения и МДС обмотки последовательного возбуждения или стабилизирующей обмотки, то можно принять, что МДС обмотки параллельного возбуждения в относительных единицах будет составлять 0,5 для двигателей серий ДП и Д смешанного возбуждения и 0,9 для двигателей серий ДП и Д параллельного возбуждения. На долю обмотки последовательного возбуждения или стабилизирующей обмотки будет приходиться остальная часть МДС. Учитывая, что эта часть соответствует МДС при протекании номинального тока, для любой силы тока МДС обмотки последовательного возбуждения можно выразить следующими формулами:
для двигателей серий ДП и Д смешанного возбуждения,
где I*п — сила тока, протекающего по обмотке последовательного возбуждения;
для двигателей параллельного возбуждения со стабилизирующей обмоткой серий ДП и Д
Полная МДС главных полюсов выражается в виде алгебраической суммы МДС обмоток последовательного и параллельного возбуждения:
В некоторых случаях для реализации повышенных (пониженных) частот вращения двигателей МДС обмотки параллельного возбуждения берут меньше (больше) номинальной.
Общий метод расчета механической характеристики двигателей постоянного тока в рассматриваемой схеме (см. рис. 2.12) включения заключается в нахождении зависимостей F* = f (Iя*) и Iп* = f (Iя*) и последующем переходе к зависимости n* = f (М*).
Зависимость силы тока в последовательной обмотке от силы тока якоря двигателя устанавливают по одному из следующих уравнений:
каждое из которых справедливо при наличии обмотки последовательного возбуждения только в одной цепи.
Соответственно зависимость ЭДС от силы тока якоря определяют по одной из следующих зависимостей:
Частоту вращения п при заданной силе тока якоря находят по формуле n = Е/ФсE, где Ф — магнитный поток двигателя; сЕ — коэффициент пропорциональности напряжения.
Для получения уравнений в относительных единицах введем следующие базисные величины: nб = nном; Iб = Iном; Еб = Uном; Фб = Фном; Rб = Rном. Используя соотношения
можно записать nном/nо = с’Е, в котором
где rдв = rя + rп; n0 — частота вращения при идеальном холостом ходе.
Тогда формулу для определения частоты вращения в относительных единицах запишем так:
так как в относительных единицах Ф* = (Е/п)*.
Магнитный поток Ф* для соответствующей силы тока якоря при известной МДС главных полюсов (F* = F*пар + F*п) определяют по универсальным нагрузочным характеристикам. Нагрузочной характеристикой называют зависимость (Е/n)* = f (F*) при постоянной силе тока якоря I*я. Так как вид нагрузочных характеристик зависит от силы тока якоря, то они изображаются в виде семейства кривых, построенных при различных значениях Iя. Характеристика при Iя = 0 является кривой намагничивания двигателя.
На рис. 2.13 показаны универсальные характеристики двигателей серий ДП и Д. Характеристики изображены в относительных единицах. За базисные величины приняты номинальная МДС главных полюсов двигателя при ПВ = 25 % и номинальный магнитный поток Ф главных полюсов при протекании по якорю двигателя тока номинальной силы при ПВ — 25 % в направлении, соответствующем двигательному режиму. Типовые нагрузочные характеристики соответствуют действительным нагрузочным характеристикам конкретных двигателей серий ДП и Д, отличаясь от характеристик, полученных на основе опыта, на 2—3 %.
Электромагнитный момент двигателя (в Н?м)
где cM — коэффициент момента.
Вращающий момент на валу двигателя отличается от электромагнитного на величину, определяемую механическими потерями и потерями в железе якоря. Таким образом, вращающий момент на валу двигателя может быть представлен в следующем виде:
где ?Р — потери мощности на трение; ?Рст — потери мощности в стали; kM— коэффициент пропорциональности моментов.
Параметр ?M* = kM* (?P* + ?Р*ст)/n* определяют по кривым, выражающим зависимость ?M* = f (Е/n)* при различных постоянных значениях частоты вращения n*. Такие кривые, построенные в относительных единицах, показаны на рис. 2.14.
Пользуясь этими кривыми, нетрудно найти момент ?М* при различных магнитных потоках главных полюсов и частотах вращения. Коэффициент момента сM можно определить, исходя из того, что при базисных силе тока, магнитном потоке и частоте вращения вращающий момент на валу двигателя также должен быть равен базисному (номинальному). Следовательно, пользуясь выражением (2.39), можно написать, что при Мдв = Мб = Мном т. е.
Определив по рис. 2.14, что для (Е/n)* = 1 и n* = 1 ?М* = 0,03, найдем
Окончательно формула для определения вращающих моментов на валу имеет вид

В этой статье описаны основные формулы, величины и их обозначения которые относятся ко всем двигателям постоянного тока.
В результате взаимодействия Iя тока якоря в проводнике L обмотки якоря с внешним магнитным полем возникает электромагнитная сила создающая электромагнитный момент М который приводит якорь во вращение с частотой n.
Противо ЭДС двигателя Eя
При вращении якоря пазовый проводник пресекает линии поля возбуждения с магнитной индукцией B и в соответствии с явлением электромагнитной индукции в проводнике наводится ЭДС Eя направленная навстречу Iя. Поэтому эта ЭДС называется противо ЭДС и она прямо пропорциональна Ф магнитному потоку и частоте вращения n.
Eя = Се * Ф * n (1)
Ce — постоянный коэффициент определяемой конструкцией двигателя.
Применив второй закон Кирхгофа получаем уравнение напряжения двигателя.
U = Eя + Iя * ∑R (2)
где ∑R — суммарное сопротивления обмотки якоря включающая сопротивление :
- обмотки якоря
- добавочных полюсов
- обмотки возбуждения (для двигателей с последовательным возбуждением)
Ток якоря Iя
Выразим из формулы 2 ток якоря.
Частота вращения якоря
Из формул 1 и 2 выведем формулу для частоты вращения якоря.
Электромагнитная мощность двигателя
Pэм = Ея Iя (5)
Электромагнитный момент
где: ω = 2*π*f — угловая скорость вращения якоря, Cм — постоянный коэффициент двигателя (включает в себя конструктивные особенности данного двигателя)
Момент на валу двигателя, т.е. полезный момент, где М0 момент холостого хода;
Р2 — полезная мощность двигателя
Лекция 25
Ранее было
установлено, что при работе машины в
генераторном режиме э. д. с. Е якоря будет
больше, чем напряжение на его зажимах,
на значение падения напряжения в цепи
якоря (14.7). В этом случае ток течет от
положительного зажима генератора во
внешнюю сеть и электромагнитный момент
машины М является тормозным (рис. 14.19,
а).
Машина постоянного
тока, подключенная к сети постоянного
тока, может работать как в генераторном,
так и в двигательном режиме. Если у
генератора с параллельным или независимым
возбуждением, подключенного к этой
сети, уменьшить ток возбуждения с таким
расчетом, чтобы э. д. с. якоря E
стала меньше напряжения сети, то ток в
цепи якоря из-за преобладания напряжения
сети над э. д. с. изменит направление, т.
е. пойдет от сети к машине. При этом
электромагнитный момент также изменит
направление и будет направлен в сторону
вращения машины, т. е. станет вращающим
(рис. 14.19, б).
Таким образом,
машина постоянного тока может быть
переведена из генераторного режима в
двигательный, при котором якорь машины
начинает потреблять из сети ток,
создаваемый разностью напряжения сети
и э. д. с. якоря:
В двигательном
режиме индуцируемая в обмотке якоря
э. д. с. направлена против протекающего
по ней тока, поэтому ее принято называть
противо-э. д. с. Значение противо-э.
д. с., так же
как и для генератора, определяется
согласно (14.3). Напряжение, приложенное
к зажимам якоря двигателя согласно
(14.10), должно уравновешивать противо-э.
д. с. и компенсировать падение напряжения
на внутреннем 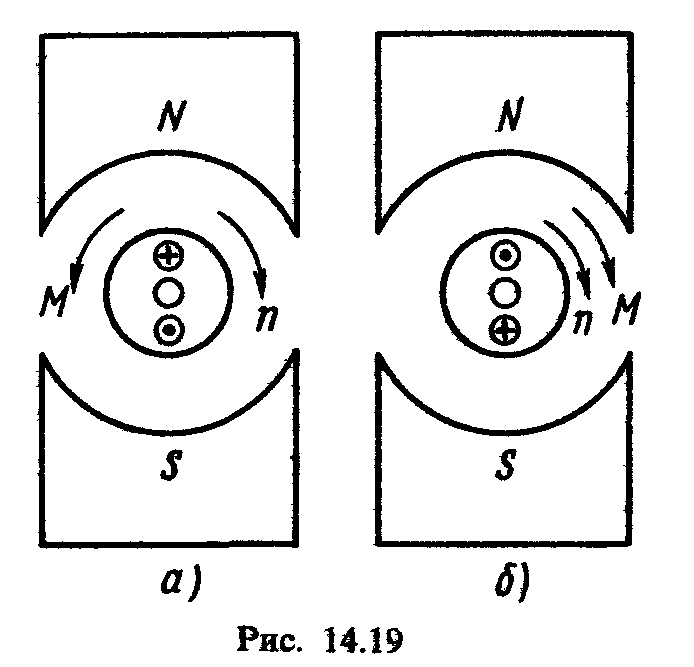
цепи якоря:
(14.11)
Умножив левую и
правую части уравнения (14.11) на ток Ia,
получим уравнение баланса мощностей
цепи якоря двигателя:
(14.12)
где UIa
— мощность, потребляемая якорем двигателя
из сети; Ia2ra
— мощность потерь в обмотке якоря; ЕIа
— электромагнитная мощность, преобразуемая
в механическую мощность вращения вала
двигателя.
Вращающий момент
двигателя определяется по формуле
(14.5), как и для генератора. Момент в
двигательном режиме имеет противоположное
направление по сравнению с генераторным
режимом.
Путем подстановки
в выражение (14.3) значения Е из равенства
(14.11) можно получить формулу для определения
частоты вращения двигателя:
(14.13)
Регулирование
частоты вращения.
Полученное выражение (14.13) показывает,
что частоту вращения двигателя постоянного
тока можно регулировать: изменением
магнитного потока Ф, изменяя соответственно
ток возбуждения; изменением питающего
напряжения U; включением добавочного
сопротивления в цепь обмотки якоря.
Изменение
направления вращения.
Если требуется изменить направление
вращения двигателя, то для этого
необходимо изменить направление
электромагнитного момента М, действующего
на якорь. Согласно (14.5), это можно
осуществить изменением направления
тока в обмотке якоря Iа
или путем изменения направления
магнитного потока Ф (тока возбуждения).
На практике это производят путем
переключения проводов, подводящих ток
к обмотке якоря или к обмотке возбуждения.
Свойство
саморегулирования.
Для того чтобы двигатель вращался с
постоянной частотой n,
развиваемый им вращающий момент М должен
быть равным создаваемому нагрузкой
тормозному моменту Mт:
(14.14)
Если равенство
(14.14) нарушается, то частота вращения
двигателя увеличивается или уменьшается
до тех пор, пока снова вращающий момент
двигателя не будет уравновешен тормозным
моментом. Таким образом, двигатели
постоянного тока обладают свойством
саморегулирования
— способностью при изменении нагрузки
автоматически устанавливать новое
значение частоты вращения, при которой
двигатель работает устойчиво. Роль
регулятора играет противо-э. д. с.,
наводимая в обмотке якоря.
Рассмотрим сущность
процесса саморегулирования. Допустим,
что тормозной момент, создаваемый
нагрузкой, уменьшился и стал меньше
вращающего момента двигателя, вследствие
чего частота вращения и последнего
начала возрастать. С увеличением n,
согласно (14.11), возрастает противо-э. д.
с. Е и, согласно (14.10) и (14.5), уменьшаются
ток якоря Iа
и вращающий момент двигателя М. Этот
процесс будет продолжаться до тех пор,
пока вращающий момент двигателя не
станет равным тормозному. Тогда рост
частоты вращения прекратится. Аналогично
протекает процесс при увеличении
тормозного момента, когда вращающий
момент двигателя становится меньше
тормозного. В этом случае частота
вращения двигателя начинает падать,
вследствие чего уменьшится противо-э.
д. с. и возрастают ток якоря и вращающий
момент. Этот процесс, так же как при
уменьшении нагрузки, прекратится, когда
M
= Mт
и n = const.
В установившемся
режиме, когда M
= Mт,
потребляемый якорем двигателя ток
определяется моментом на валу Iа
= Мт/(СМФ).
Из этого выражения следует, что при Ф =
const ток, потребляемый двигателем, всегда
пропорционален моменту на валу.
Пуск двигателей.
В момент включения двигателя в сеть его
частота вращения n
равна нулю, противо-э. д. с.
также равна нулю, а пусковой токIп
= U/ra
ограничивается только сопротивлением
обмотки якоря, которое у двигателей
средней и большой мощностей составляет
десятые — сотые доли Ом. Поэтому при
прямом пуске путем непосредственного
включения двигателя в сеть пусковой
ток был бы недопустимо большим—в
10—20 раз больше номинального. Это может
вызвать поломку вала, а также сильное
искрение под щетками. Поэтому при пуске
двигателей постоянного тока в цепь
якоря часто включают добавочный пусковой
реостат с таким сопротивлением rп,
чтобы пусковой ток не превышал допустимого
значения. Прямой пуск применяют в
основном для двигателей мощностью до
нескольких сотен ватт, а иногда мощностью
в несколько киловатт. В машинах большой
и средней мощностей допустимый пусковой
ток
а в машинах малой мощности
По мере увеличения
частоты вращения двигателя в обмотке
якоря возрастает противо-э. д. с., ток
уменьшается, вследствие чего сопротивление
пускового реостата необходимо постепенно
уменьшать. При достижении двигателем
номинальной частоты вращения пусковой
реостат полностью выводится. Чем короче
период пуска, тем меньше потери энергии
в цепи якоря.
Следует иметь в
виду, что чрезмерное уменьшение пускового
тока может привести к тому, что двигатель
вообще не сможет стронуться с места,
так как пусковой момент
не сможет преодолеть момента сопротивления
на валу двигателя. Для обеспечения
большого пускового момента при
ограниченном пусковом токе необходимо
создать возможно больший магнитный
поток, что достигается за счет увеличения
тока возбуждения с помощью специального
реостата, включаемого в цепь возбуждения
двигателя.
Ограничение
пускового тока при реостатном пуске
обычно сопровождается значительными
потерями энергии в пусковом реостате.
Для исключения этого пуск двигателя
можно осуществить при пониженном
напряжении, подводимом к его обмотке
якоря от источника с регулируемым
напряжением. В процессе пуска в этом
случае напряжение, подводимое к якорю
двигателя, плавно повышают.
Классификация
двигателей.
Двигатели постоянного тока отличаются
друг от друга способом питания обмотки
возбуждения. Двигатели постоянного
тока, как и генераторы, могут иметь
независимое, параллельное,
последовательное и смешанное возбуждение.
Двигатели с
независимым возбуждением
применяют тогда, когда напряжение на
зажимах якоря изменяется в процессе
работы или когда напряжение якоря
отличается по значению от напряжения
возбуждения.
Двигатели
последовательного возбуждения
получили широкое применение, так как
обладают рядом ценных свойств. Двигатели
со смешанным возбуждением по
своим свойствам являются промежуточными
между двигателями последовательного
и параллельного возбуждения.
Двигатели с
параллельным возбуждением,
получившие наибольшее
распространение,
— это, по существу, те же двигатели с
независимым
возбуждением, но только
питание обмотки возбуждения у них
произ-
водится от того же источника
энергии, что и питание якоря. На рис.
14.20
приведена схема двигателя с
параллельным возбуждением. В нем
обмотка
возбуждения подключена
непосредственно к сети параллельно с
обмот-
кой якоря. В цепь якоря включен
пусковой реостат rп,
а в цепь обмотки возбуждения —
регулировочный реостат rрв.
Так как обмотка возбуждения
питается
независимо от обмотки якоря непосредственно
от сети, то ток
возбуждения двигателя
параллельного возбуждения не зависит
от
тока якоря.
Если сопротивление
регулировочного реостата не меняется,
то ток возбуждения при напряжении сети
U
= const остается постоянным. Поэтому
магнитный поток двигателя при изменении
нагрузки также практически не меняется
(немного уменьшаясь при увеличении
нагрузки за счет усиления реакции
якоря). Ток I,
потребляемый двигателем из сети,
(14.15)
Обмотка возбуждения
состоит из большого числа витков
относительно тонкого провода и
обладает значительным сопротивлением
rв,
поэтому ток возбуждения Iв
мал по сравнению с током якоря, составляя
от него не более 3—4%.
Ток возбуждения
(14.16)
Характерным
свойством двигателей параллельного
возбуждения является то, что при
напряжении сети U = const и сопротивлении
цепи возбуждения
ток возбужденияIв
= const и не зависит от тока нагрузки
I.
Для оценки свойств
электрических двигателей широко
используют различные характеристики.
Наиболее распространенным режимом
работы двигателей параллельного
возбуждения является режим при U = const и
Iв
= const. В этом случае свойства двигателя
достаточно полно описываются тремя
характеристиками: моментной, скоростной
и механической. Согласно (14.15), моментная
характеристика
М = f(Iа)
будет 
(рис. 14.21, а), так как магнитный поток
двигателя параллельного возбуждения
остается постоянным при изменении тока
якоря и, следовательно, момент двигателя
прямо пропорционален току якоря.
Действительно, при Ф = const момент
Скоростной
характеристикой
двигателя постоянного тока называют
зависимость частоты его вращения от
тока якоря n
= f(Ia),
а механической
— зависимость частоты вращения двигателя
от момента n
= f(М)
при U = const и Iв
= const. Согласно (14.13), скоростная
характеристика для двигателей
параллельного возбуждения будет линейной
(рис. 14.21, а). Следовательно, линейной
будет также механическая характеристика
двигателя (рис. 14.21, б). Подставляя значение
тока якоря Iа
из (14.5) в (14.13), получим уравнение
механической характеристики:
(14.17)
Когда в цепи якоря
отсутствует добавочный реостат (rрег
= 0), механическая характеристика
называется естественной.
Механическая характеристика двигателя,
у которого в цепь якоря введен
регулировочный реостат с сопротивлением
rрег,
называется искусственной
(рис. 14.21, б). Естественная характеристика
обычно линейна и имеет слегка падающий
характер. Как механическую, так и
скоростную характеристики у двигателей
параллельного возбуждения можно считать
жесткими, так как при изменении
нагрузки от холостого хода до номинальной
частоты вращения уменьшаются на 3 — 7%.
Способность этих двигателей сохранять
частоту вращения почти неизменной при
изменении нагрузки широко используется
на практике.
С другой стороны,
частоту вращения двигателей параллельного
возбуждения можно изменять в широких
пределах с помощью регулировочного
реостата с сопротивлением rрв,
позволяющего изменять ток возбуждения
двигателя Iв
и его магнитный поток Ф и, как следует
из (14.13), частоту вращения n.
Следует особо
отметить, что при холостом ходе и
небольшой нагрузке для двигателя
параллельного возбуждения большую
опасность представляет значительное
уменьшение тока возбуждения и тем более
обрыв цепи возбуждения, когда Iв
= 0 (Ф = 0). В этом случае частота вращения
может возрасти до опасных пределов —
двигатель «идет в разнос». Кроме того,
при этом ток якоря сильно возрастает,
вследствие чего усиливается искрение
под щетками.
Для оценки
эксплуатационных свойств двигателей
широко используют рабочие
характеристики,
представляющие зависимость потребляем
мощности Р1,
тока якоря Iа,
частоты вращения n,
момента М, к. п. д. η от мощности на валу
Р2
при U = const и Iв
= const (рис. 14.22). Из рисунка видно, что с
увеличением нагрузки частота вращения
двигателя несколько уменьшается и
характеристика n
= f(Р2)
линейна, а также то, что момент якоря
растет практически прямо пропорционально
нагрузке, т. е. характеристика М = f(P2)
тоже линейна.
Характеристики
имеют вид, характерный для любых
электрических машин.
Двигатель с
последовательным возбуждением.
На рис. 14.23 приведена схема двигателя
последовательного возбуждения. Обмотка
возбуждения, обмотка якоря и пусковой
реостат rп
в этом двигателе соединяются
последовательно, поэтому ток якоря
является одновременно и током возбуждения.
В связи с этим обмотку возбуждения
двигателя выполняют с малым числом
витков из провода большего сечения, чем
в двигателе параллельного возбуждения.
При холостом ходе и малых нагрузках,
когда потребляемый двигателем ток
небольшой, м. д. с. обмотки и магнитный
поток Ф двигателя также невелики. Так
как частота вращения двигателя обратно
пропорциональна значению магнитного
потока, то при холостом ходе и малых
нагрузках она в несколько раз превышает
номинальную, представляя опасность для
целостности двигателя. Поэтому эти
двигатели нельзя запускать вхолостую
или при небольшой нагрузке (менее 20 —
25 % от номинальной), т. е. нельзя применять
для привода механизмы, работающие
вхолостую или при небольшой нагрузке.
Исключение составляют двигатели малой
мощности (десятки ватт), которые могут
быть использованы для привода механизмов,
у которых возможен холостой ход. Так
как частота вращения двигателя
(14.18)
то ее можно
регулировать как посредством изменения
Ф, так и путем изменения U.
В первом случае для регулирования
изменяют магнитный поток путем
шунтирования обмотки возбуждения
регулировочным реостатом. При этом
часть тока ответвляется через реостат,
включенный параллельно обмотке
возбуждения. Это позволяет изменять
(уменьшать) ток в обмотке возбуждения
и устанавливать требуемую частоту
вращения двигателя.
Частоту вращения
за счет изменения напряжения на зажимах
якоря регулируют, включая последовательно
с якорем реостат, на котором падает
часть напряжения сети, вследствие чего
частота вращения двигателя уменьшается.
Этот способ регулирования неэкономичен
из-за больших потерь энергии в реостате.
Характерной
особенностью двигателей последовательного
возбуждения является резкое уменьшение
частоты вращения при увеличении нагрузки.
При ненасыщенной магнитной системе
машины, когда Iа
< (0,8-0,9) Iн,
скоростная характеристика двигателя
n
= f(Ia)
имеет вид гиперболы (рис. 14.24). При больших
нагрузках (Iа
> Iн),
когда наблюдается насыщение магнитной
системы машины (Ф = const), скоростная
характеристика становится линейной.
Моментная
характеристика двигателя М = f(Ia)
при ненасыщенной магнитной системе
машины имеет вид параболы (рис. 14.24), так
как Ф = СфIа
и электромагнитный момент
(14.19)
где k — постоянная.
Таким образом, при ненасыщенной магнитной
системе машины электромагнитный момент
изменяется пропорционально квадрату
тока якоря.
В то же время
значительное увеличение нагрузки на
валу двигателя сопровождается сравнительно
небольшим ростом тока якоря. Это свойство
двигателя последовательного возбуждения
особенно ценно тогда, когда требуется
большой вращающий момент, значительно
превышающий номинальный, например при
пуске в ход двигателя в трамваях,
электровозах и т. д.
Механические
характеристики n
= f(М)
двигателя являются мягкими и имеют
гиперболический вид (рис. 14.25). Подставляя
значение тока из (14.19) в (14.18), получим
выражение, определяющее механическую
характеристику двигателя при Iа
< (0,8 – 0,9)Iн:

При насыщении
магнитной системы двигателя (Iа
> Iн)
зависимость n = f(М)
становится линейной. Изменяя сопротивление
реостата rп,
включенного последовательно с якорем,
кроме естественной характеристики
1 можно получить семейство реостатных
характеристик 2 и 3.
На рис. 14.26 приведены
рабочие характеристики двигателя
последовательного возбуждения.
Характеристики M
= f(P2)
и n = f(P2)
нелинейны, а характеристики
имеют
вид, аналогичный подобным зависимостям
для двигателя параллельного возбуждения.
На рис. 14.26 начальные участки рабочих
характеристик, изображенные штриховыми
линиями, соответствуют работе двигателя
при малой нагрузке, когда частота
вращения становится недопустимо большой.
Д
со смешанным возбуждением.
На рис. 14.27 приведена схема двигателя
смешанного (компаундного) возбуждения,
у которого имеется две обмотки возбуждения:
сериесная и шунтовая. В двигателе
магнитный поток Ф создается совместным
действием токов возбуждения шунтовой
Iвш
и сериесной Iвс
обмоток. Обмотки возбуждения можно
включать таким образом, что они будут
создавать магнитные потоки одного
(согласное включение) или противоположного
(встречное включение) направлений.
При встречном
включении с небольшой м. д. с. последовательной
обмотки можно получить двигатель с
жесткой механической характеристикой,
однако встречное включение обмоток
возбуждения применяют очень редко, так
как в этом случае ухудшаются пусковые
свойства двигателя. В этом двигателе
характер изменения частоты вращения и
вращающего момента зависит от соотношения
м. д. с. последовательной и параллельной
обмоток возбуждения. Подбирая
соответствующим образом соотношение
между м. д. с. обмоток, можно получить
необходимое изменение частоты
вращения при нагрузке, «приблизив»
двигатель по свойствам к двигателям
последовательного или параллельного
возбуждения. Следовательно, рабочие
характеристики двигателя смешанного
возбуждения являются промежуточными
между характеристиками двигателей
параллельного и последовательного
возбуждения.
Эти двигатели при
работе вхолостую не «идут в разнос»,
так как всегда имеется постоянный
магнитный поток, создаваемый параллельной
обмоткой возбуждения. Кроме того, из-за
наличия последовательной обмотки
возбуждения в них при возрастании
нагрузки увеличивается магнитный поток.
Двигатели обладают большей перегрузочной
способностью по сравнению с двигателями
параллельного возбуждения.
Соседние файлы в папке Эл.техника
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
ПРАКТИЧЕСКАЯ РАБОТА №12
«Расчет параметров двигателей постоянного тока»
ЦЕЛЬ РАБОТЫ: рассчитать ток двигателя в
номинальном режиме, частоту вращения и ток в режиме холостого хода; потери и
КПД двигателя; механические и искусственные характеристики двигателя.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ:
Коллекторные машины обладают
свойством обратимости, т. е.
они могут работать как в режиме генератора, так и в режиме двигателя. Поэтому если машину постоянного тока подключить к
источнику энергии постоянного
тока, то в обмотке возбуждения
и в обмотке якоря машины появятся токи. Взаимодействие
тока якоря с полем возбуждения создает на якоре электромагнитный момент М, который
является не тормозящим, как это имело место
в генераторе, а вращающим.
Под действием электромагнитного момента якоря машина начнет вращаться,
т. е. машина будет работать
в режиме двигателя, потребляя из сети электрическую энергию и преобразуя ее в механическую. В процессе работы двигателя его якорь
вращается в магнитном поле. В обмотке якоря индуцируется ЭДС , направление
которой можно определить по правилу
«правой руки». По своей природе она не
отличается от ЭДС, наводимой в обмотке якоря
генератора. В двигателе же ЭДС направлена против тока , и поэтому ее называют противоэлектродвижущей силой (противо-ЭДС) якоря.
Для двигателя, работающего с постоянной частотой вращения,
.
(12.1)
Из (29.1) следует, что
подведенное к двигателю напряжение
уравновешивается противо-ЭДС обмотки якоря и падением
напряжения в цепи якоря. На основании (29.1) ток якоря
.
(12.2)
Умножив обе части уравнения (29.1) на ток якоря ,
получим уравнение мощности для цепи якоря:
, (12.3)
где — мощность в цепи
обмотки якоря; — мощность электрических потерь в цепи якоря.
Для выяснения сущности
выражения проделаем следующее преобразование:
, или
.
Но,
Тогда ,
(12.4)
где
— угловая частота вращения якоря;
— электромагнитная
мощность двигателя.
Следовательно, выражение представляет собой электромагнитную мощность двигателя.
Преобразовав выражение (12.3)
с учетом (12.4), получим
.
Анализ этого уравнения
показывает, что с увеличением нагрузки на вал двигателя,
т. е. с увеличением электромагнитного момента
М, возрастает мощность в цепи обмотки якоря , т. е.
мощность на входе двигателя. Но так как напряжение, подводимое к двигателю, поддерживается неизменным , то увеличение нагрузки двигателя сопровождается ростом тока в
обмотке якоря .
В зависимости от способа
возбуждения двигатели постоянного тока, так же как и генераторы, разделяют на
двигатели с возбуждением от постоянных магнитов (магнитоэлектрические) и с
электромагнитным возбуждением. Последние в соответствии со схемой включения обмотки возбуждения относительно
обмотки якоря подразделяют на двигатели параллельного (шунтовые),
последовательного (сериесные) и смешанного (компаундные) возбуждения.
В соответствии с формулой ЭДС
частота вращения двигателя (об/мин)
.
Подставив
значение из (12.1), получим (об/мин)
, (12.5)
Частота вращения двигателя прямо пропорциональна напряжению
и обратно пропорциональна магнитному потоку возбуждения. Физически это объясняется тем, что повышение напряжения U или уменьшение потока Ф вызывает увеличение разности ; это,
в свою очередь, ведет к росту тока . Вследствие этого
возросший ток повышает вращающий момент, и
если при этом нагрузочный момент остается неизменным, то частота вращения двигателя увеличивается.
Из (29.5) следует, что регулировать частоту вращения двигателя
можно изменением либо напряжения U, подводимого к двигателю, либо
основного магнитного потока Ф, либо электрического сопротивления
в цепи якоря .
Направление вращения якоря
зависит от направлений магнитного потока возбуждения Ф
и тока в обмотке якоря. Поэтому, изменив направление какой-либо из указанных
величин, можно изменить направление вращения якоря. Следует иметь в виду, что
переключение общих зажимов схемы у рубильника не дает изменения направления вращения якоря, так как при
этом одновременно изменяется направление тока и в обмотке якоря, и в
обмотке возбуждения.
Пусковой ток якоря при
полном сопротивлении пускового реостата
. (12.7)
С появлением тока в цепи
якоря возникает пусковой момент
, под действием которого начинается
вращение якоря. По мере
нарастания частоты вращения увеличивается противо-ЭДС , что ведет к
уменьшению пускового тока и пускового момента.
Схема включения в сеть
двигателя показана на рис.
29.3, а. Характерной особенностью параллельного возбуждения
является то, что ток в обмотке возбуждения (ОВ) не зависит от тока нагрузки (тока якоря). Реостат в цепи
возбуждения служит
для регулирования тока в обмотке возбуждения и магнитного потока
главных полюсов.
Эксплуатационные свойства
двигателя определяются его рабочими
характеристиками, под которыми понимают зависимость
частоты вращения n, тока I, полезного момента M2, вращающего момента M от мощности на валу двигателя Р2 при и
(рис.
29.3, 6).
При включении стабилизирующей
обмотки согласованно с параллельной обмоткой возбуждения ее МДС
компенсирует размагничивающее
действие реакции якоря так, что поток Ф во всем
диапазоне нагрузок остается практически неизменным.
Изменение частоты вращения
двигателя при переходе от номинальной
нагрузки к х.х., выраженное в процентах, называют номинальным
изменением частоты вращения:
,
(29.8)
где —
частота вращения двигателя в режиме х.х.
Обычно для двигателей
параллельного возбуждения , поэтому характеристику частоты вращения
двигателя параллельного возбуждения называют жесткой.
Введение дополнительного
сопротивления в цепь якоря.
Дополнительное сопротивление
(реостат ) включают в цепь якоря аналогично пусковому реостату (ПР).
Однако в отличие от последнего оно должно быть рассчитано
на продолжительное протекание тока.
При включении сопротивления в цепь якоря выражение частоты (29.5)
принимает вид
, (29.12)
где — частота вращения в режиме х.х.;
— изменение частоты
вращения, вызванное падением напряжения в цепи якоря.
Частоту вращения двигателей
последовательного возбуждения можно
регулировать изменением либо напряжения , либо
магнитного потока обмотки
возбуждения. В первом случае в цепь якоря последовательно включают регулировочный реостат (рис. 29.10, а). С увеличением
сопротивления этого реостата уменьшаются напряжение на входе двигателя и
частота его вращения. Этот
метод регулирования применяют главным образом в двигателях небольшой мощности. В случае
значительной мощности двигателя этот способ неэкономичен из-за больших потерь энергии в . Кроме
того, реостат , рассчитываемый на
рабочий ток двигателя,
получается громоздким и дорогостоящим.
Регулировать частоту
вращения двигателя изменением магнитного потока можно тремя способами: шунтированием обмотки возбуждения реостатом , секционированием обмотки возбуждения и
шунтированием обмотки якоря реостатом . Включение
реостата , шунтирующего обмотку возбуждения, а также уменьшение сопротивления этого
реостата ведет к снижению
тока возбуждения , а следовательно, к росту
частоты вращения. Этот способ
экономичнее предыдущего (см. рис. 29.10, а),
применяется чаще и оценивается
коэффициентом регулирования . Обычно
сопротивление реостата принимается таким, чтобы
.
При секционировании обмотки
возбуждения отключение части витков обмотки сопровождается ростом частоты вращения. При шунтировании обмотки якоря реостатом увеличивается ток возбуждения , что вызывает уменьшение частоты вращения. Этот способ регулирования, хотя и обеспечивает глубокую регулировку, неэкономичен и применяется очень редко.
Потери в машинах постоянного
тока. В машинах
постоянного тока, как и в других электрических машинах, имеют место магнитные, электрические и
механические потери (составляющие группу основных потерь)
и добавочные потери.
Магнитные потери происходят только в сердечнике якоря, так как только этот элемент
магнитопровода машины постоянного тока подвергается перемагничиванию. Величина магнитных потерь, состоящих из потерь от гистерезиса и потерь от вихревых токов, зависит от частоты перемагничивания значений магнитной индукции в
зубцах и спинке якоря, толщины листов электротехнической стали, ее
магнитных свойств и качества изоляции этих
листов в пакете якоря.
Электрические потери в
коллекторной машине постоянного тока
обусловлены нагревом обмоток и щеточного контакта. Потери в цепи возбуждения
определяются потерями в обмотке возбуждения и в реостате, включенном в цепь
возбуждения:
(12.18)
Здесь — напряжение на зажимах цепи
возбуждения. Потери в
обмотках цепи якоря
(12.19)
где сопротивление обмоток в цепи якоря , приведенное к расчетной рабочей температуре
,
определяется по (13.4) с учетом данных, приведенных в § 13.1 и § 8.4.
Электрические потери также
имеют место и в контакте щеток:
(12.20)
где
— переходное падение напряжения, В, на
щетках обеих полярностей, принимаемое в
соответствии с маркой щеток.
Электрические потери в цепи
якоря и в щеточном контакте зависят от нагрузки машины,
поэтому эти потери называют переменными.
Механические потери. В машине
постоянного тока механические потери
складываются из потерь от трения щеток о коллектор
(12.21)
трения в подшипниках и
на вентиляцию
(12.22)
где — коэффициент трения
щеток о коллектор — поверхность соприкосновения всех щеток
с коллектором, м2; — удельное давление, Н/м2, щетки [для
машин общего назначения =(2÷3)·104 Н/м2];
окружная скорость коллектора
(м/с) диаметром (м)
. (12.23)
Механические и магнитные потери при стабильной частоте вращения можно
считать постоянными.
Сумма магнитных и
механических потерь составляют потери х.х.:
.
(12.24)
Если машина работает в качестве двигателя параллельного
возбуждения в режиме х.х., то она потребляет из сети мощность
. (12.25)
Однако ввиду небольшого
значения тока электрические потери
и
весьма малы и обычно не превышают 3% потерь
.
Поэтому, не допуская заметной ошибки, можно записать , откуда потери х.х.
. (12.26)
Таким образом, потери х.х.
(магнитные и механические) могут быть определены экспериментально.
В машинах постоянного тока
имеется ряд трудно учитываемых
потерь — добавочных. Эти потери складываются из потерь от вихревых токов
в меди обмоток, потерь в уравнительных соединениях, в стали якоря из-за неравномерного
распределения индукции при
нагрузке, в полюсных наконечниках, обусловленных пульсацией основного потока из-за наличия зубцов якоря,
и др. Добавочные потери
составляют хотя и небольшую, но не поддающуюся точному учету величину. Поэтому, согласно ГОСТу, в
машинах без компенсационной обмотки значение добавочных
потерь принимают равным 1% от полезной мощности для генераторов или 1% от подводимой мощности для двигателей. В
машинах с компенсационной
обмоткой значение добавочных потерь принимают равным соответственно
0,5%.
Мощность (Вт) на входе
машины постоянного тока (подводимая мощность):
для генератора (механическая
мощность)
(12.27)
где — вращающий
момент приводного двигателя, Н∙м;
для двигателя (электрическая
мощность)
.
(12.28)
Мощность (Вт) на выходе
машины (полезная мощность):
для генератора (электрическая
мощность)
;
(12.29)
для двигателя (механическая
мощность)
. (12.30)
Здесь и
—
момент на валу электрической машины, Н-м; — частота вращения, об/мин.
Коэффициент полезного
действия. Коэффициент
полезного действия
электрической машины представляет собой отношение мощностей отдаваемой (полезной) к подводимой (потребляемой)
,:
.
Определив суммарную мощность
вышеперечисленных потерь
, (12.31)
можно подсчитать КПД машины по одной из следующих
формул:
для генератора
; (12.32)
для двигателя
. (12.33)
Обычно КПД машин постоянного
тока составляет 0,75—0,90 для
машин мощностью от 1 до 100 кВт и 0,90—0,97 для машин мощностью свыше 100 кВт. Намного меньше КПД машин
постоянного тока малой
мощности. Например, для машин мощностью от 5 до 50 Вт = 0,15÷0,50. Указанные значения
КПД соответствуют
номинальной нагрузке машины. Зависимость КПД машины постоянного тока от нагрузки выражается графиком
, форма которого характерна для электрических машин.
Коэффициент полезного
действия электрической машины можно
определять: а) методом непосредственной нагрузки по результатам
измерений подведенной и отдаваемой
мощностей; б) косвенным методом по
результатам измерений потерь.
Метод непосредственной
нагрузки применим только для машин малой мощности, для остальных случаев применяется косвенный метод, как более точный и удобный. Установлено, что при >
80 % измерять КПД методом непосредственной
нагрузки нецелесообразно, так как он
дает большую ошибку, чем косвенный метод.
Существует несколько косвенных способов определения КПД. Наиболее прост способ холостого хода двигателя, когда потребляемая
машиной постоянного тока
мощность затрачивается только
на потери х.х. Что же касается
электрических потерь, то их определяют расчетным путем
после предварительного измерения электрических сопротивлений обмоток и приведения
их к рабочей температуре.
Пример 12.1. Двигатель постоянного тока
параллельного возбуждения
включен в сеть с напряжением 220 В. При номинальной нагрузке и частоте вращения об/мин
он потребляет ток = 43 А. Определить КПД
двигателя при номинальной нагрузке, если ток х.х. = 4 А,
а сопротивления цепей якоря = 0,25 Ом и возбуждения
= 150 Ом. При каком добавочном сопротивлении
,
включенном последовательно в цепь якоря, частота вращения двигателя будет = 1000
об/мин (нагрузочный момент )?
Решение. Ток возбуждения =
220/150 =1,47 А. Ток якоря в режиме х.х. = 4 – 1,47 = 2,53 А. Ток якоря
номинальный = 43 – 1,47 = 41,53 А. Сумма магнитных и
механических потерь = 220- 2,53 -2,532–
0,25 = 555 Вт. Электрические потери в цепи возбуждения по (12.18)
Вт.
Электрические потери в цепи
якоря по (12.19)
Вт.
Электрические потери в
щеточном контакте по (12.20)
Вт.
Подводимая к двигателю
мощность по (12.28)
Вт.
Добавочные потери
Вт.
Суммарные потери по (12.31)
Вт.
Полезная мощность двигателя
Вт.
КПД двигателя при номинальной
нагрузке
.
Из выражения (29.5) получим
ЭДС якоря при частоте вращения 1000 об/мин по (12.20)
В.
Так как ток якоря прямо
пропорционален моменту , то при
сила тока
после включения
останется
прежней А. Из выражения тока якоря (12.2) получим
Ом.
Электрические потери в
добавочном сопротивлении
Вт.
Полезная мощность двигателя при частоте вращения 1000
об/мин
Вт.
Расчет полезной мощности является приближенным, так как он
не учитывает уменьшение
механических потерь двигателя при его переходе на меньшую частоту
вращения.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
1.
Решить
задачу №1. Двигатель постоянного тока параллельного возбуждения имеет
следующие данные: номинальная мощность Рном, напряжение питания Uном,
номинальная частота вращения nном,
сопротивление обмоток в цепи якоря Σr,
сопротивление цепи возбуждения rв, падение
напряжения в щеточном контакте щеток ∆Uщ
= 2 В. Значения перечисленных
параметров приведены в табл. 12.1. Требуется определить потребляемый двигателем
ток в режиме номинальной нагрузки Iном,
сопротивление пускового реостата Rп.р., при
котором начальный пусковой ток в цепи якоря двигателя был бы равен 2,5 Iаном,
начальный пусковой момент Мп, частоту вращения n0
и
ток I0 в режиме
холостого хода, номинальное изменение частоты вращения якоря двигателя при
сбросе нагрузки. Влиянием реакции якоря пренебречь.
Таблица 12.3.
|
Параметр |
Варианты |
||||
|
1 |
2 |
3 |
4 |
5 |
|
|
Рном ,кВт |
25 |
15 |
45 |
4,2 |
18 |
|
Uном , В |
440 |
220 |
440 |
220 |
220 |
|
nном , об/мин |
1500 |
1000 |
1500 |
1500 |
1200 |
|
ηном, |
85 |
83,8 |
88 |
78 |
84 |
|
Σr, Ом |
0,15 |
0,12 |
0,13 |
0,15 |
0,12 |
|
rв |
88 |
73 |
88 |
64 |
73 |
Решение:
–
определить
потребляемую двигателем мощность при номинальной нагрузке Р1ном;
–
определить
ток, потребляемый двигателем при номинальной нагрузке Iном;
–
определить
ток в цепи обмотки возбуждения Iв;
–
определить
ток в обмотке якоря Iаном;
–
определить
начальный пусковой ток якоря при заданной кратности 2,5 Iп.р.;
–
определить
требуемое сопротивление цепи якоря при заданной кратности пускового тока 2,5 Rа= Rп.р.+
Σr= Uном/ Iап;
–
определить
сопротивление пускового реостата Rп.р.;
–
определить
ЭДС якоря в режиме номинальной нагрузки Iаном, используя
уравнение напряжений;
–
определить
отношение коэффициентов сM/ce=[pN/2πɑ]/ [pN/(60ɑ)];
–
определить
начальный пусковой момент при заданной кратности пускового тока 2,5
–
Мп= сMФ Iап;
–
определить
момент на валу двигателя при номинальной нагрузке М2ном;
–
определить
электромагнитную мощность при номинальной нагрузке Рэм.ном;
–
определить
электромагнитный момент при номинальной нагрузке Мном;
–
определить
момент холостого хода М0
=
Мном – М2ном;
–
определить
ток якоря в режиме холостого хода Iаном= М0/( сMФ);
–
определить
ЭДС якоря в режиме холостого хода Ea,
используя уравнение напряжений (принимаем ∆Uщ
= 0);
–
определить
частоту вращения якоря в режиме холостого хода n0=
Ea0/( сеФ);
–
определить
номинальное изменение частоты вращения двигателя при сбросе нагрузки .
2. Решить
задачу №2. В табл. 12.1 даны значения параметров двигателя постоянного тока
независимого возбуждения: номинальная мощность двигателя Рном,
напряжение питания цепи якоря Uном , напряжение
питания цепи возбуждения UB, частота
вращения якоря в номинальном режиме nном;
сопротивления цепи якоря Σr; и цепи возбуждения
rв,
приведенные к рабочей температуре, падение напряжения в щеточном контакте при
номинальном токе ∆Uщ
= 2 В, номинальное изменение
напряжения при сбросе нагрузки = 8,0 %, ток якоря в режиме
холостого хода I0. Требуется
определить все виды потерь и КПД двигателя.
Таблица 12.2.
|
Параметр |
Варианты |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
Рном ,кВт |
25 |
40 |
53 |
75 |
16 |
11 |
|
Uном ,В |
440 |
440 |
440 |
440 |
220 |
220 |
|
UB ,В |
220 |
220 |
220 |
220 |
220 |
110 |
|
I0, А |
6,0 |
7,5 |
8,0 |
10,8 |
8,7 |
5,8 |
|
Σr , Ом |
0,30 |
0,17 |
0,12 |
0,70 |
0,18 |
0,27 |
|
rв , Ом |
60 |
55 |
42 |
40 |
60 |
27 |
|
nном, об/мин |
2200 |
1000 |
2360 |
3150 |
1500 |
800 |
Решение:
– определить частоту вращения в режиме холостого
хода n0;
– определить ЭДС якоря в режиме холостого
хода (падением напряжения в щеточном контакте пренебрегаем ввиду его
незначительной величины в режиме холостого хода) Еа0;
– определить момент в режиме холостого
хода М0;
– определить момент на валу двигателя в
режиме номинальной нагрузки М2ном;
– определить электромагнитный момент
двигателя при номинальной нагрузке Мном;
– определить электромагнитная мощность
двигателя в режиме номинальной нагрузки Рэм.ном;
– определить тока якоря в режиме
номинальной нагрузки через ЭДС якоря в режиме холостого хода можно представить
как , сM/ce=9,55;
– определить сумму магнитных и
механических потерь двигателя, которая пропорциональна моменту холостого хода 0,105
М0n0;
– определить электрические потери в цепи
обмотки якоря Ра.э;
– определить электрические потери в
щеточном контакте якоря Рщ.э;
– определить мощность, подводимая к цепи
якоря, в номинальном режиме Р1аном;
– определить ток в обмотке возбуждения Iв;
– определить мощность в цепи возбуждения Рв;
– определить мощность, потребляемую
двигателем в режиме номинальной нагрузки Р1ном;
–
определить КПД двигателя в номинальном режиме ηном.
3. Решить
задачу №3. В табл. 12.3 приведены данные каталога на двигатели постоянного
тока независимого возбуждения серии 2П: номинальная мощность РНом,
номинальное
напряжение, подводимое к цепи якоря, Uном, номинальная
частота вращения nном, КПД
двигателя ηном,
сопротивление цепи якоря, приведенное к рабочей температуре Σr. Требуется определить сопротивление
добавочного резистора гд, который следует включить в цепь якоря,
чтобы при номинальной нагрузке двигателя частота вращения якоря составила 0,5п1ном;
построить естественную и искусственную механические характеристики двигателя.
Таблица
12.3.
|
Тип |
Рном ,кВт |
Uном,В |
nном |
ηном |
Σr , Ом |
|
2ITO200L |
7Д |
220 |
750 |
83,5 |
0,48 |
|
2П0200М |
20 |
440 |
2200 |
90 |
0,28 |
|
2ПФ200М |
30 |
440 |
2200 |
90 |
0,22 |
|
2ПФ200Ц |
20 |
220 |
1000 |
85,5 |
0,18 |
|
2ПН225М |
37 |
220 |
1500 |
86,5 |
0,07 |
|
2ПФ225М |
10 |
220 |
500 |
74,5 |
0,58 |
|
2ПО180М |
17 |
440 |
3000 |
90 |
0,31 |
Решение.
– определить ток в цепи якоря в режиме
номинальной нагрузки при пном== 750
об/мин I aном;
– определить ЭДС в режиме номинальной
нагрузки (падением напряжения в щеточном контакте пренебрегаем) Еном
;
– определить частоту вращения идеального
холостого хода (пограничная частота вращения) nоо ; – –
определить номинальный момент на валу двигателя М2ном;
– по полученным данным построить
естественную механическую характеристику (рис. 12.1, график 1);
– определить частоту вращения при включении
резистора п’ном = 0,5
пном;
– по вычисленным данным построить
искусственную механическую характеристику двигателя (рис. 12.1, график 2);

сопротивление резистора rД.
4.
Оформить отчет по практической работе.
5.
Ответить на контрольные вопросы.
6.
Сделать вывод о проделанной работе.
Рисунок 12.1.Механические характеристики
двигателя постоянного тока
КОНТРОЛЬНЫЕ ВОПРОСЫ:
1. Каким свойством обладают коллекторные машины?
2. Охарактеризуйте вращающий момент. Где он возникает?
3. Почему в двигателе постоянного тока ЭДС
называется противоэлектродвижущей силой (противо-ЭДС) якоря?
4. Что является рабочими характеристиками
двигателя?
5. Как можно регулировать частоту вращения двигателей
последовательного возбуждения?
6. От чего зависит направление вращения
якоря?
7. Виды потерь двигателя постоянного тока и
их характеристики.
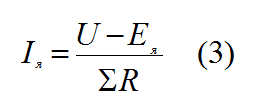



 – постоянная момента, Н∙м/А,
– постоянная момента, Н∙м/А, – электродвижущая сила, В,
– электродвижущая сила, В, – постоянная ЭДС, В∙с/рад,
– постоянная ЭДС, В∙с/рад, – угловая частота, рад/с
– угловая частота, рад/с – жесткость механической характеристики электродвигателя постоянного тока
– жесткость механической характеристики электродвигателя постоянного тока

 – механическая постоянная времени, с
– механическая постоянная времени, с