Входное и выходное сопротивление
Входное и выходное сопротивление является очень важным в электронике.
Предисловие
Ладно, начнем издалека… Как вы знаете, все электронные устройства состоят из блоков. Их еще часто называют каскады, модули, узлы и тд. В нашей статье будем использовать понятие «блок». Например, источник питания, собранный по этой схеме:
состоит из двух блоков. Я их пометил в красном и зеленом прямоугольниках.
В красном блоке мы получаем постоянное напряжение, а в зеленом блоке мы его стабилизируем. То есть блочная схема будет такой:
Блочная схема — это условное деление. В этом примере мы могли бы даже взять трансформатор, как отдельный блок, который понижает переменное напряжение одного номинала к другому. Как нам удобнее, так и делим на блоки нашу электронную безделушку. Метод «от простого к сложному» полностью работает в нашем мире. На низшем уровне находятся радиоэлементы, на высшем — готовое устройство, например, телевизор.
Ладно, что-то отвлеклись. Как вы поняли, любое устройство состоит из блоков, которые выполняют определенную функцию.
— Ага! Так что же получается? Я могу просто тупо взять готовые блоки и изобрести любое электронное устройство, которое мне придет в голову?
Да! Именно на это нацелена сейчас современная электроника 😉 Микроконтроллеры и конструкторы, типа Arduino, добавляют еще больше гибкости в творческие начинания молодых изобретателей.
На словах все выходит прекрасно, но всегда есть подводные камни, которые следует изучить, чтобы начать проектировать электронные устройства. Некоторые из этих камушков называются входным и выходным сопротивлением.
Думаю, все помнят, что такое сопротивление и что такое резистор. Резистор хоть и обладает сопротивлением, но это активное сопротивление. Катушка индуктивности и конденсатор будут уже обладать, так называемым, реактивным сопротивлением. Но что такое входное и выходное сопротивление? Это уже что-то новенькое. Если прислушаться к этим фразам, то входное сопротивление — это сопротивление какого-то входа, а выходное — сопротивление какого-либо выхода. Ну да, все почти так и есть. И где же нам найти в схеме эти входные и выходные сопротивления? А вот «прячутся» они в самих блоках радиоэлектронных устройств.
Входное сопротивление
Итак, имеем какой-либо блок. Как принято во всем мире, слева — это вход блока, справа — выход.
Как и полагается, этот блок используется в каком-нибудь радиоэлектронном устройстве и выполняет какую-либо функцию. Значит, на его вход будет подаваться какое-то входное напряжение Uвх от другого блока или от источника питания, а на его выходе появится напряжение Uвых (или не появится, если блок является конечным).
Но раз уж мы подаем напряжение на вход (входное напряжение Uвх), следовательно, у нас этот блок будет кушать какую-то силу тока Iвх.
Теперь самое интересное… От чего зависит Iвх ? Вообще, от чего зависит сила тока в цепи? Вспоминаем закон Ома для участка цепи :

Значит, сила тока у нас зависит от напряжения и от сопротивления. Предположим, что напряжение у нас не меняется, следовательно, сила тока в цепи будет зависеть от… СОПРОТИВЛЕНИЯ. Но где нам его найти? А прячется оно в самом каскаде и называется входным сопротивлением.
То есть, разобрав такой блок, внутри него мы можем найти этот резистор? Конечно же нет). Он является своего рода сопротивлением радиоэлементов, соединенных по схеме этого блока. Скажем так, совокупное сопротивление.
Как измерить входное сопротивление
Как мы знаем, на каждый блок подается какой-либо сигнал от предыдущего блока или это может быть даже питание от сети или батареи. Что нам остается сделать?
1)Замерить напряжение Uвх, подаваемое на этот блок
2)Замерить силу тока Iвх, которую потребляет наш блок
3) По закону Ома найти входное сопротивление Rвх.

Если у вас входное сопротивление получается очень большое, чтобы замерить его как можно точнее, используют вот такую схему.
Мы с вами знаем, что если входное сопротивление у нас большое, то входная сила тока в цепи у нас будет очень маленькая (из закона Ома).
Падение напряжения на резисторе R обозначим, как UR





Когда мы проводим эти измерения, имейте ввиду, что напряжение на выходе генератора не должно меняться!
Итак, давайте посчитаем, какой же резистор нам необходимо подобрать, чтобы как можно точнее замерять это входное сопротивление. Допустим, что у нас входное сопротивление Rвх=1 МегаОм, а резистор взяли R=1 КилоОм. Пусть генератор выдает постоянное напряжение U=10 Вольт. В результате, у нас получается цепь с двумя сопротивлениями. Правило делителя напряжения гласит: сумма падений напряжений на всех сопротивлениях в цепи равняется ЭДС генератора.
В результате получается цепь:
Высчитываем силу тока в цепи в Амперах

Получается, что падение напряжения на сопротивлении R в Вольтах будет:

Грубо говоря 0,01 Вольт. Вряд ли вы сможете точно замерить такое маленькое напряжение на своем китайском мультиметре.
Какой отсюда вывод? Для более точного измерения высокого входного сопротивления надо брать добавочное сопротивление также очень большого номинала. В этом случае работает правило шунта: на бОльшем сопротивлении падает бОльшее напряжение, и наоборот, на меньшем сопротивлении падает меньшее напряжение.
Измерение входного сопротивления на практике
Ну все, запарка прошла ;-). Давайте теперь на практике попробуем замерить входное сопротивление какого-либо устройства. Мой взгляд сразу упал на Транзистор-метр. Итак, выставляем на блоке питания рабочее напряжение этого транзистор-метра, то есть 9 Вольт, и во включенном состоянии замеряем потребляемую силу тока. Как замерить силу тока в цепи, читаем в этой статье. По схеме все это будет выглядеть вот так:
Итак, у нас получилось 22,5 миллиАмпер.
Теперь, зная значение потребляемого тока, можно найти по этой формуле входное сопротивление:


Выходное сопротивление
Яркий пример выходного сопротивления — это закон Ома для полной цепи, в котором есть так называемое «внутреннее сопротивление». Кому лень читать про этот закон, вкратце рассмотрим его здесь.
Что мы имели? У нас был автомобильный аккумулятор, с помощью которого мы поджигали галогенную лампочку. Перед тем, как цеплять лампочку, мы замеряли напряжение на клеммах аккумулятора:
И как только подсоединяли лампочку, у нас напряжение на аккумуляторе становилось меньше.
Разница напряжения, то есть 0,3 Вольта (12,09-11,79) у нас падало на так называемом внутреннем сопротивлении r 😉 Оно же и есть ВЫХОДНОЕ СОПРОТИВЛЕНИЕ. Его также называют еще сопротивлением источника или эквивалентным сопротивлением.
У всех аккумуляторов есть это внутреннее сопротивление r, и «цепляется» оно последовательно с источником ЭДС (Е).
Но только ли аккумуляторы и различные батарейки обладают выходным сопротивлением? Не только. Выходным сопротивлением обладают все источники питания. Это может быть блок питания, генератор частоты, либо вообще какой-нибудь усилитель.
В теореме Тевенина (короче, умный мужик такой был) говорилось, что любую цепь, которая имеет две клеммы и содержит в себе туеву кучу различных источников ЭДС и резисторов разного номинала можно привести тупо к источнику ЭДС с каким-то значением напряжения (Eэквивалентное) и с каким-то внутренним сопротивлением (Rэквивалентное).
Eэкв — эквивалентный источник ЭДС
Rэкв — эквивалентное сопротивление
То есть получается, если какой-либо источник напряжения питает нагрузку, значит, в источнике напряжения есть ЭДС и эквивалентное сопротивление, оно же выходное сопротивление.
В режиме холостого хода (то есть, когда к выходным клеммам не подцеплена нагрузка) с помощью мультиметра мы можем замерить ЭДС (E). С замером ЭДС вроде бы понятно, но вот как замерить Rвых ?
В принципе, можно устроить короткое замыкание. То есть замкнуть выходные клеммы толстым медным проводом, по которому у нас будет течь ток короткого замыкания Iкз.
В результате у нас получается замкнутая цепь с одним резистором. Из закона Ома получаем, что

Но есть небольшая загвоздка. Теоретически — формула верна. Но на практике я бы не рекомендовал использовать этот способ. В этом случае сила тока достигает бешеного значения, да вообще, вся схема ведет себя неадекватно.
Измерение выходного сопротивления на практике
Есть другой, более безопасный способ. Не буду повторяться, просто скопирую со статьи закон Ома для полной цепи, где мы находили внутреннее сопротивление аккумулятора. В той статье, мы к акуму цепляли галогенную лампочку, которая была нагрузкой R. В результате по цепи шел электрический ток. На лампочке и на внутреннем сопротивлении у нас падало напряжение, сумма которых равнялась ЭДС.
Итак, для начала замеряем напряжение на аккумуляторе без лампочки.
Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе Ur тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае E=12,09 Вольт.
Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем резисторе и на нагрузке, в данном случае на лампочке:
Сейчас на нагрузке (на галогенке) у нас упало напряжение UR=11,79 Вольт, следовательно, на внутреннем резисторе падение напряжения составило Ur=E-UR=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r:


Заключение
Входное и выходное сопротивление каскадов (блоков) в электронике играют очень важную роль. В этом мы убедимся, когда начнем рассматривать статью по согласованию узлов радиоэлектронных схем. Все качественные вольтметры и осциллографы также стараются делать с очень высоким входным сопротивлением, чтобы оно меньше сказывалось на замеряемый сигнал и не гасило его амплитуду.
С выходным сопротивлением все намного интереснее. Когда мы подключаем низкоомную нагрузку, то чем больше внутреннее сопротивление, тем больше напряжение падает на внутреннем сопротивлении. То есть в нагрузку будет отдаваться меньшее напряжение, так как разница осядет на внутреннем резисторе. Поэтому, качественные источники питания, типа блока питания либо генератора частоты, пытаются делать как можно с меньшим выходным сопротивлением, чтобы напряжение на выходе «не проседало» при подключении низкоомной нагрузки. Даже если сильно просядет, то мы можем вручную подкорректировать с помощью регулировки выходного напряжения, которые есть в каждом нормальном источнике питания. В некоторых источниках это делается автоматически.
Источник
![]() ,
,
(8.4)
где
f1
–частота
напряжения, требуемого для вращения
вала двигателя с частотой 882 об/мин, Гц;
nрасч.– расчетная частота
вращения вала двигателя, об/мин;
fсети
– частота
сети, 50 Гц;
nном.– номинальная
частота вращения вала двигателя, об/мин;
![]()
1.7.3.2
Определяем
частоту выходного напряжения от ПЧ для
большой скорости вращения по формуле
8.5
![]() ,
,
(8.5)
где
f2
–частота
напряжения, требуемого для вращения
вала двигателя с частотой 192 об/мин, Гц;
nмал.–частота вращения
вала двигателя на малой скорости, об/мин;
fсети
– частота
сети, 50 Гц;
nном.– номинальная
частота вращения вала двигателя, об/мин;
![]()
С
применением ПЧ номинальная скорость
лифта равна 1 м/с, а при движении на малой
скорости 0,22 м/с. Так же ПЧ обеспечивает
плавные переходы скорости.
 1.7.3.3
1.7.3.3
Построение тахограммы
Для
построения тахограммы используем ранее
полученные времена.
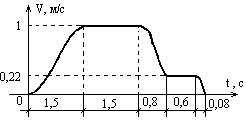
Рисунок
5 – Тахограмма лифта с использованием
ПЧ и односкоростного АД.
1.7.4
Определение моментов инерции
1.7.4.1Определяем угловую скорость
двигателя по формуле 8.6
Wдв
= nрасч.
/9,55, (8.6)
где nрасч.
– количество оборотов двигателя,
об/мин;
Wдв= 882 /9,55 = 92,4 рад/с;
1.7.4.2Определяем момент инерции при
пуске и номинальной загрузке кабины по
формуле 8.7
 ,
,
(8.7)
где JΣ1–момент
инерции при номинальной загрузке кабины,
кг*м²;
Jдв – момент инерции
двигателя, кг*м²;
m1 – масса загруженной
кабины на остановках, н;
Vк – скорость движения
кабины, м/с;
Wдв– угловая скорость двигателя, рад.
JΣ
1
= 0,048 + 454,4 * (1 / 92,4) ² = 0,1 кг*м²;
 1.7.4.3Определяем момент инерции при пуске
1.7.4.3Определяем момент инерции при пуске
пустой кабины по формуле 8.8
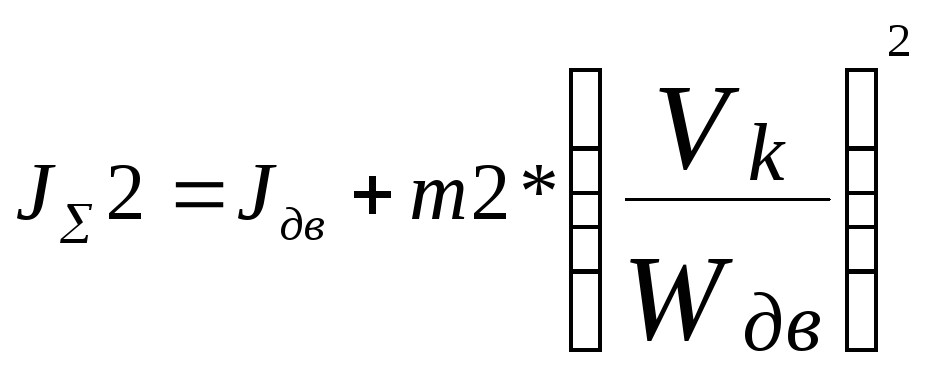 ,(8.8)
,(8.8)
где JΣ2
–момент инерции при пустой кабине,
кг*м²;
Jдв – момент инерции
двигателя, кг*м²;
m2 – масса пустой кабины
на остановках, н;
Vк – скорость движения
кабины, м/с;
Wдв– угловая скорость двигателя, рад.
JΣ
2= 0,048 +
196,7 * (1 / 92,4) ² = 0,07 кг*м²;
1.7.4.4 Определяем момент инерции при
переходе с большой скорости на малую
при полной загрузке кабины по формуле
8.9
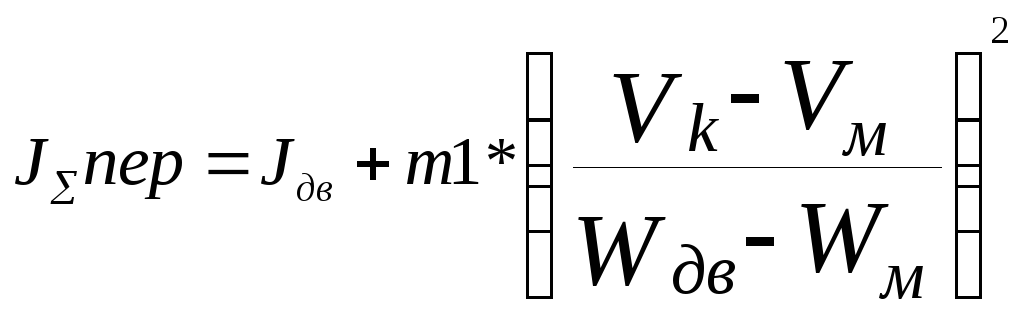 ,(8.9)
,(8.9)
где JΣпер.–момент
инерции при переходе и номинальной
загрузке кабины, кг*м²;
Jдв – момент инерции
двигателя, кг*м²;
m1 – масса загруженной
кабины на остановках, н;
Vк – скорость движения
кабины, м/с;
Wдв– угловая скорость двигателя, рад/с;
Vм – малая скорость
движения кабины, м/с;
Wм– малая угловая скорость двигателя,
рад/с;
JΣпер.
= 0,048 + 454,4 * ((1-0,22) / (92,4-20,1)) ² = 0,1 кг*м²;
 1.7.4.5Определяем момент инерции при переходе
1.7.4.5Определяем момент инерции при переходе
с большой скорости на малую при пустой
кабине по формуле 8.10
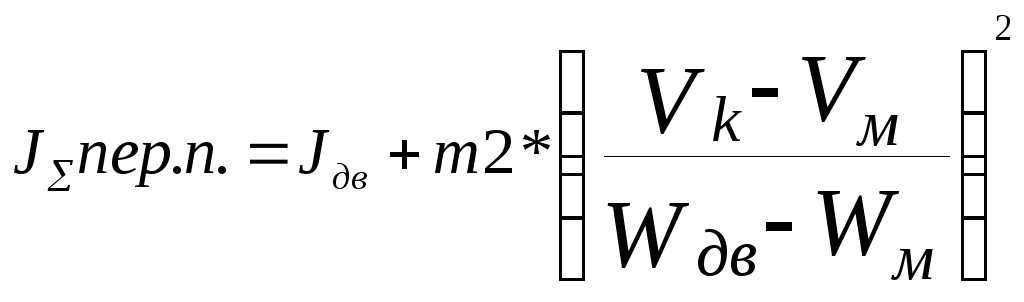 ,(8.10)
,(8.10)
где JΣпер.п.–момент
инерции при переходе пустой кабины,
кг*м²;
Jдв – момент инерции
двигателя, кг*м²;
m2 – масса пустой кабины
на остановках, н;
Vк – скорость движения
кабины, м/с;
Wдв– угловая скорость двигателя, рад/с;
Vм – малая скорость
движения кабины, м/с;
Wм– малая угловая скорость двигателя,
рад/с;
JΣпер.п
= 0,048 + 196,7 * ((1-0,22) / (92,4-20,1)) ² = 0,07 кг*м²;
1.7.4.6Определяем момент инерции на
малой скорости и полной загрузке кабины
по формуле 8.11
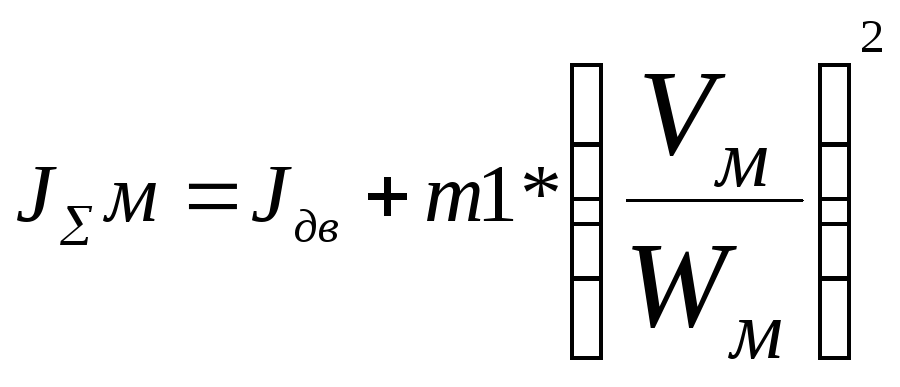 , (8.11)
, (8.11)
где JΣ1м
–момент инерции на малой скорости
и полной загрузке кабины, кг*м²;
Jдв – момент инерции
двигателя, кг*м²;
m1 – масса загруженной
кабины на остановках, н;
Vм – малая скорость
движения кабины, м/с;
Wм– малая угловая скорость двигателя,
рад/с;
JΣм=
0,048 + 454,4 * (0,22 / 20,1) ² = 0,1 кг*м²;
 1.7.4.7Определяем момент инерции на малой
1.7.4.7Определяем момент инерции на малой
скорости при пустой кабине по формуле
8.12
 ,(8.12)
,(8.12)
где JΣ1м.п.
–момент инерции на малой скорости
при пустой кабины, кг*м²;
Jдв – момент инерции
двигателя, кг*м²;
m2 – масса загруженной
кабины на остановках, н;
Vм – малая скорость
движения кабины, м/с;
Wм– малая угловая скорость двигателя,
рад/с;
JΣм.п.=
0,048 + 196,7 * (0,22 / 20,1) ² = 0,07 кг*м²;
 1.7.5
1.7.5
Построение нагрузочной диаграммы
двигателя
Для построения нагрузочной диаграммы
двигателя определим динамические
моменты на участках:
1. Пуск;
2. Переход с большей скорости на меньшую;
3. Торможение на малой скорости;
1.7.5.1Определяем динамический
момент при пуске загруженной кабины
по формуле 9.1
Мдин.
п.=
(JΣ1*
Wдв
)/tп
,(9.1)
где
Мдин.
п. –динамический
момент при пуске, н*м;
JΣ1–
момент инерции при номинальной загрузке
кабины, кг*м²;
Wдв– угловая скорость двигателя, рад/с;
tп
– время пуска
двигателя, с;
Мдин.
п. =
(0,1*92,4)/1,5=
6,16 н*м;
1.7.5.2Определяем динамический момент
при пуске пустой кабины по формуле 9.2
Мдин.
п.’=
(JΣ2*
Wдв
)/tп
,(9.2)
где
Мдин.
п.’ –динамический
момент при пуске, н*м;
JΣ2–
момент инерции при номинальной загрузке
кабины, кг*м²;
Wдв– угловая скорость двигателя, рад/с;
tп
– время пуска
двигателя, с;
Мдин.
п.’ =
(0,07*92,4)/1,5=
4,3 н*м;
 1.7.5.3Определяем динамический момент при
1.7.5.3Определяем динамический момент при
переходе с большей скорости на меньшую
загруженной кабины по формуле 9.3
Мдин.пер.=
( – JΣпер*
Wдв
)/tпер
,
(9.3)
где
Мдин.пер.
–динамический
момент при переходе с большей скорости
на меньшую загруженной кабины, н*м;
JΣпер–
момент инерции при переходе с большей
скорости на меньшую, кг*м²;
Wдв.
пер.– угловая скорость двигателя
, рад/с;
tпер
– время
перехода с большей скорости на меньшую,
с;
Мдин.пер.
= (–0,1*72,3)/0,8
= – 9
н*м;
1.7.5.4Определяем динамический момент
при переходе с большей скорости на
меньшую пустой кабины по формуле 9.4
Мдин.пер.’=
( – JΣпер.п.*
Wдв
)/tпер
,
(9.4)
где
Мдин.пер.’
–динамический
момент при переходе с большей скорости
на меньшую загруженной кабины, н*м;
JΣпер.п.–
момент инерции при переходе с большей
скорости на меньшую пустой кабины,
кг*м²;
Wдв.
пер.– угловая скорость двигателя
, рад/с;
tпер
– время
перехода с большей скорости на меньшую,
с;
Мдин.пер.’
= (–0,07*72,3)/0,8
= – 6,3
н*м;
1.7.5.5Определяем динамический момент
при торможении на малой скорости
загруженной кабины по формуле 9.5
Мдин.т.=
( – JΣм*
Wм
)/tпер
,
(9.5)
где
Мдин.т.
–динамический
момент при торможении, н*м;
JΣм–
момент инерции при переходе с большей
скорости на меньшую загруженной кабины,
кг*м²;
Wм– малая угловая скорость двигателя,
рад/с;
tт
.м. – время
торможения, с;
Мдин.т.
= (–0,1*20,1)/0,08
= –25
н*м;
 1.7.5.6Определяем динамический момент при
1.7.5.6Определяем динамический момент при
торможении на малой скорости пустой
кабины по формуле 9.6
Мдин.т.’=
( – JΣм.п.*
Wм
)/tпер
,
(9.6)
где
Мдин.т.’
–динамический
момент при торможении, н*м;
JΣм.п.–
момент инерции при переходе с большей
скорости на меньшую пустой кабины,
кг*м²;
Wм– малая угловая скорость двигателя,
рад/с;
tт
.м. – время
торможения, с;
Мдин.т.’
= (–0,07*20,1)/0,08
= –17,6
н*м;
Теперь
определяем моменты двигателя на этих
участках в двух случаях:
1.
Когда кабина загружена полностью и
движется вверх;
2.
Когда кабина пустая и движется вниз;
Определяем момент на валу двигателя
при подъеме загруженной кабины:
1.при пуске
М1=Мст1+
Мдин. п.
,
где
М1 –
момент на
валу двигателя при пуске и полностью
загруженной кабине, н*м;
Мдин.
п. –динамический
момент при пуске, н*м;
Мст1– статический
момент на валу двигателя, н*м;
М1=
64,3 + 6,16 = 70,5 н*м
2.при переходе с большей скорости
на меньшую
М2=Мст1+
Мдин.пер.
,
где
М2 –
момент на
валу двигателя при переходе с большей
скорости на меньшую, н*м;
Мдин.пер.
–динамический
момент при переходе с большей скорости
на меньшую, н*м;
Мст1– статический
момент на валу двигателя, н*м;
М2=
64,3 –
9 = 55,3 н*м
 3.при торможении на малой скорости
3.при торможении на малой скорости
М3=Мст1+
Мдин.т.
,
где
М3 –
момент на
валу двигателя при торможении на малой
скорости, н*м;
Мдин.т.
–динамический
момент при торможении на малой скорости,
н*м;
Мст1– статический
момент на валу двигателя, н*м;
М3=
64,3 –
25 = 39,3 н*м
Определяем момент на валу двигателя
при спуске пустой кабины:
1.при пуске
М1’=Мст2+
Мдин. п.’
,
где
М1’ –
момент на
валу двигателя при пуске пустой кабины,
н*м;
Мдин.
п.’ –динамический
момент при пуске, н*м;
Мст2– статический
момент на валу двигателя, н*м;
М1’=
28 + 4,3 = 32,3 н*м
2.при переходе с большей скорости
на меньшую
М2’=Мст2+
Мдин.пер.’
,
где
М2’ –
момент на
валу двигателя при переходе с большей
скорости на меньшую, н*м;
Мдин.пер.’
–динамический
момент при переходе с большей скорости
на меньшую, н*м;
Мст2– статический
момент на валу двигателя, н*м;
М2’=
28 – 6,3 = 21,7 н*м
3.при торможении на малой скорости
М3’=Мст2+
Мдин.т.’
,
где
М3’ –
момент на
валу двигателя при торможении на малой
скорости, н*м;
Мдин.т.’
–динамический
момент при торможении на малой скорости,
н*м;
М3’=
28 –
17,6 = 10,4 н*м
 1.7.5.6
1.7.5.6
Построение нагрузочной диаграммы
Теперь
можно построить нагрузочные диаграммы
работы двигателя лифта при подъеме
загруженной кабины (рисунок 6) и при
спуске пустой кабины (рисунок 7). Для
этогоиспользуем
ранее полученные моменты и времена.
Р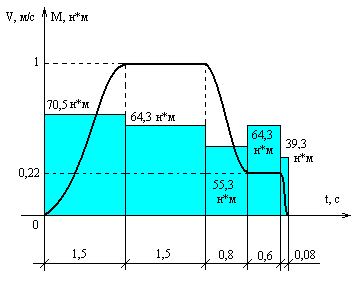 исунок
исунок
6.- Нагрузочная диаграмма работы
двигателя при подъеме загруженной
кабины и тахограмма ее движения.
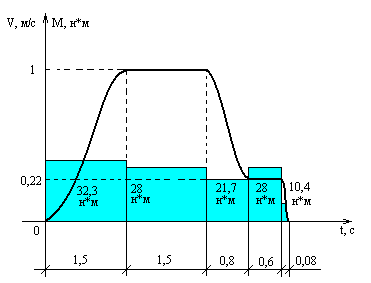
Рисунок
7 – Нагрузочная диаграмма работы
двигателя при спуске пустой кабины и
тахограмма ее движения.
 1.7.6
1.7.6
Проверка двигателя по пуску и по нагреву
1.7.6.1Условие выбора двигателя по
пуску
М1≤Mмакс
,
где М1–
максимальный момент, возникающий на
валу двигателя при пуске, н*м;Mмакс
– максимальный момент двигателя,
н*м;
70,5 < 110
Двигатель проверку по пуску прошел.
Теперь проверяем двигатель по нагреву.
1.7.6.2Условие выбора двигателя по
нагреву
Мэкв’
< Mном
Мэкв’=![]()
![]()
Мэкв’=49,9
* 0,89 = 44, 84 н*м
44,84 < 55
Двигатель проверку по нагреву прошел.
 1.8
1.8
Выбор ПЧ
1.8.1
Выбор ПЧ по
мощности двигателя и по напряжению
питания
Из
каталога выбираем ПЧ , мощность которого
равна или больше номинальной мощности
двигателя.
Выбираем
ПЧ типа ATV58HU90N4S309, его параметры представлены
в таблице 3, а его внешний вид показан
на рисунке 8.
Таблица
3 – Параметры ПЧ.
|
Тип |
Сеть |
Двигатель |
Преобразователь |
||||||
|
U |
I |
I |
Мощность |
I |
Макс. перех. |
Потери мощности |
Масса |
||
|
В. |
А. |
КА. |
кВт. |
л.с. |
А. |
А. |
Вт. |
Кг. |
|
|
ATV58 HU90N 4S309 |
380 |
17 |
5 |
5,5 |
7,7 |
13 |
17,7 |
200 |
6,9 |
Рисунок
8 – Внешний вид ПЧ.
АЦП. Методы преобразования. Преобразование напряжения в частоту, однократное интегрирование, двойное и многостадийное интегрирование, сигма-дельта
Данная статья является логическим продолжением статьи «АЦП. Параллельное кодирование, последовательное приближение». Как уже было сказано существует шесть методов преобразования аналоговых величин в цифровые, каждая со своими плюсами и минусами: параллельное кодирование, последовательное приближение, преобразование напряжения в частоту, однократное интегрирование, двойное и многостадийное интегрирование, сигма-дельта. В этой статье продолжим рассмотрение методов преобразования и рассмотрим оставшиеся.
Интегрирующие АЦП. Преобразование напряжения в частоту
Обзор принципов аналогово-цифровых преобразователей продолжат конверторы напряжение-частота (V-to-F или V/F). Здесь входной аналоговый сигнал преобразуется в непрерывный поток импульсов, чья частота пропорциональна уровню напряжения на входе. Импульсы можно получить, заряжая конденсатор током, пропорциональным входному напряжению, и разряжая затем до нулевого уровня. Для увеличения точности используется обратная связь. В одном варианте выход V/F-схемы сравнивается с уровнем на входе и поддерживается та частота, которая позволяет удерживать выход компаратора в нужном состоянии. В другой, более популярной схеме, используется метод «балансировки заряда».
Выходная частота преобразователей лежит в диапазоне от 10 kHz до 1 MHz для полного диапазона входных напряжений. Коммерческие преобразователи V/F имеют разрешение 13 разрядов (точность 0.01%) и являются примерами качественных генераторов, управляемых напряжением. Например, отличный AD650 фирмы Analog Devices имеет в рабочем диапазоне 0…10 kHz типовую нелинейность 0.002% . Он недорог и удобен для передачи по кабелю, когда требуется частота, а не цифровой код. Если скорость не важна, можно получать усреднённое цифровое значение, считая импульсы в течение определённого времени. Такая техника используется в простых цифровых щитовых приборах на 3 десятичных разряда.
Генераторы, управляемые напряжением, подобные AD650, являются асинхронными преобразователями напряжение-частота. Внутри у них есть постоянно тикающий генератор, а вывода для внешней частоты нет. Но задачу можно решать иначе. Можно пропускать на выход часть входного потока импульсов, пропорциональную в среднем входному аналоговому сигналу.
Для таких синхронных преобразователей V/F выходные импульсы появляются синхронно с внешней тактовой частотой. В каждом периоде тактовой частоты импульс может пропускаться на выход или блокироваться присутствовать или отсутствовать в зависимости от того, что требуется, чтобы средняя выходная частота была пропорциональна Vin. В общем случае расстояние между соседними импульсами постоянно меняется (но всегда пропорционально целому числу периодов тактовой частоты), т.е. на выходе нет какого-то регулярного сигнала. Выходная импульсная последовательность имеет «джиттер». Где-то, где усреднение сигнала внутренне присущее схеме свойство, это нормально. Например, так себя ведёт резистивный нагреватель с аналоговым датчиком температуры в контуре управления.
На рисунке показан усреднённый на промежутке длиной несколько секунд выходной сигнал, снятый на макете синхронного преобразователя V/F AD7741 с тактовой частотой 5 MHz .
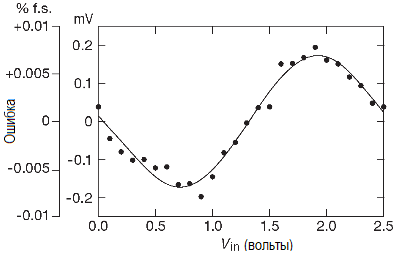
Линейность, как легко заметить, очень неплохая.
Синхронные преобразователи напряжение-частота являются простым примером «1-разрядного» АЦП. Есть и более удобные способы создания битовых последовательностей, пропорциональных среднему значению аналогового сигнала. А именно, сигма-дельта преобразователи делают подобную работу гораздо лучше. Но о них немного позже.
Интегрирующие АЦП. Однократное интегрирование
В этом методе однократного интегрирования внутренний генератор линейно возрастающего напряжения (источник тока + конденсатор) начинает цикл преобразования и одновременно запускается счётчик. Счетчик начинает накапливать импульсы стабильной тактовой частоты. Когда возрастающее напряжение сравняется со входным сигналом, компаратор остановит счёт. Полученная цифра и есть выходной код, пропорциональный входному напряжению. Блок-схема преобразователя показана на рисунке:
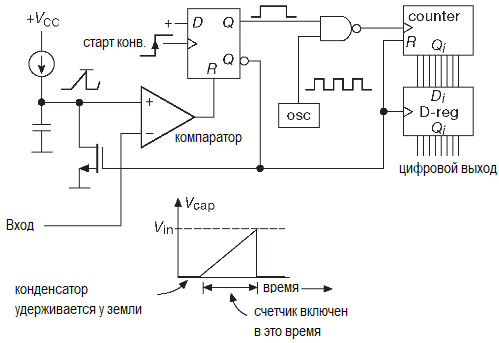
В конце цикла преобразования схема разряжает конденсатор и сбрасывает счётчик, после чего можно начинать новый цикл. Однократная интеграция проста, но не используется, когда нужна высокая точность, потому что накладывает жёсткие требования на стабильность и точность конденсатора и компаратора. Данное ограничение (и некоторые другие) отсутствует в методе «двойного интегрирования», который в настоящий момент используется везде, где нужны точные показания.
Однократные интеграторы живы и по-прежнему используются там, где абсолютная точность не требуется, но нужно равномерное разбиение диапазона по уровням. Примером может служить анализ амплитуды импульсов: пиковый детектор сохраняет максимальный уровень импульса, который затем преобразуется в адрес. Точное разделение по амплитуде является основным требованием для такой задачи, а метод последовательного приближения здесь совершенно не годится. Однократная интеграция используется также в преобразователях время-амплитуда.
Сетевые наводки
Есть несколько методов, использующих конденсатор для хранения соотношения между входным сигналом и опорным напряжением. Всё это — методы, усредняющие (интегрирующие) входной сигнал на фиксированном промежутке времени преобразования, что имеет два полезных свойства.
-
Использование одного конденсатора для сигнала и опорного напряжения позволяет не обращать внимания (до некоторой степени) на точность и стабильность ёмкости. Снижаются и требования к компаратору. Результат: при сравнимом качестве деталей точность выше, или можно получить такую же точность за меньшие деньги.
-
Выход пропорционален входному напряжению, усреднённому по фиксированному промежутку времени интегрирования. Если проводить интегрирование на промежутке, кратном периоду сетевой частоты, то преобразователь станет нечувствителен к сетевой наводке и её гармоникам во входном сигнале.
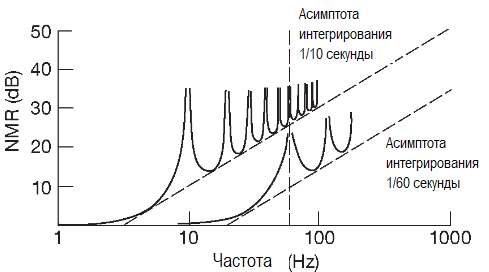
Избавиться от сетевой интерференции можно, только точно соблюдая пропорциональность времени интегрирования сетевой частоте, т.к. ошибка от даже доли процента сетевого периода приведёт к неполной компенсации наводок. Один из выходов — использование кварцевого генератора. Красивым вариантом будет фазовая автоподстройка для синхронизации рабочей частоты АЦП с сетевой частотой, снимающая все проблемы с подавлением наводок.
Недостатком интегрирующей техники является низкая по сравнению с последовательным приближением скорость преобразования.
Интегрирующие АЦП. Двойное и многостадийное интегрирование
Двойное интегрирование — красивая и активно используемая техника, которая позволяет избавиться от большей части проблем с конденсатором и компаратором. Основная идея представлена на рисунке.
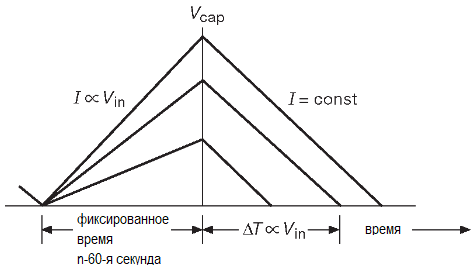
Сначала ток, точно пропорциональный входному напряжению, заряжает в течение определённого времени конденсатор. Затем конденсатор разряжается до нуля образцовым постоянным током. Время разряда пропорционально уровню входного напряжения и используется как сигнал разрешения счёта тактовых импульсов определённой частоты. Содержимое счётчика пропорционально входному напряжению.
Двойное интегрирование достигает очень высокой точности, не предъявляя жёстких требований к стабильности компонентов. В частности, не обязательно иметь точную величину ёмкости конденсатора, потому что цикл заряда и цикл разряда идут со скоростью, пропорциональной 1/C (и в уравнении взаимно компенсируются, т.е. сокращаются). Точно так же дрейф и смещение компаратора взаимно уничтожаются, т.к. конец цикла преобразования находится в той же точке и в тех же условиях, что и начало. В особо точных АЦП цикл измерения перемежается с циклом автоподстройки нуля, при котором на входе удерживается нулевое напряжение. Обе фазы проводятся одним и тем же интегратором и компаратором, поэтому вычитание результата «нулевого цикла» из результатов измерения полностью убирают все ошибки, связанные с нулевым уровнем, но не исправляют ошибок полной шкалы.
Отметим, что при двойном интегрировании не нужна даже особая стабильность и точность тактовой частоты. Время интегрирования в первой фазе формируется из целого числа циклов тактовой частоты. Если длительность цикла увеличится на 10%, то на столько же увеличится и уровень напряжения, которого достигнет напряжение на интеграторе. Значит, на столько же увеличится время полного разряда. Из-за того, что тактовая частота понизилась на 10% , число прошедших за время разряда циклов останется тем же! Единственная величина, требующая высокой стабильности в АЦП двойного интегрирования с автоподстройкой, — разрядный ток. Прецизионные источники напряжения и тока сделать относительно несложно, а уже он станет измерительным эталоном.
Преобразователи двойного интегрирования требуют высококачественных конденсаторов с наименьшей величиной диэлектрической абсорбции (эффект «памяти»). Наилучшими вариантами будут полипропиленовые, полистирольные и фторопластовые. Это неполярные конденсаторы, но внешнюю сторону фольги (она обозначается полоской) надо подключать к низкоимпедансной точке (выход ОУ интегратора). Чтобы минимизировать ошибки, значения R и C надо подбирать так, чтобы при измерении был задействован полный аналоговый диапазон интегратора. Высокая частота тактирования улучшает разрешение до тех пор, пока его период продолжает быть больше, чем время реакции компаратора.
При работе с АЦП двойного интегрирования (и вообще любого типа точных преобразователей) необходимо держать цифровой шум подальше от аналоговых цепей. В АЦП обычно имеется «аналоговая» и «цифровая» земля. Цифровые выводы АЦП очень полезно буферировать (например, с помощью ’541 — 8-канальных шинных формирователей и выводить их из Z-состояния только в момент считывания данных), отделяя от цифрового рёва микропроцессорной шины. В некоторых случаях приходится использовать оптические изоляторы. АЦП требуют хорошей фильтрации питающих линий в непосредственной близости от микросхемы. Да и вообще, следует поменьше шуметь в ходе преобразования, особенно в самый важный момент — вблизи точки срабатывания компаратора. Некоторые АЦП будто нарочно предоставляют пользователю возможность узнавать об окончании преобразования читая слово состояния. Так делать не надо! Используйте отдельную хорошо изолированную линию «BUSY».
Двойное интегрирование активно используется в цифровых мультиметрах. Этот метод недорог, точен и даёт хорошую повторяемость. Плюс он отлично подавляет сетевую наводку, да и другие виды интерференции тоже, а выходной код с ростом входного напряжения меняется строго монотонно. Но работает такой преобразователь медленно.
Стоит посмотреть на абсолютный рекорд среди интегрирующих АЦП — технику многостадийного интегрирования, придуманную фирмой Hewlett-Packard и реализованную в 8.5-разрядном вольтметре. Но сначала важный обзор методов использования аналоговых ключей.
Аналоговые ключи из стандартных логических семейств
Широко распространённые ключи ’4051 и ’4053 из состава семейства КМОП логики особенно удобны в аналоговых схемах, потому что у них есть линия отрицательного питания для аналогового канала и встроенные схемы сдвига уровней. Благодаря этому, микросхемы могут работать во всём диапазоне от -VEE до +VDD, а фактически заходя на 0.25 V за оба эти потенциала. Всего имеется три типа ключей. ’4053 — самый привлекательный (три независимых SPDT переключателя). ’4052 — пара мультиплексоров «4-в-1» и ’4051 (одиночный «8-в-1»). Привлекают они не только низкой ценой и большим числом производителей, но также высоким быстродействием и низкой ёмкостью.
Скажем, 74HC4053 имеет типичное сопротивление открытого канала 40 Ω, переключается за 20 ns и имеет ёмкость 8 pF. Если сравнивать её с микросхемами, официально предназначенными для переключения аналоговых сигналов, у ’4053 чуть меньший размах входного напряжения и нет защиты от статических разрядов (ESD). Если сравнивать с мощными КМОП переключателями, у ’4053 больше сопротивление открытого канала, но меньше ёмкость. Данный ключ хорошо вписывается в задачи переключения сигналов внутри одной печатной платы.
Одиночные версии SPDT ключей доступны в SOT23 и других компактных корпусах. Некоторые такие компоненты, например, ’1G3157 («1G» означает одиночный ключ) не имеют вывода отрицательного питания, поэтому не имеют обозначения «4053» в названии.
Рассмотрим парочку примеров, в которых ’4053 образует удобный мостик между цифровым и аналоговым миром. Второй пример с генератором пилообразного напряжения плавно переходит в тему преобразователей многостадийного интегрирования и сигма-дельта АЦП.
Программируемый генератор высоковольтных импульсов
Довольно удобно иметь генератор импульсов, сигнал на выходе которого можно включать логическим уровнем, и иметь независимую регулировку амплитуды. Последнюю задачу можно решать ЦАПом под управлением компьютера или набора ручек на панели. Простая схема делает всё изложенное, создавая сигналы с амплитудой до +100 V.
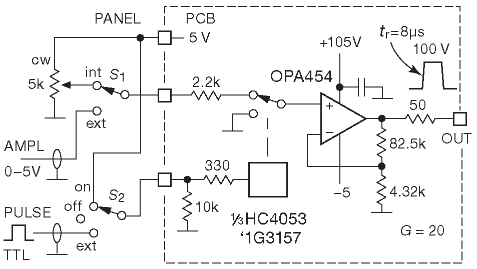
’4053 подаёт потенциал, выбираемый переключателем S1, на высоковольтный OPA454, включённый здесь неинвертирующим усилителем с G =20. ОУ не особо быстрый (время переключения около 10 μs), но зато недорог и может давать 100 mA в емкостную нагрузку. Его можно заменить на что-нибудь пошустрее, чтобы реализовать скоростные возможности ’4053 (∼20 ns). Переключатель со средней точкой S2 позволяет включать/выключать импульсы или подать на выход постоянный потенциал, чтобы проконтролировать амплитуду с помощью вольтметра.
Генератор пилообразного напряжения с переключаемым током
Схема использует очень хорошие характеристики аналоговых ключей ’4053.
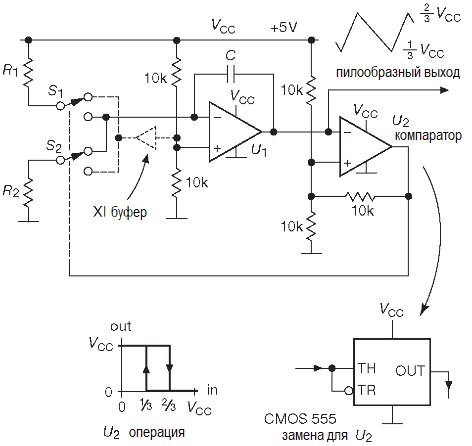
Предлагаемое переключение токов используется в АЦП многостадийного преобразования, который описывается немного дальше. Суммирующая точка интегратора на U1 заводится на среднюю точку источника питания (для работы от однополярного источника +5V). Ключи S1 и S2 типа ’HC4053, подключённые к тем же +5V, задают с помощью резисторов R1 и R2 наклон характеристики. Замыкание S1 включает источник VCC/2R1, вызывая спад напряжения интегратора, а S2 включает его рост. Пределы переключения компаратора равны 1/3 и 2/3 от VCC, ограничивая размах пилы величиной ΔV=VCC/3. Время роста напряжения равно tR=(2/3)R2C , время спада — tF=2/3R1C, а частота — f=1.5/C(R1+R2).
Скорости ключей и компаратора хватает для работы на частоте несколько мегагерц, для которой подойдут резисторы в килоомном диапазоне и конденсатор 100…500 pF. Такая ёмкость уже достаточно мала и заставляет думать об эффектах ёмкости ключей CSW, которые лежат в пределах 5…10 pF. Рассмотрим работу S1 в состоянии, показанном на схеме. Его ёмкость заряжается до +5V, после чего передаёт порцию заряда ΔQ=CSW·ΔV (где ΔV=VCC/2) в суммирующую точку, когда ключ перекидывается на нижний контакт. Такой перенос заряда вызывает скачок напряжения на выходе интегратора.
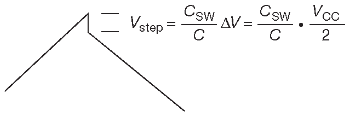
Средством борьбы с этим явлением будет удержание потенциала второго контакта на уровне суммирующей точки (часть схемы, нарисованная пунктиром).
Образцы для подражания: АЦП многостадийного преобразования фирмы Agilent
Учитывая предыдущий пример с аналоговым переключателем, разобраться с многостадийной техникой преобразования, применяемой в мультиметрах фирмы Agilent 34420 (7½ разрядов) и 3458A (8½ разрядов). Это старшие приборы инструментальных линеек Agilent, занимающие высшие ступени пьедестала уже более 20 лет. Упрощённый вариант схемы («Multislope III») используется в серии современных мультиметров, ставших промышленным стандартом — 34420 A (7½ разрядов), 34401A (6½ разрядов) и системе сбора данных 34970A (6½ разрядов). Здесь подробно разбирается работа схемы Multislope III и слегка затрагивается следующее поколение, явленное миру в 2006 — Multislope IV.
Основные принципы. Если коротко, то многостадийное преобразование стало развитием метода двойного интегрирования, т.е. многоциклового интегрирования с уравновешиванием заряда. Такой подход малочувствителен к параметрам конденсатора и учитывает накопленный остаток в конце цикла преобразования. В многостадийной технике сочетаются приёмы двойного и сигма-дельта интегрирования, а сама она является прямым переходом к сигма-дельта АЦП.
Блок-схема предельно проста и использует по большей части недорогие компоненты (исключая источники опорного напряжения и прецизионные резисторы).
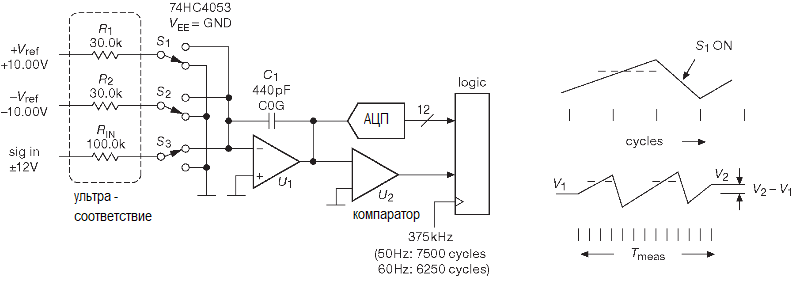
Схема включает интегратор U1, логическую часть, которая через компаратор U2 смотрит за выходом интегратора в каждом из тактов частоты 375 kHz и два ключа S1 и S2, балансирующие интегратор, закачивая и откачивая из него ток. АЦП с очень скромной точностью (12 разрядов) используется для считывания выхода интегратора в начале и конце общего цикла измерения.
Теперь, как это в принципе работает. Чтобы начать измерение, надо замкнуть ключ S3, что вызовет изменение напряжения на выходе интегратора вверх или вниз в соответствии с соотношением dV/dt= -Iin/C1= -Vin/Rin·C1. В каждом последующем такте системной частоты схема замыкает ключ S1 или S2 (согласно полярности напряжения на выходе интегратора), добавляя или вычитая образцовый ток от соответствующего опорного источника (±10 V/30 kΩ) и заставляя выход интегратора менять направление в сторону нулевого уровня. Это продолжается на протяжении достаточно большого числа тактов. Чтобы по максимуму подавить наводки от сетевой частоты желательно использовать в качестве системного времени какую-либо частоту, кратную сетевой, например, чтобы 6250 циклов соответствовало 1/60 или 1/50 секунды. В результате система получает число положительных (nP) и отрицательных (nM) циклов. Это даёт первое приближение среднего входного напряжения за время измерения.
Всё это пока не поражает точностью: при максимальном входном сигнале ±12 V получается nM – nP или ±2250 отсчётов, что соответствует 12-разрядному разрешению. А теперь следите за руками. Из-за того, что измерение продолжалось какое-то целое число тактов, не прерываясь событиями наподобие равенства нулю, как в двойном интегрировании, напряжение на интеграторе содержит дополнительные данные и позволяет провести уточнение дробной части результата, как это происходит в вереньерных шкалах. Именно для этого нужен 12-разрядный АЦП, изображенный на блок-схеме. Он используется для измерения уровня на интеграторе перед началом цикла измерения и по его окончании. Для 12-разрядного АЦП это даёт дополнительные 512 уровней разрешения внутри LSB исходной системы первого приближения, т.е. добавляет 9 бит к 12, полученным на первом этапе. В итоге получаем результат с точностью 21 разряд.
Для десяти циклов один цикл, он же «вереньерная часть» составляет 1/10, для ста — 1/100 и т.д. Для однотактного измерения всю информацию о сигнале будет содержать «вереньерная часть» ΔV.
Некоторые подробности. Это только общий обзор техники непрерывного преобразования. Здесь много о чём можно говорить: в деталях прячется целый табун дьяволов. Метод можно улучшать множеством доступных способов, добиваясь наибольшей точности в рамках исходной идеи. Здесь авторы наступят друг другу на горло и сократят комментарии до краткой выжимки из наиболее интересных и поучительных подробностей.
Некритичные компоненты
В качестве S1— S3 Agilent использовал обычные микросхемы 74HC4053 производства NXP, а в качестве C1 — массовый керамический конденсатор для поверхностного монтажа со стабильным диэлектриком NP0/C0G фирмы AVX. Этот тип конденсаторов очень дёшев, имеет малый температурный коэффициент 30 ppm/°C и пренебрежимо малую диэлектрическую абсорбцию (эффект «памяти»), особенно при таких временах переключения. Высокая точность и стабильность компаратора и АЦП тоже не нужна.
Критичные компоненты
Источник опорного напряжения устанавливает шкалу измерения и должен иметь высокую стабильность. В приборе используется один 7-вольтовый опорный источник на основе стабилитрона и два прецизионный операционных усилителя, чтобы получить 10.0 V опорного напряжения. Конкретная величина потенциала «10.0 V» неважна, т.к. будет учтена при калибровке, но это напряжение обязано быть стабильным, чтобы калибровочные значения как можно дольше отражали реальное положение вещей.
Ещё одним критичным компонентом является резисторная сборка R1 – R3 (масштабирующие резисторы в опорном источнике) и ОУ, на котором собран интегратор. Последний представляет собой композитный усилитель (OP27+AD711), имеющий высокое петлевое усиление в сочетании с низким напряжением смещения.
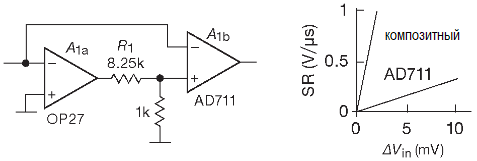
В качестве набора резисторов используется специальная точно подогнанная сборка, с хорошей стабильностью отношения. Здесь очень важен дрейф (по времени и температуре) отношения резисторов, потому что небольшое исходное расхождение также убирается заводской калибровкой.
Не показанный, но тоже важный, входной усилитель с программируемым усилением. Его усиление должно иметь высокую точность и стабильность, чтобы сохранять параметры настройки и калибровки.
Переключатели
Ключи 74HC4053 используются в схеме распределения тока. Ключи включены так, чтобы напряжения на всех выводах ключа поддерживались на близком к нулевому уровне. ’4053 используются только для переключения токов, чтобы повысить или снизить скорость роста напряжения на выходе интегратора, которая находится в точной зависимости от входного напряжения. Сопротивление открытого канала, конечно, оказывает на токи заметное влияние, но пока Ron ключей хорошо согласовано, стабильно и мало по сравнению с R1 – R3, его влияние можно учесть калибровочными циклами, которые прибор проводит в автоматическом режиме перед каждым измерением.
Для микросхем производства NXP, которые стоят в приборе, Ron имеет типовое значение 85 Ω и согласовано до 8 Ω. Очень важной особенностью является разрыв соединения перед переключением, благодаря чему выводы никогда не бывают закорочены (что замкнуло бы внутреннюю суммирующую точку на землю и проявилось бы на входе как дифференциальный сигнал, равный напряжению смещения ОУ). Одни производители упоминают данный факт в документации, другие — нет. Например, паспортные данные NXP указывают времена включения и выключения, разница между которыми и определяет время разрыва цепи 4 ns. Но прямо данное время не указывается, а, скажем, в справочных данных на DG4053 фирмы Siliconix есть параметр «Break-Before-Make Time Delay» tD=6 ns (тип.) или 2 ns (мин.).
Калибровка
Простая схема переключения токов очень удобна для калибровки и устранения эффектов неточного согласования резисторов, неточности опорного напряжения, смещений ОУ, задержек ключей и т.п. Например, когда S3 выключается (т.е. входной сигнал отсутствует), для S1 и S2 можно провести несколько последовательных циклов переключения. Накопившийся в результате этого действия потенциал ΔV на выходе интегратора отражает разницу положительного и отрицательного токов. По аналогии, подав на вход VREF, вместо сигнала, и проведя измерение можно выяснить отклонение опорных токов от номинальной величины. Перед каждым измерением с наибольшей точностью, когда разница имеет значение, прибор проводит серию таких калибровок. Естественно, обнаружить таким методом дрейф опорного источника нельзя. Чтобы поверять его, нужен внешний источник образцового напряжения, и на этом делают деньги поверочные службы.
Интервал измерений
Ранее в примере мелькала цифра Tmeas, равная одному периоду сетевой частоты или 6250 циклам частоты 375 kHz, или 1/60 (1/50) сек. Время измерения есть целое число циклов PLC (NPLC). Оно позволяет подавить наводку, а итоговая точность зависит от общей продолжительности цикла измерения. Но, согласно данным таблицы, можно делать быстрые измерения, если несколько поступиться точностью и степенью подавления сетевых наводок. Возможен также режим непрерывного измерения, при котором ключ S3 всегда замкнут (в этом режиме время измерения регулируется извне).
«Многомногостадийное измерение»
Вернёмся к исходному примеру — 8.5-разрядному мультиметру HP3458, в корне изменившему расклад сил. В нём есть четыре набора входных резисторов и ключей. Это позволяет очень сильно (почти в 600 раз) понизить скорость нарастания при приближении к моменту окончания измерения. Причём необычен отказ от использования красивого приёма — измерения остатка напряжения на интеграторе с помощью АЦП, а вместо этого проводится его линейный разряд до 0В.
Прочее
Остаётся ещё масса деталей итоговой реализации этой методики, которые описаны в руководстве по обслуживанию, статьях из HP Journal, и патентах. Например, данная техника предполагает только борьбу с насыщением интегратора, а значит, можно использовать больше одного компаратора и включать токовые ключи S1 и S2, только чтобы удерживать интегратор от насыщения. Это уменьшает число циклов переключения и связанных с ними ошибок. Есть и необычные схемные решения: ферритовые бусины на аналоговых входах ’4053 и конденсатор между суммирующей точкой интегратора и землёй.
Эволюция метода
В 2006 году Agilent представил более быструю линейку «Multislope IV» — модели 34410 A, 34411A и 34972A с USB и Ethernet на борту. Стоят они дороже, а цена на классические модели 34401A и 34970A была снижена. Заявлены модели 34460A и 34461A с графическими дисплеями и специальными интерфейсами для датчиков (34461A имеет такую же скорость измерения, как и 34401A). 34420 A замены не получил и остался единственным 7.5-разрядным (20 ppm) прибором в линейке.
От многостадийных к сигма-дельта. Многостадийные АЦП плавно подводят нас к очень широко используемой технике сигма-дельта преобразования, с которой имеют много общего. Оба используют интегрирование, при котором входной сигнал на периодической основе сравнивается с выходным напряжением интегратора. Как будет видно чуть позднее, в глубине сигма-дельта техники таятся некоторые тонкие отличия, позволяющие достигать фантастических параметров.
Сигма-дельта
Вот, наконец, дело дошло до самого лучшего метода аналого-цифрового преобразования — «сигма-дельта». Это довольно сложная тема, но, разобравшись в ней, можно понять, как достигаются параметры самых лучших по разрешению и точности (например, монотонность в диапазоне 31 разряда и более) «вольтметров» и звуковых ускорителей. Их архитектура с избыточной дискретизацией сильно упрощает входные спектральные фильтры и выполняет некоторые магические действия по удалению шума из рабочей полосы. И всё это за весьма скромные деньги. Сначала будут рассмотрены базовые принципы, а затем разобраны методы достижения гораздо более высоких параметров, нежели можно было бы ожидать.
Простая сигма-дельта система для подсчёта экспозиционной дозы солнечного света
Чтобы было с чего начинать, возвратимся к легенде пляжного приборостроения — мониторе экспозиционной дозы. Теперь экспонометр будет реализован на сигма-дельта интеграторе. Схема приведена на рисунке:
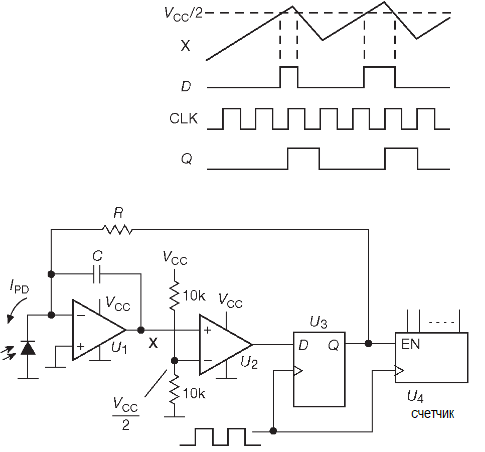
Используется вариант с синхронным дозированием заряда, который работает так же, как многостадийный интегратор. Такой способ проще, потому что не использует финальный уточняющий этап: общая доза солнечного освещения набирается простым подсчётом числа тактов, в течение которых потребовалось закачивать измерительный ток (здесь VCC/R), чтобы уравновесить вытекающий ток фотодиода IPD. Внешнее устройство сигнализирует, когда достигается установленный пользователем уровень. Сигнальная схема здесь не показана, но читатель, который знакомился с книгой последовательно, хорошо знает, как она может выглядеть.
Данное устройство представляет собой простейший сигма-дельта интегратор. Он накапливает (сигма) различия (дельта) между аналоговым входом и образцовым током, которые складываются в суммирующей точке. Оно может стать законченным аналого-цифровым преобразователем (а не простым интегратором), если добавить пару блоков:
- схему сброса перед началом работы
- элемент, считывающий показания счётчика на регулярной основе с интервалом, существенно превышающим период тактирования.
На самом деле схема может работать как АЦП и так, но на практике возможно достижение гораздо более высоких параметров, если простой счётчик заменить цифровым фильтром. Дальнейшего улучшения можно добиться каскадированием нескольких блоков «разностный усилитель — интегратор».
Все указанные улучшения будут внесены совсем скоро, но сначала надо разобраться, как работает этот простой пример.
U1 — ОУ с однополярным питанием, который может работать с сигналами вплоть до отрицательного потенциала (и даже чуть ниже). U2 — компаратор с активной подтяжкой. В низкоскоростных схемах, подобных представленной, можно использовать сдвоенный RRIO усилитель LMC6482, который работает от тех же +3.3 или +5V, что и цифровые схемы, и очень нравится авторам. Напряжение на выходе интегратора растёт пропорционально току фотодиода IPD до тех пор, пока не превысит уровень VCC/2 . После прихода очередного активного фронта напряжение на выходе интегратора начинает снижаться со скоростью, пропорциональной общему току VCC/R -IPD. В результате активная часть периода (D), т.е. та часть цикла, когда его выход «Q» триггера U3 находится в состоянии ВЫСОКИЙ, усредняется по многим циклам: D=IPDR/VCC или IPD=DVCC/R. Длительность активной фазы цикла получается из числа N (содержимого счётчика U4 и времени измерения T, т.е. D= N/fclk T. Отметим, что результат не зависит от порогового напряжения компаратора (здесь VCC/2) или напряжения на выходе интегратора (точка «X»).
Ниже приводится правильная последовательность разработки.
-
Выбрать период тактирования, который гораздо короче, нежели ожидаемое время экспонирования, например, fclk=10 Hz. Можно и больше, но тогда потребуется более длинный счётчик.
-
Выбрать номинал R так, чтобы ток через него был больше, чем предполагаемый входной ток полной шкалы: для IFS=1 μA и VCC =5V номинал R должен быть меньше 5 MΩ .
-
Выбрать C так, чтобы изменение напряжения на выходе интегратора за время одного такта было меньше с некоторым запасом, чем уровень опорного напряжения компаратора.
Для схемы, изображенной выше, можно выбрать fclk =10 Hz, R=3.3MΩ, C =100 nF , при которых напряжение в точке «X» изменяется за время одного цикла не более, чем на 1.5 V (при минимальном IPD), а значит, не войдёт в насыщение. Пиковая частота счёта равна тактовой частоте, а средняя скорость счёта несколько ниже (здесь 0.6fclk), т.е. 16-разрядного счётчика будет достаточно для накопления экспозиционной дозы, эквивалентной двум часам солнечного света.
Несколько важных моментов.
-
Общая калибровка зависит от напряжения питания VCC, которое считается стабильным и равным +5V. Кроме того, в схеме используется способность КМОП логики достигать уровней питания.
-
Выходной сигнал интегратора не обязательно является периодическим. Он колеблется вокруг опорного уровня VCC/2, и единственное, что можно гарантировать, он изменит направление движения на следующем фронте, появившемся после пересечения уровня опорного напряжения. Такое поведение нисколько не снижает общую точность, усреднённую по множеству тактов. Метод интеграции сигма-дельта систем гарантирует их от переполнения любого вида.
-
Динамический диапазон преобразователя ограничен напряжением смещения ОУ, который вызывает появление ошибки входного тока Vos/R. Для схемы выше это 2nA в худшем случае для группы «-A». Входной ток ОУ (4 pA max при максимальной температуре) совершенно незначителен по сравнению с величиной ошибки от смещения.
-
Динамический диапазон можно сильно расширить, если заменить резистор R на переключаемый источник тока, предполагается, что входной сигнал остаётся токовым.
-
Точность компаратора U2 значения не имеет. Его вообще можно выкинуть, используя в качестве порогового входной логический уровень триггера. То же самое можно сказать о точности образцового напряжения: VCC/2 выбрано просто для удобства.
Всё, что вы хотели знать о сигма-дельта преобразовании, но стеснялись спросить. Как уже говорилось, сигма-дельта интегратор превращается в преобразователь среднего входного напряжения, если снимать накапливающиеся в счётчике числа на регулярной основе — с периодом Tmeas. Естественно, для достижения приличного разрешения время измерения должно быть гораздо больше, чем период тактовой частоты. Это означает, что если требуется АЦП со скоростью преобразования 100 ksps (период опроса со сбросом 10 μs), то для частоты 10 MHz максимальное число, которое счётчик сможет накопить за 10 μs будет равно 100, что чуть не дотягивает до 7-разрядной точности. Чтобы повысить её до 16 разрядов потребуется тактовая частота 216×100 kHz или 6.5536 GHz!
Это не вдохновляет. Идея «1-разрядного» АЦП оказалась дохлой, а весь выход — поток битов, которые можно засунуть в счётчик. Но ведь известно, что идея рабочая. Существует масса 16-разрядных сигма-дельта АЦП, оцифровывающих звуковой сигнал со скоростью 96 ksps. Есть даже 20- и более разрядные, работающие с такой частотой.
ΣΔ АЦП и ЦАПы
Как будет ясно из дальнейшего ΣΔ (или ΔΣ) преобразование может идти в любом направлении: как из D в A, так и обратно. В настоящее время ΣΔ ЦАПы используются в первую очередь в звуковой области, где очень важна их отличная линейность, монотонность и низкая цена. Типовой звуковой ΣΔ ЦАП может иметь шесть 24-разрядных 192 ksps каналов с эффективным динамическим диапазоном 114 dB. А ΣΔ АЦП закрывают широкий спектр применений от точных 24-разрядных медленных преобразователей до звуковых АЦП высокого разрешения (24 бита, 96 ksps) и быстрых преобразователей с невероятными параметрами (16 разрядов 20 Msps).
В дальнейшей дискуссии говорится преимущественно о ΣΔ АЦП как из-за их важности, так и из-за того, что в их конструкции находят применение близкие к идеальным цифровым фильтрам.
На этом пути придётся разобраться с вопросом, напоминающим большой розыгрыш, а именно:
«Как получается, что 1-разрядное преобразование, идущее с несколько более высокой скоростью дискретизации (скажем, в 64 раза большей, чем обычный предел Найквиста 2 fmax даёт на выходе цифровой код высокой точности, например, 16 разрядов?»
Мысль можно сформулировать иначе: от 1-разрядного преобразования с 64-кратной избыточной передискретизацией можно ожидать итогового цифрового кода с разрядностью 6 бит (26 =64), не больше. Дальше станет ясно, что это не просто возможно, но что можно достичь гораздо лучшего результата (именно это требуется в обработке звука).
Собственно процесс ΣΔ преобразования
Базовые этапы ΣΔ преобразования показаны на рисунке
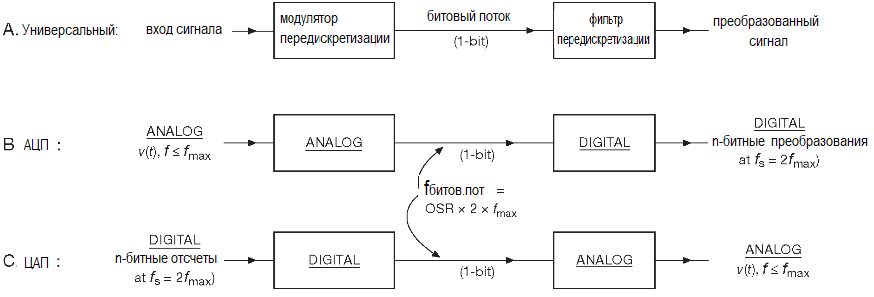
Входной сигнал с полосой, ограниченной частотой fmax (обычно это делается спектральным фильтром), преобразуется в битовый поток с помощью модулятора. Этот последний тактируется с частотой, кратной частоте предела Найквиста 2fmax, и даёт на выходе поток с частотой fbit = OSR × 2fmax, где OSR — коэффициент передискретизации. Битовый поток является только промежуточным этапом на пути получения результата: его ещё необходимо пропустить через ФНЧ.
Отметим, что и модулятор, и ФНЧ могут быть как аналоговыми, так и цифровыми. Тип зависит от конвертора: сигма-дельта АЦП состоит из аналогового модулятора и цифрового фильтра, а ЦАП — из цифрового модулятора и аналогового фильтра. Из сказанного следует, что сначала будет рассмотрен модулятор.
Модулятор. Так или иначе, но ФНЧ — это «просто фильтр», который ограничивает полосу входного сигнала. Всё самое интересное (и загадочное) творится в модуляторе. На рисунке приведена блок-схема передискретизирующего модулятора «первого порядка»
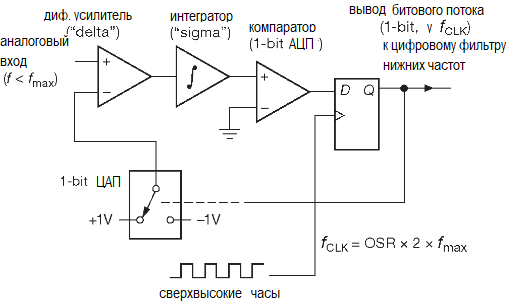
Модулятор получает на входе аналоговый сигнал амплитудой от –1 до +1V, лежащий в полосе с верхней границей fmax и создающий 1-разрядный битовый поток с частотой в OSR раз большей, чем предел Найквиста 2fmax.
В каждом цикле тактовой частоты текущее значение битовой последовательности, преобразованное в аналоговое напряжение (здесь ±1V), вычитается из входного сигнала, а разница интегрируется (самым обычным аналоговым интегратором, в данном случае неинвертирующим) и подаётся на компаратор с запоминанием. Усиление в интеграторе выбирается так, чтобы для сигнала полной шкалы на входе (здесь +1V) изменение выходного уровня за время одного периода тактовой частоты равнялось напряжению полной шкалы (+1V). Таким образом, интегратор можно рассматривать как «аналоговый аккумулятор»: для фиксированного входного напряжения V его выход увеличивается на V за один период тактового сигнала.
В результате получается быстрый поток нулей и единиц (на частоте, скажем, в 64 раза большей, чем обычная частота выборки 2fmax), соответствующий относительно медленному (в данном случае как минимум в 64 раза медленнее) изменению входного сигнала. Если условиться, что биты имеют уровень ±1V, получаем, что модулятор создаёт поток, чьё среднее значение соответствует входному сигналу. Данную схему можно рассматривать как петлю отрицательной обратной связи, которая стремится минимизировать среднюю (т.е. интегральную) ошибку между входным сигналом и выходным потоком (сравнение идёт в аналоговой форме, благодаря обратному преобразованию потока с помощью «1-разрядного ЦАПа»). Если взглянуть на схему внимательнее, то можно обнаружить, что происходит совершенно ужасная вещь: такт за тактом входной поток просто мечется между двумя предельными уровнями. Как точно заметил Боб Адамс: «Передискретизирующие преобразователи увеличивают разрешение не путём уменьшения ошибки между аналоговым входом и цифровым выходом, а заставляя ошибку появляться чаще.»
Динамический диапазон (разрешение) АЦП. Выходной цифровой ФНЧ создаёт цифровые n-разрядные числа, которые выводятся наружу. Используются обычно КИХ (FIR) фильтры.
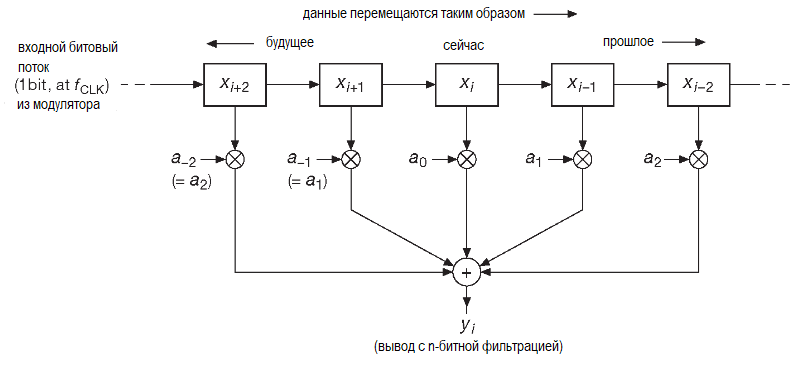
В этом случае 1-разрядный сдвиговый регистр с проходящими сквозь него единицами и нулями включает и выключает набор постоянных коэффициентов, которые суммируются с данными, получая в итоге n-разрядные выходные значения. Из-за того, что данные выходят из фильтра со скоростью передискретизации (т.е. в OSR раз быстрее, чем надо) их приходится подвергать прореживанию. Проще всего просто выкинуть лишние значения, оставляя только одно число на OSR тактов («###децимация»).
Если подойти к вопросу прямолинейно, то увеличение разрешения достигается усреднением массы 1-разрядных значений на каждой половине цикла наибольшей частоты входного спектра. Усреднённое значение битового поток отслеживает входной сигнал, и эта картина соответствует описанию Боба Адамса, а значит, всё хорошо.
Или не совсем? Рассмотрим пример: предположим, что оцифровывается звук с частотой fmax=20 kHz. Обычное АЦП (например, последовательного приближения) может работать со скоростью 48 ksps, оставляя удобный запас над предельной частотой 40 kHz. Теперь возьмём ΣΔ АЦП с типичным коэффициентом передискретизации 64, т.е. модулятор крутится на 64×48 kHz = 3.072 Msps, создавая 1-разрядный битовый поток с такой же скоростью. Фильтруем этот поток, допустим, фильтром «скользящего среднего». Цифровая фильтрация обрабатывает 64 последовательных бита одновременно. На что будет похож выход? Это просто. Когда усредняется 64 бита, на выходе может получиться только 64 65 возможных значений, т.е. в итоге получилось АЦП с разрядностью жалких 6 бит.
Каждый бит — отдельное значение, следовательно, усредняя сложением 64 однобитовых числа, получаем: если на входе все нули, выход =0, если все единицы =64. С мест поправляют: если есть состояния «0» и «64», то всего состояний 65.
Следуя той же схеме, чтобы достичь 16-разрядной точности, требуется обработать 216 = 65536 значений, что потребует выборки со скоростью приблизительно 3 гигагерца! Сигма-дельта преобразование, оказывается, не такая хорошая штука.
Что же происходит на самом деле? (Рассмотрение во временной области). Ответ на парадокс можно дать несколькими способами. В литературе по теме обычно говорится, что работа схемы квантования имеет две составляющие: идеальное преобразование и привнесение широкополосного «шума» (он состоит из разницы между реальным аналоговым сигналом и копией, восстановленной из получившейся 1-разрядной последовательности). Этот «привнесённый шум квантования» имеет широкий спектр (спасибо высокой частоте передискретизации), который заходит вверх за частоту тактирования. Важнее всего в этом процессе то, что шум квантования (который так и остаётся в выходных данных) минимален на низких частотах и растёт на высоких. Благодаря процессу модуляции большая его часть находится сильно выше fmax.
Полоса преобразования в 64 раза шире, чем 2fmax, а следовательно, даже при равномерном распределении шума в полосу сигнала с границей fmax попадёт 1/128 от общего шума квантования.
Такой спектральный состав позволяет выходному ФНЧ работать селективным подавителем большей части шума квантования в выходном потоке, сохраняя сам преобразованный сигнал. В итоге имеем гораздо большее разрешение и динамический диапазон, чем ожидалось при «тупом» рассмотрении процесса.
Приведённые выше рассуждения достаточно корректны, но не вполне удовлетворительны. Хотелось бы рассмотреть секреты динамического диапазона АЦП во временной области, не затрагивая частотную. Но в данном месте вышла некоторая заминка. Чтение опусов с названиями «Сигма-дельта АЦП раскрывают тайны» и «Сигма-дельта АЦП для идиотов» не помогло. Все такие публикации имеют слабое место: «..сигма-дельта преобразователи преодолевают данное ограничение с помощью техники сдвига шума..» и «..можно увидеть, как модулятор сдвигает шум в область высоких частот, позволяя получить более высокое разрешение» (выдержки из обеих указанных статей).
Вот как можно объяснить всё это в терминах временной области. Во-первых, ФНЧ не просто усредняет серию импульсов из живого битового потока. Вместо этого, он взвешивает каждое 1-разрядное значение с аккуратно подобранным коэффициентами, чтобы достичь наилучших параметров фильтрации. Из-за того, что отдельные отсчёты получают различный вес, появляется гораздо больше вариантов, чем просто 64 значения как в примере выше. Более того, типичный КИХ фильтр взвешивает и суммирует гораздо больше отсчётов и за гораздо большее время, чем период частоты передискретизации, т.е. уходя далеко за «интервал Найквиста» (под которым подразумевается половина периода частоты fmax). Для 64-кратной передискретизации можно использовать цифровую фильтрацию по тысячам точек (отдельным последовательным значениям внутри битового потока) каждый со своим множителем, размазывая каждый по десяткам интервалов Найквиста, чтобы получить в итоге окончательное (прореженное) число. Такой вариант достижения высоких разрешений как минимум несколько правдоподобнее, чем простое усреднение.
Продолжая в том же ключе, то, что каждый бит потока влияет на много прореженных итоговых n-разрядных выходных слов, ничего не означает. С конспирологической точки зрения, вполне правдоподобна версия, что модулятор столь умно придуман, что может создавать такой поток битов, который после прохождения через фильтр нижних частот преобразуется в n-разрядные выходные числа с очень сильно улучшенным динамическим диапазоном. То есть, не будет большой ошибкой сказать, что «всё дело в волшебном модуляторе». Но тогда вопрос надо ставить иначе: «Как столь примитивная железка (аналоговый сигма-дельта модулятор) может решать столь сложную задачу?»
Как уже отмечалось, обычно при описании сигма-дельта преобразователей говорят о «перераспределении шума» в частотной области. «Шум квантования» с плоским спектром, появляющийся в дискретизаторе «выдавливается» в область высших частот. По большей части в зону за пределами частоты выборки. Меньшее количество внутриполосного шума ведёт к увеличению точности. Вот, собственно, и все объяснения.
Итак, в сигма-дельта АЦП первого порядка шум квантования ослабляется на низких частотах, его спектр линейно расширяется вплоть до частоты передискретизации. Но частота-то избыточная, т.е. интересующий пользователя спектр расположен в низкочастотном углу (и занимает полосу согласно степени передискретизации). Другими словами, большая часть шума квантования лежит за пределами полосы сигнала. В модуляторах высоких порядков данный эффект проявляется отчётливее: график шума в модуляторе второго порядка квадратичный, кубический для третьего и т.д. Отсюда и процитированное заключение: «Сигма-дельта АЦП достигают такой точности, выдавливая шум в область высоких частот». Возможно, формулы не слишком возбуждают, но, по крайней мере, они показывают, что происходит в простой и однозначной форме.
Собственно процесс ΣΔ преобразования
И из правдоподобных аргументов во временной области, и из прямых расчётов в частотной выходит, что модулятор является ключом к высоким параметрам сигма-дельта АЦП. В их число входит способность оцифровывать аналоговый сигнал с разрешением заметно более высоким, чем коэффициент передискретизации. Более того, данный показатель растёт по мере роста сложности модулятора. Современные АЦП используют модуляторы «высоких порядков», что означает, единственный разностный усилитель и интегратор заменяется несколькими последовательными звеньями из разностного усилителя и интегратора каждое. Все звенья используют общий битовый поток
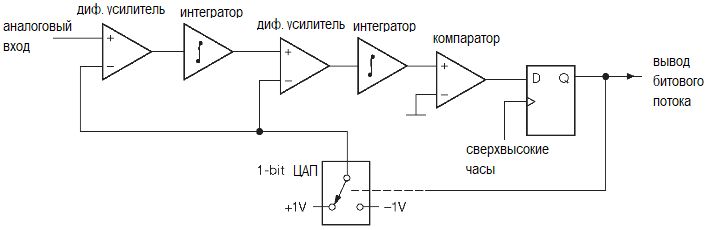
Модуляторы высоких порядков находят широкое применение, потому что расширяют динамический диапазон без увеличения коэффициента передискретизации. Кроме того, они в большей степени подавляют тон паузы, которые портят жизнь модуляторам первого порядка.
Хотя рассуждения о временной области могут быть полезны (разве что для обоснования заявленного отличного динамического диапазона), любая серьёзная аналитика должна использовать рассмотрение в частотном диапазоне. Последний показывает, что модуляторы высоких порядков (собранные на m интеграторах) изменяют спектр шума так, что внутриполосный шум квантования (от постоянного тока доfmax) подавляется в степени OSR [m+0.5], где m — порядок модулятора. Или иначе, каждое удвоение коэффициента передискретизации снижает шум квантования в такой степени, как если бы динамический диапазон увеличился на m+1/2 бита. График показывает теоретически возможный динамический диапазон сигма-дельта АЦП как функцию от коэффициента передискретизации и порядка модулятора.
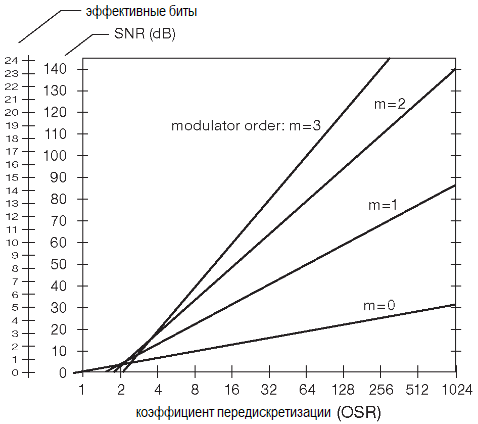
Другим способом увеличения динамического диапазона, скорости или обоих параметров разом является построение модулятора, создающего поток «слов», каждое из которых имеет разрядность больше одного бита.
Моделирование
Предположим, есть желание увидеть, как сигналы проходят через сигма-дельта АЦП. А именно, хочется получить поток битов из случайного аналогового сигнала и итоговые числа (изображаемые в виде точек на одном графике с входным сигналом), причём делать это в частотной области, где перераспределение должно быть хорошо заметно.
Подобную задачу можно решить в пакете Mathematica®, используя следующие шаги.
-
Создаётся псевдослучайный сигнал с плоским спектром и гауссовым распределением амплитуд и выводится для 8192 последовательных промежутков времени.
-
Отфильтровывается идеальным ФНЧ со срезом на уровне 1/8 от исходной частоты и нормализуется, чтобы амплитуда попала в диапазон ±1. Это будет «аналоговый входной сигнал». Максимальная частота полученного сигнала обозначается как частота Найквиста fnyq.
-
«Входной сигнал» превращается в поток битов со значениями ±1 с помощью моделирования передискретизирующего сигма-дельта модулятора первого порядка (в котором интегратор выполнен в виде отдельного цифрового аккумулятора). В примере взят коэффициент передискретизации 8×: частота тактирования будет равна fclk = 8 × 2fnyq fclk должна быть кратна 2fnyq.
-
Полученный битовый поток рассматривается как аналоговый сигнал и пропускается через ФНЧ с такой же характеристикой, как и фильтр на шаге (b), чтобы получить выходные отсчёты. Выходные отсчёты появляются с частотой 8× и требуют прореживания (например, использованием только каждого восьмого бита), чтобы превратиться в выходной сигнал АЦП с частотой 1× (т.е. в два раза большей, чем fnyq — максимальной частоты во входном сигнале).
На рисунке показан характерный кусок более длинного результата моделирования, иллюстрирующий картину во временной области.
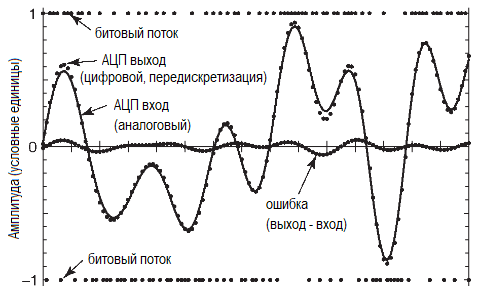
Отметки на горизонтальной оси соответствуют частоте 1× (пределу Найквиста), а отдельные точки следуют с частотой 8×. Входной сигнал — извилистая непрерывная линия, проходящая почти по точкам.
Отметки на горизонтальной оси соответствуют частоте 1× (пределу Найквиста), а отдельные точки следуют с частотой 8×. Входной сигнал — извилистая непрерывная линия, проходящая почти по точкам.
Точки — представление выходных чисел, в которых уже есть ошибка квантования, в аналоговом виде.
Поток битов показан там же в виде точек на уровнях ±1. Наконец, ошибка (цифровой выход минус аналоговый вход в каждой точке тактовой частоты 8×) — линия точек малой амплитуды. По этим графикам можно на глаз прикинуть точность преобразования. Здесь она составляет 6% от полной амплитуды и превращается в динамический диапазон SNR 16:1 или 24.
Из того же моделирования можно вывести частотный спектр входного сигнала и цифрового результата и разницу между ними (сигнал ошибки), см. рисунок
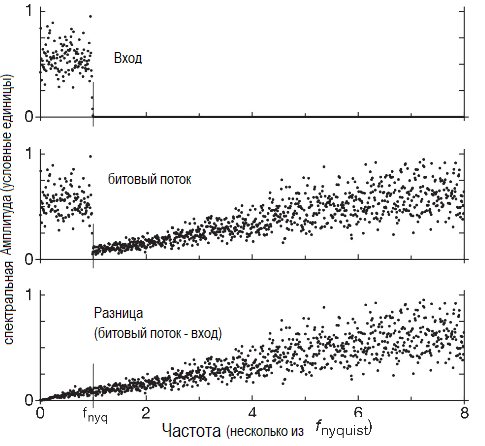
Спектр простирается до половины частоты передискретизации, т.е. до границы в 4 × 2fnyq (до 4×). Верхний график показывает плоский входной спектр, чётко срезанный идеальным фильтром на частоте fnyq. Средний график — спектр битового потока, в этом случае он рассматривается как аналоговое напряжение, которое предположительно содержит копию входного сигнала и какое-то количество шума квантования. Спектр простирается до частоты передискретизации (на рисунке обрезан на уровне «4×»). По рисунку видно, что картина соответствует ожиданиям: почти точное повторение спектра до частоты fnyq и дополнительный шум квантования, увеличивающийся пропорционально частоте. Чтобы оценить разницу, надо вычистить разность выходного и входного спектров — нижний график. Виден почти линейный рост от постоянного тока и до границы графика. Весь шум выше частоты fnyq будет вырезан выходным цифровым фильтром АЦП, через который проходит весь битовый поток. При этом фильтр работает с потоком как с набором цифровых значений.
Линейный характер спектра шума квантования в модуляторе первого порядка меняется на квадратичный в модуляторе второго порядка, и т.д. по мере роста порядка. Изменение характера графика соответствует улучшению точности (или SNR, или эффективному числу разрядов).
Что там у ЦАПов?
Как указывалось ранее, та же схема низкочастотной фильтрации битового потока, но порождаемого уже с помощью цифрового модулятора, используется в сигма-дельта цифро-аналоговых преобразователях.
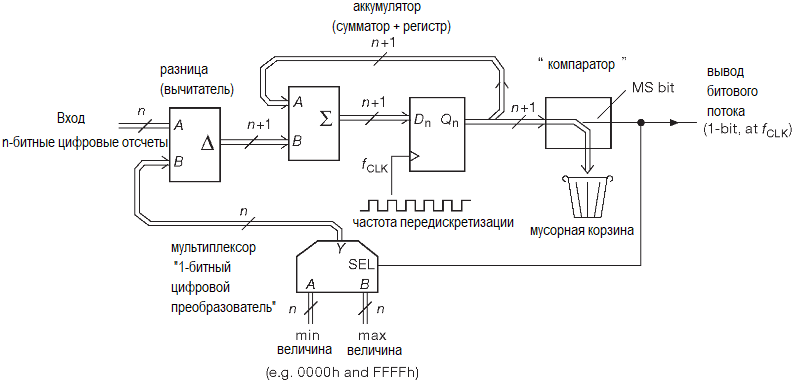
В качестве входного сигнала такой модулятор принимает n-разрядные слова. Если сравнить его с аналоговым коллегой в АЦП, рассмотренном выше, то можно обнаружить, что разностный усилитель превратился в цифровое вычитающее устройство, а интегратор — в цифровой же аккумулятор. На каждом такте его текущее содержимое складывается с новым входным словом и вновь защёлкивается до следующего такта. Аналоговый компаратор заменён на цифровой вариант, который в наиболее простом случае передаёт далее по схеме знаковый разряд (или MSB в случае беззнакового кода со смещением). В этой точке образуется поток 1-разрядных слов, которые сообщают, больше или меньше середины шкалы было содержимое аккумуляторе. Наконец, 1-разрядный ЦАП заменило «n-разрядное АЦП», которое просто подаёт на сумматор максимальное или минимальное n-разрядное число, соответствующее выходному 1-разрядному значению в нужной кодировке. Для n-разрядного беззнакового кода со смещением это будут числа из n нулей или n единиц, т.е. для 16 разрядов — 0x0000 или 0xFFFF).
Так же, как и в случае аналогового модулятора в АЦП, цифровой модулятор в ЦАПе может иметь порядок отличный от единицы. Для этого надо каскадировать связку «вычитатель-аккумулятор» (т.е. цифровой ФНЧ). Так же, как и в аналоговой схеме, модулятор не ограничивается 1-битными выходными числами. Он может, и эта опция используется достаточно часто, выдавать поток многоразрядных слов. В таком варианте несколько старших битов направляются как в выходной поток, так и в цепь цифровой обратной связи. Для 2-разрядного модулятора (четыре уровня) 2-разрядные выходные слова будут:
-
преобразованы в 4-уровневый аналоговый сигнал (например, с помощью резистивного делителя), а тот, в свою очередь, пропущен через аналоговый ФНЧ, чтобы получить в итоге аналоговое выходное напряжение;
-
одновременно превращёны в одно из четырёх n-разрядных значений перекрывающих весь диапазон чисел (для 16 разрядов это могут быть 0x0000, 0x5555, 0xAAAA и 0xFFFF) и поданы обратно на входной вычитатель.
На выходе сигма-дельта ЦАПа как и на выходе сигма-дельта АЦП, стоит фильтр нижних частот. Но у ЦАПа это аналоговый фильтр, который лишён богатых возможностей цифрового варианта. Результатом является ухудшение характеристик: увеличение прохождения тактовой частоты на выход и чувствительность к джиттеру — дрожанию фазы тактового сигнала. Это обычная проблема «непрерывных» во времени линейных схем.
Плюсы и минусы ΣΔ конверторов
Достоинства.
Линейность, монотонность, точность
1-Разрядные сигма-дельта конверторы гарантируют монотонность, они изначально линейны и спокойно достигают точности 24 разряда на звуковых частотах.
Дешевизна
Сигма-дельта АЦП используют недорогую и точную цифровую фильтрацию, а благодаря передискретизации, нуждаются в простом аналоговом спектральном фильтре на входе.
Недостатки.
Ограниченная полоса
Верхняя граница ∼10…100 Msps определяется тактовыми сигналами в гигагерцовом диапазоне.
Задержка
Встроенный в АЦП выходной цифровой фильтр имеет идеальную почти вертикальную заграждающую характеристику за счёт использования большого числа точек (последовательных первичных отсчётов АЦП, участвующих в получении результата). И по той же причине он имеет большую задержку или «латентность», измеряемую десятками периодов выборки, т.е. в случае звуковых АЦП миллисекундами.
Шум ЦАПов
Сигма-дельта ЦАПы используют аналоговые выходные фильтры, которые пропускают на выход какое-то количество цифрового шума, полностью отсутствующего в R-2R ЦАПах.
Тон паузы
АЦП с модулятором первого порядка могут создавать «тональные паузы», когда получают на входе постоянный сигнал (и вызывают этим истерику среди аудиофилов). В модуляторах более высоких порядков такой проблемы нет: шум давится за счёт действия обратных связей более высокого порядка.
Смотрите также:
АЦП. Параллельное кодирование, последовательное приближение
Насчитывается немало основных способов аналого-цифровых преобразователей (АЦП), каждый из которых обладает своими преимуществами и ограничениями. Дабы не «утяжелять» страницу, в рамках данной статьи рассмотрим только два из них. Другие способы рассмотрим отдельно. Прямо сейчас не будем углубляться в подробности самого процесса преобразования. Сконцентрируемся на общих вопросах, в числе которых: параметры (скорость, точность и т.п.), цифровой интерфейс (параллельный или последовательный, однополярный или дифференциальный и т.д.), степень интеграции (один или несколько инверторов в корпусе, отдельный или встроенный в микроконтроллер или систему на кристалле).
В большинстве случаев дело приходится иметь с готовыми АЦП-модулями или ИС, а не строить что-то своё. Но важно понимать, как работают различные методы аналого-цифровых преобразований, чтобы случайно на попасть в хитрую ловушку, свойственную какому-то конкретному варианту.
Амплитудно-частотная характеристика
Аббревиатура АЧХ расшифровывается как амплитудно-частотная характеристика. На английском этот термин звучит как «frequency response», что в дословном переводе означает «частотный отклик». Амплитудно-частотная характеристика цепи показывает зависимость уровня сигнала на выходе данного устройства от частоты передаваемого сигнала при постоянной амплитуде синусоидального сигнала на входе этого устройства. АЧХ может быть определена аналитически через формулы, либо экспериментально. Любое устройство предназначено для передачи (или усиления) электрических сигналов. АЧХ устройства определяется по зависимости коэффициента передачи (или коэффициента усиления) от частоты.
Коэффициент передачи
Что такое коэффициент передачи? Коэффициент передачи — это отношение напряжения на выходе цепи к напряжению на ее входе. Или формулой:
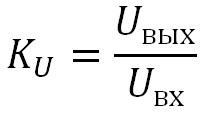
где

Uвых — напряжение на выходе цепи
Uвх — напряжение на входе цепи
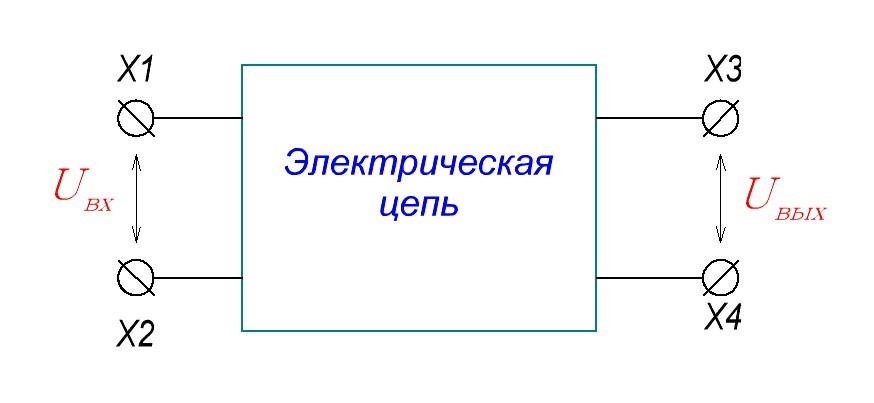
В усилительных устройствах коэффициент передачи больше единицы. Если устройство вносит ослабление передаваемого сигнала, то коэффициент передачи меньше единицы.
Коэффициент передачи может быть выражен через децибелы:
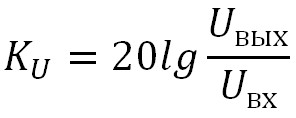
Строим АЧХ RC-цепи в программе Proteus
Для того, чтобы досконально разобраться, что такое АЧХ, давайте рассмотрим рисунок ниже.
Итак, имеем «черный ящик», на вход которого мы будем подавать синусоидальный сигнал, а на выходе черного ящика мы будем снимать сигнал. Должно соблюдаться условие: нужно менять частоту входного синусоидального сигнала, но его амплитуда должна быть постоянной.
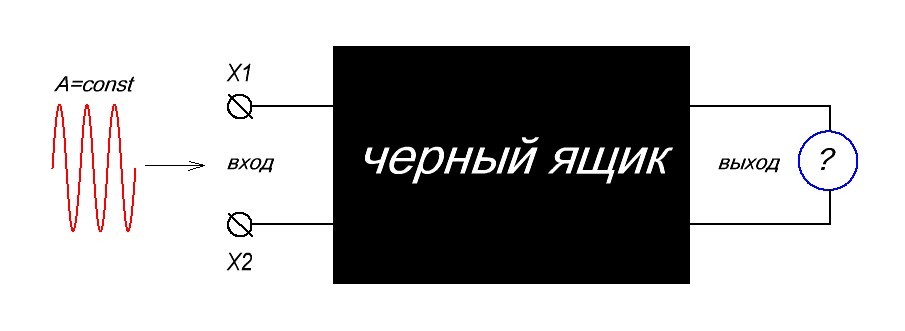
Что нам делать дальше? Надо измерить амплитуду сигнала на выходе после черного ящика при интересующих нас значениях частоты входного сигнала. То есть мы должны изменять частоту входного сигнала от 0 Герц (постоянный ток) и до какого-либо конечного значения, которое будет удовлетворять нашим целям, и смотреть, какая амплитуда сигнала будет на выходе при соответствующих значениях на входе.
Давайте разберем все это дело на примере. Пусть в черном ящике у нас будет самая простая RC-цепь с уже известными номиналами радиоэлементов.

Как я уже говорил, АЧХ может быть построено экспериментально, а также с помощью программ-симуляторов. На мой взгляд, самый простой и мощный симулятор для новичков — это Proteus. С него и начнем.
Собираем данную схему в рабочем поле программы Proteus
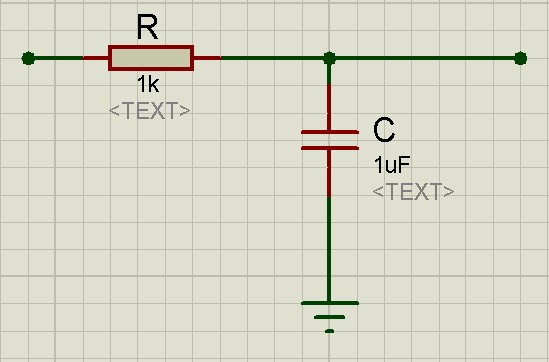
Для того, чтобы подать на вход схемы синусоидальный сигнал, мы кликаем на кнопочку «Генераторы», выбираем SINE, а потом соединяем его со входом нашей схемы.
Для измерения выходного сигнала достаточно кликнуть на значок с буквой «V» и соединить выплывающий значок с выходом нашей схемы:

Для эстетики, я уже поменял название входа и выхода на sin и out. Должно получиться как-то вот так:

Ну вот, пол дела уже сделано.
Теперь осталось добавить важный инструмент. Он называется «frequency response», как я уже говорил, в дословном переводе с английского — «частотный отклик». Для этого нажимаем кнопочку «Диаграмма» и в списке выбираем «frequency»
На экране появится что-то типа этого:
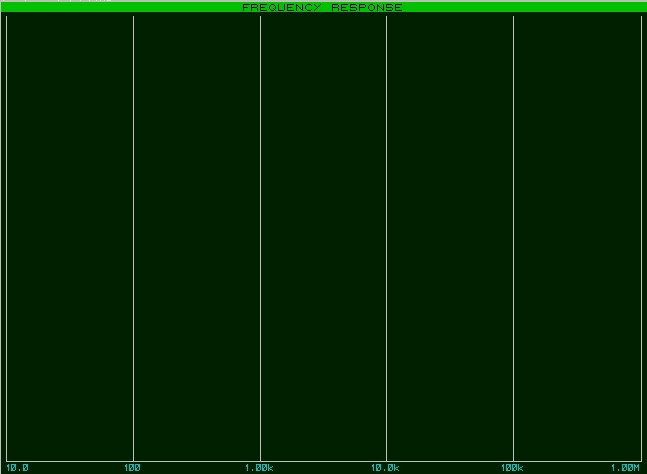
Кликаем ЛКМ два раза и открывается вот такое окошко, где в качестве входного сигнала мы выбираем наш генератор синуса (sin), который у нас сейчас задает частоту на входе.
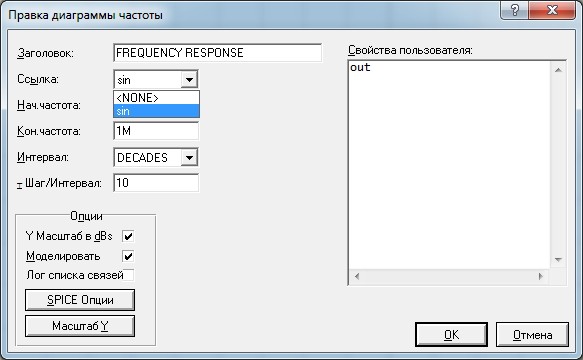
Здесь же выбираем диапазон частоты, который будем «загонять» на вход нашей цепи. В данном случае это диапазон от 1 Гц и до 1 МГц. При установке начальной частоты в 0 Герц Proteus выдает ошибку. Поэтому, ставьте начальную частоту близкую к нулю.
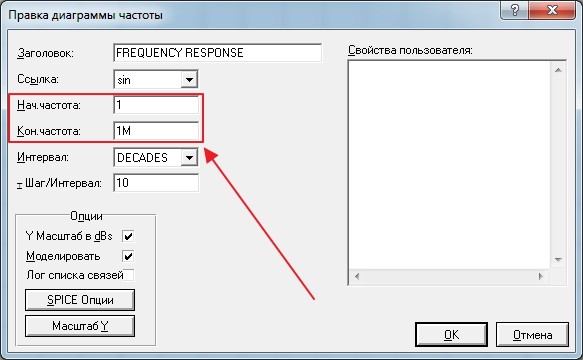
Нажимаем ОК.
Далее нажимаем ПКМ на самой табличке Frequency Response и видим вот такой выплывающий список, в котором нажимаем «Добавить трассы»

Долго не думая, выбираем в первом же окошке наш выход out
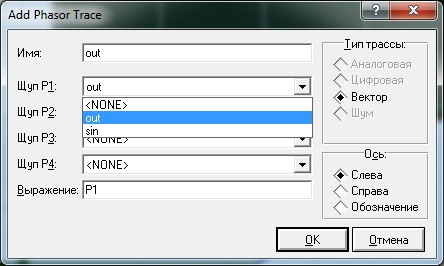
и в результате должно появится окошко с нашим выходом

Нажимаем пробел и радуемся результату
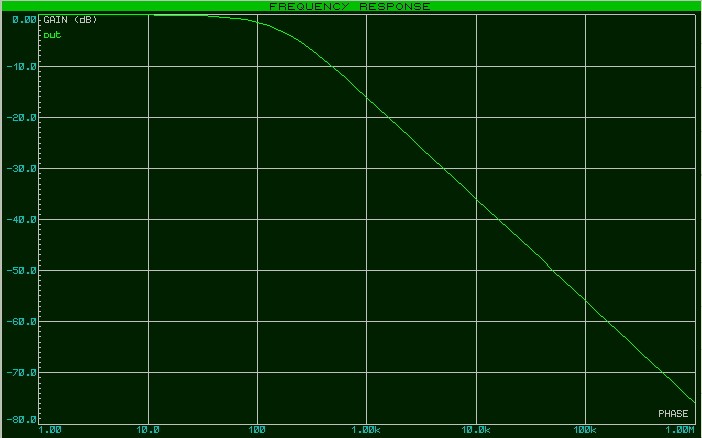
Итак, что интересного можно обнаружить, если взглянуть на нашу АЧХ? Как вы могли заметить, амплитуда на выходе цепи падает с увеличением частоты. Это означает, что наша RC-цепь является своеобразным частотным фильтром. Такой фильтр пропускает низкие частоты, в нашем случае до 100 Герц, а потом с ростом частоты начинает их «давить». И чем больше частота, тем больше он ослабляет амплитуду выходного сигнала. Поэтому, в данном случае, наша RC-цепь является самым простейшим фильтром низкой частоты (ФНЧ).
Полоса пропускания
В среде радиолюбителей и не только встречается также такой термин, как полоса пропускания. Полоса пропускания — это диапазон частот, в пределах которого АЧХ радиотехнической цепи или устройства достаточно равномерна, чтобы обеспечить передачу сигнала без существенного искажения его формы.
Как же определить полосу пропускания? Это сделать довольно легко. Достаточно на графике АЧХ найти уровень в -3 дБ от максимального значения АЧХ и найти точку пересечения прямой с графиком. В нашем случае это можно сделать легче пареной репы. Достаточно развернуть нашу диаграмму на весь экран и с помощью встроенного маркера посмотреть частоту на уровне в -3 дБ в точке пересечения с нашим графиком АЧХ. Как мы видим, она равняется 159 Герц.
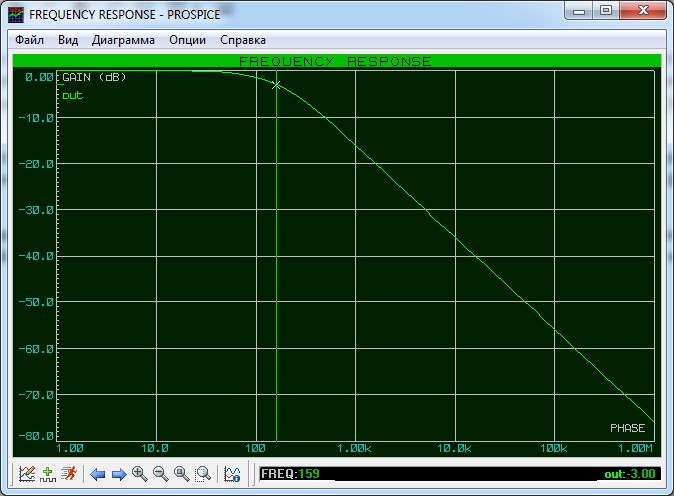
Частота, которая получается на уровне в -3 дБ, называется частотой среза. Для RC-цепи ее можно найти по формуле:
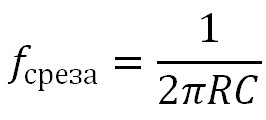
Для нашего случая расчетная частота получилась 159,2 Гц, что подтверждает и Proteus.
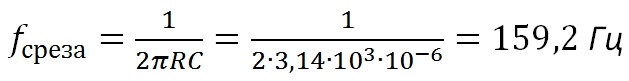
Кто не желает связываться с децибелами, то можно провести линию на уровне 0,707 от максимальной амплитуды выходного сигнала и смотреть пересечение с графиком. В данном примере, для наглядности, я взял максимальную амплитуду за уровень в 100%.
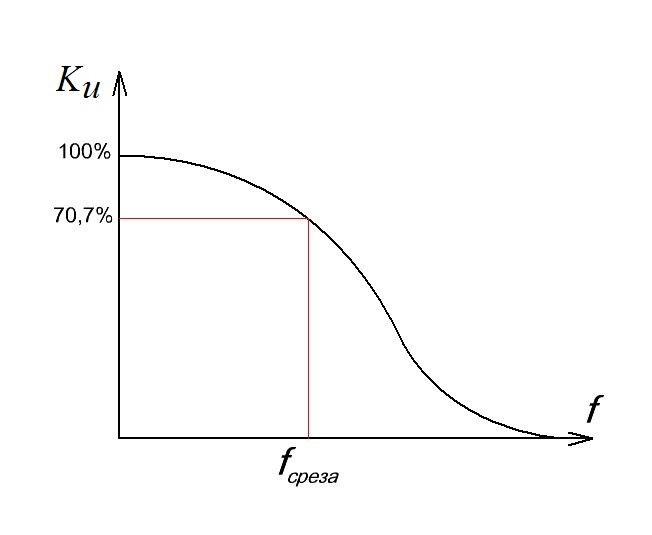
Как построить АЧХ на практике?
Как построить АЧХ на практике, имея в своем арсенале генератор частоты и осциллограф?
Итак, поехали. Собираем нашу цепь в реале:

Ну а теперь цепляем ко входу схемы генератор частоты, а с помощью осциллографа следим за амплитудой выходного сигнала, а также будем следить за амплитудой входного сигнала, чтобы мы были точно уверены, что на вход RC-цепи подается синус с постоянной амплитудой.

Для экспериментального изучения АЧХ нам потребуется собрать простенькую схемку:
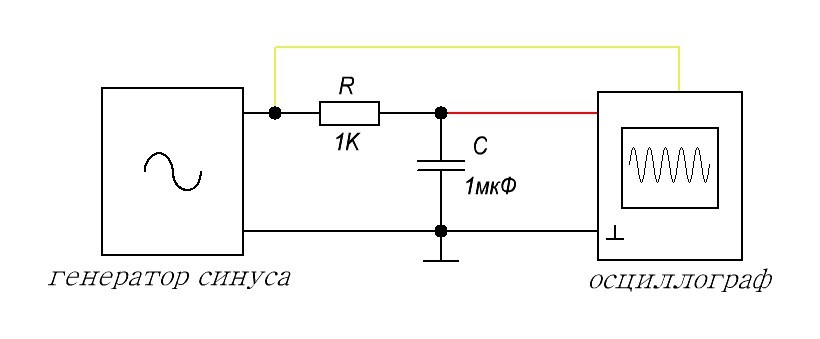
Наша задача состоит в том, чтобы менять частоту генератора и уже наблюдать, что покажет осциллограф на выходе цепи. Мы будем прогонять нашу цепь по частотам, начиная от самой малой. Как я уже сказал, желтый канал предназначен для визуального контроля, что мы честно проводим опыт.
Постоянный ток, проходящий через эту цепь, на выходе будет давать амплитудное значение входного сигнала, поэтому первая точка будет иметь координаты (0;4), так как амплитуда нашего входного сигнала 4 Вольта.
Следующее значение смотрим на осциллограмме:
Частота 15 Герц, амплитуда на выходе 4 Вольта. Итак, вторая точка (15;4)
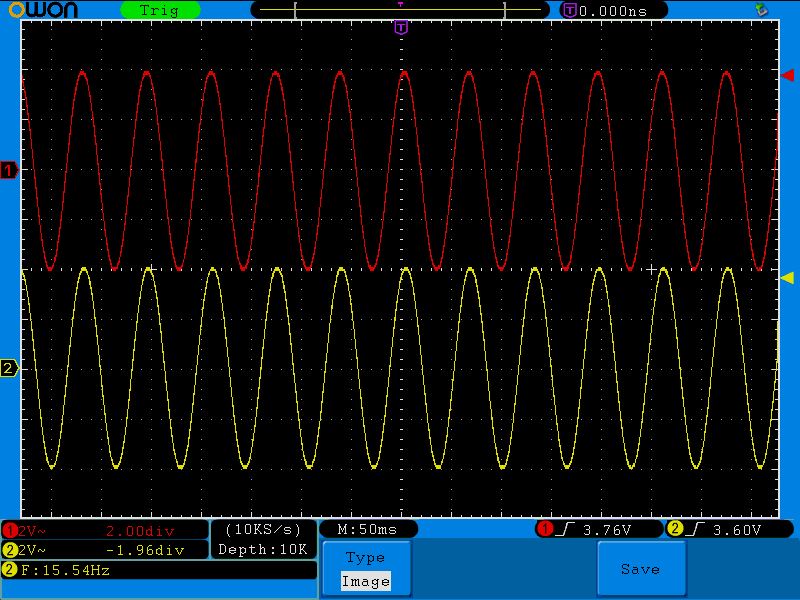
Третья точка (72;3.6). Обратите внимание на амплитуду выходного красного сигнала. Она начинает проседать.

Четвертая точка (109;3.2)
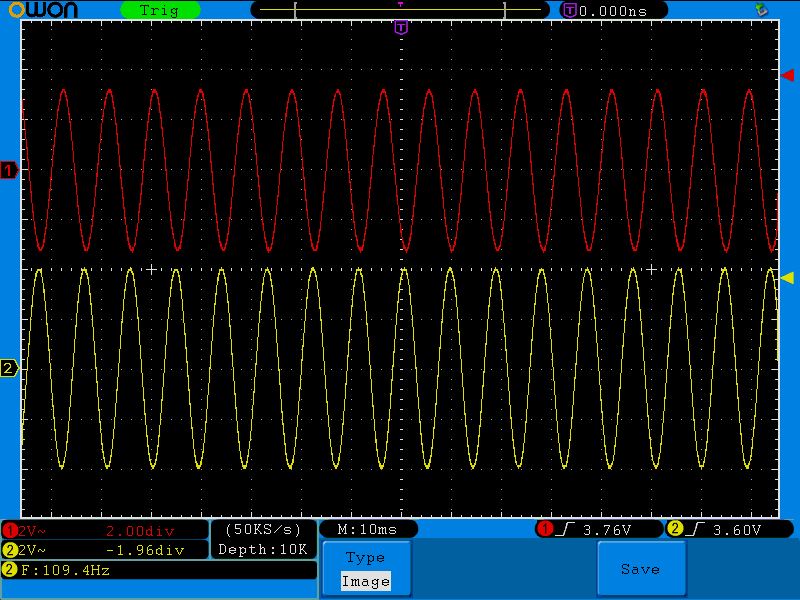
Пятая точка (159;2.8)
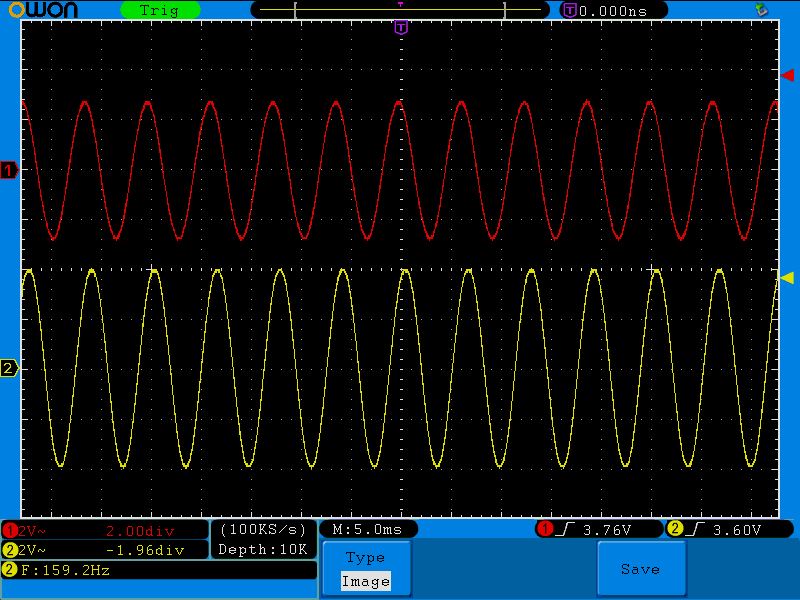
Шестая точка (201;2.4)

Седьмая точка (273;2)
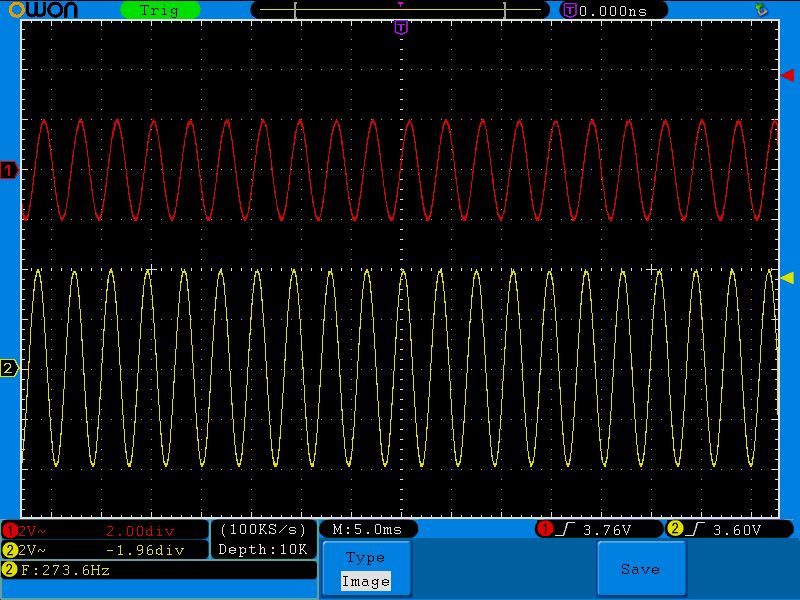
Восьмая точка (361;1.6)

Девятая точка (542;1.2)

Десятая точка (900;0.8)
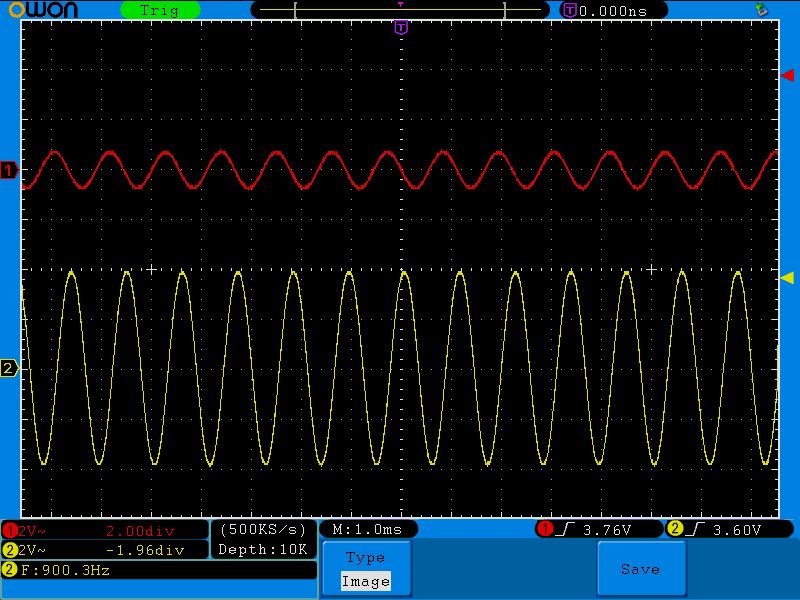
Ну и последняя одиннадцатая точка (1907;0.4)
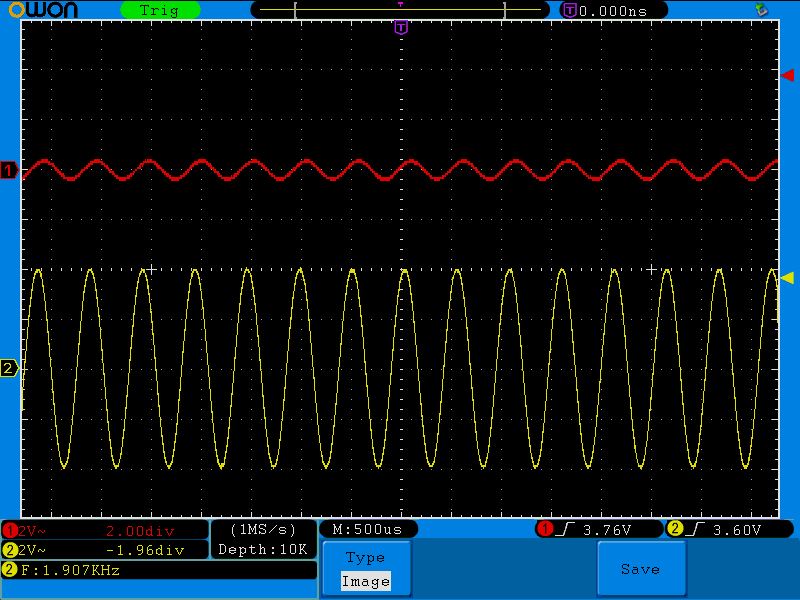
В результате измерений у нас получилась табличка:

Строим график по полученным значениям и получаем нашу экспериментальную АЧХ 😉

Получилось не так, как в технической литературе. Оно и понятно, так как по Х берут логарифмический масштаб, а не линейный, как у меня на графике. Как вы видите, амплитуда выходного сигнала будет и дальше понижаться с увеличением частоты. Для того, чтобы еще более точно построить нашу АЧХ, требуется взять как можно больше точек.
Давайте вернемся к этой осциллограмме:

Здесь на частоте среза амплитуда выходного сигнала получилась ровно 2,8 Вольт, которые как раз и находятся на уровне в 0,707. В нашем случае 100% это 4 Вольта. 4х0,707=2,82 Вольта.

АЧХ полосового фильтра
Существуют также схемы, АЧХ которых имеет вид холма или ямы. Давайте рассмотрим один из примеров. Мы будем рассматривать так называемый полосовой фильтр, АЧХ которого имеет вид холма.
Собственно сама схема:
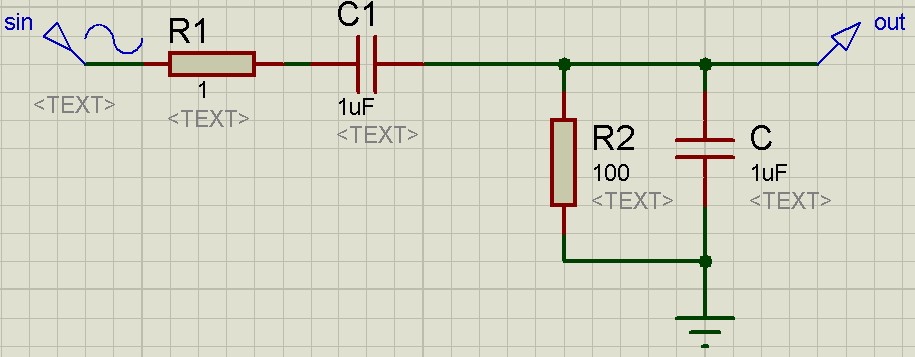
А вот ее АЧХ:

Особенность таких фильтров, что они имеют две частоты среза. Определяются они также на уровне в -3дБ или на уровне в 0,707 от максимального значения коэффициента передачи, а еще точнее Ku max/√2.

Так как в дБ смотреть график неудобно, поэтому я переведу его в линейный режим по оси Y, убирая маркер

В результате перестроения получилась такая АЧХ:
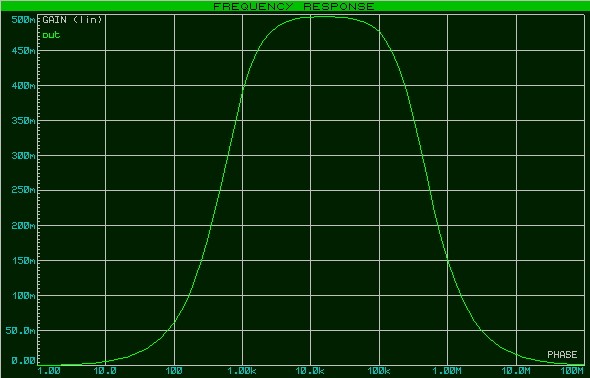
Максимальное значение на выходе составило 498 мВ при амплитуде входного сигнала в 10 Вольт. Мдя, неплохой «усилитель») Итак, находим значение частот на уровне в 0,707х498=352мВ. В результате получились две частоты среза — это частота в 786 Гц и в 320 КГц. Следовательно, полоса пропускания данного фильтра от 786Гц и до 320 КГц.
На практике для получения АЧХ используются приборы, называемые характериографами для исследования АЧХ. Вот так выглядит один из образцов Советского Союза

Фазо-частотная характеристика
ФЧХ расшифровывается как фазо-частотная характеристика, phase response — фазовый отклик. Фазо-частотная характеристика — это зависимость сдвига по фазе между синусоидальными сигналами на входе и выходе устройства от частоты входного колебания.
Разность фаз
Думаю, вы не раз слышали такое выражение, как » у него произошел сдвиг по фазе». Это выражение не так давно пришло в наш лексикон и обозначает оно то, что человек слегка двинулся умом. То есть было все нормально, а потом раз! И все :-). И в электронике такое тоже часто бывает) Разницу между фазами сигналов в электронике называют разностью фаз. Вроде бы «загоняем» на вход какой-либо сигнал, а выходной сигнал ни с того ни с сего взял и сдвинулся по времени, относительно входного сигнала.
Для того, чтобы определить разность фаз, должно выполняться условие: частоты сигналов должны быть равны. Пусть даже один сигнал будет с амплитудой в Киловольт, а другой в милливольт. Неважно! Лишь бы соблюдалось равенство частот. Если бы условие равенства не соблюдалось, то сдвиг фаз между сигналами все время бы изменялся.
Для определения сдвига фаз используют двухканальный осциллограф. Разность фаз чаще всего обозначается буквой φ и на осциллограмме это выглядит примерно так:

Строим ФЧХ RC-цепи в Proteus
Для нашей исследуемой цепи

Для того, чтобы отобразить ее в Proteus мы снова открываем функцию «frequency response»

Все также выбираем наш генератор

Не забываем проставлять испытуемый диапазон частот:

Далее нажимаем ПКМ на самой табличке Frequency Response и видим вот такой выплывающий список, в котором нажимаем «Добавить трассы»

Долго не думая, выбираем в первом же окошке наш выход out

И теперь главное отличие: в колонке «Ось» ставим маркер на «Справа»
Нажимаем пробел и вуаля!
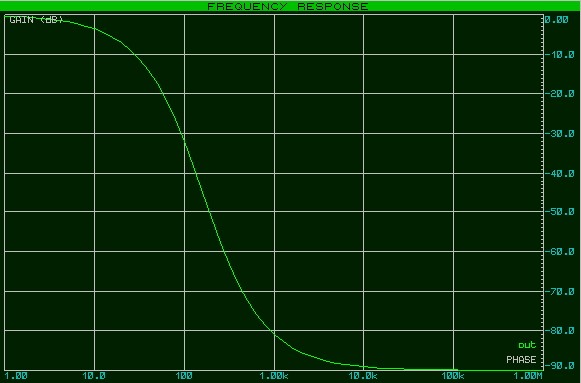
Можно его развернуть на весь экран
При большом желании эти две характеристики можно объединить на одном графике

Обратите внимание, что на частоте среза сдвиг фаз между входным и выходным сигналом составляет 45 градусов или в радианах п/4 (кликните для увеличения)

В данном опыте при частоте более 100 КГц разность фаз достигает значения в 90 градусов (в радианах π/2) и уже не меняется.
Строим ФЧХ на практике
ФЧХ на практике можно измерить также, как и АЧХ, просто наблюдая разность фаз и записывая показания в табличку. В этом опыте мы просто убедимся, что на частоте среза у нас действительно разность фаз между входным и выходным сигналом будет 45 градусов или π/4 в радианах.
Итак, у меня получилась вот такая осциллограмма на частоте среза в 159,2 Гц

Нам надо узнать разность фаз между этими двумя сигналами
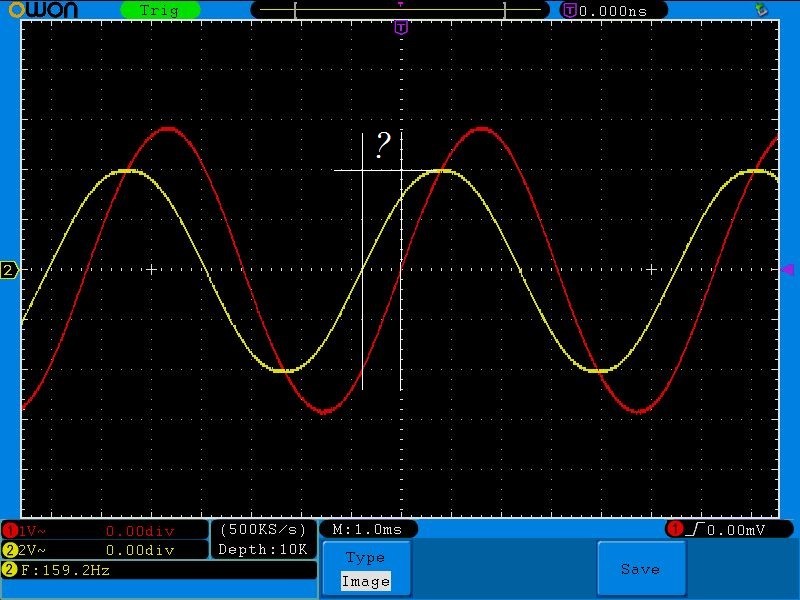
Весь период — это 2п, значит половина периода — это π. На полупериод у нас приходится где-то 15,5 делений. Между двумя сигналами разность в 4 деления. Составляем пропорцию:
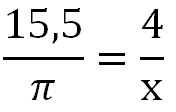
Отсюда х=0,258п или можно сказать почти что 1/4п. Следовательно, разница фаз между двумя этими сигналами равняется п/4, что почти в точности совпало с расчетными значениями в Proteus.
Если Вы лучше воспринимаете информацию через видео, то к Вашему вниманию:
Резюме
Амплитудно-частотная характеристика цепи показывает зависимость уровня сигнала на выходе данного устройства от частоты передаваемого сигнала при постоянной амплитуде синусоидального сигнала на входе этого устройства.
И еще интересная статья — последовательное и параллельное соединение проводников.
Фазо-частотная характеристика — это зависимость сдвига по фазе между синусоидальными сигналами на входе и выходе устройства от частоты входного колебания.
Коэффициент передачи — это отношение напряжения на выходе цепи к напряжению на ее входе. Если коэффициент передачи больше единицы, то электрическая цепь усиливает входной ссигнал, если же меньше единицы, то ослабляет.
Полоса пропускания — это диапазон частот, в пределах которого АЧХ радиотехнической цепи или устройства достаточно равномерна, чтобы обеспечить передачу сигнала без существенного искажения его формы. Определяется по уровню 0,707 от максимального значения АЧХ.
Учебное пособие: Четырехполюсники, электрические фильтры
МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ
(государственный технический университет)
ФИЛИАЛ «ВЗЛЕТ»
КОНСПЕКТ ЛЕКЦИЙ ПО КУРСУ
«Основы теории цепей». Часть 2.
Четырехполюсники, электрические фильтры.
Учебное пособие для студентов радиотехнической специальности.
НА ЗАСЕДАНИИ КАФЕДРЫ РЭВС
«____» ________________ 2003 года
Ахтубинск – 2003
Предисловие ко 2-й части
Во второй части конспекта по Основам теории цепей (ОТЦ) кратко изложена теория четырехполюсников (4х-П) и более подробно изложена теория электрических фильтров.
Анализ и синтез простейших электрических фильтров проводится с применением прикладной программы Mathcad 2000 (МС). Все расчеты, выполненные в среде Mathcad , проверены путем электронного моделирования по программе Electronics Workbench . Конспект, с его многочисленными примерами, может быть использован студентами при проектировании электрических фильтров на этапах разработки курсовых и дипломных проектов.
Работа написана на основе 4-х-летнего опыта применения упомянутых программ в учебном процессе.
Глава 1. Четырехполюсники
1.1 Основные определения и классификация четырехполюсников (4х-П)
Часть электрической цепи, рассматриваемая по отношению к любым двум парам ее зажимов, называется 4х-П, Рис.1.1.
| Название: Четырехполюсники, электрические фильтры Раздел: Рефераты по коммуникации и связи Тип: учебное пособие Добавлен 01:54:09 05 июня 2010 Похожие работы Просмотров: 2826 Комментариев: 19 Оценило: 4 человек Средний балл: 4.3 Оценка: неизвестно Скачать |
Рис.1.1. Схема 4х-П. Его токи и напряжения.
Понятием 4х-П пользуются тогда, когда интересуются токами и напряжениями на входе «1-1’» и на выходе «2-2’».
В качестве 4х-П могут быть представлены: трансформатор, выпрямитель, электрический фильтр и другие устройства с двумя парами зажимов.
Четырехполюсники делятся на активные и пассивные. В составе активных 4х-П имеются источники энергии. Пассивные 4х-П не содержат источников энергии.
Четырехполюсники делятся на линейные и нелинейные. Если в состав 4х-П входит хотя бы один нелинейный элемент, то такой4х-П называется нелинейным. В данной работе рассматриваются только линейные 4х-П.
По схеме внутренних соединений различают Г-образные, Т-образные, П-образные и другие 4х-П, Рис.1.2.
Рис.1.2. Электрические схемы 4х-П.
Основной смысл теории 4х-П заключается в том, что, пользуясь некоторыми обобщенными параметрами, можно находить ток и напряжение на выходе 4х-П, не производя расчетов токов и напряжений внутри заданной схемы.
1.2 Системы уравнений четырехполюсников
Уравнениями 4х-П называют комплексные уравнения, связывающие комплексные действующие значения токов и напряжений на его входе и выходе.
Линейный пассивный 4х-П, естественно, описывается линейными уравнениями.
Из четырех величин характеризующих 4х-П, две должны быть заданы, а две другие определяются из уравнения 4х-П. Всего, таким образом, может быть составлено шесть форм записи уравнений.
Если 4х-П выполняет роль передаточного звена между источником и приемником электрической энергии, то обычно пользуются уравнениями в форме А:
В этих уравнениях А11 , А12 , А21 , А22 называются коэффициентами формы А. Они, в общем случае, являются комплексными числами, модули которых зависят от частоты.
Физический смысл коэффициентов формы А можно пояснить, если мысленно выполнить опыты холостого хода и короткого замыкания.
В режиме холостого хода . Уравнение (1.1.) принимает следующий вид:
– отношение входного напряжения к выходному в режиме холостого хода;
– передаточная проводимость в режиме холостого хода.
В режиме короткого замыкания . Уравнения (1.1) принимают вид:
– передаточное сопротивление в режиме короткого замыкания;
– отношение тока на входе к току на выходе в режиме короткого замыкания.
Основное свойство коэффициентов формы А состоит в том, что определитель, составленный из этих коэффициентов, равен единице:
Из этого уравнения следует, что для составления системы (1.1) в форме А необходимо и достаточно определить только любые три коэффициента. Четвертый коэффициент определяется из (1.2).
Рассмотрим Г-образный 4х-П, изображенный на Рис.1.3, и определим для него коэффициенты формы А.
Рис.1.3. Схема Г-образного 4х-П.
При определении коэффициентов формы А будем считать, что комплексные сопротивления Z1 и Z2 заданы.
Проведем опыт холостого хода: зажимы 2-2’ – разомкнуты,
В этом случае ток на входе и напряжение на выходе определяются по закону Ома в комплексной форме:
Эти выражения можно записать так:
Отсюда получаем значения А11 и А21 , выраженные через сопротивления Z1 и Z2 :
Теперь проведем опыт короткого замыкания: зажимы 2-2’ закорочены,
При этом в цепи осталось только одно сопротивление Z1 и, следовательно:
Таким образом, коэффициенты формы А Г-образного 4х-П можно представить в виде следующей матрицы
Аналогичным образом можно получить матрицу коэффициентов формы А для Т-образного4х-П:
Кроме формы А (1,1) существуют еще пять форм записи уравнений 4х-П. Приведем еще две формы.
Полный перечень форм записи уравнений 4х-П приводится в учебниках, задачниках и справочниках по ОТЦ.
Если известны коэффициенты хотя бы одной формы записи уравнений 4х-П, то можно найти коэффициенты любой другой формы, решив систему уравнений, например (1,1) относительно искомых токов или напряжений.
1.3 Входное сопротивление, сопротивления холостого хода и короткого замыкания
Рассмотрим произвольный 4х-П с известными коэффициентами формы А, который нагружен активным сопротивлением R, Рис.1.4.
Рис.1.4. Схема 4х-П, нагруженного активным сопротивлением R
Определим входное сопротивление 4х-П Рис.1.4., т.е. сопротивление со стороны зажимов 1-1’.
По закону Ома в комплексной форме входное сопротивление есть отношение входного напряжения к входному току (1.1):
Полученное выражение входного сопротивления показывает, что 4х-П может быть применен для преобразования сопротивления между источником и приемником.
Сопротивление холостого хода 4х-П представляет собой частный случай входного сопротивления (1.5) при
Сопротивление короткого замыкания получается из (1.5) при
1.4 Передаточная функция четырехполюсника
При проектировании радиотехнических устройств широко применяются электрические фильтры, которые удобно рассматривать как 4х-П, предназначенные для передачи сигналов от входа к выходу с определенной избирательностью.
Передаточной функцией по напряжению называется отношение выходного напряжения к входному:
Модуль этого отношения представляет собой амплитудно-частотную характеристику (АЧХ), а аргумент – фазо-частотную характеристику (ФЧХ). Эти характеристики являются основными при выборе электрических фильтров.
Амплитудно-частотная характеристика показывает, во сколько раз выходное напряжение меньше (или больше) входного, ФЧХ дает сдвиг фаз между входным и выходным напряжениями.
Определим АЧХ и ФЧХ произвольного 4х-П с известными коэффициентами формы А, нагруженного активным сопротивлением R, Рис.1.4. С этой целью запишем первое уравнение системы (1.1) в следующем виде:
Поскольку коэффициенты формы А, в общем случае, являются комплексными числами, зависящими от частоты, постольку выражение в скобках (1.6) можно записать в алгебраической форме:
где а(ω) – действительная часть;
b(ω) – мнимая часть.
После этого связь входного и выходного напряжений (1.6) можно выразить следующим образом:
Для определения ФЧХ 4х-П за начало отсчета сдвига фаз между входным и выходным напряжениями примем вектор выходного напряжения , который направим по оси абсцисс, т.е. горизонтально.
При таком выборе начала отсчета положение вектора на комплексной плоскости целиком определяется величинами а(ω)и b(ω) и их знаками:
Расчет ФЧХ по (1.8) дает сдвиг фаз, выраженный в радианах. Ключ для определения этого угла показан на Рис.1.5:
j
φ
0 +
Рис.1.5. Ключ для определения сдвига фаз между входным и выходным напряжениями
На основании (1.7) комплексная передаточная функция по напряжению произвольного 4х-П с известными коэффициентами формы А и нагруженного активным сопротивлением R, принимает вид:
Модуль передаточной функции 4х-П, т.е. его АЧХ:
Таким образом, по формулам (1.8) и (1.10) можно рассчитать АЧХ и ФЧХ любого 4х-П при известных коэффициентах формы А и нагрузке R.
Пример 1.1. Задана электрическая схема Г-образного 4х-П (Рис.1.6) и его параметры R, L, C. Данный 4х-П подключен к источнику синусоидального напряжения. Необходимо найти формулы для расчета АЧХ и ФЧХ этого 4х-П.
1 2
Рис.1.6. Электрическая схема г-образного 4х-П, нагруженного активным сопротивлением R
Решение. Комплексные сопротивления плеч 4х-П:
Коэффициенты формы А (1.3):
Комплексная передаточная функция:
Модуль передаточной функции:
где
Таким образом, при известных значениях R, L, C-элементов по формулам (1.11), (1.12) можно рассчитать и построить графики АЧХ и ФЧХ Г-образного 4х-П, изображенного на Рис.1.6.
1.5 Каскадное соединение четырехполюсников
Рассмотрим так называемое каскадное соединение 4х-П (Рис.1.7), при котором входные зажимы каждого последующего 4х-П присоединяются к выходным зажимам предыдущего.
Рис.1.7. Каскадное соединение 4х-П
Эти два 4х-П, взятые вместе, можно рассматривать как один эквивалентный.
Определим параметры эквивалентного 4х-П через известные параметры первого и второго четырехполюсников.
Пусть заданы матрицы коэффициентов формы А двух каскадно соединенных 4х-П.
Из теории известно, что матрица коэффициентов формы А двух каскадно соединенных 4х-П равна произведению матриц отдельных 4х-П:
Это правило, распространяется на случай каскадного соединения любого числа 4х-П. При этом матрицы, подлежащие перемножению, записываются в порядке следования 4х-П, т.к. умножение матриц не подчиняется переместительному закону.
1.6 Одноэлементые четырехполюсники
Простейшими 4х-П являются одноэлементные 4х-П, состоящие из последовательного (Рис.1.8а) и параллельного (Рис.1.8б) двухполюсника.
Рис.1.8. Одноэлементный 4х-П
Матрицы коэффициентов формы А одноэлементных 4х-П:
С помощью этих матриц М1 и М2 можно получить коэффициенты формы А любого 4х-П, построенного по лестничной схеме. Для этого необходимо перемножить матрицы М1 и М2 столько раз, сколько раз встречаются параллельный и последовательный 2х-П.
Например, коэффициенты формы А Г-образного 4х-П получаются после перемножения матриц М1 и М2 (см.1.3):
Глава 2. Электрические фильтры нижних частот
2.1 Основные определения и классификация электрических фильтров
Электрическим фильтром называется устройство, при помощи которого электрические колебания разных частот отделяются друг от друга. Электрический фильтр представляет собой пассивный 4х-П, пропускающий сигналы в некоторой полосе частот с малым затуханием, а за пределами этой полосы сигналы проходят в нагрузку с большим затуханием.
Полоса частот, в пределах которой передаточная функция по напряжению (1.10) принимает не менее заданного значения
называется полосой пропускания. Остальная область частот называется полосой задерживания. Частоты, разделяющие эти полосы, называются граничными.
В зависимости от пропускаемого спектра частот фильтры разделяются на:
– фильтры нижних частот (ФНЧ);
– фильтры верхних частот (ФВЧ);
– полосовые фильтры (ПФ);
– заграждающие фильтры (ЗФ).
В зависимости от электрической схемы фильтры разделяются на Г-образные, Т-образные, П-образные и другие.
В зависимости от числа реактивных элементов, входящих в состав фильтра, различают фильтры первого порядка, второго порядка и т.д.
По составу элементов фильтры делятся на активные и пассивные. Активные фильтры содержат источники электрической энергии, а пассивные их не содержат.
По способу обработки сигналов фильтры делятся на аналоговые и цифровые.
В данном курсе рассматриваются только пассивные электрические фильтры, построенные на идеальных линейных R, L, C-элементах.
2.2 Общий принцип действия линейных пассивных электрических фильтров
Рассмотрим электрический фильтр, частотные характеристики которого известны и описываются формулами (1.8)и (1.10).
Пусть на вход данного фильтра поступает сигнал в виде суммы различных частот
Определим структуру сигнала на выходе фильтра.
В силу линейности фильтра, сигнал на выходе будет также представлять сумму синусоидальных напряжений. При этом изменятся амплитуды и начальные фазы составляющих, а частоты составляющих на выходе фильтра одинаковы:
Амплитуды составляющих на выходе определяются передаточной функцией фильтра (1.10):
Сдвиг фаз между входным и выходным напряжениями определяется фазо-частотной характеристикой фильтра (1.8):
В дальнейшем будем полагать, что на вход фильтра подается синусоидальное напряжение, частота которого изменяется от нуля до бесконечности.
2.3 Общая характеристика фильтров нижних частот
Фильтры нижних частот (ФНЧ) предназначены для пропускания в нагрузку сигналов малой частоты и подавления сигналов большой частоты.
Полоса пропускания ФНЧ определяется его граничными частотами:
f1 =0 – нижняя граница полосы пропускания;
f2 – верхняя граница полосы пропускания, которая определяется назначением данного конкретного фильтра.
В теории фильтров рассматриваются идеальные и реальные фильтры. Идеальным ФНЧ называется фильтр, передаточная функция которого (1.10) в полосе пропускания равна единице, а за пределами полосы пропускания она равна нулю:
Передаточная функция реального фильтра в полосе пропускания не равна единице, а в полосе задерживания – не равна нулю.
Передаточные функции по напряжению идеального и реального фильтров нижних частот показаны на Рис.2.1.
H(f)
Передаточная функция идеального ФНЧ
Передаточная функция реального ФНЧ
H1
пропускания Полоса задерживания
H22
f2 f22 f
Рис.2.1. Передаточные функции идеального и реального фильтров нижних частот
Количественную оценку избирательности фильтра целесообразно производить с помощью коэффициента прямоугольности передаточной функции по напряжению или мощности.
Для расчета коэффициента прямоугольности передаточной функции фильтра введем в рассмотрение передаточную функцию по мощности, которую определим следующим образом.
Максимально возможная мощность, которая может быть выделена в нагрузке в случае идеального фильтра, определяется по формуле:
где U1 – действующее значение входного напряжения;
R – сопротивление нагрузки.
Фактическая мощность, выделяемая в нагрузке реального фильтра, определяется действующим значением выходного напряжения, которое зависит от частоты входного напряжения:
Передаточной функцией по мощности будем называть отношение мощности, выделяемой в нагрузке реального фильтра (2.2) к мощности, выделяемой в нагрузке, идеального фильтра:
Таким образом, передаточная функция по мощности есть квадрат передаточной функции по напряжению (2.3).
Отметим, что в известных учебниках по ОТЦ частотные характеристики фильтров оцениваются затуханием, которое выражается в децибелах (дБ):
Из этой формулы следует, что фактически производится оценка затухания (ослабления) сигнала по мощности.
Поскольку физический смысл формулы (2.4) спрятан под знаком логарифма, постольку в дальнейшем будем пользоваться более простой формулой (2.3), физический смысл которой более прост и понятен.
Расчет коэффициента прямоугольности передаточной функции по мощности ФНЧ будем производить следующим образом.
Определим частоту, на которой передаточная функция по мощности составляет 5% от максимума:
За пределами этой частоты будем считать, что передаточная функция равна нулю
Определим полную площадь под кривой передаточной функции (Рис.2.1):
Определим также площадь под кривой передаточной функции в пределах полосы пропускания (0…f2 ), где передаточная функция по напряжению а передаточная функция по мощности (Рис.2.1):
Коэффициентом прямоугольности передаточной функции по мощности будем называть отношение найденных площадей:
По физической сущности коэффициент прямоугольности представляет собой коэффициент полезного использования площади под кривой передаточной функции по мощности и дает представление о степени соответствия реального фильтра идеальному с той же полосой пропускания.
2.4 Емкостной фильтр нижних частот
2.4.1 Частотные характеристики емкостного фильтра нижних частот первого порядка (ФНЧ-1)
Рассмотрим электрическую схему, изображенную на Рис.2.3, которая представляет собой простейший фильтр нижних частот первого порядка (ФНЧ-1).
1 2
Рис.2.3. Емкостной фильтр нижних частот (ФНЧ-1)
Работа ФНЧ-1:
На малых частотах емкость обладает большим сопротивлением и поэтому весь проходит только через резисторы r, R, не ответвляясь в емкость.
На больших частотах емкость обладает малым сопротивлением. Она закорачивает нагрузку и поэтому выходное напряжение мало.
Определим для этого фильтра АЧХ и ФЧХ, рассматривая его как Г-образный 4х-П, нагруженный активным сопротивлением R.
Сопротивления плеч фильтра:
Коэффициенты формы А:
Уравнение связи входного и выходного напряжений (1.6):
где – эквивалентное сопротивление при параллельном соединении R и r.
Из (2.8) получаем фазо-частотную характеристику ФНЧ-1:
Передаточные функции ФНЧ-1 принимают вид:
где – значение передаточной функции на частоте ω=0.
Теперь, по формулам (2.9) и (2.10) можно, при известных значениях R, r, C-элементов, рассчитать и построить графики АЧХ и ФЧХ простейшего фильтра нижних частот (ФНЧ-1).
При изучении частотных характеристик фильтров удобно пользоваться АЧХ ФЧХ в параметрической форме. Для этого необходимо ввести в рассмотрение приведенную, или так называемую нормированную частоту, которая, в данном случае, определяется по формуле
где – граничная частота, на которой реактивное сопротивление емкости равно активному сопротивлению
Запишем (2.9) и (2.10) в параметрической форме:
Параметрические функции (2.11) и (2.12) позволяют проводить общий анализ АЧХ и ФЧХ фильтра при заданных значениях R, r-элементах и произвольном значении емкости С.
Пример 2. Рассчитать и построить графики при следующих исходных данных:
R=100 Ом – сопротивление нагрузки;
r=5 Ом – внутреннее сопротивление источника.
Оценить коэффициент прямоугольности передаточной функции по мощности.
Результаты расчетов представлены на Рис.2.4 и Рис.2.5.
Из этих рисунков видно, что передаточная функция по мощности при частоте ν=0 принимает значение H(0)=0,98, а затем плавно уменьшается с увеличением частоты. Коэффициент прямоугольности этой функции составляет всего П=0,545. Это означает, что данный фильтр соответствует идеальному фильтру на 54,5%.
Сдвиг фаз между входным и выходным напряжениями изменяется от 0 до 90 0 . При этом выходное напряжение опережает входное.
2.4.2 Синтез емкостного фильтра нижних частот первого порядка
Синтез (проектирование) любого технического устройства начинается с разработки технического задания (ТЗ), в котором приводятся исходные данные и формулируются требования к устройству.
Применительно к ФНЧ-1 техническое задание на его проектирование можно изложить следующим образом:
1. Спроектировать емкостной фильтр нижних частот, схема которого приведена на Рис.3.2.
2. На вход фильтра подаются сигналы синусоидальной формы, частота которых изменяется от 0 до ∞.
3. Сопротивление нагрузки R, а внутреннее сопротивление источника r, (R>>r).
4. Передаточная функция по напряжению на нижней границе полосы пропускания (f1 =0) должна принимать значение, близкое к единице, а на верхней границе f2 передаточная функция должна принимать значение H(f2 )=H1 .
5. Определить потребное значение емкости, рассчитать АЧХ и ФЧХ фильтра, оценить коэффициент прямоугольности передаточной функции по мощности.
В условиях данной задачи неизвестной величиной является только емкость, которую достаточно просто можно найти из уравнения передаточной функции. Однако, в интересах общности изложения последующего материала воспользуемся передаточной функцией в параметрической форме (2.14), из которой найдем значение приведенной частоты n2 , на которой передаточная функция (2.12) принимает заданное значение H1 :
Четырехполюсники
Содержание:
Основы теории четырехполюсников и фильтров:
Электрическая цепь, имеющая два входных и два выходных зажима, называется четырехполюсником. Теория четырехполюсников в общем виде рассматривает основную проблему электротехники: передачу энергии от источника к приемнику через промежуточное звено — четырехполюсник.
Активные четырехполюсники содержат внутри себя также источники электрической энергии. Далее сначала рассматриваются пассивные четырехполюсники, не содержащие внутри себя источников энергии. Примером их могут служить линия передачи (рис. 9.1, а), трансформатор (рис. 9.1, б), мостовая схема (рис. 9.1, в), а также Т-образная (рис. 9.1, г) и П-образная (рис. 9.1, д) схемы, к зажимам I’, I” которых подключается источник, а к зажимам 2′, 2″ — приемник электрической энергии.
На рис. 9.2, а изображена в общем виде схема четырехполюсника. Здесь
Для вывода уравнений, связывающих входные и выходные напряжения и токи, удобно заменить приемник Z2 с напряжением эквивалентным источником напряжения без внутреннего сопротивления (рис. 9.2, б). Согласно, э. д. с. последнего должна быть равна Тогда можно применить метод наложения. Считая сначала существующим только источник и замыкая накоротко зажимы источника — (рис. 9.2, в), находят токи которые, очевидно, будут пропорциональны напряжению
Аналогично, при наличии источника , и коротком замыкании (рис. 9.2, г)
Здесь — комплексные коэффициенты пропорциональности, имеющие размерность проводимости; Y11 и Y12 называются входными, а Y12 и Y21 — взаимными проводимостями. Проводимости Y12 и Y21 определяют токи в короткозамкнутом выходном или входном контуре при заданном напряжении в другом контуре. При одинаковом напряжении U токи Yl2U и Y21U по принципу взаимности были бы равны между собой. Следовательно, взаимные проводимости
Действительные токи на входе и выходе четырехполюсника
Совместное решение этих уравнений дает
После введения обозначений
(9.1)
получаются уравнения четырехполюсника:
где комплексы А, В, С, D называются параметрами четырехполюсника. Между ними существует следующая связь:
Следовательно, из четырех параметров независимыми являются три.
Если входные и выходные зажимы поменять местами (рис. 9.2, д), т. е. осуществить обратное питание (индекс «о»), уравнения, очевидно, получатся аналогичными:
а параметры А’, В’, С’, D’ определятся из выражений (9.1), если индекс I заменить индексом 2 и наоборот:
Следовательно, уравнения четырехполюсника, питаемого со стороны выхода, получают вид:
Отсюда следует, что в симметричном четырехполюснике, который со стороны выходных зажимов представляет ту же цепь, что и со стороны входных, А = D и А 2 — ВС = 1.
С помощью уравнений четырехполюсника можно определить нагрузочный режим, т. е. найти , для заданных . Очевидно, уравнения четырехполюсника могут быть использованы также для определения двух любых величин из указанных, если заданы две другие.
Холостой ход и короткое замыкание четырехполюсника
При холостом ходе ток на выходе = 0 и уравнения четырехполюсника дают
При коротком замыкании напряжение на выходе = 0 и из уравнении четырехполюсника вытекает, что
Отсюда видно, что параметр А представляет собой отношение входного и выходного комплексных напряжений при холостом ходе четырехполюсника, a D — отношение входного и выходного комплексных токов при коротком замыкании.
Если при холостом ходе напряжение на выходе будет равно напряжению при нагрузке, а при коротком замыкании ток на выходе — току при нагрузке, уравнения четырехполюсника получают вид:
Следовательно, напряжение и ток I1 при любом заданном режиме работы приемника могут быть определены путем наложения соответствующих режимов холостого хода и короткого замыкания.
Чтобы осуществить это наложение, надо знать, как расположить друг относительно друга векторные диаграммы холостого хода и короткого замыкания . Для этой цели нужно измерить сдвиг фаз σ между векторами при опыте холостого хода и сдвиг фаз между векторами при опыте короткого замыкания.
После этого построение ведется в следующем порядке (рис. 9.3): строится заданная диаграмма затем под углом σ к вектору т. е. отличаются от основных уравнений четырехполюсника тем, что параметры А и D поменялись местами, строится вектор , а под углом к нему — вектор под углом β к вектору I2 строится вектор а под углом к нему — вектор После этого строятся векторы напряжения и тока на входе как суммы напряжений и токов при холостом ходе и коротком замыкании.
Так как в симметричном четырехполюснике А = D, то
т. е. угол сдвига фаз между векторами равен заданному углу сдвига фаз в нагрузке, что сразу определяет взаимное расположение векторных диаграмм холостого хода и короткого замыкания без добавочных измерений.
Указанное применение принципа наложения имеет большое значение при испытании мощных электротехнических устройств, описываемых линейными уравнениями, так как позволяет заменить опыт нагрузки, требующий источников большой мощности, опытами холостого хода и короткого замыкания при значительно меньшей мощности.
Определение параметров четырехполюсника
Если известны конкретная схема и сопротивления (проводимости) ветвей четырехполюсника, то его параметры могут быть определены расчетным путем по входным и взаимным проводимостям. Можно также исходить непосредственно из зависимостей, устанавливаемых законами Кирхгофа.
Далее в качестве примера рассмотрены простейшие схемы четырехполюсников. Так как из четырех параметров четырехполюсника независимыми являются три, простейшие схемы должны содержать три ветви, т. е. представлять собой соединение звездой (Т-образная схема, рис. 9.1, г) или треугольником (П-образная схема, рис. 9.1, д).
Для Т-образной схемы при режиме холостого хода (рис. 9.4, а) очевидны следующие соотношения:
при коротком замыкании (рис. 9.4, б)
Отсюда параметры этого четырехполюсника
Параметры П-образной схемы могут быть определены аналогичным расчетом (рис. 9.1, д). При холостом ходе
при коротком замыкании
Отсюда параметры П-схемы
Подобно тому, как при расчете цепей любой двухполюсник удобно заменить простейшим эквивалентным двухполюсником — последовательной или параллельной схемой, можно любой сложный четырехполюсник заменить простейшим эквивалентным ему, т. е. Т- или П-схемой. Решая уравнения (9.2) и (9.3), можно найти параметры этих эквивалентных схем, выразив их через параметры четырехполюсника.
Из этих выражений видно, что схемы, эквивалентные симметричным четырехполюсникам, сами тоже симметричны, так как, если А = D, то
Если конкретная схема и параметры ветвей четырехполюсника неизвестны, его параметры могут быть определены из опытов холостого хода и короткого замыкания при питании и измерениях со стороны входа и со стороны выхода. Эти измерения позволяют определить комплексы сопротивлений короткого замыкания и холостого хода при питании схемы со стороны входных зажимов — при питании схемы со стороны выходных зажимов 2′ —2″:
Как видно из этих выражений, полные сопротивления при коротком замыкании и холостом ходе связаны между собой соотношением:
поэтому из четырех вышеупомянутых опытов необходимы лишь три, а четвертый может служить для контроля.
Параметры четырехполюсника находят по формулам, вытекающим из (9.4):
Повторное сопротивление и коэффициент распространения симметричного четырехполюсника
В технике электросвязи часто применяются симметричные четырехполюсники и такое согласование их с сопротивлением нагрузки Z, при котором сопротивление между входными зажимами также равно Z, т. е.
Сопротивление Z получило название повторного. Уравнения симметричного четырехполюсника после подстановки примут вид:
Деление первого уравнения на второе дает:
откуда
и уравнения четырехполюсника, нагруженного повторным сопротивлением, будут иметь вид:
Как видно из этих уравнений, равные между собой отношения напряжений и токов на входе и выходе являются комплексным числом. Последнее может быть представлено в показательной форме:
Следовательно, у симметричного четырехполюсника, нагруженного повторным сопротивлением, выходные напряжение и ток меньше входных в раз, а их фазы — на угол β. Поэтому α называется коэффициентом затухания, β — коэффициентом фазы, — коэффициентом распространения. Коэффициент β измеряется в радианах, α—в неперах; одному неперу соответствует затухание в е = 2,718. раз.
уравнения симметричного четырехполюсника при произвольной нагрузке могут быть переписаны в другой форме:
Передаточные функции и обратные связи четырехполюсников
Как видно из предыдущего, четырехполюсник можно рассматривать как преобразователь входных величин или в выходные или . Тогда его можно характеризовать передаточной функцией К, равной отношению выходной величины к входной. Например,
Очевидно, что первая передаточная функция безразмерна, вторая имеет размерность сопротивления, третья — проводимости.
В ряде электротехнических и автоматических устройств необходимо, чтобы передаточная функция зависела от режима цепи на выходе. Для этого схема усложняется обратной связью — дополнительным четырехполюсником, питаемым выходной величиной основного четырехполюсника, например напряжением а выходная величина дополнительного четырехполюсника, например напряжение включается последовательно с источником первичного напряжения (рис. 9.5).
Пусть передаточная функция четырехполюсника обратной связи равна . Тогда входное напряжение основного четырехполюсника, передаточная функция которого
окуда передаточная функция всей системы
Из этого выражения видно, что передаточную функцию К’ системы можно изменять, регулируя передаточную функцию Ко устройства обратной связи.
Цепные схемы и электрические фильтры
Цепные схемы состоят из каскадно включенных четырехполюсников, называемых звеньями (рис. 9.6).
При этом выходные зажимы каждого предыдущего звена соединяются с входными последующего. Если все n четырехполюсника одинаковы и симметричны, а последний нагружен своим повторным сопротивлением Z, то оно будет также входным сопротивлением последнего звена, нагрузкой предпоследнего звена, его входным сопротивлением и т. д. Величина — коэффициент распространения одного звена схемы), на которую надо умножать выходные величины каждого звена, чтобы получить входные, также одинакова для всех звеньев. В результате Z является повторным сопротивлением всей цепной схемы, а ее коэффициент распространения
Тогда уравнения n-звенной цепной схемы будут:
В различных электротехнических устройствах между источником энергии и приемником включают электрические фильтры в виде четырехполюсников или цепных схем, чтобы пропустить к приемнику только токи заданного диапазона частоты.
Фильтры различаются по диапазону пропускаемых частот: низкочастотные — от 0 до заданного значения ω, высокочастотные — от ω до , полосные — от ω1 до 1 Коэффициенты часто также обозначаются через А, В, С и D.
В случае перемены направления передачи электрической энергии, а именно при передаче энергии от выводов 2 к выводам 1, в уравнениях четырехполюсника связывают напряжения и токи [см. уравнения (9-4) по форме Если заменить в (9-3) токи на —на — и решить уравнения относительно то получим уравнения четырехполюсника в форме || В ||, выраженные через коэффициенты формы || А ||. Для обратимого четырехполюсника:
Сопоставляя уравнение (9-18) с уравнениями (9-3), соответствующими направлению передачи энергии от выводов 1 к выводам 2, заключаем, что с переменой направления передачи энергии коэффициенты входящие в системы уравнений, меняются местами.
Параметры холостого хода и короткого замыкания
Было показано, что коэффициенты представляют собой входные проводимости четырехполюсника рис. 9-4, измеренные слева и справа при закороченных противоположных выводах; соответственно представляют собой входные сопротивления четырехполюсника при разомкнутых выводах.
Введя индексы «к» и «х» для обозначения режимов короткого замыкания (выводы замкнуты) и холостого хода (выводы разомкнуты), получим параметры холостого хода и короткого замыкания:
Этих параметров достаточно для составления уравнений обратимого четырехполюсника. Для записи уравнений необратимого четырехполюсника недостаточно параметров холостого хода и короткого замыкания, так как из них только три являются независимыми.
Действительно, на основании (9-19) и таблицы приложения II
и
откуда
Таким образом, параметры холостого хода и короткого замыкания, выражаемые формулами (9-19), принудительно связаны уравнением (9-20).
В случае симметричного четырехполюсника
т. е. симметричный четырехполюсник характеризуется только двумя параметрами.
Параметры холостого хода и короткого замыкания могут быть выражены через любую систему коэффициентов, например через коэффициенты А:
В свою очередь любая система коэффициентов обратимого четырехполюсника может быть выражена через параметры холостого хода и короткого замыкания. Например, для коэффициентов А получаем
и, используя (9-21), выражаем все остальные коэффициенты через
Схемы замещения четырехполюсника
На основании уравнений четырехполюсника могут быть построены различные схемы замещения, которые облегчают исследование общих свойств рассматриваемой цепи. Ниже показаны некоторые схемы замещения четырехполюсника, параметры которых выражаются через коэффициенты У, Z и А.
1 Эта формула дает двузначное решение, так как входящие в нее параметры не меняются от перекрещивания любой пары выводов.
На практике чаще всего пользуются П-образной и Т-образной схемами замещения четырехполюсника.
На рис. 9-5, а показана П-образная схема замещения четырехполюсника, в которой проводимости ветвей выражены через коэффициенты Y. При этом зависимый источник тока сохраняется в эквивалентной схеме
только в случае необратимого четырехполюсника; в схеме обратимого четырехполюсника источник тока отсутствует (см. рис. 9-6, а).
Схема рис. 9-5, о соответствует системе уравнений (9-1). Действительно, по первому закону Кирхгофа ток равен сумме токов, входящих в ветви с проводимостями Ток, входящий в первую ветвь, рдвен а ток, входящий во вторую ветвь, равен
В свою очередь ток равен сумме токов, входящих в ветви с проводимостями и тока источника Следовательно,
На рис. 9-5, б показана Т-образная схема замещения, в которой сопротивления ветвей выражены через коэффициенты Z четырехполюсника. Применив второй закон Кирхгофа, легко убедиться в тем, что данная схема соответствует уравнениям (9-2).
Схема замещения четырехполюсника содержит зависимый источник э. д. с. или тока в случае, когда четырехполюсник необратим. В схеме обратимого четырехполюсника зависимый источник отсутствует (рис. 9-6, б).
Параметры схемы замещения четырехполюсника могут быть выражены также через коэффициенты А. Так, например, пользуясь таблицей приложения II, можно в П-об-разной схеме (см. рис. 9-5, а) проводимости ветвей выразить через коэффициенты А. при этом получится схема рис. 9-5, в в случае обратимого четырехполюсника будем иметь схему рис. 9-6, а, которая часто применяется для расчета энергетических систем.
Пассивный П-образный четырехполюсник может быть преобразован в Т-образный (или наоборот) по правилу преобразования треугольника в эквивалентную звезду.
Следует заметить, что П-образ на я и Т-образная схемы замещения четырехполюсника не всегда физически реализуемы
Под физически реализуемой пассивной схемой понимается такая схема, в которой параметры r, L и С положительны. Если в какой-либо ветви схемы данное условие не выполнено, то схема физически нереализуема.
1 Это не относится к четырехполюсникам, не содержащим реактивных элементов.
Например, схема рис. 9-6, б нереализуема при отрицательном знаке действительной части т. е. если
Схемой замещения четырехполюсника может служить и мостовая схема. Мостовая схема является физически реализуемым эквивалентом для любого реально осуществимого симметричного пассивного четырехполюсника.
Схемы замещения необратимых четырехполюсников, описанные выше, применяются для анализа и расчета электрических цепей, содержащих электронные лампы и транзисторы. К этому вопросу предстоит вернуться во второй части курса.
Пример 9-1.
Рассматривая автотрансформатор (см. рис. 8-21, о) как четырехполюсник, построить для него Т-образную схему замещения.
Выбрав положительные направления токов по третьему варианту и воспользовавшись параметрами Z, найдем:
На основании рис. 9-6, б получаются следующие сопротивления ветвей Т-образной схемы:
Полученный результат совпадает с данными (см, рис. 8-21, б).
Входное сопротивление четырехполюсника при произвольной нагрузке
Обозначим через входное сопротивление четырехполюсника со стороны выводов 1, когда к выводам 2 присоединено произвольное комплексное сопротивление Z3 (рис. 9-7, а); соответственно через обозначим. входное сопротивление четырехполюсника со стороны выводов 2, когда к выводам 1 присоединено произвольное комплексное сопротивление (рис. 9-7, б).
Следовательно, входное сопротивление равно отношению напряжения к току при прямой передаче энергии:a равно отношению напряжения к-локу при обратной передаче энергии:
Входные сопротивления четырехполюсника могут быть выражены через любую систему коэффициентов четырехполюсника и комплексные сопротивления нагрузок и .
а и б — произвольная нагрузка: в и г — согласованная нагрузка.
Например, если воспользоваться системой уравнений (9-3), то, разделив первое из уравнений на второе, получим:
Аналогично при обратной передаче на основании (9-18)
Если воспользоваться таблицами приложений II и III, то можно выразить через другие коэффициенты четырехполюсника.
На практике применяются и другие выражения для . Например, в тех случаях, когда известны параметры холостого хода и короткого замыкания удобно пользоваться зависимостями от этих параметров. С этой целью выражениям (9-23) и(9-24) с учетом (9-21) придается следующий вид:
Рассмотренные выше функциональные зависимости представляют собой дробнолинейные преобразования, связывающие сопротивления на выводах четырехполюсника; они иллюстрируют одно из свойств четырехполюсника — способность преобразовывать сопротивления.
Характеристические параметры четырехполюсника
Положим, что сопротивления в схемах рис. 9-7, а и б подобраны таким образом, что и . Иначе говоря, будем считать, что существуют два сопротивления: которые удовлетворяют следующему условию: входное сопротивление четырехполюсника, нагруженного сопротивлением , равно (рис. 9-7, в); входное сопротивление четырехполюсника, нагруженного сопротивлением равно (рис. 9-7, г).
Такие два сопротивления называются характеристическими сопротивлениями несимметричного четырехполюсника.
Условие, когда четырехполюсник нагружен соответствующим характеристическим сопротивлением, называется условием согласованной нагрузки или согласованного включения.
Положив в (9-23) и (9-24)
и
получим
Совместное решение этих уравнений относительно и дает:
Введем для рассматриваемого обратимого четырехполюсника новый параметр g, удовлетворяющий условиям:
Эти условия всегда осуществимы, так как параметр g может быть комплексным. Кроме того, эти условия взаимно дополняют друг друга, так как имеющая место связь между коэффициентами (9-16) соответствует тригонометрической формуле
Параметр g в общем случае комплексный; называется мерой передачи четырехполюсника. Это — третий характеристический параметр обратимого четырехполюсника. Его действительная часть а называется собственным затуханием четырехполюсника, а мнимая часть b — коэффициентом фазы.
Физический смысл этих коэффициентов будет пояснен ниже. Выразим коэффициенты четырехполюсника формы через характеристические параметры.
На основании (9-25):
Умножение (9-26) на (9-27) и (9-28) дает:
1 Иногда этот параметр называется коэффициентом передачи, его не следует смешивать с терминами «коэффициент передачи по напряжению» и «коэффициент передачи по току». В литературе ранее применялось обозначение
Деление (9-26) на (9-27) и (9-28) дает:
В результате подстановки (9-29)—(9-32) в (9-3) получаются уравнения несимметричного обратимого четырехполюсника в гиперболической форме, соответствующие положительным направлениям токов указанным на рис. 9-4:
При согласованно подобранной нагрузке имеет место равенство
Если воспользоваться известным математическим соотношением
то уравнения (9-33) упростятся:
Отсюда следует, что при согласованно подобранной нагрузке модули напряжений и соответственно токов на входе и выходе четырехполюсника связаны уравнениями:
Множитель равен отношению амплитуд или действующих значений напряжений на входе и выходе четырехполюсника при согласованной нагрузке. В свою очередь множитель равен отношению амплитуд или действующих значений токов при той же нагрузке.
Если аргументы (углы) комплексных характеристических сопротивлений обозначить через то фазовый сдвиг напряжения на входе относительно напряжения на выходе определится величиной а фазовый сдвиг тока на выходе относительно тока на выходе — величиной
В общем случае коэффициент фазы b может быть определен как полусумма фазовых сдвигов между напряжениями и соответственно между токами на входе и выходе четырехполюсника, нагруженного согласованно. При равенстве углов и согласованно подобранной нагрузке фазовые сдвиги между напряжениями и соответственно между токами четырехполюсника одинаковы и равны b.
Характеристические параметры и g могут быть выражены через параметры холостого хода и короткого замыкания, а именно: на основании (9-21), (9-25) и (9-26)
Подстановка (9-26) в формулу ch g + sh g = приводит к выражению, связывающему характеристический параметр g с коэффициентами четырехполюсника формы ||A||,
По этой формуле g вычисляется однозначно, если подставлять под радикалы коэффициенты А в показательной форме с последующим сложением углов и делением их суммы на 2. По формуле (9-35) для тангенса принципиально невозможно получить однозначное решение, так как входные сопротивления под радикалом не изменяются от перекрещивания выводов четырехполюсника. Поэтому формула (9-36) предпочтительнее формулы (9-35) для th g.
Вычисление g по формуле для th g ведется в следующем порядке:
откуда
в результате логарифмирования
Следует отметить, что параметр g может быть также получен как половина натурального логарифма отношения произведений комплексных напряжения и тока на входе и выходе четырехполюсника при согласованной нагрузке.
Действительно, на основании (9-34)
откуда
В случае симметричного четырехполюсника характеристические сопротивленияравны друг другу:
Следовательно, входное сопротивление симметричного четырехполюсника, нагруженного характеристическим сопротивлением равно . Это означает, что всякому симметричному четырехполюснику соответствует некоторое характеристическое сопротивление обладающее следующим свойством: если нагрузить данный четырехполюсник сопротивлением то отноишия напряжения к току на входе и выходе четырехполюсника будут-одинаковыми, т. е.
На основании (9-33) уравнения симметричного четырехполюсника при произвольной нагрузке записываются в гиперболической форме (для положительных направлений рис. 9-4) так:
Если нагрузка подобрана согласованно, т. е. то
В этом случае амплитудные изменения напряжения и тока определяются множителем а фазовый сдвиг между напряжениями или токами — углом b. Собственное затухание а будет:
Величины g, а и b — безразмерные. Угол b вычисляется в радианах (рад); собственное затухание а, входящее в (9-39), принято вычислять в б е л а х (Б) или децибелах (дБ), которые определяются следующим образом.
Если полная мощность на выходе четырехполюсника в 10 раз меньше мощности на его входе, то затухание составляет 1-Б если мощность уменьшается в 100 раз, то затухание оценивается в 2 Б и т. д. Поэтому
В случае согласованно нагруженного симметричного четырехполюсника
Децибел — единица затухания, в 10 раз мейьшая бела. Затухание 1 дБ соответствует уменьшению полной мощности в 1,26 раза или уменьшению напряжения и тока в 1,12 раза.
Затуханию 1 Нп соответствует уменьшение амплитуды и действующего значения напряжения или тока в е = 2,718 раза (так как при имеем ).
Табл. 9-1 иллюстрирует зависимость затухания в децибелах от отношений полных мощностей на входе и выходе четырехполюсника;
Таблица 9-1
Затухание при различных отношениях дБ
соответствующие им отношения величин напряжений или токов симметричного четырехполюсника, нагруженного согласованно, составляют
Для перехода от децибелов к неперам или обратно можно воспользоваться приведенным выше условием:
Вносимое затухание четырехполюсника
Вносимое затухание (или усиление) является мерой оценки изменения условий передачи при включении четырехполюсника между источником и приемником.
Положим, что между источником напряжения, имеющим внутреннее сопротивление и приемником включен четырехполюсник.
Под вносимым затуханием четырехполюсника подразумевается десятикратное значение десятичного логарифма (в децибелах) или половина натурального логарифма (в неперах) отношения полной мощности 5,. которую непосредственно отдавал бы источник сопротивлению (рис. 9-8, о), к полной мощности на выходе четырехполюсника, нагруженного сопротивлением (рис, 9-8, б):
или
Мощности выражаются следующим образом:
Отношение входящее в (9-42), может быть выражено через характеристические параметры четырехполюсника и сопротивления
Пользуясь обозначениями рис. 9-8, б и уравнениями четырехполюсника, записанными в форме находим:
откуда
На основании (9-29) — (9-32)
Подстановка (9-44) в (9-43) дает:
После ряда алгебраических преобразований получается:
где
— так называемые коэффициенты отражения на входе и выходе четырехполюсника.
В связи с этим выражение (9-42) принимает следующий вид:
Следовательно, вносимое затухание состоит из пяти слагаемых. Первое слагаемое — собственное затухание четырехполюсника, второе — затухание вследствие несогласованности сопротивлений на входе четырехполюсника, третье — затухание вследствие несогласованности сопротивлений на выходе, четвертое — затухание вследствие взаимодействия несогласованностей на входе и выходе и пятое со знаком минус — затухание вследствие несогласованности сопротивлений источника и приемника.
Если вносимое затухание равно нулю, то это означает, что мощности на входе и выходе четырехполюсника равны между собой.
Когда четырехполюсник является усилителем мощности (например, в случае лампового триода или транзистора), выражения (9-40) и (9-41) дают отрицательные значения ; это указывает на то,- что вместо затухания в данном случае имеет место усиление (измеряемое в децибелах или неперах),
Передаточная функция
Передаточной функцией называется зависимость от частоты отношения комплексных амплитуд или комплексных действующих значений электрических величин на выходе и входе четырехполюсника при заданном режиме передачи. Необходимо помнить, что именно выходная электрическая величина делится на входную, а не обратно.
Передаточные функции, соответствующие отношению одноименных электрических величин, — коэффициент передачи по напряжению
и коэффициент передачи по току
представляют собой безразмерные, в общем случае комплексные, зависящие от частоты величины. Применительно к усилительным устройствам они носят название коэффициентов усиления по напряжению и току.
Отношения разноименных электрических величин — передаточное сопротивление и передаточная проводимость — имеют соответственно размерности сопротивления и проводимости и также являются в общем случае комплексными величинами, зависящими от частоты.
Зависимости модулей комплексных отношений представляют собой амплитудно-частотные, зависимости их аргументов — фазо-частотные характеристики четырехполюсника.
Под передаточной функцией понимается часто отношение операторных изображенийэлектрических величин на выходе и входе четырехполюсника»
Эти характеристики имеют важное значение для работы устройств автоматики и радиотехники.
В общем случае четырехполюсника, нагруженного произвольным сопротивлением передаточные функции могут быть выражены через любую систему коэффициентов четырехполюсника, и сопротивление
Через коэффициенты формы они выразятся следующим образом (положительные направления для токов соответствуют прямой передаче):
Н
При холостом ходе и коротком замыкании эти коэффициенты примут вид:
В случае обратной передачи, очевидно, можно написать
Отсюда видно, что для обратимого четырехполюсника коэффициент передачи по напряжению при холостом ходе и прямом направлении передачи энергии равен коэффициенту передачи по току при коротком замыкании и обратном направлении передачи энергии. В свою очередь коэффициент передачи по току при коротком замыкании и прямом направлении передачи равен коэффициенту передачи по напряжению при холостом ходе и обратном направлении передачи.
Каскадное соединение четырехполюсников, основанное на согласовании характеристических сопротивлений
На практике широко распространено каскадное или цепочечное соединение четырехполюсников, при котором входные выводы каждого последующего четырехполюсника присоединяются к выходным выводам предыдущего четырехполюсника; цепи, служащие для передачи электрической энергии (каналы связи и т. д.) обычно состоят из звеньев, следующих друг за другом.
Каскадное соединение четырехполюсников, выполненное по принципу согласования характеристических сопротивлений, заключается в том, что входное сопротивление на выводах любого четырехполюсника равно характеристическому.
Рисунок 9-9 иллюстрирует каскадное соединение двух четырехполюсников. Ввиду того что комплексное сопротивление нагрузки согласовано с выходным характеристическим сопротивлением второго четырехполюсника, входное сопротивление этого четырехполюсника равно характеристическому при этом оно служит согласованной нагрузкой для первого четырехполюсника. Поэтому входное сопротивление первого четырехполюсника также равно характеристическому
Отсюда следует, что каскадно соединенные четырехполюсники с согласованными характеристическими сопротивлениями могут быть замещены одним четырехполюсником, имеющим характеристические сопротивления, равные входному характеристическому сопротивлению первого и выходному характеристическому сопротивлению последнего четырехполюсников (рис. 9-9). Мера передачи g результирующего четырехполюсника определяется алгебраической суммой мер передачи составных четырехполюсников.
В самом деле, применительно к схеме рис. 9-9 в соответствии с (9-34)
Полученные выражения подтверждают сказанное выше: результирующий четырехполюсник имеет характеристические сопротивления и меру передачи Соответственно собственное затухание результирующего четырехполюсника а фазовый коэффициент
Было показано что передача максимума активной мощности обеспечивается, когда комплексные сопротивления источника и нагрузки являются сопряженными. Это условие не выполняется в случае согласования характеристических сопротивлений каскада в прямом и обратном направлениях, если характеристические сопротивления комплексные. Однако если они активные (включая сопротивление источника), как это нередко имеет место на практике, то обеспечивается оптимальное условие передачи мощности.
Согласование характеристических сопротивлений .широко применяется в автоматике, приборостроении и электронике.
Уравнения сложных четырехполюсников в матричной форме
Для получения параметров результирующего четырехполюсника, составленного из более простых четырехполюсников, параметры которых известны, удобно пользоваться матричной записью,
В зависимости от схемы соединения сложного четырехполюсника применяется та или иная форма уравнений, а именно:
- при каскадном соединении (рис. 9-10) —форма
- при последовательном соединении (см. рис. 9-11) — форма
- при параллельном соединении (см. рис. 9-12) — форма Каскадное соединение четырехполюсников (рис. 9-10). Уравнения
составных четырехполюсников в матричной форме
Здесь индексом а отмечены величины, относящиеся к первому четырехполюснику, а индексом 6 — величины, относящиеся ко второму четырехполюснику.
При каскадном соединении
Следовательно,
Таким образом, матрица результирующего четырехполюсника равна произведению матриц составных четырехполюсников:
Эго правило распространяется на случай каскадного соединения любого числа четырехполюсника.’ При этом матрицы, подлежащие
перемножению, записываются в порядке следования соответствующих четырехполюсников, так как умножение матриц не подчиняется переместительному закону.
Последовательное соединение четырехполюсников (рис. 9-11) Уравнения составных четырехполюсников в матричной формеимеют вид:
Таким образом, матрица результирующего четырехполюсника равна сумме матриц составных четырехполюсников:
Параллельное соединение четырехполюсника (рис. 9-12)
Уравнения составных четырехполюсников в матричной форме имеют вид:
При параллельном соединении четырехполюсников:
При параллельном соединении четырехполюсников:
Таким образом, матрица результирующего четырехполюсника равна сумме матриц Составных четырехполюсников
Правила нахождения матриц сложных четырехполюсников сведены в табл. 9-2. Они справедливы при любом числе составных четырехполюсников. Однако правила сложения матриц применимы только при равенстве токов входящего и выходящего в каждой паре выводов составных четырехполюсников, которое должно быть обеспечено тем или иным способом.
Одноэлементные четырехполюсники
Простейшими четырехполюсниками являются одноэлементные четырехполюсники, состоящие из последовательного (рис. 9-13, а) или параллельного (рис. 9-13, б) двухполюсника.
Уравнения первого из них в форме записываются следующим образом:
или, что то же,
Уравнения одноэлементного четырехполюсника с параллельной ветвью (рис. 9-13, б) в формезаписываются следующим образом:
или, что то же,
Если в первом четырехполюснике (рис. 9-13, а) положить Z = 0 или, что то же, во втором четырехполюснике (рис. 9-13, б) принять то получится уравнение
в форме
соответствующее непосредственному прямому соединению, показанному на рис. 9-14, а.
Поэтому при перекрещивании входных или выходных выводов любого четырехполюсника его матрица умножается на что равносильно перемене знаков коэффициентов А.
Г-образный четырехполюсник
Коэффициенты Г-образного четырехполюсника (см. рис. 9-15) могут быть получены непосредственно по формулам. Например, для схемы рис. 9-15, а коэффициенты формы ||Л|| согласно формулам будут:
Легко убедиться, что перекрещенному соединению (рис. 9-14, б) соответствует уравнение в формесогласно формулам будут:
Аналогично могут быть вычислены и другие коэффициенты.
Характеристические параметры Г-образного четырехполюсника могут быть вычислены по формулам (9-25) и (9-26).
Для схемы рис. 9-15, а:
Для схемы рис. 9-15, б:
При расчете электрических фильтров и в ряде других случаев за исходные схемы Г-образных четырехполюсников принимаются схемы рис. 9-15, виг, причем мера передачи Г-образного четырехполюсника обозначается через g/2, для того чтобы при согласованном каскадном соединении двух таких четырехполюсников получался Т- или П-образный четырехполюсник с мерой передачи g. При этом характеристическое сопротивление со стороны параллельной ветви обозначается через а со стороны последовательной ветви — через
На основании (9-45) или (9-46):
Эти выражения используются в теории электрических фильтров.
Т-образный и П-образный четырехполюсники
Рассматривались схемы замещения четырехполюсника и приводились схемы Т-образного и П-образного четырехполюсников. Коэффициенты таких четырехполюсников вычисляются по общей методике.
Так, для Т-образной схемы рис.
9-16 получим:
Характеристические параметры находятся по формулам (9-25) и (9-26).
Симметричные Т- и П-образные четырехполюсники можно получить согласованным каскадным соединением двух одинаковых Г-образных четырехполюсников (рис. 9-17, а и б). Результирующие четырехполюсники имеют характеристические сопротивленияопределяемые согласно (9-47), и меру передачи g, вдвое превышающую меру передачи Г-образного четырехполюсника.
С учетом (9-48) имеем:
Тот же результат получается на основании (9-26).
Симметричный мостовой четырехполюсник
Для симметричного мостового четырехполюсника (см.рис. 9-18) в соответствии с можно получить коэффициенты формы
Характеристические параметры симметричного мостового четырехполюсника находятся по формулам:
Как уже отмечалось, мостовой четырехполюсник является физически реализуемым эквивалентом для любого реально осуществимого симметричного пассивного четырехполюсника.
Обратная связь
Последовательно-параллельное соединение двух четырехполюсников представляет собой один из основных видов цепи с обратной связью, в которой напряжение на выходе воздействует на входные напряжения системы. Пусть некоторое устройство, которое назовем основным, представляет собой четырехполюсник с передаточной функцией
(рис. 9-19). Если выходное напряжение подвести к выводам другого четырехполюсника, называемого устройством обратной связи, и включить его противоположные выводы последовательно с входными выводами основного устройства, то получится система с обратной связью по напряжению.
Обозначим передаточную функцию устройства обратной связи черезОчевидно,
Следовательно, передаточная функция всей системы
или, если разделить числитель и знаменатель на
Если поменять полярность одной из пар выводов устройства обратной связи, то в знаменателе (9-51) вместо знака минус получится знак плюс.
Обратная связь, при которой напряжение, пропорциональное выходному напряжению, добавляется к входному напряжению системы так, чтоназывается положительной; если же то обратная связь называется отрицательной.
Выражение (9-51) может быть переписано так:
Если то
Это выражение показывает, что передаточная функция системы зависит от передаточной функции устройства обратной связи. Регулируя последнюю, можно воздействовать на передаточную функцию всей системы.
Методы расчета электрических цепей с использованием теории четырехполюсников
Основные теоретические сведения:
В радиотехнике обычно интересуются прохождением сигналов через произвольную сложную электрическую цепь. При этом важно установить связь между выходными и входными значениями сигнала, не рассчитывая токи и напряжения на элементах внутри цепи.
Для такого анализа цепь (или часть цепи) представляется обобщенной схемой в виде четырехполюсника. Анализ цепи в этом случае производится на основе классической теории четырехполюсников, которая устанавливает связь между токами и напряжениями, действующими на входных и выходных зажимах (полюсах).
Краткая характеристика четырехполюсников
На рис. 5.1. показан неавтономный активный четырехполюсник. В зависимости от того, какая пара переменных величин считается независимой, процессы в четырехполюсниках можно описать одной из шести форм уравнений, приведенных и табл. 5.1.
Коэффициенты уравнений характеризуют свойства четырехполюсника, зависящие только от схемы цепи и параметров ее элементов. Поэтому коэффициенты уравнения называют собственными (иногда первичными) параметрами четырехполюсника. Их можно определить экспериментально или аналитически по известной схеме цепи. Для определения параметров применяют режим холостого хода (XX) или режим короткого замыкания (КЗ) на соответствующих зажимах четырехполюсника.
Режим работы четырехполюсника выбирают так, чтобы одно из слагаемых данных уравнений (табл. 5.1) было равно нулю. Например, для выходных зажимов при XX при КЗ Далее, полагая одну из двух переменных величин (ток, напряжение) заданной, по схеме цепи рассчитывают данный параметр.
При выбранном режиме работы четырехполюсника каждый коэффициент уравнений имеет конкретный физический смысл. Например, из уравнений в форме Y (табл. 5.1) видно, что каждый коэффициент равен отношению тока к напряжению. Поэтому по физическому смыслу Y-параметры являются входными или передаточными проводимостями. В этом смысле Z- параметры являются входными или передаточными сопротивлениями.
А- и В-параметры называют передаточными, так как по физическому смыслу они являются передаточными сопротивлениями (проводимостями) или коэффициентами передачи по напряжению (току). Параметры вида Н и G называются гибридными, так как они содержат входные сопротивления (проводимости) и коэффициенты передачи по напряжению (току).
В общем случае четырехполюсник характеризуется четырьмя параметрами. Для взаимных и симметричных четырехполюсников число параметров уменьшается, так как могут быть два параметра, равных по величине. Условия взаимности и симметричности четырехполюсников для различных собственных параметров приведены в табл. 5.2.
Любая система параметров может быть выражена через каждую из других пяти систем (табл.5.3). Например, в справочнике приведены Н-параметры транзистора, а для расчета цепи необходимо знать Y-параметры транзистора. В этом случае необходимо воспользоваться формулами, расположенными на пересечении строки Y и столбца Н (табл. 5.3):
где Н — определитель матрицы Н-параметров.
Использование собственных параметров четырехполюсника позволяет при расчете любую электрическую цепь представить эквивалентной схемой замещения.
На рис. 5.2 показаны схемы замещения на базе Y-, Z- и Н-параметров. Наиболее часто схемы замещения применяют для описания электрических приборов (триодов, транзисторов), включенных в электрическую цепь.
Собственные параметры четырехполюсника не учитывают влияние внешних цепей (источника и нагрузки). Для расчета четырехполюсника с учетом этих целей применяют комплексные функции, которые иногда называют вторичными или рабочими параметрами. Эти параметры выражают через собственные параметры Y или Z.
Если источник задан напряжением или током на входе четырехполюсника, то при расчете необходимо учитывать только нагрузку. Комплексные входные и передаточные функции для этого случая приведены соответственно в табл. 5,4 и 5.5.
Расчет в ряде случаев удается упростить, если цепь представить в виде сложного четырехполюсника. Основные виды соединения двух простых четырехполюсников показаны в табл. 5.6. Матрицы параметров некоторых простых четырехполюсников приведены в табл. 5.7 и 5.8.
Примеры решения задач:
Пример 5.1.1.
Для четырехполюсника (рис. 5.3, а) определить А-параметры. Y- и Z-параметры найти по связям с полученными параметрами.
Дано:
Решение
1. Строим схемы для холостого хода и короткою замыкания на зажимах 2—2′ (рис. 5.3, б, в).
Для режима холостого хода система уравнений вида А примет вид:
Отсюда
Для определении на вход цепи рис. 5.3,6 подаем и определяем
При расчете задаемся и находим (рис. 5.3, б)
Для режима короткого замыкания система уравнений вида А примет вид
Для определения на вход цепи (рис. 5.3, в) подаем и находим . Из схемы видно, что поэтому
Подставляя по значение в исходную формулу, получаем
можно найти из соотношения
т.е.
2. Рассчитаем Y- и Z-параметры по формулам связи с А-параметрами (см. табл. 5.3):
Пример 5.1.2.
Найти матрицу А низкочастотного фильтра, изображенного на рис. 5.4, пользуясь матрицами элементарных четырехполюсников.
Решение
1. Определяем матрицу элементарного четырехполюсника (см. табл. 5.7)
2. Находим матрицу элементарного четырехполюсника (см. табл. 5.7)
3.Рассчитаем матрицу А сложного четырехполюсника при каскадном включении элементарных четырехполюсников
Пример 5.1.3.
Определить комплексную передаточную функцию по напряжению реактивного фильтра нижних частот (см. рис. 5.4), нагруженного на активное сопротивление .
Решение
1. Рассчитаем Y-параметры ненагруженного четырехполюсника. Из табл. 5.8 определим
2.Комплексную передаточную функцию по напряжению нагруженного четырехполюсника определим по формуле (см. табл. 5.5).
Учитывая, что , получаем
Методы расчета линейных активных цепей с использованием теории четырехполюсников
Основные теоретические сведения:
Цепи с электронными приборами (электронными лампами, транзисторами, операционными усилителями и т.п.), способные в определенных режимах усиливать по мощности входной сигнал, называются активными. Вследствие нелинейности вольт-амперных характеристик (ВАХ) электронных приборов такие цепи, строго говоря, являются нелинейными. Если амплитуда входного сигнала мала, а рабочая точка выбрана на линейном участке ВАХ прибора, id активные цели можно рассматривать как линейные.
В этом случае их анализ производят методами теории линейных электрорадиоцепей.
Для расчета линейных электрических цепей активные элементы заменяют их моделями, которые с определенной степенью точности отражают происходящие в них физические процессы. Paзличают математические (аналитические) и электрические модели электронных приборов. При расчете линейных активных цепей (ЛАЦ) известными методами теории цепей используют электрические модели, т. е. эквивалентные электрические схемы активных элементов. Обычно применяют два вида эквивалентных схем электронных приборов — физическую и схему на базе собственных параметров четырехполюсника.
Физическая эквивалентная схема строится на основе структуры прибора и принципа его работы, т. е. на основе так называемых физических параметром.
Рассмотрим эквивалентные схемы трех основных видов электронных приборов, применяемых для усиления сигналов. Способность прибора усиливать сигнал отражается включением в эквивалентную схему зависимого источника тока или напряжения.
На рис.5.9 схематически показано устройство плоскостного биполярного транзистора и его условное графическое изображение. В электрическую цепь транзистор может быть включен по схеме с обшей базой (ОБ), но схеме с общим эмиттером (ОЭ) или по схеме с общим коллектором (ОК). В табл. 5.9 приведены физические эквивалентные схемы биполярного транзистора для трех схем включения.
Элемент , схемы является дифференциальным сопротивлением эмиттерного перехода в прямом направлении, — дифференциальное сопротивление коллекторного перехода в обратном направлении, — сопротивление объема полупроводника базы. Обычно в транзисторах
В общем случае все физические параметры являются частотно-зависимыми. Этот факт учитывается включением в электрическую модель емкостей эмиттера и коллектора. Эти емкости достаточно малы, поэтому их влияние необходимо учитывать лишь на высоких частотах. Наиболее вредной является емкость коллектора шунтирующая источник.
В рассматриваемых схемах усилительные свойства отображены зависимыми источниками тока в цепи коллектора, которые выражены через коэффициент передачи тока;
Зависимый источник можно выразить также через коэффициент передачи тока базы:Так как то
В современных транзисторах ток базы мал по сравнению с током эмиттера. Обычно поэтому
На рис.5.10 приведены условное графическое изображение и физическая эквивалентная схема электровакуумного триода.
Эквивалентная схема характеризуется физическими параметрами: входным и внутренним сопротивлениями триода переменному току и межэлектродными емкостями, которые пунктиром показаны на условном графическом изображении. Для большинства триодов эти емкости имеют значения от 2 до 15 пФ, поэтому на низких частях их можно не учитывать.
Величины входного и внутреннего сопротивлений зависит от режима работы триода. Обычно на сетку подается отрицательное относительно катода напряжение. При этом ток сетки близок к нулю, а входное сопротивление велико – единицы – десятки мегаом. Внутреннее сопротивление триода при работе в линейном режиме обычно лежит в пределах от 10 до 30 кОм.
Зависимый источник тока в эквивалентной схеме определяется крутизной S вольт-амперной характеристики и напряжением между сеткой и катодом:
где — ток анода.
Важным параметром триода является коэффициент усиления
где — напряжение между анодом и катодом.
Современные триоды имеют коэффициент усиления от 3 до 100 и крутизну от 1 до 50 мА/В.
Рассмотренная физическая эквивалентная схема соответствует включению триода и цепь по наиболее распространенной схеме с общим катодом. Кроме того, триод может включаться в цепь по схеме с общим анодом или с обшей сеткой.
Полевой (униполярный, канальный) транзистор является полупроводниковым аналогом электровакуумного триода. На рис.5.11 схематически показано устройство полевого транзистора с управляющим переходом и каналом типа, а также его условное графическое изображение.
Сетке триода соответствует затвор (3) транзистора, катоду -исток (И), аноду – сток (С).
Физическая эквивалентная схема этого транзистора, включенного на схеме с общим истоком, показана на рис. 5.12. Видно, что эта схема аналогична схеме триода. Зависимый источник тока характеризуется крутизной ВАХ и напряжением между затвором и истоком:
где — ток стока.
Величина внутреннего сопротивления может достигать сотен килоом.
Второй тип эквивалентных схем электронных приборов основан на представлении их линейными невзаимными четырехполюсниками. В этом случае параметрами активных элементов являются коэффициенты уравнений четырехполюсников (см. табл. 5.1). Поэтому эквивалентными схемами электронных приборов являются схемы замещения четырехполюсников на базе соответствующих параметров (см. рис. 5.2). Аналогично физическим эквивалентным схемам усилительные свойства электронных приборов отражаются зависимыми источниками.
В настоящее время основными параметрами транзисторов считаются гибридные Н-параметры, так как они наиболее просто измеряются. Именно эти параметры приводятся во всех справочниках. При расчете некоторых цепей удобнее применять Y-napaметры. Переход от одних параметров к другим производится по известным формулам связи собственных параметров четырехполюсников разных систем (см. табл. 5.3).
Н- и Y-параметры называются низкочастотными мало сигнальными, так как они справедливы лишь на низких частотах и для входных сигналом с малыми амплитудами. При работе электронных приборов на низких частотах все их параметры являются вещественными.
Параметры электронных приборов как четырехполюсников, в отличие от физических параметров, существенно зависят от схемы включения прибора в цепь. Поэтому к цифровому индексу параметра добавляют соответствующую букву.
Например, матрицы Н-параметров транзисторов, включенных по схеме с ОЭ и по схеме с ОБ, соответственно имеют вид:
Аналогично записываются матрицы Y-параметров.
Зная параметры прибора для одной схемы включения, можно найти его параметры для другой схемы. В табл. 5.10 приведены формулы, связывающие -параметры транзистора при различных схемах включения в цепь.
Н-параметры так же, как и Y-параметры, непосредственно связаны с физическими параметрами электронного прибора. Некоторые формулы, определяющие эту связь для биполярных транзисторов, приведены в табл. 5.11 и 5.12.
Отметим физический смысл Н-параметров транзистора, который следует из уравнений четырехполюсника в форме Н (см. табл. 5.1).
В систему Н-параметров входят величины:
. — входное сопротивление при коротком замыкании выходных зажимов транзистора
— коэффициент обратной связи по напряжению при холостом ходе на входных зажимах;
— коэффициент передачи тока ( или в зависимости от схемы включения) при
— выходная проводимость транзистора при холостом ходе на входе
По физическому смыслу выходная проводимость есть внутренняя проводимость транзистора;
Для полевого транзистора или электровакуумного триода эквивалентную схему можно упростить. Наиболее часто эти приборы включают в цепь по схеме с общим катодом (истоком). При этом входное сопротивление велико, поэтому ток сетки (затвора) близок к нулю.
Из уравнений в форме (см. табл. 5.1) видно, что Поэтому эти активные элементы характеризуются двумя параметрами:
Расчет линейных активных целей (ЛАЦ) с использованием рассмотренных эквивалентных схем активных элементов может производиться по известным методам. В настоящее время наиболее часто применяют MУH, MKT, метод сигнальных графов.
Введение в эквивалентные схемы активных элементов зависимых (управляемых) источников позволяет исключить из расчета независимые источники цепи (источники питания), которые обеспечивают заданный режим работы. При этом зависимые источники работают на частоте сигнала, подаваемого на вход цепи.
Таким образом, при расчете полагают, что в цепи действует один независимый источник сигнала на входе. Поэтому расчет цепи проводят обычным способом, определяя заданные токи (напряжения) или комплексные функции.
Особенность расчета ЛАЦ по MKT или МУН состоит в следующем. Электрическая схема цепи заменяется эквивалентной схемой, в которой активные элементы заменяются физическими эквивалентными схемами или схемами на базе параметров четырехполюсника. Далее, в соответствии с выбранным методом расчета составляются по общим правилам контурные или узловые уравнения.
Например, допустим, что схема имеет три независимых контура. Источник сигнала включен в первый контур, а зависимый источник электронного прибора находится в третьем контуре. В соответствии с MKT система контурных уравнений в матричной форме будет иметь вид
В этом случае матрица контурных сопротивлений описывает только пассивные элементы цепи. Условимся называть такие матрицы матрицами пассивной части цепи и обозначим соответственно или Эти матрицы являются симметричными относительно главных диагоналей, т. е.
Зависимые источники активных элементов неизвестны, они определяются токами (напряжениями) в цепи. Поэтому их необходимо выразить через контурные токи (при MKT) или через узловые напряжения (при МУН) и перенести в соответствующие элементы правой части уравнений.
После преобразований все уравнения, кроме первого, будут иметь нулевые правые части. При этом матрица Z или Y характеризует цепь с учетом активных элементов. Такую матрицу будем называть полной.
Так как электронной прибор является невзаимным (однонаправленным), то полная матрица будет несимметричной, т. е. в общем случае
Полная матрица Z или Y позволяет но известным формулам через определители рассчитать любую комплексную функцию цепи.
Эти методы расчета обычно называют методами эквивалентных схем. Они отличаются наглядностью, простатой и логичностью действий, позволяют использовать любые эквивалентные схемы активных элементов. Однако их применение ограничено, так как для сложных многокаскадных цепей метод становится громоздким.
Представление зависимых источников через искомые точки или напряжения, перенос этих величин в левые части уравнений имеют общие закономерности. Исследования этих закономерностей позволило обобщить (формализовать) методы расчета. Суть обобщения состоит в том, что можно по известным правилам составлять полную матрицу сопротивлений (проводимостей) цепи, не составляя систему уравнений.
Рассмотрим обобщенный метод узловых напряжений (ОМУН). Сущность этого метода состоит в следующем. Электронные приборы в схеме заменяют физической эквивалентной схемой, затем по известным правилам определяют независимые узлы и для них составляют матрицу пассивной части цепи, включая физические параметры электронного прибора. Далее в эту матрицу вписывают так называемые управляющие параметры, учитывающие зависимые источники активных элементов. Полученная в результате этого матрица является полной матрицей активной линейной цепи, позволяющей произвести расчет заданных величин.
Управляющим параметрам называют коэффициент (по модулю) при узловом напряжении, которое создает ток зависимого источника активного элемента. Он рассчитывается непосредственно из выражения для зависимого источника тока.
Для биполярного транзистора Ток эмиттера зависит от сопротивления ветви эмиттера (внутреннего и внешнего) и от приложенного к ней узлового напряжения. Например, если то
Проводимость и является управляющим параметром, который вписывается в два элемента матрицы . В общем случае ток эмиттера может определяться разностью двух узловых напряжений: В этом случае управляющий параметр необходимо вписать в четыре элемента матрицы.
Номера строк этих элементов определяются номерами узлов цепи, к которым подключен зависимый источник тока , а номера столбцов – номерами узловых напряжений, создающих этот ток. Например, пусть источник включен между узлами 3 и 5, а управляется он узловым напряжением . Тогда управляющий параметр необходимо вписать в элементы матрицы.
Параметр вписывают со знаком плюс, если источник и напряжение относительно своих углов направлены одинаково. Например, в элемент параметр необходимо вписать со знаком плюс, если ток источника направлен к узлу 5, а напряжение — к узлу 3 (или оба направлены от узлов). В противном случае необходимо ставить знак минус.
Необходимо помнить, что при определении направления напряжения относительно -го узла необходимо учитывать его знак в формуле для расчета эмиттерного тока.
Для расчета ЛАЦ применяют также другой вариант ОМУН, принципиально отличающийся от рассмотренного выше. Сущность этого метода состоит в следующем. Для расчета составляют эквивалентную схему цепи, из которой исключают все активные элементы. Точки включения электродов этих элементов на схеме считаются узлами. Для этой схемы по известным правилам МУН составляют матрицу
Электронные приборы описывают матрицами Y-параметров. Для получения полной матрицы цепи элементы матрицы Y-napaметров необходимо вписать в одноименные элементы матрицы Далее расчет ведется обычным способом.
Если электронный прибор включен в цепь определенно, т. е. по схеме с общим электродом, то он характеризуется четырьмя параметрами, например:
В общем случае электронный прибор включается в цепь неопределенно, т. е. без общего электрода. При этом на всех электродах имеется напряжение относительно базисного узла (относительно земли).
Пример неопределенного включения транзистора показан на рис. 5.13. В этом случае транзистор описывается не четырьмя, а девятью Y-параметрами. Такая матрица формируется на основе параметров транзистора с определенной схемой включения. Для схемы, прицеленной на рис. 5.13, матрица Y-параметров транзистора имеет вид:
Можно показать, что такая матрица является неопределенной, т. е. суммы ее элементов в каждой строке и в каждом столбце тождественно равны нулю. На основании этого свойства определяют дополнительные параметры. Например: и.т.д.
Чтобы получить правильную полную матрицу проводимостей ЛАЦ, необходимо знать правила вписывания Y-параметров электронных приборов. Если, например, электроды транзистора включены к узлам с номерами то строки и столбцы неопределенной матрицы необходимо обозначить соответственно этими же номерами (см. ). Тогда элементы этой матрицы вписываются в элементы матрицы имеющие те же номера.
Примеры решения задач:
Пример 5.2.1.
Рассчитать комплексный коэффициент передачи по напряжению однокаскадного транзисторного усилителя (рис. 5.14) методом контурных токов (MKT). Транзистор представить физической схемой замещения.
Решение
1. Составим эквивалентную схему транзисторного усилителя по переменному току (рис. 5.15).
2. Выполним эквивалентные преобразования сопротивлений в схеме (рис. 5.16).
3. Выберем независимые контуры и зададим положительное направление контурных токов в них (рис. 5.16).
4. Составим систему уравнении по MKT:
5. Выразим ток эмиттеpa через контурный ток
6. Подставим ток эмиттера в уравнения
7. Сгруппируем подобные слагаемые в уравнениях
.
8. Рассчитаем ток по формуле Крамера
9. Рассчитаем выходное напряжение транзисторного усилителя
10. Рассчитаем комплексный коэффициент передачи по напряжению транзисторного усилителя
Пример 5.2.2.
Рассчитать комплексный коэффициент передачи по напряжению однокаскадного транзисторного усилителя (рис. 5.17) MKT. Транзистор представить схемой замещения на базе Н-параметров.
1. Составим эквивалентную комплексную схему транзисторного усилителя по переменному току (рис. 5.18).
2.Выполним эквивалентные преобразования сопротивлений в схеме и преобразуем источник тока в эквивалентный источник ЭДС (рис. 5.19):
3. Выберем независимые контуры и зададим положительное направление в них контурных токов.
4. Составим систему уравнений по MKT:
5. Выразим ток и напряжение через контурные токи:
6. Подставим их выражения в уравнения:
7. Сгруппируем подобные слагаемые в уравнениях:
8. Рассчитаем комплексный ток третьего контура
9. Рассчитаем выходное напряжение транзисторного усилителя
10. Рассчитаем комплексный коэффициент передачи по напряжению транзисторного усилителя
Пример 5.2.3. Рассчитать комплексный коэффициент передачи по напряжению однокаскадного транзисторного усилителя (рис. 5.20) ОМУН. Транзистор представить физической схемой замешения.
Решение
1. Составим эквивалентную комплексную схему транзисторного усилителя по переменному току (рис. 5.21).
2. Выберем независимые углы и зададим положительное направление узловых напряжений.
3. Составим матрицу проводимостей пассивной части схемы.
4. Определим управляющий параметр. Из схемы видно, что поэтому источник тока
Отсюда получим управляющий параметр:
5. Впишем управляющий параметр в матрицу
Источник тока включен в узлы 3 и 4, а управляется он узловым напряжением третьего узла . Поэтому параметр необходимо вписать в элементы матрицы
Ток источника направлен от yзла 3, а напряжение с учетом знака в формуле (5.1) направлено к. узлу. Поэтому в элемент параметр вписывается со знаком минус. Рассуждая аналогично, найдем, что в элемент параметр необходимо вписать со знаком плюс. После вписывания получим полную матрицу Y проводимостей усилителя
6. Рассчитаем комплексный коэффициент передачи усилителя по формуле (см. табл. 4.1)
где — алгебраические дополнения полной матрицы проводимостей, получаемые из нее путем вычеркивания соответствующих строк (в данном случае первой) и столбцов (первого и четвертого соответственно).
Пример 5.2.4.
Рассчитать Y-параметры транзистора — 623 В.
Дано:
Решение
1. Рассчитаем параметр транзистора по формуле (см. табл. 5.9)
2. Рассчитаем -параметры транзистора, включенного в схему с общей базой, по формулам пересчета параметров (см. табл. 5.3):
3. Используя основное свойство неопределенной матрицы, составим матрицу Y-параметров транзистора
4. Составим матрицу -параметров транзистора, включенного по схеме с общим эмиттером
Пример 5.2.5.
Рассчитать комплексный коэффициент передачи по напряжению однокаскадного транзисторного усилителя (см. рис. 5.20) ОМУН. Транзистор описать матрицей Y-параметров.
Решение
1.Составим эквивалентную комплексную схему однокаскадного транзисторного усилителя без учета транзистора (рис. 5.22).
2. Выберем независимые узлы и зададим положительное направление узловых напряжений.
3. Составим матрицу проводимостей пассивной части схемы
4. Впишем матрицу проводимостей пассивной части схемы в матрицу Y-параметров транзистора, включенного по схеме с общим эмиттером
5. Рассчитаем комплексный коэффициент передачи по напряжению
Пример 5.2.6.
Рассчитать комплексный коэффициент передачи по напряжению однокаскадного транзисторного усилители (рис. 5.23) МУН. Транзистор представить схемой замещения на базе Y-параметров. Построить АЧХ усилителя в диапазоне
Дано:
Решение
1. Составим эквивалентную комплексную схему транзисторного усилителя по переменному току (рис. 5.24).
2. Выберем независимые узлы и зададим положительное направление узловых напряжений.
3. Составим систему уравнений по МУН
4. Выразим напряжения через узловые напряжения:
5. Подставим значения напряжений в систему уравнений (5.2):
6. Сгруппируем подобные слагаемые в уравнениях (5.3):
7. Запишем матрицу проводимостей из полученной системы уравнений (5.4)
8. Подставим числовые значения и матрицу проводимостей
9. Рассчитаем комплексный коэффициент передачи по напряжению:
После подстановки и преобразований получим
Модуль комплексного коэффициента передачи определяется выражением
10. Рассчитаем значения модуля комплексного коэффициента передачи по напряжению и диапазоне частот
По результатам расчета построим график АЧХ и среде Mathcad (рис. 5.25).
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Линейные диаграммы
- Круговые диаграммы
- Цепи с взаимной индукцией
- Трехфазные цепи
- Нелинейные электрические цепи
- Магнитные цепи и их расчёт
- Цепи переменного тока
- Символический метод расчета цепей
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
№75 Уравнения четырехполюсника.
Четырехполюсником называется часть электрической цепи или схемы, содержащая два входных вывода (полюса) для подключения источника энергии и два выходных вывода для подключения нагрузки. К четырехполюсникам можно отнести различные по назначению технические устройства: двухпроводную линию, двухобмоточный трансформатор, фильтры частот, усилители сигналов и др.
Теория четырехполюсников устанавливает связь между режимными параметрами на входе (U1, I1) и режимными параметрами на его выходе (U2, I2), при этом процессы, происходящие внутри четырехполюсника, не рассматриваются. Таким образом, единая теория четырехполюсника позволяет анализировать различные по структуре и назначению электрические цепи, которые могут быть отнесены к классу четырехполюсников.
Если четырехполюсник не содержит внутри себя источников энергии, то он называется пассивным (обозначается буквой П), если внутри четырехполюсника имеются источники, то он называется активным (обозначается буквой А).
В настоящей главе анализируются пассивные линейные четырехполюсники. На электрических схемах четырехполюсники условно обозначаются прямоугольником с двумя парами выводов: 1 и 1′ – входные выводы, 2 и 2′ – выходные выводы (рис. 75.1). Соответственно напряжение и ток на входе индексируются цифрой 1 (U1, I1) , а на выходе – цифрой 2 (U2, I2).
Установим связь между параметрами режима входа (U1, I1) и выхода (U2, I2). Для этой цели согласно теореме о компенсации заменим нагрузку Z2 источником ЭДС Е2 = U2 = I2Z2 и найдем токи по методу наложения от каждого ис¬=точника в отдельности (рис. 75.2 а, б):
где Y11, Y22 – входные проводимости входа и выхода, Y12 = Y21 – взаимная проводимость между входом и выходом.
Выразим из полученных уравнений режимные параметры на входе:
– комплексные кэффициенты четырехполюсника
С учетом принятых обозначений система основных уравнений четырехполюсника получит вид
Система основных уравнений четырехполюсника формы А:
Уравнения четырехполюсника часто записывают в матричной форме:
где матрица коэффициэнтов формы А:
Выразим соотношение между коэффициентами четырехполюсника:
A•D – B•C=1 – уравнение связи между коэффициентами. Уравнение связи показывает, что независимыми являются только три из четырех коэффициентов четырехполюсника.
Поменяем местами в схеме рис. 75.1 источник и приемник энергии. В новой схеме рис. 75.3 направления токов изменятся на противоположные.
Уравнения четырехполюсника с учетом изменения направлений токов примут вид:
Преобразуем полученную систему уравнений следующим образом. Умножим члены уравнения (1) на D, члены уравнения (2) на В и вычтем почленно из 1-го уравнения 2-ое. В результате получим:
Умножим члены уравнения (1) на С, члены уравнения (2) на А и вычтем из 1-го уравнения 2-ое. В результате получим:
Новая система уравнений четырехполюсника получила название формы В:
Четырехполюсник называется симметричным, если перемена местами входных и выходных выводов не влияет на режим остальной цепи, частью ко¬торой является четырёхполюсник. Для симметричного четырёхполюсника выполняются следующие условия:
Кроме названных форм уравнений четырехполюсника А и В применяются на практике еще четыре формы, а именно формы Z, Y, H и G. Структура этих уравнений приведена ниже:
– система основных уравнений четырехполюсника формы Z:
– система основных уравнений четырехполюсника формы Y:
– система основных уравнений четырехполюсника формы H:
– система основных уравнений четырехполюсника формы G:
Для уравнений формы Z, Y, H и G принята следующая ориентация токов и напряжений относительно выводов четырехполюсника (рис.75.4).
Соотношения между коэффициентами четырехполюсника различных форм приводятся в справочной литературе, однако их нетрудно получить, выполнив преобразование одной формы уравнений в другую. Например, пусть заданы коэффициенты формы А (А, В, С, D) и требуется определить коэффициенты формы Z(Z11, Z12, Z21, Z22). Для этого в уравнениях формы A изменим знак тока I2 и решим их относительно переменных U1 и U2:
Сравнивая полученные выражения с уравнениями четырехполюсника формы Z, находим соотношения между коэффициентами двух форм:
[spoiler title=”источники:”]
http://www.evkova.org/chetyirehpolyusniki
http://toehelp.com.ua/lectures/075.html
[/spoiler]
