Звуковая волна – период, длина, частота и скорость распространения
Калькуляторы онлайн перевода длины звуковой, инфразвуковой или ультразвуковой
волны в частоту и наоборот. Таблица соответствия
нот полного звукоряда частотам.
Звуковая волна – это механические колебания, которые в результате колебаний молекул вещества распространяются в какой-либо
среде (в газе, жидкости или твёрдом теле) и, достигнув органов слуха человека, воспринимаются им как звук. Источник, создающий
возмущение (колебания воздуха), называется источником звука.
Как уже было сказано, для распространения звука необходима какая-либо упругая среда. Поэтому в вакууме ори, не ори – тебя никто не
услышит, по причине того, что звуковые волны распространяться не смогут, так как там нечему колебаться.., да и слушать там, по большому
счёту, тоже некому.
Так же, как и в случае с электромагнитными волнами, соотношение, связывающее длину звуковой волны с частотой колебаний,
в общем случае выглядит следующим образом:
λ (м) = V (м/сек) / F (Гц), где V (м/сек) – это скорость распространения
звука в среде.
Период колебаний также не претерпел никаких изменений и по-прежнему равен:
T(сек) = 1 / F (Гц) = λ (м) / V (м/сек).
Частота колебаний звукового сигнала F (Гц) – это параметр стабильный, практически не зависящий от среды распространения.
А вот скорость звука V (м/сек), а соответственно и длина звуковой волны – это величины, которые зависят
не только от плотности вещества, но и от его упругости, а в случае с жидкостями и газами ещё – и от температуры, и атмосферного
давления.
Зависимость скорости звуковой волны от свойств упругой среды легко прослеживается по следующей формуле:
V (м/сек) = √Eупр (паскаль) / ρ (кг/м3)
,
где Eупр представляет собой модуль объёмной упругости среды, а ρ – плотность среды.
Модуль упругости, так же как и плотность – это справочные величины, прописанные для конкретных материалов.
В качестве примера, ниже приведена таблица величины скорости распространения звука в различных средах:
| Среда | Скорость звука, м/сек |
| Воздух при 0° | 331 |
| Воздух при 30° | 350 |
| Вода | 1450 |
| Медь | 3800 |
| Дерево | 4800 |
| Железо | 4900 |
| Сталь | 5600 |
Для газов параметры модуля объёмной упругости и плотности имеют ярко выраженную зависимость от температуры и атмосферного давления.
Если углубиться, то скорость звука в газах можно вычислить по следующей формуле:
V (м/сек) = √γ*Ратм / ρ ,
где
γ = cp/сv – это отношение удельной теплоёмкости при постоянном давлении
к удельной теплоёмкости при постоянном объёме, а Pатм – атмосферное давление,
которое связано с температурой газообразной среды.
Поэтому, чтобы никого сильно не грузить, приведу и приближённую зависимость скорости звука (при нормальном
атмосферном давлении) от температуры среды:
V (м/сек) = (331 + 0,6 * T°), где 331 м/сек – это скорость звука при 0°С,
а T° – температура в градусах Цельсия.
Теперь можно совместить формулы и получить простое соотношение, связывающее длину звуковой волны с частотой колебаний с учётом
температуры среды:
λ (м) = (331 + 0,6 * T°) / F (Гц).
Всё это без лишнего напряга несложно посчитать при помощи листа бумаги или деревянных счёт, ну а для пущего упрощения жизни человека,
приведу и пару он-лайн считалок для перевода одного из параметров в другой.
Калькуляторы предполагают расчёты длины и частоты звуковой волны для воздушной среды при нормальном атмосферном
давлении (760 мм ртутного столба).
Онлайн калькулятор расчёта длины звуковой волны по частоте
|
Частота звуковых колебаний f |
||
Температура Т(°С) (по умолчанию 20°) |
||
Длина волны |
Онлайн калькулятор расчёта частоты по длине звуковой волны
|
Длина волны λ при заданной Т |
||
Температура Т(°С) (по умолчанию 20°) |
||
Частота колебаний |
Полный диапазон звуковых частот условно находится в пределах:
16…20 000 Гц.
Ниже ( 0,001…16Гц ) – инфразвук.
Выше ( 20…100кГц ) – низкочастотный ультразвук,
ещё выше (100кГц…1МГц) – высокочастотный ультразвук.
А для интересующихся приведу таблицу соответствия нот стандартного музыкального звукоряда частотам.
| Частота (Гц) | ||||||||||||
| Октава | Нота | |||||||||||
| До | До – диез | Ре | Ми – бемоль | Ми | Фа | Фа – диез | Си | Си- диез | Ля | Соль-бемоль | Соль | |
| C | C# | D | Eb | E | F | F# | G | G# | A | Bb | B | |
| 0 | 16.35 | 17.32 | 18.35 | 19.45 | 20.60 | 21.83 | 23.12 | 24.50 | 25.96 | 27.50 | 29.14 | 30.87 |
| 1 | 32.70 | 34.65 | 36.71 | 38.89 | 41.20 | 43.65 | 46.25 | 49.00 | 51.91 | 55.00 | 58.27 | 61.74 |
| 2 | 65.41 | 69.30 | 73.42 | 77.78 | 82.41 | 87.31 | 92.50 | 98.00 | 103.8 | 110.0 | 116.5 | 123.5 |
| 3 | 130.8 | 138.6 | 146.8 | 155.6 | 164.8 | 174.6 | 185.0 | 196.0 | 207.7 | 220.0 | 233.1 | 246.9 |
| 4 | 261.6 | 277.2 | 293.7 | 311.1 | 329.6 | 349.2 | 370.0 | 392.0 | 415.3 | 440.0 | 466.2 | 493.9 |
| 5 | 523.3 | 554.4 | 587.3 | 622.3 | 659.3 | 698.5 | 740.0 | 784.0 | 830.6 | 880.0 | 932.3 | 987.8 |
| 6 | 1047 | 1109 | 1175 | 1245 | 1319 | 1397 | 1480 | 1568 | 1661 | 1760 | 1865 | 1976 |
| 7 | 2093 | 2217 | 2349 | 2489 | 2637 | 2794 | 2960 | 3136 | 3322 | 3520 | 3729 | 3951 |
| 8 | 4186 | 4435 | 4699 | 4978 | 5274 | 5588 | 5920 | 6272 | 6645 | 7040 | 7459 | 7902 |
Random converter
- Калькуляторы
- Акустика — звук
Калькулятор звуковой частоты и длины волны
Этот калькулятор определяет длину волны звуковых колебаний (только звуковых!), если известны их частота и скорость распространения звука в среде. Он также может рассчитать частоту, если известны длина волны и скорость или скорость звука, если известны частота и длина волны.
Пример: Рассчитать длину звуковой волны, распространяющейся в морской воде от гидроакустического преобразователя с частотой 50 кГц, если известно, что скорость звука в соленой воде равна 1530 м/с.
Частота
f
Длина волны
λ
Скорость звука
v
или Среда
Поделиться ссылкой на этот калькулятор, включая входные параметры
Для расчета выберите среду или введите скорость звука, затем введите частоту и нажмите кнопку Рассчитать для расчета длины волны. Можно также ввести длину волны и рассчитать частоту.
Определения и формулы
Звук — это волновой процесс. Если струна скрипки или арфы колеблется, в окружающем ее воздуха образуются зоны сжатия и разрежения, которые и представляют собой звук. Эти зоны сжатия и разрежения перемещаются по воздуху в форме продольных волн, которые имеют ту же частоту, что и источник звука. В продольных волнах молекулы воздуха движутся параллельно движению волны. Воздух сжимается в том же направлении, в котором распространяются звуковые волны. Эти волны передают энергию голоса или колеблющейся струны. Отметим, что воздух не перемещается, когда звуковая волна проходит через него. Перемещаются только колебания, то есть зоны сжатия и разрежения. Более громкие звуки получаются при более сильных сжатиях и разрежениях.

Спектр звуковых колебаний. 1 — землетрясения, молнии и обнаружение ядерных взрывов; 2 — акустический диапазон; 3 — Слух животных; 4, Ультразвуковая очистка; 5. Терапевтическое применение ультразвука; 6 — Неразрушающий контроль и медицинская ультразвуковая диагностика; 7 — Акустическая микроскопия; 8 — Инфразвук; 9 — Слышимый диапазон; 10 — Ультразвук
Количество этих колебаний в секунду называется частотой и измеряется в герцах. Период колебаний — это длительность одного цикла колебаний, измеренная в секундах. Длина волны — это расстояние между двумя соседними повторяющимися зонами волнового процесса. Если предположить, что скорость распространения волны в среде постоянная, то длина волны обратно пропорциональна частоте.
При 20 °C звук распространяется в сухом воздухе со скоростью около 343 метра в секунду или 1 километр приблизительно за 3 секунды. Звук распространяется быстрее в жидкостях и еще быстрее в твердых телах. Например, в воде звук распространяется в 4,3 раза быстрее, чем в воздухе, в стекле — в 13 раз и в алмазе в 35 раз быстрее, чем в воздухе.
Хотя звуковые волны и морские волны движутся намного медленнее электромагнитных волн, уравнение, описывающее их движение будет одинаковым для всех трех типов волн:

или

где
f — частота волны,
v — скорость распространения волны и
λ — длина волны
Продольные и поперечные волны
В различных средах звук распространяется в виде различных видов волн. В жидкостях и газах звук распространяется в виде продольных волн. В твердых телах звук может распространяться как в виде продольных, так и в виде поперечных волн.
Для лучшего понимания обоих типов волн удобно воспользоваться механическим аналогом, которым послужит пружина Слинки. Эта пружина представляет собой модель среды (жидкости или газа). Если ее растянуть, а затем сжимать, а затем отпускать один конец, сжатие в форме волны перемещается вперед, передавая таким образом энергию с одного конца пружины в другой. Если звук распространяется в жидкости или газе, он идет от источника в форме периодических сжатий и разрежений газа или жидкости, которые перемещаются от источника звука.
Мы можем сравнить витки пружины с молекулами воздуха или воды, которые сталкиваются друг с другом. Поскольку направление движения этих сжатий и разрежений параллельно направлению движения самой волны, такие волны называются продольными.
Если начать двигать один конец пружины перпендикулярно ее оси, то создается поперечная волна. Она называется поперечной, потому что движение витков пружины перпендикулярно направлению движения волны по пружине. В такой волне энергия передается вдоль пружины, а ее витки движутся в направлении, перпендикулярном передаче энергии.
Отметим, что в нашем эксперименте пружина представляет собой среду, в которой распространяется волна, и эта среда не движется вместе с волной. Она только колеблется. Это поведение волны легко наблюдать в твердом теле, однако это справедливо также для воздуха, воды и вообще любой жидкости или газа. То есть, колебания переносятся молекулами жидкости или газа, в то время как среднее положение молекул среды не изменяется с течением времени. Это справедливо для любых типов волн.
Примеры
Возьмем на клавиатуре несколько нот и покажем их частоту и длину волны. Предположим, что звук движется в воздухе со скоростью 340 м/с. Тогда можно рассчитать длину волны нот:
| Научное и традиционное название ноты | Частота, Гц | Период, мс | Длина волны, см |
|---|---|---|---|
| A3, ля малой октавы | 220 | 4,55 | 156 |
| A4, ля первой октавы | 440 | 2,27 | 78 |
| A5, ля второй октавы | 880 | 1,14 | 39 |
| A6, ля третьей октавы | 1760 | 0,57 | 19,5 |
Акустика — звук
На этих страницах размещены конвертеры единиц измерения, позволяющие быстро и точно перевести значения из одних единиц в другие, а также из одной системы единиц в другую. Конвертеры пригодятся инженерам, переводчикам и всем, кто работает с разными единицами измерения.
Мы работаем над обеспечением точности конвертеров и калькуляторов TranslatorsCafe.com, однако мы не можем гарантировать, что они не содержат ошибок и неточностей. Вся информация предоставляется «как есть», без каких-либо гарантий. Условия.
Если вы заметили неточность в расчётах или ошибку в тексте, или вам необходим другой конвертер для перевода из одной единицы измерения в другую, которого нет на нашем сайте — напишите нам!
Канал Конвертера единиц TranslatorsCafe.com на YouTube
Как найти частоту звуковых колебаний
Звуком называют волны механических деформаций, распространяющиеся в любой достаточно упругой среде (жидкостях, твердых телах, газах). Как и другие волны, звук характеризуется, в частности, частотой колебаний. В зависимости от начальных условий найти частоту звука можно разными способами.

Вам понадобится
- – калькулятор;
- – физический справочник;
- – тахометр;
- – звуковой датчик;
- – осциллограф.
Инструкция
Найдите частоту звуковых колебаний, если известна длина их волн и скорость звука в среде, где они распространяются. Вычисления следует производить по формуле F=V/L. Здесь V – скорость звука в среде, а L – длина волны (известная величина). Значения скоростей звука для разных сред можно узнать из физических справочников. Так, для воздуха при нормальных условиях (температуре в районе 20°C и давлении, близком к атмосферному) это значение составляет 341 м/с. Поэтому, например, звуковые колебания в воздухе с длиной волны в 0,25 м будут иметь частоту 341/0,25=1364 Гц.
Найти частоту звуковых колебаний, зная их период, можно по простой формуле: F=1/T. Обратите внимание на то, что для получения корректных значений частоты, представленных в герцах, период T должен быть выражен системе СИ, то есть иметь размерность в секундах.
Для получения частоты звуковых колебаний, распространяющихся в реальной среде, осуществите физический эксперимент. Примените специализированное устройство – тахометр. Сегодня тахометры, как правило, имеют высокую точность измерений и отображают информацию в готовом виде на цифровом индикаторе.
При отсутствии тахометра для нахождения частоты звука можно воспользоваться микрофоном или другим звуковым датчиком с достаточной чувствительностью, а также осциллографом. Подключите датчик к осциллографу и создайте условия для получения сигнала (например, поместите датчик в исследуемую среду). Подберите чувствительность осциллографа так, чтобы колебания на экране отображались с достаточной амплитудой. Путем подстройки частоты развертки добейтесь отображения устойчивой картинки. Узнайте период звуковых колебаний, ориентируясь на шкалу прибора. Найдите частоту, используя способ, описанный во втором шаге.
Обратите внимание
При вычислениях, связанных с получением значений частоты звука, всегда переводите все известные значения в систему СИ.
Полезный совет
Если дополнительно требуется найти циклическую частоту звуковых колебаний, рассчитайте ее по формуле w=2*PI*F, где F – частота, выраженная в герцах, полученная одним из описанных способов.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Download Article
Download Article
Frequency, also called wave frequency, is a measurement of the total number of vibrations or oscillations made within a certain amount of time. There are a few different ways to calculate frequency based on the information you have available to you. Keep reading to learn some of the most common and useful versions.
-

1
Learn the formula. The formula for frequency, when given wavelength and the velocity of the wave, is written as: f = V / λ[1]
- In this formula, f represents frequency, V represents the velocity of the wave, and λ represents the wavelength of the wave.
- Example: A certain sound wave traveling in the air has a wavelength of 322 nm when the velocity of sound is 320 m/s. What is the frequency of this sound wave?
-

2
Convert the wavelength into meters, if necessary. If the wavelength is given in nanometers, you need to convert this value into meters by dividing it by the number of nanometers in a single meter.[2]
- Note that when working with extremely small numbers or extremely large numbers, it is generally easier to write the values in scientific notation. The values will be shown in and out of their scientific notation forms for this example, but when writing your answer for homework, other schoolwork, or other formal forums, you should stick with scientific notation.
- Example: λ = 322 nm
- 322 nm x (1 m / 10^9 nm) = 3.22 x 10^-7 m = 0.000000322 m
Advertisement
-

3
Divide the velocity by the wavelength. Divide the velocity of the wave, V, by the wavelength converted into meters, λ, in order to find the frequency, f.[3]
- Example: f = V / λ = 320 / 0.000000322 = 993788819.88 = 9.94 x 10^8
-

4
Write your answer. After completing the previous step, you will have completed your calculation for the frequency of the wave. Write your answer in Hertz, Hz, which is the unit for frequency.
- Example: The frequency of this wave is 9.94 x 10^8 Hz.
Advertisement
-

1
Learn the formula. The formula for the frequency of a wave in a vacuum is almost identical to that of a wave not in a vacuum. Since there are no outside influences on the velocity of the wave, though, you would use the mathematical constant for the speed of light, which electromagnetic waves would travel at under these conditions. As such, the formula is written as: f = C / λ[4]
- In this formula, f represents frequency, C represents the velocity or speed of light, and λ represents the wavelength of the wave.
- Example: A particular wave of electromagnetic radiation has a wavelength of 573 nm when passing through a vacuum. What is the frequency of this electromagnetic wave?
-

2
Convert the wavelength into meters, if necessary. When the problem gives you the wavelength in meters, no further action is needed. If, however, the wavelength is given in micrometers, you need to convert this value into meters by dividing it by the number of micrometers in a single meter.
- Note that when working with extremely small numbers or extremely large numbers, it is generally easier to write the values in scientific notation. The values will be shown in and out of their scientific notation forms for this example, but when writing your answer for homework, other schoolwork, or other formal forums, you should stick with scientific notation.
- Example: λ = 573 nm
- 573 nm x (1 m / 10^9 nm) = 5.73 x 10^-7 m = 0.000000573
-

3
Divide the speed of light by the wavelength. The speed of light is a constant, so even if the problem does not provide you with a value, the value remains 3.00 x 10^8 m/s. Divide this value by the wavelength converted into meters.[5]
- Example: f = C / λ = 3.00 x 10^8 / 5.73 x 10^-7 = 5.24 x 10^14
-

4
Write your answer. With this, you should have calculated the value of the frequency of the wave. Write your answer in Hertz, Hz, the unit for frequency.
- Example: The frequency of this wave is 5.24 x 10^14 Hz.
Advertisement
-

1
Learn the formula. Frequency and the time taken to finish a single wave oscillation are inversely proportional. As such, the formula for calculating frequency when given the time taken to complete a wave cycle is written as: f = 1 / T
- In this formula, f represents frequency and T represents the time period or amount of time required to complete a single wave oscillation.
- Example A: The time for a certain wave to complete a single oscillation is 0.32 seconds. What is the frequency of this wave?
- Example B: In 0.57 seconds, a certain wave can complete 15 oscillations. What is the frequency of this wave?
-

2
Divide the number of oscillations by the time period. Usually, you will be told how long it takes to complete a single oscillation, in which case, you would just divide the number 1 by the time period, T. If given a time period for numerous oscillations, however, you will need to divide the number of oscillations by the overall time period required to complete them.[6]
- Example A: f = 1 / T = 1 / 0.32 = 3.125
- Example B: f = 1 / T = 15 / 0.57 = 26.316
-

3
Write your answer. This calculation should tell you the frequency of the wave. Write your answer in Hertz, Hz, the unit for frequency.
- Example A: The frequency of this wave is 3.125 Hz.
- Example B: The frequency of this wave is 26.316 Hz.
Advertisement
-

1
Learn the formula. When told the angular frequency of a wave but not the standard frequency of that same wave, the formula to calculate the standard frequency is written as: f = ω / (2π)[7]
- In this formula, f represents the frequency of the wave and ω represents the angular frequency. As with any mathematical problem, π stands for pi, a mathematical constant.
- Example: A particular wave rotates with an angular frequency of 7.17 radians per second. What is the frequency of that wave?
-

2
Multiply pi by two. In order to find the denominator of the equation, you need to double the value of pi, 3.14.
- Example: 2 * π = 2 * 3.14 = 6.28
-

3
Divide the angular frequency by the double of pi. Divide the angular frequency of the wave, given in radians per second, by 6.28, the doubled value of pi.[8]
- Example: f = ω / (2π) = 7.17 / (2 * 3.14) = 7.17 / 6.28 = 1.14
-

4
Write your answer. This final bit of calculation should indicate what the frequency of the wave is. Write your answer in Hertz, Hz, the unit for frequency.
- Example: The frequency of this wave is 1.14 Hz.
Advertisement
Add New Question
-
Question
What is the frequency if 80 oscillations are completed in 1 second?

Frequency is the number of oscillations completed in a second. The answer would be 80 Hertz.
-
Question
Do atoms have a frequency and, if so, does it mean everything vibrates?

Atoms have energy. Energy is often characterized as vibration. Vibration possesses frequency. So, yes, everything could be thought of as vibrating at the atomic level.
-
Question
What’s the definition of frequency?

The rate at which a vibration occurs that constitutes a wave, either in a material (as in sound waves), or in an electromagnetic field (as in radio waves and light), usually measured per second. The rate at which something occurs or is repeated over a particular period of time or in a given sample.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Thanks for submitting a tip for review!
Things You’ll Need
- Calculator
- Pencil
- Paper
References
About This Article
Article SummaryX
To calculate the frequency of a wave, divide the velocity of the wave by the wavelength. Write your answer in Hertz, or Hz, which is the unit for frequency. If you need to calculate the frequency from the time it takes to complete a wave cycle, or T, the frequency will be the inverse of the time, or 1 divided by T. Display this answer in Hertz as well. Keep reading to learn how to calculate frequency from angular frequency!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,511,586 times.
Did this article help you?
Физика > Частота звуковых волн
Чему равна частота звуковой волны – частота, длина и скорость звука. Изучите единицу измерения, формулу частоты звуковой волны, что определяет, диапазон.
Частота – количество повторяющихся событий за временную единицу.
Задача обучения
- Объединить частоту, длину и скорость звука.
Основные пункты
- Частота основывается на длине и звуковой скорости:

- Период – длительность цикла повторяющегося события. Выступает обратной частоте.
- Единица измерения – Герц (количество циклов в секунду).
Термины
- Частота – количество периодического события за временную единицу: f = n/t.
- Герц – один период в секунду, единица частоты (Гц).
- Период – длительность цикла в повторяющемся событии.
Звуковые волны обладают частотой, то есть количеством вхождений повторяющегося события за временную единицу.
Частота колебаний звуковой волны основывается на длине волны и скорости звука: ![]()
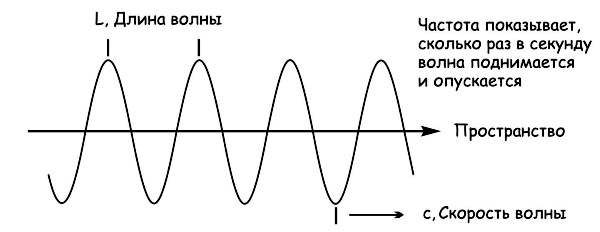
Нижний рисунок демонстрирует связь частоты и длины.

Звуковая волна формируется из источника, вибрирующего на частоте (f), и распространяется при v на длине λ
Частота звуковой волны определяет и другие характеристики. Можно использовать частоту и длину, чтобы отыскать скорость волны. Не забывайте, что она зависит от того, в какой среде перемещается звук. Высокие показатели появляются в твердых веществах. Формула: vs = fλ.
Период – длительность цикла повторяющегося события. В анимации показаны различные частоты и периоды (от наименьшего к наивысшему).

Три мигающих огонька: от самой низкой частоты (сверху) до наивысшей (снизу). F – частота в Герцах. Т – период в секундах
Герц
Единица измерения – Герц (Гц). Это количество циклов в секунду: 100 Гц = 100 циклам.
Различные виды улавливают разные частотные диапазоны. Люди способны услышать 20 – 200000 Гц, а собаки до 60000 Гц. У летучих мышей диапазон вырастает до 120000 Гц. Последние применяют ультразвук, чтобы сориентироваться в пространстве или найти объекты. Звуковые волны отбиваются от предметов. Животное улавливает, сколько времени нужно на возврат, и понимает, какая дистанция образовалась. Это эхолокация.
