Как найти частоты колебаний маятников - Сайт, где вы сможете решить свои вопросы

Примеры движения

Колебательное движение является одним из наиболее распространенных в природе. Например, можно представить себе струны музыкальных инструментов, качели или голосовые связки человека.

В физике колебаниями называются процессы, которые повторяются через равные промежутки времени. Подобные движения рассматривается посредством нескольких моделей:

тела, подвешенного на пружине (двигающееся по направлению вверх-вниз);
груза на нитке;
электрического контура и других.

Амплитуда, период и частота

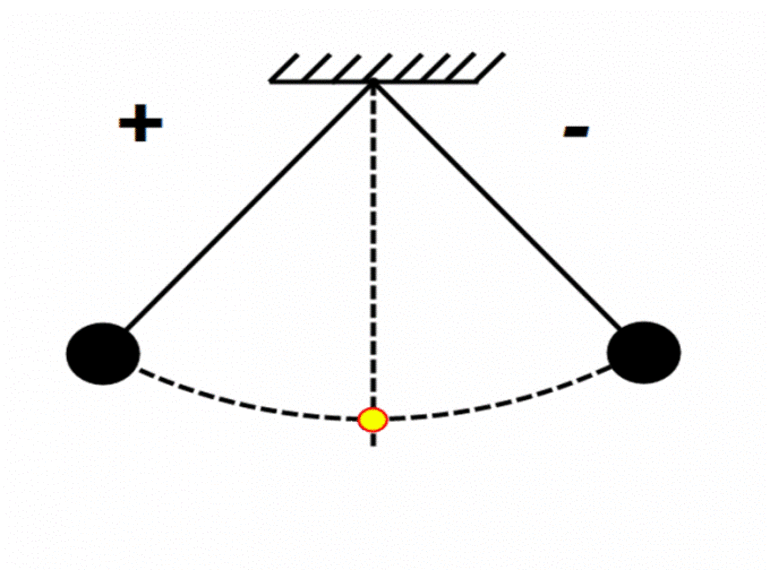
Если подвесить одновременно два груза на две разные нити и запустить их, то можно заметить, что расстояние отклонения груза от среднего положения до крайнего — разное.

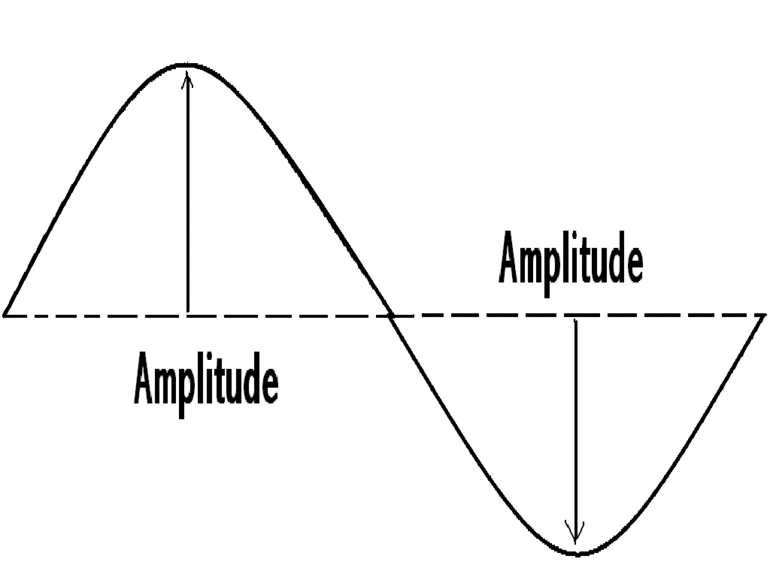
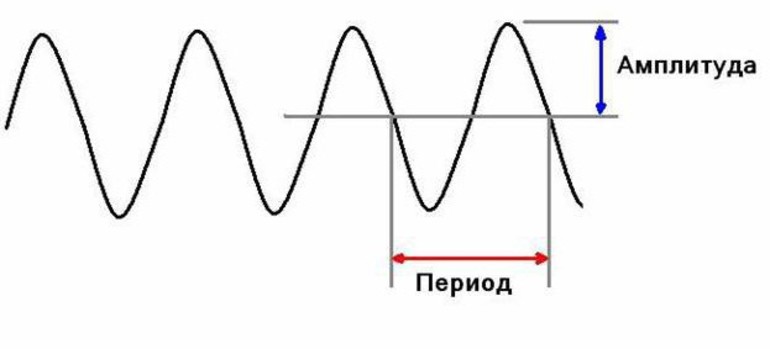
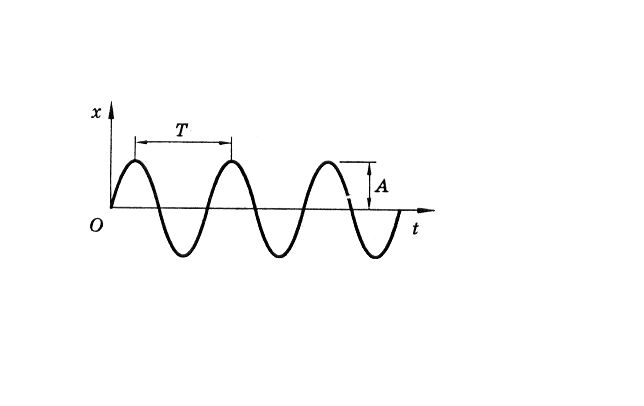
Это величина носит название амплитуды. Обозначается буквой А и измеряется в системе Си в метрах. Также для обозначения подобного движения применяются следующие термины:

Время, за которое маятник приходит в одно и то же положение, называется периодом колебаний.
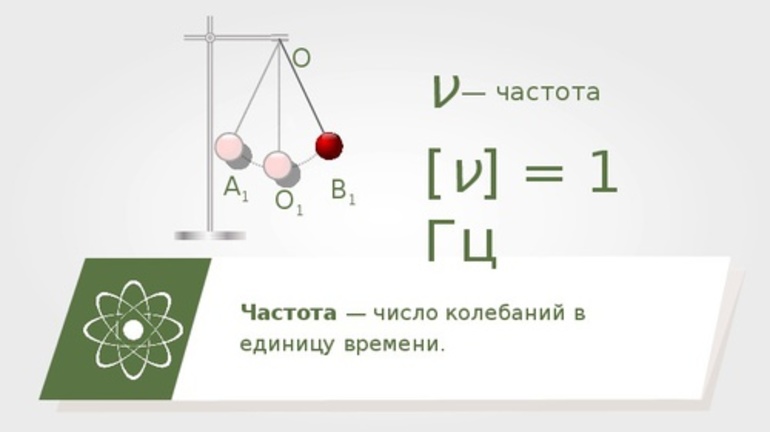
Количество колебаний в единицу времени представляет собой частоту. Она измеряется в Герцах (Гц). Имеет обратную зависимость от периода.
Циклическая частота колебаний (угловая, круговая) представляет собой количество колебаний за 2 π секунд. Обозначается греческой буквой омега. Она вводится для упрощения расчетов в теоретической физике и электронике. Единица измерения циклической частоты рад/с.
Если имеется два графика функций с одинаковой частотой, но сдвинуты относительно друг друга, то различна их фаза колебаний.

Выделяют понятие свободных колебаний. Когда системе, например, математическому маятнику, придают импульс, чтобы начать движение, дальнейшие его колебания (самостоятельные) будут считаться свободными.

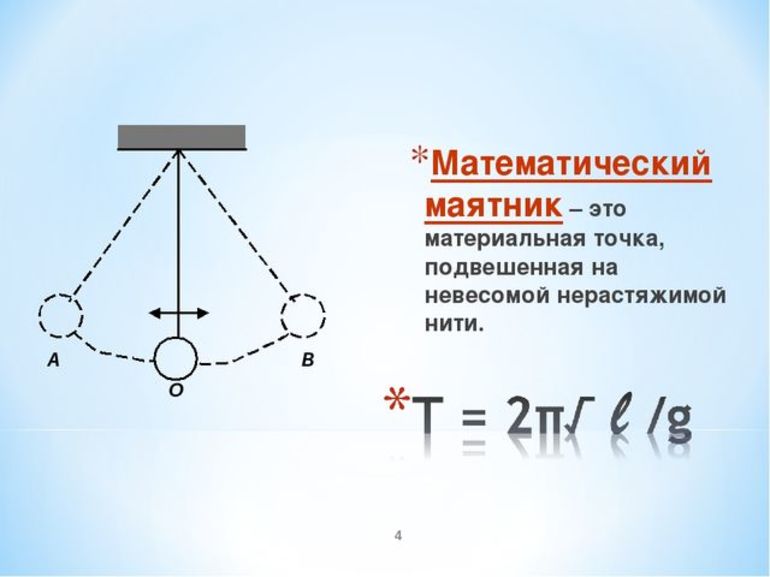
Математический маятник

Эта модель рассматривает движение груза, подвешенного на нитке. Описывается система, в которой масса нитки намного меньше массы груза, а ее длина намного больше его размеров.

Также нить должна быть невесомой и нерастяжимой.

Груз в этом случае считается материальной точкой.

При выполнении этих условий частота колебаний маятника и период не будут зависеть от массы груза. Движение математического маятника рассматривается при небольшом угле отклонения (α). Последний измеряется в радианах, поэтому приблизительно соответствует по значению его синусу и тангенсу. Этот же угол пропорционален отношению смещения на длину нити:

α=x/l.

На маятник действует синусовая составляющая силы тяжести и тангенсовая сила натяжения нити. Согласно второму закону Ньютона: ma=-mgsin (α). Откуда можно получить a=-gx/l

Вторая производная уравнения движения дает a=-(ω)^2x

Таким образом: -gx/l=-(ω)^2x -> ω ^2=g/l.

Период: T=2π /ω T=2π*sqrt (g/l)

Это формула Галилея, которая описывает движение математического маятника.

Формула частоты колебаний для математического маятника: v=sqrt (l/g)/2π.

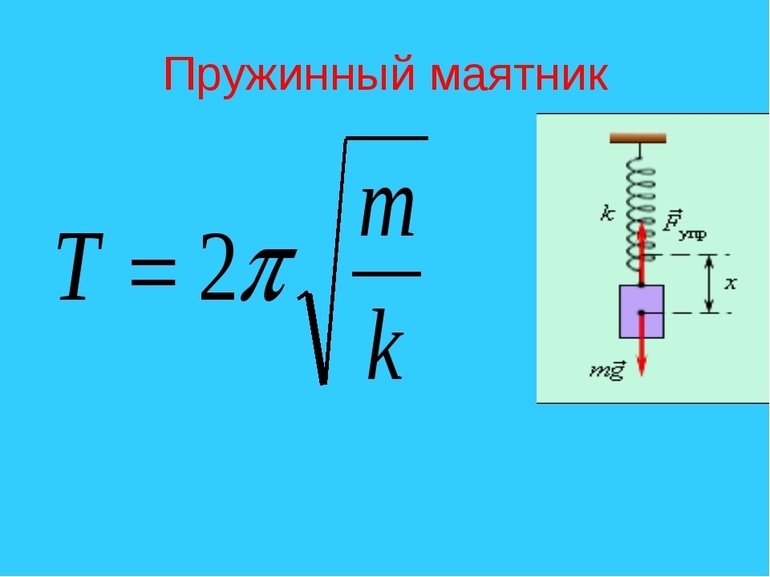
Пружинный маятник

Подобным термином называется система, в которой движения совершает груз, подвешенный на легкой пружине.

Тело находится в положении равновесия, если пружина не деформирована. Если ее растянуть или сжать, то система начнет колебания под действием силы упругости, которая направлена на приведение маятника в положение равновесия.

Сила упругости пропорциональна смещению тела (x), но направлена противоположно. Коэффициент пропорциональности между этими двумя величинами носит название жесткости пружины (k). Таким образом:

F=-kx.

Сила упругости достигает наибольшей величины в положении максимального отклонения тела (амплитуда, смещение) от равновесия. В этой точке наибольшую величину имеет и ускорение.

По мере того, как тело приближается к положению равновесия, уменьшается сила упругости и ускорение. В средней точки обе величины равны нулю, но ненулевое значение имеет скорость тела. Поэтому груз не останавливается, а продолжает движение.

После прохождения положения равновесия он двигается в обратном направлении по инерции, а сила упругости тянет его назад. Благодаря трению воздуха скорость уменьшается, и маятник останавливается.

Все эти модели можно отнести к классическому гармоническому осциллятору — системе, которая имеет одну степень свободы и описывается единственным уравнением.

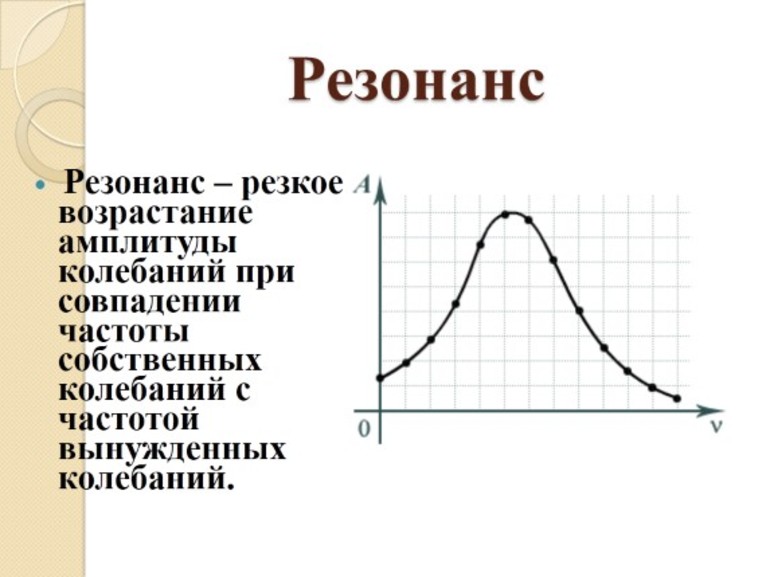
Явление резонанса

Это понятие имеет особое значение для описания колебаний. Если имеется некое воздействие, частота которого приближается к собственной частоте системы, то последняя реагирует резким увеличением амплитуды.

Явление резонанса можно представить себе на примере того же математического маятника. Для этого необходимо маятник привязать к веревке, к которой привязать еще один такой же, но с более длинной нитью. При этом длина нитки второго маятника может регулироваться. Если привести в движение оба маятника, а длину второй нитки постепенно изменять, то можно будет заметить, что амплитуда увеличивается по мере приближения размеров обеих ниток.

В этом случае первый маятник будет приемником колебаний, а второй — передатчиком. Причиной увеличения амплитуды является колебание подвески с такой же частотой.

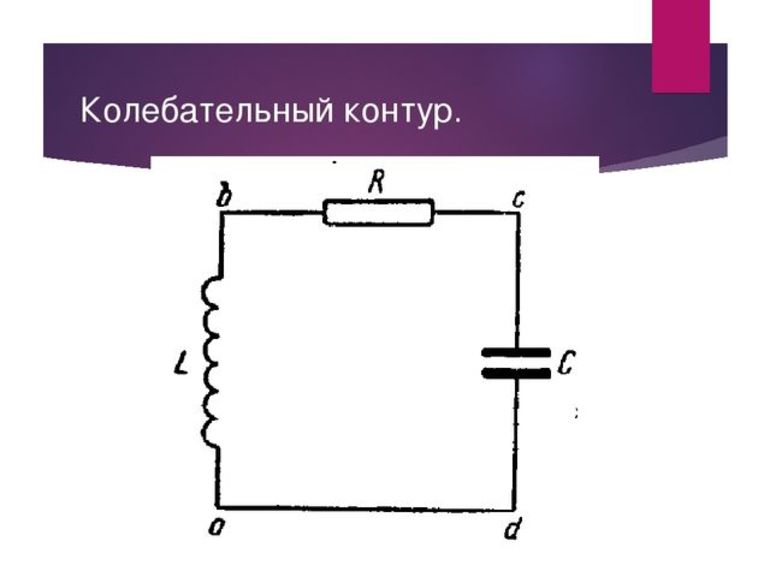
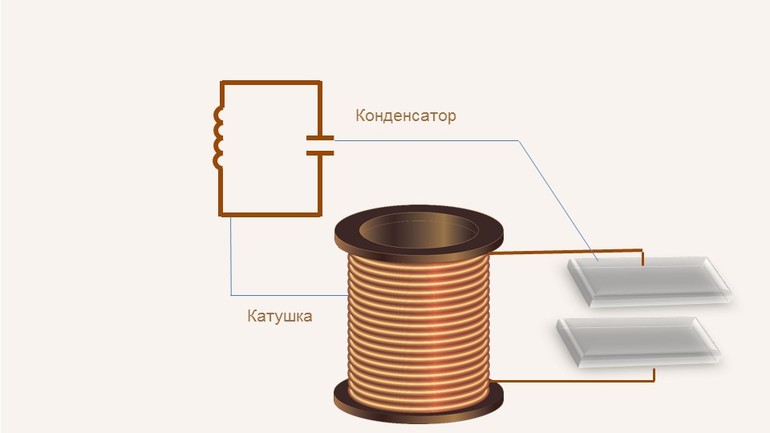
Колебательный контур

Является еще одним примером колебаний, на котором основаны все радиоприемники. Контур играет роль приемника сигнала.

В простейшем примере представляет собой замкнутую цепь из катушки индуктивности и конденсатора. При определенных обстоятельствах в подобном контуре могут возникать и поддерживаться электрические колебания.

Для возбуждения колебаний необходимо подключить источник постоянного напряжения к конденсатору и зарядить его. После этого источник убрать, а цепь замкнуть.

Конденсатор разряжается через катушку индуктивности, а в цепи создается ток, интенсивность которого увеличивается по мере разряда конденсатора. Вокруг катушки создается магнитное поле.

Электрический заряд конденсатора преобразовался в магнитное поле. После этого магнитное поле катушки будет уменьшаться, а конденсатор обратно заряжаться. Процесс повторяется циклически и описывается теми же характеристиками, что и механические колебания: частотой, амплитудой и периодом.

Они являются свободными и затухающими. Чтобы их поддерживать, необходимо периодически заряжать конденсатор.

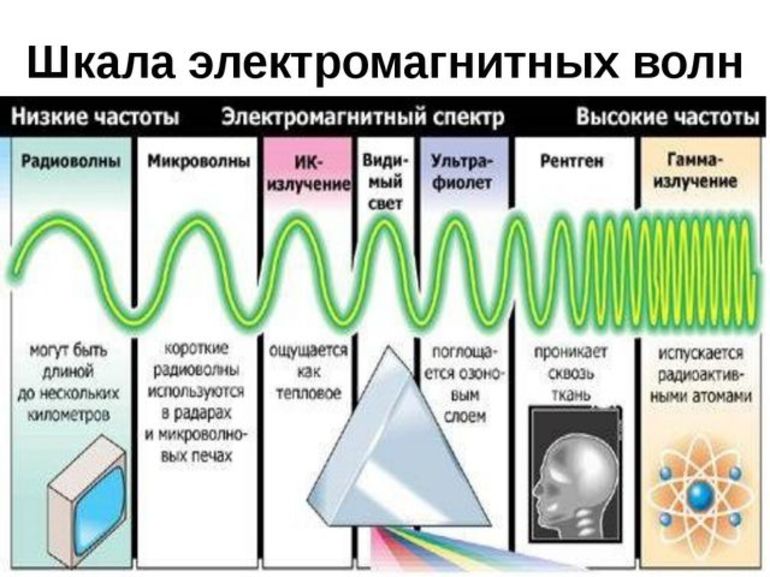
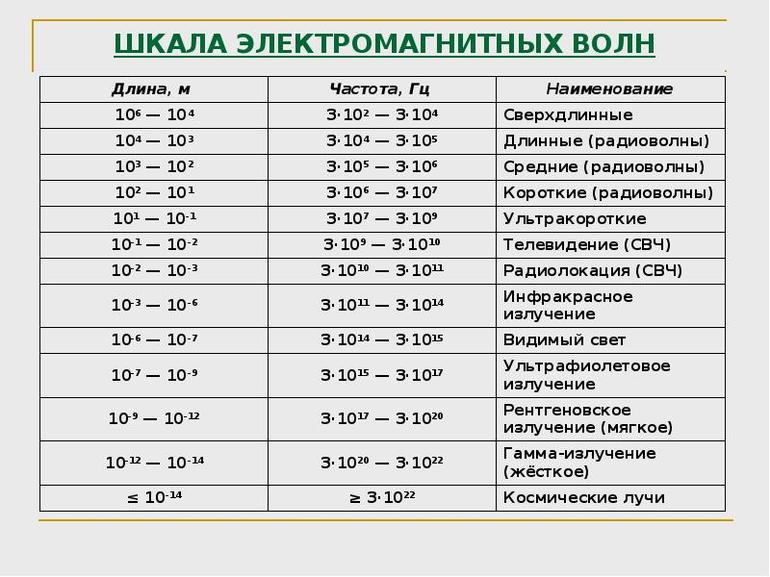
Звук и электромагнитные волны

Понятие частоты вводится и для звуковых и электромагнитных волн. Первые представляют собой колебания плотности среды. Вторые — изменение со временем напряженности магнитного и электрического полей.

От частоты звука зависит его тональность. Этим свойством пользуются для стандартизации описания музыки и создания музыкальных инструментов — каждой ноте соответствует своя частота.

До 16 Гц человеческое ухо не воспринимает, так же как и выше 20 КГЦ. Более высокие частоты используются в эхолокации, ультразвуковой диагностике.

Частота электромагнитных волн также определяет их способность взаимодействовать с человеческим организмом. Рентгеновское излучение проходит насквозь, при этом взаимодействуя с молекулами, вызывая их ионизацию. Ультразвук провоцирует процессы загара, фотосинтеза. Радиоволновое излучение практически не оказывает прямого воздействия, но хорошо подходит для передачи информации. В видимом диапазоне частота определяет цвет.

Есть также такая характеристика, как частота колебаний молекул. Она зависит от температуры тела и определяет его агрегатное состояние.

Таким образом, частота колебаний описывает большое количество процессов и оказывает воздействие на их характеристики.

Источник

Формула частоты колебаний пружинного маятника в физике

Формула частоты колебаний пружинного маятника

Частота колебаний

Определение

Частота колебаний ($nu$) является одним из параметров, которые характеризуют колебания Это величина обратная периоду колебаний ($T$):

[nu =frac{1}{T}left(1right).]

Таким образом, частотой колебаний называют физическую величину, равную числу повторений колебаний за единицу времени.

[nu =frac{N}{Delta t}left(2right),]

где $N$ – число полных колебательных движений; $Delta t$ – время, за которые произошли данные колебания.

Циклическая частота колебаний (${omega }_0$) связана с частотой $nu $ формулой:

[nu =frac{{omega }_0}{2pi }left(3right).]

Единицей измерения частоты в Международной системе единиц (СИ) является герц или обратная секунда:

[left[nu right]=с^{-1}=Гц.]

Пружинный маятник

Определение

Пружинным маятником называют систему, которая состоит из упругой пружины, к которой прикреплен груз.

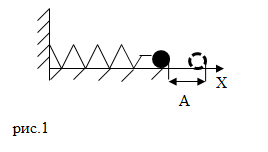
Допустим, что масса груза равна $m$, коэффициент упругости пружины $k$. Масса пружины в таком маятнике обычно не учитывается. Если рассматривать горизонтальные движения груза (рис.1), то он движется под действием силы упругости, если систему вывели из состояния равновесия и предоставили самой себе. При этом часто считают, что силы трения можно не учитывать.

Уравнения колебаний пружинного маятника

Пружинный маятник, который совершает свободные колебания – это пример гармонического осциллятора. Пусть он выполняет колебания вдоль оси X. Если колебания малые, выполняется закон Гука, то уравнение движения груза запишем как:

[ddot{x}+{omega }^2_0x=0left(4right),]

где ${omega }^2_0=frac{k}{m}$ – циклическая частота колебаний пружинного маятника. Решение уравнения (4) это функция синуса или косинуса вида:

[x=A{cos left({omega }_0t+varphi right)=A{sin left({omega }_0t+{varphi }_1right) } }left(5right),]

где ${omega }_0=sqrt{frac{k}{m}}>0$- циклическая частота колебаний пружинного маятника, $A$ – амплитуда колебаний; ${(omega }_0t+varphi )$ – фаза колебаний; $varphi $ и ${varphi }_1$ – начальные фазы колебаний.

Частота колебаний пружинного маятника

Из формулы (3) и ${omega }_0=sqrt{frac{k}{m}}$, следует, что частота колебаний пружинного маятника равна:

[nu =frac{1}{2pi }sqrt{frac{k}{m}} left(6right).]

Формула (6) справедлива в случае, если:

пружина в маятнике считается невесомой;
груз, прикрепленный к пружине, является абсолютно твердым телом;
крутильные колебания отсутствуют.

Выражение (6) показывает, что частота колебаний пружинного маятника увеличивается с уменьшением массы груза и увеличением коэффициента упругости пружины. Частота колебаний пружинного маятника не зависит от амплитуды. Если колебания не являются малыми, сила упругости пружины не подчиняется закону Гука, то появляется зависимость частоты колебаний от амплитуды.

Примеры задач с решением

Пример 1

Задание. Период колебаний пружинного маятника составляет $T=5cdot {10}^{-3}с$. Чему равна частота колебаний в этом случае? Какова циклическая частота колебаний этого груза?

Решение. Частота колебаний – это величина обратная периоду колебаний, следовательно, для решения задачи достаточно воспользоваться формулой:

[nu =frac{1}{T}left(1.1right).]

Вычислим искомую частоту:

[nu =frac{1}{5cdot {10}^{-3}}=200 left(Гцright).]

Циклическая частота связана с частотой $nu $ как:

[{omega }_0=2pi nu left(1.2right).]

Вычислим циклическую частоту:

[{omega }_0=2pi cdot 200approx 1256 left(frac{рад}{с}right).]

Ответ. $1) nu =200$ Гц. 2) ${omega }_0=1256 frac{рад}{с}$

Пример 2

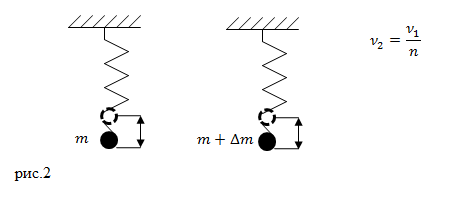
Задание. Массу груза, висящего на упругой пружине (рис.2), увеличивают на величину $Delta m$, при этом частота уменьшается в $n$ раз. Какова масса первого груза?

Решение. Будем считать, что грузы на пружине совершают свободные гармонические колебания, тогда за основу решения задачи примем формулу:

[nu =frac{1}{2pi }sqrt{frac{k}{m}} left(2.1right).]

Для первого груза частота будет равна:

[{nu }_1=frac{1}{2pi }sqrt{frac{k}{m}} left(2.2right).]

Для второго груза:

[{nu }_2=frac{1}{2pi }sqrt{frac{k}{m+Delta m}} left(2.2right).]

По условию задачи ${nu }_2=frac{{nu }_1}{n}$, найдем отношение $frac{{nu }_1}{{nu }_2}:frac{{nu }_1}{{nu }_2}=sqrt{frac{k}{m}cdot frac{m+Delta m}{k}}=sqrt{1+frac{Delta m}{m}}=n left(2.3right).$

Получим из уравнения (2.3) искомую массу груза. Для этого обе части выражения (2.3) возведем в квадрат и выразим $m$:

[1+frac{Delta m}{m}=n^2to frac{Delta m}{m}=n^2-1to m=frac{Delta m}{n^2-1}.]

Ответ. $m=frac{Delta m}{n^2-1}$

Читать дальше: формула частоты.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник

Частота колебаний маятника

4.3

Средняя оценка: 4.3

Всего получено оценок: 198.

4.3

Средняя оценка: 4.3

Всего получено оценок: 198.

Маятник – простейшая колебательная система, в которой можно изучать особенности колебательных процессов. Колебания, происходящие в маятнике, обладают рядом характеристик, важнейшей из которых является частота. Рассмотрим частоту колебаний маятника более подробно.

Маятник и процессы, происходящие в нем

Изначально под термином «маятник» понимался груз, подвешенный на нити, который может совершать свободные качания под действием силы тяжести. Такой маятник называется «нитяным». Идеальной моделью нитяного маятника является математический маятник, который отличается отсутствием потерь, точечным размером массы и нерастяжимой нитью.

Рис. 1. Нитяной маятник.

Сила тяжести в маятнике может быть заменена на силу упругости. Такой маятник называется «пружинным».

Как показывает опыт, пружинный маятник по своему поведению очень мало отличается от нитяного, являясь его близким аналогом. Аналогом ускорения свободного падения в нитяном маятнике является жесткость пружины в пружинном маятнике, аналогом длины является масса груза.

Рис. 2. Пружинный маятник.

В обоих маятниках свободные колебания возникают потому, что при выведении их из равновесия возникает сила, направленная в сторону равновесия, тем большая, чем больше отклонение.

В точке наибольшего отклонения маятник обладает потенциальной энергией, которая по мере движения превращается в кинетическую. В точке равновесия потенциальная энергия равна нулю, а вся энергия маятника имеет кинетическую форму. Поэтому маятник не может остановиться, и будет продолжать движение, при этом кинетическая энергия будет уменьшаться переходя в потенциальную. В противоположной точке отклонения вся кинетическая энергия перейдет в потенциальную, и станет равной нулю. Маятник начнет обратный ход, при котором потенциальная энергия снова будет переходить в кинетическую.

Идеальный маятник не имеет потерь энергии, а поэтому колебания будут незатухающими.

Частота колебаний маятника

Для получения формулы, выражающей частоту колебаний маятника, вспомним, что колебания совершаются под действием силы, тем большей, чем больше отклонение от равновесия. Например, для пружинного маятника с жесткостью пружины $k$ сила будет равна $F=-kx$, а значит ускорение, приобретаемое грузом, по второму закону Ньютона будет равно:.

$$a=-{kxover m}$$

Ускорение является второй производной координаты. То есть:

$$x”=-{kover m}x$$

В высшей математике доказывается, что единственная функция, удовлетворяющая данному условию – это круговая функция (синус или косинус):

$$x(t)=A cos sqrt{kover m}t$$

Сравним эту формулу с формулой гармонических колебаний:

$$x(t)=A cos( omega t+varphi)$$

Можно видеть, что коэффициент $sqrt {kover m}$ представляет собой круговую частоту. А значит, частота колебаний маятника равна:

$$nu={omega over 2pi}={1over 2pi}sqrt {kover m}$$

Процессы, происходящие в нитяном маятнике, очень близки к процессам, происходящим в пружинном. Поэтому частота колебаний нитяного маятника имеет формулу такого же вида, только в ней жесткость пружины является аналогом ускорения свободного падения, а аналогом массы является длина маятника:

$$nu={1over 2pi}sqrt {mathrm{g}over l}$$

На графике частота колебаний маятника равна количеству полных колебаний, происходящих в единицу времени:

Рис. 3. График колебаний маятника.

Что мы узнали?

И в нитяном и в пружинном маятнике колебания возникают потому, что при выведении их из положения равновесия возникает сила, стремящаяся вернуть маятник в равновесие, тем большая, чем больше отклонение. Единственная функция, удовлетворяющая этому условию – это круговая функция, частоту которой можно получить из ее формулы или графика.

Тест по теме

Доска почёта

Чтобы попасть сюда – пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.3

Средняя оценка: 4.3

Всего получено оценок: 198.

А какая ваша оценка?

Источник

Частота математического маятника

Виктор Матвеевич Скоков

Эксперт по предмету «Физика»

Задать вопрос автору статьи

Замечание 1

Колебаниям математический маятника – тела с точечной массой, подвешенного на упругой нити – свойственен изохронизм. Это значит, что их частота не зависит от амплитуды и массы подвешенного тела. Такая система обладает свойствами гармонического осциллятора – устройства, график движения тела, в котором представляет собой синусоиду.

Функция, описывающая гармонические колебания:

$varphi (t) = varphi_0 cdot cos(omega_0 + alpha)$, где:

$ alpha$- начальная фаза колебаний,
$varphi_0$ – их амплитуда,
$omega_0$ – циклическая частота.

Циклическая частота связана с длиной подвеса математического маятника зависимостью:

$omega_0 = sqrt{frac{g}{l}}$,

где $g$ – ускорение свободного падения, $l$ – длина нити.

Эта зависимость получается исходя из того, что при малых отклонениях от вертикали касательную (тангенциальную) составляющую силы, тянущей маятник по дуге, можно найти как сумму векторов силы упругости нити (направлена от тела к центру вращения вдоль нити) и силы тяжести (направлена вертикально вниз). Ускорение, создаваемое касательной силой, относится к ускорению свободного падения в следующем соотношении:

$a = g cdot frac{x}{l}$,

где $l$ – длина нити, $x$ – модуль касательной силы.

Поскольку же уравнение колебательного движения выглядит как

$a = – omega_0^2 cdot x$,

где $omega_0$ – частота циклических колебаний, можно подставить в формулу для нахождения периода колебаний полученное соотношение:

$T = frac{2pi}{omega_0}; omega_0 = sqrt{frac{g}{l}} implies T = 2pi cdot sqrt{frac{l}{g}}$

Частоту можно найти как величину, обратную периоду.

$f = frac{1}{T}$

Пример 1

Найти частоту колебаний маятника с длиной подвеса 1 м.

$T = 2 cdot 3,14 cdot sqrt{frac{1}{9,8}} approx 2 с$.

$f = frac{1}{2} = 0,5$