Перейти к содержимому
Частота среза — частота, на которой частотная характеристика пересекает 0 дБ.
Частота сопряжения — частота, на которой частотная характеристика меняет наклон.

Эти понятия относятся к теории автоматического управления. Частота среза используется при анализе устойчивости системы управления. Чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы фаза разомкнутой системы не достигала −180° на частоте среза.
Частота среза имеет другое определение в обработке сигналов. Там под частотой среза подразумевают частоту сопряжения, а понятием частота сопряжения не пользуются. В обработке сигналов нет необходимости анализировать устойчивость системы.
Понятия раскрываются в книге Бесекерского и Попова «Теория систем автоматического регулирования» 2003 года. Приведу пару цитат, где вводятся эти понятия.
Первая цитата со страницы 59:
Точку пересечения прямой с осью нуля децибел (осью частот) можно найти, положив L(ω)=0 или, соответственно, A(ω)=1. Отсюда получаем так называемую частоту среза л. а. х.,
При этом в книге частота среза обозначается как ωср.
На странице 66 описывается апериодическое звено первого порядка:
Наиболее просто, практически без вычислительной работы, строится так называемая асимптотическая л. а. х. На стандартной сетке проводится вертикальная прямая через точку с частотой, называемой сопрягающей частотой ω=1/T.
При чем эта «вертикальная прямая» проводится в точке изменения наклона частотной характеристики.
Скриншот этой страницы с полным описанием:

Как
было показано в п. 3.2.1, передаточные и
частотные функции последовательно
соединенных звеньев перемножаются, а
их логарифмические характеристики —
складываются, т.е.
 ,
,
 ,
, ,
,
![]() ,
,
![]() .
.
Отсюда
вытекает правило построения ЛАЧХ и ЛФЧХ
разомкнутой одноконтурной САУ: строят
логарифмические характеристики звеньев
и затем их графически складывают.
Но
для построения асимптотической ЛАЧХ
применяют более простой метод, который
сформулируем после рассмотрения
конкретного примера.
Пример
4.6
Построить
асимптотическую ЛАЧХ для разомкнутой
цепи САУ с передаточной функцией
![]() ,
,
где
![]() ,
,![]() с,
с,![]() с,
с,![]() с.
с.
По
виду передаточной функции можно
заключить, что система состоит из
последовательно соединенных интегрирующего,
форсирующего, инерционного звеньев и
звена второго порядка.
Определим,
каким является звено второго порядка,
рассчитав его коэффициент демпфирования:
![]() .
.
Поскольку
![]() ,
,
звено второго порядка является
колебательным.
Рассчитаем
частоты сопряжения по соотношению
![]() ,
,
где![]() — постоянная времени
— постоянная времени![]() -го
-го
звена:
![]() ,
,
![]() ,
,![]() ,
,
где
![]() — частота сопряжения инерционного
— частота сопряжения инерционного
звена,![]() — частота сопряжения форсирующего
— частота сопряжения форсирующего
звена,![]() — частота сопряжения колебательного
— частота сопряжения колебательного
звена.
Соответственно
логарифмы частот сопряжения равны
![]() дек,
дек,
![]() ,
,![]() дек.
дек.
Будем
считать, что коэффициент передачи
интегрирующего звена равен коэффициенту
передачи разомкнутой цепи САУ, а
коэффициенты передачи всех остальных
звеньев равны единице. Определим величину
![]() дБ.
дБ.
На
рис. 4.15 показан процесс построения
асимптотической ЛАЧХ разомкнутой цепи
САУ.
Характеристики
звеньев построены на рис. 4.15, где
соответственно ломаные линии 1, 2, 3, 4
являются ЛАЧХ интегрирующего, инерционного,
форсирующего и колебательного звеньев.
Так как коэффициенты передачи всех
звеньев, кроме интегрирующего, приняты
единичными, то ЛАЧХ этих звеньев при
![]() совпадают с осью частот.
совпадают с осью частот.
Просуммировав
графически ЛАЧХ всех звеньев, получим
характеристику 5, являющуюся асимптотической
ЛАЧХ разомкнутой цепи САУ.
Из
этого примера видно, что суммарную
характеристику легко можно построить,
не изображая характеристик отдельных
звеньев. Поэтому при построении ЛАЧХ
разомкнутых САУ вначале проводят первую
асимптоту через точку с координатами
![]()
![]() с наклоном
с наклоном![]() ,
,
где![]() равно разности между числами идеальных
равно разности между числами идеальных
интегрирующих и дифференцирующих
звеньев. После каждой сопрягающей
частоты наклон ЛАЧХ изменяют, причем
изменение наклона определяется типом
звена, давшим сопрягающую частоту.
Причем если у колебательного звена <
0,4, на соответствующей частоте необходимо
изобразить «горб» в соответствии с
величиной .

Рис.
4.15 — Построение асимптотической ЛАЧХ
разомкнутой цепи
Возможно
и решение обратной задачи — восстановление
передаточной функции по ее асимптотической
ЛАЧХ.
Пример
4.7.
По
заданной на рис. 4.16 асимптотической
ЛАЧХ одноконтурной разомкнутой системы
требуется восстановить ее передаточную
функцию.

Рис.
4.16 — Восстановление передаточной
функции по
асимптотической
ЛАЧХ
Величина
наклона первой асимптоты (по мере роста
частоты) указывает на присутствие в
структуре системы интегрирующего звена.
Для
первой асимптоты поэтому справедливо
уравнение (см. характеристики интегрирующего
звена):
![]() .
.
Определить
параметр
![]() можно, отсчитав с графика координаты
можно, отсчитав с графика координаты
любой точки этой асимптоты. Например
![]() ,
,
![]() ,
,![]() ,
,![]() .
.
После
первой по величине частоты сопряжения
наклон ЛАЧХ изменился на плюс 20 дБ/дек.
Такой наклон имеет ЛАЧХ форсирующего
звена. Следовательно, в структуре системы
есть форсирующее звено. Анализируя
изменение наклонов асимптот ЛАЧХ можно
заключить, что помимо упомянутых типовых
звеньев в систему включены колебательное
звено, еще одно форсирующее и инерционное
звенья.
В
общем виде передаточная функция будет
следующей:
![]()
По
частотам сопряжения рассчитаем
соответствующие постоянные времени:
![]() ;
;
![]() ;
;![]() с;
с;
![]() ;
;
![]() ;
;![]() с;
с;
![]() ;
;
![]() ;
;![]() с;
с;
![]() ;
;
![]() ;
;![]() с.
с.
По
всплеску ЛАЧХ на частоте сопряжения
колебательного звена определим
коэффициент демпфирования:
![]()
![]()
![]()
Окончательный
ответ:
![]()
Следует
отметить, что восстановление передаточной
функции САУ по асимптотической ЛАЧХ
возможно в том случае, если система
содержит только минимально-фазовые
звенья. Если же в ней имеются особые
звенья (неминимально-фазовые,
иррациональные, звенья чистого
запаздывания), эта задача не имеет
однозначного решения, т.к. асимптотические
ЛАЧХ этих звеньев такие же, как и у
минимально-фазовых звеньев (см. подраздел
3.3).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Построение логарифмических частотных характеристик
Страницы работы
Содержание работы
2 ПОСТРОЕНИЕ ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
2.1 Построение ЛАЧХ
нескорректированной исходной системы
Определим значение коэффициента добротности системы ![]() и сопоставим его со значением
и сопоставим его со значением ![]() из условия:
из условия:
![]() ,
,
Так как значение коэффициента добротности менее
значения заданного по условию, т.е.:
![]()
![]() ,
,
то в заданную систему необходимо ввести дополнительный
элемент, которым выступает усилитель и включить его в схему последовательно
рисунок 2.
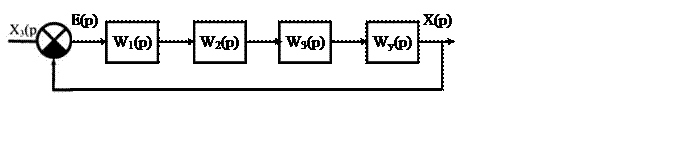 |
Рисунок 2 – функциональная схема САУ с дополнительным
блоком
Соответственно коэффициент усиления данного блока
должен быть равен:
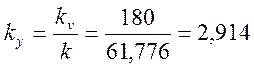 .
.
Исходя из полученной функциональной схемы передаточная
функция разомкнутой системы будет представлена виде:
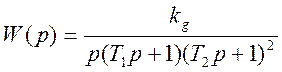 ,
,
где ![]() .
.
Определяем частоты сопряжения:
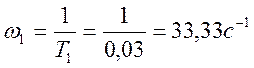 ;
;
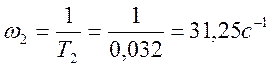 .
.
Запишем в общем виде амплитудно-фазочастотную характеристику
передаточной функции:
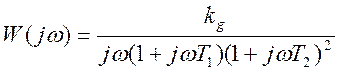 .
.
Логарифмическая амплитудно-частотная
характеристика:
![]() .
.
Логарифмическая фазовая частотная характеристика:
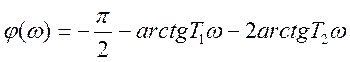 .
.
Подставим в формулы значения коэффициентов, получим
следующие значения логарифмических характеристик:
![]() ,
,
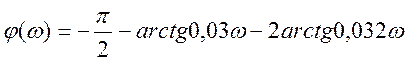 .
.
По полученным выражениям строим ЛАЧХ и ЛФЧХ исходной
нескорректированной системы (Приложение А).
2.2 Построение ЛАЧХ желаемой системы
При построении желаемой ЛАЧХ всю область частот
разбивают на три области: НЧ (низких частот), СЧ (средних частот) и ВЧ
(высоких частот).
Вид ЛАЧХ в СЧ области определяет динамику системы.
Частота среза wср
определяется следующим образом:
wср»(0,6–0,9)wп,
где wп определяется следующим образом. Из рисунка 3
определяем величину Pmax и производим следующие вычисления:
Рмin= 1 – Рмах,
![]() .
.
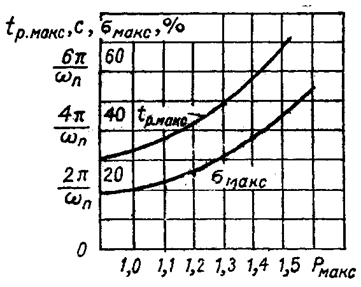 |
Рисунок 3 – Номограмма для определения Pmax и tp
Принимаем значение Рmax = 1,3,
тогда
Рмin= 1 – 1,3 = -0,3,
![]() ,
,
![]() ,
,
где ![]() – из условия.
– из условия.
Так как условие выполняется, то произвожу дальнейшие
вычисления, а именно определяю величину wп. Из рисунка 3 видно, что при величине Рmax = 1,3, формула для вычисления данной величины будет иметь вид:
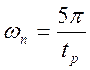 ,
,
где tp = 1,4 – из условия.
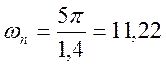 с-1.
с-1.
В итоге определяю частоту среза wср:
![]() с-1.
с-1.
По графикам, приведенным на рисунке 4 найдем запасы устойчивости
по фазе и амплитуде.
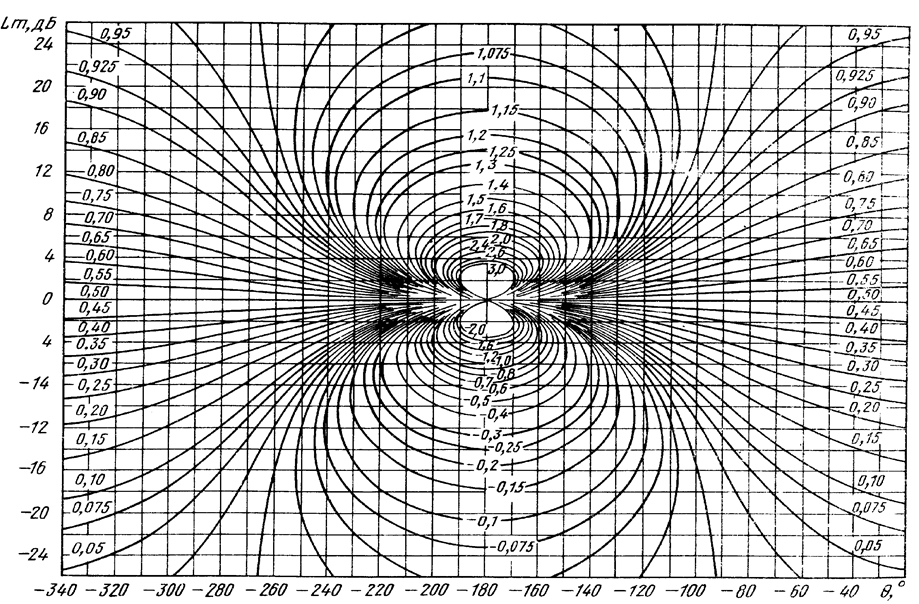
Рисунок 4 – Определение запасов амплитуд и фаз
L1 = 13,8 L2 = -12,8 Δφ = 400
Участок средней частоты будет лежать в пределах запаса
по амплитуде с наклоном в 20дБ/дек вправо и влево от частоты среза wср.
Соединение участка средних частот с низкой частотой
желаемой ЛАЧХ будет осуществляться исходя из следующих соображений. Поскольку
участок низкой частоты ЛАЧХ строится с учетом коэффициента передачи разомкнутой
системы и по этому определяет ошибку системы в статическом режиме, то
низкочастотный участок желаемой ЛАЧХ принимаем низкочастотную асимптоту ЛАЧХ
некорректированной системы с нужным коэффициентом усиления. При этом будет получена
заданная точность в статическом режиме, область низких частот определяет точность
отображения входного сигнала. Соединение проводим таким образом, чтобы в
интервале частот от wL1 до wср, где
значение ординаты находятся между L1 и 0 (L1 ≥ Lж(w),Lж(w) ≥ 0), запас стойкости по фазе
(излишек фазы) Δφ(w) был не меньше, чем запас стойкости Δφ, найденный из
условий обеспечений заданного значения перерегулирования, т.е. чтобы
выполнялось неравенство Δφ(w) ≥ Δφ. Частота соединения wс2, при
котором удовлетворяется это условие, может быть найдено с помощью номограммы на
рисунке 5. Для нахождения wс2 необходимо вычислить точку на оси номограммы и
провести прямую параллельную оси абцис, до пересечения с кривой Δφ, из
полученной точки опустить перпендикуляр на ось абцис и получивши величину w|с2 вычислить:
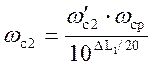 .
.
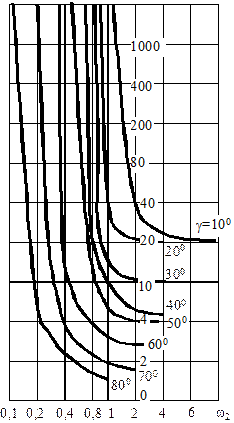
Рисунок 5 – Номограмма для определения w|с2
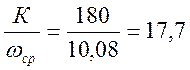
Δφ =
400
Соответственно точка полученная на номограмме w|с2 = 0,83.
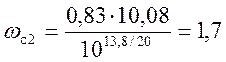 с-1.
с-1.
Область высоких частот незначительно влияет на
качество, поэтому высокочастотный участок желаемой ЛАЧХ проводится так, чтобы
разница наклонов между асимптотами некорректированной ЛАЧХ и желаемой ЛАЧХ не
превышала 20 дБ/дек. Начиная с последней частоты соединения, желаемая ЛАЧХ
совпадает с ЛАЧХ нескорректированной системы.
Исходя из вышесказанного строю желаемую ЛАЧХ
(приложение А) и определяю все частоты сопряжения, а также их постоянные
времени и общий вид передаточной функции разомкнутой скорректированной системы:
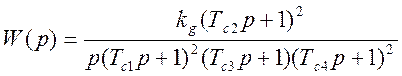 ;
;
![]() с-1,
с-1, 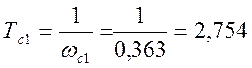 с;
с;
![]() с-1,
с-1, 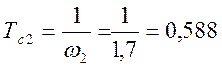 с;
с;
![]() с-1,
с-1, 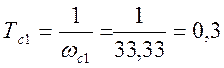 с;
с;
![]() с-1,
с-1, 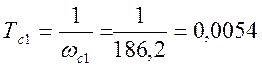 с.
с.
По полученным частотам сопряжения запишем в общем виде амплитудно-фазочастотную характеристику
передаточной функции скорректированной системы:
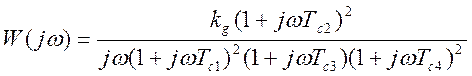 .
.
Логарифмическая амплитудно-частотная
характеристика желаемой ЛАЧХ:
![]()
![]() .
.
Логарифмическая фазовая частотная характеристика желаемой
ЛАЧХ:
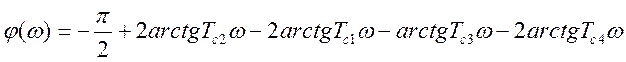 .
.
Подставим в формулы значения коэффициентов, получим
следующие значения логарифмических характеристик:
![]()
![]() ,
,
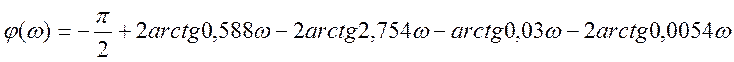 .
.
По полученным выражениям строим ЛФЧХ исходной скорректированной
системы (Приложение А).
2.3 Оценка качества скорректированной системы на предмет
соответствия поставленным требованиям
Моделирование систем на ЭВМ позволяет быстро получить
графики переходных процессов в различных частях системы, вводить различные
дополнительные блоки для улучшения качества системы или для получения
необходимых параметров. Виртуальная среда для моделирования подобных систем MathLab Simulink
содержит весь необходимый набор блоков для получения скорректированной системы
и позволяет получить все необходимые графики переходных процессов.
Построим схему моделирования скорректированной системы на
рисунке 6 и произведем её анализ.
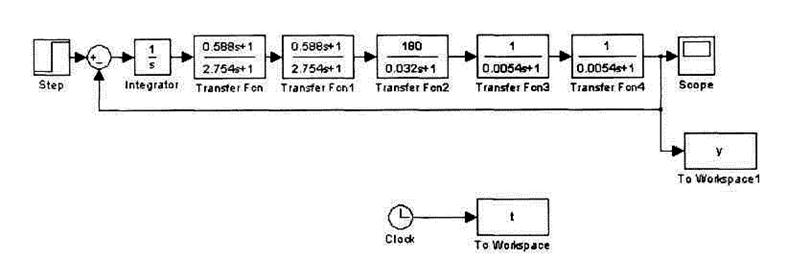
Рисунок 6 – Схема моделирования скорректированной
системы
Анализ проводим по полученному графику переходного процесса
представленном на рисунке 7.
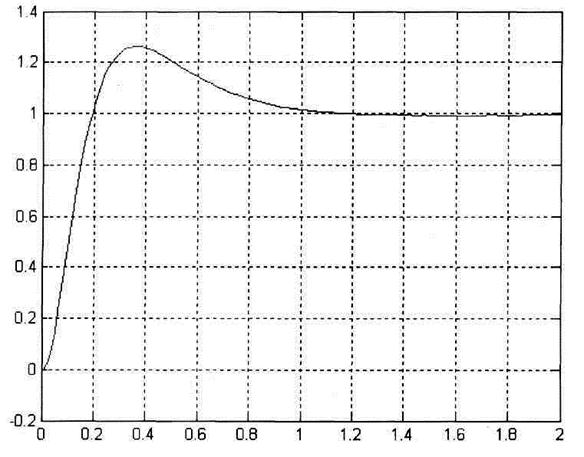
Рисунок 7 – График переходного процесса
Анализ результатов моделирования показывает, что
система удовлетворяет поставленным требованиям:
время переходного процесса не превышает 1,4 с.;
перерегулирование составляет 25% <40%.
Исходя из всех предыдущих расчётов и вычислений можно
судить о том, что мы получили удовлетворяющую всем условиям скорректированную
систему и можем приступать к проектированию корректирующего устройства.
Похожие материалы
- Построение фазового портрета системы автоматического управления методом припасовывания
- Построение фазовый портрет системы автоматического управления методом припасовывания
- Построение характеристик переходного процесса
Информация о работе
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание – внизу страницы.
Частота – сопряжение
Cтраница 4
Наклон ЛАХ на частотах сопряжения, принадлежащих знаменателю, изменяется на – 20 дБ / декаду, а на частотах сопряжения, принадлежащих числителю, на 20 дБ / декаду.
[46]
Здесь предполагается, что система при размыкании в точке А остается устойчивой и коэффициент усиления по контуру внешней обратной связи в области частоты сопряжения много больше единицы. Кроме того, предполагается, что при размыкании к предшествующей точке схемы подключается сопротивление, эквивалентное сопротивлению отключаемой цепи.
[47]
Как видно из полученных зависимостей, для сопряжения с малой величиной б важно обеспечить достаточно малую разность фазовых характеристик обоих каналов только в районе частоты сопряжения. За 5 пределами этой области фазовые сдвиги могут быть любыми.
[48]
Переход от ЛЧД к ЛАХ заключается в определении обычными методами коэффициента усиления усилителя на средних частотах и построении асимптот ЛАХ по известным из ЛЧД частотам сопряжения и наклонам на участках между ними.
[49]
Наличие перерегулирования определяется главным образом присутствием в ЛАЧХ участков с наклоном – 40 дБ / дек и более, непосредственно примыкающих к среднечастотной асимптоте при частотах сопряжения QI, и QIB соответственно. Приближение достаточно протяженного низкочастотного участка с наклоном – 40 дБ / дек к частоте среза вызывает увеличение перерегулирования. Напротив, если Q1H значительно удалена от Qc, перерегулирование невелико. Аналогично удаление QJB от йс в высокочастотной области также уменьшает влияние на качество регулирования участков с отрицательным наклоном, большим 20 дБ / дек.
[50]
Выбор резисторов и конденсаторов двухзвенного фильтра основывается на том, что, во-первых, задается напряжение на выводе VRMS, а во-вторых, каждое звено должно иметь частоту сопряжения ( полюс) на частоте ниже двойной частоты сети. На выводе VRMS действует постоянное напряжение, пропорциональное среднему и действующему значениям синусоидального сетевого напряжения.
[52]
При частоте среза сос имеется запас устойчивости по фазе Yi – Для увеличения коэффициента усиления на низких частотах без существенного уменьшения запаса устойчивости по фазе необходимо, чтобы частота сопряжения а ] / Т1, определяемая наименьшей из постоянных времени контура, была ниже частоты среза на 2 – Ь 3 октавы.
[53]
Сопряжение входного и гетеродинного контура на верхней частоте приводит к нарушению сопряжения на нижней частоте, поэтому для большей точности сопряжения контуров операции настройки на нижней и верхней частотах сопряжения повторяют до тех пор, пока не прекратится увеличение выходного напряжения и не будет обеспечена требуемая чувствительность по всему диапазону. При правильном сопряжении контуров ослабление сигнала зеркального канала и реальная чувствительность должны быть не хуже нормы для данного типа радиоприемника.
[54]
При этом должны учитываться различные факторы: обеспечение работы обоих каналов IB линейной области, минимизация уровня шумов и дрейфа нуля, сложность схемной реализации, отсутствие провала АЧХ на частоте сопряжения, требования обеспечения устойчивости в большом после перегрузок.
[55]
Указанные три типа обратных ЛАЧХ разомкнутых ИСП и соответствующие им обратные передаточные функции однозначно определяются тремя параметрами: частотой со о2 / 7 где Т – период работы импульсного элемента, частотой сопряжения второй низкочастотной и среднечастотной асимптот co i и частотой сопряжения среднечастотной и высокочастотной асимптот со 2 – Формирование желаемых ЛАЧХ состоит в определении сопрягающих частот желаемой ЛАЧХ, обеспечивающих либо минимальную дисперсию ошибки 62Л либо минимальное значение показателя колебательности М, либо компромиссный выбор между ними. Необходимо заметить, что тип желаемой ЛАЧХ определяется как требованиями, предъявляемыми к ИСП, так и способом коррекции.
[56]
Указанные три типа обратных ЛАЧХ разомкнутых ИСП и соответствующие им обратные передаточные функции однозначно определяются тремя параметрами: частотой со о2 / 7 где Т – период работы импульсного элемента, частотой сопряжения второй низкочастотной и среднечастотной асимптот co i и частотой сопряжения среднечастотной и высокочастотной асимптот со 2 – Формирование желаемых ЛАЧХ состоит в определении сопрягающих частот желаемой ЛАЧХ, обеспечивающих либо минимальную дисперсию ошибки 62Л либо минимальное значение показателя колебательности М, либо компромиссный выбор между ними. Необходимо заметить, что тип желаемой ЛАЧХ определяется как требованиями, предъявляемыми к ИСП, так и способом коррекции.
[57]
ОУ высокой точности, прежде всего необходимо выбрать параметры основных узлов: коэффициенты усиления Ко, Ki, Kz, Km, Кю ( см. рис. 3 – 3, 3 – 5), допустимый уровень помех на входе каждого узла, частотные характеристики, частоты сопряжения, величины линейных диапазонов выходных напряжений, входные и выходные сопротивления.
[58]
Частоты сопряжения ffli, Ю2, коз получены в соответствии со значениями постоянных времени.
[60]
Страницы:
1
2
3
4
5
Обновлено: 18.05.2023
Данная статья познакомит вас с концепцией фильтрации и подробно объяснит назначение и характеристики RC фильтров нижних частот.
Временная область и частотная область
Когда вы смотрите на электрический сигнал на осциллографе, вы видите линию, которая представляет изменения напряжения относительно времени. В любой конкретный момент времени сигнал имеет только одно значение напряжения. На осциллографе вы видите представление сигнала во временной области.
Типовая осциллограмма проста и интуитивно понятна, но она также имеет некоторые ограничения, поскольку она напрямую не раскрывает частотный состав сигнала. В отличие от представления во временной области, в котором один момент времени соответствует только одному значению напряжения, представление в частотной области (также называемое спектром) передает информацию о сигнале посредством определения различных частотных компонентов, которые представлены одновременно.
Рисунок 1 – Представления во временной области синусоидального (вверху) и прямоугольного (внизу) сигналов Рисунок 2 – Частотные представления синусоидального (вверху) и прямоугольного (внизу) сигналов
Что такое фильтр?
Если у вас нет большого опыта анализа частотной области, вы можете быть не уверены в том, что представляют собой эти частотные компоненты и как они сосуществуют в сигнале, который не может иметь несколько значений напряжения одновременно. Давайте рассмотрим краткий пример, который поможет прояснить эту концепцию.
Сигнал, видимый на осциллографе, будет по-прежнему представлять собой только одну последовательность напряжений с одним значением на момент времени, но он будет выглядеть по-другому, поскольку его изменения во временной области теперь должны отражать как синусоидальную волну 5 кГц, так и высокочастотные колебания шума.
Однако в частотной области синусоида и шум являются отдельными частотными компонентами, которые присутствуют одновременно в этом одном сигнале. Синусоидальная волна и шум занимают разные участки представления сигнала в частотной области (как показано на диаграмме ниже), и это означает, что мы можем отфильтровать шум, направив сигнал через схему, которая пропускает низкие частоты и блокирует высокие частоты.

Рисунок 3 – Представление аудиосигнала и высокочастотного шума в частотной области
Типы фильтров
В зависимости от особенностей амплитудно-частотных характеристик фильтры можно распределить по широким категориям. Если фильтр пропускает низкие частоты и блокирует высокие частоты, он называется фильтром нижних частот. Если он блокирует низкие частоты и пропускает высокие частоты, это фильтр верхних частот. Существуют также полосовые фильтры, которые пропускают только относительно узкий диапазон частот, и режекторные фильтры, которые блокируют только относительно узкий диапазон частот.

Рисунок 4 – Амплитудно-частотные характеристики фильтров
Фильтры также могут быть классифицированы в соответствии с типами компонентов, которые используются для реализации схемы. Пассивные фильтры используют резисторы, конденсаторы и катушки индуктивности; эти компоненты не способны обеспечить усиление, и, следовательно, пассивный фильтр может только сохранять или уменьшать амплитуду входного сигнала. Активный фильтр, напротив, может фильтровать сигнал и применять усиление, поскольку он включает в себя активный компонент, такой как транзистор или операционный усилитель.

Рисунок 5 – Этот активный фильтр нижних частот основан на популярной топологии Саллена-Ки
В данной статье рассматривается анализ и проектирование пассивных фильтров нижних частот. Эти схемы играют важную роль в самых разных системах и приложениях.
RC фильтр нижних частот
Чтобы создать пассивный фильтр нижних частот, нам нужно объединить резистивный элемент с реактивным элементом. Другими словами, нам нужна схема, которая состоит из резистора и либо конденсатора, либо катушки индуктивности. Теоретически, топология фильтров нижних частот резистор-индуктивность (RL) эквивалентна, с точки зрения фильтрующей способности, топологии фильтров нижних частот резистор-конденсатор (RC). Однако на практике версия резистор-конденсатор встречается гораздо чаще, и, следовательно, оставшаяся часть этой статьи будет посвящена RC фильтру нижних частот.

Рисунок 6 – RC фильтр нижних частот
Как вы можете видеть на схеме, пропускающая нижние частоты частотная характеристика RC фильтра создается путем установки резистора последовательно с путем прохождения сигнала и конденсатора параллельно нагрузке. На схеме нагрузка является отдельным компонентом, но в реальной цепи она может представлять что-то гораздо более сложное, например, аналого-цифровой преобразователь, усилитель или входной каскад осциллографа, который вы используете для измерения амплитудно-частотной характеристики фильтра.
Мы можем интуитивно проанализировать фильтрующее действие топологии RC фильтра нижних частот, если поймем, что резистор и конденсатор образуют частотно-зависимый делитель напряжения.

Рисунок 7 – RC фильтр нижних частот перерисован так, чтобы он выглядел как делитель напряжения
Когда частота входного сигнала низкая, полное сопротивление конденсатора будет высоким относительно полного сопротивления резистора; таким образом, большая часть входного напряжения падает на конденсаторе (и на нагрузке, которая параллельна конденсатору). Когда входная частота высокая, полное сопротивление конденсатора будет низким по сравнению с полным сопротивлением резистора, что означает, что на резисторе падает большее напряжение, и меньшее напряжение передается на нагрузку. Таким образом, низкие частоты пропускаются, а высокие частоты блокируются.
Частота среза
Диапазон частот, для которого фильтр не вызывает значительного ослабления, называется полосой пропускания, а диапазон частот, для которых фильтр вызывает существенное ослабление, называется полосой задерживания. Аналоговые фильтры, такие как RC фильтр нижних частот, переходят из полосы пропускания в полосу задерживания всегда постепенно. Это означает, что невозможно идентифицировать одну частоту, на которой фильтр прекращает пропускать сигналы и начинает их блокировать. Однако инженерам нужен способ, чтобы удобно и кратко охарактеризовать амплитудно-частотную характеристику фильтра, и именно здесь в игру вступает понятие частоты среза.
Частота среза RC фильтра нижних частот фактически является частотой, на которой амплитуда входного сигнала уменьшается на 3 дБ (это значение было выбрано, поскольку уменьшение амплитуды на 3 дБ соответствует снижению мощности на 50%). Таким образом, частоту среза также называют частотой -3 дБ, и на самом деле это название является более точным и более информативным. Термин полоса пропускания относится к ширине полосы пропускания фильтра, и в случае фильтра нижних частот полоса пропускания равна частоте -3 дБ (как показано на диаграмме ниже).

Рисунок 8 – Данная диаграмма показывает общие особенности амплитудно-частотной характеристики RC фильтра нижних частот. Ширина полосы пропускания равна частоте -3 дБ.
Как объяснялось выше, пропускающее низкие частоты поведение RC фильтра обусловлено взаимодействием между частотно-независимым импедансом резистора и частотно-зависимым импедансом конденсатора. Чтобы определить подробности амплитудно-частотной характеристики фильтра, нам нужно математически проанализировать взаимосвязь между сопротивлением (R) и емкостью (C); мы также можем манипулировать этими значениями, чтобы разработать фильтр, который соответствует точным спецификациям. Частота среза (fср) RC фильтра нижних частот рассчитывается следующим образом:
Давайте посмотрим на простой пример. Значения конденсаторов являются более сдерживающими, чем значения резисторов, поэтому мы начнем с распространенного значения емкости (например, 10 нФ), а затем воспользуемся формулой для определения необходимого значения сопротивления. Цель состоит в том, чтобы разработать фильтр, который будет сохранять аудиосигнал 5 кГц и подавлять шум 500 кГц. Мы попробуем частоту среза 100 кГц, а позже в этой статье мы более тщательно проанализируем влияние этого фильтра на обе частотные составляющие.
Таким образом, резистор 160 Ом в сочетании с конденсатором 10 нФ даст нам фильтр, который дает амплитудно-частотную характеристику, близкую к необходимой.
Расчет амплитудно-частотной характеристики фильтра
Мы можем рассчитать теоретическое поведение фильтра нижних частот, используя частотно-зависимую версию типового расчета делителя напряжения. Выходное напряжение резистивного делителя напряжения выражается следующим образом:

Рисунок 9 – Резистивный делитель напряжения
RC фильтр использует эквивалентную структуру, но вместо R2 у нас конденсатор. Сначала мы заменим R2 (в числителе) на реактивное сопротивление конденсатора (XC). Далее нам нужно рассчитать величину полного сопротивления и поместить его в знаменатель. Таким образом, мы имеем
Реактивное сопротивление конденсатора указывает величину противодействия протеканию тока, но, в отличие от активного сопротивления, величина противодействия зависит от частоты сигнала, проходящего через конденсатор. Таким образом, мы должны рассчитать реактивное сопротивление на определенной частоте, и формула, которую мы используем для этого, следующая:
В приведенном выше примере схемы R ≈ 160 Ом, и C = 10 нФ. Предположим, что амплитуда Vвх равна 1 В, поэтому мы можем просто удалить Vвх из расчетов. Сначала давайте рассчитаем амплитуду Vвых на частоте необходимой нам синусоиды:
Амплитуда необходимого нам синусоидального сигнала практически не изменяется. Это хорошо, поскольку мы намеревались сохранить синусоидальный сигнал при подавлении шума. Этот результат неудивителен, поскольку мы выбрали частоту среза (100 кГц), которая намного выше частоты синусоидального сигнала (5 кГц).
Теперь посмотрим, насколько успешно фильтр ослабит шумовую составляющую.
Амплитуда шума составляет всего около 20% от первоначального значения.
Визуализация амплитудно-частотной характеристики фильтра
Наиболее удобным способом оценки влияния фильтра на сигнал является изучение графика его амплитудно-частотной характеристики. На этих графиках, часто называемых графиками Боде, амплитуда (в децибелах) откладывается по вертикальной оси, а частота – по горизонтальной оси; горизонтальная ось обычно имеет логарифмический масштаб, поэтому физическое расстояние между 1 Гц и 10 Гц такое же, как физическое расстояние между 10 Гц и 100 Гц, между 100 Гц и 1 кГц и так далее. Такая конфигурация позволяет нам быстро и точно оценить поведение фильтра в очень широком диапазоне частот.

Рисунок 10 – Пример графика амплитудно-частотной характеристики
Каждая точка на кривой указывает амплитуду, которую будет иметь выходной сигнал, если входной сигнал имеет величину 1 В и частоту, равную соответствующему значению на горизонтальной оси. Например, когда частота входного сигнала равна 1 МГц, амплитуда выходного сигнала (при условии, что амплитуда входного сигнала равна 1 В) будет 0,1 В (поскольку –20 дБ соответствует уменьшению в десять раз).
Общий вид этой кривой амплитудно-частотной характеристики станет вам очень знакомым, если вы будете проводить больше времени со схемами фильтров. Кривая почти идеально плоская в полосе пропускания, а затем, по мере приближения частоты входного сигнала к частоте среза, скорость ее спада начинает увеличиваться. В конечном итоге скорость изменения затухания, называемая спадом, стабилизируется на уровне 20 дБ/декада, то есть уровень выходного сигнала уменьшается на 20 дБ при каждом увеличении частоты входного сигнала в десять раз.
Оценка производительности фильтра нижних частот
Если мы построим амплитудно-частотную характеристику фильтра, который мы разработали ранее в этой статье, то увидим, что амплитудный отклик на 5 кГц, по сути, равен 0 дБ (т.е. почти нулевое затухание), а амплитудный отклик на 500 кГц составляет приблизительно –14 дБ (что соответствует коэффициенту передачи 0,2). Эти значения согласуются с результатами расчетов, которые мы выполнили в предыдущем разделе.
Фазовый сдвиг фильтра низких частот
До сих пор мы обсуждали способ, которым фильтр изменяет амплитуду различных частотных составляющих в сигнале. Однако реактивные элементы цепи в дополнение к влиянию на амплитуду всегда вносят сдвиг фазы.
Понятие фазы относится к значению периодического сигнала в определенный момент цикла. Таким образом, когда мы говорим, что схема вызывает сдвиг фазы, то имеем в виду, что она создает смещение между входным и выходным сигналами: входной и выходной сигналы больше не начинают и заканчивают свои циклы в один и тот же момент времени. Значение сдвига фазы, например, 45° или 90°, показывает, какое было создано смещение.
Каждый реактивный элемент в цепи вводит сдвиг фазы на 90°, но этот фазовый сдвиг происходит не сразу. Фаза выходного сигнала, так же как и амплитуда выходного сигнала, изменяется постепенно по мере увеличения частоты входного сигнала. В RC фильтре нижних частот у нас есть один реактивный элемент (конденсатор), и, следовательно, схема в конечном итоге будет вводить сдвиг фазы на 90°.
Как и в случае амплитудно-частотной характеристикой, фазо-частотную характеристику легче всего оценить, изучив график, на котором частота на горизонтальной оси приведена в логарифмическом масштабе. Приведенное ниже описание дает общее представление, а затем вы можете заполнить детали, изучив график.
- Сдвиг фазы изначально равен 0°.
- Он постепенно увеличивается до достижения 45° на частоте среза; на этом участке характеристики скорость изменения увеличивается.
- После частоты среза сдвиг фазы продолжает увеличиваться, но скорость изменения уменьшается.
- Скорость изменения становится очень малой, когда сдвиг фазы асимптотически приближается к 90 °.
Фильтры нижних частот второго порядка
До сих пор мы предполагали, что RC фильтр нижних частот состоит из одного резистора и одного конденсатора. Эта конфигурация является фильтром первого порядка.
Добавляя один реактивный элемент к фильтру, например, переходя от первого порядка ко второму или от второго к третьему, мы увеличиваем максимальный спад на 20 дБ/декада. Более крутой спад приводит к более быстрому переходу от низкого затухания к высокому затуханию, и это может привести к улучшению производительности, когда нет широкой полосы частот, отделяющей необходимые частотные компоненты от шумовых компонентов.

Рисунок 12 – RC фильтр нижних частот второго порядка
Хотя эта топология, безусловно, создает характеристику второго порядка, она широко не используется – как мы увидим в следующем разделе, ее амплитудно-частотная характеристика часто уступает амплитудно-частотной характеристике активного фильтра второго порядка или RLC фильтра второго порядка.
Амплитудно-частотная характеристика RC фильтра второго порядка
Мы можем попытаться создать RC фильтр нижних частот второго порядка, разработав фильтр первого порядка в соответствии с необходимой частотой среза, а затем соединив два этих каскада первого порядка последовательно. Это даст фильтр, который имеет аналогичную общую амплитудно-частотную характеристику и максимальный спад 40 дБ/декада вместо 20 дБ/декада.
Однако если мы посмотрим на АЧХ более внимательно, то увидим, что частота –3 дБ снизилась. RC фильтр второго порядка ведет себя не так, как ожидалось, поскольку эти два звена не являются независимыми – мы не можем просто соединить эти две звена вместе и проанализировать схему как фильтр нижних частот первого порядка, за которым следует идентичный фильтр нижних частот первого порядка.
Кроме того, даже если мы вставим буфер между этими двумя звеньями, чтобы первое RC звено и второе RC звено могли работать как независимые фильтры, затухание на исходной частоте среза будет составлять 6 дБ вместо 3 дБ. Это происходит именно потому, что два звена работают независимо – первый фильтр вносит затухание 3 дБ на частоте среза, а второй фильтр добавляет еще 3 дБ затухания.

Рисунок 13 – Сравнение амплитудно-частотных характеристик фильтров нижних частот второго порядка
Правообладателем опубликованных на форуме текстовых и графических материалов является Clippu Net.
Всё содержимое форума не подлежит дальнейшему воспроизведению и/или распространению в какой-либо форме, иначе как с разрешения Clippu Net.
О ФОРУМЕ
Форум по автозвуку и домашним акустическим системам. Информационный портал для тех, чья жизнь тесно связанна с качественной музыкой.
Полезные советы, примеры инсталляций car и home audio систем. Видео библиотеки и фото альбомы с тематическим содержанием. Партнёрские программы. Доска объявлений.
Частота среза — частота, на которой частотная характеристика пересекает 0 дБ.
Частота сопряжения — частота, на которой частотная характеристика меняет наклон.
Эти понятия относятся к теории автоматического управления. Частота среза используется при анализе устойчивости системы управления. Чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы фаза разомкнутой системы не достигала −180° на частоте среза.
Частота среза имеет другое определение в обработке сигналов. Там под частотой среза подразумевают частоту сопряжения, а понятием частота сопряжения не пользуются. В обработке сигналов нет необходимости анализировать устойчивость системы.
Первая цитата со страницы 59:
Точку пересечения прямой с осью нуля децибел (осью частот) можно найти, положив L(ω)=0 или, соответственно, A(ω)=1. Отсюда получаем так называемую частоту среза л. а. х.,
При этом в книге частота среза обозначается как ωср.
На странице 66 описывается апериодическое звено первого порядка:
Наиболее просто, практически без вычислительной работы, строится так называемая асимптотическая л. а. х. На стандартной сетке проводится вертикальная прямая через точку с частотой, называемой сопрягающей частотой ω=1/T.
В разных источниках вижу разные определения для этого понятия.
1)частота на которой коэфициент усиления падает на 3 дб.
2)частота на которой КУ равен нулю.
Почему такая разница?
Вот я определяю частоту среза графически для того чтобы оценить устойчивость системы по аплитуде и фазе. Каким определением частоты среза я должен пользоваться?
Есть еще такое понятие как сопрягающая частота – это частота, граница ачх двух звеньев, и она в целом тоже может быть определена на урове -3 дб.
С точки зрения теории автоматического управления ответ строго однозначен: частота среза – это частота, где “падающая” ЛАЧХ пересекает ось абсцисс. Эта частота соответствует единичному усилению, т. к. 20lg1=0. Частота среза разомкнутой системы, например, показывает, устойчива ли данная система при замыкании: если на частоте среза ФЧХ проходит выше уровня -π, то данная система устойчива при замыкании, а отличие ФЧХ от -π на частоте среза, численно выражает запас устойчивости. Как видите, ни о каких 3-х или там 10-ти децибеллах речи не идет, частота среза является математически обоснованной величиной: дело в том, что если ФЧХ на частоте среза проходит ниже уровня -π, то это равнозначно изменению знака обратной связи с отрицательной на положительную, что как раз-таки и выводит систему из устойчивости. Чтоб не сомневаться, руководствуйтесь книжками по ТАУ, там терминология соблюдается неукоснительно.

То есть вашь вариант по уровню -3 дб?
А если не применимо к звуку?
Я говорил об исследовании системы радиоавтоматики на устойчивость.
Вот другое определение.
EBM — значит Эстрадная Балдёжная Музыка Мудрец (10989) но тогда хз, я колонками и усилителями занимался
Уже такие вопросы были, вниз страницу пролистни.
КУ не может быть равен нулю, если только в ИДЕАЛЬНОМ фильтре частот, такие существуют или нет – не знаю, по моему нет. На практике происходит примерно как на этом графике, то есть заметно уменьшается КУ, но не падает резко до нуля, постепенно всё. На картинке – фильтр высоких частот, то есть низкие он не пропускает (почти)

Это все понятно, а конкретное значение частоты среза по ЛАЧХ как определить? По уровню в минус 3 дб?
Вот есть другое определение частоты среза.
Идущий найдет дорогу Просветленный (34569) Карабас π’дорас, ну вообще в интернете написано, что приблизительно в точке где падает на 3дБ – начинается полоса задержания. То есть находишь эту точку, смотришь какой частоте соответствует точка, и эта частота будет являться частотой среда. Но вообще нас в вузе по другому учили, но это было в программе, опять же не без графика, к сожалению не помню что сделать нужно было. Запомнилось только что что-то делили на корень из двух.
Идущий найдет дорогу Просветленный (34569) Карабас π’дорас, про определение я тебе доходчиво обьяснил. Оба определения правильные по сути, но первое оно реальное, а второе для идеальных фильтров. Где реальный, а где идеальный фильтр – видно на второй картинке. Что непонятного то?
Зависит от критерия. Для усилителей частота среза АЧХ – уровень 1,5 дБ. Для акустики (измерения по воздуху) 15 дБ. Для автомагнитол 3 дБ. Для китайцев – произвольное значение.
Уровень среза – частота, при которой АЧХ пересекает линию с заранее заданным уровнем.
Я это так понимаю.
Читайте также:
- Расскажите о правлении сегунов в японии кратко
- Янка сипаков биография кратко
- Кризис римской империи кратко
- Поздравления с 80 летием мужчине своими словами кратко и ясно
- Международные отношения от вестфальского мира до великой французской революции кратко
