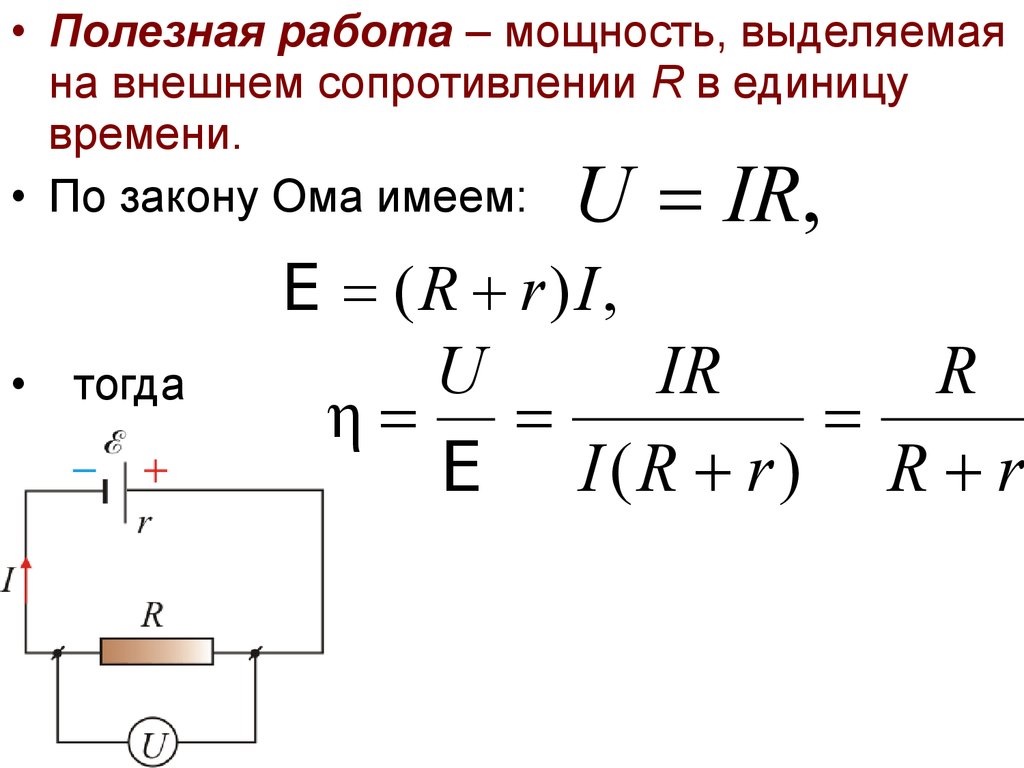
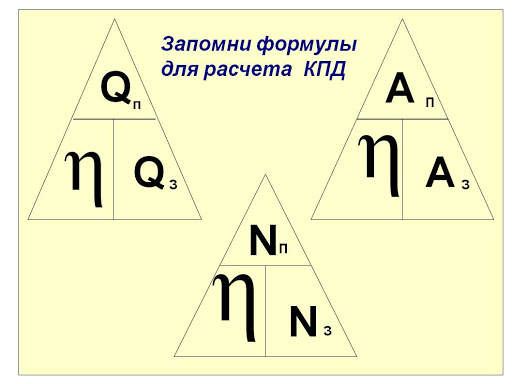
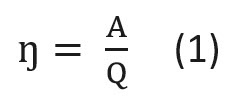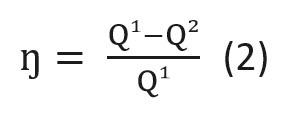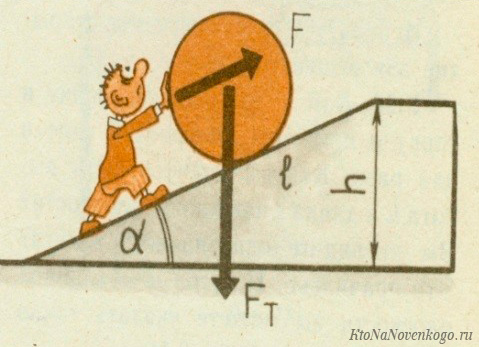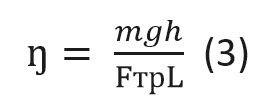Коэффицие́нт поле́зного де́йствия (КПД) — характеристика эффективности системы (устройства, машины) в отношении преобразования или передачи энергии. Определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой; обозначается обычно η («эта»)[1]. КПД является безразмерной величиной и часто выражается в процентах. Часто применяется в переносном смысле как метафора эффективности чего-либо без привязки к расчётам.
Определение[править | править код]
Математически КПД определяется как
где А — полезная работа (энергия), а Q — затраченная энергия.
Если КПД выражается в процентах, эту формулу иногда записывают в виде
.
Здесь умножение на 

В силу закона сохранения энергии и в результате неустранимых потерь энергии КПД реальных систем всегда меньше единицы, то есть невозможно получить полезной работы больше или столько, сколько затрачено энергии.
КПД теплово́го дви́гателя — отношение совершённой полезной работы двигателя к энергии, полученной от нагревателя. КПД теплового двигателя может быть вычислен по следующей формуле
,
где 

.
Другие похожие показатели[править | править код]
Не все показатели, характеризующие эффективность энергетических процессов, соответствуют вышеприведённому описанию. Даже если они традиционно или ошибочно называются «коэффициент полезного действия», они могут иметь другие свойства, в частности, превышать 100 %.
КПД котлов[править | править код]
КПД котлов на органическом топливе традиционно рассчитывается по низшей теплоте сгорания; при этом предполагается, что влага продуктов сгорания покидает котёл в виде перегретого пара. В конденсационных котлах эта влага конденсируется, теплота конденсации полезно используется. При расчёте КПД по низшей теплоте сгорания он в итоге может получиться больше единицы. В данном случае корректнее было бы считать его по высшей теплоте сгорания, учитывающей теплоту конденсации пара; однако при этом показатели такого котла трудно сравнивать с данными о других установках.
Тепловые насосы и холодильные машины[править | править код]
Достоинством тепловых насосов как нагревательной техники является возможность получать больше теплоты, чем расходуется энергии на их работу. Холодильная машина может отвести от охлаждаемого конца больше теплоты, чем затрачивается энергии на организацию процесса.
Эффективность машин характеризует холодильный коэффициент[en]
,
где 

Для тепловых насосов используют термин коэффициент трансформации
,
где 

В идеальной машине 

Наилучшими показателями производительности для холодильных машин обладает обратный цикл Карно: в нём холодильный коэффициент
,
где 

Примечания[править | править код]
- ↑ Зубарев Д. Н. Коэффициент полезного действия // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 484—485. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
- ↑ Холодильный коэффициент // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
Литература[править | править код]
- Пёрышкин А. В. Физика. 8 класс. — Дрофа, 2005. — 191 с. — 50 000 экз. — ISBN 5-7107-9459-7..
Формула КПД и как его вычислить для тепловой машины или механизма
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Эта аббревиатура вряд ли требует расшифровки: она неизвестна разве что тем, у кого в школе был «неуд» по физике.
Но для забывчивых всё же напомним, что под этим сокращением скрывается коэффициент полезного действия. Что же собой представляет эта величина?
Поговорим о ней простым и понятным языком – это может пригодиться даже в повседневной жизни.
Что такое КПД в физике и какова его формула
Для выполнения какой-либо работы необходимо затратить определённое количество энергии. Чтобы ехал велосипед, вы тратите мышечную энергию крутя педали. Чтобы двигался автомобиль, используется энергия сжигаемого топлива (бензина, солярки или газа).
Для горения лампочки требуется энергия электрического тока. Список можно продолжать до бесконечности. Точку можно поставить на солнечной энергии, благодаря которой существует жизнь на Земле.
Далее возникает логичный вопрос: а насколько эффективно расходуется эта энергия? В идеале хотелось бы, чтобы вся она шла «в дело», то есть использовалась только по прямому назначению. Но, к сожалению, на практике такого не бывает.
Затраченная энергия будет всегда больше, чем полезная работа, так как для достижения основной цели (движение, подъём груза, освещение, отопление и т.д.) часть энергии неизбежно уйдёт на неустранимые потери (преодоление силы трения, нагрев электропроводки, выброс продуктов горения в атмосферу и т.д.). Понятно, что чем меньше такие потери, тем лучше.
Критерием того, насколько эффективно работает система (устройство, агрегат, двигатель, машина и т.д.), служит показатель, получивший название коэффициент полезного действия (КПД).
Иными словами, коэффициент полезного действия показывает, какова доля полезной работы в общих энергозатратах. Математически КПД (чаще всего обозначается символом ŋ) определяется по формуле:
где A — полезная энергия (работа);
Q — энергия, затраченная на совершение полезной работы.
Понятно, что ŋ – величина безразмерная и не может быть больше единицы (да и равной единице она может быть чисто теоретически).
Выражается она в виде десятичной дроби либо в процентах (в последнем случае в формулу вставляется множитель х100).
Так, если КПД равен 0,9 (90%), то это значит, что 10% полезной мощности составили безвозвратные потери.
КПД теплового двигателя (машины)
Под тепловым двигателем понимается машина (агрегат), в которой энергия, высвобождающаяся в процессе расширения рабочего тела, преобразуется в механическую работу.
В качестве рабочего тела обычно выступает газ или газообразные вещества (пары бензина, водяной пар и т.п.).
Тепловые машины работают по замкнутому циклу. Это значит, что процесс преобразования энергии и сопутствующей теплопередачи периодически повторяется, а рабочее тело совершает круговой цикл, возвращаясь в исходное состояние.
К тепловым двигателям относятся:
- поршневые (паровые машины, двигатели внутреннего сгорания);
- роторные/турбинные (газовые или паровые турбины АЭС и ТЭЦ);
- реактивные (авиация);
- ракетные (космическая техника).
Используя положения предыдущего параграфа, КПД тепловой машины можно сформулировать как отношение полезной работы, совершённой за один цикл, к энергии (количеству теплоты), поступившей от энергоносителя (нагревателя).
Тогда формулу (1) можно преобразовать следующим образом:
где Q1 — количество теплоты, полученное двигателем от нагревателя за цикл;
Q2 — количество теплоты, отданное двигателем охладителю (холодильнику) за цикл;
Q1 – Q2 – количество теплоты, которое пошло на совершение работы.
Предположим, что Q1 = Q2, то есть на совершение полезной работы ничего не осталось – вся энергия «ушла в трубу». Тогда и КПД будет нулевым. Если же Q2 = 0, то есть вся энергия отдана полезной работе (потери отсутствуют), то коэффициент полезного действия будет равен 1.
Но это теория, на практике ни то ни другое нереалистично. В первом случае двигатель просто бесполезен, во втором – идеален, но недосягаем.
Значения КПД для различных типов тепловых двигателей приведены ниже.
Самым большим КПД обладают тепловые двигатели, работающие на основе цикла Карно (процесс назван в честь французского инженера, открывшего это явление в 1824 г.). В термодинамике оно характеризует круговой цикл, включающий в себя две стадии: расширение и сжатие рабочего тела.
Причём на протяжении обеих стадий попеременно проходят два процесса: изотермический (протекающий при постоянной температуре), и адиабатический (протекающий без теплообмена с окружающей средой). Максимальное значение КПД здесь достигается за счёт того, что тела с разной температурой не контактируют, а значит, без осуществления работы теплопередача исключается.
КПД механизма — по какой формуле вычисляют
Человек придумал разнообразные механизмы, с помощью которых можно поднимать тяжёлые грузы на определённую высоту. Так, для подъёма ведра с водой из колодца изобрели ворот, для подъёма автомобиля – домкрат. При помощи лебёдки и наклонной плоскости египтяне построили свои грандиозные пирамиды.
Пользуясь этими приспособлениями, человек редко вспоминает об их КПД. В качестве примера рассмотрим этот показатель для наклонной плоскости.
Принцип расчёта КПД остаётся неизменным: нужно найти отношение полезной работы ко всей затраченной энергии. То есть опять-таки используем общую формулу (1), сделав соответствующие преобразования.
Предположим, тело массой m нужно поднять (точнее затолкать или затянуть) на высоту h. При постоянной скорости подъёма полезная работа будет равна произведению силы тяжести (mg) на высоту (h).
Затраченная работа определяется произволением силы толчка или тяги F на длину наклонной плоскости L. Заметим, что толчковое (тяговое) усилие идёт на преодоление силы трения Fтр.
Таким образом, КПД такого простейшего механизма можно посчитать по формуле:
Несложный анализ показывает, что коэффициент полезного действия наклонной плоскости обратно пропорционален силе трения и длине аппарели. Последняя, в свою очередь, зависит от угла наклона: чем он больше, тем короче аппарель.
Как можно увеличить КПД
Современная наука постоянно ищет пути повышения коэффициента полезной модности двигателей и отдельных механизмов, внедряя новые технические решения и технологические инновации.
Чем выше будет КПД, тем экономичней будет двигатель, тем больше энергоресурсов удастся сберечь.
Тепловой двигатель
Из формулы (2) следует, что для увеличения КПД есть два пути: а) повышение температуры нагревателя; б) понижение температуры холодильника. Оба пути малоперспективны.
Нагреватель нельзя разогревать до бесконечности, так как любой материал имеет предел жаропрочности. Холодильником почти всегда служит окружающая среда, а внедрение в систему дополнительного теплообменника (например, баллона с жидким азотом) нецелесообразно: это резко увеличит вес, габариты и стоимость двигателя.
Установлено, что на коэффициент полезного действия не влияют характеристики рабочего тела. Что же остаётся?
А остаётся немало практически реализуемых способов, таких как уменьшение трения в механических узлах, минимизация теплопотерь путём достижения максимально полного сгорания топлива, создание обтекаемых форм для снижения лобового сопоставления (воздуха или воды) и т.д.
Учитывая, что в механике хорошим показателем на сегодняшний день считается КПД 30-40%, учёным и практикам есть над чем работать.
Наклонная плоскость
Из формулы (3) следует, что для повышения КПД нужно снижать силу трения (прежде всего, путём создания гладких соприкасающихся поверхностей) и увеличивать угол наклона. Но! При крутом уклоне силёнок для поднятия тяжёлого груза может и не хватить.
В заключение отметим, что в электротехнике ситуация с КПД обстоит гораздо лучше (показатель в 95% для электродвигателя – норма). На то есть объективные причины, объяснение которых выходит за рамки рассматриваемой темы.
Чему равен КПД цикла, проводимого с идеальным одноатомным газом? Ответ приведите в процентах, округлить до целых.
Спрятать решение
Решение.
КПД тепловой машины определяется как отношение полезной работы и переданного рабочему телу тепла за цикл: Определим сперва полезную работу за цикл, на диаграмме
этой величине соответствует площадь цикла:
Передаваемое газу тепло рассчитаем при помощи первого начала термодинамики:
Рассмотрим последовательно все участки цикла. На участке 1 — 2 газ не совершает работы, а изменение его внутренней энергии (с учетом уравнения Клапейрона-Менделеева) равно:
Так как изменение внутренней энергии положительно, газ получает тепло на этом участке. На участке 2 — 3 газ совершает работу
Изменение его внутренней энергии на этом участке:
Следовательно, на этом участке газ получает тепло
На участке 3 — 1 газ совершает отрицательную работу, он остывает, а значит, его внутренняя энергия уменьшается, следовательно, на этом участке он отдает тепло, а не получает. Окончательно, все полученное газом за цикл тепло равно
Таким образом, КПД цикла равно
Ответ: 10.
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
|
Приведено полное решение, включающее следующие элементы: I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом; II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии задачи, и стандартных обозначений величин, используемых при написании физических законов); III) представлены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями); IV) представлен правильный ответ с указанием единиц измерения искомой величины |
2 |
|
Правильно записаны все необходимые положения теории, физические законы, закономерности, и проведены преобразования, направленные на решение задачи, но имеется один или несколько из следующих недостатков. Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. И (ИЛИ) В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения и не зачёркнуты. И (ИЛИ) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. И (ИЛИ) Отсутствует пункт IV, или в нём допущена ошибка (в том числе в записи единиц измерения величины) |
1 |
|
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1 или 2 балла |
0 |
| Максимальный балл | 2 |
п.1. Полезная работа и затраченная работа
Полезной называется работа по подъёму грузов или преодолению какого-либо сопротивления.
Затраченной (полной) называется работа, совершённая приложенной силой.
Примеры полной и полезной работы
Затраченная работа равна сумме:
- полезной работы;
- работы против силы трения в различных частях механизма;
- работы по перемещению различных составных элементов механизма.
Поэтому всегда (A_text{полезная}lt A_text{затраченная})
п.2. КПД механизма
Коэффициент полезного действия механизма – это отношение его полезной работы к затраченной работе. $$ eta=frac{A_text{п}}{A_text{з}}cdot 100text{%} $$
Поскольку в реальных механизмах всегда (A_text{п}lt A_text{з}), $$ frac{A_text{п}}{A_text{з}}lt 1. $$
Следовательно КПД реальных механизмов (etalt 100text{%}).
Только в идеальном механизме, в котором нет потерь на трение, и все составные элементы не имеют веса, (A_text{п}=A_text{з}) и (eta=100text{%}).
КПД никогда не может быть выше (100text{%}).
КПД реальных механизмов можно увеличить за счет снижения трение в подвижных узлах и уменьшения веса всех составных элементов конструкции.
Для этого нужны новые смазочные вещества и лёгкие, но прочные конструкционные материалы.
п.3. Задачи
Задача 1. По наклонной плоскости поднимают груз массой 50 кг, прикладывая к нему силу 250 Н, направленную вдоль плоскости. Чему равен КПД плоскости, если её длина 10 м, а высота 3 м?
Дано:
(m=50 text{кг})
(gapprox 10 text{м/с}^2)
(F=250 text{Н})
(L=10 text{м})
(h=3 text{м})
__________________
(eta-?)
Полезная работа по подъему груза begin{gather*} A_text{п}=mgh. end{gather*} Затраченная работа на перемещение груза вдоль наклонной плоскости begin{gather*} A_text{з}=FL. end{gather*} КПД плоскости: begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{mgh}{FL}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{50cdot 10cdot 3}{250cdot 10}cdot 100text{%}=60text{%} end{gather*} Ответ: 60%
Задача 2. С помощью подвижного блока поднимают груз массой 200 кг, прикладывая силу 1200 Н. Чему равен КПД блока?
Дано:
(m=200 text{кг})
(gapprox 10 text{м/с}^2)
(F=1200 text{Н})
__________________
(eta-?)
Полезная работа по подъему груза на высоту (h): begin{gather*} A_text{п}=mgh. end{gather*} Подвижный блок дает выигрыш в силе в 2 раза и проигрыш в расстоянии. Т.е. при работе нужно вытянуть трос длиной (2h). Затраченная работа: begin{gather*} A_text{з}=Fcdot 2h. end{gather*} КПД блока begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{mgh}{2Fh}cdot 100text{%}=frac{mg}{2F}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{200cdot 10}{2cdot 1200}cdot 100text{%}approx 83,3text{%} end{gather*} Ответ: 83,3%
Задача 3. Груз массой 245 кг с помощью рычага равномерно подняли на высоту 6 см. При этом к длинному плечу рычага была приложена сила 500 Н, а точка приложения силы опустилась на 30 см. Найдите КПД рычага.
Дано:
(m=245 text{кг})
(gapprox 10 text{м/с}^2)
(h_2=6 text{см}=0,6 text{м})
(F_1=500 text{Н})
(h_1=30 text{см}=0,3 text{м})
__________________
(eta-?)
Полезная работа по подъему груза на высоту (h_2): begin{gather*} A_text{п}=mgh_2. end{gather*} Затраченная работа по опусканию длинного плеча рычага: begin{gather*} A_text{з}=F_1h_1. end{gather*} КПД рычага begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{mgh_2}{F_1h_1}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{245cdot 10cdot 0,06}{500cdot 0,3}cdot 100text{%}=frac{147}{150}cdot 100text{%}=98text{%} end{gather*} Ответ: 98%
Задача 4. Чему равен КПД гидравлической машины, если для равномерного подъема груза массой 1,2 т к меньшему поршню прикладывают силу 160 Н? Площади поршней равны 5 см2 и 500 см2.
Дано:
(m=1,2 text{т}=1200 text{кг})
(gapprox 10 text{м/с}^2)
(F_1=160 text{Н})
(S_1=5 text{см}^2=5cdot 10^{-4} text{м}^2)
(S_2=500 text{см}^2=5cdot 10^{-2} text{м}^2)
__________________
(eta-?)
При опускании малого поршня на высоту (h_1) из малого в большой цилиндр вытекает объем жидкости равный $$ V=S_1h_1=S_2h_2Rightarrow frac{h_2}{h_1}=frac{S_1}{S_2} $$ Полезная работа по подъему груза на высоту (h_2): begin{gather*} A_text{п}=mgh_2. end{gather*} Затраченная работа по опусканию поршня малого цилиндра: begin{gather*} A_text{з}=F_1h_1. end{gather*} КПД гидравлической машины begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{mgh_2}{F_1h_1}cdot 100text{%}=frac{mgS_1}{F_1S_2}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{1200cdot 10cdot 5cdot 10^{-4}}{160cdot 5cdot 10^{-2}}cdot 100text{%}=frac{600}{800}cdot 100text{%}=75text{%} end{gather*} Ответ: 75%
Задача 5*. Груз массой 12 кг поднимают с помощью подвижного блока массой 3 кг. Чему равен КПД блока?
Дано:
(M=12 text{кг})
(m=3 text{кг})
__________________
(eta-?)
Полезная работа по подъему груза на высоту (h): begin{gather*} A_text{п}=Mgh. end{gather*} Подвижный блок дает выигрыш в силе в 2 раза. Поэтому достаточно приложить силу, равную половине суммы весов груза и блока: begin{gather*} F=frac 12(M+m)g end{gather*} При этом будет проигрыш в расстоянии. Потребуется вытянуть трос длиной (2h). Затраченная работа, приложенная к тросу: begin{gather*} A_text{з}=Fcdot 2h=frac 12(M+m)gcdot 2h=(M+m)gh. end{gather*} КПД подвижного блока begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{Mgh}{(M+m)gh}cdot 100text{%}=frac{M}{M+m}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{12}{12+3}cdot 100text{%}=80text{%} end{gather*} Ответ: 80%
Задача 6. Сколько воды можно поднять из колодца глубиной 36 м за 1 ч, если мощность электродвигателя равна 5 кВт, КПД всей установки равно 70%?
Дано:
(N=5 text{кВт}=5cdot 10^3 text{Вт})
(eta=70text{%}=0,7)
(h=36 text{м})
(t=1 text{ч}=3600 text{с})
(gapprox 10 text{м/с}^2)
__________________
(m-?)
Полезная работа по подъему груза на высоту (h): begin{gather*} A_text{п}=Mgh. end{gather*} Затраченная работа электродвигателя: begin{gather*} A_text{з}=Nt. end{gather*} КПД установки begin{gather*} eta=frac{A_text{п}}{A_text{з}}=frac{mgh}{Nt} end{gather*} Масса воды begin{gather*} m=frac{eta Nt}{gh} end{gather*} Получаем: begin{gather*} m=frac{0,7cdot 5cdot 10^3cdot 3600}{10cdot 36}=35cdot 10^3 (text{кг})=35 text{т} end{gather*} Ответ: 35 т
Задача 7*. КПД подвижного блока при подъеме первого груза равен 80%, а при подъеме второго груза – 90%. Масса какого груза больше и во сколько раз? Трением в блоке можно пренебречь.
Дано:
(eta_1=80text{%}=0,8)
(eta_2=90text{%}=0,9)
__________________
(frac{M_2}{M_1}-?)
КПД подвижного блока массой (m), с помощью которого поднимают груз массой (M) begin{gather*} eta=frac{M}{M+m} end{gather*} (см. Задачу 5 выше). Масса груза begin{gather*} eta(M+m)=MRightarrow eta m=(1-eta)MRightarrow M=frac{eta}{1-eta}m end{gather*} Получаем: begin{gather*} M_1=frac{0,8}{1-0,8}m=4m,\[6pt] M_2=frac{0,9}{1-0,9}m=9m end{gather*} Масса второго груза больше.
Отношение масс begin{gather*} frac{M_2}{M_1}=frac{9m}{4m}=2,25 (text{раз}) end{gather*} Ответ: масса второго груза больше в 2,25 раз
п.4. Лабораторная работа №13. Определение КПД наклонной плоскости
Цель работы
Научиться проводить измерения и рассчитывать КПД простого механизма на примере наклонной плоскости. Исследовать зависимость КПД наклонной плоскости от высоты.
Теоретические сведения
Работа по подъему тела весом (P) вертикально на высоту (h) (из точки C в точку B): $$ A_text{CB}=Ph $$
Работа по перемещению того же тела силой (F), направленной вдоль наклонной плоскости длиной (L) (из точки A в точку B): $$ A_text{AB}=FL $$
В обоих случаях тело перемещается с нулевого уровня AC, где (h_0=0), на уровень с высотой (h) в точку B. Работа сторонних сил в этом случае равна изменению потенциальной энергии тела: $$ A=A_text{CB}=A_text{AB}=Delta E_p $$
Получаем уравнение для идеальной наклонной плоскости (без трения): $$ Ph=FL $$
При наличии трения получаем неравенство: $$ Phlt FL $$
Полезная и затраченная работа для наклонной плоскости: $$ A_text{п}=Ph, A_text{з}=FL $$
КПД наклонной плоскости: $$ eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{Ph}{FL}cdot 100text{%} $$
Затраченная работа равна сумме полезной работы и работы по преодолению силы трения: $$ A_text{з}=A_text{п}+F_text{тр}L $$
Откуда сила трения равна: $$ F_text{тр}=frac{A_text{з}-A_text{п}}{L}=frac{FL-Ph}{L}=F-Pfrac hL $$
Вес (P) и сила (F) определяются в работе с помощью динамометра с ценой деления (d=0,1 text{Н}).
Абсолютная погрешность прямых измерений $$ Delta_F=Delta_P=frac d2=0,05 text{Н}. $$
Сила (F) определяется в серии из пяти опытов с вычислением средних величин.
Высота наклонной плоскости (h) и длина наклонной плоскости (L) определяются с помощью мерной ленты с ценой деления (d=5 text{мм}). Абсолютная погрешность (Delta_L=2,5 text{мм}).
Относительные погрешности измерений вычисляются как обычно.
Относительная погрешность расчета КПД: $$ delta_eta=delta_F+delta_P+delta_h+delta_L $$
Абсолютная погрешность расчета КПД: $$ Delta_eta=etacdot delta_eta $$
Приборы и материалы
Доска длиной от 70 см, штатив с муфтой и лапкой, брусок массой не менее 300 г, мерная лента, динамометр.
Ход работы
1. Измерьте мерной лентой длину доски (L).
2. Определите вес бруска (P) с помощью динамометра.
3. Соберите наклонную плоскость: закрепите один конец доски в лапке штатива на высоте около (h=frac L3.)
4. Положите брусок на наклонную плоскость, прикрепите к нему динамометр и равномерно тяните по наклонной плоскости. Следите, чтобы динамометр располагался параллельно наклонной плоскости. Запишите измеренное значение (F). Повторите измерение (F) в серии из пяти опытов.
5. Соберите новую наклонную плоскость: закрепите один конец доски в лапке штатива на высоте около (h=frac L4). Перейдите на шаг 4 и повторите серию опытов для определения (F).
6. Рассчитайте КПД для двух исследованных наклонных плоскостей. Найдите относительные и абсолютные погрешности расчетов КПД.
7. Для каждой из наклонных плоскостей укажите величину полезной и затраченной работы, найдите силу трения.
8. Сделайте выводы о зависимости силы трения и КПД от высоты наклонной плоскости.
Результаты измерений и вычислений
Длина наклонной плоскости (доски) begin{gather*} L=80 text{см}=800 text{мм},\[7pt] Delta_L=2,5 text{мм},\[6pt] delta_L=frac{Delta_L}{L}=frac{2,5}{800}approx 0,0031=0,31text{%} end{gather*}
Вес бруска begin{gather*} P=4,4 text{Н},\[7pt] Delta_P=0,05 text{Н},\[6pt] delta_P=frac{Delta_P}{P}=frac{0,05}{4,4}approx 0,0011=1,1text{%} end{gather*}
1. Наклонная плоскость высотой (h=27 text{см})
Высота наклонной плоскости begin{gather*} h=27 text{см}=270 text{мм},\[7pt] Delta_h=2,5 text{мм},\[6pt] delta_h=frac{Delta_h}{h}=frac{2,5}{270}approx 0,0093=0,93text{%} end{gather*}
Определение силы тяги (F) в серии опытов
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| $$ F, H $$ | 2,9 | 2,8 | 3,0 | 2,7 | 2,8 | 14,2 |
| $$ Delta_F, H $$ | 0,06 | 0,04 | 0,16 | 0,14 | 0,04 | 0,44 |
begin{gather*} F_text{ср}=frac{sum F_i}{5}=frac{14,2}{5}=2,84 (text{Н}),\[6pt] Delta_{Ftext{ср}}=frac{sum Delta_{Fi}}{5}=frac{0,44}{5}approx 0,09 (text{Н}),\[6pt] F=(2,84pm 0,09) text{Н},\[7pt] delta_F=frac{0,09}{2,84}approx 0,032=3,2text{%} end{gather*}
Полезная работа: $$ A_text{П}=Ph=4,4cdot 0,27=1,188 (text{Дж}) $$
Затраченная работа: $$ A_text{З}=FL=2,84cdot 0,8=2,272 (text{Дж}) $$
Сила трения: $$ F_text{тр}=F-Pfrac hL=2,84-4,4cdot frac{0,27}{0,8}approx 1,36 (text{Н}) $$
КПД наклонной плоскости: $$ eta=frac{A_text{П}}{A_text{З}}=frac{1,188}{2,272}approx 0,523=52,3text{%} $$
Погрешности расчета КПД: $$ delta_eta=delta_F+delta_P+delta_h+delta_L=0,032+0,011+0,0093+0,0031=0,0554approx 0,056=5,6text{%} $$
При расчете (delta_eta) использовали округление с избытком. $$ Delta_eta=0,523cdot 0,056approx 0,029=2,9text{%} $$
Окончательно получаем: $$ eta=(52,3pm 2,9)text{%}, delta_eta=5,6text{%} $$
2. Наклонная плоскость высотой (h=20 text{см})
Высота наклонной плоскости begin{gather*} h=20 text{см}=200 text{мм},\[7pt] Delta_h=2,5 text{мм},\[6pt] delta_h=frac{Delta_h}{h}=frac{2,5}{200}approx 0,013=1,3text{%} end{gather*}
Определение силы тяги (F) в серии опытов
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| $$ F, H $$ | 2,4 | 2,6 | 2,5 | 2,6 | 2,5 | 12,6 |
| $$ Delta_F, H $$ | 0,12 | 0,08 | 0,02 | 0,08 | 0,02 | 0,32 |
begin{gather*} F_text{ср}=frac{sum F_i}{5}=frac{12,6}{5}=2,52 (text{Н}),\[6pt] Delta_{Ftext{ср}}=frac{sum Delta_{Fi}}{5}=frac{0,32}{5}approx 0,06 (text{Н}),\[6pt] F=(2,52pm 0,06) text{Н},\[7pt] delta_F=frac{0,06}{2,52}approx 0,024=2,4text{%} end{gather*}
Полезная работа: $$ A_text{П}=Ph=4,4cdot 0,2=0,88 (text{Дж}) $$
Затраченная работа: $$ A_text{З}=FL=2,52cdot 0,8=2,016 (text{Дж}) $$
Сила трения: $$ F_text{тр}=F-Pfrac hL=2,52-4,4cdot frac{0,2}{0,8}approx 1,42 (text{Н}) $$
КПД наклонной плоскости: $$ eta=frac{A_text{П}}{A_text{З}}=frac{0,88}{2,016}approx 0,437=43,7text{%} $$
Погрешности расчета КПД: $$ delta_eta=delta_F+delta_P+delta_h+delta_L=0,024+0,011+0,013+0,0031=0,0511approx 0,052=5,2text{%} $$
При расчете (delta_eta) использовали округление с избытком. $$ Delta_eta=0,437cdot 0,052approx 0,023=2,3text{%} $$
Окончательно получаем: $$ eta=(43,7pm 2,3)text{%}, delta_eta=5,2text{%} $$
Выводы
На основании полученных результатов можно сделать следующие выводы.
В работе проводился расчет КПД наклонной плоскости постоянной длины, но разной высоты.
Для высоты около (h=frac L3):
- полезная и затраченная работы: (A_text{П}=1,188 (text{Дж}), A_text{З}=2,272 (text{Дж}))
- сила трения: (F_text{тр}=1,36 (text{Н}))
- КПД: (eta=(52,3pm 2,9)text{%}, delta_eta=5,6text{%})
Для высоты около (h=frac L4):
- полезная и затраченная работы: (A_text{П}=0,88 (text{Дж}), A_text{З}=2,016 (text{Дж}))
- сила трения: (F_text{тр}=1,42 (text{Н}))
- КПД: (eta=(43,7pm 2,3)text{%}, delta_eta=5,2text{%})
Таким образом, с уменьшением высоты:
- сила трения растет;
- КПД наклонной плоскости падает.
Все задачи, поставленные перед исследованием, успешно выполнены.
Что такое КПД
Коэффициент полезного действия машины или механизма – это важная величина, характеризующая энергоэффективность данного устройства. Понятие используется и в повседневной жизни. Например, когда человек говорит, что КПД его усилий низкий, это значит, что сил затрачено много, а результата почти нет. Величина измеряет отношение полезной работы ко всей совершенной работе.
Согласно формуле, чтобы найти величину, нужно полезную работу разделить на всю совершенную работу. Или полезную энергию разделить на всю израсходованную энергию. Этот коэффициент всегда меньше единицы. Работа и энергия измеряется в Джоулях. Поделив Джоули на Джоули, получаем безразмерную величину. КПД иногда называют энергоэффективностью устройства.
Если попытаться объяснить простым языком, то представим, что мы кипятим чайник на плите. При сгорании газа образуется определенное количество теплоты. Часть этой теплоты нагревает саму горелку, плиту и окружающее пространство. Остальная часть идет на нагревание чайника и воды в нем. Чтобы рассчитать энергоэффективность данной плитки, нужно будет разделить количество тепла, требуемое для нагрева воды до температуры кипения на количество тепла, выделившееся при горении газа.
Данная величина всегда ниже единицы. Например, для любой атомной электростанции она не превышает 35%. Причиной является то, что электростанция представляет собой паровую машину, где нагретый за счет ядерной реакции пар вращает турбину. Большая часть энергии идет на нагрев окружающего пространства. Тот факт, что η не может быть равен 100%, следует из второго начала термодинамики.
Примеры расчета КПД
Пример 1. Нужно рассчитать коэффициент для классического камина. Дано: удельная теплота сгорания березовых дров – 107Дж/кг, количество дров – 8 кг. После сгорания дров температура в комнате повысилась на 20 градусов. Удельная теплоемкость кубометра воздуха – 1,3 кДж/ кг*град. Общая кубатура комнаты – 75 кубометров.
Чтобы решить задачу, нужно найти частное или отношение двух величин. В числителе будет количество теплоты, которое получил воздух в комнате (1300Дж*75*20=1950 кДж ). В знаменателе – количество теплоты, выделенное дровами при горении (10000000Дж*8 =8*107 кДж). После подсчетов получаем, что энергоэффективность дровяного камина – около 2,5%. Действительно, современная теория об устройстве печей и каминов говорит, что классическая конструкция не является энергоэффективной. Это связано с тем, что труба напрямую выводит горячий воздух в атмосферу. Для повышения эффективности устраивают дымоход с каналами, где воздух сначала отдает тепло кладке каналов, и лишь потом выходит наружу. Но справедливости ради, нужно отметить, что в процессе горения камина нагревается не только воздух, но и предметы в комнате, а часть тепла выходит наружу через элементы, плохо теплоизолированные – окна, двери и т.д.
Пример 2. Автомобиль проделал путь 100 км. Вес машины с пассажирами и багажом – 1400 кг. При этом было затрачено14 литров бензина. Найти: КПД двигателя.
Для решения задачи необходимо отношение работы по перемещению груза к количеству тепла, выделившемуся при сгорании топлива. Количество тепла также измеряется в Джоулях, поэтому не придется приводить к другим единицам. A будет равна произведению силы на путь( A=F*S=m*g*S). Сила равна произведению массы на ускорение свободного падения. Полезная работа = 1400 кг x 9,8м/с2 x 100000м=1,37*108 Дж
Удельная теплота сгорания бензина – 46 МДж/кг=46000 кДж/кг. Восемь литров бензина будем считать примерно равными 8 кг. Тепла выделилось 46*106*14=6.44*108 Дж. В результате получаем η ≈21%.
Единицы измерения
Коэффициент полезного действия – величина безразмерная, то есть не нужно ставить какую-либо единицу измерения. Но эту величину можно выразить и в процентах. Для этого полученное в результате деления по формуле число необходимо умножить на 100%. В школьном курсе математики рассказывали, что процент – этот одна сотая чего-либо. Умножая на 100 процентов, мы показываем, сколько в числе сотых.
От чего зависит величина КПД
Эта величина зависит от того, насколько общая совершенная работа может переходить в полезную. Прежде всего, это зависит от самого устройства механизма или машины. Инженеры всего мира бьются над тем, чтобы повышать КПД машин. Например, для электромобилей коэффициент очень высок – больше 90%.
А вот двигатель внутреннего сгорания, в силу своего устройства, не может иметь η, близкий к 100 процентам. Ведь энергия топлива не действует непосредственно на вращающиеся колеса. Энергия рассеивается на каждом передаточном звене. Слишком много передаточных звеньев, и часть выхлопных газов все равно выходит в выхлопную трубу.
Как обозначается
В русских учебниках обозначается двояко. Либо так и пишется – КПД, либо обозначается греческой буквой η. Эти обозначения равнозначны.
Символ, обозначающий КПД
Символом является греческая буква эта η. Но чаще все же используют выражение КПД.
Мощность и КПД
Мощность механизма или устройства равна работе, совершаемой в единицу времени. Работа(A) измеряется в Джоулях, а время в системе Си – в секундах. Но не стоит путать понятие мощности и номинальной мощности. Если на чайнике написана мощность 1 700 Ватт, это не значит, что он передаст 1 700 Джоулей за одну секунду воде, налитой в него. Это мощность номинальная. Чтобы узнать η электрочайника, нужно узнать количество теплоты(Q), которое должно получить определенное количество воды при нагреве на энное количество градусов. Эту цифру делят на работу электрического тока, выполненную за время нагревания воды.
Величина A будет равна номинальной мощности, умноженной на время в секундах. Q будет равно объему воды, умноженному на разницу температур на удельную теплоемкость. Потом делим Q на A тока и получаем КПД электрочайника, примерно равное 80 процентам. Прогресс не стоит на месте, и КПД различных устройств повышается, в том числе бытовой техники.
Напрашивается вопрос, почему через мощность нельзя узнать КПД устройства. На упаковке с оборудованием всегда указана номинальная мощность. Она показывает, сколько энергии потребляет устройство из сети. Но в каждом конкретном случае невозможно будет предсказать, сколько конкретно потребуется энергии для нагрева даже одного литра воды.
Например, в холодной комнате часть энергии потратится на обогрев пространства. Это связано с тем, что в результате теплообмена чайник будет охлаждаться. Если, наоборот, в комнате будет жарко, чайник закипит быстрее. То есть КПД в каждом из этих случаев будет разным.
Формула работы в физике
Для механической работы формула несложна: A = F x S. Если расшифровать, она равна приложенной силе на путь, на протяжении которого эта сила действовала. Например, мы поднимаем груз массой 15 кг на высоту 2 метра. Механическая работа по преодолению силы тяжести будет равна F x S = m x g x S. То есть, 15 x 9,8 x 2 = 294 Дж. Если речь идет о количестве теплоты, то A в этом случае равняется изменению количества теплоты. Например, на плите нагрели воду. Ее внутренняя энергия изменилась, она увеличилась на величину, равную произведению массы воды на удельную теплоемкость на количество градусов, на которое она нагрелась.
Мощность и коэффициент полезного действия электродвигателей
Электрические двигатели имеют высокий коэффициент полезного действия (КПД), но все же он далек от идеальных показателей, к которым продолжают стремиться конструкторы. Все дело в том, что при работе силового агрегата преобразование одного вида энергии в другой проходит с выделение теплоты и неминуемыми потерями. Рассеивание тепловой энергии можно зафиксировать в разных узлах двигателя любого типа. Потери мощности в электродвигателях являются следствием локальных потерь в обмотке, в стальных деталях и при механической работе. Вносят свой вклад, пусть и незначительный, дополнительные потери.
Расчет КПД.
Магнитные потери мощности
При перемагничивании в магнитном поле сердечника якоря электродвигателя происходят магнитные потери. Их величина, состоящая из суммарных потерь вихревых токов и тех, что возникают при перемагничивании, зависят от частоты перемагничивания, значений магнитной индукции спинки и зубцов якоря. Немалую роль играет толщина листов используемой электротехнической стали, качество ее изоляции.
Механические и электрические потери
Механические потери при работе электродвигателя, как и магнитные, относятся к числу постоянных. Они складываются из потерь на трение подшипников, на трение щеток, на вентиляцию двигателя. Минимизировать механические потери позволяет использование современных материалов, эксплуатационные характеристики которых совершенствуются из года в год. В отличие от них электрические потери не являются постоянными и зависят от уровня нагрузки электродвигателя. Чаще всего они возникают вследствие нагрева щеток, щеточного контакта.
Падает коэффициент полезного действия (КПД) от потерь в обмотке якоря и цепи возбуждения. Механические и электрические потери вносят основной вклад в изменение эффективности работы двигателя.
Добавочные потери
Добавочные потери мощности в электродвигателях складываются из потерь, возникающих в уравнительных соединениях, из потерь из-за неравномерной индукции в стали якоря при высокой нагрузке. Вносят свой вклад в общую сумму добавочных потерь вихревые токи, а также потери в полюсных наконечниках. Точно определить все эти значения довольно сложно, поэтому их сумму принимают обычно равной в пределах 0,5-1%. Эти цифры используют при расчете общих потерь для определения КПД электродвигателя.
КПД и его зависимость от нагрузки
Коэффициент полезного действия (КПД) электрического двигателя это отношение полезной мощности силового агрегата к мощности потребляемой. Этот показатель у двигателей, мощностью до 100 кВт находится в пределах от 0,75 до 0,9. для более мощных силовых агрегатов КПД существенно выше: 0,9-0,97. Определив суммарные потери мощности в электродвигателях можно достаточно точно вычислить коэффициент полезного действия любого силового агрегата. Этот метод определения КПД называется косвенным и он может применяться для машин различной мощности.
Для маломощных силовых агрегатов часто используют метод непосредственной нагрузки, заключающийся в измерениях потребляемой двигателем мощности. КПД электрического двигателя не является величиной постоянной, своего максимума он достигает при нагрузках около 80% мощности.
Достигает он пикового значения быстро и уверенно, но после своего максимума начинает медленно уменьшаться. Это связывают с возрастанием электрических потерь при нагрузках, более 80% от номинальной мощности. Падение коэффициента полезного действия не велико, что позволяет говорить о высоких показателях эффективности электродвигателей в широком диапазоне мощностей.
В чем измеряется КПД
Коэффициент полезного действия (кпд), характеристика эффективности системы (устройства, машины) в отношении преобразования или передачи энергии; определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой; обозначается обычно h = Wпол/Wcyм.
В электрических двигателях кпд — отношение совершаемой (полезной) механической работы к электрической энергии, получаемой от источника; в тепловых двигателях — отношение полезной механической работы к затрачиваемому количеству теплоты; в электрических трансформаторах — отношение электромагнитной энергии, получаемой во вторичной обмотке, к энергии, потребляемой первичной обмоткой.
Для вычисления кпд разные виды энергии и механическая работа выражаются в одинаковых единицах на основе механического эквивалента теплоты, и др. аналогичных соотношений. В силу своей общности понятие кпд позволяет сравнивать и оценивать с единой точки зрения такие различные системы, как атомные реакторы, электрические генераторы и двигатели, теплоэнергетические установки, полупроводниковые приборы, биологические объекты и т. д.
Из-за неизбежных потерь энергии на трение, на нагревание окружающих тел и т. п. кпд всегда меньше единицы. Соответственно этому кпд выражается в долях затрачиваемой энергии, т. е. в виде правильной дроби или в процентах, и является безразмерной величиной. Кпд тепловых электростанций достигает 35—40%, двигателей внутреннего сгорания — 40—50%, динамомашин и генераторов большой мощности—95%, трансформаторов—98%.
В чем измеряется КПД.
Кпд процесса фотосинтеза составляет обычно 6—8%, у хлореллы он достигает 20—25%. У тепловых двигателей в силу второго начала термодинамики кпд имеет верхний предел, определяемый особенностями термодинамического цикла (кругового процесса), который совершает рабочее вещество. Наибольшим кпд обладает Карно цикл. Различают кпд отдельного элемента (ступени) машины или устройства и кпд, характеризующий всю цепь преобразований энергии в системе. Кпд первого типа в соответствии с характером преобразования энергии может быть механическим, термическим и т. д. Ко второму типу относятся общий, экономический, технический и др. виды кпд. Общий кпд системы равен произведению частных кпд, или кпд ступеней.
В технической литературе кпд иногда определяют т. о., что он может оказаться больше единицы. Подобная ситуация возникает, если определять кпд отношением Wпол/Wзатр, где Wпол — используемая энергия, получаемая на «выходе» системы, Wзатр — не вся энергия, поступающая в систему, а лишь та её часть, для получения которой производятся реальные затраты.
Например, при работе полупроводниковых термоэлектрических обогревателей (тепловых насосов) затрата электроэнергии меньше количества теплоты, выделяемой термоэлементом. Избыток энергии черпается из окружающей среды. При этом, хотя истинный кпд установки меньше единицы, рассмотренный кпд h = Wпол/Wзатр может оказаться больше единицы.
Примеры расчета КПД.
Для чего нужен расчет КПД
Коэффициент полезного действия электрической цепи – это отношение полезного тепла к полному. Для ясности приведем пример. При нахождении КПД двигателя можно определить, оправдывает ли его основная функция работы затраты потребляемого электричества. То есть его расчет даст ясную картину, насколько хорошо устройство преобразовывает получаемую энергию. Обратите внимание! Как правило, коэффициент полезного действия не имеет величины, а представляет собой процентное соотношение либо числовой эквивалент от 0 до 1. КПД находят по общей формуле вычисления, для всех устройств в целом. Но чтобы получить его результат в электрической цепи, вначале потребуется найти силу электричества.
По физике известно, что любой генератор тока имеет свое сопротивление, которое еще принято называть внутренняя мощность. Помимо этого значения, источник электричества также имеет свою силу. Дадим значения каждому элементу цепи: сопротивление – r; сила тока – Е; резистор (внешняя нагрузка) – R. Полная цепь Итак, чтобы найти силу тока, обозначение которого будет – I, и напряжение на резисторе – U, потребуется время – t, с прохождением заряда q = lt. Рассчитать работу источника тока можно по следующей формуле: A = Eq = EIt. В связи с тем, что сила электричества постоянна, работа генератора целиком преобразуется в тепло, выделяемое на R и r. Такое количество можно рассчитать по закону Джоуля-Ленца: Q = I2 + I2 rt = I2 (R + r) t.
Формулы расчета КПД.
Затем приравниваются правые части формулы: EIt = I2 (R + r) t. Осуществив сокращение, получается расчет: E = I(R + r). Произведя у формулы перестановку, в итоге получается: I = E R + r. Данное итоговое значение будет являться электрической силой в данном устройстве. Произведя таким образом предварительный расчет, теперь можно определить КПД.
Расчет КПД электрической цепи Мощность, получаемая от источника тока, называется потребляемой, определение ее записывается – P1. Если эта физическая величина переходит от генератора в полную цепь, она считается полезной и записывается – Р2. Чтобы определить КПД цепи, необходимо вспомнить закон сохранения энергии.
В соответствии с ним, мощность приемника Р2 будет всегда меньше потребляемой мощности Р1. Это объясняется тем, что в процессе работы в приемнике всегда происходит неизбежная пустая трата преобразуемой энергии, которая расходуется на нагревание проводов, их оболочки, вихревых токов и т.д. Чтобы найти оценку свойств превращения энергии, необходим КПД, который будет равен отношению мощностей Р2 и Р1.
Итак, зная все значения показателей, составляющих электроцепи, находим ее полезную и полную работу: А полезная. = qU = IUt =I2Rt; А полная = qE = IEt = I2(R+r)t. В соответствии этих значений, найдем мощности источника тока: Р2 = А полезная /t = IU = I2 R; P1 = А полная /t = IE = I2 (R + r). Произведя все действия, получаем формулу КПД: n = А полезная / А полная = Р2 / P1 =U / E = R / (R +r). У этой формулы получается, что R выше бесконечности, а n выше 1, но при всем этом ток в цепи остается в низком положении, и его полезная мощность мала.
Каждый желает найти КПД повышенного значения. Для этого необходимо найти условия, при которых P2 будет максимален. Оптимальные значения будут: dP2 / dR = 0. Далее определить КПД можно формулами: P2 = I2 R = (E / R + r)2 R; dP2 / dR = (E2 (R + r)2 — 2 (r + R) E2 R) / (R + r)4 = 0; E2 ((R + r) -2R) = 0. В данном выражении Е и (R + r) не равны 0, следовательно, ему равно выражение в скобках, то есть (r = R). Тогда получается, что мощность имеет максимальное значение, а коэффициент полезного действия = 50 %. Как видно, найти коэффициент полезного действия электрической цепи можно самостоятельно, не прибегая к услугам специалиста. Главное –соблюдать последовательность в расчетах и не выходить за рамки приведенных формул.
Примеры расчета КПД
Пример 1. Нужно рассчитать коэффициент для классического камина. Дано: удельная теплота сгорания березовых дров – 107Дж/кг, количество дров – 8 кг. После сгорания дров температура в комнате повысилась на 20 градусов. Удельная теплоемкость кубометра воздуха – 1,3 кДж/ кг*град. Общая кубатура комнаты – 75 кубометров.
Чтобы решить задачу, нужно найти частное или отношение двух величин. В числителе будет количество теплоты, которое получил воздух в комнате (1300Дж*75*20=1950 кДж ). В знаменателе – количество теплоты, выделенное дровами при горении (10000000Дж*8 =8*107 кДж). После подсчетов получаем, что энергоэффективность дровяного камина – около 2,5%. Действительно, современная теория об устройстве печей и каминов говорит, что классическая конструкция не является энергоэффективной. Это связано с тем, что труба напрямую выводит горячий воздух в атмосферу.
Для повышения эффективности устраивают дымоход с каналами, где воздух сначала отдает тепло кладке каналов, и лишь потом выходит наружу. Но справедливости ради, нужно отметить, что в процессе горения камина нагревается не только воздух, но и предметы в комнате, а часть тепла выходит наружу через элементы, плохо теплоизолированные – окна, двери и т.д.
Расчет коэффициента полезного действия.
Пример 2. Автомобиль проделал путь 100 км. Вес машины с пассажирами и багажом – 1400 кг. При этом было затрачено14 литров бензина. Найти: КПД двигателя.
Для решения задачи необходимо отношение работы по перемещению груза к количеству тепла, выделившемуся при сгорании топлива. Количество тепла также измеряется в Джоулях, поэтому не придется приводить к другим единицам. A будет равна произведению силы на путь( A=F*S=m*g*S). Сила равна произведению массы на ускорение свободного падения. Полезная работа = 1400 кг x 9,8м/с2 x 100000м=1,37*108 Дж
Удельная теплота сгорания бензина – 46 МДж/кг=46000 кДж/кг. Восемь литров бензина будем считать примерно равными 8 кг. Тепла выделилось 46*106*14=6.44*108 Дж. В результате получаем η ≈21%.
КПД в механике
Главный секрет заключается в том, что эта формула подойдет для всех видов КПД.
Запоминаем!КПД не может быть больше 100%. В реальной жизни и 100 не встречается, но больше сотни даже в задачах нет. Это значит, что если в задаче получается значение больше 100%, то мы в ответ пишем 100. И никак иначе.
КПД
η = (Aполезная/Aзатраченная) * 100%
η — коэффициент полезного действия [%]
Aполезная — полезная работа [Дж]
Aзатраченная — затраченная работа [Дж]
Дальше мы просто заменяем полезную и затраченную работы на те величины, которые ими являются.
Давайте разберемся на примере задачи.
Задача
Чтобы вкатить санки массой 4 кг в горку длиной 12 метров, мальчик приложил силу в 15 Н. Высота горки равна 2 м. Найти КПД этого процесса. Ускорение свободного падения принять равным g ≃9,8 м/с^2
Запишем формулу КПД.
η = (Aполезная/Aзатраченная) * 100%
Теперь задаем два главных вопроса:
Ради чего все это затеяли?
Чтобы санки в горку поднять — то есть ради приобретения телом потенциальной энергии. Значит в данном процессе полезная работа равна потенциальной энергии санок.
Потенциальная энергия
Еп = mgh
Еп — потенциальная энергия [Дж]
m — масса тела [кг]
g — ускорение свободного падения [м/с^2]
h — высота [м]
На планете Земля g ≃9,8 м/с^2
За счет чего процесс происходит?
За счет мальчика, он же тянет санки. Значит затраченная работа равна механической работе
Механическая работа
А = FS
A — механическая работа [Дж]
F — приложенная сила [Н]
S — путь [м]
Заменим формуле КПД полезную работу на потенциальную энергию, а затраченную — на механическую работу:
η = Eп/A * 100% = mgh/FS * 100%
Подставим значения:
η = 4*9,8*2/15*12 * 100% = 78,4/180 * 100% ≃ 43,6 %
Ответ: КПД процесса приблизительно равен 43,6 %
КПД в термодинамике
В термодинамике КПД — очень важная величина. Она полностью определяет эффективность такой штуки, как тепловая машина.
- Тепловой двигатель (машина) – это устройство, которое совершает механическую работу циклически за счет энергии, поступающей к нему в ходе теплопередачи.
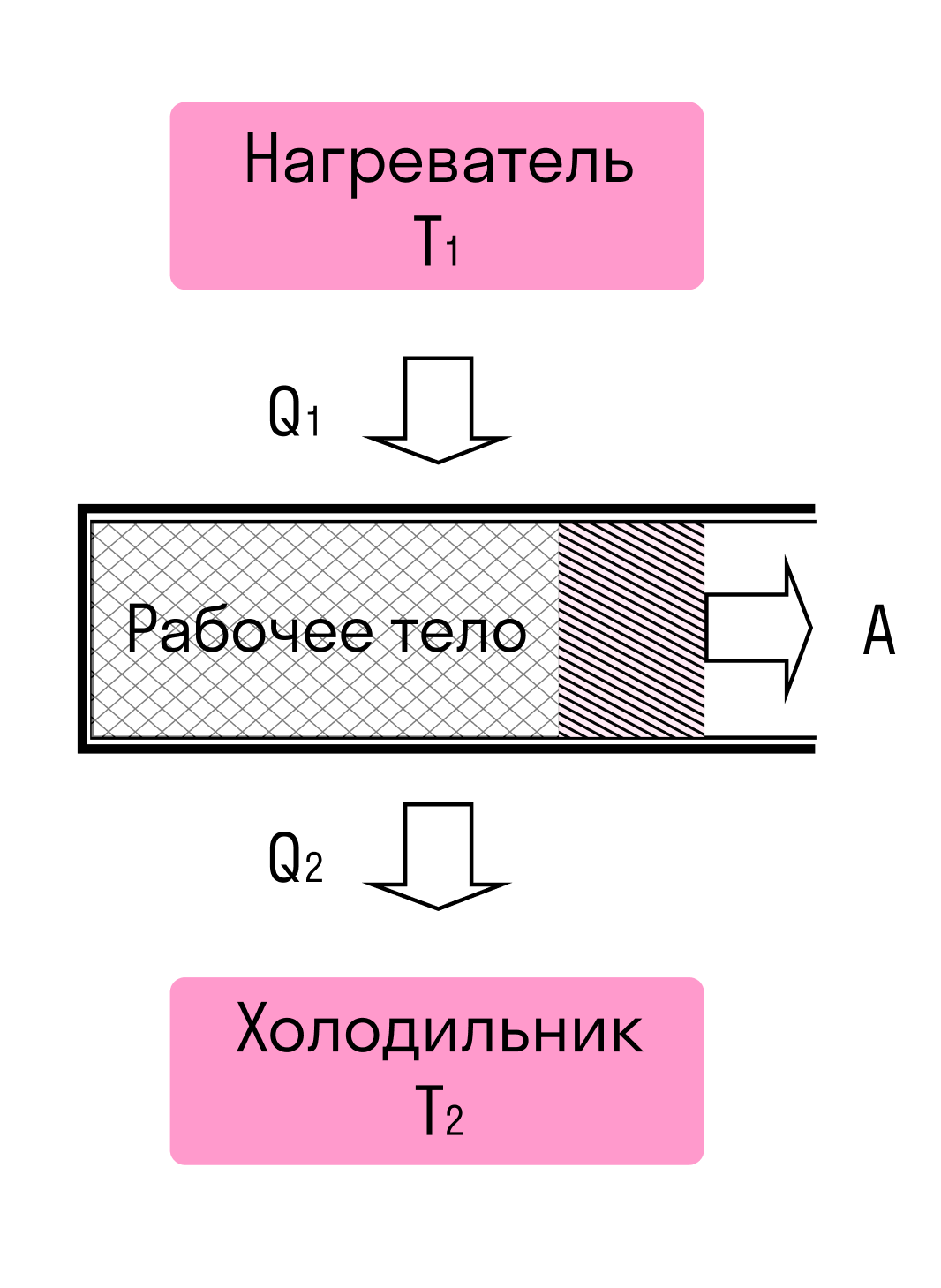
Схема теплового двигателя выглядит так:
У теплового двигателя обязательно есть нагреватель, который (не может быть!) нагревает рабочее тело, передавая ему количество теплоты Q1 или Qнагревателя (оба варианта верны, это зависит лишь от учебника, в котором вы нашли формулу).
- Рабочее тело — это тело, на котором завязан процесс (чаще всего это газ). Оно расширяется при подводе к нему теплоты и сжимается при охлаждении. Часть переданного Q1 уходит на механическую работу A. Из-за этого производится движение.
Оставшееся количество теплоты Q2 или Qхолодильника отводится к холодильнику, после чего возвращается к нагревателю и процесс повторяется.
КПД такой тепловой машины будет равен:
КПД тепловой машины
η = (Aполезная/Qнагревателя) * 100%
η — коэффициент полезного действия [%]
Aполезная — полезная работа (механическая) [Дж]
Qнагревателя — количество теплоты, полученное от нагревателя[Дж]
Если мы выразим полезную (механическую) работу через Qнагревателя и Qхолодильника, мы получим:
A = Qнагревателя — Qхолодильника.
Подставим в числитель и получим такой вариант формулы.
КПД тепловой машины
η = Qнагревателя — Qхолодильника/Qнагревателя * 100%
η — коэффициент полезного действия [%]
Qнагревателя — количество теплоты, полученное от нагревателя[Дж]
Qхолодильника — количество теплоты, отданное холодильнику [Дж]
А возможно ли создать тепловую машину, которая будет работать только за счет охлаждения одного тела?
Точно нет! Если у нас не будет нагревателя, то просто нечего будет передавать на механическую работу. Любой такой процесс — когда энергия не приходит из ниоткуда — означал бы возможность существования вечного двигателя.
Поскольку свидетельств такого процесса в мире не существует, то мы можем сделать вывод: вечный двигатель невозможен. Это второе начало термодинамики.
Запишем его, чтобы не забыть:
Невозможно создать периодическую тепловую машину за счет охлаждения одного тела без изменений в других телах.
Задача
Найти КПД тепловой машины, если рабочее тело получило от нагревателя 20кДж, а отдало холодильнику 10 кДж.
Решение:
Возьмем формулу для расчета КПД:
η = Qнагревателя — Qхолодильника/Qнагревателя * 100%
Подставим значения:
η = 20 — 10/20 *100% = 50%
Ответ: КПД тепловой машины равен 50%
Идеальная тепловая машина: цикл Карно
Давайте еще чуть-чуть пофантазируем: какая она — идеальная тепловая машина. Кажется, что это та, у которой КПД равен 100%.
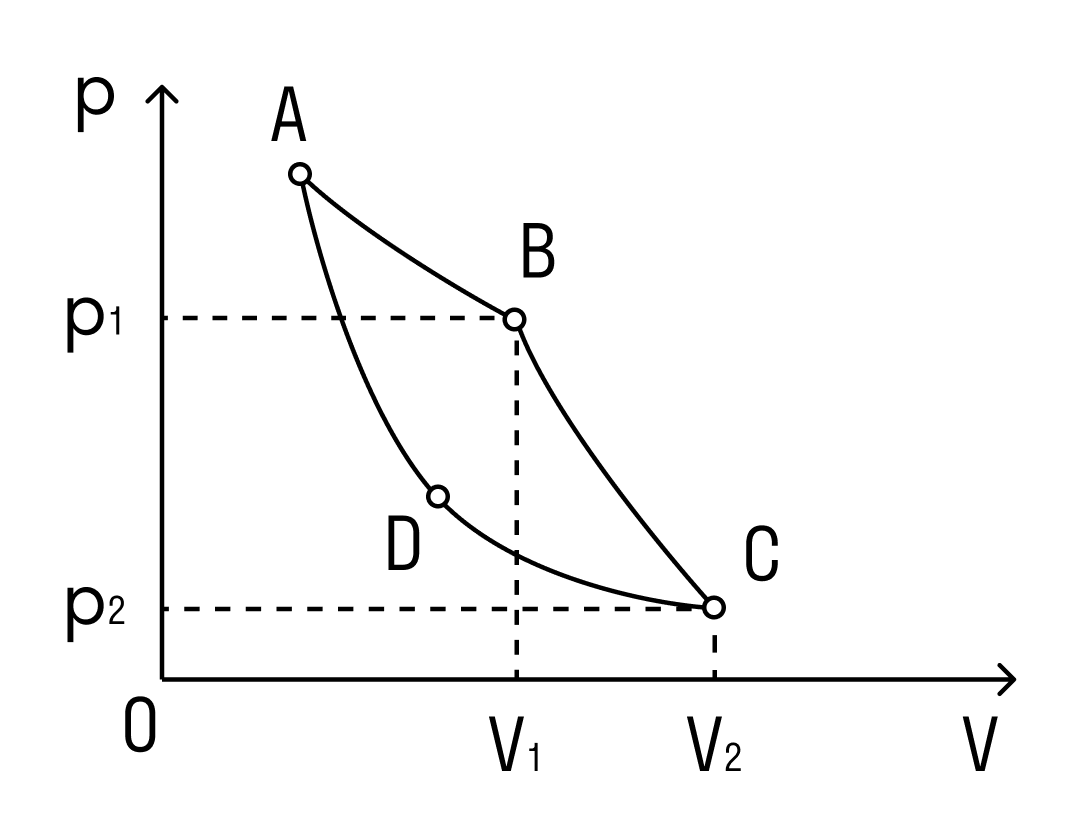
На самом деле понятие «идеальная тепловая машина» уже существует. Это тепловая машина, у которой в качестве рабочего тела взят идеальный газ. Такая тепловая машина работает по циклу Карно. Зависимость давления от объема в этом цикле выглядит следующим образом
А КПД для цикла Карно можно найти через температуры нагревателя и холодильника.
КПД цикла Карно
η = Tнагревателя — Tхолодильника /Tнагревателя *100%
η — коэффициент полезного действия [%]
Tнагревателя — температура нагревателя[Дж]
Tхолодильника — температура холодильника [Дж]
КПД в электродинамике
Мы каждый день пользуемся различными электронными устройствами: от чайника до смартфона, от компьютера до робота-пылесоса — и у каждого устройства можно определить, насколько оно эффективно выполняет задачу, для которой оно предназначено, просто посчитав КПД.
Вспомним формулу:
КПД
η = Aполезная/Aзатраченная *100%
η — коэффициент полезного действия [%]
Aполезная — полезная работа [Дж]
Aзатраченная — затраченная работа [Дж]
Для электрических цепей тоже есть нюансы. Давайте разбираться на примере задачи.
Задачка, чтобы разобраться
Найти КПД электрического чайника, если вода в нем приобрела 22176 Дж тепла за 2 минуты, напряжение в сети — 220 В, а сила тока в чайнике 1,4 А.
Решение:
Цель электрического чайника — вскипятить воду. То есть его полезная работа — это количество теплоты, которое пошло на нагревание воды. Оно нам известно, но формулу вспомнить все равно полезно
Количество теплоты, затраченное на нагревание
Q = cm(tконечная-tначальная)
Q — количество теплоты [Дж]
c — удельная теплоемкость вещества [Дж/кг*˚C]
m — масса [кг]
tконечная — конечная температура [˚C]
tначальная — начальная температура [˚C]
Работает чайник, потому что в розетку подключен. Затраченная работа в данном случае — это работа электрического тока.
Работа электрического тока
A = (I^2)*Rt = (U^2)/R *t = UIt
A — работа электрического тока [Дж]
I — сила тока [А]
U — напряжение [В]
R — сопротивление [Ом]
t — время [c]
То есть в данном случае формула КПД будет иметь вид:
η = Q/A *100% = Q/UIt *100%
Переводим минуты в секунды — 2 минуты = 120 секунд. Теперь намм известны все значения, поэтому подставим их:
η = 22176/220*1,4*120 *100% = 60%
Ответ: КПД чайника равен 60%.
Давайте выведем еще одну формулу для КПД, которая часто пригождается для электрических цепей, но применима ко всему. Для этого нужна формула работы через мощность:
Работа электрического тока
A = Pt
A — работа электрического тока [Дж]
P — мощность [Вт]
t — время [c]
Подставим эту формулу в числитель и в знаменатель, учитывая, что мощность разная — полезная и затраченная. Поскольку мы всегда говорим об одном процессе, то есть полезная и затраченная работа ограничены одним и тем же промежутком времени, можно сократить время и получить формулу КПД через мощность.
КПД
η = Pполезная/Pзатраченная *100%
η — коэффициент полезного действия [%]
Pполезная — полезная мощность [Дж]
Pзатраченная — затраченная мощность [Дж]
Физическая формула КПД
Существует определенная формула для нахождения КПД. Она звучит следующим образом: чтобы найти КПД в физике, нужно количество энергии разделить на проделанную системой работу. То есть КПД — это отношение затраченной энергии к выполненной работе. Отсюда можно сделать простой вывод, что тем лучше и эффективнее система или тело, чем меньше энергии затрачивается на выполнение работы.
Сама формула выглядит кратко и очень просто Ƞ будет равняться A/Q. То есть Ƞ = A/Q. В этой краткой формулы и фиксируют нужные нам элементы для вычисления. То есть A в этом случае является использованной энергией, которая потребляется системой во время работы, а большая буква Q, в свою очередь, будет являться затраченной A, или опять же затраченной энергией.
В идеале КПД равен единице. Но, как это обычно бывает, он её меньше. Так происходит по причине физики и по причине, конечно же, закона о сохранении энергии.
Все дело в том, что закон сохранения энергии предполагает, что не может быть получено больше А, чем получено энергии. И даже единице этот коэффициент будет равняться крайне редко, поскольку энергия тратится всегда. И работа сопровождается потерями: к примеру, у двигателя потеря заключается в его обильном нагреве.
Итак, формула КПД:
Ƞ=А/Q, где
- A — полезная работа, которую выполняет система.
- Q — энергия, которую потребляет система.
Применение в разных сферах физики
Примечательно, что КПД не существует как понятие нейтральное, для каждого процесса есть свой КПД, это не сила трения, он не может существовать сам по себе.
Рассмотрим несколько из примеров процессов с наличием КПД.
К примеру, возьмем электрический двигатель. Задача электрического двигателя — преобразовывать электрическую энергию в механическую. В этом случае коэффициентом будет являться эффективность двигателя в отношении преобразования электроэнергии в энергию механическую. Для этого случая также существует формула, и выглядит она следующим образом: Ƞ=P2/P1. Здесь P1 — это мощность в общем варианте, а P2 — полезная мощность, которую вырабатывает сам двигатель.
Нетрудно догадаться что структура формулы коэффициента всегда сохраняется, меняются в ней лишь данные, которые нужно подставить. Они зависят от конкретного случая, если это двигатель, как в случае выше, то необходимо оперировать затрачиваемой мощностью, если работа, то исходная формула будет другая.
Теперь мы знаем определение КПД и имеем представление об этом физическом понятии, а также об отдельных его элементах и нюансах. Физика — это одна из самых масштабных наук, но её можно разобрать на маленькие кусочки, чтобы понять. Сегодня мы исследовали один из этих кусочков.
Видео
Это видео поможет вам понять, что такое КПД.
Как устроен тепловой двигатель
Любой тепловой двигатель состоит из трех основных частей:
- рабочего тела;
- нагревателя;
- холодильника.
В основе работы двигателя лежит циклический процесс.
Нагреватель с помощью, например, сгорания топливной смеси выделяет большое количество теплоты и передает ее рабочему телу.
Рабочее тело, например пар, газ или жидкость, при нагревании расширяется и совершает работу, к примеру, вращает турбину или перемещает поршень.
Холодильник нужен, чтобы вернуть рабочее тело в начальное состояние. Он поглощает часть энергии рабочего тела. Таким образом обеспечивается цикличность, и тепловой двигатель работает непрерывно.
Идеальный тепловой двигатель Карно
Модель двигателя Карно разработал французский физик С. Карно.
Рабочая часть двигателя Карно — поршень в заполненном газом цилиндре. Двигатель Карно — идеальная машина, она возможна только в теории. Поэтому в ней силы трения между поршнем и цилиндром и тепловые потери считаются равными нулю.
Механическая работа максимальна, если рабочее тело выполняет цикл, состоящий из двух изотерм и двух адиабат. При изотермическом расширении работа газа совершается за счет внутренней энергии нагревателя. При адиабатном процессе — за счет внутренней энергии расширяющегося газа. В этом цикле нет контакта тел с разной температурой, поэтому исключена теплопередача без совершения работы. Такой цикл называют циклом Карно.
Адиабатический процесс — это термодинамический процесс, происходящий без теплообмена с окружающей средой (Q=0).
Изотермический процесс — это термодинамический процесс, происходящий при постоянной температуре. Так как у идеального газа внутренняя энергия зависит только от температуры, то переданное газу количество тепла Q идет полностью на совершение работы A (Q=A).
Функционирует двигатель Карно следующим образом:
- Цилиндр вступает в контакт с горячим резервуаром, и газ расширяется при постоянной температуре. На этой фазе газ получает от горячего резервуара тепло.
- Цилиндр окружается теплоизоляцией, за счет чего количество тепла, имеющееся у газа, сохраняется. Газ продолжает расширяться, пока его температура не упадет до температуры холодного теплового резервуара.
- На третьей фазе теплоизоляция снимается. Газ в цилиндре, будучи в контакте с холодным резервуаром, сжимается, отдавая при этом часть тепла холодному резервуару.
- Когда сжатие достигает определенной точки, цилиндр снова окружается теплоизоляцией. Газ сжимается за счет поднятия поршня до тех пор, пока его температура не сравняется с температурой горячего резервуара. После этого теплоизоляция удаляется, и цикл повторяется вновь с первой фазы.
Примечание
Чем больше разница между температурами нагревателя и холодильника, тем больше КПД двигателя Карно.
Трактовка понятия
Электродвигатель и другие механизмы выполняют определённую работу, которая называется полезной. Устройство, функционируя, частично растрачивает энергию. Для определения эффективности работы применяется формула ɳ= А1/А2×100%, где:
- А1 — полезная работу, которую выполняет машина либо мотор;
- А2 — общий цикл работы;
- η – обозначение КПД.
Показатель измеряется в процентах. Для нахождения коэффициента в математике используется следующая формула: η= А/Q, где А — энергия либо полезная работа, а Q — затраченная энергия. Чтобы выразить значение в процентах, КПД умножается на 100%. Действие не несёт содержательного смысла, так как 100% = 1. Для источника тока КПД меньше единицы.
В старших классах ученики решают задачи, в которых нужно найти КПД тепловых двигателей. Понятие трактуется следующим образом: отношение выполненной работы силового агрегата к энергии, полученной от нагревателя. Расчет производится по следующей формуле: η= (Q1-Q2)/Q1, где:
- Q1 — теплота, полученная от нагревательного элемента;
- Q2 — теплота, отданная холодильной установке.
Максимальное значение показателя характерно для циклической машины. Она оперирует при заданных температурах нагревательного элемента (Т1) и холодильника (Т2). Измерение осуществляется по формуле: η= (Т1-Т2)/Т1. Чтобы узнать КПД котла, который функционирует на органическом топливе, используется низшая теплота сгорания.
Плюс теплового насоса как нагревательного прибора заключается в возможности получать больше энергии, чем он может затратить на функционирование. Показатель трансформации вычисляется путём деления тепла конденсации на работу, затрачиваемую на выполнение данного процесса.