| Магнитный поток | |
|---|---|
 |
|
| Размерность | ML2T−2I−1 |
| Единицы измерения | |
| СИ | Вб |
| СГС | Мкс |
| Примечания | |
| Скалярная величина |
| Классическая электродинамика |
|---|
 |
| Электричество · Магнетизм |
|
Электростатика Закон Кулона |
|
Магнитостатика Закон Био — Савара — Лапласа |
|
Электродинамика Векторный потенциал |
|
Электрическая цепь Закон Ома |
|
Ковариантная формулировка Тензор электромагнитного поля |
| См. также: Портал:Физика |
Магни́тный пото́к — поток вектора магнитной индукции 






Важнейшая физическая формула, в которую входит магнитный поток, — выражение для закона электромагнитной индукции Фарадея.
Определение магнитного потока[править | править код]

Разбиение поверхности на малые участки

Изменение вектора нормали к поверхности
Магнитным потоком через бесконечно малый элемент поверхности 
,
где 


.
Магнитным потоком через поверхность конечной площади называется интеграл от 
.
Направление вектора 
В случае однородного поля и плоской поверхности магнитный поток рассчитывается как 
Единицы измерения магнитного потока[править | править код]
В СИ единицей магнитного потока является вебер (Вб, размерность — Вб = В·с =
кг·м²·с-2·А-1), в системе СГС — максвелл (Мкс, 1 Вб = 108 Мкс).
Приборы для измерения потока[править | править код]
Прибор для измерения магнитных потоков называется флюксметром (от лат. fluxus — «течение» и греч. metron — мера) или веберметром.
Некоторые свойства магнитного потока[править | править код]
В соответствии с теоремой Гаусса для магнитной индукции, поток вектора магнитной индукции 

.
Это означает, что в классической электродинамике невозможно существование магнитных зарядов, которые создавали бы магнитное поле подобно тому, как электрические заряды создают электрическое поле.
В соответствии с теоремой Стокса, магнитный поток 


,
поскольку имеет место связь 
Переменный во времени магнитный поток[править | править код]
По закону электромагнитной индукции Фарадея, если магнитный поток через некоторую поверхность изменяется со временем, то создаётся электродвижущая сила
в контуре, на который натянута данная поверхность. Если вдоль такого контура «проложен» электрический провод, то в нём возникнет индукционный ток. Изменение потока со временем может быть вызвано изменением вектора магнитной индукции 
Квантование магнитного потока[править | править код]
При рассмотрении ряда квантовых явлений, таких как эффект Ааронова — Бома или квантовый эффект Холла, используется квант магнитного потока:
,
где 

Опыты с неодносвязным сверхпроводником (например, со сверхпроводящим кольцом) показывают, что магнитный поток через кольцо всегда кратен половине кванта магнитного потока, откуда следует, что носители тока в сверхпроводнике являются парами связанных элементарных зарядов. Это прямое подтверждение теории БКШ, согласно которой сверхпроводимость обусловлена электронными парами (куперовскими парами):
Вб (в СИ);
Гаусс·см2 (в СГС),
— скорость света.
Экспериментально квантование магнитного потока было обнаружено в 1961 году.
См. также[править | править код]
- Уравнения Максвелла
- Электродвигатель постоянного тока
- Потокосцепление
- Индуктивность
Магнитный поток
Содержание:
-
Что такое магнитный поток
- В чем измеряется, обозначение и размерность
- От чего зависит величина основного магнитного потока
-
Чему равен магнитный поток, как найти
- Скорость изменения магнитного потока через контур
- Какой формулой определяется величина магнитного потока
- Связь магнитного потока и работы сил магнитного поля
Что такое магнитный поток
Магнитный поток — величина, характеризующая число магнитных силовых линий поля, проходящих через замкнутый контур.
Майкл Фарадей опытным путем пришел к выводу, что при любом соприкосновении проводника и магнитных линий по проводнику проходит заряд (triangle Q). Этот заряд прямо пропорционален количеству( triangle Ф) пересеченных линий и обратно пропорционален сопротивлению R контура. Пересечение линий вызывается или движением проводника, или изменением поля.
Позже, представляя замкнутый контур, в котором действует ЭДС индукции, Джеймс Клерк Максвелл подсчитывал количество силовых линий (triangle Ф), пересекаемых контуром за время (triangle t). Ф он при этом отождествлял с магнитным потоком сквозь всю поверхность.
В чем измеряется, обозначение и размерность
Единица измерения — вебер, сокращенно Вб. Он обозначается буквой Ф.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Размерность — выражение, демонстрирующее связь физической величины с другими величинами данной системы, разложение ее на сомножители из других величин.
Размерность магнитного потока — (В times с = кг times м^{2} times с^{-2} times А^{-1}.)
От чего зависит величина основного магнитного потока
Его можно изменить следующими способами:
- изменив площадь контура;
- изменив угол его наклона;
- изменив магнитное напряжение.
Чему равен магнитный поток, как найти
Магнитный поток в случае однородного магнитного поля равен произведению модуля индукции В этого поля, площади S плоской поверхности, через которую вычисляется поток, и косинуса угла (varphi) между направлением индукции В и нормали к данной поверхности.
Нормаль — перпендикуляр к плоскости контура.
Также поток можно вычислить через индуктивность, которая пропорциональна отношению полного, или суммарного потока к силе тока.
Обозначение суммарного потока — буква ( psi). Он равен сумме потоков, проходящих через всю поверхность. И в простом случае, где рассматриваются одинаковые потоки, проходящие через одинаковые витки катушки, и в случаях, когда поверхность имеет очень сложную форму, эта пропорциональность сохраняется.
Скорость изменения магнитного потока через контур
Закон электромагнитной индукции Фарадея в интегральном виде выглядит следующим образом:
(;underset С{oint;};(overrightarrow{Е;}times;doverrightarrow l) = – frac{1}{c}frac{d}{dt}int underset S{int;};(overrightarrow{B} times doverrightarrow{S}).)
Интеграл в левой части уравнения — циркуляция вектора (overrightarrow{Е;}) по замкнутому контуру С, это отражает знак интеграла, записанный с кругом. В правой части — скорость изменения потока Ф, который вычисляется как интеграл по поверхности S, «натянутой» на С.
Интеграл — целое, определяемое как сумма его бесконечно малых частей.
Если считать изменение потока в замкнутом контуре равномерным, то закон Фарадея примет следующий вид:
(epsilon_{i} = – frac{triangleФ}{triangle t}.)
Какой формулой определяется величина магнитного потока
Математически величину Ф описывают двумя формулами:
(Ф;=;sum_{triangle S};;Btriangle S = B times S times cosvarphi. )
Связь магнитного потока и работы сил магнитного поля
Герман Гельмгольц первым связал закон Фарадея и закон сохранения энергии. Возьмем проводник с током I, находящийся внутри однородного магнитного поля, которое перпендикулярно плоскости контура, и перемещающийся в нем. Под влиянием силы Ампера F проводник перемещается на отрезок dx. Сила F производит работу dA = IdФ.
Работу источника тока можно измерить, сложив работу на джоулеву теплоту и работу по перемещению проводника внутри поля:
(epsilon Idt = I^{2}Rdt + IdФ.)
(I = frac{epsilon – frac{dФ}{dt}}{R}.)
Насколько полезной была для вас статья?
Рейтинг: 4.40 (Голосов: 5)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Вероятно, термин «поток» ассоциируется у вас с потоком воды. Если бы вы хотели описать этот поток количественно, то имели бы в виду определенное количество воды, протекающей через поперечное сечение в определенной точке. Такой поток может нести большое или малое количество воды в зависимости от скорости воды и площади этого поперечного сечения.
Магнитный поток — это физическая величина, тесно связанная с явлением электромагнитной индукции. Это сложная величина, довольно абстрактная. Но, как вы правильно догадались, его название берет свое начало в гидродинамике. Здесь, однако, нет потока материи через поверхность, есть только векторы магнитной индукции B, «пронзающие» поверхность и иногда «скользящие» по ней.
Представьте себе однородное магнитное поле, описываемое вектором магнитной индукции B. Мы помещаем плоскую поверхность с полем S в это поле совершенно произвольным образом, то есть под любым углом по отношению к вектору B (рис. 1). Теперь определим вектор B, перпендикулярный плоскости поверхности. Пусть длина этого вектора равна величине поверхности.

Потоком вектора магнитной индукции ФB через поверхность S называется скалярное произведение векторов B и S.

Итак можно дать следующее определение термину «магнитный поток»:
Магнитный поток — это поток вектора магнитной индукции B через некоторую поверхность. Для бесконечно малого участка равен произведению модуля | B | на площадь участка dS и косинус угла α между B и нормалью n к плоскости участка. Для поверхности конечных размеров находится как сумма (интеграл) по её малым фрагментам.
Википедия
Зависимости магнитного потока
Используя формулу, можно увидеть, что магнитный поток зависит от трех переменных: магнитного поля B, площади S и угла α.
Магнитный поток линейно зависит от B и S. Например, если увеличить площадь S, но оставить магнитное поле B и угол α прежними, то магнитный поток будет больше. Поэтому большая площадь означает большой поток, а маленькая площадь — маленький магнитный поток.
Если, с другой стороны, увеличить магнитное поле B, то магнитный поток также увеличится. Сильное магнитное поле приводит к большому потоку, слабое поле — к малому магнитному потоку.
В целом, чем больше магнитное поле B или площадь S, тем больше магнитный поток.
Ситуация с углом α немного сложнее. Представьте, что ваша поверхность перпендикулярна магнитному полю, тогда ваш угол α = 0° . Здесь у вас самый большой магнитный поток. Если теперь шаг за шагом увеличивать угол, магнитный поток уменьшается. Когда вы достигаете α = 90°, магнитный поток равен нулю, потому что магнитное поле параллельно поверхности. После этого он снова начинает увеличиваться.
Единица измерения и обозначение магнитного потока
Магнитное поле B имеет единицу Тесла (T), а площадь — единицу квадратный метр м2 .
Поток является скалярной величиной и его единицей измерения является вебер (Вб): 1 Вб = 1 Т * м2 , то есть [Ф] = Т * м2 . Обозначается магнитный поток как Ф (символ формулы — греческая фи).
Примеры
Приведенные ниже примеры дадут вам лучшее понимание того, что представляет собой новая концепция и аналогия с потоком воды.
- В случае, показанном на рис. 2, поток магнитного поля с магнитной индукцией B через поверхность S составляет: ФB = B * S и при этом его значение максимально, так как:


2. А в каком случае при ненулевой магнитной индукции ФB = 0 ?

Определение магнитного потока показывает, что это тот случай, когда:

потому что cos 90° = 0.
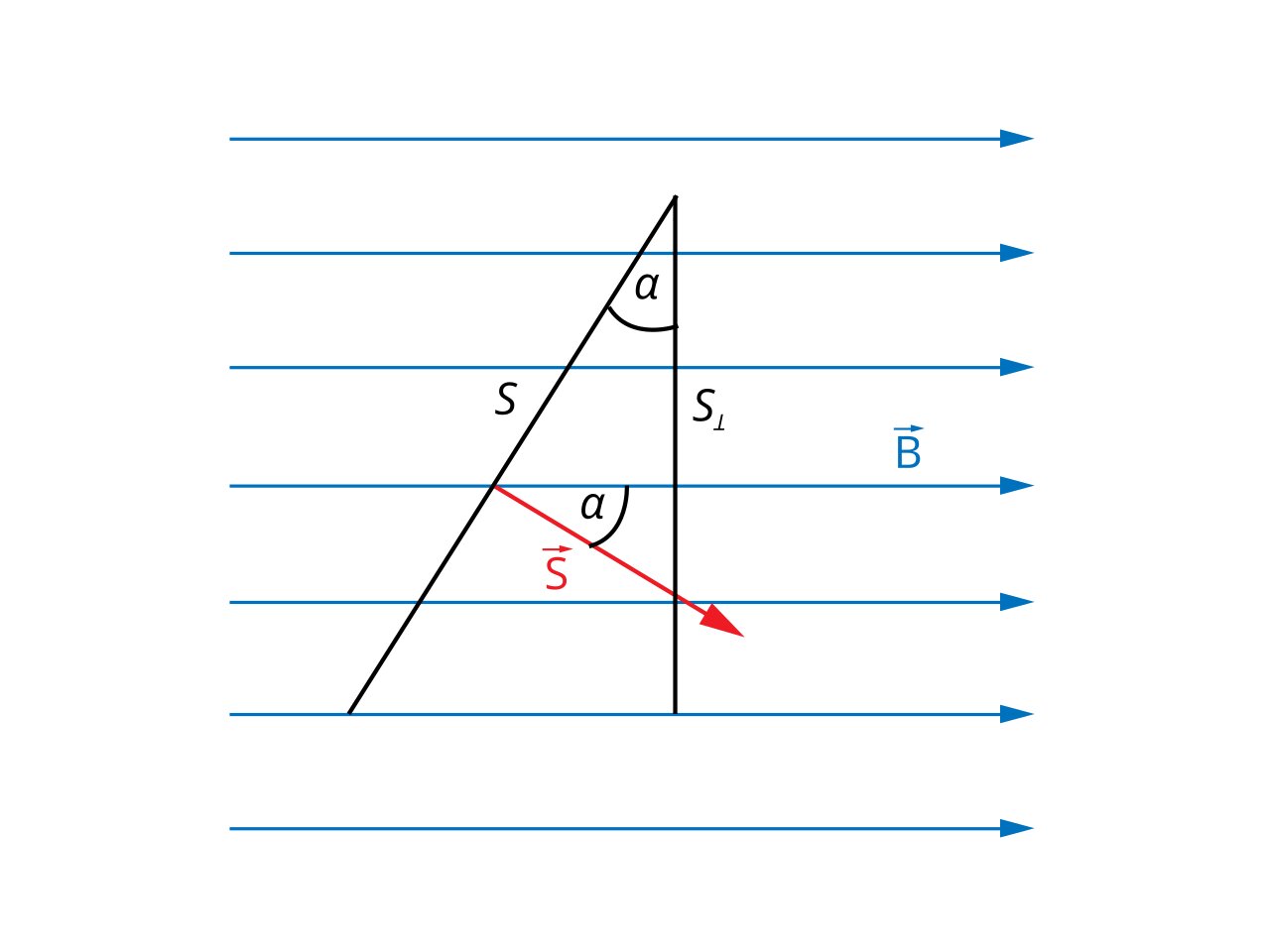
На рис. 3 мы видим, как в этой ситуации располагается плоская поверхность относительно векторов магнитной индукции.
Обратите внимание, что ФB можно представить как произведение В и S⟂, где S⟂ = S * cos α. Аналогично, вы всегда можете рассчитать величину потока магнитного поля, умножив составляющую магнитной индукции, перпендикулярную поверхности, на величину площади поверхности (см. рис. 4а. и 4б.).

Как можно рассчитать поток магнитного поля, если поле неоднородно и/или поверхность искривлена? Мы делим поверхность, через которую мы должны вычислить поток, на такие маленькие участки, что можно считать, что они плоские и поле однородное. Все это для того, чтобы можно было применить определение потока. Поэтому мы вычисляем небольшие «потоки» и суммируем их. Описанная процедура называется вычислением поверхностного интеграла, который записывается в виде:

Вычислять такие интегралы совсем не обязательно, но полезно понимать смысл такой процедуры.
Понятие магнитного потока
Таким образом, для описания явления электромагнитной индукции было введено понятие «магнитный поток», характеризующее «охват поля» рамкой. В этом понятии объединяются все величины, от которых зависит наведенная в рамке ЭДС – индукция поля, площадь и ориентация рамки. Для обозначения используется большая греческая буква Ф (фи):
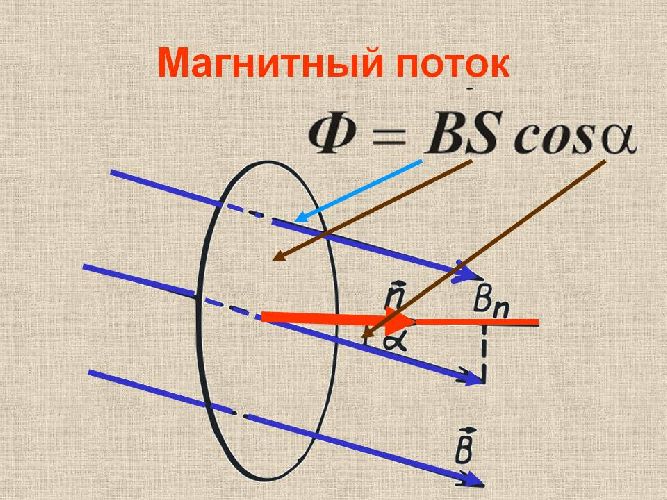
$$Ф=BScosalpha$$
Таким образом, магнитный поток – это величина, равная произведению индукции магнитного поля, площади проводящего контура, и косинуса угла между нормалью к контуру и направлением линий индукции.
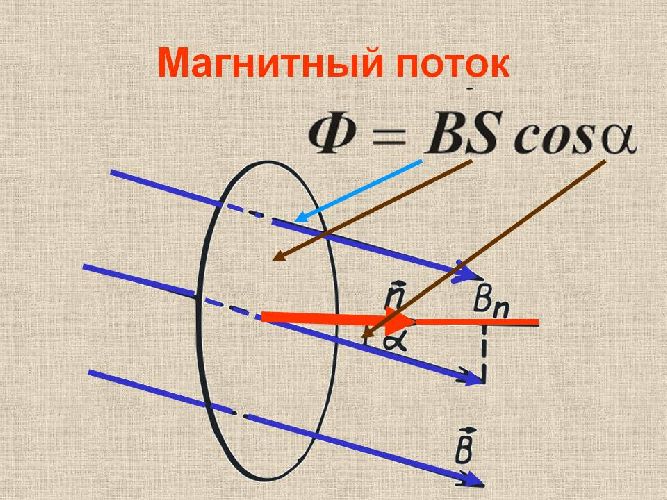
Рис. 2. Магнитный поток Ф=BScosa.
Из приведенной формулы магнитного потока можно вывести определение его единицы – вебер(Вб):
$$1Вб=1Тл×1м^2×cosalpha$$,
то есть, магнитный поток 1 Вебер – это магнитный поток, проходящий через рамку площадью 1 квадратный метр, которая ориентирована перпендикулярно линиям однородного магнитного поля с индукцией 1Тесла.

Для понимания термина «магнитный поток» можно представить аналогию с обычным водяным потоком. Водяной поток, как правило, зависит от напора воды (аналог индукции) и площади сечения трубы (аналог площади рамки), а поскольку вода, в отличие от магнитного поля, всегда заключена внутрь трубы, то водяной поток всегда ориентирован поперек сечения трубы, и значение косинуса в формуле всегда равно единице.
Определение
Определение
Потоком вектора магнитной индукции (магнитным потоком) (Ф) через площадку S называют скалярную величину равную:
[Ф=BScosalpha ={ B}_nS=overrightarrow{B}overrightarrow{S}left(1right),]
где $alpha $ угол между $overrightarrow{n}$ и $overrightarrow{B}$, $overrightarrow{n}$ — нормаль к площадке S.
Ф равен количеству линий магнитной индукции, которые пересекают площадку S (рис.1). Поток магнитной индукции может быть положительным и отрицательным. Знак потока зависит от выбора положительного направлении нормали к площадке S. Обычно, положительное направление нормали связывают с направлением обхода контура током. За положительное направление нормали принимают поступательное перемещение правого винта, при вращении его по току.
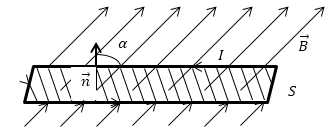
Рис. 1
В том случае, если магнитное поле неоднородно, S не является плоской, то поверхность можно разбить на элементарные площадки dS, которые рассматриваются как плоские, а поле на этой площадке можно считать однородным. В таком случае магнитный поток (dФ) можно через такую поверхность определить как:
[dФ=BdScosalpha =overrightarrow{B}doverrightarrow{S}left(2right).]
Тогда полный поток через поверхность S находится как:
[Ф=intlimits_S{BdScosalpha =intlimits_S{overrightarrow{B}doverrightarrow{S}}left(3right).}]
Основная единица измерения магнитного потока в системе СИ — вебер (Вб). $1 Вб=frac{1Тл}{1м^2}$.
Чему равен магнитный поток, как найти
Магнитный поток в случае однородного магнитного поля равен произведению модуля индукции В этого поля, площади S плоской поверхности, через которую вычисляется поток, и косинуса угла (varphi) между направлением индукции В и нормали к данной поверхности.
Нормаль — перпендикуляр к плоскости контура.
Также поток можно вычислить через индуктивность, которая пропорциональна отношению полного, или суммарного потока к силе тока.
Обозначение суммарного потока — буква ( psi). Он равен сумме потоков, проходящих через всю поверхность. И в простом случае, где рассматриваются одинаковые потоки, проходящие через одинаковые витки катушки, и в случаях, когда поверхность имеет очень сложную форму, эта пропорциональность сохраняется.
Скорость изменения магнитного потока через контур
Закон электромагнитной индукции Фарадея в интегральном виде выглядит следующим образом:
(;underset С{oint;};(overrightarrow{Е;}times;doverrightarrow l) = – frac{1}{c}frac{d}{dt}int underset S{int;};(overrightarrow{B} times doverrightarrow{S}).)
Интеграл в левой части уравнения — циркуляция вектора (overrightarrow{Е;}) по замкнутому контуру С, это отражает знак интеграла, записанный с кругом. В правой части — скорость изменения потока Ф, который вычисляется как интеграл по поверхности S, «натянутой» на С.
Интеграл — целое, определяемое как сумма его бесконечно малых частей.
Если считать изменение потока в замкнутом контуре равномерным, то закон Фарадея примет следующий вид:
(epsilon_{i} = – frac{triangleФ}{triangle t}.)
Проводящая рамка в магнитном поле
Явление электромагнитной индукции состоит в том, что при изменении поля, пронизывающего проводящую рамку или катушку, в ней возникает электродвижущая сила (ЭДС):

Рис. 1. Электромагнитная индукция, опыт Фарадея.
Энергия используемого в этом опыте магнитного поля характеризуется магнитной индукцией. Однако, при попытке описать наблюдаемое явление выяснилось, что одной этой величины мало.
Если выписать в таблицу значения ЭДС, наводимые магнитным полем, имеющим одну и ту же плотность магнитных линий, в разных условиях, то окажется, что ЭДС, возникающая в квадратной рамке, имеет гораздо большее значение, чем ЭДС в длинной узкой рамке (при одном периметре).
А наибольшая ЭДС возникает в круглом витке.
Причиной этого оказался разный «охват поля» рамкой. Площадь длинной узкой рамки невелика, она «охватывает» малое «количество поля», и ЭДС в ней также мала. У квадратной рамки площадь при одинаковом периметре больше, а у круглого витка – она наибольшая, в результате рамка «охватывает» большее «количество поля», и ЭДС в такой рамке тоже получается больше.
Не менее важной оказалась ориентация рамки по отношению к направлению магнитного поля. Наибольшая ЭДС возникает, если проводящая рамка перпендикулярна линиям магнитной индукции. Если плоскость рамки параллельна этим линиям – то независимо от ее площади и силы магнитного поля ЭДС в рамке не возникнет.
Измерительные приборы
Линии магнитной индукции
Магнитные потоки, определимые с помощью специальных приборов – флюксметров, измеряются и в лабораторных, и в полевых условиях. Приборы ещё называют веберметрами. Особенностью такого измерительного аппарата магнитоэлектрической системы (МЭС) является то, что ток подводится к перемещающейся бескаркасной рамке через спирали, не имеющие момента противодействия (безмоментные).
Внимание! В тот момент, когда ток отсутствует, указатель прибора не имеет фиксированного положения в пределах шкалы.
Схема применения и устройства флюксметра
Прибор состоит из следующих деталей, отмеченных на рис. выше:
- испытуемый постоянный магнит – 1;
- рамка измерительная – 2;
- рамка прибора – 3;
- магнит прибора – 4;
- рамка корректирующего устройства – 5;
- головка регулировки корректирующей рамки – 6;
- переключатель «работа – коррекция» – 7.
Флюксметр не может измерять слабые МП из-за низкой чувствительности.
Теорема Гаусса для магнитной индукции
Cила тока: формула
Великий немецкий учёный Карл Гаусс, который отличился в математике, физике и астрономии, вывел закон (теорему) в области магнетизма. Он доказал, что, в отличие от электрического поля, создаваемого электрическими зарядами, МП не создаётся зарядами магнитными. Их попросту не существует в классической электродинамике.
Информация.Теорема, которую вывел Гаусс, принадлежит к главным законам электродинамики и является частью системы уравнений Максвелла. Она описывает соотношение между потоком напряжённости электрополя, пронизывающего замкнутую произвольную поверхность, и суммой зарядов, помещающихся в очерченном этой поверхностью объёме. Сумма выражена в алгебраической форме.
В отношении магнитной индукции поток В→, проходящий через замкнутую поверхность S, имеет нулевое значение.
Поток вектора магнитной индукции
Некоторые свойства магнитного потока
В соответствии с теоремой Гаусса для магнитной индукции, поток вектора магнитной индукции B{displaystyle mathbf {B} }
через любую замкнутую поверхность S{displaystyle S}
равен нулю:
Φ=∮SB⋅dS=0{displaystyle Phi =oint limits _{S}mathbf {B} cdot {text{d}}mathbf {S} =0}
.
Это означает, что в классической электродинамике невозможно существование магнитных зарядов, которые создавали бы магнитное поле подобно тому, как электрические заряды создают электрическое поле.
В соответствии с теоремой Стокса, магнитный поток Φ{displaystyle Phi }
через поверхность, «натянутую» на некий контур L{displaystyle L}
, можно выразить через циркуляцию векторного потенциала A{displaystyle mathbf {A} }
магнитного поля по этому контуру:
Φ=∮LA⋅dl{displaystyle Phi =oint limits _{L}mathbf {A} cdot mathbf {dl} }
,
поскольку имеет место связь B=rotA{displaystyle mathbf {B} ={rm {{rot}mathbf {A} }}}
. Этот поток не зависит от конфигурации натянутой поверхности.
Закон электромагнитной индукции Фарадея
Закон электромагнитной индукции (закон Фарадея):
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:
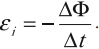
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из ( N ) витков, то ЭДС индукции:
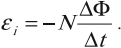
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ( R ):
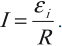
При движении проводника длиной ( l ) со скоростью ( v ) в постоянном однородном магнитном поле с индукцией ( vec{B} ) ЭДС электромагнитной индукции равна:
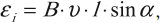
где ( alpha ) – угол между векторами ( vec{B} ) и ( vec{v} ).
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
- вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Электрическая зависимость
Британский физик Майкл Фарадей не сомневался в единственной природе явлений магнетизма в своей теореме. Изменяющийся во времени фон создаёт электронный и магнитный вид. В 1831 году Фарадей обнаружил появление индукции, которая легла в основу устройства для генераторов, преобразующих механическую энергию в электронную. А в 1835 г. немецкий математик Карл Гаусс определил аксиому, описывающую обозначение и зависимость напряжённости поля от величины заряда.
Появление электрической индукции замечено в появлении тока в проводящей цепи, которая либо лежит на изменяющемся во времени фоне, либо движется на непременном участке таким образом, что фактически число магнитных витков проникает в контуры трансформаций.
Для своих многочисленных экспериментов Фарадей воспользовался двумя катушками, магнитом, переключателем постоянного тока и гальванометром. Электронный поток мог зависеть и намагничивать кусок железа.
В результате экспериментов Фарадея были заложены основные особенности возникновения электрической индукции, и ток появляется:
- в одной из катушек во время замыкания или размыкания электронной цепи внутри другой части;
- когда энергия протекает в одном из элементов с поддержкой реостата;
- при перемещении катушек относительно друг друга;
- когда неизменный магнит движется относительно.
В замкнутом проводящем контуре ток появляется, когда число линий магнитной индукции изменяется, создавая плоскость, ограниченную цепью. И чем раньше перевести количество рядов МИ, тем больше генерируется индукционный ток в рамке. Это является основной причиной конфигурации численности последовательностей индукции.
Явление позволяет содержать и изменять число линий МИ, делая плоскость площадки, ограниченной неподвижной проводящей цепью, из-за конфигурации тока в катушке, расположенной рядом. Происходит максимальное изменение количества последовательностей МИ из-за смещения схемы на неоднородном фоне, плотность линий которого может изменяться на месте.
Переменный во времени магнитный поток
По закону электромагнитной индукции Фарадея, если магнитный поток через некоторую поверхность изменяется со временем, то создаётся электродвижущая сила
E=−dΦdt{displaystyle {mathcal {E}}=-{frac {rm {{d}Phi }}{rm {{d}t}}}}
в контуре, на который натянута данная поверхность. Если вдоль такого контура «проложен» электрический провод, то в нём возникнет индукционный ток. Изменение потока со временем может быть вызвано изменением вектора магнитной индукции B{displaystyle mathbf {B} }
и/или геометрии контура.
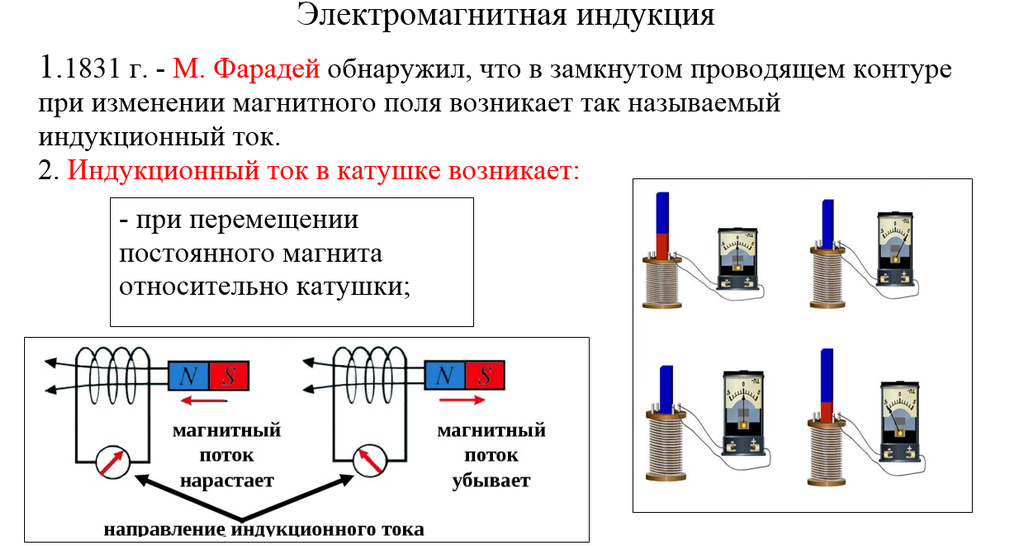
Правило Ленца
Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Алгоритм решения задач с использованием правила Ленца:
- определить направление линий магнитной индукции внешнего магнитного поля;
- выяснить, как изменяется магнитный поток;
- определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
- по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.
Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
Постоянные магниты, электромагниты.
Источником магнитного поля (МП) могут служить постоянные магниты. Они изготавливаются из магнетита. В природе он известен как оксид железа. Это минерал чёрной окраски, имеющий молекулярное строение FeO·Fe2O3. Свойства магнитов известны с давних времён. Магниты имеют два полюса – северный и южный.
Постоянные магниты можно классифицировать по следующим критериям:
- материал, из которого изготовлен магнит;
- форма;
- сфера использования.
Магниты с постоянными полюсами изготавливаются из различных материалов:
- ферритов – прессованных изделий из порошков оксида железа и оксидов иных металлов;
- редкоземельных – нодимовых (NdFeB), самариевых (SmCo), литых (сплавы металлов), полимерных (магнитопласты).
Форма магнитов самая различная:
- цилиндрическая (прямоугольная);
- подковообразная;
- кольцеобразная;
- дискообразная.
Важно! В зависимости от формы изменяется месторасположение полюсов, соответственно, и направление магнитных линий у поля.
Направление линий МП в зависимости от формы магнита
Постоянные магниты нашли широкое применение в различных отраслях народного хозяйства:
- МРТ – медицинский прибор для диагностики человеческого организма;
- приводы жёстких дисков в современных компьютерах;
- в радиотехнике, при изготовлении динамиков;
- производство декоративных украшений с применением магнитов на полимерной основе.
В двигателях постоянного тока такие магниты вмонтированы в корпус индуктора.
Электромагниты.
Следующей разновидностью устройства, предназначенного для создания МП, является электромагнит. При протекании через его обмотку электрического тока сердечник становится магнитом. Следственно, электромагнит состоит из следующих частей:
- сердечник (магнитопровод);
- обмотка.
Это своеобразная катушка индуктивности, называемая соленоидом.
Сердечник может быть выполнен из ферримагнитного материала или листового набора электротехнической стали.
Обмотка намотана проводом из алюминия или меди, покрытого изоляцией.
Электромагниты (ЭМ) можно классифицировать по следующим параметрам:
- магниты постоянного тока – нейтральные;
- магниты постоянного тока – поляризованные;
- устройства переменного тока.
Нейтральные ЭМ – создание магнитного потока происходит так, что величина притяжения увеличивается с повышением силы тока и не подчиняется направлению движения электронов.
Поляризованные ЭМ в своём составе содержат:
- рабочую обмотку – для создания рабочего Φ;
- постоянный магнит – для наведения поляризующего Φ.
Обмотки ЭМ переменного тока питаются синусоидальным током, поэтому их Φ меняется по периодическому закону.
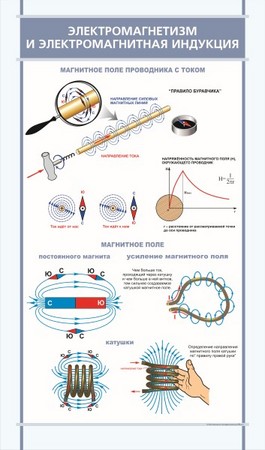
Явление электромагнитной индукции
Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
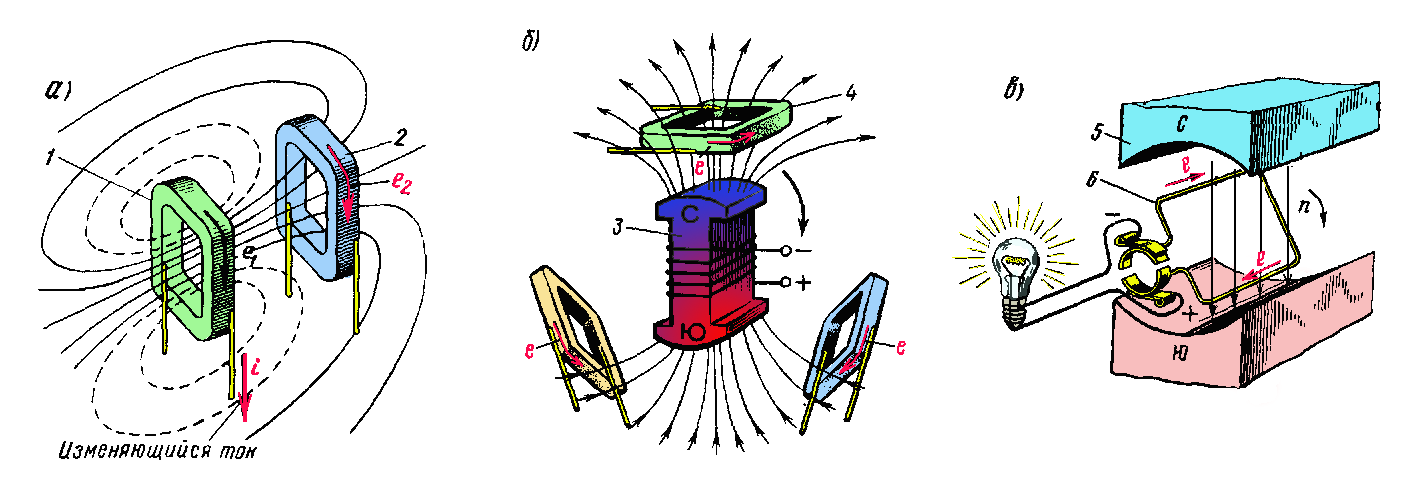
Опыты Фарадея
- На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
- Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
- Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.

Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Объяснения возникновения индукционного тока
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
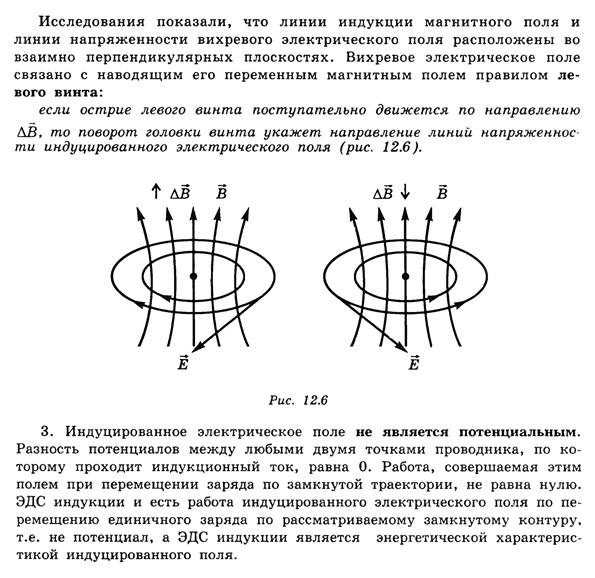
Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.
Свойства вихревого электрического поля:
- источник – переменное магнитное поле;
- обнаруживается по действию на заряд;
- не является потенциальным;
- линии поля замкнутые.
Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.
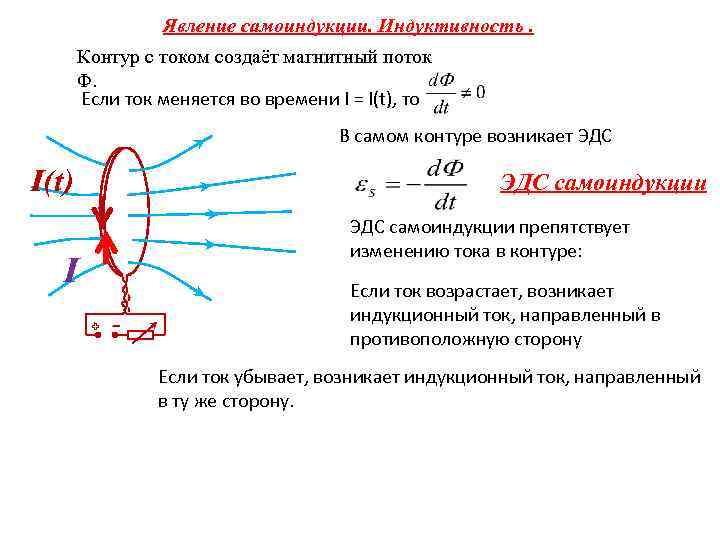
Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.
При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.
В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.
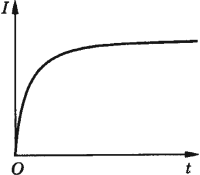
Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.
При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.
Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.
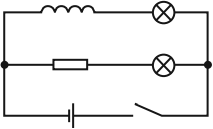
Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.
При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.
ЭДС самоиндукции ( varepsilon_{is} ), возникающая в катушке с индуктивностью ( L ), по закону электромагнитной индукции равна:
ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке
Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ( Phi ) через контур из этого проводника пропорционален модулю индукции ( vec{B} ) магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.
Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:
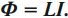
Индуктивность – коэффициент пропорциональности ( L ) между силой тока ( I ) в контуре и магнитным потоком ( Phi ), создаваемым этим током:
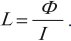
Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.
Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:
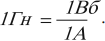
Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.
Магнитным потоком через площадь ( S ) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ( B ), площади поверхности ( S ), пронизываемой данным потоком, и косинуса угла ( alpha ) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):
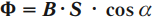
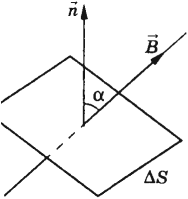
Обозначение – ( Phi ), единица измерения в СИ – вебер (Вб).
Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции:
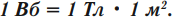
Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла ( alpha ) магнитный поток может быть положительным (( alpha ) < 90°) или отрицательным (( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Основное отличие – магнитный поток от плотности магнитного потока
В магнетизме несколько физических величин, таких как магнитный поток, плотность магнитного потока и напряженность магнитного поля, используются для объяснения поведения или влияния магнитных полей. Некоторые люди используют эти термины взаимозаменяемо. Но они имеют разные и особые значения. главное отличие между магнитным потоком и плотностью магнитного потока является то, что Магнитный поток является скалярной величиной, тогда как плотность магнитного потока является векторной величиной. Магнитный поток – это скалярное произведение плотности магнитного потока и вектора площади. Эта статья пытается дать четкое объяснение магнитного потока и плотности магнитного потока.
Магнитный поток является важным скалярным значением в магнетизме. Обычно магнитные поля визуализируются с использованием линий магнитного поля. Величина поля представлена плотностью силовых линий. Стрелки линий поля представляют направление магнитного поля. Что касается линий магнитного поля, магнитный поток через данную поверхность прямо пропорционален общему количеству линий поля, проходящих через нее. Однако линии поля не являются реальными линиями в пространстве. Это просто воображаемые линии, используемые в качестве простой модели для объяснения магнитных влияний движущихся заряженных частиц и магнитных материалов.
Магнитный поток в постоянном магнитном поле можно математически выразить как, = B.S.
ɸ – магнитный поток через векторную поверхность, B – плотность магнитного потока, а S – площадь поверхности. Другими словами, магнитный поток через данную площадь поверхности равен скалярному произведению (точечному произведению) плотности магнитного потока и вектора площади.
В более общем смысле магнитный поток можно выразить как ɸ = ɸ B.dS.
Легко показать, что магнитный поток через любую замкнутую поверхность равен нулю. Но магнитный поток через открытую поверхность может быть либо нулевым, либо ненулевым. Электродвижущая сила создается изменяющимся магнитным потоком, который проходит через проводящую петлю. Это явление является основным принципом работы генераторов. Согласно Закон индукции Фарадеявеличина электродвижущей силы, индуцированной в проводящей петле изменяющимся магнитным потоком, равна скорости изменения магнитного потока, который связан с петлей.
Магнитный поток, который также известен как «магнитная индукцияЭто еще одна важная величина в магнетизме. Плотность магнитного потока определяется как величина магнитного потока через единицу площади, расположенную перпендикулярно направлению магнитного поля. Это векторная величина, обычно обозначаемая B.
Единица СИ магнитного потока равна Тесла (Т), Гаусс (G) Единица измерения плотности магнитного потока, измеряемая C.G.S. он также широко используется, особенно когда речь идет о слабых плотностях магнитного потока, потому что один Тесла равен 10000 Г.
Плотность магнитного потока в данной точке (δB→), произведенный текущим элементом, определяется уравнением Био-Савара.
Здесь я ток, δl→ является вектором с бесконечно малой величиной, а rˆ является единичным вектором r. Это очень важное уравнение при работе с магнитными полями, создаваемыми токонесущими проводами или цепями. Плотность магнитного потока, создаваемого проводником с током, зависит от нескольких факторов, таких как геометрия провода, величина и направление тока и положение точки, в которой должна быть найдена плотность магнитного потока. Био-закон Саварта является комбинацией всех этих факторов. Таким образом, его можно использовать для расчета результирующей плотности магнитного потока B в любой заданной точке из проводника с током.
Плотность магнитного потока (B) внутри материальной среды равна магнитной проницаемости этой среды (µ), умноженной на напряженность магнитного поля (H). Это может быть выражено как B = µH. Магнитная проницаемость ферромагнитных материалов увеличивается до определенного значения при увеличении напряженности приложенного магнитного поля. После этого оно уменьшается по мере увеличения напряженности поля. Таким образом, плотность магнитного потока также приближается к уровню насыщения и затем уменьшается при дальнейшем увеличении напряженности магнитного поля в соответствии с уравнением B = µH. Это явление известно как магнитное насыщение.
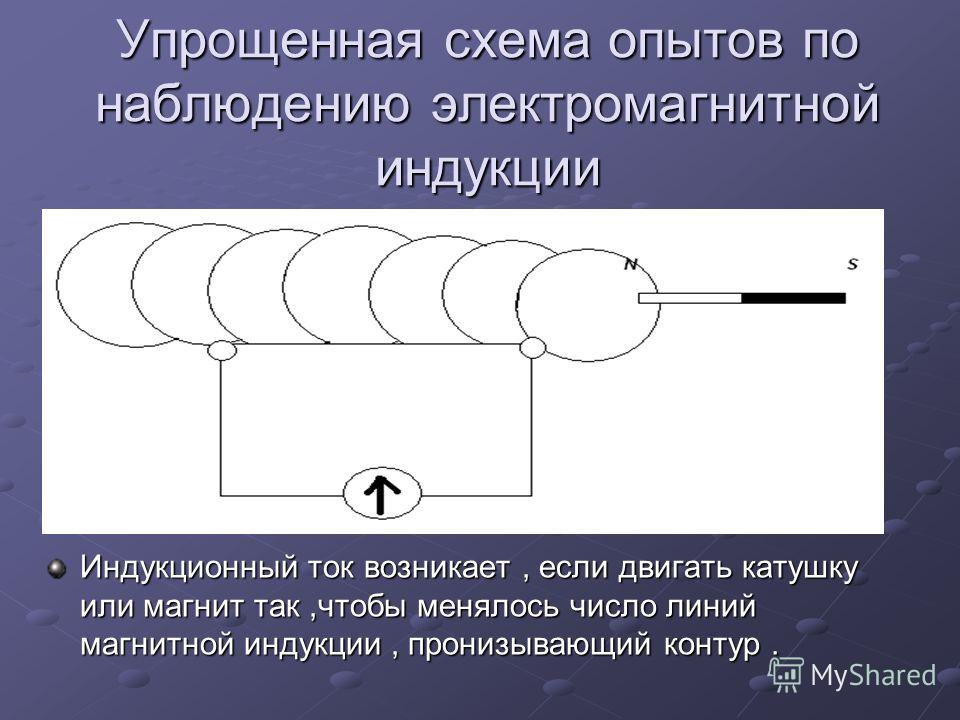
Наблюдение за спектрами
В соответствии с плотностью линий магнитного поля (МП) можно увидеть величину вектора индукции, а согласно направленности силовых рядов — его течение. Наблюдение за спектрами постоянного тока и катушки на самом деле показывает, что при удалении проводника индукция МП уменьшается и довольно быстро.
Магнитный фон называется:
- С различным выведением в разных точках — гетерогенным. Неоднородный фон — это часть прямолинейного и радиального тока, вне соленоида, неизменённого магнита и т. д.
- С индукцией во всех точках — однородным полем. Графически такой МФ представлен силовыми линиями, которые считаются равноотстоящими параллельными частями. Этот случай является фоном изнутри длинного соленоида, а также полем между близкими соседними плоскими наконечниками электромагнита.
Произведение индукции поля, проникающего в контур от его области, называется потоком МИ или элементарным МП. Определение было дано и изучено британским физиком Фарадеем. Он отметил, что эта концепция на самом деле позволяет глубже рассмотреть совместный характер магнитных и электрических явлений.
Обозначая поток буквой f, площадью контура S и углом между направлением вектора индукции B и нормальной частью n к области α, можно написать магнитный поток формулой:
F = S cos α.
МП является скалярным размером. Например, поскольку плотность силовых рядов случайного магнитного поля равна его индукции, он уравнивается всему количеству линий, которые проникают в цепь. С изменением поля поток, который пронизывает контур, также меняется.
Единица измерения магнитного потока — вебер. Определение СИ струи считается линия, площадь которой 1 м², оказавшаяся на равномерном фоне с индукцией 1 Вт / м2 и перпендикулярная вектору. Это устройство будет обозначаться:
1 Вт = 1 Вт / м2 — 1 м².
ЭДС индукции
Каков механизм возникновения индукционного тока? Это мы обсудим позже. Пока ясно одно: при изменении магнитного потока, проходящего через контур, на свободные заряды в контуре действуют некоторые силы — сторонние силы, вызывающие движение зарядов.
Как мы знаем, работа сторонних сил по перемещению единичного положительного заряда вокруг контура называется электродвижущей силой (ЭДС):
. В нашем случае, когда меняется магнитный поток сквозь контур, соответствующая ЭДС называется ЭДС индукции и обозначается
.
Итак, ЭДС индукции
— это работа сторонних сил, возникающих при изменении магнитного потока через контур, по перемещению единичного положительного заряда вокруг контура.
Природу сторонних сил, возникающих в данном случае в контуре, мы скоро выясним.
Особенности течения
Скорость изменения магнитного потока генерирует электронный фон, имеющий замкнутые блоки питания (вихревое поле). Этот фон рассматривается в проводнике как циркуляция внешних сил. Это явление называется электрической индукцией, а мощность, которую можно определить, генерируемая в этом случае, является индуцированной ЭДС поверхности.
Поток подчёркивает вероятность характеристики всего магнита или видов других источников МП. Если индукция выдвигает на первый план вероятность, характерную её эффекту в любой отдельной точке, поток будет целым. Это вторая по значимости особенность поля. Если МИ функционирует как силовая часть МП, поток считается её энергетической линией.
Возвращаясь к экспериментам, можно сказать, что фактически любая электромагнитная катушка может рассматриваться как 1 закрытая. Это схема, по которой будет течь магнитный поток вектора индукции, тогда ток МИ электронов будет замечен при потокосцеплении.
Таким образом, непосредственно под действием струи в замкнутом проводнике образуется электронный фон. И в течение этого времени он будет генерировать ток.
Взаимодействие магнита с контуром
Итак, приближение или удаление магнита приводит к появлению в контуре индукционного тока, направление которого определяется правилом Ленца. Но ведь магнитное поле действует на ток! Появится сила Ампера, действующая на контур со стороны поля магнита. Куда будет направлена эта сила?
Если вы хотите хорошо разобраться в правиле Ленца и в определении направления силы Ампера, попробуйте ответить на данный вопрос самостоятельно. Это не очень простое упражнение и отличная задача для С1 на ЕГЭ. Рассмотрите четыре возможных случая.
1. Магнит приближаем к контуру, северный полюс направлен на контур.
2. Магнит удаляем от контура, северный полюс направлен на контур.
3. Магнит приближаем к контуру, южный полюс направлен на контур.
4. Магнит удаляем от контура, южный полюс направлен на контур.
Не забывайте, что поле магнита не однородно: линии поля расходятся от северного полюса и сходятся к южному. Это очень существенно для определения результирующей силы Ампера. Результат получается следующий.
Если приближать магнит, то контур отталкивается от магнита. Если удалять магнит, то контур притягивается к магниту. Таким образом, если контур подвешен на нити, то он всегда будет отклоняться в сторону движения магнита, словно следуя за ним. Расположение полюсов магнита при этом роли не играет .
Уж во всяком случае вы должны запомнить этот факт — вдруг такой вопрос попадётся в части А1
Результат этот можно объяснить и из совершенно общих соображений — при помощи закона сохранения энергии.
Допустим, мы приближаем магнит к контуру. В контуре появляется индукционный ток. Но для создания тока надо совершить работу! Кто её совершает? В конечном счёте — мы, перемещая магнит. Мы совершаем положительную механическую работу, которая преобразуется в положительную работу возникающих в контуре сторонних сил, создающих индукционный ток.
Итак, наша работа по перемещению магнита должна быть положительна . Это значит, что мы, приближая магнит, должны преодолевать силу взаимодействия магнита с контуром, которая, стало быть, является силой отталкивания .
Теперь удаляем магнит. Повторите, пожалуйста, эти рассуждения и убедитесь, что между магнитом и контуром должна возникнуть сила притяжения.
Электромагнитная индукция в движущемся проводнике
Эксперименты показывают, что ЭДС индукции возникает в любом отрезке проводника, движущемся в магнитном поле и пересекающем линии магнитной индукции. ЭДС индукции в таком «микрогенераторе» можно рассчитать с помощью схемы, представленной на Рис.1. По параллельным металлическим «рельсам», замкнутым с одной стороны проводящей перемычкой AB, в однородном поле с магнитной индукцией B с постоянной скоростью v скользит проводящий «мостик» CD длиной l . За время dt магнитный поток, пронизывающий контур ABCD, возрастает на величину dФ = Bvl·dt, откуда
Согласно основному закону электромагнитной индукции ЭДС, индуктируемая в контуре, определяется соотношением
Так как все элементы контура, кроме «мостика», неподвижны относительно магнитного поля, то (2) — это и есть ЭДС, возникающая в движущемся проводнике.
Эта же ЭДС возникает и в незамкнутом проводящем отрезке, движущемся в магнитном поле (Рис. 2). Считается, что при перемещении проводящего отрезка в магнитном поле силой, «разделяющей» заряды q в проводнике и создающей на концах такого «микрогенератора» индукционную ЭДС, является магнитная составляющая силы Лоренца:

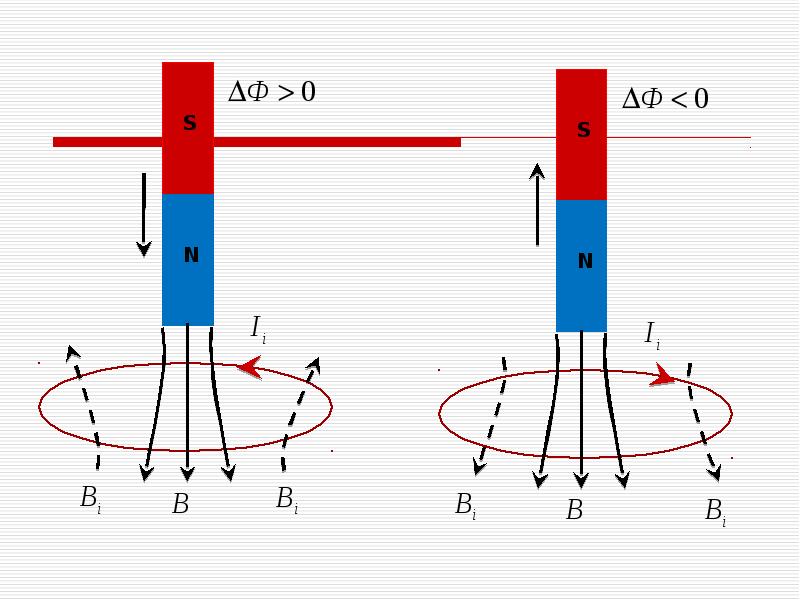

Если скорость движения проводника постоянна, то и ЭДС индукции остается постоянной. В момент остановки заряды в проводнике под действием кулоновских сил «схлопываются» и микрогенератор практически мгновенно разряжается.
ЭДС в таком индукционном микрогенераторе возникает вследствие того, что проводник пересекает линии магнитного поля с некоторой скоростью v. Назовем (для краткости) такой способ генерации ЭДС электромагнитной индукции «способом пересечения». Процесс электромагнитной индукции «с пересечением» можно схематически представить так:
пересечение → возникновение силы Лоренца → перемещение зарядов → образование ЭДС
Электромагнитные волны
Электромагнитное поле образуется вокруг движущихся заряженных частиц и распространяется в пространстве по уже известному волновому принципу. Такое распространение электромагнитного поля происходит при помощи электромагнитных волн или электромагнитных возмущений, подчиняясь физическим законам волновой природы. В отличие от механических волн (которые не могут существовать отдельно от какой-либо среды), электромагнитные волны могут проявляться без участия частиц, вещества и среды, например в вакууме. Электромагнитные волны в виде электромагнитных возмущений распространяются во все стороны от источника излучения. Для излучения ощутимой электромагнитной волны желательно наличие быстрого заряда с хорошим ускорением колебаний высокой частоты, например несколько десятков тысяч герц.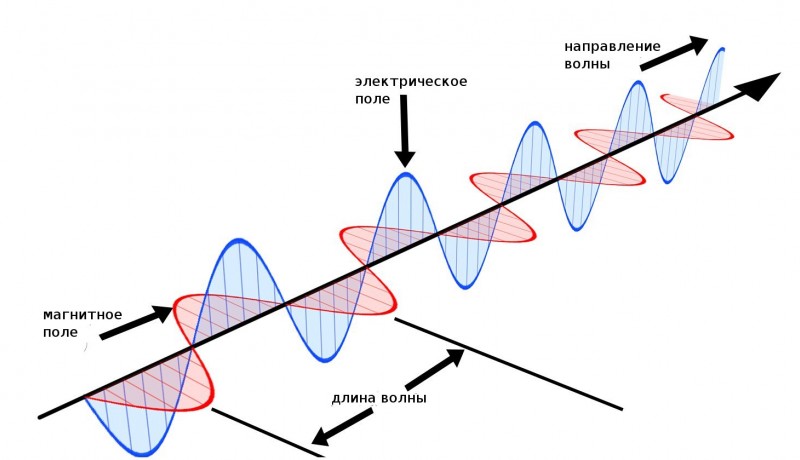
Электромагнитная волна обладает определёнными характеристиками, присущими любой волне. Скорость такой волны равняется скорости света и составляет 300000 км/с. Так же электромагнитные волны всегда поперечные по своей природе. Выражается в том, что линии магнитной индукции (магнитного поля) и силовые линии (электрического поля) перпендикулярны друг другу.
Если магнитное поле характеризует векторная величина магнитной индукции (B), то образованное из него вихревое электрическое поле характеризуется напряжённостью (E). Напряжённость электрического поля так же величина векторная и направленная, выражается в 1 Ньютон/Кулон (Н/Кл). Таким вкратце предстаёт явление электромагнитной индукции тока и сопутствующие электрические и магнитные.
Линии магнитного поля и свойства
Полезно вспомнить общие сведения о магнитном поле. Оно образуется вокруг проводника, по которому двигаются электрические заряды или протекает электрический ток. В этом случае образуется сразу два вида поля — электрическое и магнитное поля. Таким образом, вокруг проводника/провода с током будет наблюдаться и электрическое и одновременно магнитное поле, т.к. они оба возникают при условии протекания электрического тока. 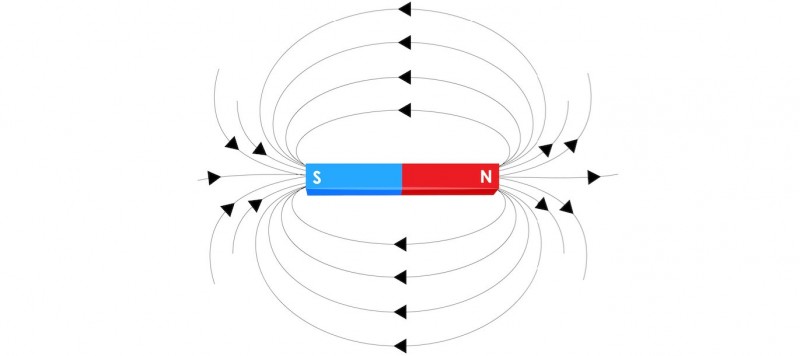
Появившись, магнитное поле имеет свойство воздействовать на другие движущиеся электрические заряды, а точнее на сторонний электрический ток, например, протекающий в другом проводнике поблизости от первого. Такое воздействие магнитного поля материально и определяется степенью — оно может быть сильнее или слабее. В автомобиле, для примера, такое взаимодействие можно наблюдать на примере проводки, которая способна оказывать ощутимое влияние друг на друга и создавать наводки/помехи, отчётливо слышимые в динамиках.
Советуем изучить Автомобильная антенна своими руками
Магнитное поле с его сферической формой образуется линиями, которые можно представить вокруг объекта под напряжением и даже увидеть при помощи мелкой металлической крошки. Таких магнитных линий вокруг объекта будет большое количество, вместе они образуют целый спектр. Направление магнитных линий определяется магнитной стрелкой. Магнитные линии всегда замкнуты, поэтому у них нет понятия «начало линии» или «конец линии». Эти линии никогда не пересекаются, не завиваются и не взаимодействуют друг с другом. Магнитные линии в совокупности формируют форму магнитного поля и по их «кучности» в какой-то точке пространства можно судить о силе магнитного воздействия в этом месте.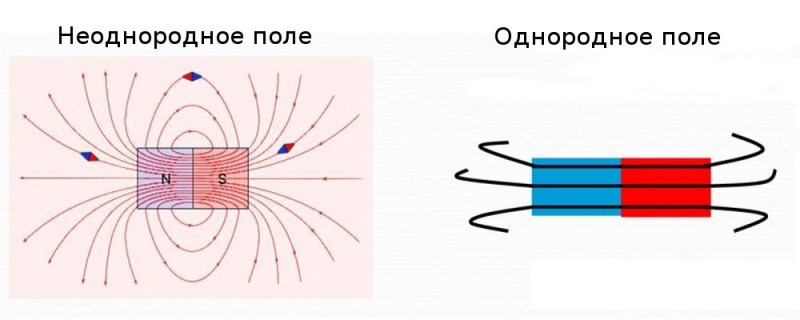
Если линии располагаются параллельно друг относительно друга и в целом упорядоченно, если их плотность более менее равномерна, то такие линии образуют однородное магнитное поле. Наоборот, если линии искривляются в пространстве и разрежены друг относительно друга, то они своей совокупностью образуют неоднородное магнитное поле. Эти два вида магнитного поля отличаются друг от друга во многом:
- Магнитная сила воздействия неоднородного поля различна в той или иной точке пространства, тогда как эта сила одинакова по модулю и направлению у однородного поля.
По взаиморасположению линий в пространстве: у однородного поля линии параллельны друг другу и кучность их одинакова; у неоднородного поля линии искривляются и кучность их различна.
Неоднородное поле находится вне магнита или проводника с электрическим током, тогда как однородное поле образуется внутри магнита.
Однородные магнитные поля чаще всего наблюдаются внутри катушки с большим количеством витков (например в катушке динамика) или внутри обычного полосового магнита, тогда как неоднородное магнитное поле чаще всего располагается вне магнита, например вокруг силового кабеля питания.
Основные формулы раздела «Электромагнитная индукция»

Алгоритм решения задач по теме «Электромагнитная индукция»:
1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
2. Записать формулу:
- закона электромагнитной индукции;
- ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.
3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.
4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).
5. Решить полученную систему уравнений относительно искомой величины.
6. Решение проверить.
Источники:
- https://obrazovaka.ru/fizika/magnitnyy-potok-formula.html
- https://spravochnick.ru/fizika/postoyannoe_magnitnoe_pole/potok_vektora_magnitnoy_indukcii_magnitnyy_potok_/
- https://wiki.fenix.help/fizika/magnitnyj-potok
- https://amperof.ru/teoriya/formula-magnitnogo-potoka.html
- https://wiki2.org/ru/%D0%9C%D0%B0%D0%B3%D0%BD%D0%B8%D1%82%D0%BD%D1%8B%D0%B9_%D0%BF%D0%BE%D1%82%D0%BE%D0%BA
- https://fizi4ka.ru/egje-2018-po-fizike/jelektromagnitnaja-indukcija.html
- https://nauka.club/fizika/magnitn%D1%83i-potok.html
- https://ru.strephonsays.com/difference-between-magnetic-flux-and-magnetic-flux-density
- https://ege-study.ru/ru/ege/materialy/fizika/elektromagnitnaya-indukciya/
- https://encom74.ru/elektromagnitnaa-indukcia-fenomen-voznikausij-v-inducirovannom-pole/
Предыдущая
ИнформацияПечатные платы что это и их назначение?
Следующая
ИнформацияГистерезис в электротехнике и электронике: о самом главном
Магнитный поток


3.9
Средняя оценка: 3.9
Всего получено оценок: 124.
3.9
Средняя оценка: 3.9
Всего получено оценок: 124.
Для количественного описания явления электромагнитной индукции необходимо введение понятия магнитного потока. Рассмотрим эту тему подробнее.
Проводящая рамка в магнитном поле
Явление электромагнитной индукции состоит в том, что при изменении поля, пронизывающего проводящую рамку или катушку, в ней возникает электродвижущая сила (ЭДС):

Энергия используемого в этом опыте магнитного поля характеризуется магнитной индукцией. Однако, при попытке описать наблюдаемое явление выяснилось, что одной этой величины мало.
Если выписать в таблицу значения ЭДС, наводимые магнитным полем, имеющим одну и ту же плотность магнитных линий, в разных условиях, то окажется, что ЭДС, возникающая в квадратной рамке, имеет гораздо большее значение, чем ЭДС в длинной узкой рамке (при одном периметре).
А наибольшая ЭДС возникает в круглом витке.
Причиной этого оказался разный «охват поля» рамкой. Площадь длинной узкой рамки невелика, она «охватывает» малое «количество поля», и ЭДС в ней также мала. У квадратной рамки площадь при одинаковом периметре больше, а у круглого витка – она наибольшая, в результате рамка «охватывает» большее «количество поля», и ЭДС в такой рамке тоже получается больше.
Не менее важной оказалась ориентация рамки по отношению к направлению магнитного поля. Наибольшая ЭДС возникает, если проводящая рамка перпендикулярна линиям магнитной индукции. Если плоскость рамки параллельна этим линиям – то независимо от ее площади и силы магнитного поля ЭДС в рамке не возникнет.
Понятие магнитного потока
Таким образом, для описания явления электромагнитной индукции было введено понятие «магнитный поток», характеризующее «охват поля» рамкой. В этом понятии объединяются все величины, от которых зависит наведенная в рамке ЭДС – индукция поля, площадь и ориентация рамки. Для обозначения используется большая греческая буква Ф (фи):
$$Ф=BScosalpha$$
Таким образом, магнитный поток – это величина, равная произведению индукции магнитного поля, площади проводящего контура, и косинуса угла между нормалью к контуру и направлением линий индукции.
Из приведенной формулы магнитного потока можно вывести определение его единицы – вебер(Вб):
$$1Вб=1Тл×1м^2×cosalpha$$,
то есть, магнитный поток 1 Вебер – это магнитный поток, проходящий через рамку площадью 1 квадратный метр, которая ориентирована перпендикулярно линиям однородного магнитного поля с индукцией 1Тесла.

Для понимания термина «магнитный поток» можно представить аналогию с обычным водяным потоком. Водяной поток, как правило, зависит от напора воды (аналог индукции) и площади сечения трубы (аналог площади рамки), а поскольку вода, в отличие от магнитного поля, всегда заключена внутрь трубы, то водяной поток всегда ориентирован поперек сечения трубы, и значение косинуса в формуле всегда равно единице.

Что мы узнали?
Для описания явления электромагнитной индукции в проводящем контуре необходимо учесть индукцию магнитного поля, «охват» поля контуром и ориентацию контура. Все эти факторы объединяются в понятии «магнитный поток». Изменение магнитного потока приводит к возникновению ЭДС в контуре. Постоянный магнитный поток ЭДС не вызывает.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
3.9
Средняя оценка: 3.9
Всего получено оценок: 124.
А какая ваша оценка?











