Как найти чему равен угол преломления - Сайт, где вы сможете решить свои вопросы

Преломление света.

Закон преломления (частный случай).
Обратимость световых лучей.
Закон преломления (общий случай).
Полное внутреннее отражение.
Разберем задачи ЕГЭ по теме: Преломление света.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: закон преломления света, полное внутреннее отражение.

На границе раздела двух прозрачных сред наряду с отражением света наблюдается его преломление – свет, переходя в другую среду, меняет направление своего распространения.

Преломление светового луча происходит при его наклонном падении на поверхность раздела (правда, не всегда – читайте дальше про полное внутреннее отражение). Если же луч падает перпендикулярно поверхности, то преломления не будет – во второй среде луч сохранит своё направление и также пойдёт перпендикулярно поверхности.

к оглавлению ▴

Закон преломления (частный случай).

Мы начнём с частного случая, когда одна из сред является воздухом. Именно такая ситуация присутствует в подавляющем большинстве задач. Мы обсудим соответствующий частный случай закона преломления, а уж затем дадим самую общую его формулировку.

Предположим, что луч света, идущий в воздухе, наклонно падает на поверхность стекла, воды или какой-либо другой прозрачной среды. При переходе в среду луч преломляется, и его дальнейший ход показан на рис. 1.

Рис. 1. Преломление луча на границе “воздух–среда”

В точке падения проведён перпендикуляр (или, как ещё говорят, нормаль) к поверхности среды. Луч , как и раньше, называется падающим лучом, а угол alpha между падающим лучом и нормалью – углом падения. Луч – это преломлённый луч; угол beta между преломлённым лучом и нормалью к поверхности называется углом преломления.

Всякая прозрачная среда характеризуется величиной , которая называется показателем преломления этой среды. Показатели преломления различных сред можно найти в таблицах. Например, для стекла n=1,6 , а для воды n=1,33 . Вообще, у любой среды ; показатель преломления равен единице только в вакууме. У воздуха , поэтому для воздуха с достаточной точностью можно полагать в задачах n=1 (в оптике воздух не сильно отличается от вакуума).

Закон преломления (переход “воздух–среда”).

1) Падающий луч, преломлённый луч и нормаль к поверхности, проведённая в точке падения, лежат в одной плоскости.
2) Отношение синуса угла падения к синусу угла преломления равно показателю преломления среды:

$frac{displaystyle sinalpha }{displaystyle sinbeta }=n$ . (1)

Поскольку из соотношения (1) следует, что , то есть – угол преломления меньше угла падения. Запоминаем: переходя из воздуха в среду, луч после преломления идёт ближе к нормали.

Показатель преломления непосредственно связан со скоростью распространения света в данной среде. Эта скорость всегда меньше скорости света в вакууме: . И вот оказывается,что

$n=frac{displaystyle c }{displaystyle v }$ . (2)

Почему так получается, мы с вами поймём при изучении волновой оптики. А пока скомбинируем формулы . (1) и (2):

$frac{displaystyle sinalpha }{displaystyle sinbeta }=frac{displaystyle c }{displaystyle v }$ . (3)

Так как показатель преломления воздуха очень близок единице, мы можем считать, что скорость света в воздухе примерно равна скорости света в вакууме . Приняв это во внимание и глядя на формулу . (3), делаем вывод: отношение синуса угла падения к синусу угла преломления равно отношению скорости света в воздухе к скорости света в среде.

к оглавлению ▴

Обратимость световых лучей.

Теперь рассмотрим обратный ход луча: его преломление при переходе из среды в воздух. Здесь нам окажет помощь следующий полезный принцип.

Принцип обратимости световых лучей. Траектория луча не зависит от того, в прямом или обратном направлении распространяется луч. Двигаясь в обратном направлении, луч пойдёт в точности по тому же пути, что и в прямом направлении.

Согласно принципу обратимости, при переходе из среды в воздух луч пойдёт по той же самой траектории, что и при соответствующем переходе из воздуха в среду (рис. 2) Единственное отличие рис. 2 от рис. 1 состоит в том, что направление луча поменялось на противоположное.

Рис. 2. Преломление луча на границе “среда–воздух”

Раз геометрическая картинка не изменилась, той же самой останется и формула (1): отношение синуса угла alpha к синусу угла beta по-прежнему равно показателю преломления среды. Правда, теперь углы поменялись ролями: угол beta стал углом падения, а угол alpha – углом преломления.

В любом случае, как бы ни шёл луч – из воздуха в среду или из среды в воздух – работает следующее простое правило. Берём два угла – угол падения и угол преломления; отношение синуса большего угла к синусу меньшего угла равно показателю преломления среды.

Теперь мы целиком подготовлены для того, чтобы обсудить закон преломления в самом общем случае.

к оглавлению ▴

Закон преломления (общий случай).

Пусть свет переходит из среды 1 с показателем преломления $n_{displaystyle 1}$ в среду 2 с показателем преломления $n_{displaystyle 2}$ . Среда с большим показателем преломления называется оптически более плотной; соответственно, среда с меньшим показателем преломления называется оптически менее плотной.

Переходя из оптически менее плотной среды в оптически более плотную, световой луч после преломления идёт ближе к нормали (рис. 3). В этом случае угол падения больше угла преломления: .

Наоборот, переходя из оптически более плотной среды в оптически менее плотную, луч отклоняется дальше от нормали (рис. 4). Здесь угол падения меньше угла преломления:

Оказывается, оба этих случая охватываются одной формулой – общим законом преломления, справедливым для любых двух прозрачных сред.

Закон преломления.
1) Падающий луч, преломлённый луч и нормаль к поверхности раздела сред, проведённая в точке падения, лежат в одной плоскости.
2) Отношение синуса угла падения к синусу угла преломления равно отношению показателя преломления второй среды к показателю преломления первой среды:

$frac{displaystyle sinalpha }{displaystyle sinbeta }=frac{displaystyle n_{displaystyle 2}}{displaystyle n_{displaystyle 1}}$ . (4)

Нетрудно видеть, что сформулированный ранее закон преломления для перехода “воздух–среда” является частным случаем данного закона. В самом деле, полагая в формуле (4) $n_{displaystyle 1}=1, n_{displaystyle 2}=n$ , мы придём к формуле (1).

Вспомним теперь, что показатель преломления – это отношение скорости света в вакууме к скорости света в данной среде: $n_{displaystyle 1}=c/v_{displaystyle1}, n_{displaystyle 2}=c/v_{displaystyle2}$ . Подставляя это в (4), получим:

$frac{displaystyle sinalpha}{displaystyle sinbeta }=frac{displaystyle v_{displaystyle 1}}{displaystyle v_{displaystyle 2}}$ . (5)

Формула (5) естественным образом обобщает формулу (3). Отношение синуса угла падения к синусу угла преломления равно отношению скорости света в первой среде к скорости света во второй среде.

к оглавлению ▴

Полное внутреннее отражение.

При переходе световых лучей из оптически более плотной среды в оптически менее плотную наблюдается интересное явление – полное внутреннее отражение. Давайте разберёмся, что это такое.

Будем считать для определённости, что свет идёт из воды в воздух. Предположим, что в глубине водоёма находится точечный источник света , испускающий лучи во все стороны. Мы рассмотрим некоторые из этих лучей (рис. 5).

Рис. 5. Полное внутреннее отражение

Луч $SO_{displaystyle 1}$ падает на поверхность воды под наименьшим углом. Этот луч частично преломляется (луч $O_{displaystyle 1} A_{displaystyle 1}$ ) и частично отражается назад в воду (луч $O_{displaystyle 1} B_{displaystyle 1}$ ). Таким образом, часть энергии падающего луча передаётся преломлённому лучу, а оставшаяся часть энергии -отражённому лучу.

Угол падения луча $S O_{displaystyle 2}$ больше. Этот луч также разделяется на два луча – преломлённый и отражённый. Но энергия исходного луча распределяется между ними по-другому: преломлённый луч $O_{displaystyle 2} A_{displaystyle 2}$ будет тусклее, чем луч $O_{displaystyle 1} A_{displaystyle 1}$ (то есть получит меньшую долю энергии), а отражённый луч $O_{displaystyle 2} B_{displaystyle 2}$ – соответственно ярче, чем луч $O_{displaystyle 1} B_{displaystyle 1}$ (он получит большую долю энергии).

По мере увеличения угла падения прослеживается та же закономерность: всё большая доля энергии падающего луча достаётся отражённому лучу, и всё меньшая – преломлённому лучу. Преломлённый луч становится всё тусклее и тусклее, и в какой-то момент исчезает совсем!

Это исчезновение происходит при достижении угла падения $alpha _{0}$ , которому отвечает угол преломления $90^{circ}$ . В данной ситуации преломлённый луч должен был бы пойти параллельно поверхности воды, да идти уже нечему – вся энергия падающего луча целиком досталась отражённому лучу .

При дальнейшем увеличении угла падения преломлённый луч и подавно будет отсутствовать.

Описанное явление и есть полное внутреннее отражение. Вода не выпускает наружу лучи с углами падения, равными или превышающими некоторое значение $alpha _{0}$ – все такие лучи целиком отражаются назад в воду. Угол $alpha _{0}$ называется предельным углом полного отражения.

Величину $alpha _{0}$ легко найти из закона преломления. Имеем:

$frac{displaystyle sinalpha _{0}}{displaystyle sin90^{circ}}=frac{displaystyle 1}{displaystyle n}$ .

Но $sin90^{circ}=1$ , поэтому

$sinalpha _{0}=frac{displaystyle 1}{displaystyle n}$ ,

откуда

$alpha _{0}=arcsinfrac{displaystyle 1}{displaystyle n}$ .

Так, для воды предельный угол полного отражения равен:

$alpha _{0}=arcsinfrac{displaystyle 1}{1,33} approx 48,8^{circ}$ .

Явление полного внутреннего отражения вы легко можете наблюдать дома. Налейте воду в стакан, поднимите его и смотрите на поверхность воды чуть снизу сквозь стенку стакана. Вы увидите серебристый блеск поверхности – вследствие полного внутреннего отражения она ведёт себя подобно зеркалу.

Важнейшим техническим применением полного внутреннего отражения является волоконная оптика. Световые лучи, запущенные внутрь оптоволоконного кабеля (световода) почти параллельно его оси, падают на поверхность под большими углами и целиком, без потери энергии отражаются назад внутрь кабеля. Многократно отражаясь, лучи идут всё дальше и дальше, перенося энергию на значительное расстояние. Волоконно-оптическая связь применяется, например, в сетях кабельного телевидения и высокоскоростного доступа в Интернет.

к оглавлению ▴

Разберем задачи ЕГЭ по теме: Преломление света.

Задача 1. Нижняя грань AC прозрачного клина посеребрена и представляет собой плоское зеркало. Угол при вершине клина $alpha = 30^{circ}$ . Луч света падает из воздуха на клин перпендикулярно грани AB, преломляется и выходит в воздух через ту же грань AB, но уэе под углом преломления $beta = 90^{circ}$ Определите показатель преломления материала клина. Сделайте рисунок, поясняющий ход луча в клине.

Дано:
$alpha = 30^{circ}$
$beta = 90^{circ}$
n-?
Решение. Решение задач по геометрической оптике необходимо начинать с построения чертежа (рисунка), моделирующего условия, описанные в тексте задачи.

Световой луч падает на прозрачный клин перпендикулярно стороне АВ (см.рис.1). В этом случае, световой луч не преломляется на границе раздела воздух-клин, так как угол падения равен 0, соответственно, угол преломления также равен 0. Следовательно, внутри клина световой луч попадает на нижнюю грань АС, которая представляет собой плоское зеркало. Согласно рис.1 величина угла $alpha_1=180^{circ}-(alpha+90^{circ})=90^{circ}-alpha.$

$alpha_1=90^{circ}-30^{circ}=60^{circ}.$

Тогда угол падения луча на плоское зеркало будет равен
$90^{circ}-alpha_1=90^{circ}-60^{circ}=30^{circ}.$

То есть угол падения равен $alpha=30^{circ}$ .
Согласно закону отражения света, угол падения светового луча равен углу отражения. В треугольнике МКО угол КОМ образован суммой двух углов α, поэтому он равен 60°. Тогда угол падения светового луча на грань АВ также будет равен $2alpha=60^{circ}$ (равенство накрест лежащих углов).
На следующем этапе задачи надо применить закон преломления света, так как луч переходит из одной среды в другую.
$frac{sin{2alpha}}{sinbeta}=frac{1}{n}$
При записи этой формулы учтено, что второй средой является воздух с показателем преломления равным 1, а первой средой является материал клина с показателем преломления n, который необходимо определить. Из последней формулы можно выразить и рассчитать n.

$n=frac{sinbeta}{sin2alpha}$

$n=frac{sin90^{circ}}{sin(2cdot 30^{circ})}=frac{sin90^{circ}}{sin60^{circ}}approx 1,15$

Ответ: 1,15

Задача 2. На тонкую собирающую линзу от удалённого источника падает пучок параллельных лучей (см. рисунок). Как изменится положение изображения источника, создаваемого линзой, если между линзой и её фокусом поставить
плоскопараллельную стеклянную пластинку с показателем преломления n (на рисунке положение пластинки отмечено пунктиром)? Ответ поясните, указав, какие физические закономерности Вы использовали. Сделайте рисунок, поясняющий ход лучей до и после установки плоскопараллельной стеклянной пластинки.

Решение. Рассмотрим ход световых лучей от удаленного источника через линзу при отсутствии плоскопараллельной стеклянной пластинки (см.рис.1).

Луч 1-1ʹ проходит через оптический центр линзы и не преломляется. Луч 2-2ʹ идет через фокус и после прохождения через линзу, идет параллельно главной оптической оси. Пересечение этих двух лучей дает действительное изображение удаленного источника, которое расположено в фокальной плоскости линзы. Этот факт также можно доказать, используя формулу тонкой линзы.

$frac{1}{d}+frac{1}{f}=frac{1}{F} (1)$

Так как источник света расположен на расстоянии то $frac{1}{d}rightarrow 0.$

Тогда формула тонкой линзы (1) примет вид $frac{1}{f}=frac{1}{F},$ следовательно, f=F, т.е. изображение формируется в фокальной плоскости линзы.

Рассмотрим ход световых лучей через плоскопараллельную стеклянную пластинку. Для этого необходимо использовать закон преломления света.

Рис.2

Согласно рис.2 угол падения луча на пластину равен α. Закон преломления света на границе раздела воздух-пластинка имеет вид:

$frac{sinalpha}{sinbeta}=frac{n}{1}=n (1).$

Здесь учтено, что показатель преломления воздуха равен 1, а пластинки n.
При переходе светового луча из пластинки в воздух, закон преломления света будет иметь вид:

$frac{sinbeta}{singamma}=frac{1}{n} (2).$

В этом случае первой средой является пластинка с показателем преломления n, а второй средой будет воздух с показателем преломления равным 1.
Из (1) и (2) выразим и .

Так как правые части этих уравнений равны, то

Отсюда вытекает равенство углов . Следовательно, луч, падающий на стеклянную пластину, выходит из нее, оставаясь параллельным входящему лучу. Но при этом выходящий луч немного смещается вверх.

Исходя из этого можно сделать вывод, что изображение удаленного источника после прохождения через плоскопараллельную стеклянную пластину, не изменится. Из удаленного источника выходит бесконечное количество параллельных лучей, которые собираются в фокальной плоскости линзы.

Ответ: не изменится.

Задача 3. Ученик провел опыт по преломлению света, представленный на фотографии. Как изменится при уменьшении угла падения угол преломления светового пучка и скорость света, распространяющегося в стекле? Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшиться
3) не изменится
Запишите в таблицу выбранные цифры для каждой величины. Цифры в ответе могут повторяться.

Угол преломления	Скорость света в стекле

Решение. Для ответа на первый вопрос задачи необходимо применить закон преломления света для границы раздела воздух-стекло.

$frac{sinalpha}{sinbeta}=frac{n}{1}=n.$

Показатель преломления стекла равен n, а воздуха 1.
При уменьшении угла падения α, будет уменьшаться и значение Так как показатель преломления стекла не изменяется, то значение sinbeta так же будет уменьшаться. Поэтому угол преломления уменьшится.

Для ответа на второй вопрос надо учесть, что скорость света в данной среде определяется значением показателя преломления $v_{cp}=frac{c}{n},$ где с – скорость света в вакууме, а n – показатель преломления среды (стекла). Так как эти обе величины не изменяются, то скорость света в стекле так же не изменяется.

Ответ: 23.

Задача 4. Чему равен синус предельного угла полного внутреннего отражения при переходе света из вещества с n_1=1,5 в вещество с n_2=1,2 ?

Решение.

Явление полного внутреннего отражения наблюдается при переходе светового луча из оптически более плотной среды в оптически менее плотную (см.рис.1). Источник света S должен находиться в среде с большим показателем преломления.

Для нахождения синуса угла полного внутреннего отражения необходимо воспользоваться законом преломления света.

$frac{sinalpha_{np}}{sinbeta}=frac{n_2}{n_1} (1)$

При полном внутреннем отражении преломленный луч скользит по границе раздела двух сред и угол преломления $beta=90^{circ}$ . С учетом того, что $sin90^{circ}=1$ уравнение (1) примет вид:

$sinalpha_{np}=frac{1,2}{1,5}=0,8$

$sinalpha_{np}=0,8$

Ответ: 0,8.

Если вам нравятся наши материалы – записывайтесь на курсы подготовки к ЕГЭ по физике онлайн

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Преломление света.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Рассмотрим падение плоской волны на границу, разделяющую две прозрачные однородные диэлектрические среды с показателями преломления и . Будем считать, что граница представляет собой плоскость (так как в пределах бесконечно малой области любую поверхность можно считать плоской). Будем также считать, что сама граница раздела свет не поглощает.

После прохождения границы раздела двух сред падающая плоская волна (луч ) разделяется на две волны: проходящую во вторую среду (луч ) и отраженную (луч ) (рис.3.1.1).

Рис.3.1.1. Преломление и отражение света на границе двух сред. На рис.3.1.1 N – вектор нормали к поверхности в точке падения единичной длины . Поместим начало координат в точку падения. Определим следующие величины:

Угол падения – это угол между лучом , падающим на преломляющую или отражающую поверхность, и нормалью к поверхности в точке падения.

Угол преломления – это угол между преломленным лучом и нормалью к поверхности в точке преломления.

Угол отражения – это угол между отраженным лучом и нормалью к поверхности в точке отражения.

3.1.1. Закон преломления

После прохождения светом границы раздела двух сред необходимо определить направление распространения преломленной волны и отраженной волны , ираспределение энергии между отраженной и преломленной волной.

None уравнение падающей плоской волны.

(3.1.1) уравнение преломленной плоской волны

(3.1.2) уравнение отраженной плоской волны

$O_{displaystyle 2} B_{displaystyle 2}$

(3.1.3) где , , – оптические векторы падающей, отраженной и преломленной волн, – волновое число, – радиус-вектор произвольной точки. Здесь мы используем соотношения скалярной теории, поскольку закон преломления одинаков для векторных и скалярных волн.

Из уравнений падающей и преломленной плоской волны следует, что на границе раздела двух сред у падающей и преломленной волн амплитуды могут быть различны, но должны совпадать значения эйконалов (этого требует условие физической реализуемости, так как иначе волна будет иметь разрыв на границе раздела):

(3.1.4) Равенство (3.1.4) соблюдается на границе раздела, то есть для всех , перпендикулярных вектору нормали. Таким образом, выражение (3.1.4) можно записать в виде: при или: при То есть , если . Выполнение этих условий возможно тогда и только тогда, когда . Таким образом, можно вывести формулировки закона преломления в векторной форме:

(3.1.5) где – некоторый скаляр, или: (3.1.6) или:

Так как длина оптического вектора равна показателю преломления среды (, ), то из выражения (3.1.7) и определения векторного произведения можно вывести классический закон преломления Снеллиуса (Snell law).

Закон преломления (refraction law):

качественная часть закона:
падающий луч, преломленный луч и нормаль к поверхности раздела двух сред в точке падения лежат в одной плоскости.

количественная часть закона:
произведение показателя преломления на синус угла между лучом и нормалью сохраняет свое значение при переходе в следующую среду:

Чтобы найти скаляр , домножим скалярно выражение (3.1.5) на вектор нормали :

, следовательно

где.

Величина имеет большое значение в математическом аппарате расчета лучей (ray tracing) на компьютере.

[custom_ads_shortcode1]

3.1.2. Закон отражения

Закон отражения можно вывести в векторной форме аналогично закону преломления, подставив вместо оптического вектора преломленного луча оптический вектор отраженного луча (рис.3.1.2).

Рис.3.1.2. Отражение света на границе двух сред. Закон отражения (reflection law):

Закон отражения можно вывести как частный случай закона преломления при (это просто прием для удобства расчета лучей в геометрической оптике, в отрицательном значении показателя преломления нет никакого физического смысла). Тогда случай отражения можно не выделять, а включать его в закон преломления при условии, что (рис.3.1.3).

Рис.3.1.3. Отражение света на границе двух сред.

Величина в таком случае будет равна: (3.1.12)

[custom_ads_shortcode2]

3.1.3. Полное внутреннее отражение

Если угол падения невелик, то часть поля отражается, а часть преломляется. Однако, при переходе из более плотной среды в менее плотную , при некотором угле падения синус угла преломления по закону преломления должен быть больше единицы, что невозможно. Поэтому в таком случае преломления не происходит, а происходит полное внутреннее отражение (ПВО, entire inner reflection) (рис.3.1.4):

Рис.3.1.4. Полное внутреннее отражение. Условие полного внутреннего отражения: (3.1.13) Явление ПВО широко используется в оптической технике благодаря тому, что при ПВО отражается 100% энергии, то есть потерь энергии нет. Таким образом, ПВО позволяет решить задачу полного отражения света: в зависимости от угла падения луч или почти полностью проходит, или почти полностью отражается. Нарушенное полное внутреннее отражение (НПВО), которое возникает при оптическом контакте границы раздела со средой, используется в спектроскопии. Решение задач на определение законы преломления и отражения рассматривается в практическом занятии “Правило знаков в оптике. Основные законы распространения света”.

Если пустить световой луч из воздуха в воду, то на границе двух сред он немного изменит свое направление и в воде пойдет под иным углом. Угол между перпендикулярной прямой к границе двух сред и лучом в воде уменьшится. Это угол преломления (γ). Угол между перпендикулярной прямой и падающим лучом — это угол падения (α). Изменение направления луча связано с разной плотностью сред. Вода по сравнению с воздухом более плотная среда, свет в ней распространяется медленнее. Так как свет — это волна, то это приводит к изменению его направления.

$O_{displaystyle 1} B_{displaystyle 1}$

Если световой луч выходит из воды в воздух, то он снова меняет свое направление. В данном случае угол между лучом и перпендикуляром к границе сред увеличится. Если луч изначально шел из воздуха в воду, а потом вышел из воды в воздух, и обе границы сред параллельны друг другу, то угол луча станет таким, каким был до входа в воду. Луч выйдет из воды параллельно тому, как он вошел в нее, но будет лежать на другой прямой из-за того, что в воде он менял свое направление. Таким образом, при переходе светового луча из менее плотной среды в более плотную угол падения больше угла преломления (α > γ). При его переходе из более плотной среды в менее плотную угол падения меньше угла преломления (α < γ).

Если луч падает перпендикулярно к границе раздела сред, то угол падения будет равен углу преломления (α = γ = 0°). То есть, можно сказать, преломления не произойдет. Углы падения и преломления всегда лежат в одной плоскости.

Кроме пары сред воздух-вода, также можно привести примеры пар других прозрачных сред, в которых луч преломляется из-за их разной плотности. Например, вакуум-воздух, воздух-стекло и др.

$SO_{displaystyle 1}$

Понятно, что с увеличением угла падения, увеличивается угол преломления (даже если он меньше угла падения). Однако отношение углов падения и преломления не сохраняется. То есть если угол падения был 20° и его увеличить в 2 раза, то это не значит, что угол преломления, который допустим был 15° также увеличится в 2 раза.

Однако для определенной пары двух сред всегда сохраняется отношение синусов углов падения и преломления. То есть sin α / sin γ = const. Это отношение называется показателем преломления для двух сред и обозначается буквой n. Если в качестве угла α всегда брать угол движения луча в менее плотной среде, то чем больше n тем сильнее преломление для данной пары сред.

Одним из важных законов распространения световой волны в прозрачных веществах является закон преломления, сформулированный в начале XVII века голландцем Снеллом. Параметрами, фигурирующими в математической формулировке явления преломления, являются показатели и углы преломления. В данной статье рассмотрено, как ведут себя световые лучи при переходе через поверхность разных сред.

[custom_ads_shortcode3]

Что собой представляет явление преломления?

Главное свойство любой электромагнитной волны – это ее прямолинейное движение в гомогенном (однородном) пространстве. При возникновении любой неоднородности волна испытывает в большей или меньшей мере отклонение от прямолинейной траектории. Этой неоднородностью может быть наличие сильного гравитационного или электромагнитного поля в определенной области пространства. В данной статье эти случаи не будут рассмотрены, а будет уделено внимание именно неоднородностям, связанным с веществом.

Эффект преломления луча света в его классической формулировке означает резкое изменение одного прямолинейного направления движения этого луча на другое при переходе через поверхность, разграничивающую две разные прозрачные среды.

Следующие примеры удовлетворяют данному выше определению:

переход луча из воздуха в воду;
из стекла в воду;
из воды в алмаз и т. д.

Единственной причиной, обуславливающей описанный эффект, является различие скоростей движения электромагнитных волн в двух разных средах. Если такого различия не будет, или оно будет несущественным, то при переходе через поверхность раздела луч сохранит свое первоначальное направление распространения.

Разные прозрачные среды имеют различную физическую плотность, химический состав, температуру. Все эти факторы сказываются на скорости света. Например, явление миража – это прямое следствие преломления света в нагретых до разных температур слоях воздуха вблизи земной поверхности.

[custom_ads_shortcode1]

Главные законы преломления

Этих законов два, причем их может проверить каждый, если вооружится транспортиром, лазерной указкой и толстым куском стекла.

Перед тем как сформулировать их, стоит ввести некоторые обозначения. Показатель преломления записывают символом n_i, где i – идентифицирует соответствующую среду. Угол падения обозначают символом θ (тета один), угол преломления- θ (тета два). Оба угла отсчитываются относительно не плоскости раздела, а нормали к ней.

Закон № 1. Нормаль и два луча (θ и θ) лежат в одной плоскости. Этот закон полностью аналогичен 1-му закону для отражения.

Закон № 2. Для явления преломления всегда справедливо равенство:

n* sin (θ) = n * sin (θ).

В приведенной форме это соотношение запомнить проще всего. В других формах оно выглядит менее удобно. Ниже приводятся еще два варианта записи закона №2:

$O_{displaystyle 1} A_{displaystyle 1}$

sin (θ) / sin (θ) = n/ n;

sin (θ) / sin (θ) = v/ v.

Где v_i – скорость волны в i-той среде. Вторая формула легко получается из первой прямой подстановкой выражения для n_i:

n_i = c / v_i.

Оба приведенных закона являются результатом многочисленных опытов и обобщений. Однако их можно математически получить, пользуясь так называемым принципом наименьшего времени или принципом Ферма. В свою очередь, принцип Ферма выводится из принципа Гюйгенса – Френеля о вторичных источниках волн.

[custom_ads_shortcode2]

Особенности закона № 2

n* sin (θ) = n* sin (θ).

Видно, что чем больше показатель n (плотная оптическая среда, в которой скорость света сильно уменьшается), тем ближе будет θ к нормали (функция sin (θ) монотонно возрастает на отрезке [0^o, 90^o]).

Показатели преломления и скорости движения электромагнитных волн в средах – это табличные величины, измеренные экспериментально. Например, для воздуха n составляет 1,00029, для воды – 1,33, для кварца – 1,46, а для стекла – около 1,52. Сильно свет замедляет свое движение в алмазе (почти в 2,5 раза), его показатель преломления равен 2,42.

Приведенные цифры говорят, что любой переход луча из отмеченных сред в воздух будет сопровождаться увеличением угла (θ>θ). При изменении направления луча справедлив обратный вывод.

Показатель преломления зависит от частоты волны. Указанные выше цифры для разных сред соответствуют длине волны 589 нм в вакууме (желтый цвет). Для синего света эти показатели будут несколько больше, а для красного – меньше. Стоит отметить, что угол падения равен углу преломления луча только в одном единственном случае, когда показатели n1 и n2 одинаковые.

Далее рассмотрены два разных случая применения этого закона на примере сред: стекло, воздух и вода.

[custom_ads_shortcode3]

Луч переходит из воздуха в стекло или воду

Стоит рассмотреть два случая для каждой среды. Можно взять для примера углы падения 15^o и 55^o на границу стекла и воды с воздухом. Угол преломления в воде или в стекле можно рассчитать по формуле:

θ = arcsin (n/ n* sin (θ)).

Первой средой в данном случае является воздух, то есть n = 1,00029.

Подставляя в выражение выше известные углы падения, получится:

$frac{displaystyle sinalpha _{0}}{displaystyle sin90^{circ}}=frac{displaystyle 1}{displaystyle n}$

(n = 1,33): θ = 11,22^o (θ= 15^o) и θ = 38,03^o (θ= 55^o);

(n = 1,52): θ = 9,81^o (θ= 15^o) и θ = 32,62^o (θ= 55^o).

Полученные данные позволяют сделать два важных вывода:

n=1

Поскольку угол преломления из воздуха в стекло меньше, чем для воды, то стекло изменяет направление движения лучей несколько сильнее.
Чем больше угол падения, тем сильнее от первоначального направления отклоняется луч.

[custom_ads_shortcode1]

Свет движется из воды или стекла в воздух

Любопытно рассчитать, чему равен угол преломления для такого обратного случая. Расчетная формула остается той же самой, что и в предыдущем пункте, только теперь показатель n = 1,00029, то есть, соответствует воздуху. Получится

при движении луча из воды:

(n = 1,33): θ = 20,13^o (θ= 15^o) и θ = не существует (θ = 55^o);

при движении луча из стекла:

(n = 1,52): θ = 23,16^o (θ= 15^o) и θ = не существует (θ = 55^o).

Для угла θ= 55^o не получается определить соответствующий θ. Связано это с тем, что он оказался больше 90^o. Эта ситуация называется полным отражением внутри оптически плотной среды.

Этот эффект характеризуется критическими углами падения. Рассчитать их можно, приравняв в законе № 2 sin (θ) единице:

θ_1c = arcsin (n / n).

Подставляя в это выражение показатели для стекла и воды, получится:

(n = 1,33): θ_1c = 48,77^o;

(n = 1,52): θ_1c = 41,15^o.

Любой угол падения, который будет больше полученных значений для соответствующих прозрачных сред, приведет к эффекту полного отражения от поверхности раздела, то есть преломленного луча не будет существовать.

Преломление света – это изменение направления луча на границе двух сред разной плотности.

Пояснение: луч света, упав в воду, меняет свое направление на границе двух сред (то есть на поверхности воды). Луч буквально преломляется. Это явление и называют преломлением света. Оно происходит из-за того, что у воды и воздуха разные плотности. Вода плотнее воздуха, и у луча света, упавшего на ее поверхность, замедляется скорость. Таким образом, вода – оптически более плотная среда.

None Угол преломления (γ) – это угол, образуемый преломленным лучом и перпендикуляром к точке падения луча на поверхности раздела двух сред.

Пояснение:

Луч упал на поверхность воды в какой-то определенной точке и преломился (см.рисунок). Проведем от этой точки перпендикуляр в ту же сторону, в какую «ушел» преломленный луч – в нашем случае перпендикуляр направлен в сторону дна водоема. Угол, образуемый этим перпендикуляром и преломленным лучом, и называют углом преломления.

Если свет идет из оптически менее плотной среды в оптически более плотную среду, то угол преломления всегда меньше угла падения.

None Для любых двух сред с различной оптической плотностью верна формула:

sin α = n
sin γ где n – постоянная величина, не зависящая от угла падения.

None Возьмем три луча, падающих в воду.

None При замере окажется, что углы преломления этих лучей составляют соответственно 23°, 33° и 42°.

Если составить соотношение углов падения и углов преломления, то получим одно и то же число:

sin 30° sin 45° sin 60°
≅ 1,3
sin 23° sin 33° sin 42° Таким образом, если мы разделим угол падения луча в воду и угол его преломления, то получим 1,3. Это постоянная величина (n), которую и находят с помощью приведенной выше формулы.

Падающий луч, преломленный луч и перпендикуляр, проведенный от точки падения луча, лежат в одной плоскости.

Источники:

aco.ifmo.ru
scienceland.info
fb.ru
test1.czl23.ru

Источник

Refraction is an important term used in the Ray Optics branch of Physics. Refraction of light is defined as the change in direction or the bending of a wave passing from one medium to another due to the change in speed of the wave. Some natural phenomena occurring in nature where refraction of light takes place are the twinkling of stars, the formation of mirages and Rainbows, Optical illusions, and many more. The major cause of refraction to occur is the change in the speed of waves in different mediums, which is different due to the difference between the densities of the mediums. e.g. the speed of light in a vacuum is maximum. Snell’s Law provides a quantitative description of the amount of bending of a wave, that depends on the refractive index of the two mediums. Let’s learn more about refraction like the Laws of Refractions, Causes of Refraction, Types of Refraction, Examples, and Applications of Refractions in the article below.

What is Refraction of Light?

The bending of a light wave when it passes from one medium to another due to the change in the speed of the light traveling the two different media is called the Refraction of light.

This phenomenon also occurs with sound, water, and other waves. Because of this bending of waves that are responsible for the refraction of light, we have lenses, magnifying glasses, prisms, and rainbows. Due to this phenomenon, our eyes would not be able to focus, without the refraction of light.

As shown in the above figure, light travels from Medium 1 to Medium 2. Please note that these mediums can be different materials or substances with different densities. So when an incident ray from medium 1 travels to another medium 2, the refracted ray bends either towards the normal or away from the normal (depending upon the densities of the mediums).

Here are the definitions of important terms used to study Refraction:

Normal – The point of the surface at which an optical phenomenon occurs is called the normal. In simple words, it is termed the point of incidence. It is shown by a dotted line drawn perpendicular to the surface of the refracting material, in a ray diagram.
Incident Ray – The light rays that strike the refracting surface, at the separation of two media are called the Incident Ray.
Refracted Ray – The light rays that bend after passing into another medium are called the Refracted Ray.
Angle of Incidence – This is the angle between the incident ray and the normal. It is represented by ∠i and it is also called an Incident angle.
Angle of Refraction – This is the angle between refracted ray and the normal. It is represented by ∠r and it is also called a Refracted angle.

Laws of Refraction of Light

The refraction of light traveling through different mediums follows some laws. There are two laws of refraction as stated below which at the sight of refraction, the light follows, and we see the refracted image of the object.

The reflected, incident, and the normal at the point of incidence all will tend to lie in the same plane.
Secondly, the ratio of the sine of the angle of the incidence and refraction is constant which is termed Snell’s law.

sin i / sin r = Constant (n)

where i is the angle of incidence, r is the angle of refraction, the constant value depends on the refractive indexes of the two mediums.

What is the Refractive Index?

The Refractive index also called the index of refraction enables us to know how fast light travels through the material medium.

Refractive Index is a dimensionless quantity. For a given material or medium, the refractive index is considered the ratio between the speed of light in a vacuum (c) to the speed of light in the medium (v) on which it goes. The Refractive index for a medium is represented by small n, and it is given by the following formula:

n = c / v

where

c is the speed of the light in a vacuum, and

v is the speed of light in the medium.

The given velocities of light in different media can give the refractive index by the following also where the first medium is not vacuum:

n₂₁ = v₁ / v₂

where n₂₁is the refractive index of 2 with respect to 1.

Based on the given refractive index of the material or medium, the light ray either changes its direction or bends at the junction which separates the two given media. If the light ray travels from a certain medium to another of a slightly higher refractive index, it bends towards the normal in that case when traveling from rarer to a denser medium, or else it bends away from the normal when traveling from denser to rarer medium.

Snell’s Law

Snell’s law provides the degree or extent of refraction that occurs through a relationship between the incident angle, refracted angles, and the refractive indices of a given pair of media.

According to Snell’s law, the ratio of the sine of the incident angle to the sine of the refracted angle is a constant, for any light of a given color or for any given pair of media. The constant value is called the refractive index of the second medium with respect to the first.

Snell’s Law is given by the relation,

or

where,

i and r are the angle of incidence and refraction,

n is the refractive index and n₁ and n₂ are the refractive indices of medium 1 and 2, and

v₁ and v₂ are the speed of light in medium 1 and 2 respectively.

Causes of Refraction of Light

As it is known that when light travels in different mediums its speed varies. e.g. light passes through the air than in a glass. Hence, it can be said that, due to the change in the speed of light in different mediums that the light rays are refracted.

To understand the causes of refraction of light in much depth let’s understand What are rarer and denser mediums? and Types of Refractions as:

What are Rarer and Denser mediums?

Rarer medium (or Optically Rarer medium) is a medium in which the speed of light is more. For example, Air is optically rarer medium as compared to glass and water.

Denser medium (or Optically Denser medium) is a medium in which the speed of light is less. For example, Glass is optically denser medium as compared to air.

Types of Refraction

The refraction of light occurs in different ways depending on the medium through which the light travels.

Refraction from denser to rarer medium – When light rays pass through rarer to a denser medium, the light rays bend towards the normal. Due to this the angle of refraction is smaller than the angle of incidence. e.g. In the case when light rays pass from air to water or from air to glass, it bends towards normal. It is because of the reason that the speed of light rays reduces while passing from air to glass or water.
Refraction from rarer to denser medium – When light rays pass from denser to rarer medium, the light rays bend away from the normal. Due to this the angle of refraction becomes more than the angle of incidence. e.g. In case when light rays pass from water to air or glass to air, light rays bend away from the normal. The speed of light rays becomes greater while passing from glass or water to air.

Characteristics of Refraction

Some of the important characteristics of Refraction are:

The frequency of light does not change when it travels from one medium to another, but the velocity and wavelength of light changes.

A ray of light bends when it travels from one optical medium to another with a variable refractive index. For a specific pair of media, the ratio of the sine of the angle of incidence to the sine of the angle of refraction is constant.

The relationship between a medium’s refractive index and the speed of light in that medium is as follows:

where,

i and r are the angle of incidence and refraction,

n is the refractive index and n₁ and n₂ are the refractive indices of medium 1 and 2, and

v₁ and v₂ are the speed of light in medium 1 and 2 respectively.

Effects of Refraction of Light

When anything interrupts the light waves, it causes refraction of the light. Light also moves mostly in the form of waves, much like most other materials.

As shown below, the pencil seems deformed in the water because light cannot travel through the water as rapidly as it can through the air. The pencil has a tiny magnification effect due to the light refraction, which makes the angle appear larger than it actually is and makes the pencil appear crooked.

Examples of Refraction of Light

The stars twinkle in the night sky due to the refraction of their light.
Looming and Mirage formation, both occur due to the optical illusions caused by the refraction of light.
The formation of rainbows in the sky and VIBGYOR, when white light passes through the prism are also major examples of refraction.
A swimming pool always seems or looks much shallower than it really is because of the light that comes from the bottom of the pool bends at the surfaces due to the refraction of light.

Applications of Refraction of Light

Refraction has many wide and common applications in optics and also in technology. A few of them are given below:

A lens uses the refraction phenomenon to form an image of an object or body for various purposes, such as magnification.
Spectacles that are worn by people with defective vision use the principle of refraction.
Refraction is used in peepholes of the house doors for safety, in cameras, inside movie projectors, and also in telescopes.

Solved Examples on Refraction of Light

Example 1: What is the constant value if the angle of incidence is 22° and the angle of refraction is given to be 15°?

Solution:

As we know,

sin i / sin r = constant

Given sin i = sin 22° and sin r = sin 22°

Putting the values of angles from log table we get

sin 22° / sin 15° = 1.44

Hence, the value of constant or refractive index is 1.44.

Example 2: What is the constant value if the angle of incidence is 30° and the angle of refraction is given to be 46°?

Solution:

Since, the

sin i / sin r = constant

Given sin i= sin 30° and sin r= sin 46°

Putting the values of angles from log table we get

sin 30° / sin 46° = 1.44

Hence, the constant is 1.44.

Example 3: What is the value of the sine of the angle of incidence if the angle of refraction is given to be sin 35°? Given the value of refractive index 1.33.

Solution:

As we know,

{sin i}/{sin r} =constant

Given constant= 1.33 and sin r = sin 35° = 0.57

Putting the values of angles from log table we get

sin i / sin 35° = 1.33

sin i = 1.33 × 0.57

= 0.75

Example 4: Calculate the speed of light in diamond with respect to air. Take the absolute refractive index of glass from the table.

Solution:

As we know we can calculate refractive index by the following formula,

n = c/v

where refractive index of diamond n= 2.42, c = 3 × 10⁸ m/s

Hence, the velocity or speed of light in glass is v_d = 1.24 × 10⁸ m/s

FAQs based on Refraction of light

Question 1: Define the term Refraction.

Answer:

The change that occurs in the direction of a wave when light passes from one medium to the other is known as refraction of light.

Question 2: When is the refraction of light not possible?

Answer:

When the light is incident perpendicular to the boundary or surface, refraction of light is not possible.

Question 3: What is the difference between reflection and refraction in light?

Answer:

The bouncing back of light when it strikes a smooth surface is called Reflection. While the bending of a light ray when it travels from one medium to other is called refraction of light.

Question 4: Give an example of the Refraction of light.

Answer:

There are many examples of refraction of light observed in our daily life like the Twinkling of stars. The Twinkling of stars is because of the atmospheric refraction occurs by the light from the star undergoing a gradual change in the medium.

Источник

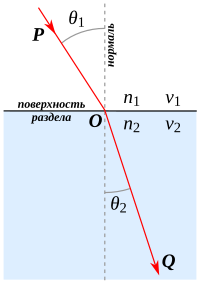
Зако́н Сне́ллиуса (также Снелля или Снелла) описывает преломление света на границе двух прозрачных сред. Также применим и для описания преломления волн другой природы, например, звуковых. Теоретическое объяснение закона Снеллиуса см. в статье Преломление.

Закон был открыт в 1621 году голландским математиком Виллебрордом Снеллиусом^[1]. Несколько позднее опубликован (и, вероятно, независимо переоткрыт) Рене Декартом.

Формулировка[править | править код]

Угол падения света на поверхность связан с углом преломления соотношением:

${displaystyle n_{1}sin theta _{1}=n_{2}sin theta _{2},}$

где $n_{1}$

— показатель преломления среды, из которой свет падает на границу раздела;

$theta _{1}$

— угол падения света — угол между падающим на поверхность лучом и нормалью к поверхности;

$n_{2}$

— показатель преломления среды, в которую свет попадает, пройдя границу раздела;

$theta _{2}$

— угол преломления света — угол между прошедшим через поверхность лучом и нормалью к поверхности.

Вывод закона

Пусть vec{k} лежит в плоскости чертежа. Пусть ось направлена горизонтально, ось — вертикально. Из соображений симметрии следует, что vec{k'} и (для падающей, отраженной и преломленной волны, соответственно) должны лежать в одной плоскости.

Выделим из падающего луча плоскополяризованную составляющую, у которой угол между и плоскостью произволен. Тогда если выбрать начальную фазу равной нулю, то:

${displaystyle E=E_{m}e^{i(omega t-{vec {k}}{vec {r}})}=E_{m}e^{i(omega t-k_{x}x-k_{y}y)};}$

${displaystyle E'=E'_{m}e^{i(omega 't-{vec {k'}}{vec {r}})}=E'_{m}e^{i(omega 't-k'_{x}x-k'_{y}y+alpha ')};}$

${displaystyle E''=E''_{m}e^{i(omega ''t-{vec {k''}}{vec {r}})}=E''_{m}e^{i(omega ''t-k''_{x}x-k''_{y}y+alpha '')}.}$

Результирующее поле в первой и второй среде равны соответственно:

${displaystyle E_{1}=E+E'=E_{m}e^{i(omega t-k_{x}x-k_{y}y)}+E'_{m}e^{i(omega 't-k'_{x}x-k'_{y}y+alpha ')};}$

${displaystyle E_{2}=E''=E''_{m}e^{i(omega ''t-k''_{x}x-k''_{y}y+alpha '')}.}$

Очевидно, что тангенциальные составляющие E_1 и E_2 должны быть равны на границе раздела то есть при

Тогда:

${displaystyle E_{m}e^{i(omega t-k_{x}x)}+E'_{m}e^{i(omega 't-k'_{x}x+alpha ')}=E''_{m}e^{i(omega ''t-k''_{x}x+alpha '')}.}$

Для того, чтобы последнее уравнение выполнялось для всех необходимо, чтобы , а для того, чтобы оно выполнялось при всех необходимо, чтобы:

${displaystyle k_{x}=k'_{x}=k''_{x}Leftrightarrow ksin {alpha }=k'sin {alpha '}=k''sin {alpha ''}Leftrightarrow {cfrac {omega }{v_{1}}}sin {alpha }={cfrac {omega }{v_{1}}}sin {alpha '}={cfrac {omega }{v_{2}}}sin {alpha ''},}$

где $v_{1}$

и $v_{2}$

— скорости волны в первой и второй среде соответственно.

Отсюда следует, что ${displaystyle {cfrac {sin {alpha }}{sin {alpha ''}}}={cfrac {v_{1}}{v_{2}}}=n_{12}blacksquare .}$

Область применимости закона[править | править код]

Закон Снеллиуса хорошо определён для случая «геометрической оптики», то есть в случае, когда длина волны достаточно мала по сравнению с размерами преломляющей поверхности, вообще же говоря, работает в рамках приближённого описания, каковым и является геометрическая оптика.

Если ${displaystyle n_{1}sin theta _{1}>n_{2},}$ имеет место полное внутреннее отражение (преломлённый луч отсутствует, падающий луч полностью отражается от границы раздела сред).

Следует заметить, что в случае анизотропных сред (например, кристаллов с низкой симметрией или механически деформированных твердых тел) преломление подчиняется несколько более сложному закону. При этом возможна зависимость направления преломленного луча не только от направления падающего, но и от его поляризации (см. двойное лучепреломление).

Закон Снеллиуса не описывает соотношение интенсивностей и поляризаций падающего, преломленного и отраженного лучей, рассматриваемые в более детальных формулах Френеля.

Исторический очерк[править | править код]

Первым закон преломления света, то есть зависимость угла преломления от угла падения, попытался экспериментально определить знаменитый античный астроном Клавдий Птолемей в пятой книге своего трактата «Оптика»^[en]. Птолемей измерил, как меняется угол преломления в зависимости от угла падения при изменении последнего от ${displaystyle 10^{circ }}$ до ${displaystyle 80^{circ },}$ и составил таблицы для трёх вариантов смены среды: воздух-вода, воздух-стекло и вода-стекло. Например, для случая воздух-вода таблица Птолемея следующая (для сравнения приведены также современные данные и величина ошибки)^[2]^[3]:

Углы преломления по Птолемею и по современным данным (воздух-вода)

Угол падения, градусов	10°	20°	30°	40°	50°	60°	70°	80°
Данные Птолемея	8° 0′	15° 30′	22° 30′	29° 0′	35° 0′	40° 30′	45° 30′	50° 0′
Современные данные	7° 29′	14° 52′	22° 01′	28° 49′	35° 04′	40° 30′	44° 48′	47° 36′
Величина ошибки	+31′	+38′	+29′	+11′	−4′	0′	+42′	+144′

Историки пришли к выводу, что реально Птолемей измерял отклонение луча только в районе 60° и близких к нему углов, потому что во всех трёх таблицах для этого значения ошибка равна нулю, а для других углов выполнил линейную аппроксимацию с подобранными им коэффициентами. Однако на деле зависимость угла преломления от угла падения нелинейна, поэтому у Птолемея получились большие ошибки^[2]^[4].

Арабский физик и астроном XI века Ибн аль-Хайсам в своей «Книге оптики^[en] (1021 год) также рассуждает на эту тему и приводит свои таблицы, близкие к птолемеевским, однако не делает попыток выразить искомый закон математически^[3].

В 1990 году арабский историк науки Рошди Рашед^[en], специализирующийся на поиске арабского вклада в мировую науку, опубликовал статью, в которой сообщил, что он нашёл два фрагмента арабской рукописи малоизвестного учёного X века ибн Саля, одного из учителей Ибн аль-Хайсама. Рашед также сообщил, что он сумел реконструировать текст, из которого следует, что ибн Саль открыл и правильно сформулировал закон Снеллиуса. Независимые подтверждения для утверждений Рашеда пока отсутствуют. Требуется также объяснить, почему никто из последователей ибн Саля, включая его ученика Ибн аль-Хайсама, не упоминает об этом фундаментальном достижении, и почему сам ибн Саль не сообщает, какими экспериментами он доказал своё открытие^[5]^[3].

В Европе первая формулировка закона преломления обнаружена в неопубликованной рукописи английского математика Томаса Хэрриота (1602 год). Немецкий астроном Иоганн Кеплер, занимавшийся проблемой выбора наилучшей формы зажигательных линз, просил Хэрриота сообщить подробности открытого тем закона, но Хэрриот ограничился отправкой уточнённых таблиц, сославшись на то, что плохое здоровье не позволяет ему выразить закон в форме, подходящей для публикации^[6].

Ещё одно оставшееся неопубликованным открытие этого закона произошло в 1621 году, когда нидерландский математик Виллеброрд Снелл (Снеллиус) записал закон преломления в форме, равносильной современной: «в одних и тех же средах отношение косекансов углов падения и преломления остаётся постоянным». Скоропостижная смерть в 1626 году помешала Снеллу обнародовать своё открытие, однако слухи о нём разошлись, а набросок статьи Снелла сохранился и находится в библиотеке Амстердамского университета^[7].

Позже «закон Снеллиуса» был независимо открыт и опубликован Рене Декартом в трактате «Рассуждение о методе» (приложение «Диоптрика», 1637). Приоритет Снелла установил Христиан Гюйгенс в 1703 году (в трактате «Диоптрика»), спустя 77 лет после смерти Снелла, когда этот закон уже был общеизвестен; Гюйгенс также обосновал (в труде «Трактат о свете^[en]») вывод закона Снеллиуса из волновой теории света и принципа Гюйгенса — Френеля. Недоброжелатели обвинили Декарта в плагиате, подозревая, что во время одного из своих визитов в Лейден Декарт услышал об открытии Снелла и смог ознакомиться с его рукописями^[8]. Однако никаких доказательств плагиата нет, а самостоятельный путь Декарта к этому открытию подробно изучен историками^[9]^[10].

Принцип Ферма[править | править код]

Луч света попадает из точки A в точку B за минимальное время.

Известный принцип^[11] о движении светового луча по пути между двумя точками, который требует наименьшего времени можно использовать для доказательства закона преломления. Пусть скорость света в двух средах составляет $v_{1}$ и $v_{2}$ , тогда время движения между точками А и В зависит от выбора точки P на границе между средами:

${displaystyle T={frac {sqrt {a^{2}+x^{2}}}{v_{1}}}+{frac {sqrt {b^{2}+(d-x)^{2}}}{v_{2}}},.}$

Эта функция будет иметь минимум когда её производная равна нулю^[12]:

${displaystyle {frac {dT}{dx}}={frac {x}{v_{1}{sqrt {a^{2}+x^{2}}}}}+{frac {-(d-x)}{v_{2}{sqrt {b^{2}+(d-x)^{2}}}}}=0,.}$

Здесь синусы углов можно выразить через треугольники:

${displaystyle {frac {x}{sqrt {a^{2}+x^{2}}}}=sin alpha ,,qquad {frac {d-x}{sqrt {b^{2}+(d-x)^{2}}}}=sin beta }$

Производная приводится к виду

${displaystyle {frac {sin alpha }{v_{1}}}-{frac {sin beta }{v_{2}}}=0,,}$

из чего следует, что

${displaystyle {frac {sin alpha }{sin beta }}={frac {v_{1}}{v_{2}}},.}$

Это выражение представляет собой закон Снеллиуса^[13].

Векторная формула[править | править код]

Пусть ${displaystyle scriptstyle {vec {v}}_{1}}$ и ${displaystyle scriptstyle {vec {v}}_{2}}$ лучевые векторы падающего и преломленного световых лучей, то есть векторы, указывающие направления лучей и имеющие длины ${displaystyle scriptstyle |{vec {v}}_{1}|=n_{1}}$ и ${displaystyle scriptstyle |{vec {v}}_{2}|=n_{2},}$ а единичный нормальный вектор к преломляющей поверхности в точке преломления. Тогда:

${displaystyle {vec {v}}_{2}={vec {v}}_{1}+left({sqrt {{frac {n_{2}^{2}-n_{1}^{2}}{({vec {v}}_{1}cdot {vec {n}})^{2}}}+1}}-1right)({vec {v}}_{1}cdot {vec {n}}){vec {n}}.}$

Примечания[править | править код]

↑ Снеллиус — латинизированная форма оригинальной фамилии Снелл
↑ ¹ ² Бронштэн В. А. Клавдий Птолемей / Отв. ред. А. А. Гурштейн. — М.: Наука, 1988. — С. 157—161. — 239 с.
↑ ¹ ² ³ Sabra A. I. (1981), Theories of Light from Descartes to Newton, Издательство Кембриджского университета. (ср. Pavlos Mihas, Use of History in Developing ideas of refraction, lenses and rainbow, p. 5, Demokritus University, Фракия, Греция.)
↑ Ptolemy (ca. 100-ca. 170). Eric Weinstein’s World of Scientific Biography. Дата обращения: 28 июля 2021. Архивировано 27 апреля 2006 года.
↑ Dr. Gorden Videen. Whose Law of Refraction? Архивная копия от 27 июля 2021 на Wayback Machine, Optics & Photonics News (May 2008) Архивная копия от 27 июля 2021 на Wayback Machine
↑ Kwan, A.; Dudley, J.; Lantz, E. (2002). “Who really discovered Snell’s law?”. PhysicsWorld. 15 (4): 64. DOI:10.1088/2058-7058/15/4/44.
↑ Розенбергер Ф. История физики. — М.—Л.: ГИТТЛ, 1934. — Т. 2. — С. 94—95.
↑ Снеллиус // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
↑ Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II. — С. 32.
↑ Дорфман Я. Г. Всемирная история физики. С древнейших времён до конца XVIII века. — Изд. 3-е. — М.: ЛКИ, 2010. — С. 198—199. — 352 с. — ISBN 978-5-382-01091-5.
↑ Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. Том 3: Излучение. Волны. Кванты. Перевод с английского (издание 4). — Эдиториал УРСС. — ISBN 5-354-00701-1.
↑ Ландсберг, Г. С. Оптика: учебное пособие для вузов. — 6-е изд. стереот. — М.: ФИЗМАТЛИТ, 2003. — С. 252. — 848 с. — ISBN 5-9221-0314-8.
↑ Снелля закон // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.

Ссылки[править | править код]

Элементы большой науки: Закон Снеллиуса

Источник

Основные законы геометрической оптики были известны задолго до установления физической природы света. Большая часть из них выводятся из общего принципа, описывающего поведение волн. Впервые этот принцип выдвинул современник Ньютона Христиан Гюйгенс.

Принцип Гюйгенса

Каждая точка среды, до которой дошло возмущение, сама становится источником вторичных волн.

Чтобы, зная положение волновой поверхности в момент времени t, найти ее положение в следующий момент времени t + ∆t, нужно каждую точку волновой поверхности рассматривать как источник вторичных волн. Поверхность, касательная ко всем вторичным волнам, представляет собой волновую поверхность в следующий момент времени. Этот принцип подходит для описания волн любой природы (световых, механических, электромагнитных и пр.).

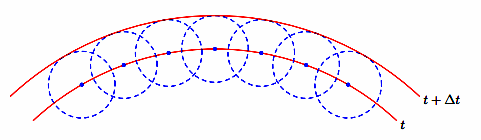
Для механических волн принцип Гюйгенса имеет наглядное толкование: частицы среды, до которых доходят колебания, колеблясь, приводят в движение соседние частицы среды, с которыми они взаимодействуют.

Закон прямолинейного распространения света

В оптически однородной среде свет распространяется прямолинейно.

Опытным доказательством этого закона служат резкие тени, отбрасываемые непрозрачными телами при освещении светом источника небольших размеров («точечного источника»).

Другим доказательством может служить известный опыт по прохождению света далекого источника сквозь небольшое отверстие, в результате чего образуется узкий световой пучок. Этот опыт приводит к представлению о световом луче как о геометрической линии, вдоль которой распространяется свет.

Внимание!

Законы геометрической оптики выполняются приближенно при условии, что размеры препятствий на пути световых волн много больше длины волны. Так, закон прямолинейного распространения света нарушается и понятие светового луча утрачивает смысл, если свет проходит через очень малые отверстия.

Пример №1. Здание, освещенное солнечными лучами, отбрасывает тень длиной L = 36 м. Вертикальный шест высотой h = 2,5 м отбрасывает тень длиной l = 3 м. Найдите высоту H здания.

Так как шест и здание расположены вертикально, они параллельны. Так как на них светит один и тот же источник света, то угол падения лучей одинаков. Следовательно, треугольники, образованные стеной зданий, лучом солнца и землей, а также землей, лучом солнца и шестом, подобны. Отсюда можно сделать вывод, что отношение высоты здания к высоте шеста будет отношению длины тени здания к длине тени шеста:

Hh=Ll

H2,5=363=12

H=12·2,5=30 (м)

Закон отражения света

Рассмотрим отражение плоской волны (см. рис. ниже).

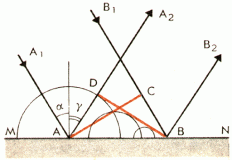
Пусть:

MN — отражающая поверхность.
A₁A и B₁B — два параллельных луча падающей плоской волны.
AC — волновая поверхность плоской волны.
α и γ— угол падения и отражения лучей A₁A и B₁B.

Определение

Плоская волна — волна, волновые поверхности которой представляют собой плоскости.

Угол падения — угол между падающим лучом и перпендикуляром к отражающей поверхности.

Угол отражения — угол между перпендикуляром к отражающей поверхности и отраженным лучом.

Волновую поверхность отраженной волны можно получить, если провести огибающую вторичных волн, центры которых лежат на границе раздела сред. Различные участки волновой поверхности AC достигают отражающей границы неодновременно. Возбуждение колебаний в точке A начинается раньше, чем в точке B, на время Δt=CBv (v — скорость волны).

В момент, когда волна достигнет точки B, и в этой точке начнется возбуждение колебаний, вторичная волна в точке A уже будет представлять собой полусферу радиусом r = AD = v∆t = CB. Радиусы вторичных волн от источников, находящихся между точками A и B, меняются так, как показано на рисунке выше.

Огибающей вторичных волн является плоскость DB, касательная к сферическим поверхностям. Она является волновой поверхностью отраженной волны. Отраженные лучи AA₂ и BB₂ перпендикулярны волновой поверхности DB. Между ними образуется угол γ, являющийся углом отражения.

Так как AD = CB и треугольники ADB и ACB прямоугольные, то углы DBA и CAB равны. Но угол α= ∠CAB, а γ= ∠DBA как углы с перпендикулярными сторонами. Следовательно, α=γ.

Закон отражения света

Угол падения равен углу отражения. Падающий луч, луч отраженный и перпендикуляр, восстановленный в точке падения, лежат в одной плоскости.

Пример №2. Луч света падает на плоское зеркало. Угол падения α равен 20°. Чему равен угол между падающим и отражённым лучами?

Поскольку, согласно закон отражения света, угол падения равен углу отражения, то угол между падающим и отражённым лучами равен удвоенному углу α. Следовательно, он равен 40°.

Закон преломления света

На границе двух разнородных сред свет меняет направление распространения. Часть его энергии возвращается в первую среду, то есть, происходит отражение света. Если же вторая среда прозрачна, то часть света проходит через границу, разделяющую первому и вторую среду. При этом он меняет свое направление. Это явление называется преломлением света.

Преломление света на границе двух сред легко продемонстрировать с помощью стакана, воды и карандаша. Если опустить карандаш в пустой стакан, то он будет выглядеть таким же прямым, как и всегда (см. рисунок слева). Если же опустить карандаш в стакан, заполненный водой, мы увидим, что его часть под водой будто бы «преломилась».

Закон преломления света, который определяет взаимное расположение луча падающего, луча преломленного и перпендикуляра, восстановленного в точке падения, был открыт опытным путем в XVII веке. Но его можно доказать, основываясь на принципе Гюйгенса.

Известно, что скорость света достигает максимального значения только в вакууме. При распространении в среде скорость света снижается. Преломление света при переходе из одной среды в другую вызвано различием в скоростях распространения света в той и другой среде. Обозначим скорость распространения волны в первой среде как v1, а во второй — как v2.

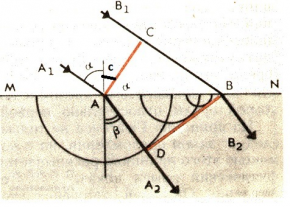
Пусть на плоскую границу раздела двух сред (к примеру, из воздуха в воду) падает плоская световая волна (см. рисунок выше). Волновая поверхность AC перпендикулярна лучам A₁A и B₁B. Поверхности MN сначала достигнет луч A₁A. B₁B достигнет ее через некоторое время, которое можно определить отношением:

Δt=CBv1

В момент, когда вторичная волна в точке B только начинает возбуждаться, волна от точки A уже имеет вид полусферы, радиус которой определяется выражением:

AD=v2Δt

Волновую поверхность преломленной волны можно получить, проведя поверхность, касательную всем вторичным волнам во второй среде, центры которых лежат на границе раздела сред. В данном случае, ею является плоскость BD. Она является огибающей вторичных волн.

Угол падения α равен CAB в треугольнике ABC (стороны одного из этих углов перпендикулярны сторонам другого). Следовательно:

CB=v1Δt=ABsinα

Угол преломления β равен углу ABD в треугольнике ABD. Поэтому:

AD=v2Δt=ABsinβ

Поделим первое выражение на второе и получим:

sinαsinβ=v1v2=n

Закон преломления света

Падающий луч, луч преломленный и перпендикуляр, восстановленный в точке падения, лежат в одной плоскости. Отношение синуса угла падения к синусу угла преломления есть величина постоянная для двух сред.

Пример №3. Угол падения параллельных лучей на плоскопараллельную пластинку равен 60^о. Найдите расстояние между точками, в которых из пластины выходят параллельные лучи, если расстояние между лучами, прошедшими сквозь пластину, равно 0,7 м.

Сначала построим рисунок хода лучей до пластины, внутри нее и после нее. Расстояние между лучами, прошедшими сквозь пластину, обозначим за l. Оно равна длине перпендикуляра, соединяющего эти лучи.

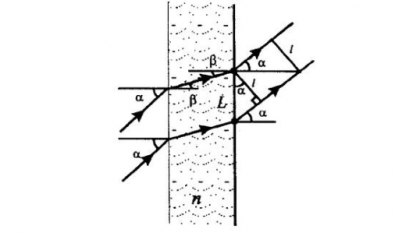
Значение величины угла β, который составляет нормаль к пластине и направлением распространения луча в ней, определяется законом преломления света:

sinαsinβ=n

Луч выходит из пластины под некоторым углом γ таким, что:

sinβsinγ=1n

Следовательно:

n=sinγsinβ=sinαsinβ

Отсюда: sinγ=sinα или γ= α. Если вспомнить геометрические законы, можно сделать вывод, что расстояние между пластинами, являющееся гипотенузой прямоугольного треугольника, можно вычислить путем деления катета на косинус угла между ним и гипотенузой:

L=lcos60°=0,70,5=1,4 (м)

Величина n — относительный показатель преломления.

Физический смысл показателя преломления заключается в том, что он равен отношению скоростей света в средах, на границе между которыми происходит преломление.

n=v1v2

Различают также абсолютный показатель преломления — показатель преломления среды относительно вакуума. Он равен синусу угла падения к синусу угла преломления при переходе светового луча из вакуума в данную среду.

Поскольку в вакууме скорость света максимальна, абсолютный показатель преломления можно выразить формулой:

n=cv1

где v1 — скорость света в среде, c — скорость света в вакууме.

Между абсолютными и относительными показателями преломления есть взаимосвязь. Пусть скорость распространения света в первой среде равна v1, во второй — v2. Тогда абсолютные показатели преломления для первой и второй среды равны:

n1=cv1

n2=cv2

Тогда относительный показатель преломления при переходе света из первой среды во вторую будет равен отношению абсолютного показателя преломления второй среды к абсолютному показателю преломления первой среды:

n=v1v2=n2n1

Внимание!

Среду с меньшим абсолютным показателем преломления принято называть оптически менее плотной средой, а среду с большим абсолютным показателем преломления — оптически более плотной.

Пример №4. Определить показатель преломления воды относительно алмаза.

n=nвnа

Абсолютные показатели преломления воды и алмаза — постоянные табличные величины.

n=1,332,42≈0,55

Полное отражение

Закон преломления света позволяет объяснить интересное и практически важное явление — полное отражение света.

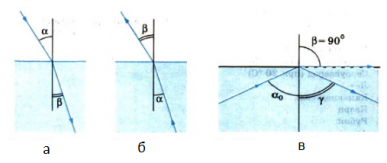
При прохождении света из оптически менее плотной среды в более плотную, к примеру, из воздуха в стекло или воду, v1>v2. Следовательно, согласно закону преломления показатель преломления n > 1. Поэтому α > β (см. рисунок а). В результате преломления луч приближается к перпендикуляру, восстановленному к точке падения луча.

Если же направить луч света в обратном направлении — из оптически более плотной среды в оптически менее плотную вдоль ранее преломленного луча (см. рисунок б), то закон преломления запишется следующим образом:

sinαsinβ=v2v1=1n

Преломленный луч по выходе из оптически более плотной среды будет направлен по линии ранее падавшего луча, поэтому α < β, т. е. преломленный луч в этом случае отдаляется от перпендикуляра, восстановленного в точке падения к границе раздела сред. По мере увеличения угла α угол преломления β также увеличивается. При этом, согласно закону преломления света, он всегда будет больше угла α. Наконец, при некотором угле падения α значение угла преломления β приблизится к 90°, и преломленный луч будет направлен почти по границе раздела двух сред (см. рисунок в). Наибольшему возможному углу преломления β = 90° соответствует угол падения α₀.

Попробуем выяснить, что произойдет при α > α₀. При падении света на границу двух сред световой луч, как мы уже говорили ранее, частично отражается и частично преломляется. Но при α > α₀ преломление света невозможно. Значит, луч должен полностью отразиться. Это явление и называется полным отражением света.

Примеры полного отражения света:

блеск от ограненного алмаза;
блеск капель росы на солнце;
внутреннее отражение предметов, находящихся под водой.

Определение

Угол полного отражения — угол падения α₀, соответствующий углу преломления 90°.

При sin β = 1 (что соответствует углу 90°) угол полного отражения можно определить по формуле:

sinα0=1n

Пример №5. Луч света, идущий из толщи воды, полностью отражается от ее поверхности. Выйдет ли луч в воздух, если на поверхность воды налить слой кедрового масла?

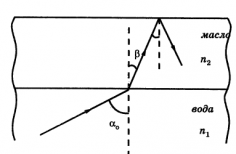
Синус угла полного отражения для луча, идущего из воды к воздуху:

sinα0=1n1

sinα0 n1=1

где n1 — показатель преломления воды.

Запишем закон преломления света для случая, когда на поверхность воды налито масло:

Тогда синус угла полного отражения для луча, идущего из воды к маслу:

sinα0sinβ=n2n1

где n2 — показатель преломления масла.

Тогда:

sinβ=1n2

Эта формула соответствует случаю, когда угол β является углом полного отражения. Следовательно, луч света за пределы масляной пленки в воздух не выйдет.

Практическое применение явления полного отражения света

Явление полного отражения света применяют в волоконной оптике для передачи света и изображения по пучкам прозрачных гибких волокон — световодов. Световод — это стеклянное волокно цилиндрической формы, покрытое оболочкой из прозрачного материала с меньшим, чем у волокна, показателем преломления.

За счет многократного полного отражения свет может быть направлен, либо по прямому, либо по изогнутому пути (см. рисунок слева). Волокна собираются в жгуты. При этом по каждому из волокон передается какой-нибудь элемент изображения (см. рисунок справа). Жгуты из волокон используются, например, в медицине для исследования внутренних органов.

В последнее время волоконная оптика широко используется для быстрой передачи компьютерных сигналов. По волоконному кабелю передается модулированное лазерное излучение.

Задание EF17610

Ученик провёл опыт по преломлению монохроматического света, представленный на фотографии.

Затем вся установка была помещена в воду. Как изменятся частота световой волны, длина волны, падающей на стекло, и угол преломления?

Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.

Алгоритм решения

1.Описать эксперимент, проведенный учеником.

2.Установить, как изменяется частота световой волны при перемещении установки из воздуха в воду.

3.Установить, как при этом изменяется длина световой волны.

4.Установить, как при этом изменяется угол преломления.

Решение

Ученик направил луч монохроматического света на стекло под углом 30 градусов к нормали. При этом луч вышел под углом 20 градусов. Это говорит о том, что свет из менее плотной оптической среды попал в более плотную.

Частота световой волны — характеристика, не зависящая от условий распространения этой волны. Поэтому при перемещении установки из воздуха в воду частота останется прежней.

Чтобы установить, как меняется длина световой волны и угол преломления. Нужно рассчитать изменение показателя преломления света. Относительный показатель преломления в первом и втором опыте будет соответственно равен:

sinαsinβ=nвоздух−стекло

sinαsinγ=nвода−стекло

Относительные показатели преломления можем выразить через абсолютные:

nвоздух−стекло=nстеклоnвоздух

nвода−стекло=nстеклоnвода

Абсолютный показатель преломления — табличная величина. Мы возьмем приблизительный значения: для воздуха — 1, для воды — 1,33, для стекла — 1,5. В действительности абсолютный показатель преломления стекла может составлять от 1,43 до 2,17. Но это не столь важно, поскольку важно лишь то, что он в любом случае больше абсолютного показателя преломления воды.

Получим:

nвоздух−стекло=1,51=1,5

nвода−стекло=1,51,33≈1,3

Видно, что при перемещении из воздуха показатель преломления уменьшился. Тогда:

sinαsinγ=1,3

Так как числитель в левой части уравнения остался прежним, а число в правой части уменьшилось, то синус угла преломления увеличился. Поскольку синус угла находится в прямой зависимости от величины угла, то и угол преломления увеличился.

Длина волны определяется формулой:

λ=vν

Учтем, что скорость распространения света в более плотной среде уменьшается. Если скорость уменьшилась, то длина воды тоже уменьшилась, поскольку между ними существует прямо пропорциональная зависимость.

Ответ: 321

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18593

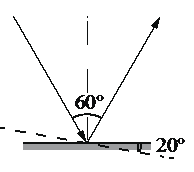Свет падает на горизонтальное плоское зеркало. Угол между падающим и отражённым лучами равен 60°. Каким станет угол между этими лучами, если повернуть зеркало на 20°, как показано на рисунке?

Алгоритм решения

1.Записать известные данные.

2.Зарисовать рисунок после поворота зеркала.

3.Представить решение задачи в общем виде.

4.Подставить неизвестные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Угол между падающим и отраженным углом: γ1 = 60^о.

• Угол поворота угла: φ = 20^о.

Построим рисунок с учетом того, что зеркало повернули:

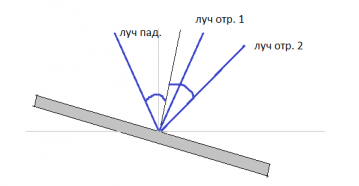
Поскольку угол падения, равен углу отражения, то:

α1+β1=60°

α1=β1

2α1=60°

α1=60°2=30°

На рисунке видно, что после переворачивания зеркала угол падения α увеличился на угол переворота:

α=α1+φ=30°+20°=50°

Так как угол падения равен углу отражения, то:

α=β=50°

Отсюда угол между лучом падающим и лучом отраженным равен:

γ=α+β=50°+50°=100°

Ответ: 100

pазбирался: Алиса Никитина | обсудить разбор

Задание EF19015

На дне бассейна с водой находится небольшая лампочка. На поверхности воды плавает круглый плот – так, что центр плота находится точно над лампочкой. Определите глубину бассейна Н, если минимальный радиус плота, при котором свет от лампочки не выходит из воды, R = 2,4 м. Сделайте рисунок, поясняющий решение. Толщиной плота пренебречь. Показатель преломления воды n = 4/3.

Алгоритм решения

1.Записать исходные данные.

3.Записать закон полного отражения.

4.Выполнить решение в общем виде.

5.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Радиус круглого плота: R = 2,4 м.

• Показатель преломления воды: n = 4/3.

Выполним рисунок. Проведем перпендикуляры к поверхности: перпендикуляр от точечного источника света, а также нормали, проведенные через края плота.

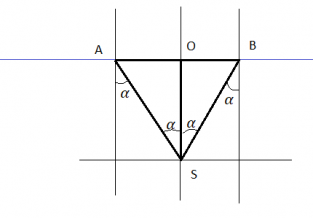
Чтобы свет лампочки не выходил из воды, лучи света от лампочки, направленные к границе между краем плота и поверхностью воды, должны полностью отражаться. Это возможно только при выполнении следующего условия:

sinα=1n

Поскольку вершина S треугольника ABS лежит строго под центром круглого плота, этот треугольник является равнобедренным. Причем перпендикуляр, восстановленный к основанию треугольника AB — SO — делит это основание на 2 равные стороны. Одновременно он делит угол S этого треугольника на 2 равные части, так как он является одновременно перпендикуляром, медианой и биссектрисой.

Пусть α — угол падения луча. Тогда угол OSB будет равен этому углу как накрест лежащие углы.

Треугольник OSB — прямоугольный. Причем искомая величина — глубина бассейна — является одним из его катетов. Из курса геометрии известно, что катет равен произведения второго катета на котангенс прилежащего угла. Второй катет в нашем случае — радиус круглого плота. Прилежащий угол равен углу падения. Следовательно:

H=Rcotα

Котангенс угла определяется как отношение косинуса этого угла к его синусу:

cotα=cosαsinα

Косинус угла можем выразить из основного тригонометрического тождества:

sin2α+cos2α=1

Следовательно:

cosα=√1−sin2α

Отсюда котангенс равен:

cotα=√1−sin2αsinα

Тогда глубина бассейна:

H=Rcotα=R√1−sin2αsinα

Из закона полного отражения вспомним, что синус угла падения есть величина, обратная показателю преломления воды. Тогда эта формула примет вид:

H=R√1−(1n)21n=Rn√1−1n2

Подставим известные данные и получим:

H=2,4·43⎷1−1(43)2=3,2√1−916=3,2√74≈0,8·2,65=2,12 ⎛⎜⎜⎝м⎞⎟⎟⎠

Ответ: 2,12

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17706

Стеклянную линзу (показатель преломления стекла n_стекла = 1,54), показанную на рисунке, перенесли из воздуха (n_{воздуха} = 1) в воду (n_воды = 1,33). Как изменились при этом фокусное расстояние и оптическая сила линзы?

Ответ:

а) Фокусное расстояние уменьшилось, оптическая сила увеличилась.

б) Фокусное расстояние увеличилось, оптическая сила уменьшилась.

в) Фокусное расстояние и оптическая сила увеличились.

г) Фокусное расстояние и оптическая сила уменьшились.

Алгоритм решения

1.Установить характер преломления лучей линзой при ее перемещении из воздуха в воду.

2.Выяснить, как от этого зависят фокусное расстояние и оптическая сила линзы.

Решение

Чтобы узнать, что произойдет с лучами света при прохождении их сквозь линзу, погруженную воду, найдем относительные показатели преломления:

nвоздух−стекло=nстеклоnвоздух=1,541=1,54

nвода−стекло=nстеклоnвода=1,541,33≈1,16

Видно, что относительный показатель преломления уменьшился. Значит, преломленный линзой луч будет менее отклоняться от нормали, проведенной в точке падения на линзу. Следовательно, чтобы достигнуть главной оптической оси, ему придется пройти большее расстояние. Это говорит о том, что фокусное расстояние линзы увеличится.

Оптическая сила линзы — величина, обратная ее фокусному расстоянию. Если оно увеличится, то оптическая сила уменьшится.

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 7.2k

Источник

Преломление света.

Закон преломления (частный случай).

Обратимость световых лучей.

Закон преломления (общий случай).

Полное внутреннее отражение.

Разберем задачи ЕГЭ по теме: Преломление света.

3.1.1. Закон преломления

3.1.2. Закон отражения

3.1.3. Полное внутреннее отражение

Что собой представляет явление преломления?

Главные законы преломления

Особенности закона № 2

Луч переходит из воздуха в стекло или воду

Свет движется из воды или стекла в воздух

What is Refraction of Light?

Laws of Refraction of Light

What is the Refractive Index?

Snell’s Law

Causes of Refraction of Light

What are Rarer and Denser mediums?

Types of Refraction

Characteristics of Refraction

Effects of Refraction of Light

Examples of Refraction of Light

Applications of Refraction of Light

Solved Examples on Refraction of Light

FAQs based on Refraction of light

Формулировка[править | править код]

Область применимости закона[править | править код]

Исторический очерк[править | править код]

Принцип Ферма[править | править код]

Векторная формула[править | править код]

Примечания[править | править код]

Ссылки[править | править код]

Закон прямолинейного распространения света

Закон отражения света

Закон преломления света

Полное отражение

Практическое применение явления полного отражения света

Вам также может понравиться

Как составить региональный бюджет

Как исправить чтобы не было обновлений на виндовс 7

Как найти число безработных в стране

Добавить комментарий Отменить ответ