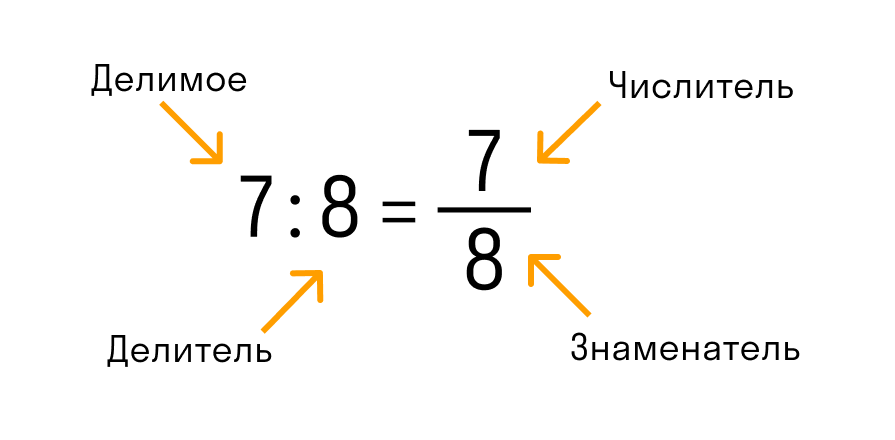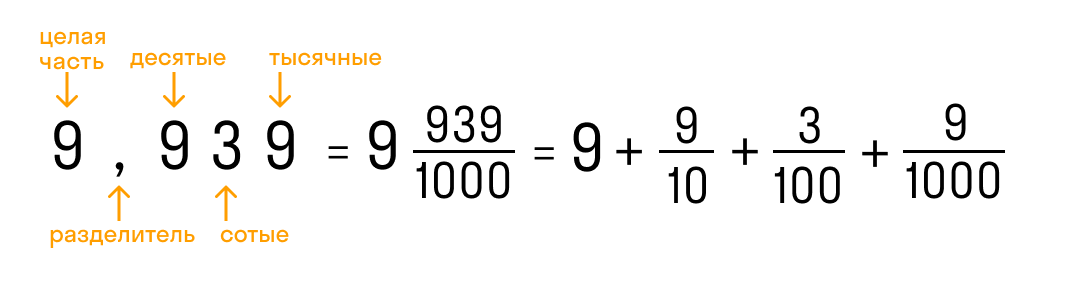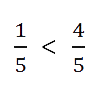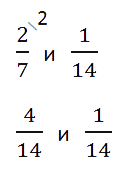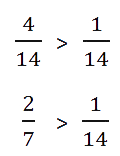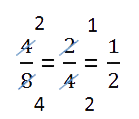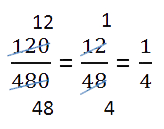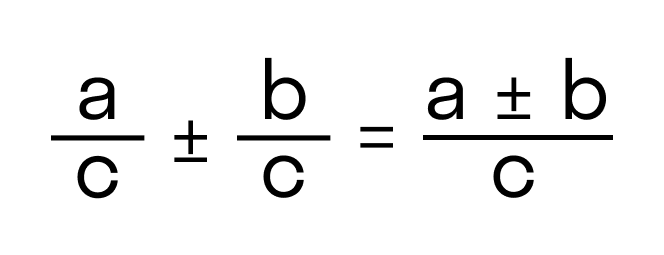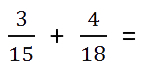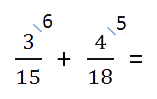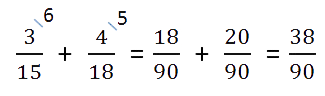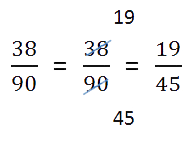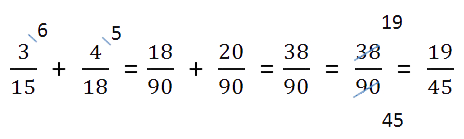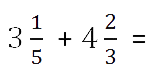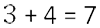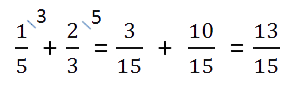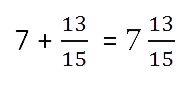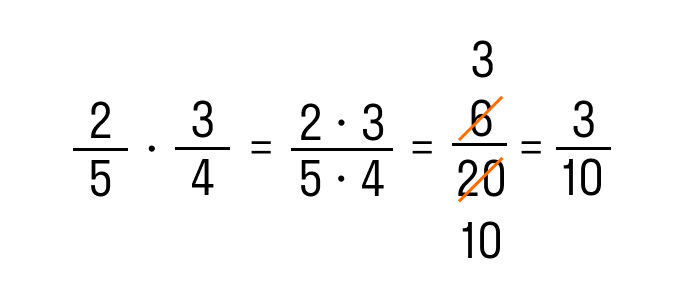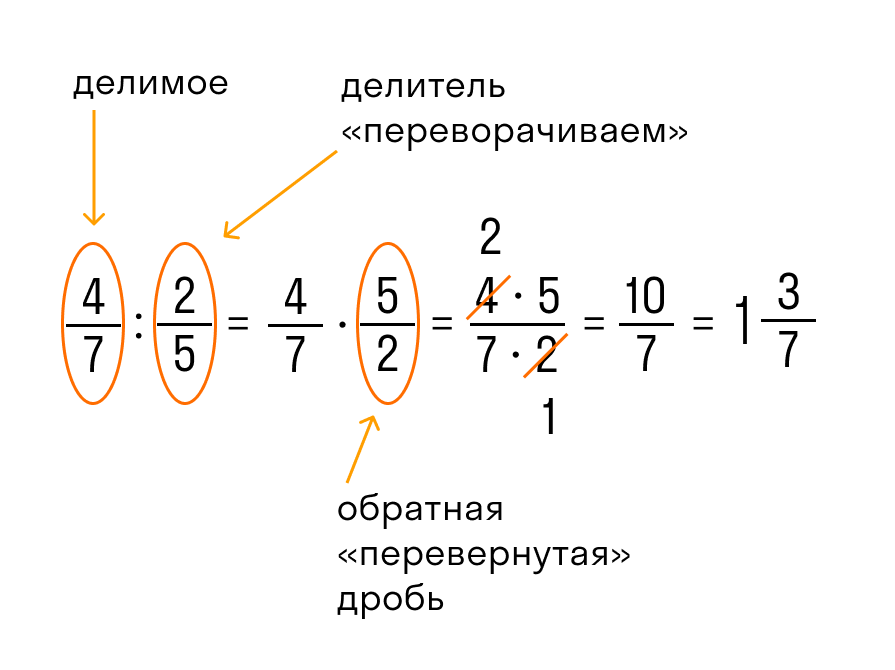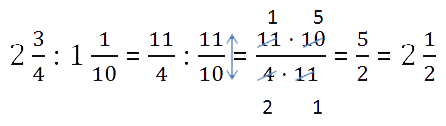В данной публикации мы рассмотрим, каким образом можно найти дробь от целого числа и наоборот – как найти число, если известно, чему равна определенная дробь от него. Также разберем примеры решения задач для лучшего понимания и закрепления теоретического материала.
- Нахождение дроби от числа
- Нахождение числа по значению дроби
Нахождение дроби от числа
Чтобы найти часть от целого числа n, которая представлена дробью, нужно умножить эту дробь (например, a/b) на данное число n.
Дробь от числа = n ⋅
a/b
=
n ⋅ a/b
Пример 1
Решение
5/12
⋅ 24 =
5 ⋅ 24/12
=
120/12
= 10
Пример 2
Решение
4/9
⋅ 7 =
4 ⋅ 7/9
=
28/9
=3
1/9
Таким образом, результат нахождения дроби числа не всегда бывает целым числом.
Примечание: если дробь является смешанной, сперва ее следует представить в виде неправильной и только потом выполнять умножение.
Нахождение числа по значению дроби
Если известно сколько число n занимает в числе m, и эта доля выражена в виде дроби, то для нахождения числа m используется формула:
Пример:
Один ряд кинозала вмещает 20 кресел, что составляет
2/5
от всей вместимости зала. Определите, сколько всего посадочных мест в зале.
Решение
Общее количество кресел равняется:
20 :
2/5
= 20 ⋅
5/2
=
20 ⋅ 5/2
= 50
Доля целого
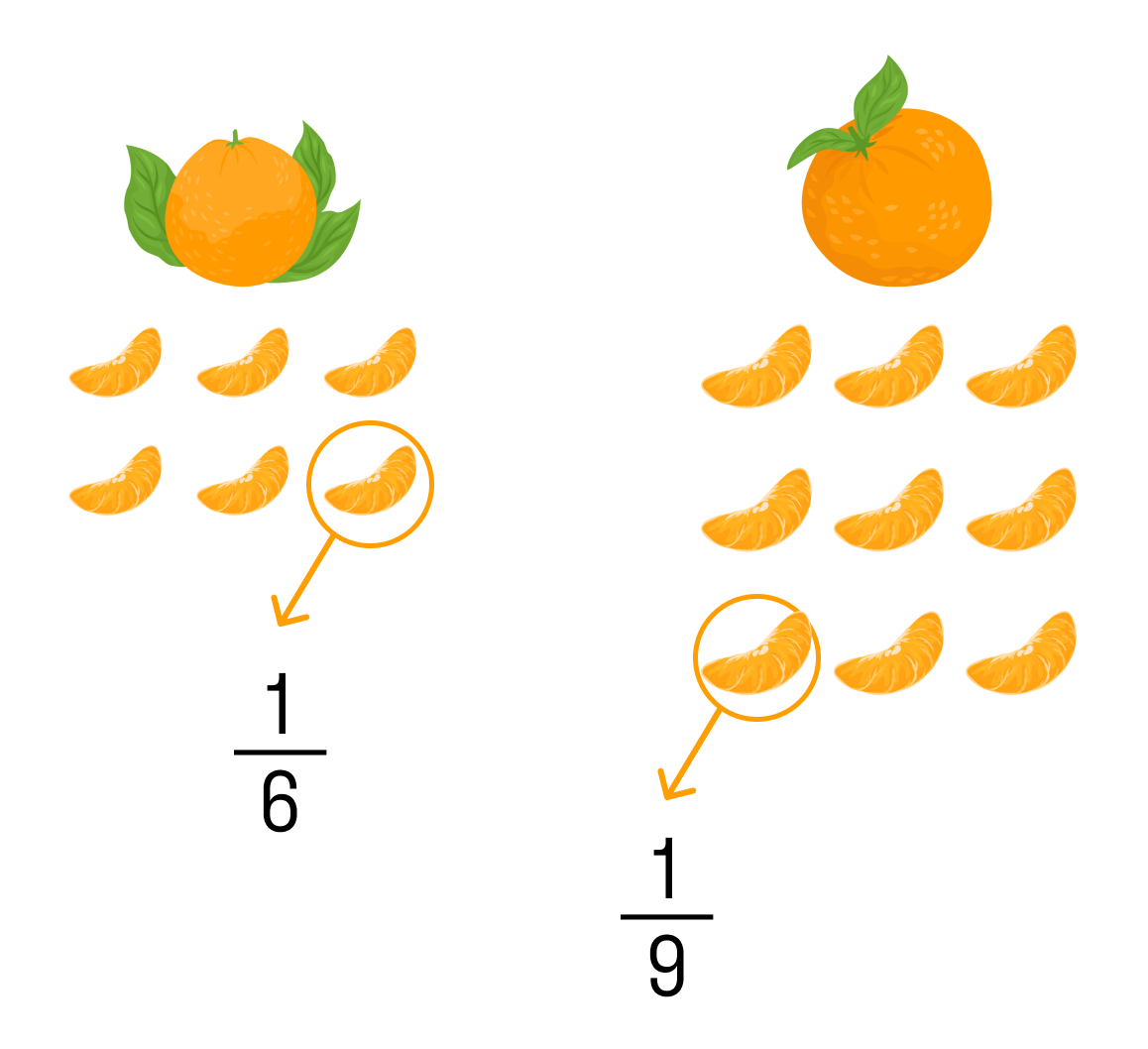
Доля это каждая из равных частей, на которые поделено целое.
Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.
У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.
- Половина — одна вторая доля предмета или 1/2.
- Треть — одна третья доля предмета или 1/3.
- Четверть — одна четвертая доля предмета или 1/4.
Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Как устроена обыкновенная дробь
Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.
Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.
Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.
Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.
Черта между числителем и знаменателем — символ деления.
Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.
Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.
Как устроена десятичная дробь
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
- 0,3
- 4,23
- 9,939
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства дробей
Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:
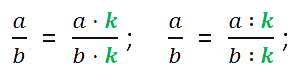
- Дробь не имеет значения, если знаменатель равен нулю.
- Дробь равна нулю, если числитель равен нулю, а знаменатель — нет.
- Две дроби a/b и c/d называются равными, если a * d = b * c.
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде, если в знаменателе обыкновенной дроби числа 10, 100, 1000 и т. д.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби, если в знаменателе обыкновенной дроби числа 10, 100, 1000 и т. д. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Действия с дробями
С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.
Сравнение дробей
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
Сравним 1/5 и 4/5. Как рассуждаем:
- В обеих дробях знаменатель равен 5.
- В первой дроби числитель равен 1, во второй дроби равен 4.
1 < 4
- Поэтому первая дробь 1/5 меньше второй 4/5.
Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.
Сравним 1/2 и 1/8. Как рассуждаем:
Представим, что у нас есть торт. Так как знаменатель первой дроби равен 2, то делим торт на две части и забираем себе одну, то есть половину торта.
Знаменатель второй дроби равен 8, делим торт на восемь частей и забираем крохотный кусочек. Половина торта больше больше маленького кусочка.
Таким образом 1/2 > 1/8.
Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.
Пример. Сравнить 2/7 и 1/14.
Как рассуждаем:
- Приведем дроби к общему знаменателю:
- Сравним дроби с одинаковыми знаменателями:
Ответ: 2/7 > 1/14.
Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.
Чтобы сравнить дроби с разными числителями и знаменателями, нужно:
- привести дроби к общему знаменателю;
- сравнить полученные дроби.
Чтобы привести дроби к общему знаменателю, нужно:
- Найти общее кратное знаменателей дробей, которое станет их общим знаменателем.
- Разделить общий знаменатель на знаменатель данных дробей, то есть найти для каждой дроби дополнительный множитель.
- Умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Сокращение дробей
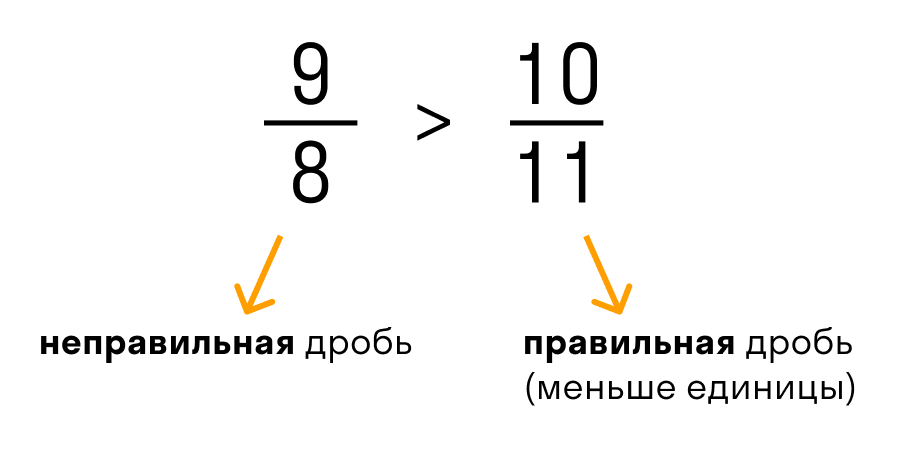
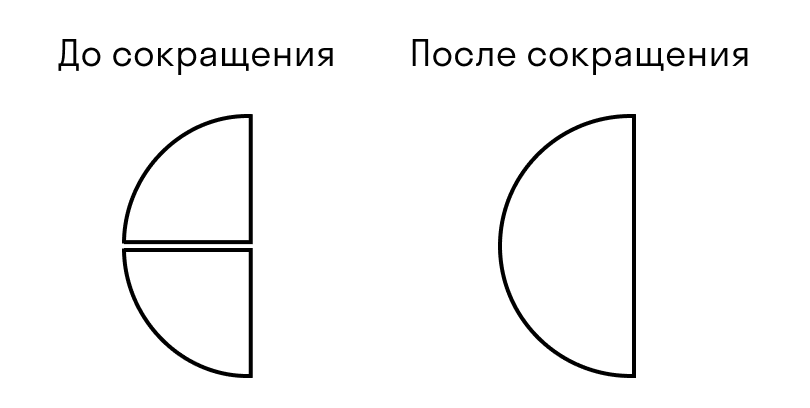
Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.
Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.
В этом примере делим обе части дроби на двойку.
Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.
Сложение и вычитание дробей
При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.
Не забудьте проверить, можно ли сократить дробь и выделить целую часть.
При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).
Вот, что делать:
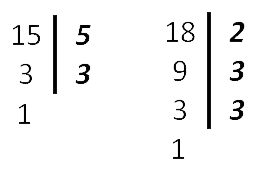
- Найдем наименьшее общее кратное для определения единого делителя.
Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.
НОК (15, 18) = 3 * 2 * 3 * 5 = 90
- Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:
90 : 15 = 6,
90 : 18 = 5.
Полученные числа запишем справа сверху над числителем.
- Воспользуемся одним из основных свойств дробей: перемножим числитель и знаменатель на дополнительный множитель. После умножения знаменатель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.
- Проверим полученный результат:
- если числитель больше знаменателя, нужно преобразовать дробь в смешанное число;
- если есть что сократить, нужно выполнить сокращение.
Ход решения одной строкой:
Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:
- Сложить целые части.
- Сложить дробные части.
Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.
- Суммировать полученные результаты.
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.
Умножение и деление дробей
Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:
Не забываем про сокращение. Это может облегчить вычисления.
Чтобы умножить два смешанных числа, надо:
- преобразовать смешанные дроби в неправильные;
- перемножить числители и знаменатели дробей;
- сократить полученную дробь;
- если получилась неправильная дробь, преобразовать в смешанную.
Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:
- числитель первой умножить на знаменатель второй, результат произведения записать в числитель новой дроби;
- знаменатель первой умножить на числитель второй, результат произведения записать в знаменатель новой дроби.
Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.
Числа, произведение которых равно 1, называют взаимно обратными.
Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.
Для деления смешанных чисел необходимо:
- представить числа в виде неправильных дробей;
- разделить то, что получилось друг на друга.
Здравствуйте, дорогие читатели, подписчики и гости канала. В этой статье рассмотрим различные вычисления с дробями, которые встречаются в шестом задании ОГЭ по математике. В июле 2.07.2021 года состоится последняя пересдача по математике в основной этап. Дополнительный этап будет уже в сентябре.
Давайте начнем разбор заданий.
1) Умножение дробь на дробь. Чтобы умножить дробь на дробь, нужно числитель умножить на числитель, знаменатель на знаменатель, при возможности сократить.
2) Деление дроби на дробь. При делении дробь на дробь, первая дробь переписывается, вторая дробь переворачивается, а деление заменяется на умножение.
3) Вычитание и умножение дробей. Несколько действий.
Способ №1. Находим общий знаменатель при вычитании. Чтобы найти общий знаменатель, нужно найти такое число, которое будет делиться на первое и второе число. В нашем случае это числа 10 и 20. Общий знаменатель 20.
Способ №2. Распределительный закон умножения. Чтобы умножить число на сумму можно умножить это число на каждое слагаемое, и результат сложить. Также это действует и при вычитании.
Также встречаются выражения, в которых не стоит находить общий знаменатель, поскольку это будет сложно. Приведу два примера:
Пример №1
Пример №2
4) Умножение целого числа на дробь. При умножении целого числа на дробь, целое число умножается на числитель, а знаменатель остается без изменений.
5) Сложение, деление и умножение смешанных чисел.
При сложении, вычитании, умножении и делении смешанных чисел иногда легче перевести смешанное число в неправильную дробь. Чтобы смешанное число перевести в неправильную дробь, нужно целую часть умножить на знаменатель, к полученному значению прибавить числитель дробной части и записать это в числитель, а знаменатель оставить прежним.
6) Вынесение общего множителя за скобку.
7) Действия с десятичными дробями
В итоге у нас получилось, что числитель дроби умножили на 100 (10*10=100), значит и знаменатель дроби тоже умножаем на 100, чтобы значение дроби не изменилось.
И еще один пример:
8) Десятичные дроби и действия со степенями
При возведении отрицательного числа в четную степень, получится число положительное. При возведении отрицательного числа в нечетную степень, получится число отрицательное.
И последнее выражение
Для отработки этих примеров, можно воспользоваться сайтом. Там много аналогичных задания, а эта статья вам будет в помощь при их решений.
Спасибо, что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.
Download Article
Download Article
Calculating fractions are one of the most useful math skills to develop. Before you begin working with them, learn how to identify parts and types of fractions. Then you can move on to adding and subtracting them. For more complex calculations, learn how to multiply and divide them. In most cases, you’ll also need to simplify or reduce the fraction.
-
1
Find a fraction. Fractions are written as 1 number placed over a dividing line with 1 number below it.
-
2
Identify the numerator. The number on top is called the numerator and it tells you how many parts of the fraction there are.[1]
- For example, in the fraction 1/5, 1 is the numerator.
Advertisement
-
3
Locate the denominator. The number on the bottom is called the denominator. This number tells you how many parts make up the whole number.[2]
- For example, in the fraction 1/5, 5 is the denominator so there should be 5 parts in the fraction.
-
4
Determine if the fraction is proper or improper. If the numerator is less than the denominator, the fraction is proper. For an improper fraction, the numerator is greater than the denominator.[3]
- For example, 3/4 is a proper fraction and 5/3 is an improper fraction.
- If you have a whole number with a fraction, it’s called a mixed fraction. For example, 1 1/2 is a mixed fraction.
Advertisement
-
1
Identify fractions with like denominators. If you need to add or subtract fractions, they need to have common denominators before you make your calculations. Look at the denominator on the fractions to see if they’re the same (like).
-
2
Find a common denominator if the denominators are unlike. If your denominators aren’t the same, you’ll need to change the fractions so they have the same denominators. To find a common denominator, multiply each part of a fraction by the denominator of the other fraction.[4]
- For example, to find a common denominator for 1/3 + 2/5, multiply the 1 and 3 by 5 and multiply the 2 and 5 by 3. You should get 5/15 + 6/15. Then you can calculate the fractions.
-
3
Add or subtract the numerators to calculate the fractions. Once you’ve found a common denominator and multiplied the numerators if necessary, you’re ready to add or subtract. Add or subtract the numerators and place the result over a dividing line. Put the common denominator below the line.[5]
- For example, 3/6 – 2/6 = 1/6.
- Avoid adding or subtracting denominators.
-
4
Simply the sum if necessary. If you’ve had to find a common denominator, you may end up with a large fraction that can be simplified. For example, if you added 8/32 +12/32, you’d get 20/32. This can be reduced to 5/8.[6]
Advertisement
-
1
Turn mixed fractions or whole numbers into improper fractions. To make it easier to multiply, you’ll need to work with proper or improper fractions. If you have a whole number or mixed fraction that you want to multiply, turn it into its fraction.
- For example, to multiply 2/5 by 7, turn 7 into a fraction. Then you can multiply 2/5 by 7/1.
- If you have a mixed fraction such as 1 1/3, turn it into an improper fraction, 4/3 before you multiply.
-
2
Multiply the numerators and denominators. Instead of adding the numerators, multiply both of them and write the result over your dividing line. You’ll also need to multiply the denominators and put the result under the line.[7]
- For example, to multiply 1/3 by 3/4, multiply 1 by 3 to get the numerator. Multiply 3 by 4 to get the denominator. Your answer will be 3/12.
-
3
Simplify your result. In many cases, you’ll need to reduce the result to a simplified fraction, especially if you started with improper fractions.Identify the greatest common factor and use it to simplify the numerator and denominator.[8]
- For example, if your answer is 3/12, 3 is the greatest common factor. Reduce the fraction by 3 to get 1/4.
Advertisement
-
1
Invert the second fraction. The simplest way to divide fractions, even those with unlike denominators, is to flip the second fraction before you calculate the sum.
- For example, with 5/4 ÷ 1/2 you should flip the 1/2 fraction so it appears as 2/1.
-
2
Multiply the numerators and denominators. Multiply the fractions straight across to multiply the numerators. Put the result over a dividing line and multiply the denominators. Put the result under the dividing line.[9]
- To continue the example, you’d multiply 5/4 by 2/1 to get 10/4.
-
3
Simplify the results, if needed. If your answer is an improper fraction or can be reduced, simplify the fraction. Use the greatest common factor to reduce the fraction.[10]
- For example, the greatest common factor for 10/4 is 2 so your simplified answer is 5/2.
- Since this is an improper fraction, turn it into a whole number with a fraction. 5/2 becomes 2 1/2.
Advertisement
Add New Question
-
Question
What is 5/8 times 16?
To multiply a fraction by a whole number, multiply the numerator by the whole number to get the new numerator. The denominator remains unchanged. (5/8)(16) = 80/8 = 10.
-
Question
How do I calculate 2/3 × -5/6?
(2/3)(-5/6) = [(2)(-5)] / [(3)(6)] = -10/18 = -5/9.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Always write your fractions neatly to reduce your risk for calculation errors.
-
If you’re working with complex fractions, you’ll need to take a few extra steps to simplify them, but that’s still a necessary part of the process.
Advertisement
References
About This Article
Article SummaryX
To calculate fractions by adding or subtracting, start by finding a common denominator of the two numbers. Simply multiply the fraction by the denominator of the other fraction to make the denominators the same. For example, to find a common denominator for 1/3 + 2/5, multiply the 1 and 3 by 5 and multiply the 2 and 5 by 3 to get 5/15 + 6/15. Then, add or subtract the numerators, and use the common denominator as the denominator for your answer. For example, 5/15 + 6/15 would be 11/16. Be sure to simplify your answer if possible! If you want to learn how to multiply fractions together, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 90,762 times.
Reader Success Stories
-
Pavithra Poojani
Mar 19, 2020
“Thanks for the explanation, it helped me to be successful.”
Did this article help you?
Калькулятор дробей
- Главная
- /
- Математика
- /
- Арифметика
- /
- Калькулятор дробей
Если вам необходимо произвести математические операции с дробями воспользуйтесь нашим онлайн калькулятором:
Просто заполните необходимые поля и получите ответ и подробное решение.
Данный калькулятор может работать как с положительными, так и с отрицательными дробями.
При этом нужно помнить, что:
− ac = a− c = − ac
Всегда нужно использовать только последний вариант.
Сложение дробей
С одинаковыми знаменателями
При сложении дробей с одинаковыми знаменателями складываются только числители, а знаменатель остаётся прежним.
Формула
ac + bc = a + bc
Пример
Для примера сложим следующие дроби с равными знаменателями:
27 + 47 = 2 + 47 = 67
С разными знаменателями
При сложении дробей с разными знаменателями для начала необходимо привести дроби к общему знаменателю. А затем сложить числители.
Формула (универсальная)
ac + bd = a⋅d + b⋅cc⋅d
Пример №1
Для примера сложим следующие дроби с разными знаменателями:
12+13=1⋅32⋅3+1⋅23⋅2=36+26=3+26=56
Пример №2
Существуют также частные случаи, когда знаменатель одной дроби можно привести к знаменателю второй. Например:
12+14=1⋅22⋅2+14=24+14=2+14=34
Этот же пример можно решить и применяя вышеуказанную универсальную формулу:
12+14=1⋅42⋅4+1⋅24⋅2=48+28=4+28=68=34
Обратите внимание, что мы сократили дробь:
68=3 ⋅ 24 ⋅ 2=34
Сложение смешанных чисел
Смешанные числа – это такие числа, у которых есть как дробная часть, так и целая.
Преобразуя в неправильную дробь
Для начала смешанное число (дробь) нужно преобразовать в неправильную дробь, а потом можно складывать как в предыдущих примерах.
Формула
a bc + d ef = b + a ⋅ cc + e + d ⋅ ff
Пример
Для примера сложим два смешанных числа:
312+123=1+3⋅22+2+1⋅33=72+53=7⋅32⋅3+5⋅23⋅2=216+106=21+106=316=5⋅6+16=5⋅66 + 16=516
Обратите внимание, что из полученной неправильной дроби мы выделили целую часть:
316=5⋅6+16=5⋅66 + 16=516
Складывая целую и дробную части отдельно
Целую и дробную части смешанных чисел можно складывать по отдельности.
Формула
a bc + d ef = (a + d) + (bc + ef)
Пример
Решим предыдущий пример этим способом:
3 12 + 1 23 = (3+1)+(12+23) = 4+1⋅32⋅3+2⋅23⋅2=4+36+46=4+3+46=4+76=4+116 = 516
Вычитание дробей
Вычитание дробей происходит по тем же принципам, что и сложение.
С одинаковыми знаменателями
Формула
ac − bc = a − bc
Пример
Для примера вычтем одну дробь из другой с равными знаменателями:
35−25=3−25=15
С разными знаменателями
Тут также, как и при сложении, дроби нужно подвести под общий знаменатель, а затем вычитать.
Формула
ac − bd = a⋅d − b⋅cc⋅d
Пример
Для примера вычтем одну дробь из другой, с разными знаменателями:
34−13=3⋅34⋅3−1⋅43⋅4=912−412=9−412=512
Вычитание смешанных чисел
Для начала смешанные числа преобразуем в неправильные дроби, потом приводим полученные дроби к общему знаменателю, а затем вычтем одну из другой. Далее выделяем целую часть если она есть.
Формула
a bc − d ef = b + a ⋅ cc − e + d ⋅ ff
Пример
312−123=1+3⋅22−2+1⋅33=72−53=7⋅32⋅3−5⋅23⋅2=216−106=21−106=116=1⋅6+56=1⋅66 + 56=156
Умножение дробей
При умножении дробей неважно одинаковые или разные у них знаменатели. Числитель одной дроби умножается на числитель другой, а знаменатели тоже перемножаются между собой.
Формула
ac ⋅ be = a ⋅ bc ⋅ e
Давайте рассмотрим несколько примеров:
Пример №1
Умножим дроби с одинаковыми знаменателями:
13⋅23=1⋅23⋅3=29
Пример №2
Умножим дроби с разными знаменателями:
13⋅24=1⋅23⋅4=212=1⋅26⋅2=16
Пример №3
Умножим смешанные числа:
112⋅223=1+1⋅22⋅2+2⋅33=32⋅83=3⋅82⋅3=246=4
Деление дробей
При делении одной дроби на другую также неважно одинаковые или разные у них знаменатели. Чтобы разделить одну дробь на другую нужно перемножить числитель первой дроби и знаменатель второй, а знаменатель первой умножить на числитель второй.
Формула
ac : be = a ⋅ ec ⋅ b
Давайте рассмотрим несколько примеров:
Пример №1
Разделим одну дробь на другую с таким же знаменателем:
23:13=23⋅31=2⋅33⋅1=63=2
Пример №2
Делим дроби с разными знаменателями:
12:23=12⋅32=1⋅32⋅2=34
Пример №3
Деление смешанных чисел:
412:223=1+4⋅22:2+2⋅33=92:83=92⋅38=9⋅32⋅8=2716=1⋅16+1116=1⋅1616 + 1116=11116