Задачи с векторами только на первый взгляд кажутся сложными, особенно если задача связана с трехмерным пространством. Но не стоит пугаться ведь если разобраться по-лучше в данной тематике задачи решаются в два счета. Так например в данной статье мы разберем тематику определения координат вектора, исходными данными для которого известны координаты начальной и конечной точки.
Для того чтобы определить координаты некоторого вектора MN⃗vec{MN}, зная координаты начала и конца, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки.
Задача 1
Рассмотрим первый вариант задачи. Вектор задан в двухмерном пространстве {x,y}. Тогда у каждой точки вектора существует две координаты, соответственно относящиеся к оси ОХ и ОУ. Формула для определения координаты вектора в таком случае принимает вид:
MN⃗=Mx−Nx;My−Ny.vec{MN}={M_x{-N}_x;M_y{-N}_y}.
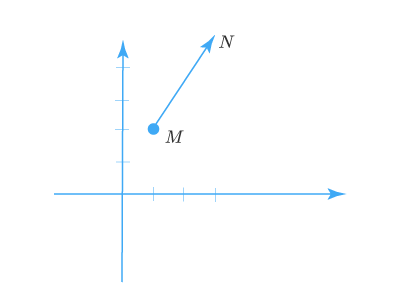
Рассмотрим на примере: На некоторой плоскости заданы точки M и N, координаты которых равны соответственно (1,2) и (3,5). Необходимо найти координаты вектора MN⃗vec{MN}
Решение
Возьмем некоторую плоскость ОХУОХУ и отметим точки ММ и NN. Затем соединим исходные точки и рассчитаем координаты полученного вектора. MN⃗={3−1;5−2}=2;3.vec{MN}=left{3-1;5-2right}={2;3}.
Вот так вот мы получили простое решение искомой задачи. Вариация таких задач может сочетать в себе нахождение не только координат вектора, но и отдельных координат исходных точек вектора.
Но у меня задача может быть не только одно- или двухмерное, но также трехмерное или как мы будем называть их n-мерное. Формула тогда в таком случае немного изменит вид, но смысл не меняется.
Задача 2
Сформулируем формулу для определения координат вектора расположенного в n-мерном пространстве.
Такое пространство подразумевает координаты точек в виде M(M1;M2;M3;..;Mn)M(M_1;M_2{;M}_3;..{;M}_n) и формула примет вид:
MN⃗=Mx−Nx;My−Ny;..;Mn−Nn.vec{MN}={M_x{-N}_x;M_y{-N}_y{;..;M}_n{-N}_n}.
Рассмотрим задачу на примере 5-мерного пространства. Необходимо найти координаты точки N вектора
MN⃗={3,8,4,1,7}vec{MN}={3,8,4,1,7}, если известны координаты точки M(1,9,6,7,4).M(1,9,6,7,4).
Решение
Не стоит пугаться при виде слов 5-мерное пространство, т.к. рисовать данную систему координат не обязательно. Стоит лишь правильно понимать и применять формулу которую мы рассмотрели выше. Перепишем ее еще раз для нашего случая.
MN⃗={M1−N1;M2−N2;M3−N3;M4−N4;M5−N5}.vec{MN}= {M_1{-N}_1;M_2{-N}_2{;M_3{-N}_3{;M}_4{-N}_4;M}_5{-N}_5}.
Тогда рассмотрим систему:
{1−N1=39−N2=86−N3=47−N4=14−N5=7begin{cases}1-N_1=3 \
9-N_2=8 \
6-N_3=4\
7-N_4=1\
4-N_5=7end{cases}
и решив данную систему, получим
{N1=−2N2=1N3=2N4=6N5=−3begin{cases}N_1=-2\
N_2=1\
N_3=2\
N_4=6\
N_5=-3\ end{cases}
Тогда получим ответ на задачу N(−2,1,2,6,−3).N(-2,1,2,6,-3).
В данной публикации мы рассмотрим формулы, с помощью которых можно найти координаты вектора, заданного координатами его начальной и конечной точек, а также разберем примеры решения задач по этой теме.
- Нахождение координат вектора
- Примеры задач
Нахождение координат вектора
Для того, чтобы найти координаты вектора AB, нужно из координат его конечной точки (B) вычесть соответствующие координаты начальной точки (A).
Формулы для определения координат вектора
| Для плоских задач | AB = {Bx – Ax; By – Ay} |
| Для трехмерных задач | AB = {Bx – Ax; By – Ay; Bz – Az} |
| Для n-мерных векторов | AB = {B1 – A1; B2 – A2; … Bn – An} |
Примеры задач
Задание 1
Найдем координаты вектора AB, если у его точек следующие координаты: A = (2; 8), B = (5; 12).
Решение:
AB = {5 – 2; 12 – 8} = {3; 4}.
Задание 2
Определим координаты точки B вектора AB = {6; 14}, если координаты точки A = (2; 5).
Решение:
Координаты точки B можно вывести из формулы для расчета координат вектора:
Bx = ABx + Ax = 6 + 2 = 8.
By = ABy + Ay = 14 + 5 = 19.
Таким образом, B = (8; 19).
Вспомним, что при умножении вектора на число
k≠0
мы получаем два коллинеарных (параллельных) вектора, которые или сонаправлены, если
k>0
, или противоположно направлены, если
k<0
. Длины векторов различаются (k) раз.
Справедливо и обратное суждение.
Если ненулевые векторы коллинеарны, то обязательно можно найти число
k≠0
так, что
b→=k⋅a→
.
Для неколлинеарных векторов справедливо суждение, что каждый вектор на плоскости можно представить в виде
c→=k⋅a→+m⋅b→
. Говорят, что вектор
c→
разложен по векторам
a→
и
b→
, а числа (k) и (m) называют коэффициентами разложения.
Это справедливо для любого вектора на плоскости, причём коэффициенты определяются единственным образом.
Выберем два не коллинеарных вектора на осях системы координат. Пусть длина каждого из них будет равна единичному отрезку в этой системе координат. Эти векторы называют координатными векторами и обозначают
i→
и
j→
.
Если от начала координат отложить вектор
a→
, то его можно разложить по векторам
i→
и
j→
следующим образом:
a→=3⋅i→+2⋅j→
.
В этом разложении коэффициенты координатных векторов называют координатами вектора
a→
.
Это записывают как
a→3;2
.
Любой вектор, который равен с вектором
a→
, можно переместить и отложить от начала координат. Следовательно, можем сделать вывод.
Равные векторы имеют равные координаты.
Но в то же время в координатной системе можно переместить векторы
i→
и
j→
, таким образом определить координаты векторов независимо от их места расположения в координатной системе.
Легко понять, что разница между абсциссами (координатами x) конечной и начальной точки вектора и есть абсцисса вектора, а разница между ординатами (координатами y) конечной и начальной точки вектора есть ордината вектора.
Связь между координатами противоположных векторов следует из того, что, если умножить вектор на (-1), результатом будет противоположный вектор.
У противоположных векторов противоположные координаты.
Важно понять ещё несколько интересных связей между координатами векторов одинаковой длины.
Способы вычисления координат вектора
Содержание:
- Что такое координаты вектора — какие операции можно производить
- Способы представления, как записываются
- Методы вычисления координат вектора
- Примеры задачи на нахождение координат вектора
Что такое координаты вектора — какие операции можно производить
Три попарно перпендикулярные прямые с определенными направлениями и единицей измерения в геометрии составляют систему координат в пространстве. Точка, в которой пересекаются данные прямые, представляет собой начало координат.
Оси координат:
- (Ox) — ось абсцисс.
- (Oy) — ось ординат.
- (Oz) — ось аппликат.
Через две прямые, которые пересекаются, можно построить плоскость. Таким образом, образуются три координатные плоскости в виде:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- ((Oxy));
- ((Oyz));
- ((Oxz)).
Определить положение точки (А) в пространстве можно с помощью трех координат (x, y) и (z).
Координата x является понятием абсциссы точки (A), координата y — определяет ординату точки (A), координата (z) — аппликату точки (A).
Запись имеет следующий вид:
(A(x;y;z)).
Варианты расположения точки:
- в том случае, когда точка расположена на оси (Ox), ее координаты — (X(x;0;0));
- при нахождении точки на оси (Oy) она характеризуется координатами (Y(0;y;0));
- если точка принадлежит оси (Oz), ее координаты — (Z(0;0;z));
- точка, лежащая в плоскости (Oxy), обладает координатами (A1(x;y;0));
- в том случае, когда расположение точки совпадает с плоскостью (Oyz,) она обладает координатами (A2(0;y;z));
- если точка расположена в плоскости (Oxz), то данная точка имеет координаты ( A3(x;0;z)).
Допустим, что в системе координат существуют некие единичные векторы (overrightarrow { i }), (overrightarrow { j }) и (overrightarrow { k }), которые были отложены от начала координат. В этом случае допустимо определить прямоугольный базис. Какой-либо вектор раскладывается на единичные вектора и записывается в виде:
(overrightarrow {OA}=x⋅overrightarrow { i }+y⋅overrightarrow { j }+z⋅overrightarrow { k })
Коэффициенты (x), (y) и ( z) могут иметь одно единственное значение и являются координатами вектора.
Определение
В прямоугольной системе координат (Х0у) проекции х и у вектора (overrightarrow {OA}) на оси абсцисс и ординат называют координатами вектора. То есть координаты вектора являются числами, описывающими положение вектора относительно координатной плоскости.
Координатами вектора, начало которого совпадает с точкой (A(x1; y1)), а конец — соответствует точке (B(x2; y2)), называют числа:
(a1 = x2 — x1);
(a2 = y2 — y1).
Координаты вектора записывают в таком виде:
(overrightarrow {OA}{x;y;z}).
Правила записи с помощью координат:
Координаты суммы векторов при наличии известных координат векторов:
Координаты разности векторов при заданных координатах векторов:
Координаты произведения вектора на число при наличии определенных координатах вектора:
Длина, которой обладает вектор:
Координаты вектора при заданных координатах, которыми характеризуются начальная и конечная точки вектора:
Расстояние по модулю, на которое удалены две точки с заданными координатами:
Координаты серединной точки отрезка, когда заданы координаты начальной и конечной точек отрезка:
Координаты вектора обладают следующими свойствами:
- Какие-либо равные векторы в единой системе координат обладают идентичными координатами.
- Координаты коллинеарных векторов пропорциональны в том случае, когда ни один из векторов не обладает нулевым значением.
- Квадрат длины какого-либо вектора определяется как сумма квадратов его координат.
- В процессе умножения вектора на действительное число каждая его координата умножается на это число.
- Когда требуется сложить вектора, следует определить сумму соответствующих координат данных векторов.
- Скалярное произведение пары векторов соответствует сумме произведений их соответствующих координат.
Способы представления, как записываются
Общепринятой является запись координат вектора в виде:
((х, у)).
Непосредственно вектор обозначают, как:
(overrightarrow {AB} =(х, у)).
Координаты вектора записывают в круглых скобках рядом с буквенным обозначением вектора:
(overrightarrow {AB} (a_1 ;a_2 ))
или
(overrightarrow a (a_1 ;a_2 ))
В некоторых случаях допустимо использовать запись координат вектора без буквенного обозначения, то есть со знаком вектора над скобками:
(overrightarrow {(a_1 ;a_2 )})
Нулевой вектор обладает нулевыми координатами:
(overrightarrow 0 (0;0))
Методы вычисления координат вектора
В том случае, когда определены координаты начала и конца вектора (overline{AB}: Aleft(x_{1} ;; y_{1} right),; Bleft(x_{2} ;; y_{2} right)), при вычислении его координат требуется от координат конца отнять соответствующие координаты начала:
(overline{AB}=left(x_{2} -x_{1} ;; y_{2} -y_{1} right))
Формула определения координат вектора для двухмерных задач: в рассматриваемом случае вектор ( overline{AB} )с заданными координатами точек (A(х1;у1) и B(x2;y2)) можно найти по формуле:
(overline{AB}=(x2 – x1 ; y2 – y1).)
Формула определения координат вектора для пространственных задач: если требуется решить пространственную задачу на нахождение вектора (overline{AB}), координаты точек (A(х1;у1;z1) и B(x2;y2;z2)) которого известны, следует воспользоваться формулой:
(overline{AB}=(x2 – x1 ; y2 – y1; z2 – z1))
С помощью вычисления координат вектора можно определить его характеристики, в том числе найти длину вектора. Зная координаты, достаточно просто построить вектор.
Примеры задачи на нахождение координат вектора
Задача 1
Существуют пары точек:
(A(-3; 7), B(2; -1));
(С(5; 0), D(11; 8).
)
Необходимо определить координаты векторов:
(overrightarrow {AB} ,overrightarrow {CD} .)
Решение:
С целью вычисления координат вектора необходимо из координат его конца (точки B) вычесть координаты начала (точки A):
(overrightarrow {AB} (2 – ( – 3); – 1 – 7))
(overrightarrow {AB} (5; – 8).)
Аналогичным способом можно рассчитать координаты второго вектора:
(overrightarrow {CD} (11 – 5;8 – 0))
(overrightarrow {CD} (6;8))
Ответ: (overrightarrow {AB} (5; – 8); overrightarrow {CD} (6;8).)
Задача 2
Требуется вычислить координаты вектора (overline{AB}) при условии, что:
(Aleft(-1;; 2right), Bleft(2;; -3right))
Решение
Определить координаты, которым характеризуется вектор (overline{AB}), исходя из известных по заданию координат его начальной точки (Aleft(-1;; 2right)) и конечной точки (Bleft(2;; -3right)), можно путем вычитания из координат конечной точки соответствующих координат начальной точки. Таким образом, первым и единственным действием в данном случае является:
(overline{AB}=left(2-left(-1right), ;; -3-2right)=left(3;; -5right))
Ответ: (overline{AB}=left(3;; -5right))
Задача 3
Необходимо определить координаты точки (A), которая представляет собой начало вектора (overline{AB}=left(0;; -4;; 3right)), а концом вектора является точка (Bleft(-1;; 6;; 1right).)
Решение
Предположим, что точка (A ) обладает следующими координатами:
(Aleft(a_{1} ;; a_{2} ;; a_{3} right))
В таком случае, вектор (overline{AB}), при условии, что точка (Bleft(-1;; 6;; 1right)), характеризуется следующими координатами:
(overline{AB}=left(-1-a_{1} ;; 6-a_{2} ;; 1-a_{3} right)=left(0;; -4;; 3right))
Зная, что равенство двух векторов достигается при равенстве соответствующих координат этих векторов, можно записать следующие уравнения для вычисления неизвестных координат, которыми характеризуется точка (А):
(-1-a_{1} =0Rightarrow a_{1} =-1)
(6-a_{2} =-4Rightarrow a_{2} =10)
(1-a_{3} =3Rightarrow a_{3} =-2)
В результате:
(Aleft(-1;; 10;; -2right))
Ответ: (Aleft(-1;; 10;; -2right))
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Метод координат
- Координаты вектора
Прямоугольная система координат (декаротова система координат) — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Для задания прямоугольной системы координат нужно провести две взаимно перпендикулярные прямые, на каждой из них выбрать направление (оно обозначается стрелкой) и выбрать единицу измерения отрезков.
На рисунке выше оси 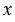
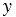
Отложим от начала координат О единичные векторы 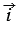
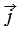
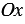
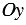
Векторы 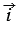
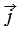
Координатные векторы не коллинеарны, поэтому любой вектор 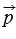
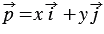
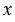
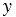
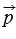
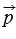
Координаты вектора записывают в фигурных скобках после обозначения вектора: 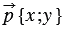
На рисунке выше 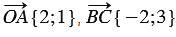
Нулевой вектор можно представить в виде 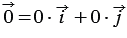
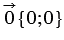
Если векторы 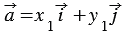
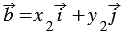
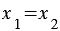
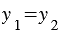
Правила, позволяющие по координатам векторов находить координаты их суммы, разности и произведения вектора на число:
10. Каждая координата суммы двух и более векторов равна сумме соответствующих координат этих векторов.
Доказательство
Дано: 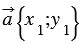
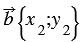
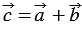
Доказать: 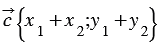
Доказательство:
По условию 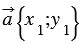
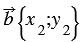
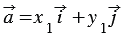
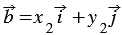
Сложим последние два равенства и применим свойства сложения векторов и умножения вектора на число, получим: 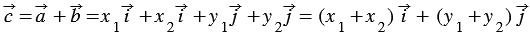
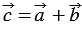

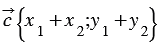
20. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.
Доказательство
Дано: 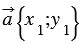
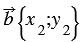
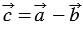
Доказать: 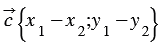
Доказательство:
По условию 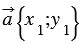
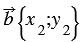
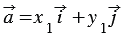
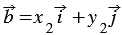
Вычтем из равенства (1) равенство (2) и применим свойства сложения векторов и умножения вектора на число, получим: 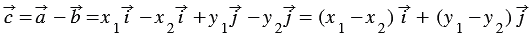
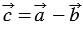
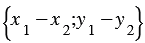
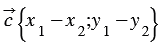
30. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
Доказательство
Дано: 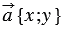
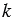
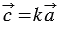
Доказать: 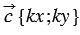
Доказательство:
По условию 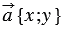
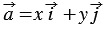
Умножим последнее равенство на число 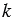
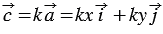
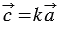
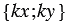
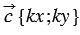
Данные правила позволяют определить координаты любого вектора, представленного в виде алгебраической суммы данных векторов с известными координатами.
Пример
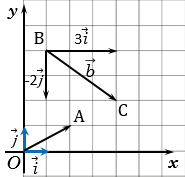
Найти координаты вектора 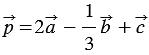
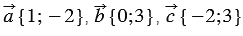
Решение:
По правилу 30 вектор 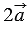
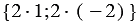
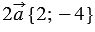
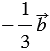
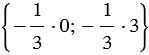
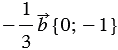
Так как 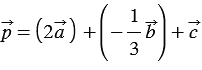
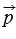
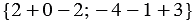
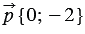
Ответ: 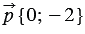
Советуем посмотреть:
Разложение вектора по двум неколлинеарным векторам
Связь между координатами вектора его начала и конца
Простейшие задачи в координатах
Уравнение линии на плоскости
Уравнение окружности
Уравнение прямой
Взаимное расположение двух окружностей
Метод координат
Правило встречается в следующих упражнениях:
7 класс
Задание 931,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 932,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 944,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 945,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 5,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 18,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 24,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 989,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1008,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 7,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник