Исходные
данные для расчета берутся из
кинематического раздела: крутящий
момент Т1
(Н∙мм) и частота вращения n1(мин.-1)
на червяке; крутящий момент Т2
(Н∙мм) и частота вращения n2
(мин.-1)
на червячном колесе (параметры червяка
имеют индекс 1, червячного колеса –
индекс 2); передаточное число u
червячной передачи.
Последовательность
расчета:
а)
по значению передаточного числа u
по таблице 18 выбирается число заходов
червяка z1;
б)
определяется число зубьев червячного
колеса z2=u∙z1.
Если получается нецелое число, его
округляют до ближайшего большего или
меньшего целого числа
.
должно
быть больше 28 из условия неподрезания
зубьев;
в)
определяется уточненное передаточное
число u*=
/z1.
Определяется изменение передаточного
числа
;
г)
определяется ориентировочное значение
коэффициента q
диаметра червяка по соотношению q
= (0,22…0,33)
,
коэффициент должен быть в полученных
пределах, но с учетом модуля передачи
m
(после определения m
по таблице 19);
д)
выбирается материал червячной передачи:
для червяка принимается углеродистая
сталь 45 термоулучшенная, имеющая HRC≤45.
Для выбора материала червячного колеса
необходимо ориентировочно определить
скорость скольжения Vck
в передаче по формуле:
,
(5.17)
где
n1
–
частота вращения червяка, мин.-1;
Т2
– крутящий момент на валу червячного
колеса, Н∙мм;
по
полученному значению Vck
выбирается из трех групп материал для
венца червячного колеса, на стр. 63;
е)
определяются допускаемые напряжения
для червячного колеса, являющегося
менее прочным элементом пары по контактным
напряжениям [σ]H
и по изгибным [σ]F
напряжениям по таблицам 22, 23 и 24;
ж)
определяется межосевое расстояние а,
по формуле [5]:
,
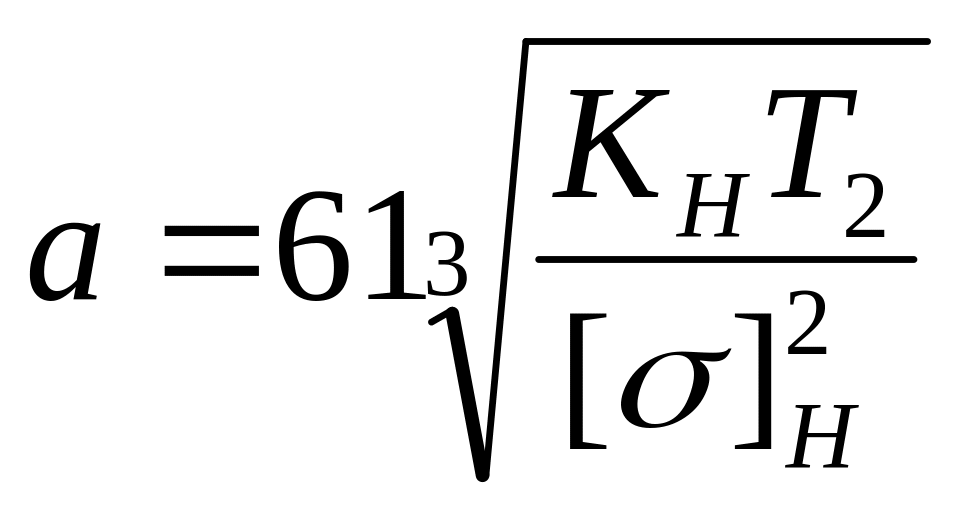
(5.18)
где
КН
– коэффициент нагрузки, предварительно
КН=1,1…1,3;
Т2
– крутящий момент на валу колеса, Н∙мм;
[σ]H
– допускаемое контактное напряжение,
Н/мм2
(определено в пункте (е));
з)
определяется осевой модуль передачи
m=(1,5…1,7)a/
,
по таблице 19 по определенному m
и
ранее определенному в пункте (г) q,
назначаются уточненные значения m*
и q*;
и)
уточняется межосевое расстояние
а*=0,5m*(
+q*);
к)
уточняется коэффициент концентрации
нагрузки КНβ*
по формуле:
КНβ*=1
+(
/Q)3(1–ψ),
(5.19)
где
Q
– коэффициент деформации червяка,
зависящий от q*и
z1,
определяется по таблице
26;
Таблица
26 – Значение коэффициента Q
деформации червяка, от z1
и
q*
|
Заходность z1 |
q |
||||||
|
7,1 |
8 |
9 |
10 |
11 |
12,5 |
14 |
|
|
1 |
57 |
72 |
89 |
108 |
127 |
157 |
190 |
|
2 |
45 |
57 |
71 |
86 |
102 |
125 |
132 |
|
4 |
37 |
47 |
58 |
70 |
82 |
101 |
123 |
ψ
– отношение среднего по времени момента
к максимальному (при постоянной нагрузке
ψ=0, при переменной (когда задана
циклограмма нагружения) определяется
выражением [5],
);
л)
уточняется коэффициент КНV*
динамической нагрузки, для чего –
определяется уточненная окружная
скорость на червяке по формуле:
;
(5.20)
-
определяется
уточненный угол подъема витка червяка
по делительному цилиндру по формуле
γ*=arctg(z1/q*); -
уточняется
скорость скольжения
;
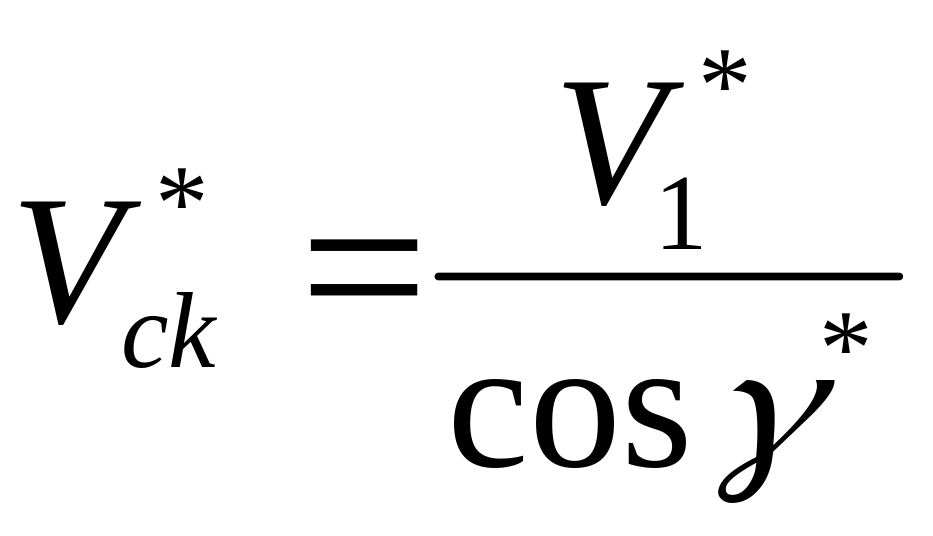
(5.21) -
по
Vck*
назначается степень точности червячной
передачи по таблице 27; -
по
определенной по таблице 27 степени
точности и скорости скольжения Vck
по таблице 28 определяется уточненное
значение КНV*;
м)
уточняется коэффициент нагрузки
КН*=КНβ*∙КНV*;
н)
по скорости скольжения Vck
уточняется допускаемое напряжение
по
таблицам 22, 23, 24;
о)
уточняется КПД червячной передачи по
формуле (5.4):
,
где
γ* – угол подъема витка червяка, формула
(5.1), (γ*=arctg(z1/q*);
ρ’
– приведенный угол трения, определяется
по Vck
по таблице 21;
Таблица
27 – Значение степени точности передачи
|
Степень точности |
Cкорость не |
Обработка |
Примечание |
|
7 |
10 |
Червяк |
Передача |
|
8 |
5 |
Червяк |
Передачи |
|
9 |
2 |
Червяк |
Передачи |
Таблица
28 – Уточненное значение коэффициента
КНV*
|
Степень |
Скорость |
|||||
|
до |
1,5…3,0 |
3,0…7,5 |
7,5…12 |
12…16 |
16…25 |
|
|
6 |
– |
– |
1,0 |
1,1 |
1,3 |
1,5 |
|
7 |
1,0 |
1,0 |
1,1 |
1,2 |
– |
– |
|
8 |
1,1…1,2 |
1,2…1,3 |
1,4 |
– |
– |
– |
|
9 |
1,2…1,3 |
– |
– |
– |
– |
– |
п)
уточняется крутящий момент Т2
на червячном колесе
;
р)
по уточненным значениям делается
проверка действительных контактных
напряжений в зубьях червячного колеса
по формуле (5.8):
,
проверяется
рациональность проектирования
;
с)
проверяется прочность зубьев червячного
колеса на изгиб по формуле (5.13) с
соответствующими уточнениями [5]:
,
где
КF
–
коэффициент нагрузки при расчете на
изгиб равен коэффициенту нагрузки КН
при расчете на контактную прочность,
так как расчет в том и другом случае
проводится для зубьев червячного колеса,
т.е. КF*=КН*;
– коэффициент
формы зуба определяется по эквивалентному
(фиктивному) числу зубьев zv2
(zv2=
/cos3γ*)
червячного колеса по таблице 29;
Таблица
29 – Значение коэффициента формы зуба
|
zv2 |
28 |
30 |
32 |
35 |
37 |
40 |
45 |
50 |
60 |
80 |
100 |
150 |
|
YF |
1,80 |
1,76 |
1,71 |
1,64 |
1,61 |
1,55 |
1,48 |
1,45 |
1,40 |
1,34 |
1,30 |
1,27 |
m*
– осевой модуль был уточнен в подпункте
(з);
q*
– коэффициент диаметра червяка был
уточнен в подпункте (з);
– число
зубьев колеса было уточнено в подпункте
(б);
определяется
действительное изгибное напряжение в
зубьях колеса[5]:
;
т)
определяются основные геометрические
размеры червячной передачи (рисунки 13
и 15):
червяк:
d1=m*q*
– диаметр делительной окружности;
da1=d1+2m*
– диаметр окружности выступов витков;
df1=d1
–
2,4m*
– диаметр окружности впадин витков;
b1≥
(11+0,67
)m*,
при z1=1
и 2;
b1≥
(12,5+0,09
)m*
при z1=3
и 4 – длина нарезанной части червяка;
червячное
колесо:
d2=m*
– делительный диаметр червячного
колеса;
da2=d2+2m*
– диаметр окружности выступов зубьев
червячного колеса;
df2
–
диаметр окружности впадин зубьев
червячного колеса;
наибольший
диаметр червячного колеса dam2
и ширина венца b2
определяются по таблице 20 в зависимости
от z1.
Соседние файлы в папке 1415
- #
- #
- #
- #
- #
- #
- #
- #
Расчет червячной передачи
Классификация червячных передач. По исполнению червячные передачи различают четыре вида по расположению червяка относительно червячного колеса, а также разделяются на открытые и закрытые (рис. 89).
Рис. 89. Классификация червячных передач по расположению червяка: а – с нижним расположением червяка, б – с верхним расположением червяка, в – с боковым расположением червяка, г – с вертикальным расположением чкервяка.
По назначению червячные передачи делятся на кинематические и силовые. По форме наружной поверхности червяка различают два основных вида червячных передач: цилиндрические, или просто червячные передачи (с цилиндрическими червяками) и глобоидные (с глобоидными червяками). В зависимости от формы профиля резьбы цилиндрических червяков различают червяки: архимедовы (
), конволютные (
), эвольвентные (
) и с вогнутым профилем витков (рис. 90).
Рис.90. Классификация по форме профиля червяка: а – цилиндрический архимедов, б – глобоидный, в – цилиндрический эвольвентный, г – с вогнутым профилем витков.
Назначение. Червячные передачи относится к механическим передачам зацепления с непосредственным контактом и предназначены для передачи вращательного движения между скрещивающимися валами (с углом, как правило 900) при необходимости реализации больших передаточных чисел (
). Червячная передача состоит из винта, называемого червяком, и червячного колеса, представляющего собой разновидность косозубого зубчатого колеса. Резьба червяка может быть однозаходной или многозаходной, а также правой или левой. Наиболее распространена правая резьба с числом заходов zx = 1…4.
Преимущества. Возможность передачи вращения между скрещивающимися валами и получения больших передаточных чисел в малых габаритах одной пары зацепления. Плавность и бесшумность работы. Компактность и простота эксплуатации. Возможность самоторможения. Высокая кинематическая точность.
Недостатки. Относительно низкий КПД. Большие потери мощности, что не позволяет использовать для передачи больших нагрузок и мощностей. Повышенный износ и склонность к заеданию контактирующих поверхностей. Необходимость применения дорогостоящих антифрикционных материалов и режущих инструментов, что повышает стоимость передачи относительно зубчатых.
Сферы применения. Червячные передачи применяются при мощности до 60кВт, в некоторых случаях до 200кВт, при передаточном числе 
с КПД 
. Наибольшее распространение получили червячные передачи в приводах электротранспорта, подьемнотранспортных механизмах, лебедках любых типов, кинематических приводах делительных механизмов станков и механизмов.
Геометрический расчет. Для червяков и колес червячных цилиндрических передач модуль т, мм, нормализован по ряду: 1,0; 1,25; 1,6; 2,0; 2,5; 3,15; 4,0; 5,0; 6,3; 8,0; 10,0; 12,5; 16,0; 20,0; 25,0.
Передаточное отношение передачи
, (15.1)
где 
– соответственно, число витков (заходов) червяка и зубьев колеса.
Число витков червяка принимают в зависимости от передаточного отношения передачи:
– 
при 
;
– 
при 
;
– 
при 
Для червячных передач номинальные значения передаточных чисел и стандартизованы ГОСТ2185 – 66 Номинальные значения передаточных чисел и для червячных редукторов следующие:
1-й ряд 1,00; 1,25; 1,60; 2,00; 2,50; 3,15; 4,0; 5,0; 6,3; 8,0; 10,0;12,5; 16; 20…
2-й ряд 1,12; 1,40; 1,80; 2,24; 2,80; 3,55; 4,5; 5,6; 7,1; 9,0; 11,2; 14; 18; 22,4…
При выборе стандартных параметров первый ряд предпочтительнее второго, а принятые значения передаточных чисел для червячных передач не должны отличаться от расчетных не более чем на 4%.
Для червячных цилиндрических передач с углом скрещивания осей червяка и колеса, равным 90° по ГОСТ 2144 – 76 нормализованы: делительные углы подъема витков червяка, длина червяка и межосевые расстояния:
1-й ряд 
40;50;63;80;100;125; 160; 200; 250; 315; 400; 500.
2-й ряд – – – – – – 140; 180; 225; 280; 355; 450.
Размеры червячного колеса определяются по таким же расчетным зависимостям как для зубчатых колес. Для унификации стандартного инструмента, применяемого при нарезании червяков и червячных колес, отношение делительного диаметра 
червяка к расчетному модулю т, называемое коэффициентом диаметра червяка q, нормализуют по ГОСТ 19672 – 74 в пределах 
= 6,3…25. Рекомендуется принимать 
, при этом 
.
Стандартом установлено два ряда значений коэффициентов диаметра червяка q:
1-й ряд 6,3; 8; 10; 12,5; 16; 20; 25;
2-й ряд 7,5; 9; 11,2; 14; 18; 22,4.
В мелкомодульных передачах коэффициент диаметра червяка q рекомендуется брать больше, так как червяки в них могут оказаться недостаточно жесткими.
Тангенс делительного угла подъема витков червяка и угла наклона зубьев колеса
. (15.2)
Значения делительного угла подъема витков червяка в зависимости от его параметров приведены в таблице 15.1.
Таблица 15.1 Делительный угол подъема витков червяка
|
Z1 |
q |
||||||
|
16 |
14 |
12 |
10 |
9 |
8 |
7,5 |
|
|
1 |
3°34’35” |
4°05’09” |
4°45’49” |
5°42’38” |
6°20’25” |
7°07’30” |
7°35’41” |
|
2 |
7°07’30” |
8°07’48” |
9°27’44” |
11°18’36” |
12°31’44” |
14°02’10” |
14°55’53” |
|
3 |
10°37’15” |
12°05’40” |
14°02’10” |
16°41’56” |
18°26’06” |
20°33’22” |
21°48’00” |
|
4 |
14°02’10” |
15°56’43” |
18°25’06” |
21°48’05” |
23°57’45” |
26°33’54” |
28°04’21” |
Основные геометрические параметры червячной передачи без смещения показаны на рис. 91 определяются по зависимостям:
– делительные и начальные диаметры червяка и колеса:
, (15.3)
; (15.4)
– диаметры вершин червяка и колеса:
, (15.5)
; (15.6)
– диаметры впадин червяка и колеса:
, (15.7)
. (15.8)
Рис. 91. Геометрические параметры червячной передачи
В червячной передаче без смещения высота зубьев и витков
. (15.9)
Для передачи без смещения делительное межосевое расстояние а и межосевое расстояние aw:
, (15.10)
Модуль червячного зацепления проверяется по зависимости
. (15.11)
Наибольший диаметр червячного колеса определяется по формуле
. (15.12)
Условный угол обхвата 
червяка венцом зубчатого колеса определяется из условия:
. (15.13)
Длина нарезанной части червяка принимают:
при 
и 2 
;
при 
и 4 
. (15.14)
Ширина венца зубчатого колеса
при 
;
при 
.
Остальные размеры зубчатого колеса принимаются такими как для зубчатых колес. Смещение цилиндрической червячной передачи с архимедовым червяком осуществляется только за счет колеса, размеры червяка, за исключением диаметра начального цилиндра, не изменяются. Предельное значение коэффициента смещения при отсутствии подрезания и заострения зубьев червячного колеса рекомендуется принимать 
. Отрицательного смещения следует избегать из-за снижения прочности зубьев на изгиб.
Минимальное число зубьев колеса в силовой червячной передаче принимают =26…28. При выборе и в зависимости от передаточного числа и необходимо иметь в виду, что для передачи без смещения во избежание подрезания зубьев колеса должно быть z2 > 28.
Кинематический и силовой расчеты. Векторы окружных скоростей червяка 
и v2 червячного колеса составляют между собой такой же угол, как угол, под которым перекрещиваются валы передачи, т. е. обычно угол, равный 90°. Каждая из скоростей определяется по соответствующей формуле:
,
. (15.15)
От окружной скорости колеса зависит выбор степени точности передачи. Из 12 степеней точности изготовления червячных передач, регламентируемых ГОСТ 13675-68 для силовых передач предусмотрены 5, 6, 7, 8 и 9-я степени точности. В общем машиностроении чаще всего пользуются 7, 8 и 9-й степенями точности. Выбор степени точности червячной передачи в зависимости от окружной скорости колеса 
, обработки червяка и колеса и области применения передачи можно производить по табл. 15.2.
Таблица 15.2. Степени точности червячных передач
|
Степень точности |
Окружная скорость колеса υ, м/с, не более |
Обработка |
Примечание |
|
7 – я |
10 |
Червяк закален, отшлифован и отполирован. Колесо нарезают шлифованными червячными фрезами. Обработка под нагрузкой |
Передачи с повышенными скоростями и малым шумом, высокими требованиями к габаритам |
|
8 – я |
5 |
Червяк с НВ≤350 нешлифованный. Колесо нарезают нешлифованной червячной фрезой или «летучкой». Обработка под нагрузкой |
Передачи среднескоростные со средними требованиями к шуму, габаритам и точности |
|
9 – я |
2 |
Червяк с НВ≤350 нешлифованный. Колесо нарезают любым способом |
Передачи низкоскоростные, кратковременно работающие, и ручные с пониженными требованиями |
Скорость скольжения представляет собой геометрическую разность этих скоростей и определяется по формуле
, (15.16)
или по зависимости
. (15.17)
Выбор материала червячного колеса в основном зависит от скорости скольжения витков резьбы червяка по зубьям колеса.
Сила взаимодействия между витками резьбы червяка и зубьями червячного колеса может быть разложена на три взаимно перпендикулярные составляющие: окружную, осевую и радиальную силы. Окружная сила червяка 
, равная и направленная противоположно осевой силе колеса 
:
. (15.18)
Окружная сила 
колеса равна осевой силе червяка 
, но направлена противоположно ей:
. (15.19)
Радиальная сила 
для червяка и колеса
, (15.20)
где 
стандартный угол профиля витков червяка.
Коэффициент полезного действия червячного редуктора при ведущем червяке с учетом потерь в зацеплении, в опорах и наразбрызгивание и перемешивание масла
, (15.21)
Коэффициент полезного действия червячного редуктора при ведущем колесе с учетом изменения направления сил трения
. (15.22)
Значения коэффициента трения, а следовательно и приведенного угла трения принимается в зависимости от скорости скольжения в передаче. Приведенные углы трения при работе червячного колеса из оловянистой бронзы по стальному червяку даны в табл.15.3.
Таблица 15.3 Приведенные углы трения
|
υск, м/с |
φ’ |
υск, м/с |
φ’ |
|
0,01 |
5°40’…6°50′ |
2,5 |
1°40’…2°20′ |
|
0,1 |
4°30’…5°10′ |
3,0 |
1°30’…2°00′ |
|
0,5 |
3°10’…3°40′ |
4,0 |
1°20’…1°40′ |
|
1,0 |
2°30’…3°10′ |
7,0 |
1°00’…1°30′ |
|
1,5 |
2°20’…2°50′ |
10 |
0°55’…1°20′ |
|
2,0 |
2°00’…2°30′ |
Критерии работоспособности. Учитывая виды повреждений основными критериями работоспособности червячной передачи являются контактная и изгибная прочность зубьев червячного колеса. В связи с тем что поверхностное разрушение зубьев колеса зависит от контактных напряжений, а поломка – от напряжений изгиба, зубья червячных колес, так же как и зубья зубчатых колес, рассчитывают на прочность по контактным напряжениям и напряжениям изгиба. При проектировочном расчете червячных передач редукторов определяют требуемое по условию контактной прочности межосевое расстояние передачи; затем проверяют зубья колеса на изгиб. В большинстве случаев оказывается, что расчетные напряжения изгиба значительно ниже допускаемых. Лишь в случае мелко – модульного зацепления при большом числе зубьев колеса (z2 > 100) может оказаться, что прочность на изгиб недостаточна. При этом приходится изменить размеры зацепления и вновь производить проверку. Помимо указанных расчетов для червячных передач выполняют расчет червяка на жесткость и тепловой расчет червячного редуктора.
Проектные расчеты червячных передач.
Расчет зубьев на контактную прочность. При проектировочном расчете зубьев червячных колес на контактную прочность определяется межосевое расстояние передачи:
, (15.23)
где 
– коэффициент концентрации нагрузки, которым определяется неравномерность распределения нагрузок по длине контактных линий в результате погрешностей в зацеплении и деформации зубьев колеса и витков резьбы червяка,
– коэффициент динамической нагрузки, учитывающий динамическую нагрузку, возникающую в зацеплении, 
– допускаемые контактные напряжения, 
– расчетный момент на червячном колесе.
Число зубьев колеса 
в проектном расчете определяется по формуле (15.1) в зависимости от принятого числа заходов резьбы червяка 
и передаточного числа и передачи 
. Значение коэффициента диаметра червяка 
принимают стандартным. Предварительно принимают 
. В проектировочных расчетах предварительно принимают 
.
После определения расчетного межосевого расстояния его значения округляют до ближайшего стандартного. Находят модуль зацепления по зависимости (15.11) и полученное значение округляют до ближайшего стандартного. Для получения стандартных размеров передачи найденные значения корректируют величиной межосевого расстояния либо коэффициентом диаметра червяка 
, числом зубьев колеса , а затем определяются геометрические, кинематические и силовые параметры передачи.
Допускаемое контактное напряжение для зубьев червячных колес из оловянных и аналогичных им бронз определяют из условия сопротивления материала зубьев поверхностной усталости:
, (15.24)
где 
– предел прочности бронзы при растяжении (табл.15.4); 
– коэффициент твердости витков червяка при 
– 
, при 
– 
; KHL – коэффициент долговечности.
Коэффициент долговечности KHL определяют в зависимости от отношения 
– базового числа циклов нагружения, при котором определяется предел контактной выносливости и 
– эквивалентного числа нагружения зубьев передачи с учетом режима ее работы. Базовое число циклов напряжений в зубьях принимают для этих материалов 
. При эквивалентном числе циклов нагружения зубьев колес меньше базового 
, то принимают 
и коэффициент долговечности KHL =1. В случае когда эквивалентное число циклов нагружения зубьев больше базового то
. (15.25)
Если при расчете 
, то принимают 
и коэффициент долговечности в этом 
.
Таблица 15.4 Механические характеристики материалов червячных колес
|
Марка бронзы или чугуна |
Способ отливки |
σВ |
σВ.И |
σТ |
|
БрОФ10-1 |
В песок |
200 |
– |
120 |
|
БрОФ10-1 |
В кокиль |
260 |
– |
150 |
|
БрОФН |
Центробежный |
290 |
– |
170 |
|
БрАЖ9-4 |
В песок |
400 |
– |
200 |
|
СЧ15 |
В песок |
150 |
320 |
– |
|
СЧ18 |
В песок |
180 |
360 |
– |
Эквивалентное число циклов напряжений при работе передачи с постоянной нагрузкой
, (15.26)
где 
– частота вращения червячного колеса, 
; t – продолжительность работы передачи под нагрузкой за расчетный срок службы, ч.
При работе передачи с переменными нагрузками
, (15.27)
где Tmax максимальный крутящий момент, передаваемый зубчатым колесом в течение времени t0 за весь срок службы передачи при частоте вращения колеса п0; 
– передаваемые зубчатым колесом крутящие моменты в течение времени соответственно при частоте вращения 
.
Для материалов червячных колес из твердых бронз и чугунов с невысокими антифрикционными свойствами, материалов склонных к заеданию, значения допускаемых контактных напряжений представлены в таблице 15.5. в зависимости от скорости скольжения в передаче.
Таблица 15.5. Допускаемые контактные напряжения для материалов, склонных к заеданию
|
Материал |
Скорость скольжения υск, м/с |
|||||||
|
червячного колеса |
червяка |
0,5 |
1 |
2 |
3 |
4 |
6 |
8 |
|
БрАЖ9-4 |
Закаленная сталь |
220 |
215 |
210 |
205 |
200 |
190 |
180 |
|
СЧ15 или СЧ20 |
Сталь 20 или 20Х цементированная |
130 |
115 |
90 |
– |
– |
– |
– |
|
СЧ15 или СЧ18 |
Сталь 45 или Ст6 |
115 |
100 |
70 |
– |
– |
– |
– |
Расчеты на изгибную прочность зубьев. Расчет зубьев червячных колес на изгиб по сравнению с аналогичным расчетом зубьев зубчатых колес усложняется тем, что форма сечений зубьев червячных колес по ширине переменная и основания зубьев расположены не по прямой линии, а по дуге окружности. Проектировочный расчет зубьев червячных колес на изгибную прочность выполняется для отрытых передач прочность при этом определяется модуль зубьев передачи:
, (15.28)
где 
– коэффициент формы зуба колеса, 
– коэффициент концентрации нагрузки при изгибе зубьев, 
– коэффициент динамической нагрузки на изгиб, 
– угол подъема витков червяка и угла наклона зубьев колеса, (для червячных передач 
и 
), 
– допускаемые напряжения изгиба зуба колеса.
Коэффициенты и имеют те же значения, что и при расчете на контактную прочность, то есть 
и 
Значения коэффициента формы зубьев червячного колеса принимают по таблице 15.6. в зависимости от эквивалентного числа зубьев 
:
. (15.29)
Таблица 15.6. Коэффициент формы зуба червячного колеса
|
Zυ2 |
20 |
24 |
26 |
28 |
30 |
32 |
35 |
37 |
|
YF2 |
1,98 |
1,88 |
1,85 |
1,80 |
1,76 |
1,71 |
1,64 |
1,61 |
|
Zυ2 |
40 |
45 |
50 |
60 |
80 |
100 |
150 |
300 |
|
YF2 |
1,55 |
1,48 |
1,45 |
1,40 |
1,34 |
1,30 |
1,27 |
1,24 |
Допускаемое напряжение на изгиб 
для зубьев червячных колес из бронзы:
– при работе зубьев одной стороной
; (15.30)
– при работе зубьев обеими сторонами (в реверсивной передаче)
, (15.31)
где 
и 
– соответственно предел текучести и предел прочности при растяжении для бронзы (табл.15.4). 
– коэффициент долговечности.
, (15.32)
где 
– базовое число циклов на изгиб зубьев колеса, 
– эквивалентное число циклов нагружений на изгиб.
Базовое число циклов напряжений на изгиб 
, а эквивалентное число циклов напряжений при работе передачи с постоянной нагрузкой
, (15.33)
где – частота вращения рассчитываемого зубчатого колеса, ; t – продолжительность работы передачи под нагрузкой за расчетный срок службы, ч.
При работе передачи с переменными нагрузками
, (15.34)
где Tmax – максимальный крутящий момент, передаваемый зубчатым колесом в течение времени t0 за весь срок службы передачи при частоте вращения колеса п0; 
– передаваемые зубчатым колесом крутящие моменты в течение времени соответственно при частоте вращения 
.
Если 
, то принимают 
, а если 
, то принимают 
.
Допускаемое напряжение на изгиб 
для зубьев червячных колес из чугуна: при работе зубьев одной стороной
, (15.35)
а при работе зубьев обеими сторонами
, (15.36)
где 
– предел прочности чугуна при изгибе ( табл. 15.4).
Проверочные расчеты зубчатых передач.
Расчет зубьев на контактную прочность. Проверочный расчет зубьев червячных колес на контактную прочность выполняется по известным геометрическим параметрам передачи по зависимости:
. (15.37)
При постоянной нагрузке коэффициент концентрации нагрузки 
, а при переменной зависит от жесткости червяка и определяется по зависимости
, (15.38)
где 
– коэффициент деформации червяка, который определяется по табл.15.7; х – коэффициент, учитывающий характер изменения нагрузки; при постоянной нагрузке х = 1, при переменной и при значительных колебаниях нагрузки .
Таблица 15.7 Коэффициент деформации червяка
|
Z1 |
Коэффициент деформации |
||||||
|
7,5 |
8 |
9 |
10 |
12 |
14 |
16 |
|
|
1 |
63 |
72 |
89 |
108 |
147 |
179 |
194 |
|
2 |
50 |
57 |
71 |
86 |
117 |
149 |
163 |
|
3 |
46 |
51 |
61 |
76 |
103 |
131 |
144 |
|
4 |
42 |
47 |
58 |
70 |
94 |
120 |
131 |
Коэффициент динамической нагрузки KHv зависит от скорости скольжения и степени точности передачи. Значения коэффициента принимается по таблице 15.8.
Таблица 15.8 Коэффициент 
динамической нагрузки червячной передачи
|
Степень точности |
Скорость скольжения υs, м/с |
|||
|
до 1,5 |
св. 1,5 до 3 |
св. 3 до 7,5 |
св. 7,5 до 12 |
|
|
6 – я |
– |
– |
1 |
1,1 |
|
7 – я |
1 |
1 |
1,1 |
1,2 |
|
8 – я |
1,15 |
1,25 |
1,4 |
– |
|
9 – я |
1,25 |
– |
– |
– |
При действии в червячной передаче кратковременных перегрузок требуется проверка рабочих поверхностей зубьев червячных колес на контактную прочность по максимальному контактному напряжению:
, (15.39)
где 
– максимальное расчетное напряжение при перегрузке зубьев максимальным моментом 
; 
– допускаемое максимальное контактное напряжение для зубьев червячных колес; 
– расчетное контактное напряжение, вызываемое расчетным моментом 
и определяемое по формуле (15.24).
Для зубьев червячных колес из оловянистых бронз 
, где 
– предел текучести материала зубьев при растяжении; для зубьев из безоловянистых бронз 
, для зубьев из чугуна 
Расчет зубьев на изгибную прочность. Проверочный расчет зубьев червячного колеса на изгиб выполняется по известным геометрическим параметрам передачи при выбранной степени точности изготовления зубьев колес по зависимости
. (15.40)
Для червячного колеса при действии кратковременных перегрузок зубья колес проверяют на пластическую деформацию или хрупкий излом при изгибе от максимальной нагрузки:
, (15.41)
где 
– максимальное расчетное напряжение на изгиб в зубьях черовячного колеса при их перегрузке максимальным моментом 
; 
– допускаемое максимальное напряжение на изгиб для зубьев; 
– расчетное напряжение на изгиб для зубьев, вызываемое расчетным моментом 
и определяемое по формуле (15.40).
Значение допускаемых максимальных напряжений на изгиб для зубьев из бронз 
, для зубьев из чугуна 
(табл.15.5).
Задача 15.1. Выполнить расчет червячной передачи. Выполнить проектный и проверочный расчеты (на контактную и изгибную прочность) червячной передачи. Параметры циклограммы нагружения червячного колеса: момент на колесе 
, продолжительность работы 
; 
, 
; 
, 
. Передаточное число 
, передача нереверсивная. Частота вращения червяка 
. Материал червяка – сталь 40ХН с поверхностной закалкой ТВЧ до твердости поверхности витков 
.
Решение. Проектный расчет. Выбор материала венца червячного колеса.
Предварительно принимаем оловянную бронзу БрО10Ф-1, отлитую в кокиль с характеристиками (табл.15.4) предел текучести 
МПа и предел прочности 
МПа.
Выбор числа витков червяка. При передаточном числе червячной передачи 
принимаем число витков червяка 
.
Число зубьев червячного колеса (15.1)
.
Принимаем 
.
Уточняем фактическое передаточное отношение
=
.
Проверка отклонения передаточного отношения от номинального
.
Выбор коэффициента диаметра червяка. Предварительно принимаем 
Выбираем ближайший больший стандартный коэффициента диаметра червяка 
.
Частота вращения червячного колеса
.
Определение эквивалентного числа циклов нагружений зубьев колеса при работе передачи с переменными нагрузками и постоянной частоте вращения по (15.27)
Коэффициент долговечности при расчете на контактную прочность по (15.25)
0,84.
Допустимые контактные напряжения для червячного колеса для материала БрО10Ф-1 по табл.15.4 и формуле (15.24)
,
где 
– коэффициент твердости витков червяка при 
– 
.
Расчетное межосевое расстояние передачи по формуле (15.23)
=
= 244,9мм.
где предварительно принимаем 
.
Принимаем ближайшее стандартное значение межосевого расстояния 
250мм.
Расчетный модуль червячной передаче по формуле (15.11)
8,7мм.
Принимаем ближайшее стандартное значение модуля 
мм.
Уточнение межосевого расстояния для червячного зацепления без смещения по формуле (15.10)
230мм.
Для получения выбранного стандартного межосевого расстояния принимаем новое значение коэффициента диаметра червяка 
.
Фактическое межосевое расстояние
244мм.
Проверка отклонения межосевого расстояния от стандартного номинального
.
Расчет геометрических и кинематических параметров передачи (рис.15.1)
Делительные и начальные диаметры червяка и колеса по формулам (15.3) и (15.4):
=128мм,
= 360мм.
Диаметры вершин червяка и колеса по формулам (15.5) и (15.6):
=144мм,
= 376мм.
Диаметры впадин червяка и колеса по формулам (15.7) и (15.8):
= 108,8мм,
= 340,8мм.
Высота зубьев и витков по формуле (15.9)
= 17,6мм
Наибольший диаметр червячного колеса определяется по формуле (15.15)
388мм.
Ширина венца зубчатого колеса при 
= 108мм.
Принимаем стандартный размер 
мм.
Условный угол обхвата 
червяка венцом зубчатого колеса определяется по (15.13):
= 0,75.
= 48,60.
Длина нарезанной части червяка по формуле (15.14) при
= 109,6мм.
Принимаем стандартное значение 
110мм.
Тангенс угол подъема линий витка червяка и наклона зубьев колеса по формуле (15.2):
0,125.
По табл. 15.1 определяем угол подъема 
.
Окружная скорость по формуле (15.15):
для червяка 
= 6,5м/с,
для колеса 
= 0,82м/с.
Скорость скольжения по формуле (15.16)
= 6,55м/с.
При данной окружной скорости колеса по табл. 15.2 принимаем 7-ую степень точности червячной передачи.
Проверочные расчеты червячной передачи Проверочный расчет на контактную прочность зубьев червячного колеса.
Определение коэффициента концентрации нагрузки 
.
При переменной нагрузке коэффициент концентрации нагрузки зависит от жесткости червяка и определяется по формуле (15.38).
1,0.
где 
– коэффициент деформации червяка, который определяется по табл.15.7; х – коэффициент, учитывающий характер изменения нагрузки при переменной 
.
Определение коэффициента динамической нагрузки 
.
Коэффициент динамической нагрузки KHv зависит от скорости скольжения и степени точности передачи и определяется по таблице 15.8. При 7-ой степени точности и скорости скольжения 
6,55м/с, 
=1,1.
Расчетное контактное напряжение на зубьях червячного колеса по формуле (15.37)
Следовательно, условие контактной прочности выполняется.
Проверочный расчет на изгибную прочность зубьев червячного колеса.
Эквивалентное число циклов нагружений зубьев колеса на изгиб при переменной нагрузке и постоянной частоте вращения по формуле (15.34)
=
циклов.
Коэффициент долговечности зубьев на изгиб определяется по формуле (15.32)
0,7.
Допускаемые напряжения изгиба зубьев по формуле (15.30)
Для зубьев червячных колес из бронзы при работе зубьев одной стороной
40,8МПа.
где прочностные характеристики материала БрО10Ф-1 по табл.15.4 
=150МПа – предел текучести, 
=260МПа – предел прочности.
Эквивалентное число зубьев червячного колеса по формуле (15.29)
46.
Коэффициент формы зуба червячного колеса по таблице 15.6. 
1,49.
Принимаем 
1,1.
Расчетные напряжения изгиба зубьев червячного колеса по формуле (15.40)
Следовательно, условие прочности зубьев червячного колеса на изгиб обеспечено.
КПД спроектированного редуктора по формуле (15.21)
0,78…0,79.
Опубликовано 05 Окт 2014 Рубрика: Механика |
Червячная передача оказывается в реальной практике инженера, как ни странно, наиболее часто востребованной, смещая на второй план и зубчатую, и цепную, и ременную передачи. Причинами такого положения дел являются простота и общая итоговая дешевизна изготовления…
…червячной передачи при ее высокой компактности с возможностью получения очень большого передаточного числа, а при необходимости и обеспечения условия самоторможения.
Червячная передача работает плавно и бесшумно. Минусом червячной передачи является низкий КПД и, как следствие, нагревание (иногда достаточно сильное) при работе.
Для изготовления элементов зацепления червячной передачи нужны токарный и зубофрезерный станки. Червяк легко изготовит токарь средней квалификации, а зубофрезеровщику нужно будет нарезать всего одно червячное колесо (при изготовлении зубчатой передачи нужно нарезать шестерню и колесо). В идеале профиль, диаметр, шаг и число заходов червячной фрезы для нарезания зубьев колеса должны быть точно такими же, как и у червяка. То есть — фреза должна быть своеобразной копией червяка.
Червячные передачи бывают с цилиндрическими архимедовыми, цилиндрическими эвольвентными, цилиндрическими конволютными и вогнутыми глобоидными червяками. В этой статье будет рассмотрена получившая наиболее широкое распространение червячная передача с архимедовым червяком.
Для унификации (минимизации номенклатуры) зубонарезного инструмента и повышения взаимозаменяемости червяков и колес значения межосевых расстояний aw и номинальных значений передаточных чисел u червячных передач регламентируются ГОСТ 2144-76, а значения модулей m и коэффициентов диаметра червяка q — ГОСТ 19672–74.
Червяки традиционно изготавливают из закаленной конструкционной стали, а зубчатые венцы колес – чаще всего из бронзы или чугуна.
На рисунке ниже показано сечение червяка и червячного колеса плоскостью проходящей через центр колеса и перпендикулярной оси червяка.
Уважающих труд автора прошу скачать файл после подписки на анонсы статей (подписные формы — в конце статьи и наверху страницы).
Ссылка на скачивание файла программы: raschet-chervyachnoy-peredachi (xls 197KB).
Программа размещена на 6-и листах файла MS Excel.
Уникальность программы состоит в том, что она, представляя собой три независимых блока, позволяет выполнить «прямой» проектный, «обратный» проектный и «ремонтный» расчеты!
1. «Прямой» проектный расчет в Excel размещен на листе «Проект-1».
По 9-и исходным данным программа выдает 57 расчетных параметров и на листе «Проект-1 (табл.)» автоматически формирует таблицы к чертежам червяка и червячного колеса!
Пользователь выбирает режим работы передачи, расчетный ресурс, передаточное число, материал червячного колеса, вводит значения частоты вращения червяка и вращающего момента на валу червячного колеса и через мгновение получает выполненный расчет червячной передачи!!!
По заданным нагрузкам и скоростям рассчитываются геометрические параметры передачи.
2. «Обратный» проектный расчет червячной передачи размещен на листе «Проект-2».
По 12-и исходным данным программа рассчитывает 46 параметров и на листе «Проект-2 (табл.)» также автоматически формирует таблицы к чертежам червяка и червячного колеса!
В отличие от первого варианта расчета в данном случае пользователь может, задав основные геометрические параметры передачи, определить ее нагрузочную способность – рассчитать максимально допустимый момент на валу червячного колеса.
3. «Ремонтный» расчет передачи в Excel размещен на листе «Ремонт».
По 6-и данным, полученным в результате замеров вышедшей из строя червячной передачи, программа вычисляет 20 геометрических параметров и на листе «Ремонт(табл.)» автоматически формирует таблицы к чертежам!
Получив эти данные, можно воспользоваться расчетом «Проект-2» и определить нагрузочные возможности ремонтируемой червячной пары.
Способы определения передаточного числа редуктора
Существует несколько возможностей определить передаточное отношение червячного редуктора без специальных инструментов и навыков. Данную процедуру проделает любой.
Самый популярный и простой способ определения передаточного числа не только червячного редуктора (он подходит ко всем видам: цилиндрический, конический и т. д.) не требующий разборки агрегата, а определяется на месте, если есть возможность прокрутить валы – быстроходный вал прокручивается столько раз, чтобы тихоходный вал сделал один оборот. Какое количество оборотов будет у быстроходного вала в итоге, то и есть передаточное число редуктора. Согласитесь, не сложно.
Этот способ будет посложнее, но и в нем нет ничего уникального. Он подойдет тем, кто хочет подобрать червячную пару на уже существующий корпус редуктора с дальнейшей его сборкой и установкой на место работы. Или для тех, у кого старый редуктор вышел из строя и прокрутить валы не представляется возможным. Причин может быть много, решение одно:
- Нужно посчитать количество зубьев на червячном колесе:
- Потом количество заходов витка на валу червяка:
И теперь делим количество заходов витка на количество зубьев колеса, получаем передаточное число редуктора.
*витков на валу может быть от 1 до 10 в зависимости от типа редуктора.
Червячная передача
Червячная передача состоит из червячного колеса и червяка. Последний представляет собой винт с одним или несколькими витками (заходами), например с тремя (рис. 9.25), определенного профиля.
Различают передачи с цилиндрическим червяком — делительные поверхности у червяка и колеса цилиндрические (рис. 9.26, а) и глобоидным — делительная поверхность у червяка является частью поверхности тора (рис. 9.26,6), у колеса — цилиндрическая (рис. 9.26, в).
Примечание. На рисунках обозначения даны как бы для разъединенных колес и червяков. Поэтому для удобства дальнейшего их использования опущены нижние индексы «w».
Боковые поверхности витков могут быть линейчатыми (геликоидными) и нелинейчатыми.
Наиболее широко применяют три типа линейчатых цилиндрических червяков: архимедов (ZA), эвольвентный (ZI) и конволютный (ZN).
У архимедова червяка боковые поверхности винтовых витков ограничены архимедовыми геликоидами, их торцовые сечения (торцовый профиль) — спиралями Архимеда (см. рис. 9.25) При их изготовлении направление режущей прямолинейной кромки резца, образующей поверхность, пересекает геометрическую ось червяка под некоторым постоянным углом.
У эвольвентного червяка аналогичные поверхности ограничены эвольвентными (развертывающимися) геликоидами. Их торцовые сечения — эвольвенты окружности (см. рис. 9.25). Направления режущих кромок резцов касательны к винтовым линиям червяка.
У конволютного червяка аналогичные поверхности — конволютные геликоиды. Их торцовые сечения — удлиненные или укороченные эвольвенты (см. рис. 8.10). Направления режущих кромок резцов касательны к цилиндрическим поверхностям, оси которых совпадают с осью червяка.
Осевое сечение витков указанных червяков — равнобочная трапеция с углом 40°. У некорригированных червячных передач aw=0,5(d1+d2), высоты головки зуба колеса и витка червяка равны модулю m=р/pi (см. рис. 9.26), ножек—1,2m.
Делительный диаметр колеса d2, как и у некорригированных цилиндрических и конических зубчатых передач, равен mz2.
Следовательно, диаметр окружности вершин зубьев
da2 = d2 + 2m = m (z2+2), впадин — df2=m(z2—2,4).
Делительный диаметр червяка d1=mq, где q— коэффициент червяка, значения которого приведены в ГОСТ 2144—76*. Диаметр вершин витков червяка da1=d1+2m=m(q+2), впадин df1=m(q-2,4)=d1-2,4m.
Вместо числа зубьев у червяка указывают число витков z1 (заходов), равное 1…4. В число параметров передачи входит ход витка — p21=pz1=pi*m*z1 и делительный угол подъема линии витка ?=p/pi*d1.
На рабочих чертежах червяков и колес часть параметров помещают на изображениях, часть — в таблицах, аналогичных
указанным на рис. 9.13 и 9.21. Их полное содержание см. в ГОСТ 2.406—76* для цилиндрических червяков и колес и в ГОСТ 2.407—75 — для глобоидных.
На учебных чертежах некоторые графы таблиц оставляют незаполненными или исключают (рис. 9.27 и 9.28). При составлении чертежа (эскиза, см; в п. 10.1) с натуры измеряют возможно точнее da (у колес и глобоидных червяков в среднем сечении), высоту витка или зуба и, принимая h=2,2m, вычисляют модуль. Полученные значения сверяют со стандартными модулями (см. с. 291) и при расхождении принимают ближайшее, используемое в дальнейших расчетах. Измеряют р, подсчитывают z1 и z2.
Делительный диаметр червяка определяют из формулы d1=da1-2m. Зная d1 и т, можно определить q— коэффициент диаметра червяка, который можно использовать для уточнения расчетов, так как он может иметь значения 8; 9; 10; 11,2; 12,5; 14; 16; 18; 20; 25 (ГОСТ 2144—76*).
Угол подъема вычисляют по формуле (с точностью до минут) или определяют измерением его на развертке поверхности цилиндрического червяка, которую легко получить, обернув червяк листом бумаги и оттиснув на нем винтовые линии.
Если чертежи червяка и колеса выполняют при деталировании чертежа общего вида, то он должен содержать соответствующие параметры. При их отсутствии параметры определяют путем обмера соответствующих элементов изображения.
Изображение червяков надо выполнять, как показано на рис. 9.27 и 9.29.
Шероховатость боковых поверхностей зубьев и витков наносят на линиях делительных поверхностей.
Изготовляют червяки и колеса из стали (например, стали 45, 40Х и др.), бронзы (например, БрОЦО5-3-5) и полимеров. Для экономии дорогостоящей бронзы из нее изготовляют только зубчатый венец, укрепляемый тем или иным способом на ступице из чугуна или дешевой стали (рис. 9.30). Такие чертежи оформляют как сборочные.
Нарезание червячных колес
При проектировании создается модель червячного колеса. По ней легко определится со способом нарезки:
Торцевой требует инструмента, в точности повторяющего червяк. Дает хорошую точность и чистоту обработки. Фрезу выставлять сложно, необходимо, чтобы в конце обработки она имела положение относительно колеса, в точности соответствующее червяку.
Нарезка зубьев на венце
По наружному диаметру червячное колесо имеет полукруглое углубление. Это позволяет лучше прилегать деталям по эвольвенте и смещать ось, увеличивая площадь контакта. Центр радиуса углубления должен совпадать с осью червяка.
Фрезы для нарезания червячного колеса должны быть с таким же наружным диаметром, как червяк. Внешне она повторяет форму ведущей детали, только вместо непрерывной линии резьбы ряды резцов. Режущая пластина по форме точно повторяет нитку резьбы, но шире нее на размер зазора. В результате конфигурация ответной детали – червячного колеса, точно повторяет формы резьбы, впадины совпадают с выступами нитей.
Фреза выставляется в плоскости оси червяка, касаясь его поверхности. Зубчатый венец вращается вокруг вертикальной оправки или собственного вала, обеспечивая тангенциальную подачу наружной поверхности относительно оси режущего инструмента. Нарезка червячных колес происходит при синхронном движении инструмента и детали, вращающихся вокруг своих осей. Отношение скорости вращения определяется передаточным числом. С каждым оборотом венец придвигается ближе к вращающейся фрезе.
Подача режущего инструмента возможна снизу и сверху. Но в большинстве случаев используют радиальную нарезку, как наиболее удобную и точную.
Ремонтная нарезка
Иногда надо сделать одну деталь, чтобы заменить ее в редукторе. В мастерской не всегда имеется полный набор фрез со всеми нормализованными диаметрами.
Если червячное колесо нарезать фрезой большим диаметром, чем радиус червяка, то прилегание будет хуже, пятно контакта меньше. Линия скольжения сместится к вершине зуба. При нарезке меньшим диаметром с таким же модулем, нагрузка будет на вершину нити резьбы. Погрешность можно компенсировать смещением инструмента и регулировкой расстояния между осями. Но трение и износ все равно будут больше, КПД упадет.
Нарезать червячное колесо фрезой с диаметром больше червяка можно для беззазорного сцепления. В этом случае используется специальная фреза с разными углами профиля для правой и левой стороны. Ось фрезы выворачивается в сторону увеличения наклона зуба. Обычные зубофрезерные станки надо переделывать для обработки беззазорного сцепления.
Из-за отсутствия зазора между рабочими элементами, поверхность быстро стирается и приходится постоянно производить регулировку. Беззазорные сцепления применяются при высокой точности и большой нагрузке с малой активностью пары, например, в прокатных станах для регулировки прижима валков – толщины прокатываемого металла.
Для изготовления одного или нескольких колес с нестандартными размерами может применяться оправка с одним резцом по форме впадины между зубьями. Инструмент вращается постоянно. Колесо вращается синхронно с инструментом. После каждого оборота реза проворачивается на размер модуля зуба и за полный оборот, подвигается к оправке с резцом на глубину реза.
Недостаток способа изготовления венца в длительности процесса. Один резец обрабатывает деталь в несколько раз дольше, чем фреза. Учитывая стирание резца, надо делать черновую и чистовую обработку.
Червячное колесо отличается от других своим внешним видом и способом обработки. Оно делается точно под определенный червяк.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Конструкции и расчет редукторов
бенности для оловяниетых бронз, имеющих пониженные пределы прочности. При неизменном межосевом расстоянии с увеличением z2 напряжения изгиба зубьев колеса возрастают, так как одновременно с уменьшением модуля уменьшаются диаметр червяка и ширина колеса, которая пропорциональна наружному диаметру червяка. Зубья червячных колес могут быть нарезаны червячными фрезами или фасонными резцами.
Параметры червячных передач следует выбирать с таким расчетом, чтобы колесо можно было нарезать червячной фрезой. Нарезка зубьев червячных колес „летучкой” производительнее, но качество зацепления более низкое, чем при нарезке червячной фрезой.
При нарезании червячных колес „летучкой” число зубьев z2 не должно содержать общих множителей с числом витков червяка (z1).
Число заходов червяка выбирается по табл. 250. С увеличением числа заходов червяка при заданном коэффициенте диаметра червяка q увеличивается значение делительного угла подъема γ, а следовательно, уменьшаются потери на трение в зацеплении, т. е. повышается КПД редуктора. Одновременно увеличивается диаметр червячного колеса и габаритные размеры редуктора. Вследствие увеличения диаметра колеса уменьшаются усилия в зацеплении, что позволяет уменьшить размеры подшипниковых опор или увеличить их долговечность. Если для обеспечения заданного передаточного числа приходится уменьшить число заходов червяка, то КПД передачи снизится.
При кратковременной работе передачи с большими (относительно величины времени цикла) перерывами в целях получения наибольшей компактности передачи рационально назначать наименьшее значение z1, так как в этом случае понижение КПД передачи, вследствие уменьшения угла γ, не окажет существенного влияния на тепловой баланс редуктора. При продолжительной работе редуктора и больших передаваемых мощностях первостепенное значение будет иметь КПД редуктора.
В этом случае малые значения z1, повлекут за собой увеличение потерь на трение в зацеплении, вследствие чего могут возникнуть затруднения в обеспечении теплового баланса. В подобных случаях при и> 15 рекомендуется z1 = 2, а число зубьев z2 должно равняться 50…80.
Коэффициент диаметра червяка q характеризует относительную толщину червяка и должен быть равен 8…20.
При выборе коэффициента q необходимо учитывать следующее: при заданном передаточном числе требуемое межосевое расстояние, обеспечивающее контактную прочность поверхностей зубьев колеса и витков червяка, можно получить соответствующим подбором модуля m число заходов червяка z1 и коэффициента q, так чтобы соблюдалось условие
При наличии корригирования аω = 0,5m(q + z2 + 2х).
Расчет геометрических параметров
Число зубьев червячного колеса z2 В общем случае: z2=uz1=20·2=40;
округляется до ближайшего целого числа; допускается изменение величины z2, после чего уточняется окончательное значение u
Принимаем z2 = 39. Уточненное значение u = 39:2 = 19,5
Продолжение табл. 128
| Параметры и обозначения | Формулы и указания | Числовые значения | |
| Коэффициент смещения червяка x | x= aw/m– 0,5(z2+q)=160/6,3-0,5(39+10)
Коэффициент смещения червяка рекомендуется принимать в пределах 1 ≥ x >-1 |
0,897 | |
| Межосевое расстояние (если х входит в исходные данные) aw | aw = 0,5(z2+q+2x)m | — | |
| Расчет диаметров червяка и червячного колeca | |||
| Делительный диаметр:
червяка d1 колеса d2 |
d1 = qm = 10·6,3
d2 = z2m = 39·6,3 |
63мм
245,7мм |
|
| Начальный диаметр червяка dw1
Делительный угол подъема γ Начальный угол подъема γw Основной угол подъема γb |
74,30мм
γ = 11º19′ γw = 9º37′ γb= 22°52′ |
||
| Основной диаметр червяка db
Высота витка червяка h1 Читайте также: Как сделать сбросной клапан для компрессора Высота головки витка червяка hа1 |
29,89мм
13,84мм 6,3мм |
||
| Диаметр вершин | витков червяка da1
зубьев колеса da2 |
75,6мм
269,6мм |
|
| Наибольший диаметр червячного колеса dаe2 | 279,05мм
Принимаем dae2=279мм |
||
Расчет размеров, характеризующих форму нарезанной части червяка и венца червячного колеса
Радиус кривизны переходной кривой червяка pf1
Длина нарезанной части червяка b1
pf1 = pf*m = 0,3·6,3
Определяют по формулам табл. 129
b1 ≥ (12 + 0,1z2)m = (12 + 0,1 · 39)6,3 = 100,17мм
1,9мм
Принимаем для шлифованного червяка b1=125мм
Ширина венца червячного колеса b2 Рекомендуется принимать:
b2 ≤ 0,75da1 при z1 ≤ 3;
b2 ≤ 0,67da1 при z1=4;
В данном примере
b2 = 0,75da1=0,75·75,6
56,7мм; принимаем b2=55мм
