Как найти четные примеры

Что такое чётная функция

Обратимся к определению чётности функции через формулу.

Другими словами, нужно в формулу функции вместо «x» подставить
«−x». Затем сравнить полученный результат с формулой исходной функцией.

Если в итоге «y(−x)» будет равен исходной функции
«y(x)», значит, эта функция чётная.

Давайте разбираться на практике.

Разбор примера

Выяснить, является ли функция чётной или нечётной:

у = 2x⁴

Подставим «−x» вместо «x» в исходную функцию «у = 2x⁴».
Если в итоге мы получим исходную функцию, значит, она чётная.

у(−x) = 2(−x)⁴ = …

При возведении в чётную степень
отрицательного числа всегда
получается положительное число.

у(−x) = 2(−x)⁴ = 2x⁴

Проверим, выполняется ли условие чётности функции «у(−x) = у(x)».

у(−x) = у(x) Значит, функция у = 2x4 чётная

После подстановки «−x»
мы получили исходную функцию «у = 2x⁴». Условие чётности функции
«у(−x) = у(x)» выполнено.

Ответ: функция «у = 2x⁴» чётная.

Что такое нечётная функция

Порядок анализа функции на нечётность:

1. подставить «−x» в исходную функцию, чтобы получить «у(−x)»;
2. вычислить «−у(x)»;
3. сравнить «у(−x)» и «−у(x)». Если они равны,
   то функция нечётная.

Разбор примера

Выяснить, является ли функция чётной или нечётной:

у = 3x ⁵

Подставим «−x» вместо «x» в формулу функции
«у(x) = 3x ⁵».

у(−x) = 3(−x) ⁵ = …

При возведении в нечётную степень
отрицательного числа получается отрицательное число.

у(−x) = 3(−x) ⁵ = −3x ⁵

Теперь получим «−у(x)».
Для этого умножим левую и правую часть исходной функции
«у = 3x ⁵»
на «−1».

Сравним полученные результаты «у(−x)» и
«−у(x)».

у(−x) = −3x5 −у(x) = −3x5

у(−x) = −у(x) Значит, функция у(x) = 3x 5 является нечётной

Ответ: функция «у(x) = 3x ⁵» нечётная.

Функции, которые не являются ни чётными, ни нечётными

Разбор примера

Выяснить, является ли функция чётной или нечётной:

у = x ³ − 2

Проверим, является ли функция
«у = x ³ − 2» чётной.
По определению чётной функции
должно выполняться условие
«у(−x) = у(x)».

Подставим «−x» вместо «x» в исходную функцию
«у = x ³ − 2».

у(−x) = (−x) ³ − 2 = …

Возведение в нечётную степень отрицательного числа даст отрицательное число.

у(−x) = (−x) ³ − 2 =
−x ³ − 2

Сравним исходную функцию «y(x)» и полученную «y(−x)»,
чтобы проверить, является ли функция «у = x ³ − 2» чётной.

у(x) = x 3 − 2 у(−x) = −x 3 − 2

у(−x) ≠ у(−x) Функция у(x) = x 3 − 2 не является чётной

Теперь проверим, является ли функция «у(x) = x ³ − 2»
нечётной. По определению
нечётной функции
должно выполняться условие:
«у(−x) = −у(x)».

Функцию «у(−x)» мы рассчитали выше. Осталось вычислить
«−у(x)». Для этого умножим левую и правую часть исходной функции
«у = x ³ − 2»
на «−1».

Используем
правило раскрытия скобок.
Так как перед скобкой «(x ³ − 2)» стоит знак минуса, все слагаемые
внутри поменяют знак на противоположный.

Сравним «−y(x)» и «−y(x)».

у(−x) = −x 3 − 2 −у(x) = −x 3 + 2

у(−x) ≠ у(−x) Функция «у(x) = x 3 − 2» не является нечётной

Ответ: функция «у(x) = x ³ − 2» не является ни чётной, ни нечётной.

Другие примеры чётных и нечётных функций

Разбор примера

Выяснить, является ли функция чётной или нечётной:

у = x ² − x + 1

Проверим, является ли функция
«у = x ² − x + 1» чётной,
то есть должно выполняться условие
«у(−x) = у(x)».

Подставим «−x» вместо «x» в формулу функции.

у(−x) = (−x) ² − (−x) + 1 = …

При возведении в чётную степень получается положительное число.

Раскроем скобки «− (−x)» по правилу раскрытия скобок: минус на минус даёт плюс.

Сравним полученную «у(−x)» с исходной функцией «у(x)».

у(x) = x 2 − x + 1 у(−x) = x 2 + x + 1

у(−x) ≠ у(−x) Функция у(x) = = x 2 − x + 1 не является чётной

Проверим, является ли функция
«у = x ² − x + 1»
нечётной функцией.
Для этого должно выполняться условие:
«у(−x) = −у(x)».

Выражение «у(−x)»
мы уже посчитали выше. Теперь вычислим «у(−x)».
Умножим левую и правую часть исходной функции на «(−1)».

Используем правило раскрытия скобок.
При умножении на «(−1)» все слагаемые внутри скобок
поменяют свой знак на противоположный.

−у(x) = −x ² + x − 1

Сравним полученные «у(−x)» и «−у(x)».

у(−x) = x 2 + x + 1 −у(x) = = −x 2 + x − 1

у(−x) ≠ у(−x) Функция у(x) = x 2 − x + 1 не является нечётной

Ответ: функция «у = x ² − x + 1» не является ни чётной, ни нечётной.

---

Разбор примера

Исследуйте на чётность функцию:

у = √x − 1 · √x + 1

По определению чётности функции «у(−x) = у(x)». Вычислим «у(−x)»,
подставив «(−x)» вместо «x».

Вынесем «(−1)» из каждого корня. После этого каждое слагаемое внутри корней поменяет знак на противоположный.

Умножим «(−1)» на «(−1)»,
используя правило знака: минус на минус дает плюс.

От перемены мест множителей произведение не меняется. Поменяем местами
«√x − 1» и
«√x + 1».

Проверим, выполняется ли
условие чётности
функции «у(−x) = у(x)».

у(x) = = √x − 1 · √x + 1 у(−x) = = √x − 1 · √x + 1

у(−x) = у(x) Функция у = = √x − 1 · √x + 1 является чётной

Ответ: функция «у = √x − 1 · √x + 1» является чётной.

---

Разбор примера

Показать, что функция не является чётной и не является нечётной:

По определению чётности функции «y(−x) = y(x)».
Вычислим «y(−x)».

Подставим «−x» в исходную функцию
«у = ».

Сравним «у(−x)» и «у(x)».

у(−x) ≠ у(x) Значит, функция y = не является чётной

Проверим функцию «y = » на нечётность.

По определению нечётности функции «y(−x) = −y(x)». Функцию
«y(−x)» мы вычислили ранее. Вычислим «−y(x)».

Для этого умножим левую и правую часть исходной функции
на «−1».

Сравним «у(−x)» и «−у(x)».

у(−x) ≠ −у(x) Значит, функция y = не является нечётной

Ответ: функция «y = »
не является ни чётной, ни нечётной.

---

Ваши комментарии

Оставить комментарий:

---

Была ли эта статья полезной?

Чётные и нечётные функции

11 декабря 2021

Сегодня мы разберём:

1. Определение чётных и нечётных функций
2. Как проверить, является функция чётной или нечётной
3. Как выглядят графики чётных и нечётных функций
4. Дополнение. Задачи с параметром

1. Определение

Определение 1. Функция $fleft( x right)$, определённая на множестве $M$, называется чётной, если:

1. $M$ — симметричное относительно нуля множество.
2. $fleft( -x right)=fleft( x right)$.

Определение 2. Функция $fleft( x right)$, определённая на множестве $M$, называется нечётной, если:

1. $M$ — симметричное относительно нуля множество.
2. $fleft( -x right)=-fleft( x right)$.

Определение 3. Во всех остальные случаях, когда функция $fleft( x right)$ не является ни чётной,
ни нечётной, её называют функцией общего вида.

Примеры чётных функций:

• Квадратичная: $fleft( x right)={{x}^{2}}$; любая степенная функция с чётным показателем: ${{x}^{4}}$, ${{x}^{8}},$ да хоть ${{x}^{128}}$.
• Модуль: $fleft( x right)=left| x right|$. С модулем будет отдельный разговор — он обращает любую функцию в чётную.

Примеры нечётных функций:

• Любая степенная функция с нечётным показателем: $fleft( x right)={{x}^{3}}$, ${{x}^{5}}$, ${{x}^{2n+1}}$.
• Корень третьей степени: $fleft( x right)=sqrt[3]{x}$.
• Обратная пропорциональность: $fleft( x right)={1}/{x};$.

2. Исследование функции на чётность

Чтобы узнать, является функция чётной или нечётной (или вообще общего вида), нужны две проверки:

1. Область определения. Если она не симметрична относительно нуля, то функция общего вида. Если симметрична — переходим ко второй проверке.
2. Зная $fleft( x right)$, считаем $fleft( -x right)$ и $-fleft( x right)$. Если $fleft( -x right)=-fleft( x right)$, то функция нечётная. А если $fleft( -x right)=fleft( x right)$, то функция чётная.

Главное, чтобы функция была задана формулой, а не таблицей, графиком или ещё как. Тогда исследование на чётность занимает несколько секунд. Мы сейчас убедимся в этом, но сначала важное замечание.

Что значит «симметричное относительно нуля множество»? Это значит, что если $xin M$, то и $-xin M$. Малейшее нарушение этого правила — хотя бы в одной точке — и множество уже не симметрично.

Примеры симметричных множеств:

[begin{align} & left( -infty ;+infty right) \ & left( -5;0 right)bigcup left( 0;5 right) \ & left[ -sqrt{2}-1;sqrt{2}+1 right] \ end{align}]

Примеры несимметричных множеств:

[begin{align} & left( -infty ;9 right)bigcup left( 9;+infty right) \ & left[ -3;3 right) \ & left[ 0;+infty right) \ end{align}]

Первые два множества несимметричны всего в одной точке (кстати, какой?). Но этого достаточно, чтобы прекратить исследование и отнести функцию к общему виду.

Разберём несколько примеров. Для начала — стандартный:

Исследуйте на чётность / нечётность функцию

[fleft( x right)={{x}^{3}}-4x]

Эта функция определена для всех действительных чисел: $xin mathbb{R}$. Это симметричное относительно нуля множество. Пока всё хорошо.

Считаем $fleft( -x right)$ и $-fleft( x right)$:

[begin{align} fleft( -x right) & ={{left( -x right)}^{3}}-4cdot left( -x right)= \ & =-{{x}^{3}}+4x; \ -fleft( x right) & =-left( {{x}^{3}}-4x right)= \ & =-{{x}^{3}}+4x end{align}]

Получили, что $fleft( -x right)=-fleft( x right)$. Значит, функция нечётная.

А вот более хитрый случай:

Исследуйте на чётность / нечётность функцию

[fleft( x right)=frac{x}{4-x}]

Область определения. Перед нами рациональная дробь. Её знаменатель должен быть отличен от нуля:

[begin{align} 4-x & ne 0 \ x & ne 4 \ end{align}]

Следовательно, область определения

[M=left( -infty ;4 right)bigcup left( 4;+infty right)]

Это множество несимметрично, поскольку $x=-4$ принадлежит этому множеству, а $x=4$ не принадлежит. Всё: функция $fleft( x right)$ — общего вида.

Дальше попробуйте сами:

Исследуйте на чётность / нечётность функцию

[begin{align} fleft( x right) & =frac{x-3}{x-3} \ gleft( x right) & =frac{3}{2+left| x right|} \ kleft( x right) & ={{left( 5-x right)}^{3}}-{{left( 5+x right)}^{3}} \ end{align}]

Ответ: $fleft( x right)$ — общего вида; $gleft( x right)$ — чётная; $kleft( x right)$ — нечётная.

Умение быстро определять чётность — чрезвычайно полезный навык. Особенно когда вы начнёте решать задачи с параметрами и всевозможные варианты ДВИ.

3. График чётной и нечётной функции

Всего два факта, которые нужно знать:

Теорема 1. График чётной функции $y=fleft( x right)$ симметричен относительно оси $OY$.

Теорема 2. График нечётной функции $y=fleft( x right)$ симметричен относительно начала координат.

Чтобы построить график чётной функции, достаточно построить его правую часть (для $xge 0$), а затем симметрично отразить относительно оси $OY$.

С нечётной функцией, на первый взгляд, всё то же самое. Сначала вновь строим правую часть графика (для $xge 0$), а затем отражаем её относительно начала координат. Однако практика показывает, что центральная симметрия даётся начинающим ученикам чуть сложнее, чем осевая.

Ниже приведены графики нескольких чётных функций. Попробуйте построить их самостоятельно.

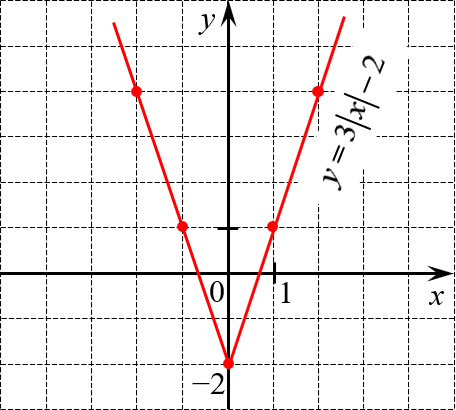
Постройте график функции

[y=3left| x right|-2]

Функция чётная. Пусть $xge 0$. Тогда функция примет вид

[y=3x-2]

Это линейная функция. Её график — прямая. С учётом отражения относительно оси $OY$ получим:

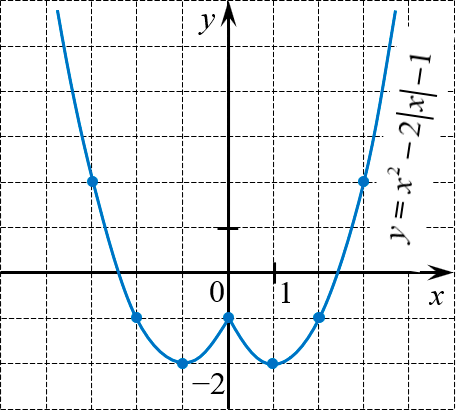
Постройте график функции

[y={{x}^{2}}-2left| x right|-1]

Функция чётная. При $xge 0$ видим привычную квадратичную функцию

[y={{x}^{2}}-2x-1]

Её график — парабола с вершиной ${{x}_{0}}={-b}/{2a};={2}/{2};=1$. После отражения получим

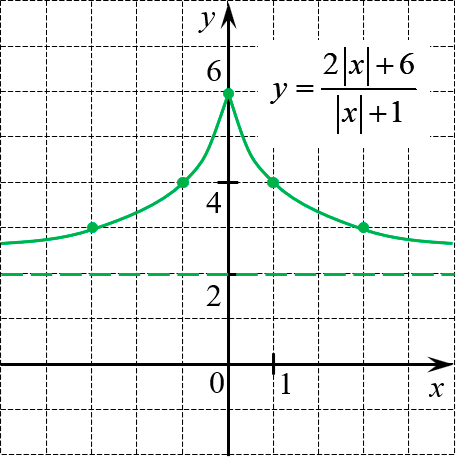
Постройте график функции

[y=frac{2left| x right|+6}{left| x right|+1}]

Функция чётная. При $xge 0$ получим привычную рациональную дробь. Выделим целую часть:

[y=frac{4}{x+1}+2]

Это обычная гипербола, сдвинутая на 1 влево и на 2 вверх. Итого получим:

Обратите внимание на последний график. При всяком сдвиге и симметрии желательно показывать не только новое положение самого графика, но и положение всех ориентиров: вспомогательная система координат, вертикальные и горизонтальные асимптоты (особенно актуально для гипербол) и т.д.

Зачем всё это нужно? Исследование функции на чётность и нечётность незаменимо для решения сложных уравнений и задач с параметром:

1. Графический метод решения задач с параметром;
2. Метод мажорант;
3. Вместе с периодичностью используется в тригонометрии.

4. Дополнение. Задачи с параметром

Чётность функций редко встречается сама по себе. Прежде всего это инструмент для решения сложных задач.

Известно, что $fleft( x right)={{x}^{8}}+a{{x}^{4}}+1$ и $fleft( 2 right)=353$. Найдите $fleft( -2 right)$ и значение параметра $a$.

Решение. Очевидно, что функция $fleft( x right)$ чётная:

[begin{align} fleft( -x right) & ={{left( -x right)}^{8}}+a{{left( -x right)}^{4}}+1= \ & ={{x}^{8}}+a{{x}^{4}}+1=fleft( x right) end{align}]

Следовательно можем найти $fleft( -2 right)$:

[fleft( -2 right)=fleft( 2 right)=353]

Кроме того, подставим $x=2$ и $fleft( 2 right)=353$ в формулу, задающую функцию:

[begin{align} 353 & ={{2}^{8}}+acdot {{2}^{4}}+1 \ 16a& =96 \ a& =6 end{align}]

Задача решена. Ответы:

[begin{align} fleft( -2 right) & =353; \ a & =6. end{align}]

И ещё одна задача. Попробуйте решить её самостоятельно:

Известно, что $fleft( x right)=frac{6075}{{{x}^{5}}+k{{x}^{3}}}$ и $fleft( 3 right)=15$. Найдите $fleft( -3 right)$ и значение параметра $k$.

Решение. Функция чётная при любом $kin mathbb{R}$ (докажите это!), поэтому

[fleft( -3 right)=-fleft( 3 right)=-15]

Поскольку $fleft( 3 right)=15$, имеем:

[begin{align} fleft( 3 right) & =frac{6075}{{{3}^{5}}+kcdot {{3}^{3}}}=frac{15}{1} \ & … \ k& =6 end{align}]

Ответ: $fleft( -3 right)=-15$; $k=6$.

А чтобы действительно разобраться с чётностью, обязательно изучите ещё две темы:

• Сдвиги графиков вдоль осей;
• Графики функций с модулем.

После этого половина задач с параметром перестанет казаться вам сложными.:)

Смотрите также:

1. Задача B15 — исследование функции с помощью производной
2. Тест к уроку «Что такое числовая дробь» (средний)
3. Следствия из теоремы Виета
4. C2: расстояние между двумя прямыми
5. Процент: налоги и зарплата. Считаем с помощью коэффициентов

Четные и нечетные функции

Функция называется четной, если ее область определения симметрична относительно нуля и для любого x из ее области определения выполняется равенство

График четной функции симметричен относительно оси ординат.

Например,  — четные функции.

Функция называется нечетной, если ее область определения симметрична относительно нуля и для любого x из ее области определения выполняется равенство

График нечетной функции симметричен относительно начала координат.

Например,  — нечетные функции.

Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида.

Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задания:

1. Проверьте, является ли функция четной (нечетной). 

Область определения функции

Проверим, является ли чётной или нечётной. Если функция четна. Если функция нечетна.

— значит, функция нечётная, её график симметричен относительно нуля.

2. Проверьте, является ли функция четной (нечетной).

Область определения: все действительные числа.

— чётная, как сумма двух чётных функций.

Её график симметричен относительно оси y.

3. Проверьте, является ли функция четной (нечетной).

Область определения функции симметрична относительно нуля.

— чётная, её график симметричен относительно оси y.