Как найти четвертую сторону четырехугольника по вписанной окружности
В четырехугольник ABCD вписана окружность, и Найдите четвертую сторону четырехугольника.
Это задание ещё не решено, приводим решение прототипа.
В четырехугольник ABCD вписана окружность, AB = 10, BC = 11 и CD = 15. Найдите четвертую сторону четырехугольника.
В четырехугольник можно вписать окружность тогда и только тогда, когда AB + CD = BC + AD, значит,
Как найти четвертую сторону четырехугольника по вписанной окружности
Задание 6. В четырёхугольник ABCD вписана окружность, АВ = 8 , ВС = 4 и CD = 25. Найдите четвёртую сторону четырёхугольника.

Так как в четырехугольник вписана окружность, то он обладает свойством, что сумма его противоположных сторон равна, т.е.
Найдем сторону AD из этого равенства, получим
Четырехугольники, вписанные в окружность. Теорема Птолемея
Вписанные четырёхугольники и их свойства
Определение 1 . Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, вписанным в окружность, или вписанным четырёхугольником .

Теорема 1 . Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180° .
Доказательство . Угол ABC является вписанным углом, опирающимся на дугу ADC (рис.1). Поэтому величина угла ABC равна половине угловой величины дуги ADC . Угол ADC является вписанным углом, опирающимся на дугу ABC . Поэтому величина угла ADC равна половине угловой величины дуги ABC . Отсюда вытекает, что сумма величин углов ABC и ADC равна половине угловой величины дуги, совпадающей со всей окружностью, т.е. равна 180° .
Если рассмотреть углы BCD и BAD , то рассуждение будет аналогичным.
Теорема 1 доказана.
Теорема 2 (Обратная к теореме 1) . Если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.
Доказательство . Докажем теорему 2 методом «от противного». С этой целью рассмотрим окружность, проходящую через вершины A , B и С четырёхугольника, и предположим, что эта окружность не проходит через вершину D . Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точка D лежит внутри круга (рис.2).

Продолжим отрезок CD за точку D до пересечения с окружностью в точке E , и соединим отрезком точку E с точкой A (рис.2). Поскольку четырёхугольник ABCE вписан в окружность, то в силу теоремы 1 сумма величин углов ABC и AEC равна 180° . При этом сумма величин углов ABC и ADC так же равна 180° по условию теоремы 2. Отсюда вытекает, что угол ADC равен углу AEC . Возникает противоречие, поскольку угол ADC является внешним углом треугольника ADE и, конечно же, его величина больше, чем величина угла AEC , не смежного с ним.
Случай, когда точка D оказывается лежащей вне круга, рассматривается аналогично.
Теорема 2 доказана.
Перечисленные в следующей таблице свойства вписанных четырёхугольников непосредственно вытекают из теорем 1 и 2.
Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.
| Фигура | Рисунок | Свойство |
| Окружность, описанная около параллелограмма |  |
Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. |
| Окружность, описанная около ромба |  |
Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. |
| Окружность, описанная около трапеции |  |
Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. |
| Окружность, описанная около дельтоида |  |
Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. |
| Произвольный вписанный четырёхугольник |  |
Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.
| Окружность, описанная около параллелограмма | |
 |
Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. |
| Окружность, описанная около ромба | |
 |
Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. |
| Окружность, описанная около трапеции | |
 |
Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. |
| Окружность, описанная около дельтоида | |
 |
Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. |
| Произвольный вписанный четырёхугольник | |
 |
| Окружность, описанная около параллелограмма |
 |
Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Окружность, описанная около ромба

Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Окружность, описанная около трапеции

Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
Окружность, описанная около дельтоида

Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.
Произвольный вписанный четырёхугольник

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:


где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Теорема Птолемея
Теорема Птолемея . Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.
Доказательство . Рассмотрим произвольный четырёхугольник ABCD , вписанный в окружность (рис.3).

Докажем, что справедливо равенство:

Для этого выберем на диагонали AC точку E так, чтобы угол ABD был равен углу CBE (рис. 4).

Заметим, что треугольник ABD подобен треугольнику BCE . Действительно, у этих треугольников по два равных угла: угол ABD равен углу CBE (по построению точки E ), угол ADB равен углу ACB (эти углы являются вписанными углами, опирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:

откуда вытекает равенство:
 |
(1) |
Заметим, что треугольник ABE подобен треугольнику BCD . Действительно, у этих треугольников по два равных угла: угол ABE равен углу DBC (углы ABD и EBC равны по построению, угол DBE – общий), угол BAC равен углу BDC (эти углы являются вписанными углами, пирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:
[spoiler title=”источники:”]
http://self-edu.ru/ege2016_36.php?id=21_6
http://www.resolventa.ru/spr/planimetry/ofcircle.htm
[/spoiler]
Вопросы
Знаток
(373),
закрыт
12 лет назад
Наталья Королева
Гуру
(3350)
12 лет назад
Если в условии упоминается, что этот четырехугольник можно вписать в окружность, то AB*CD=AD*BC ( то есть произведение двух противоположных сторон равно произведению двух других противоположных сторон).

vitalikfilippo
+10
Решено
9 лет назад
Геометрия
5 – 9 классы
В четырёхугольнике abcd вписана окружность ab=8, bc=7, cd=31. Найти четвёртую сторону четырёхугольника
Смотреть ответ
1
Ответ
5
(1 оценка)
1

Bulik228
9 лет назад
Светило науки – 28 ответов – 0 раз оказано помощи
По свойству вписанности окружности, чтобы в четырехугольник вписать окружность, у этого четырехугольника суммы противоположных сторон должны быть равны, т.е.
AB+DC = BC + AD
8+31 = 7+AD ;
(8+31) – 7 = 32 ;
Ответ : AD, или четвертая сторона четырехугольника = 32
(1 оценка)
https://vashotvet.com/task/4510352
Геометрия,
вопрос задал appolinariy0609,
8 месяцев назад
Ответы на вопрос
Ответил momogahari
1
Ответ: 4 см
Объяснение:
По условию,окружность вписанная,значит по свойству:
ВС+АD=AB+CD
12+AD=7+9
AD=4
Приложения:
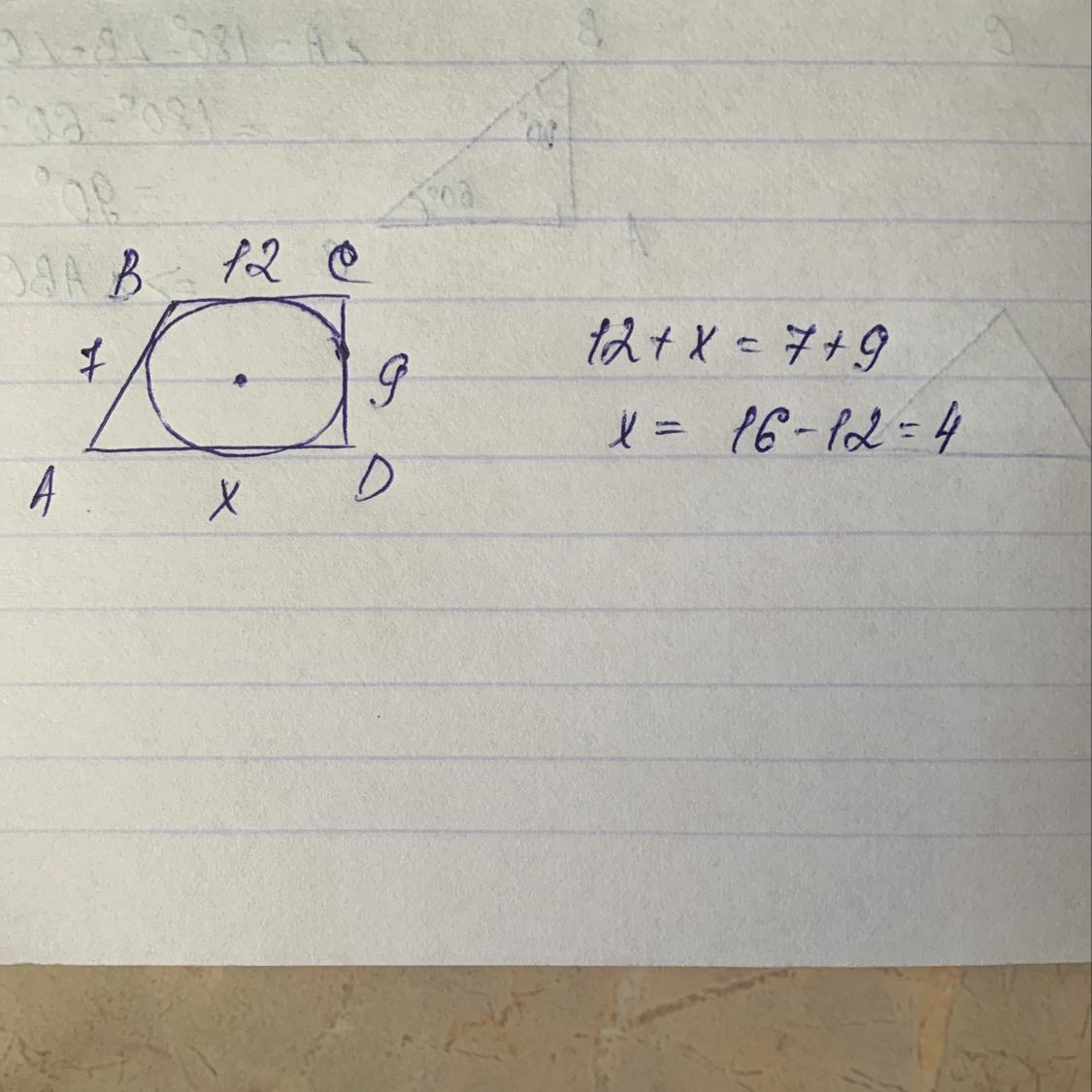
Предыдущий вопрос
Следующий вопрос
Новые вопросы
Геометрия,
29 дней назад
Найдите площадь ромба изображенного на рисунке если а=11, а r=4…
Русский язык,
29 дней назад
Составте предложение, где темнее наречие(форму темнее не изменять)…
Алгебра,
8 месяцев назад
Математика 8 класс пожалуйста с объяснением…
Математика,
8 месяцев назад
Знайдіть невідомий член пропорції х:52=4:13…
Математика,
6 лет назад
Решить уравнение 500-400:(х+43)=495…
Обществознание,
6 лет назад
как вы думаете зачем каждому человеку надо быть добрым…
В четырёхугольник ABCD вписана окружность, AB = 8, BC = 5 и CD = 27. Найдите четвёртую сторону четырёхугольника.
Источники: fipi, os.fipi, Основная волна 2019, Досрочная волна 2013
Решение:
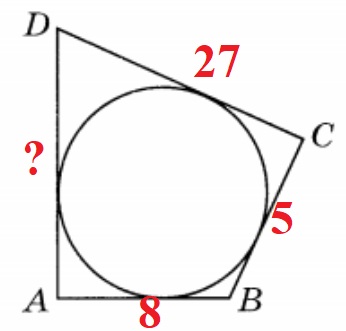
У четырёхугольника описанного около окружности сумма длин противоположных сторон равна:
AD + BC = DC + AB
AD + 5 = 27 + 8
AD = 27 + 8 – 5
AD = 30
Ответ: 30.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 16
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
