Формулировка задачи: Найти четырехзначное число, кратное N, любые две соседние цифры которого отличаются на K. В ответе укажите любое такое число.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 19 (Задачи на цифровую запись числа).
Для решения таких задач нужно знать основные признаки делимости чисел, а также уметь раскладывать составной делитель на взаимно простые множители. Рассмотрим, как решаются подобные задачи на примере.
Пример задачи:
Найти четырехзначное число, кратное 44, любые две соседние цифры которого отличаются на 1. В ответе укажите любое такое число.
Решение:
Чтобы четырехзначное число делилось на 44, нужно чтобы оно делилось на 11 и 4. Чтобы четырехзначное число делилось на 4, оно должно заканчиваться на 00 или число, составленное из 2 последних цифр, должно делиться на 4. Чтобы четырехзначное число делилось на 11, нужно чтобы сумма цифр на четных местах была равна сумме цифр на нечетных местах или чтобы эти суммы отличались на 11.
Для начала переберем все двухзначные числа, которые делятся на 4, состоящие из цифр, которые отличаются ровно на единицу:
00, 04, 08, 16, 20, 24, 28, 36, 40, 44, 48, 52, 60, 64, 68, 72, 80, 84, 88, 92, 96 – делятся на 4, но цифры отличаются не на 1
12, 32, 56, 76 – делятся на 4 и цифры отличаются на 1
Получили 4 возможных варианта окончаний четырехзначного числа. Теперь нужно подобрать 2 начальные цифры, чтобы разница между соседними цифрами была равна 1:
Для 12: 1012, 1212, 3212
Для 32: 1232, 3232, 3432, 5432
Для 56: 3456, 5456, 5656, 7656
Для 76: 5676, 7676, 7876, 9876
Проверим, какие из подобранных чисел делятся на 11:
1012: 1 + 1 = 0 + 2
1212: 1 + 1 ≠ 2 + 2
3212: 3 + 1 = 2 + 2
1232: 1 + 3 = 2 + 2
3232: 3 + 3 ≠ 2 + 2
3432: 3 + 3 = 4 + 2
5432: 5 + 3 ≠ 4 + 2
3456: 3 + 5 ≠ 4 + 6
5456: 5 + 5 = 4 + 6
5656: 5 + 5 ≠ 6 + 6
7656: 7 + 5 = 6 + 6
5676: 5 + 7 = 6 + 6
7676: 7 + 7 ≠ 6 + 6
7876: 7 + 7 = 8 + 6
9876: 9 + 7 ≠ 8 + 6
В качестве ответа можно указать числа 1012, 3212, 1232, 3432, 5456, 7656, 5676, 7876.
Ответ: 1012 или 3212 или 1232 или 3432 или 5456 или 7656 или 5676 или 7876
Эту задачу можно решать в уме, она не требует сложных математических выкладок. Просто порассуждайте, каким должно быть это число. Итак, формулировка задачи следующая:
Формулировка задачи
Какое наименьшее четырехзначное натуральное число делится и на 5, и на 9 и состоит только из четных цифр?
Решение 1
Целое число делится и на 5, и на 9 ровно тогда, когда оно делится на 45.
Поскольку мы ищем число, имеющее только четные цифры, его последняя цифра — одна из 0, 2, 4, 6 или 8, поэтому само число четное. Таким образом, мы ищем четное число, кратное 45.
Четное число кратно 45 ровно тогда, когда оно кратно 90. Это означает, что мы ищем наименьшее четырехзначное число, кратное 90, которое имеет только четные цифры.
Наименьшее четырехзначное число, кратное 90, равно 1080, но первая цифра этого числа равна 1, что нечетно. Каждое из следующих 10 кратных 90 имеет первую цифру, равную 1, поэтому искомое число должно быть больше 2000.
Четырёхзначные числа, кратные 90, которые имеют тысячную цифру 2 это 2070, 2160, 2250, 2340, 2430, 2520, 2610, 2700, 2790, 2880, 2970, а единственное число в этом списке, у которого все четные цифры, — это 2880.
Следовательно, 2880 — это наименьшее четырехзначное число, кратное 5, кратное 9 и имеющее только четные цифры.
Решение 2
Предположим, что это число abcd, где a, b, c и d — цифры. Поскольку число делится на 5, мы должны иметь, что d = 0 или d не равно 5.
Наименьшее значение а равно 2, поскольку оно должно быть четным и больше 0 (четырехзначное число не может иметь а = 0). Итак, мы попытаемся найти такое число где a = 2.
Чтобы число делилось на 9, мы должны иметь сумму a + b + c + d, делящуюся на 9. Подставив a = 2 и d = 0, получим, что
2 + b + c + 0 = 2 + b + c делится на 9.
Так как b и c четны, то 2 + b + c четно, а значит, не может равняться 9. Таким образом, мы попытаемся найти b и c так, чтобы 2 + b + c = 18, что является наименьшим кратным 9, которое больше 9. Это уравнение преобразуется в b + c = 16.
Поскольку b и c четны и удовлетворяют условию 0 ≤ b ≤ 9 и 0 ≤ c ≤ 9, то единственная возможность это b = c = 8.
Получаем ответ: 2880
Получилось ли у вас решить задачку самостоятельно? 😁
Всего: 68 1–20 | 21–40 | 41–60 | 61–68
Добавить в вариант
Найдите четырёхзначное натуральное число, меньшее 1360, которое делится на каждую свою цифру и все цифры которого различны и не равны нулю. В ответе укажите какое-нибудь одно такое число.
Найдите четырехзначное число, кратное 66, все цифры которого различны и четны. В ответе укажите какое-нибудь такое число.
Найти четырехзначное число, кратное 44, любые две соседние цифры которого отличаются на 1. В ответе укажите любое такое число.
Найдите четырёхзначное число, кратное 45, все цифры которого различны и чётны. В ответе укажите какое-нибудь одно такое число.
Найдите четырёхзначное натуральное число, кратное 4, сумма цифр которого на 1 больше их произведения. В ответе укажите какое-нибудь одно такое число.
Цифры четырёхзначного числа, кратного 5, записали в обратном порядке и получили второе четырёхзначное число. Затем из первого числа вычли второе и получили 2448. Приведите ровно один пример такого числа.
Цифры четырёхзначного числа, кратного 5, записали в обратном порядке и получили второе четырёхзначное число. Затем из первого числа вычли второе и получили 2457. Приведите пример такого числа.
Найдите четырёхзначное число, большее 1500, но меньшее 2000, которое делится на 24 и сумма цифр которого равна 21. В ответе укажите какое-нибудь одно такое число.
Найдите четырёхзначное число, большее 5500, но меньшее 6000, которое делится на 36 и сумма цифр которого равна 27. В ответе укажите какое-нибудь одно такое число.
Найдите четырёхзначное число, большее 1500, но меньшее 2000, которое делится на 24 и сумма цифр которого равна 24. В ответе укажите какое-нибудь одно такое число.
Найдите четырёхзначное число, большее 2000, но меньшее 3000, которое делится на 60 и сумма цифр которого равна 12. В ответе укажите какое-нибудь одно такое число.
Найдите четырёхзначное число, большее 2000, но меньшее 4000, которое делится на 18 и каждая следующая цифра которого больше предыдущей. В ответе укажите какое-нибудь одно такое число.
Найдите четырёхзначное число, большее 3000, но меньшее 3500, которое делится на 12 и каждая следующая цифра которого больше предыдущей. В ответе укажите какое-нибудь одно такое число.
Найдите четырёхзначное число, большее 7000, но меньшее 9000, которое делится на 50 и каждая следующая цифра которого меньше предыдущей. В ответе укажите какое-нибудь одно такое число.
Найдите четырёхзначное число, большее 6500, но меньшее 7500, которое делится на 15 и каждая следующая цифра которого меньше предыдущей. В ответе укажите какое-нибудь одно такое число.
Найдите четырёхзначное число, большее 4000, но меньшее 6500, которое делится на 60 и каждая следующая цифра которого меньше предыдущей. В ответе укажите какое-нибудь одно такое число.
Найдите четырёхзначное число, большее 4000, но меньшее 6000, которое делится на 20 и каждая следующая цифра которого меньше предыдущей. В ответе укажите какое-нибудь одно такое число.
Найдите четырёхзначное число, большее 3500, но меньшее 5500, которое делится на 40 и каждая следующая цифра которого меньше предыдущей. В ответе укажите какое-нибудь одно такое число.
Найдите четырёхзначное число, большее 1000, но меньшее 1300, которое делится на 18 и сумма цифр которого равна 18. В ответе укажите какое- нибудь одно такое число.
Найдите четырёхзначное число, большее 3500, но меньшее 4000, которое делится на 24 и сумма цифр которого равна 24. В ответе укажите какое-нибудь одно такое число.
Всего: 68 1–20 | 21–40 | 41–60 | 61–68
МатематикаЗадачи по математике
Unick
9 сентября 2018 · 318,9 K
Компьютерный инженер и математик, веб-программист и интернет-маркетолог, кинокритик и… · 10 нояб 2020 · дубасов.рф
Действительно, какой смысл использовать при решении подобной задачи формулы комбинаторики, факториалов и прочего?
Рассуждая логически, внимательный человек обратит внимание на то, что в список всех четырехзначных чисел войдут все возможные числа в рамках десятичной системы счисления, а именно: 1000, 1001, … 9998, 9999.
Ответ: можно составить 9000 четырёхзначных чисел.
24,8 K
Комментировать ответ…Комментировать…
Сингулярист, любитель занимательной математики, распространитель идей · 4 сент 2020
а чего такие сложные решения? комбинаторика. факториал? Отвечаю для школьника 3 класса: Всё ведь просто: 1000, 1001, 1002, ….., 9998, 9999. Итого: 10000-1000=9000
Ровно девять тысяч чисел. Без повторов, да, нужен комбинаторный анализ
69,0 K
Я думаю что чисел10 или даже больше
Комментировать ответ…Комментировать…
Если цифры могут повторяться, то:
– самое маленькое четырёхзначное число – 1000
– Самое большое – 9999
– 9999 – 1000 + 1 = 9000
Это и есть искомое количество.
Кстати, вопрос можно было сформулировать так – “Сколько существует четырёхзначных чисел?” Читать далее
18,8 K
Комментировать ответ…Комментировать…
Инженер-радиофизик, преподаватель физической культуры и спорта · 15 дек 2021
Из разных A⁴₁₀ – A⁴₉ = 10!/6! – 9!/5! = 10•9•8•7 – 9•8•7•6 = 9•8•7•4 = 2016
или из любых 10⁴ – 10³ = 9000
4,7 K
Комментировать ответ…Комментировать…
Человек и программист, отвечаю за еду 🙂 Подписывайтесь, приглашайте в ответы, буду рад… · 11 сент 2018
Пусть имеется k групп элементов, причем i-я группа состоит из ni-элементов. Выберем по одному элементу из каждой группы. Тогда общее число N способов, которыми можно произвести такой выбор, определяется соотношением N=n1*n2*n3*…*nk.
n1 = 9 (В качестве первого числа можно выбрать все кроме 0)
n2 = 10 (Все можно выбрать)
n3 = 10
n4 = 10
N = 9 * 10 * 10 * 10 = 9 * 1000… Читать далее
23,8 K
Комментировать ответ…Комментировать…
от 0,001 до 9,999 -9000 вариантов,
от 10,01 до 99,99 – 8100 вариантов,
от 100,1 до 999,9 – 8100 вариантов,
от 1000 до 9999 – 9000 вариантов.
Итого – 34200 вариантов.
2,1 K
Запятая не предусмотрена.
Комментировать ответ…Комментировать…
Эта задача на факториалы.
У нас есть 10 цифр, из них надо составить n четырехзначных чисел.
1) Если цифры в числе могут повторяться, то это обычный факторил из 10 цифр по 4 цифры в числе, его можно посчитать так:
n = 10!/(10-4)!=5040
2) Если цифры в числе не могут повторяться, то здесь решение усложняется:
n = 10!/(10-4)!-10!/(10-3)!=5040-720=4320 Читать далее
104,1 K
Я считаю данный ответ сомнительным.
Комментировать ответ…Комментировать…
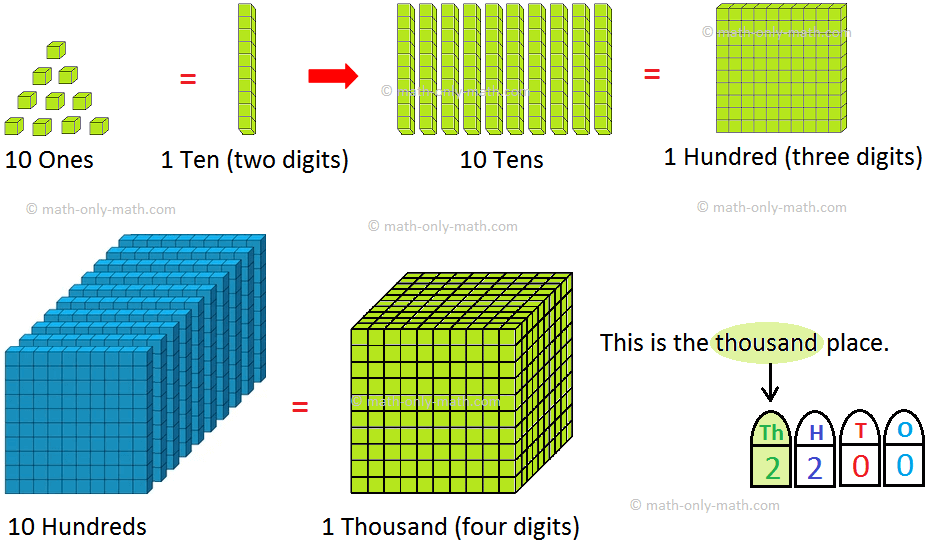
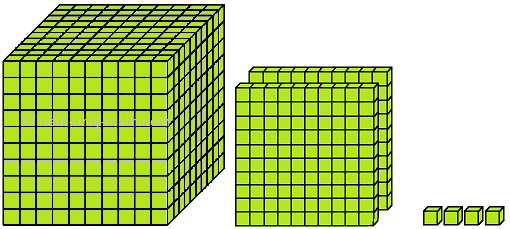
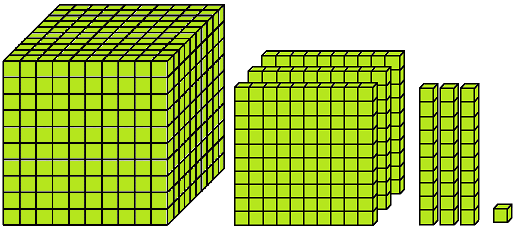
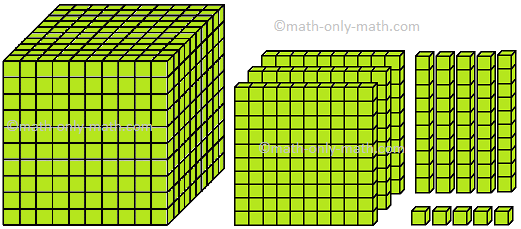
We have learned one, two and three digits numbers.
Now, we will study 4-digit numbers.
We add 1 to 999 to get the smallest four digit number. eg. 999 + 1 = 1000.
What are Four Digit Numbers?
We may divide 4-digit numbers in 9 groups.
(i) 1000 to 1999 (one thousand to one thousand nine hundred ninety nine)
(ii) 2000 to 2999 (two thousand to two thousand nine hundred ninety nine)
(iii) 3000 to 3999 (three thousand to three thousand nine hundred ninety nine)
(iv) 4000 to 4999 (four thousand to four thousand nine hundred ninety nine)
(v) 5000 to 5999 (five thousand to five thousand nine hundred ninety nine)
(vi) 6000 to 6999 (six thousand to six thousand nine hundred ninety nine)
(vii) 7000 to 7999 (seven thousand to seven thousand nine hundred ninety nine)
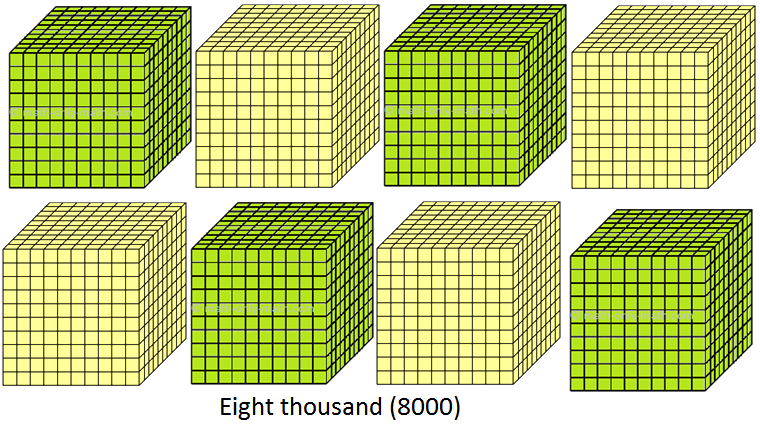
(viii) 8000 to 8999 (eight thousand to eight thousand nine hundred ninety nine)
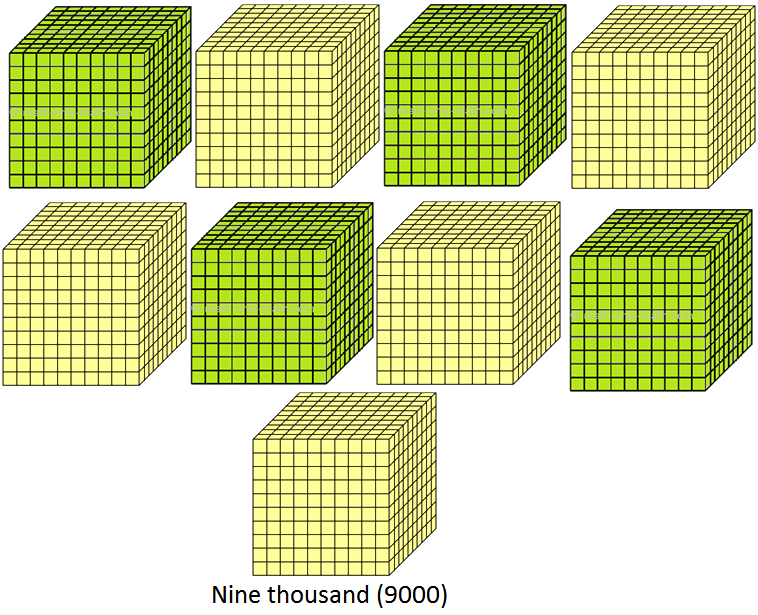
(ix) 9000 to 9999 (nine thousand to nine thousand nine hundred ninety nine)
Note: Four digit numbers begin with 1000.
Four Digits Numbers in Thousands:
If all the numbers of one digit, then two digits and then
three digits are placed step by step to the right of 1 Thousand according to their
place values, the numbers from 1001 to 1999 are formed.
1000, 1001, 1002, 1003, 1004, 1005, 1006, 1007, 1008, 1009,
1010, 1011, 1012, 1013, 1014, 1015, 1016, 1017, 1018, 1019,
1020, 1021, 1022, 1023, 1024, 1025, 1026, 1027, 1028, 1029,
1030, 1031, 1032, 1033, 1034, 1035, 1036, 1037, 1038, 1039,
1040, 1041, 1042, 1043, 10144, 1045, 1046, 1047, 1048, 1049,
1050, 1051, 1052, 1053, 1054, 1055, 1056, 1057, 1058, 1059,
1060, 1061, 1062, 1063, 1064, 1065, 1066, 1067, 1068, 1069,
1070, 1071, 1072, 1073, 1074, 1075, 1076, 1077, 1078, 1079,
1080, 1081, 1082, 1083, 1084, 1085, 1086, 1087, 1088, 1089,
1090, 1091, 1092, 1093, 1094, 1095, 1096, 1097, 1098, 1099,
1110, 1111, …………………., 1199, 1200, …………………., 1299, 1300,
1301, …………………………., 1399, 1400,
…………………, 1499, 1500, 1501, …………………., 1899, 1900, 1901,
………………….., 1921, …………………., 1971, …………………., 1981, ………………………, 1991, ………………….,
1999.
Similarly, 2000, …………….., 2199, ………………….., 2299, ……………………,
2799, ……………………, 2899, ………………….., 2999 are formed.
Thus, we reach upto 3999, ……………….., 4999, …………………, 5999,
…………………, 6999, …………………, 7999, …………………, 8999, ………………….., 9999.
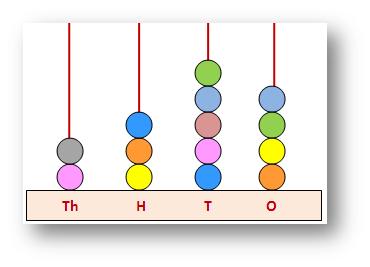
Shown below are some
four digit numbers on the abacus:
|
2354
Two thousand three hundred fifty four |
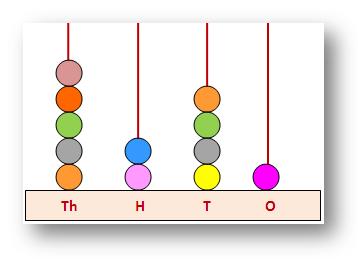
5241
Five thousand two hundred forty one |
Mike has 999 lollipops. He has made 9 packets of 100 lollipops
in each. He is now left with 99 lollipops. How many more lollipops does Mike
need to make another packet of 100 lollipops?
99 + 1 = 100
By having 1 more lollipop, Mike can make another packet of
100 lollipops.
Mike has now 10 packets of 100 lollipops in each.
|
10 hundreds = 1 thousand = 1000 Thus, Mike has 1000 lollipops in all. 1000 is a 4-digit number and is read as ‘one thousand’. |
1 packet = 100 lollipops 2 packets = 100 + 100 = 200 lollipops 3 packets = 200 + 100 = 300 lollipops 4 packets = 300 + 100 = 400 lollipops 5 packets = 400 + 100 = 500 lollipops 6 packets = 500 + 100 = 600 lollipops 7 packets = 600 + 100 = 700 lollipops 8 packets = 700 + 100 = 800 lollipops 9 packets = 800 + 100 = 900 lollipops |
1000 is the smallest 4-digit number. 9999 is the largest 4-digit number.
|
Digit One-digit Two-digit Three-digit Four-digit |
Largest Number 9 99 999 9999 |
Smallest Number 0 10 100 1000 |
9 + 1 = 10
99 + 1 = 100
999 + 1 = 1000
Let us now learn some 4-digit number names.
|
|
|
1325 is read as ‘One thousand three hundred twenty-five’ |
|
|
|
1538 is read as ‘One thousand five hundred thirty-eight’ |
|
|
|
1243 is read as ‘One thousand two hundred forty-three’ |
|
|
|
1456 is read as ‘One thousand four hundred fifty-six’ |
|
|
|
1513 is read as ‘One thousand five hundred thirteen’ |
|
|
|
1204 is read as ‘One thousand two hundred four’ |
|
|
|
1331 is read as ‘One thousand three hundred thirty-one’ |
|
|
|
1355 is read as ‘One thousand three hundred fifty-five’ |
|
|
|
2043 is read as ‘Two thousand forty-three’ |
Note: 1. The largest 4-digit number is 9999.
2. The smallest 4-digit number is 1000.
Forming 4-Digit Numbers:
4-Digit Numbers in Expand Form and Short Form:
|
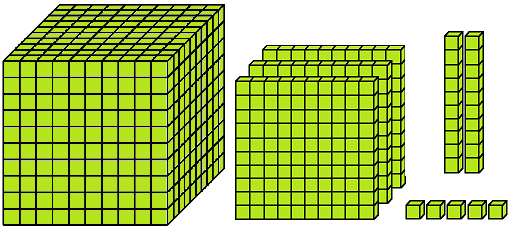
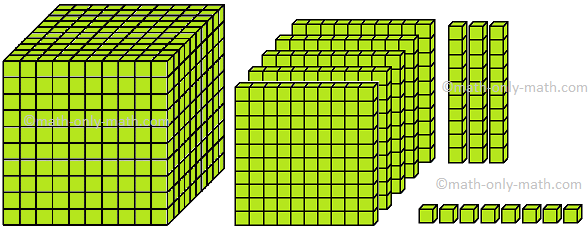
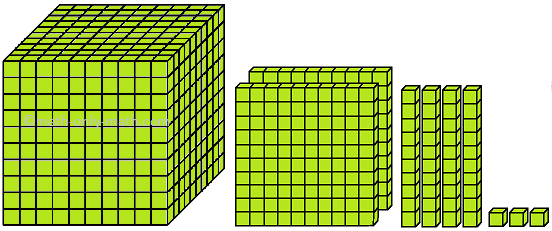
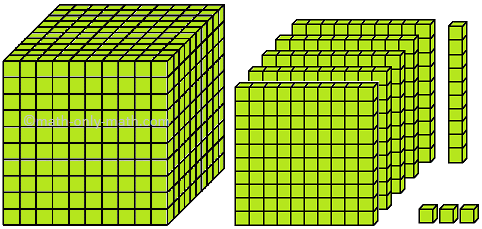
(i) 1 thousand + 4 hundreds + 6 tens + 4 ones (ii) 2 thousand + 6 hundreds + 3 tens + 1 one (iii) 5 thousand + 1 hundred + 3 tens + 2 ones (iv) 9 thousand + 9 hundreds + 9 tens + 9 ones (v) 4 thousands + 5 hundreds + 0 tens + 3 ones (vi) 6 thousands + 3 hundreds + 0 tens + 0 ones (vii) 7 thousands + 2 hundreds + 2 tens + 5 ones (viii) 3 thousands + 0 hundred + 1 ten + 6 ones (ix) 8 thousands + 7 hundreds + 4 tens + 7 ones (x) 1 thousand + 8 hundreds + 5 tens + 8 ones (xi) 2 thousands + 5 hundreds + 7 tens + 9 ones (xii) 1 thousand + 4 hundreds + 6 tens + 9 ones |
= 1000 + 400 + 60 + 4 = 2000 + 600 + 30 + 1 = 5000 + 100 + 30 + 2 = 9000 + 900 + 90 + 9 = 4000 + 500 + 0 + 3 = 6000 + 300 + 0 + 0 = 7000 + 200 + 20 + 5 = 3000 + 0 + 10 + 6 = 8000 + 700 + 40 + 7 = 1000 + 800 + 50 + 8 = 2000 + 500 + 70 + 9 = 1000 + 400 + 60 + 9 |
= 1460 = 2631 = 5132 = 9999 = 4503 = 6300 = 7225 = 3016 = 8747 = 1858 = 2579 = 1469 |
Forms of Numbers:
I. Write in the short forms. One has been done for you.
|
(i) 2000 + 700 + 50 + 8 (ii) 3000 + 400 + 60 + 2 (iii) 1000 + 300 + 40 + 5 (iv) 4000 + 200 + 30 + 5 (v) 6000 + 200 + 70 + 9 (vi) 5000 + 800 + 60 + 7 (vii) 7000 + 100 + 60 + 5 (viii) 8000 + 900 + 80 + 4 (ix) 9000 + 500 + 30 + 6 (x) 3000 + 800 + 00 + 2 |
= 2758 = ___________ = ___________ = ___________ = ___________ = ___________ = ___________ = ___________ = ___________ = ___________ |
Answer:
1. (ii) 3462
(iii) 1345
(iv) 4235
(v) 6279
(vi) 5867
(vii) 7165
(viii) 8984
(ix) 9536
(x) 3802
II. Write in the long forms. One has been done for you.
|
(i) 7684 (ii) 5053 (iii) 6734 (iv) 8635 (v) 9896 (vi) 3338 (vii) 4725 (viii) 2431 (ix) 1876 (x) 3707 (xi) 2980 (xii) 8579 |
= 7000 + 600 + 80 + 4 = __________________ = __________________ = __________________ = __________________ = __________________ = __________________ = __________________ = __________________ = __________________ = __________________ = __________________ |
Answer:
2. (ii) 5000 + 0 + 50 + 3
(iii) 6000 + 700 + 30 + 4
(iv) 8000 + 600 + 30 + 5
(v) 9000 + 800 + 90 + 6
(vi) 3000 + 300 + 30 + 8
(vii) 4000 + 700 + 20 + 5
(viii) 2000 + 400 + 30 + 1
(ix) 1000 + 800 + 70 + 6
(x) 3000 + 700 + 0 + 7
(xi) 2000 + 900 + 80 + 0
(xii) 8000 + 500 + 70 + 9
Writing Numbers:
III. Write in numbers:
(i) Five thousand eight hundred and fifty three
(ii) Nine thousand and two hundred
(iii) Two thousand eight hundred and four
(iv) Six thousand five hundred and ten
(v) Three thousand seven hundred and ninety five
(vi) One thousand nine hundred and forty two
(vii) Four thousand six hundred and eighty six
(viii) Seven thousand four hundred and sixty six
(ix) Eight thousand three hundred and seventy nine
(x) Three thousand nine hundred and thirty four
(xi) Two thousand five hundred and eighty seven
(xii) Four thousand two hundred and thirty five
(xiii) Seven thousand nine hundred and eight
Answer:
III. (i) 5853
(ii) 9200
(iii) 2804
(iv) 6510
(v) 3795
(vi) 1942
(vii) 4686
(viii) 7466
(ix) 8379
(x) 3934
(xi) 2587
(xii) 4235
(xiii) 7908
IV. Write the number names:
(i) 1530
(ii) 9217
(iii) 5645
(iv) 4872
(v) 3356
(vi) 2968
(vii) 1530
(viii) 6729
(ix) 8800
(x) 2874
(xi) 3507
(xii) 4235
(xiii) 6879
Answer:
IV. (i) One thousand five hundred thirty
(ii) Nine thousand two hundred seventeen
(iii) Five thousand six hundred forty five
(iv) Four thousand eight hundred seventy two
(v) Three thousand three hundred fifty six
(vi) Two thousand nine hundred sixty eight
(vii) One thousand five hundred thirty
(viii) Six thousand seven hundred twenty nine
(ix) Eight thousand eight hundred
(x) Two thousand eight hundred seventy four
(xi) Three thousand five hundred seven
(xii) Four thousand two hundred thirty five
(xiii) Six thousand eight hundred seventy nine
Numbers Fun:
V. Write forward consecutive numbers:
(i) 1001, ………….., ………….., ………….., ………….., ………….., …………..,
………….., ………….., …………..
(ii) 1340, ………….., ………….., ………….., ………….., ………….., …………..,
………….., ………….., …………..
(iii) 2550, ………….., ………….., ………….., ………….., ………….., …………..,
………….., ………….., …………..
(iv) 3025, ………….., ………….., ………….., ………….., ………….., …………..,
………….., ………….., …………..
(v) 4386, ………….., ………….., ………….., ………….., ………….., …………..,
………….., ………….., …………..
(vi) 5991, ………….., ………….., ………….., ………….., ………….., …………..,
………….., ………….., …………..
(vii) 6033, ………….., ………….., ………….., ………….., ………….., …………..,
………….., ………….., …………..
(viii) 7732, ………….., ………….., ………….., ………….., ………….., …………..,
………….., ………….., …………..
Answer:
V. (i) 1002, 1003, 1004, 1005, 1006, 1007, 1008, 1009, 1010
(ii) 1341, 1342, 1343, 1344, 1345, 1346, 1347, 1348, 1349
(iii) 2551, 2552, 2553, 2554, 2555, 2556, 2557, 2558, 2559
(iv) 3026, 3027, 3028, 3029, 3030, 3031, 3032, 3033, 3034
(v) 4387, 4388, 4389, 4390, 4391, 4392, 4393, 4394, 4395
(vi) 5992, 5993, 5994, 5995, 5996, 5997, 5998, 5999, 6000
(vii) 6034, 6035, 6036, 6037, 6038, 6039, 6040, 6041, 6042
(viii) 7733, 7734, 7735, 7736, 7737, 7738, 7739, 7740, 7741
VI. Write backwards consecutive numbers
(i) 1068, ………….., ………….., ………….., ………….., ………….., …………..,
………….., ………….., …………..
(ii) 6880, ………….., ………….., ………….., ………….., ………….., …………..,
………….., ………….., …………..
(iii) 9999, ………….., ………….., ………….., ………….., ………….., …………..,
………….., ………….., …………..
(iv) 5119, ………….., ………….., ………….., ………….., ………….., …………..,
………….., ………….., …………..
(v) 3425, ………….., ………….., ………….., ………….., ………….., …………..,
………….., ………….., …………..
(vi) 2500, ………….., ………….., ………….., ………….., ………….., …………..,
………….., ………….., …………..
Answer:
VI. (i) 1067, 1066, 1065, 1064, 1063, 1062, 1061, 1060, 1059
(ii) 6879, 6878, 6877, 6876, 6875, 6874, 6873, 6872, 6871
(iii) 9998, 9997, 9996, 9995, 9994, 9993, 9992, 9991, 9990
(iv) 5118, 5117, 5116, 5115, 5114, 5113, 5112, 5111, 5110
(v) 3424, 3423, 3422, 3421, 3420, 3419, 3418, 3417, 3416
(vi) 2499, 2498, 2497, 2496, 2495, 2494, 2493, 2492, 2491
VII. Complete the patterns:
(i) 8002, 8004, 8006, ………….., ………….., ………….., …………..,
………….., ………….., …………..
(ii) 9015, 9020, 9025, ………….., ………….., ………….., …………..,
………….., ………….., …………..
(iii) 7005, 7010, 7015, ………….., ………….., ………….., …………..,
………….., ………….., …………..
(iv) 6340, 6350, 6360, ………….., ………….., ………….., …………..,
………….., ………….., …………..
(v) 5000, 5006, 5012, ………….., ………….., ………….., …………..,
………….., ………….., …………..
(vi) 1100, 1200, 1300, ………….., ………….., ………….., …………..,
………….., ………….., …………..
Answer:
VII. (i) 8004, 8006, 8008, 8010, 8012, 8014, 8016, 8018, 8020
(ii) 9020, 9025, 9030, 9035, 9040, 9045, 9050, 9055, 9060
(iii) 7010, 7015, 7020, 7025, 7030, 7035, 7040, 7045, 7050
(iv) 6350, 6360, 6370, 6380, 6390, 6400, 6410, 6420, 6430
(v) 5006, 5012, 5018, 5024, 5030, 5036, 5042, 5048, 5054
(vi) 1200, 1300, 1400, 1500, 1600, 1700, 1800, 1900, 2000
VIII. Write the successor numbers (the number after):
(i) 4530 …………..
(ii) 6625 …………..
(iii) 2836 …………..
(iv) 1014 …………..
(v) 8590 …………..
(vi) 5417 …………..
(vii) 6879 …………..
(viii) 5792 …………..
(ix) 7876 …………..
(x) 5327 …………..
(xi) 9891 …………..
(xii) 5109 …………..
(xiii) 1999 …………..
(xiv) 3579 …………..
(xv) 4284 …………..
(xvi) 2029 …………..
Answer:
VIII. (i) 4531
(ii) 6626
(iii) 2837
(iv) 1015
(v) 8591
(vi) 5418
(vii) 6880
(viii) 5793
(ix) 7877
(x) 5328
(xi) 9892
(xii) 5110
(xiii) 1100
(xiv) 3580
(xv) 4285
(xvi) 2030
IX. Write the predecessors numbers (the number before)
(i) ………….. 3560
(ii) ………….. 5871
(iii) ………….. 9090
(iv) ………….. 8099
(v) ………….. 7418
(vi) ………….. 3464
(vii) ………….. 8254
(viii) ………….. 2726
(ix) ………….. 5381
(x) ………….. 7002
(xi) ………….. 3004
(xii) ………….. 3507
(xiii) ………….. 6231
(xiv) ………….. 4117
(xv) ………….. 1990
(xvi) ………….. 2001
Answer:
IX. (i) 3559
(ii) 5870
(iii) 9089
(iv) 8098
(v) 7417
(vi) 3463
(vii) 8253
(viii) 2725
(ix) 5380
(x) 7001
(xi) 3003
(xii) 3506
(xiii) 6230
(xiv) 4116
(xv) 1989
(xvi) 2000
X. Write the numbers before and after:
(i) ………….. 1995 …………..
(ii) ………….. 2010 …………..
(iii) ………….. 7328 …………..
(iv) ………….. 5609 …………..
(v) ………….. 8003 …………..
(vi) ………….. 9320 …………..
(vii) ………….. 6037
…………..
(viii) ………….. 5469 …………..
(ix) ………….. 7452 …………..
(x) ………….. 4230 …………..
(xi) ………….. 3000 …………..
(xii) ………….. 7989 …………..
Answer:
X. (i) 1994; 1996
(ii) 2009; 2011
(iii) 7327; 7329
(iv) 5608; 5610
(v)8002; 8004
(vi) 9319; 9321
(vii) 6036; 6038
(viii) 5468; 5470
(ix) 7451; 7453
(x) 4229; 4231
(xi) 2999; 3001
(xii) 7988; 7990
XI. Write the numbers between:
(i) 3057 ………….. 3059
(ii) 1574 ………….. 1576
(iii) 3898 ………….. 3900
(iv) 6407 ………….. 6409
(v) 3281 ………….. 3283
(vi) 5000 ………….. 5002
(vii) 8342 ………….. 8344
(viii) 2318 ………….. 2320
(ix) 9836 ………….. 9838
(x) 4201 ………….. 4203
(xi) 1810 ………….. 1812
(xii) 7999 ………….. 8001
Answer:
XI.
(i) 3058
(ii) 1575
(iii) 3899
(iv) 6408
(v) 3282
(vi) 5001
(vii) 8343
(viii) 2319
(ix) 9837
(x) 4202
(xi) 1811
(xii) 8000
Place value in 4-digits numbers:
A place value depends upon the position of a digit in a
given number.
A place value keeps increasing, when a number moves from
right to left.
1 one, place value = 1 1 or 1
8 tens, place value = 8 10 or 80
6 hundreds, place value = 6 100 or 600
3 thousands, place value = 4 1000 or 4000
3746 = 3 thousands + 7 hundreds + 4 tens + 6 ones
= 3000 + 700
+ 40 + 6
3rd Grade Math Lessons
From Four Digit Numbers to HOME PAGE
Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.