Как найти числа переноса

Методы определения чисел переноса.

Для определения чисел переноса используют
три метода.

По методу Гитторфа определяют
аналитическим путем изменение
количества электролита в анодном или
катодном пространстве электрохимической
системы при прохождении через нее
постоянного тока и рассчитывают
числа переноса по формуле

(10)

где n
— изменение содержания электролита;
определяемое аналитически вблизи
каждого из электродов, г-экв; F—
число Фарадея, Кл моль^-1; Q
— общее количество электричества,
пропущенное через
электрохимическую систему и определяемое
кулонометрически.

В настоящее время применяют кулонометры
— системы, в которых весь ток
расходуется лишь на одну электрохимическую
реакцию — трех типов: весовые —
серебряные и медные; объемные — водородные
и ртутные; титрационные — чаще других
используют анодное
растворение серебра (кулонометр В. А.
Кистяковского) или электролитическое
окисление ионов иода.

Найденные по формуле (10) числа переноса
не учитывают гидратацию ионов и перенос
молекул растворителя через мембраны,
разделяющие приэлектродные пространства
при электролизе,
поэтому они называются эффективными,
или кажущимися. При
выборе в качестве системы отсчета
растворителя в целом расчет чисел
переноса (особенно для концентрированных
растворов) следует
проводить по уравнению

(11)

где

и

— начальное и конечное содержания
электролита в катодном пространстве,

г-экв;

и

—
начальная и конечная
концентрации воды там же.

По методу движущейся границы определяют
расстояние l, на которое
перемещается граница между двумя
окрашенными или разной плотности
растворами с одним общим ионом в узкой
вертикальной
трубке сечением s
под действием постоянной разности
потенциалов за определенный
промежуток времени 
при выполнении условий:

1) регулирующего соотношения Кольрауша
(с точностью до 10%):

(12)

где t /t_инд– числа переноса в исследуемом и
индикаторном растворах; С, С_инд
— соответствующие концентрации;

2) число переноса индикаторного раствора
меньше исследуемого, т.е.
;

3) индикаторный раствор имеет большую,
чем исследуемый, плотность и
располагается в нижнем слое — сохраняется
резкая граница
между растворами при электролизе.

Число переноса в этом методе рассчитывают
по формуле

(13)

где С — концентрация исследуемого
раствора; z₊
— заряд иона; С₊ —
концентрация иона; V
= ls — объем раствора,
прошедшего по трубке за время .
Видно, что формула (13) идентична (10).
Отметим, что при
выборе в качестве системы отсчета
растворителя в соотношение (13)
нужно ввести поправку на изменение
объема V,
связанное с перемещением по трубке
из-за электродных
реакций воды:

(14)

Также различают метод
определения чисел переноса ионов,
связанный с
измерением диффузионного
потенциала в концентрационных цепях с
переносом.

В растворе перенос электричества
осуществляется ионами, причем каждый
вид ионов переносит определенное
количество электричества в зависимости
от содержания данных ионов в растворе,
их валентности и скорости движения в
электрическом поле.

Общее количество электричества е,
прошедшего через раствор, складывается
из количества электричества, перенесенного
всеми ионами:

(15)

Доля количества электричества,
перенесенного ионами i,
называется числом переноса t_i:

(16)

Для раствора электролита АВ, диссоциирующего
по схеме

АВА⁺+В^–

числа переноса могут быть выражены
равенствами:

(17)

где е_ки е_а– количество
электричества, перенесенное катионами
А⁺и анионами В^–соответственно.

Отсюда

Поскольку количество электричества,
перенесенное ионами данного вида,
пропорционально скорости их движения,
то числа переноса можно определить
через абсолютные скорости ионов:

(18)

Или, учитывая, что =
uF , через
подвижности (электропроводности) ионов:

(19)

Числа переноса зависят от подвижности
всех ионов в растворе, природы растворителя,
концентрации и температуры. Влияние
изменения концентрации незначительно;
при концентрации растворов ниже 0,2 н.
числа переноса практически остаются
постоянными. Благодаря этому можно
легко определить значение t_iпри бесконечном разбавлении путем
экстраполяции. Зная число переноса и
эквивалентную электропроводность при
бесконечном разбавлении, можно рассчитать
подвижность ионов, решая уравнение:

(20)

С увеличением температуры за счет
неодинаковой степени дегидратации
ионов А⁺ и В^– числа переноса
выравниваются и стремятся к 0,5.

Установка
для определения чисел переноса.

Схема
лабораторной
установки для определения чисел переноса
показана рис.
2

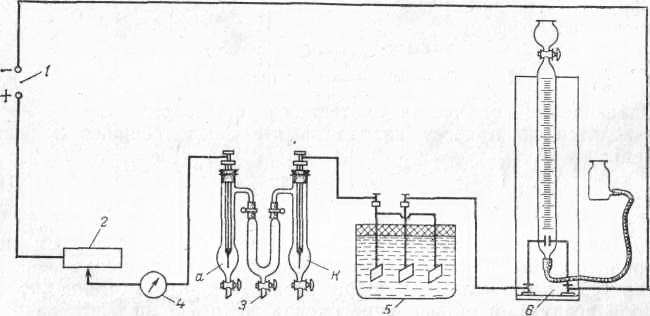
Рис. 2 Схема установки для определения
чисел переноса ионов:

/—источник
постоянного тока; 2
—
реостат; 3
—
электролизер для определения чисел
переноса ионов (а — анодный сосуд; к –
катодный сосуд); 4 — миллиамперметр; 5 —
медный кулонометр; 6
—
газовый кулонометр.

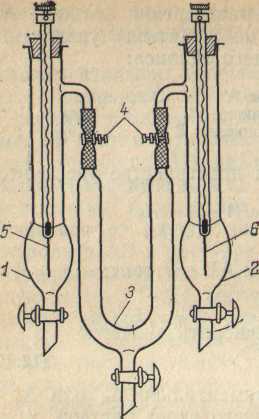
Рис. 3 Электролизер
для определения чисел
переноса ионов:

/ —
анодный сосуд; 2
— катодный
сосуд; 3
—
соединительный сосуд; 4
—
зажимы; 5, 6
—
электроды.

Поскольку при
измерении чисел переноса необходимо
определять изменение
содержания электролита у каждого
электрода отдельно, то в электролизере
3 анодное и катодное пространство
должны быть в достаточной степени
разделены. Для этой цели удобно
пользоваться прибором, изображенным
на рис. 3.

Кулонометры. Количество протекающего
через цепь электричества определяется
с помощью кулонометров — приборов,
основанных на электрохимическом принципе
действия. Расчет
количества электричества производится
на основании
законов электролиза Фарадея. Необходимым
условием при
этом является протекание на электроде
одного единственного
электрохимического процесса, отсутствие
побочных химических
реакций и механических потерь продукта,
т. е. электродный процесс должен
проходить с выходом по току 100%.

По методам определения
количества образующихся веществ
кулонометры подразделяются на
весовые, объемные и титрационные.

Медный кулонометр
(весовой) состоит
из медных электродов — пластинок,
погруженных в раствор CuSO₄.
На границе раздела «электрод — электролит»
протекают процессы:

Сu²⁺
+ 2е^–

Сu (на катоде)

Сu
— 2e^–

Сu²⁺ (на аноде)

Определение количества протекающего
электричества e_F
производится
по привесу катода за счет выделившейся
на нем меди:

e_F
= m/31,77 (21)

где т — масса выделившейся меди, г;
31,77 — химический эквивалент меди.

Точность показаний кулонометра 0,1—0,5%-
Основным источником
погрешностей является частичное
растворение медных электродов
в кислом растворе, особенно в присутствии
кислорода воздуха, и образование
оксида меди (I) за счет
реакции на катоде:

Си²⁺
+ е^–

Cu+

в нейтральном
растворе и при малых плотностях тока,
а также осаждение
меди на катоде в губчатой форме
при высоких плотностях тока. Для
повышения точности показаний кулонометра
рекомендуется в
качестве электролита использовать
раствор следующего состава:

CuSO₄*5H₂O
– 150 г/л; H₂SO₄
– 50 г/л; С₂Н₅ОН – 50 г/л; вести
электролиз при умеренных
плотностях тока на катоде в пределах
от 2 до 20 мА-см^-2. В
объемных кулонометрах количества
выделяющихся
на электродах веществ определяют
измерением их объемов.
Примером такого типа приборов является
газовый кулонометр. Кулонометр состоит
из градуированной бюретки, в нижний
конец которой впаяны два платиновых
электрода. Бюретку и уравнительную
склянку заполняют 0,5 М раствором
сульфата натрия.Для
повышения точности показаний кулонометра
рекомендуется перед каждым опытом
насыщать раствор электролита водородом
и кислородом. С этой целью собирают
установку согласно рис.2, в которую
включают только один газовый кулонометр
(электролизер 3 и другие кулонометры
не включаются) и пропускают ток 50 мА
в течение 5—10 мин. Электролиз ведут
при открытом кране. Затем, поднимая
уравнительную склянку, заполняют
газовую бюретку раствором настолько,
чтобы в ней оставалось примерно 1—2 мл
газа. После этого закрывают кран,
уровни растворов в бюретке
и склянке приводят к одной и той же
высоте и отсчитывают объем V₁
оставшегося в бюретке газа. Очевидно,
давление газа в
бюретке при этих условиях будет равно
атмосферному. Аналогично
определяется объем V₂
газовой смеси и по окончании основного
опыта. Разность V₂—V₁
= V будет соответствовать
объему гремучей смеси, выделившейся в
кулонометре за
время опыта.

Количество электричества определяют
по формуле:

e_F
= 4/3(p–h)V/(RT) (22)

где р — внешнее давление, мм рт.
ст.; h — давление насыщенного пара воды
при температуре опыта, мм рт. ст. (см.
Справочник, Р, табл. 21).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

From Wikipedia, the free encyclopedia

In chemistry, ion transport number, also called the transference number, is the fraction of the total electric current carried in an electrolyte by a given ionic species i:^[1]

${displaystyle t_{i}={frac {I_{i}}{I_{text{tot}}}}}$

Differences in transport number arise from differences in electrical mobility. For example, in an aqueous solution of sodium chloride, less than half of the current is carried by the positively charged sodium ions (cations) and more than half is carried by the negatively charged chloride ions (anions) because the chloride ions are able to move faster, i.e., chloride ions have higher mobility than sodium ions. The sum of the transport numbers for all of the ions in solution always equals unity:

${displaystyle sum _{i}t_{i}=1}$

The concept and measurement of transport number were introduced by Johann Wilhelm Hittorf in the year 1853.^[2] Liquid junction potential can arise from ions in a solution having different ion transport numbers.

At zero concentration, the limiting ion transport numbers may be expressed in terms of the limiting molar conductivities of the cation ( ${displaystyle lambda _{0}^{+}}$ ), anion ( ${displaystyle lambda _{0}^{-}}$ ), and electrolyte ( $Lambda _{0}$ ):

${displaystyle t_{+}=nu ^{+}cdot {frac {lambda _{0}^{+}}{Lambda _{0}}}}$

and

${displaystyle t_{-}=nu ^{-}cdot {frac {lambda _{0}^{-}}{Lambda _{0}}},}$

where ${displaystyle nu ^{+}}$ and ${displaystyle nu ^{-}}$ are the numbers of cations and anions respectively per formula unit of electrolyte.^[1] In practice the molar ionic conductivities are calculated from the measured ion transport numbers and the total molar conductivity. For the cation ${displaystyle lambda _{0}^{+}=t_{+}cdot {tfrac {Lambda _{0}}{nu ^{+}}}}$ , and similarly for the anion. In solutions, where ionic complexation or associaltion are important, two different tramsport/tramsference numbers can be defined. ^[3]

The practical importance of high (i.e. close to 1) transference numbers of the charge-shuttling ion (i.e. Li+ in lithium-ion batteries) is related to the fact, that in single-ion devices (such as lithium-ion batteries) electrolytes with the transfer number of the ion near 1, concentration gradients do not develop. A constant electrolyte concentration is maintained during charge-discharge cycles. In case of porous electrodes a more complete utilization of solid electroactive materials at high current densities is possible, even if the ionic conductivity of the electrolyte is reduced.^[4]^[5]

Experimental measurement[edit]

There are several experimental techniques for the determination of transport numbers.^[6] The Hittorf method is based on measurements of ion concentration changes near the electrodes. The moving boundary method involves measuring the speed of displacement of the boundary between two solutions due to an electric current.^[7]

Hittorf method[edit]

This method was developed by German physicist Johann Wilhelm Hittorf in 1853.^[7], and is based on observations of the changes in concentration of an electrolyte solution in the vicinity of the electrodes. In the Hittorf method, electrolysis is carried out in a cell with three compartments: anode, central, and cathode. Measurement of the concentration changes in the anode and cathode compartments determines the transport numbers.^[8] The exact relationship depends on the nature of the reactions at the two electrodes. For the electrolysis of aqueous copper(II) sulfate (CuSO₄) as an example, with Cu²⁺(aq) and SO2−4(aq) ions, the cathode reaction is the reduction Cu²⁺(aq) + 2 e⁻ → Cu(s) and the anode reaction is the corresponding oxidation of Cu to Cu²⁺. At the cathode, the passage of coulombs of electricity leads to the reduction of moles of Cu²⁺, where is the Faraday constant. Since the Cu²⁺ ions carry a fraction $t_{+}$ of the current, the quantity of Cu²⁺ flowing into the cathode compartment is ${displaystyle t_{+}(Q/2F)}$ moles, so there is a net decrease of Cu²⁺ in the cathode compartment equal to ${displaystyle (1-t_{+})(Q/2F)=t_{-}(Q/2F)}$ .^[9] This decrease may be measured by chemical analysis in order to evaluate the transport numbers. Analysis of the anode compartment gives a second pair of values as a check, while there should be no change of concentrations in the central compartment unless diffusion of solutes has led to significant mixing during the time of the experiment and invalidated the results.^[9]

Moving boundary method[edit]

This method was developed by British physicists Oliver Lodge in 1886 and William Cecil Dampier in 1893.^[7] It depends on the movement of the boundary between two adjacent electrolytes under the influence of an electric field. If a colored solution is used and the interface stays reasonably sharp, the speed of the moving boundary can be measured and used to determine the ion transference numbers.

The cation of the indicator electrolyte should not move faster than the cation whose transport number is to be determined, and it should have same anion as the principle electrolyte. Besides the principal electrolyte (e.g., HCl) is kept light so that it floats on indicator electrolyte. CdCl₂ serves best because Cd²⁺ is less mobile than H⁺ and Cl⁻ is common to both CdCl₂ and the principal electrolyte HCl.

For example, the transport numbers of hydrochloric acid (HCl(aq)) may be determined by electrolysis between a cadmium anode and an Ag-AgCl cathode. The anode reaction is Cd → Cd²⁺ + 2 e⁻ so that a cadmium chloride (CdCl₂) solution is formed near the anode and moves toward the cathode during the experiment. An acid-base indicator such as bromophenol blue is added to make visible the boundary between the acidic HCl solution and the near-neutral CdCl₂ solution.^[10] The boundary tends to remain sharp since the leading solution HCl has a higher conductivity that the indicator solution CdCl₂, and therefore a lower electric field to carry the same current. If a more mobile H⁺ ion diffuses into the CdCl₂ solution, it will rapidly be accelerated back to the boundary by the higher electric field; if a less mobile Cd²⁺ ion diffuses into the HCl solution it will decelerate in the lower electric field and return to the CdCl₂ solution. Also the apparatus is constructed with the anode below the cathode, so that the denser CdCl₂ solution forms at the bottom.^[1]

The cation transport number of the leading solution is then calculated as

${displaystyle t_{+}={frac {z_{+}cLAF}{IDelta t}}}$

where ${displaystyle z_{+}}$ is the cation charge, c the concentration, L the distance moved by the boundary in time Δt, A the cross-sectional area, F the Faraday constant, and I the electric current.^[1]

Concentration cells[edit]

This quantity can be calculated from the slope of the function ${displaystyle E_{mathrm {T} }=f(E)}$ of two concentration cells, without or with ionic transport.

The EMF of transport concentration cell involves both the transport number of the cation and its activity coefficient:

${displaystyle E_{mathrm {T} }=-z{frac {RT}{F}}int _{I}^{II}t_{+}dln a_{+/-}}$

where $a_{2}$ and $a_{1}$ are activities of HCl solutions of right and left hand electrodes, respectively, and ${displaystyle t_{M}}$ is the transport number of Cl⁻.

Electrophoretic magnetic resonance imaging method[edit]

This method is based on magnetic resonance imaging of the distribution of ions comprising NMR-active nuclei (usually 1H, 19F, 7Li) in an electrochemical cells upon application of electric current ^[11]

Notes[edit]

^ ^a ^b ^c ^d Peter Atkins and Julio de Paula, Physical Chemistry (8th ed. Oxford University Press, 2006) p.768-9 ISBN 0-7167-8759-8
^ Pathways to Modern Chemical Physics by Salvatore Califano (Springer 2012) p.61 ISBN 9783642281808
^ http://lacey.se/science/transference/
^ M. Doyle, T. F. Fuller and J. Newman, “The importance of the lithium ion transference number in lithium/polymer cells.” Electrochim Acta, 39, 2073 (1994) 10.1016/0013-4686(94)85091-7
^ http://lacey.se/science/transference/
^ http://lacey.se/science/transference/
^ ^a ^b ^c Laidler K.J. and Meiser J.H., Physical Chemistry (Benjamin/Cummings 1982) p.276-280 ISBN 0-8053-5682-7
^ Electrochemistry Dictionary – H Corrosion Doctors.
^ ^a ^b Principles and Applications of Electrochemistry D.R.Crow (4th ed., CRC Press 1994) p.165-169 ISBN 0748743782
^ Transport numbers and ionic mobilities by the moving boundary method, G. A. Lonergan and D. C. Pepper, J. Chem. Educ., 1965, 42 (2), p. 82. doi:10.1021/ed042p82
^ Klett, Matilda; Giesecke, Marianne; Nyman, Andreas; Hallberg, Fredrik; Lindström, Rakel Wreland; Lindbergh, Göran; Furó, István (2012). “Quantifying Mass Transport during Polarization in a Li Ion Battery Electrolyte by in Situ 7Li NMR Imaging”. Journal of the American Chemical Society. 134 (36): 14654–14657. doi:10.1021/ja305461j. PMID 22900791.

External links[edit]

Aqueous Symple Electrolytes Solutions, H. L. Friedman, Felix Franks

Источник

Числа переноса ионов. Методы определения чисел переноса. Числа переноса истинные и кажущиеся. Зависимость чисел переноса от концентрации и температуры.

Одним из важнейших понятий в электрохимии является число переноса ионов. В электролитах электричество переносится одновременно положительными и отрицательными ионами, поэтому возникает вопрос, каково участие в этом процессе ионов каждого знака.

Количество переносимого электричества определяется концентрацией ионов и скоростью их движения; когда концентрации катионов и анионов одинаковы, участие их в переносе электричества зависит лишь от относительной скорости их движения. Так как скорости движения катионов и анионов могут быть существенно различными, потому и числа переноса должны быть разными. Это было установлено Гитторфом (1854).

Числом переноса ионов называется доля прошедшего через электролит электричества, перенесенная данным родом ионов:

t₊ = , t_– = , t₊ + t_– = = 1 ;

I₊ = , I_– = , I = I₊ + I_– = ;

t₊ = = = , t_– = = = .

Таким образом, число переноса равно отношению скорости движения (или подвижности) данного иона к сумме скоростей движения (или подвижностей) катиона и аниона. Так как подвижности катиона и аниона изменяются с концентрацией и температурой в общем случае неодинаково, то и числа переноса зависят от концентрации и температуры, хотя эта зависимость более слабая.

Выведенное соотношение позволяет вычислить числа переноса, если известны значения подвижностей ионов. С другой стороны, опытное определение чисел переноса дает возможность вычислить подвижности.

Видно, что число переноса не является характеристикой только данного иона, так как зависит от подвижности парного с ним иона. Таким образом, число переноса t_i характеризует не индивидуальное свойство иона, а роль этого иона в миграционном переносе зарядов в данном растворе электролита. В бинарном растворе число переноса зависит от подвижности второго иона, а в многокомпонентном растворе еще и от соотношения концентраций компонентов раствора. Например, число переноса хлорид-иона в растворе НCl меньше, чем в растворе КCl той же концентрации, поскольку ионы водорода более подвижны, чем ионы калия.

Экспериментально числа переноса определяются по изменению концентрации ионов у электродов (метод Гитторфа).

+ Анод Катод –

А + + + + + + + + + + + + + + + + + +

– – – – – – – – – – – – – – – – – –

Б + + + + + + + + + + + + +

+ + + + +

– – – – – – – – – – – – – – – – – –

В – – – + + + + + + + + + + + + + + +

– – – – – – – – – – – – – – – + + +

I II III

Рис. 29. Определение чисел переноса ионов по методу Гитторфа

Рассмотрим схему движения ионов (переноса электричества) в растворе HCl при электролизе (см. рис. 29). Разделим мысленно ванну с электролитом на три отделения: I – анодная часть (анолит), II – центральная часть, III – катодная часть (католит). В процессе электролиза в отделении II концентрация электролита не изменяется, в отделениях I и III – изменяется. Схема А: до электролиза концентрация раствора во всех отделениях одинакова (в каждом из отделений находится по 6 пар ионов). Схема Б: абсолютная скорость движения Н⁺ приблизительно в 5 раз больше, чем скорость Cl^–, поэтому в течение определенного промежутка времени при электролизе ионы Н⁺ пройдут слева направо путь, в 5 раз больший, чем ионы Сl^– за то же время справа налево. В результате в катодном пространстве появится 6 лишних ионов водорода, а в анодном – столько же лишних ионов хлора. Схема В: эти ионы разряжаются на электродах и выделяются в виде газов. В анодном пространстве остается одна пара ионов, в катодном – 5 пар. Убыль электролита у анода Dс_а (5 пар ионов) в 5 раз больше убыли электролита у катода Dс_к (1 пара ионов). Отношение Dс_а/Dс_к равно отношению абсолютных скоростей катиона и аниона и равно отношению их подвижностей:

= = .

Числа переноса определяются из соотношений

t₊ = = , t_– = = ,

и в рассмотренном примере t₊(H⁺) » 5/6 = 0,83 , t_–(Cl^–) » 1/6 = 0,17 , откуда видно, что количество ионов данного типа, участвующих в переносе электричества, никак не связано с количеством ионов, передавших свой заряд электроду.

Для успешного применения метода Гитторфа необходимо, чтобы на границе электрод – раствор при пропускании электрического тока не происходили побочные процессы (например, разряд молекул растворителя) и чтобы время пропускания тока не было очень длительным (тогда можно пренебречь выравниванием концентрации за счет диффузии через пористую перегородку). В результате этого изменения концентрации оказываются небольшими, и это повышает требования к аналитическим методам, при помощи которых определяют изменение содержания соли.

Определенные по методу Гитторфа числа переноса называются кажущимися числами переноса; они не являются истинными, так как этот метод не учитывает сольватации ионов. Измеряемые в методе Гитторфа концентрации определяются не только количеством катионов и анионов, но и количеством растворителя, перенесенного этими ионами в виде сольватных оболочек. Оболочки ионов разных знаков неодинаковы по величине.

Существование рассмотренного эффекта можно легко установить, прибавив к электролиту недиссоциирующее на ионы вещество, например, сахар или мочевину. Учитывая изменение концентрации прибавленного неэлектролита при определении чисел переноса, можно ввести поправку на перенос воды из анодного пространства в катодное в виде сольватных оболочек и найти истинные числа переноса t₊ и t_–. Но обычно в значения чисел переноса, найденные опытным путем по методу Гитторфа, поправки не вводятся.

Существуют и другие методы определения чисел переноса. В лекции 57 будет рассмотрен метод, в котором для определения чисел переноса измеряется ЭДС концентрационной цепи 2-го рода (электрохимической цепи, состоящей из двух одинаковых электродов, отличающихся концентрацией электролита). В этой цепи имеется жидкостная граница – граница между двумя растворами одинаковой природы и разной концентрации, через которую происходит перенос ионов в соответствии с их числами переноса. ЭДС такой цепи зависит от числа переноса катиона либо аниона.

Еще один метод определения чисел переноса – метод движущейся границы. Сущность этого метода состоит в том, что растворы двух солей, имеющих одинаковый ион, помещают в узкую вертикальную трубку, причем так, что они образуют резкую границу раздела. Раствор-индикатор в трубке находится внизу и имеет большую плотность. Вверху трубки находится исследуемый раствор. При выполнении некоторых условий граница двух растворов не размывается при пропускании электрического тока. Например, концентрацию исследуемого раствора подбирают таким образом, чтобы выполнялось регулирующее соотношение Кольрауша:

Определяя положение границы через определенный промежуток времени, можно рассчитать число переноса.

Например, пусть растворы солей KCl и BaCl₂ имеют общий анион Cl^–. Раствор KCl – исследуемый, а BaCl₂ – индикатор. Тогда регулирующее соотношение Кольрауша имеет вид

Через растворы пропускают электрический ток и наблюдают за перемещением границы раздела. Если за время t через систему прошло q Кулонов, то количество электричества, перенесенное катионами К⁺, равно t₊q. Заряд t₊q должен быть равен заряду всех катионов К⁺, которые содержались в объеме V, определенном по перемещению границы. Поэтому t₊q = z₊Fc₊V, откуда

Аналогично можно оценить число переноса аниона.

Зависимость чисел переноса от концентрации обычно невелика. Экстраполяция этой зависимости к нулевой концентрации дает предельные числа переноса t_i^o. Однако в некоторых случаях число переноса сильно изменяется с концентрацией и может оказаться равным нулю и даже меньше нуля (например, для концентрированного раствора CdI₂ t₊ < 0). Это можно объяснить образованием комплексных анионов CdI₄^2–.

При не очень высоких концентрациях полностью диссоциирующего бинарного электролита наблюдается следующая закономерность в зависимости t_i от концентрации. Если t_i^o = 0,5, то при увеличении концентрации раствора число переноса остается практически неизменным. Если t_i^o < 0,5, то с ростом концентрации соли число переноса уменьшается, а если t_i^o > 0,5 – увеличивается.

Влияние температуры на числа переноса незначительно. Во многих случаях числа переноса при повышении температуры приближаются к 0,5, то есть подвижности катиона и аниона становятся почти одинаковы.

Растворы одной и той же соли в разных растворителях имеют различные числа переноса; это объясняется, в основном, различной степенью сольватации катионов и анионов в зависимости от растворителя.

Источник

Определение числа единиц переноса ()

1. Метод графического интегрирования – заключается в том, что на диаграмме, построенной в координатах находят площадь, ограниченную кривой, осью абцисс (х) и вертикальными прямыми, проведенными через точки на оси абцисс и , являющимися пределами интегрирования. Эта площадь с учетом масштабов по осям x и y, равна числу единиц переноса:

;

где: – число единиц “” в 1 см по оси абцисс;

– число единиц “” в 1 см по оси ординат.

Тогда из уравнения .

2. Графический метод – рабочая линия – прямая, равновесная зависимость нелинейна. Для определения строят диаграмму y – x, на которую наносят рабочую линию AB (прямая ) и линию равновесия OC (прямая ), затем проводят среднюю линию MN, проходящую через точки, делящие пополам отрезки ординат между рабочей линией и линией равновесия. Затем из точки В, характеризующей конечное состояние газа, проводят линию BD до пересечения со средней линией и продолжают ее до точки Е, при этом отрезок BD=DE. Затем из точки Е восстанавливают перпендикуляр EF до пересечения с рабочей линией и ставят точку F, причем EF=2KD=KL. Отрезок EF показывает изменение концентрации газа, равной одной единице переноса (ступенька BEF). Продолжая аналогичное построение ступенек до начального состояния газа (точка А), определяем , если в конце получается неполная ступенька, то ее принимаем за полную: .

3. Метод численного интегрирования – рабочая линия нелинейна, равновесная зависимость линейна. Суть метода заключается в том, что на диаграмме y – x отрезок делят на два равных участка. Вертикальные отрезки между рабочей линией AB и линией равновесия OC, проведенные из точек состояния газа в начале и в конце процесса (точка А, точка В), а также средней точки М, показывают значения движущей силы прцесса:

Пример 1

Объемная концентрация NH₃в воздухе =0,12 кг/м³, T=300K, P=кПа

Мольная масса NH₃– (M_k=17), мольная масса носителя (инертного газа – воздуха) М_ог=29

Решение:

кг/кмоль.

Тогда: объемная концентрация кмоль/м³

мольная: кмоль/кмоль

массовая: кг/кг

Парциальное давление компонента: кПа

Относительная концентрация: .

Пример 2

Концентрация поташа (K₂CO₃) после поглощения его водой:

=200 кг/м³, М_к=138 кг/кмоль,

Концентрация H₂S:

=15 кг/м³, =34 кг/кмоль, =1200 кг/м³

Растворитель – вода, М_ж=18 кг/кмоль

Выразить состав раствора в мольных долях

Решение:

мольных доль;

м.д.

Пример 3

Определить количество поглощаемого NH₃, расход поглотителя (L) и движущую силу процесса при абсорбции аммиака водой из смеси его с воздухом G₀=13600 м³/ч, (=0,1 мПа, t₀=0), – 5%, =0,27

Содержание аммиака в жидкости =0,0020 кмоль NH₃/кмоль H₂O;

=20⁰С , =20⁰С. Давление газа в абсорбере P₀= Па.

Рещение:

Расчет материального баланса: т.к. содержание аммиака в исходно смеси не превышает 10% то выражение концентраций приведем в относительных концентрациях

G=G₀(1-0,05)=13600(1-0,05)=12920 м³/ч – расход воздуха

или 12920/22,4=576,8 кмоль/ч

Относительный мольный состав газовой фазы:

Y₁=5/(100-5)=0,0526 кмоль NH₃/кмоль возд. – в начале;

Y₂=0,27/(100-0,27)=0,0027 кмоль NH₃/кмоль возд. – в конце.

Количество NH₃ , поступающего на абсорбцию:

M_нач===30,34 кмоль/ч;

M_к= ==1,56 кмоль/ч;

М= M_нач-M_к=30,34-1,56=28,78 кмоль/ч.

Пример 4

Требуется поглотить чистой водой 1 т. SO₂ в час из газов, содержащих 5% – SO₂, 95% – N_2.

Q_ж взято на 20% больше Q_ж мин необходимого,

=90%, P_ат=760 мм.рт.ст., t_ж=20⁰С,

Растворимость SO₂в воде при t=20⁰с

Концентрация SO₂, %	1	0,7	0,5	0,3	0,2	0,15	0,1	0,05	0,02
Парциальное давление SO₂над раствором, мм.рт.ст.	59	39	26	14,1	8,4	5,8	3,2	1,2	0,5

Определить .

Решение:

Парциальное давление компонента газовой смеси

P_i=мм.рт.ст.

Такому давлению соответствует концентрация в растворе 0,69%, т.е. в 100кг воды – 69кг SO₂

Общее количество поглощаемого SO₂по заданию – 1000кг

Поэтому минимальное количество орошающей жидкости:

Q_{ж мин}===145000 кг/ч=145м³/ч;

Действительное количество жидкости:

Q_ж==174 м³/ч

Из уравнения материального баланса .

Давление на выходе из аппарата P_вых==3,95 мм.рт.ст..

Содержание SO₂в абсорбенте, выходящем из аппарата

= Q_ж, т.е. ==0,575 кг на 100кг

Такому содержанию SO₂ соответствует парциальное давление 30,87 мм.рт.ст.

=38-30,87=7,13 мм.рт.ст.

=(7,13+3,95)/2=5,54 мм.рт.ст.=730 Па

Пример 5

Рассчитать количество поглощенного СO₂, расход поглотителя и движущую силу процесса

При абсорбции СO₂водой из газовой смеси состава:

СO₂ – 30,2%, CO – 4%, H₂ – 48%, N₂ – 17,8%.

Расход газа: V=10000м³/ч (при н.у.)

G₁=452,5 кмоль/ч

Давление 1,6 мПа

Орошение водой (X_н=0) t=25⁰с

Степень извлечения СO₂: =95%

Решение:

Т.к. содержание СO₂>10%, то выражение концентрации выбираем в мольных долях (если бы , то в относительных концентрациях).

По уравнению W=

Мольная доля СO₂на входе в аппарат:

=0,302,

а количество СO_2:

M₁= =136,65 кмоль/час.

Количество поглощенного СO₂

W= =129,82 кмоль/час.

Количество газа, выходящего из аппарата:

G₂= G₁-W=452,5-129,82=322,66 кмоль/час

Количество СO₂ в выходящем газе:

M₂= M₁-W=136,65-129,82=6,83 кмоль/час.

Мольная доля СO₂ в уходящем газе:

= M₂/ G₂=6,83/322,66=0,021 (2,1%).

Построение рабочей характеристики процесса по закону Генри:

Закон Генри: .

;

где: , – коэффициенты при , , ;

– парциальное давление в газе.

МПа.

Закон Дальтона: МПа.

Из закона Генри: ;

из уравнения ;

где: – равновесная концентрация в газе;

– равновесная линия процесса.

В С

А

x 10³

Определение расхода абсорбента:

кмоль/ч;

увеличенный в 1,3 раза: кмоль/ч,

тогда: ,

а содержание в выходящей воде:

– равновесная концентрация в газе.

Тогда: .

Построение рабочей линии процесса: уравнение рабочей линии имеет вид кривой:

;

Бесплатная лекция: “24 Промежуточный и итоговый контроль” также доступна.

где: – удельный расход поглотителя: .

Применим метод Симпсона – заменим кривую линию АВ ломаной АЕВ.

Для точки Е: .

Определим значение из уравнения:

;

Источник

Методы определения чисел переноса.

Experimental measurement[edit]

Hittorf method[edit]

Moving boundary method[edit]

Concentration cells[edit]

Electrophoretic magnetic resonance imaging method[edit]

See also[edit]

Notes[edit]

External links[edit]

Рекомендуемые материалы

Пример 1

Пример 2

Пример 3

Пример 5

А

Добавить комментарий Отменить ответ

Методы определения чисел переноса.

Experimental measurement[edit]

Hittorf method[edit]

Moving boundary method[edit]

Concentration cells[edit]

Electrophoretic magnetic resonance imaging method[edit]

See also[edit]

Notes[edit]

External links[edit]

Рекомендуемые материалы

Пример 1

Пример 2

Пример 3

Пример 5

А

Вам также может понравиться

Как найти внутренние инвестиции это

Работа как найти аниме

Как найти численность населения в атласе

Добавить комментарий Отменить ответ