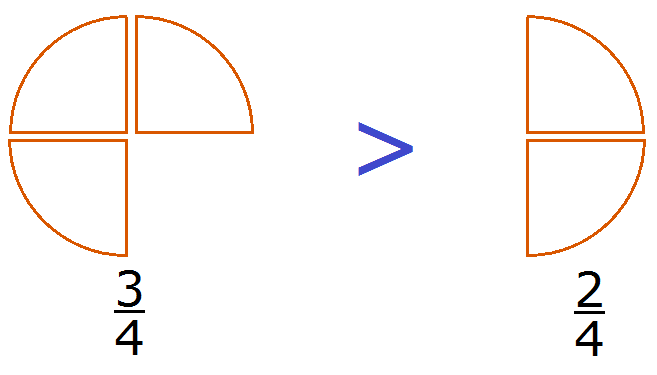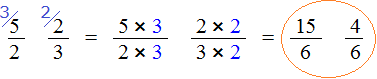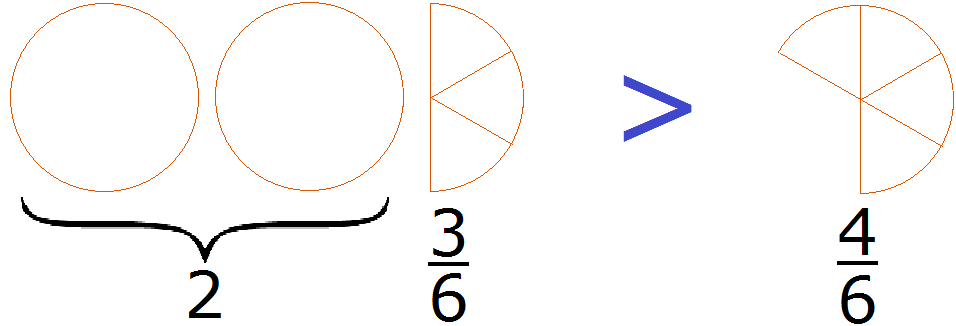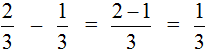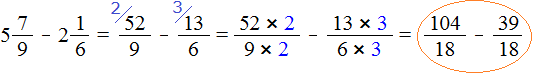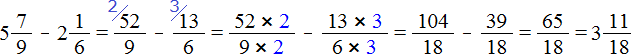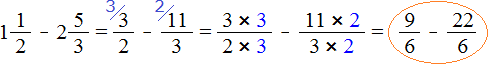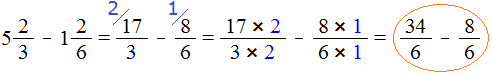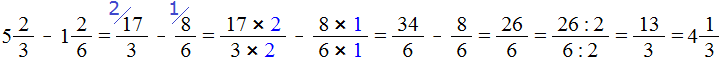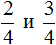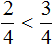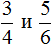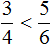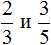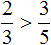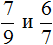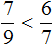Данная статья рассматривает сравнение дробей. Здесь мы выясним, какая из дробей больше или меньше, применим правило, разберем примеры решения. Сравним дроби как с одинаковыми, так и разными знаменателями. Произведем сравнение обыкновенной дроби с натуральным числом.
Сравнение дробей с одинаковыми знаменателями
Когда производится сравнение дробей с одинаковыми знаменателями, мы работаем только с числителем, а значит, сравниваем доли числа. Если имеется дробь 37, то она имеет 3 доли 17, тогда дробь 87 имеет 8 таких долей. Иначе говоря, если знаменатель одинаковый, производится сравнение числителей этих дробей, то есть 37 и 87 сравниваются числа 3 и 8.
Отсюда следует правило сравнения дробей с одинаковыми знаменателями: из имеющихся дробей с одинаковыми показателями считается большей та дробь, у которой числитель больше и наоборот.
Это говорит о том, что следует обратить внимание на числители. Для этого рассмотрим пример.
Произвести сравнение заданных дробей 65126 и 87126.
Решение
Так как знаменатели дробей одинаковые, переходим к числителям. Из чисел 87 и 65 очевидно, что 65 меньше. Исходя из правила сравнения дробей с одинаковыми знаменателями имеем, что 87126 больше 65126.
Ответ: 87126>65126.
Сравнение дробей с разными знаменателями
Сравнение таких дробей можно соотнести со сравнением дробей с одинаковыми показателями, но имеется различие. Теперь необходимо дроби приводить к общему знаменателю.
Если имеются дроби с разными знаменателями, для их сравнения необходимо:
- найти общий знаменатель;
- сравнить дроби.
Рассмотрим данные действия на примере.
Произвести сравнение дробей 512 и 916.
Решение
В первую очередь необходимо привести дроби к общему знаменателю. Это делается таким образом: находится НОК, то есть наименьший общий делитель, 12 и 16. Это число 48. Необходимо надписать дополнительные множители к первой дроби 512 , это число находится из частного 48:12=4, для второй дроби 916 – 48:16=3. Запишем получившееся таким образом: 512=5·412·4=2048 и 916=9·316·3=2748.
После сравнения дробей получаем, что 2048<2748. Значит, 512 меньше 916.
Ответ: 512<916.
Имеется еще один способ сравнения дробей с разными знаменателями. Он выполняется без приведения к общему знаменателю. Рассмотрим на примере. Чтобы сравнить дроби ab и cd, приводим к общему знаменателю, тогда b·d, то есть произведение этих знаменателей. Тогда дополнительные множители для дробей будут являться знаменатели соседней дроби. Это запишется так a·db·d и c·bd·b. Используя правило с одинаковыми знаменателями, имеем, что сравнение дробей свелось к сравнениям произведений a·d и c·b. Отсюда получаем правило сравнения дробей с разными знаменателями: если a·d>b·c, тогда ab>cd, но если a·d<b·c, тогдаab<cd. Рассмотрим сравнение с разными знаменателями.
Произвести сравнение дробей 518 и 2386.
Решение
Данный пример имеет a=5, b=18, c=23 и d=86. Тогда необходимо вычислить a·d и b·c. Отсюда следует, что a·d=5·86=430 и b·c=18·23=414. Но 430>414, тогда заданная дробь 518 больше, чем 2386.
Ответ: 518>2386.
Сравнение дробей с одинаковыми числителями
Если дроби имеют одинаковые числители и разные знаменатели, тогда можно выполнять сравнение по предыдущему пункту. Результат сравнения возможет при сравнении их знаменателей.
Имеется правило сравнения дробей с одинаковыми числителями: из двух дробей с одинаковыми числителями больше та дробь, которая имеет меньший знаменатель и наоборот.
Рассмотрим на примере.
Произвести сравнение дробей 5419 и 5431.
Решение
Имеем, что числители одинаковые, значит, что дробь, имеющая знаменатель 19 больше дроби, которая имеет знаменатель 31. Это понятно, исходя из правила.
Ответ: 5419>5431.
Иначе можно рассмотреть на примере. Имеется две тарелки, на которых 12 пирога, анна другой 116. Если съесть 12 пирога, то насытишься быстрей, нежели только 116. Отсюда вывод, что наибольший знаменатель при одинаковых числителях является наименьшим при сравнении дробей.
Сравнение дроби с натуральным числом
Сравнение обыкновенной дроби с натуральным числом идет как и сравнение двух дробей с записью знаменателей в виде 1. Для детального рассмотрения ниже приведем пример.
Необходимо выполнить сравнение 638 и 9.
Решение
Необходимо представить число 9 в виде дроби 91. Тогда имеем необходимость сравнения дробей 638 и 91. Далее следует приведение к общему знаменателю путем нахождения дополнительных множителей. После этого видим, что нужно сравнить дроби с одинаковыми знаменателями 638 и 728. Исходя из правила сравнения, 63<72, тогда получаем 638<728. Значит, заданная дробь меньше целого числа 9, то есть имеем 638<9.
Ответ: 638<9.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Не только простые числа можно сравнивать, но и дроби тоже. Ведь дробь — это такое же число как, к примеру, и натуральные числа. Нужно знать только правила, по которым сравнивают дроби.
Сравнение дробей с одинаковыми знаменателями.
Если у двух дробей одинаковые знаменатели, то такие дроби сравнить просто.
Чтобы сравнить дроби с одинаковыми знаменателями, нужно сравнить их числители. Та дробь больше у которой больше числитель.
Рассмотрим пример:
Сравните дроби (frac{7}{26}) и (frac{13}{26}).
Знаменатели у обоих дробей одинаковые равны 26, поэтому сравниваем числители. Число 13 больше 7. Получаем:
(frac{7}{26} < frac{13}{26})
Сравнение дробей с равными числителями.
Если у дроби одинаковые числители, то больше та дробь, у которой знаменатель меньше.
Понять это правило можно, если привести пример из жизни. У нас есть торт. К нам в гости могут прийти 5 или 11 гостей. Если придут 5 гостей, то мы разрежем торт на 5 равных кусков, а если придут 11 гостей, то разделим на 11 равных кусков. А теперь подумайте в каком случаем на одного гостя придется кусок торта большего размера? Конечно, когда придут 5 гостей, кусок торта будет больше.
Или еще пример. У нас есть 20 конфет. Мы можем поровну раздать конфеты 4 друзьям или поровну поделить конфеты между 10 друзьями. В каком случае у каждого друга будет конфет больше? Конечно, когда мы разделим только на 4 друзей, количество конфет у каждого друга будет больше. Проверим эту задачу математически.
(frac{20}{4} > frac{20}{10})
Если мы до решаем эти дроби, то получим числа (frac{20}{4} = 5) и (frac{20}{10} = 2). Получаем, что 5 > 2
В этом и заключается правило сравнения дробей с одинаковыми числителями.
Рассмотрим еще пример.
Сравните дроби с одинаковым числителем (frac{1}{17}) и (frac{1}{15}) .
Так как числители одинаковые, больше та дробь, где знаменатель меньше.
(frac{1}{17} < frac{1}{15})
Сравнение дробей с разными знаменателями и числителями.
Чтобы сравнить дроби с разными знаменателями, необходимо дроби привести к общему знаменателю, а потом сравнить числители.
Пример:
Сравните дроби (frac{2}{3}) и (frac{5}{7}).
Сначала найдем общий знаменатель дробей. Он будет равен числу 21.
(begin{align}&frac{2}{3} = frac{2 times 7}{3 times 7} = frac{14}{21}\\&frac{5}{7} = frac{5 times 3}{7 times 3} = frac{15}{21}\\ end{align})
Потом переходим к сравнению числителей. Правило сравнения дробей с одинаковыми знаменателями.
(begin{align}&frac{14}{21} < frac{15}{21}\\&frac{2}{3} < frac{5}{7}\\ end{align})
Сравнение неправильной и правильной дроби.
Неправильная дробь всегда больше правильной. Потому что неправильная дробь больше 1, а правильная дробь меньше 1.
Пример:
Сравните дроби (frac{11}{13}) и (frac{8}{7}).
Дробь (frac{8}{7}) неправильная и она больше 1.
(1 < frac{8}{7})
Дробь (frac{11}{13}) правильная и она меньше 1. Сравниваем:
(1 > frac{11}{13})
Получаем, (frac{11}{13} < frac{8}{7})
Вопросы по теме:
Как сравнить дроби с разными знаменателями?
Ответ: надо привести к общему знаменателю дроби и потом сравнить их числители.
Как сравнивать дроби?
Ответ: сначала нужно определиться к какой категории относятся дроби: у них есть общий знаменатель, у них есть общий числитель, у них нет общего знаменателя и числителя или у вас правильная и неправильная дробь. После классификации дробей применить соответствующее правило сравнения.
Что такое сравнение дробей с одинаковыми числителями?
Ответ: если у дробей одинаковые числители, та дробь больше у которой знаменатель меньше.
Пример №1:
Сравните дроби (frac{11}{12}) и (frac{13}{16}).
Решение:
Так как нет одинаковых числителей или знаменателей, применяем правило сравнения с разными знаменателями. Нужно найти общий знаменатель. Общий знаменатель будет равен 96. Приведем дроби к общему знаменателю. Первую дробь (frac{11}{12}) умножим на дополнительный множитель 8, а вторую дробь (frac{13}{16}) умножим на 6.
( begin{align}&frac{11}{12} = frac{11 times 8}{12 times 8} = frac{88}{96}\\&frac{13}{16} = frac{13 times 6}{16 times 6} = frac{78}{96}\\ end{align})
Сравниваем дроби числителями, та дробь больше у которой числитель больше.
( begin{align}&frac{88}{96} > frac{78}{96}\\&frac{11}{12} > frac{13}{16}\\ end{align})
Пример №2:
Сравните правильную дробь с единицей?
Решение:
Любая правильная дробь всегда меньше 1.
Задача №1:
Сын с отцом играли в футбол. Сын из 10 подходов в ворота попал 5 раз. А папа из 5 подходов попал в ворота 3 раза. Чей результат лучше?
Решение:
Сын попал из 10 возможных подходов 5 раз. Запишем в виде дроби (frac{5}{10} ).
Папа попал из 5 возможных подходов 3 раз. Запишем в виде дроби (frac{3}{5} ).
Сравним дроби. У нас разные числители и знаменатели, приведем к одному знаменателю. Общий знаменатель будет равен 10.
(begin{align}&frac{3}{5} = frac{3 times 2}{5 times 2} = frac{6}{10}\\&frac{5}{10} < frac{6}{10}\\&frac{5}{10} < frac{3}{5}\\ end{align})
Ответ: у папы результат лучше.
#хакнем_математика 👈 рубрика, содержащая интересный, познавательный контент по математике как для школьников, так и для взрослых 🥳
Цикл статей “Дроби”
Первая часть Вторая часть Третья часть
Четвертая часть Пятая часть Шестая часть
КАК СРАВНИВАТЬ ОБЫКНОВЕННЫЕ ДРОБИ?
Здравствуйте, уважаемые читатели! В этой статье будут рассмотрены различные способы сравнения обыкновенных дробей. Должен предупредить, что этот вопрос обсуждается
в учебниках, предназначенных как для четвёртого класса, так и в последующих — вплоть до седьмого. Причём, одно и то же сравнение осуществляется в них подчас различными способами.
Вот номер из каталога заданий ОГЭ-2021 на тему данной статьи, а следующий за ним номер взят из пособия к ОГЭ-2017 под редакцией И.В. Ященко.
Прежде чем читать дальше, решите эти задания и сравните ответы, а возможно и решения, с решениями автора, которые будут приведены ниже.
Вот два правила сравнения обыкновенных дробей, изучаемые
в четвёртом классе.
I. Из двух обыкновенных дробей с одинаковыми знаменателями больше та, у которой больше числитель (обратно: меньше та, у которой меньше числитель).
Поскольку часто обыкновенная дробь является результатом деления натуральных чисел, то становится очевидно, что это правило следует из хорошо знакомого четвероклассникам свойства деления: чем больше делимое при неизменном делителе, тем больше частное.
Прежде чем переходить к следующему правилу, необходимо
для отработки соответствующего навыка, предоставить четвероклассникам возможность подобного сравнения, которое вполне возможно провести устно.
II. Из двух обыкновенных дробей с одинаковыми числителями больше та, у которой меньше знаменатель (обратно: меньше та, у которой больше знаменатель).
И это правило следует из свойства деления, когда при неизменном делимом частное уменьшается при возрастании делителя и увеличивается при его уменьшении.
На отработку навыка использования этого правила следует потратить больше времени и использовать большее число соответствующих примеров.
Вот, например, как решаются вышеприведённые задания из каталога «ОГЭ-2021».
№ 12 (337381)
Поскольку, a > b, то, в соответствии с правилом II,
ОТВЕТ. 2.
Ещё одним способом сравнения двух обыкновенных дробей
служит сравнение каждой из них с каким-нибудь числом.
В третьей статье цикла мы таким образом сравнили правильные и неправильные дроби.
Обычно возможность такого сравнения легко замечается учениками.
Сравним, например, дроби
Очевидно, что
№ 2.1. (первая цифра — № задания, вторая — № варианта)
В соответствии с правилом I имеем:
Проверим число 11/23:
ОТВЕТ: 3
Хорошо считающий «в уме» ученик может использовать для подобных сравнений различные дроби:
и многие другие.
В пятом классе для сравнения дробей вида
можно использовать единичный отрезок числового луча.
В самом деле, первой дроби, чтобы стать единицей, «не хватает» всего лишь
а значит точка, изображающая дробь
дальше от отметки 1 и ближе к отметке 0 по сравнению c точкой, соответствующей дроби
(см. рисунок).
Но тогда
Этот результат можно обобщить для любых натуральных значений m и n, при m<n:
Проведём это обобщение с помощью универсального метода сравнения
двух обыкновенных дробей путём приведения к общему знаменателю, в соответствии с правилом I.
Очевидно, что числа «n» и «n+1» взаимно просты, поскольку
при делении второго из них на любой, кроме единицы, делитель первого даёт в остатке число 1.
Имеем обыкновенные дроби
Умножим и числитель, и знаменатель каждой из них на знаменатель другой, воспользовавшись при этом распределительным свойством умножения относительно сложения (которое лично я считаю самым важным в курсе школьной математики!):
Замечу для семиклассников: мы попутно доказали формулу сокращённого умножения «произведение разности и суммы двух чисел равно разности их квадратов».
В результате получили верное неравенство
В некоторых случаях для сравнения удобно приводить дроби к общему числителю, чтобы воспользоваться правилом II.
Требуется, например, сравнить дроби
Вместо того, чтобы затеваться с поиском наименьшего общего знаменателя, приведём эти дроби к общему числителю. Для этого и числитель, и знаменатель первой дроби умножим на 3, а числитель и знаменатель второй — на 2.
Получим верное равенство
Заданные дроби равны…Что ж, случается и такое!
Если вам было интересно, не забудьте подписаться на наш канал и хэштег #хакнем_математика
Автор: #себихов_александр 71 год, много лет проработал конструктором-технологом микроэлектронных приборов и узлов в одном из НИИ г. Саратова, затем преподавателем математики и физики.
Другие статьи автора:
Цикл статей “Дроби”
1 статья 2 статья 3 статья 4 статья 5 статья 6 статья 7статья [Текущая]
Содержание:
- Равные дроби
- Принципы сравнения дробей
- Сравнение дробей с разными знаменателями
Равные дроби
Пример
Задание. Найти при каком значении $x$ и $y$ дроби $frac{x}{3}$ и $frac{4}{y}$ будут равны.
Решение. Заданные дроби равны, то есть $frac{x}{3}=frac{4}{y}$ , если равны их числители и знаменатели
соответственно. А тогда имеют место следующие равенства:
$x=4$ $3=y$ или $x=4$ $y=3$
Ответ. $x=4, y=3$
Две дроби считаются равным, если величины, выражаемые этими числами при одной и той же единице измерения, равны между собой.
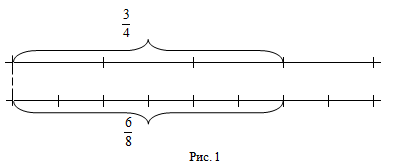
Например. Дроби $frac{3}{4}$ и
$frac{6}{8}$ равны, так как две длины, из которых одна составляет $frac{3}{4}$ м, а вторая – $frac{6}{8}$ м, равны (рис 1).
Принципы сравнения дробей
Из двух дробей с одинаковыми знаменателями больше та, числитель которой больше.
Например. $frac{7}{18}>frac{5}{18}$ , так как $7>5$
Из двух дробей с одинаковыми числителями больше та, знаменатель которой меньше.
Например. $frac{7}{3}>frac{7}{6}$, так как $3<6$ .
Любая правильная дробь меньше 1.
Например. $frac{4}{5} < 1$
Неправильная дробь, числитель которой равен знаменателю, равна 1.
Например. $frac{3}{3}=1, frac{7}{7}=1$
Неправильная дробь, у которой числитель больше знаменателя, больше 1.
Например. $frac{7}{6}>1$
Любая правильная дробь меньше произвольной неправильной дроби.
Например. $frac{4}{5}<frac{5}{4}$
В общем случае дроби по величине сравниваются следующим образом. Умножают числитель первой дроби на
знаменатель второй, а знаменатель первой на числитель второй. И сравнивают полученные произведения. Если первое
из этих произведений больше/равно/меньше второго, то соответственно и первая дробь больше/равно/меньше второй.
Например. $frac{5}{6}>frac{7}{9}$ , так как $5 cdot 9>6 cdot 7 Leftrightarrow 45>42$
Сравнение дробей с разными знаменателями
Чтобы сравнить дроби с разными знаменателями, их нужно вначале привести к одинаковому (одному) знаменателю. Для этого
приводят либо к общему знаменателю, либо числитель и знаменатель первой дроби домножают на знаменатель второй и наоборот,
числитель и знаменатель второй дроби на знаменатель первой. И далее дроби сравнивать как дроби с одинаковым знаменателем
(описано выше).

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Сравнить дроби
$frac{3}{4}$ и $frac{5}{7}$
Решение. Приведем дроби к общему знаменателю, для этого
числитель и знаменатель
первой дроби домножим на 7 (знаменатель второй дроби); а числитель и знаменатель второй дроби – на 4, будем иметь:
$frac{3 cdot 7}{4 cdot 7}$ и $frac{5 cdot 4}{7 cdot 4}$
$frac{21}{28}$ и $frac{20}{28}$
Первая дробь больше: $frac{21}{28}>frac{20}{28} Leftrightarrow frac{3}{4}>frac{5}{7}$ , так как ее числитель $21 > 20$
Ответ. $frac{3}{4}>frac{5}{7}$
Читать следующую тему: основное свойство дроби.
Продолжаем изучать дроби. Сегодня мы поговорим об их сравнении. Тема интересная и полезная. Она позволит новичку почувствовать себя учёным в белом халате.
Суть сравнения дробей заключается в том, чтобы узнать какая из двух дробей больше или меньше.
Чтобы ответить на вопрос какая из двух дробей больше или меньше, пользуются операциями отношения, такими как больше (>) или меньше (<).
Ученые-математики уже позаботились о готовых правилах, позволяющие сразу ответить на вопрос какая дробь больше, а какая меньше. Эти правила можно смело применять.
Мы рассмотрим все эти правила и попробуем разобраться, почему происходит именно так.
Сравнение дробей с одинаковыми знаменателями
Дроби, которые нужно сравнить, попадаются разные. Самый удачный случай это когда у дробей одинаковые знаменатели, но разные числители. В этом случае применяют следующее правило:
Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше. И соответственно меньше будет та дробь, у которой числитель меньше.
Например, сравним дроби и
и ответим какая из этих дробей больше. Здесь одинаковые знаменатели, но разные числители. У дроби
числитель больше, чем у дроби
. Значит дробь
больше, чем
. Так и отвечаем. Отвечать нужно с помощью значка больше ( > )
Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на четыре части. пиццы больше, чем
пиццы:
Каждый согласится с тем, что первая пицца больше, чем вторая.
Сравнение дробей с одинаковыми числителями
Следующий случай это когда числители дробей одинаковые, но знаменатели разные. Для таких случаев предусмотрено следующее правило:
Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше. И соответственно меньше та дробь, у которой знаменатель больше.
Например, сравним дроби и
. У этих дробей одинаковые числители. У дроби
знаменатель меньше, чем у дроби
. Значит дробь
больше, чем дробь
. Так и отвечаем:
Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на три и четыре части. пиццы больше, чем
пиццы:
Каждый согласится с тем, что первая пицца больше, чем вторая.
Сравнение дробей с разными числителями и разными знаменателями
Нередко случается так, что приходиться сравнивать дроби с разными числителями и разными знаменателями. Например, сравнить дроби и
.
Чтобы ответить на вопрос, какая из этих дробей больше или меньше, нужно привести их к одинаковому (общему) знаменателю. Затем можно будет легко определить какая дробь больше или меньше.
Приведём дроби и
к одинаковому (общему) знаменателю. Найдём наименьшее общее кратное (НОК) знаменателей обеих дробей. НОК знаменателей дробей
и
это число 6.
Теперь находим дополнительные множители для каждой дроби. Разделим НОК на знаменатель первой дроби . НОК это число 6, а знаменатель первой дроби это число 2. Делим 6 на 2, получаем дополнительный множитель 3. Записываем его над первой дробью:
Теперь найдём второй дополнительный множитель. Разделим НОК на знаменатель второй дроби . НОК это число 6, а знаменатель второй дроби это число 3. Делим 6 на 3, получаем дополнительный множитель 2. Записываем его над второй дробью:
Умножим дроби на свои дополнительные множители:
Мы пришли к тому что дроби, у которых были разные знаменатели, превратились в дроби, у которых одинаковые знаменатели. А как сравнивать такие дроби мы уже знаем. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше:
Правило правилом, а мы попробуем разобраться почему больше, чем
. Для этого выделим целую часть в неправильной дроби
. В дроби
ничего выделять не нужно, поскольку эта дробь уже правильная.
После выделения целой части в дроби , получим следующее выражение:
Теперь можно легко понять, почему больше, чем
. Давайте нарисуем эти дроби в виде пицц:
2 целые пиццы и пиццы, больше чем
пиццы.
Вычитание смешанных чисел. Сложные случаи.
Вычитая смешанные числа иногда можно обнаружить, что всё идёт не так гладко как хотелось бы.
При вычитании чисел уменьшаемое должно быть больше вычитаемого. Только в этом случае будет получен нормальный ответ.
Например, 10 − 8 = 2
10 — уменьшаемое
8 — вычитаемое
2 — разность
Уменьшаемое 10 больше вычитаемого 8, поэтому мы получили нормальный ответ 2.
А теперь посмотрим, что будет если уменьшаемое окажется меньше вычитаемого. Пример 5 − 7 = −2
5 — уменьшаемое
7 — вычитаемое
−2 — разность
В этом случае мы выходим за пределы привычных для нас чисел и попадаем в мир отрицательных чисел, где нам ходить пока рано, а то и опасно. Чтобы работать с отрицательными числами, нужна соответствующая математическая подготовка, которую мы ещё не получили.
Если при решении примеров на вычитание вы обнаружите, что уменьшаемое меньше вычитаемого, то можете пока пропустить такой пример. Работать с отрицательными числами допустимо только после их изучения.
С дробями ситуация та же самая. Уменьшаемое должно быть больше вычитаемого. Только в этом случае можно будет получить нормальный ответ. А чтобы понять больше ли уменьшаемая дробь, чем вычитаемая, нужно уметь сравнить эти дроби.
Например, решим пример 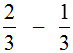
Это пример на вычитание. Чтобы решить его, нужно проверить больше ли уменьшаемая дробь, чем вычитаемая. больше чем
поэтому смело можем вернуться к примеру и решить его:
Теперь решим такой пример
Проверяем больше ли уменьшаемая дробь, чем вычитаемая. Обнаруживаем, что она меньше:
В этом случае разумнее остановиться и не продолжать дальнейшее вычисление. Вернёмся к этому примеру, когда изучим отрицательные числа.
Смешанные числа перед вычитанием тоже желательно проверять. Например, найдём значение выражения .
Сначала проверим больше ли уменьшаемое смешанное число, чем вычитаемое. Для этого переведём смешанные числа в неправильные дроби:
Получили дроби с разными числителями и разными знаменателями. Чтобы сравнить такие дроби, нужно привести их к одинаковому (общему) знаменателю. Не будем подробно расписывать как это сделать. Если испытываете затруднения на этом моменте, обязательно изучите действия с дробями.
После приведения дробей к одинаковому знаменателю, получаем следующее выражение:
Теперь нужно сравнить дроби и
. Это дроби с одинаковыми знаменателями. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.
У дроби числитель больше, чем у дроби
. Значит дробь
больше, чем дробь
.
А это значит что уменьшаемое больше, чем вычитаемое
А значит мы можем вернуться к нашему примеру и смело решить его:
Пример 3. Найти значение выражения
Проверим больше ли уменьшаемое, чем вычитаемое.
Переведём смешанные числа в неправильные дроби:
Получили дроби с разными числителями и разными знаменателями. Приведем данные дроби к одинаковому (общему) знаменателю:
Теперь сравним дроби и
. У дроби
числитель меньше, чем у дроби
, значит дробь
меньше, чем дробь
А это значит, что и уменьшаемое меньше, чем вычитаемое
А это гарантировано приведёт нас в мир отрицательных чисел. Поэтому разумнее остановиться на этом месте и не продолжать вычисление. Продолжим его после изучения отрицательных чисел.
Пример 4. Найти значение выражения
Проверим больше ли уменьшаемое, чем вычитаемое.
Переведём смешанные числа в неправильные дроби:
Получили дроби с разными числителями и разными знаменателями. Приведем их к одинаковому (общему) знаменателю:
Теперь нужно сравнить дроби и
. У дроби
числитель больше, чем у дроби
. Значит дробь
больше, чем дробь
.
А это значит, что уменьшаемое больше, чем вычитаемое
Поэтому мы смело можем продолжить вычисление нашего примера:
Сначала мы получили ответ . Эту дробь мы сократили на 2 и получили дробь
, но такой ответ нас тоже не устроил и мы выделили целую часть в этом ответе. В итоге получили ответ
.
Задания для самостоятельного решения
Задание 1. Сравнить дроби:
Решение:
Задание 2. Сравнить дроби:
Решение:
Задание 3. Сравнить дроби:
Решение:
Задание 4. Сравнить дроби:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже