Как найти число базисных решений - Сайт, где вы сможете решить свои вопросы

Базисные (основные) и свободные (неосновные) переменные. Общее и базисное решения системы линейных алгебраических уравнений. Первая часть.

В теме “Теорема Кронекера-Капелли” было указано, что если ранг расширеной матрицы системы $widetilde{A}$ и ранг матрицы системы $A$ равны между собой, то заданная система линейных алгебраических уравнений (СЛАУ) совместна, т.е. имеет решение. Вопрос о количестве этих решений разрешим с помощью следствия из теоремы Кронекера. Согласно ему, если $rang A=rangwidetilde{A} = n$ ($n$ – количество неизвестных), то СЛАУ имеет единственное решение. Если же $rang A=rangwidetilde{A} < n$, то количество решений заданной СЛАУ бесконечно.

Особый интерес представляет именно случай $rang A=rangwidetilde{A} < n$, которым и займёмся в этой теме. Так как $rang A=rangwidetilde{A}$, то обозначим эти ранги просто буквой $r$, т.е. $rang A=rangwidetilde{A}=r$. Итак, $r < n$ и система неопределена, т.е. имеет бесконечное количество решений.

Что означает фраза “ранг матрицы равен $r$”? Она означает, что есть хотя бы один минор $r$-го порядка, который не равен нулю. Напомню, что такой минор называется базисным. Базисных миноров может быть несколько. При этом все миноры, порядок которых выше $r$, равны нулю или не существуют.

Если коэффициенты при $r$ переменных совместной СЛАУ образуют базисный минор матрицы системы $A$, то эти $r$ переменных называют базисными или основными. Остальные $n-r$ переменных именуют свободными или неосновными.

Выбрать $r$ базисных переменных в общем случае можно различными способами. В примерах я покажу наиболее часто используемый способ выбора.

Решение СЛАУ, в котором все свободные переменные равны нулю, называется базисным.

Во всех изложенных ниже примерах матрицу системы будем обозначать буквой $A$, а расширенную матрицу системы – буквой $widetilde{A}$.

Пример №1

Решить СЛАУ $
left { begin{aligned}
& 3x_1-6x_2+9x_3+13x_4=9\
& -x_1+2x_2+x_3+x_4=-11;\
& x_1-2x_2+2x_3+3x_4=5.
end{aligned} right.$. Если система является неопределённой, указать базисное решение.

Решение

Итак, мы имеем СЛАУ, у которой 3 уравнения и 4 переменных: $x_1$, $x_2$, $x_3$, $x_4$. Так как количество переменных больше количества уравнений, то такая система не может иметь единственное решение (чуть позже мы строго докажем это предложение на основе теоремы Кронекера-Капелли). Найдём решения СЛАУ, используя метод Гаусса:

$$
left( begin{array} {cccc|c}
3 & -6 & 9 & 13 & 9 \
-1 & 2 & 1 & 1 & -11 \
1 & -2 & 2 & 3 & 5 end{array} right) rightarrow
left|begin{aligned}
& text{поменяем местами первую и третью}\
& text{строки, чтобы первым элементом}\
& text{первой строки стала единица.}
end{aligned}right| rightarrow \

rightarrowleft( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 5\
-1 & 2 & 1 & 1 & -11 \
3 & -6 & 9 & 13 & 9
end{array} right)
begin{array} {l} phantom{0} \ r_2+r_1\ r_3-3r_1 end{array} rightarrow

left( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 5\
0 & 0 & 3 & 4 & -6 \
0 & 0 & 3 & 4 & -6
end{array}right)
begin{array} {l} phantom{0} \ phantom{0}\r_3-r_2end{array} rightarrow \

rightarrowleft( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 5\
0 & 0 & 3 & 4 & -6 \
0 & 0 & 0 & 0 & 0
end{array}right)
$$

Мы завершили прямой ход метода Гаусса, приведя расширенную матрицу системы к ступенчатому виду. Слева от черты расположены элементы преобразованной матрицы системы, которую мы также привели к ступенчатому виду. Напомню, что если некая матрица приведена к ступенчатому виду, то её ранг равен количеству ненулевых строк.

И матрица системы, и расширенная матрица системы после эквивалентных преобразований приведены к ступенчатому виду; они содержат по две ненулевых строки. Вывод: $rang A=rangwidetilde{A} = 2$.

Итак, заданная СЛАУ содержит 4 переменных (обозначим их количество как $n$, т.е. $n=4$). Кроме того, ранги матрицы системы и расширенной матрицы системы равны между собой и равны числу $r=2$. Так как $r < n$, то согласно следствию из теоремы Кронекера-Капелли СЛАУ является неопределённой (имеет бесконечное количество решений).

Найдём эти решения. Для начала выберем базисные переменные. Их количество должно равняться $r$, т.е. в нашем случае имеем две базисные переменные. Какие именно переменные (ведь у нас их 4 штуки) принять в качестве базисных? Обычно в качестве базисных переменных берут те переменные, которые расположены на первых местах в ненулевых строках преобразованной матрицы системы, т.е. на “ступеньках”. Что это за “ступеньки” показано на рисунке:

На “ступеньках” стоят числа из столбцов №1 и №3. Первый столбец соответствует переменной $x_1$, а третий столбец соответствует переменной $x_3$. Именно переменные $x_1$ и $x_3$ примем в качестве базисных.

В принципе, если вас интересует именно методика решения таких систем, то можно пропускать нижеследующее примечание и читать далее. Если вы хотите выяснить, почему можно в качестве базисных взять именно эти переменные, и нельзя ли выбрать иные – прошу раскрыть примечание.

Примечание. показатьскрыть

Базисные переменные выбраны: это $x_1$ и $x_3$. Остальные $n-r=2$ переменных (т.е. $x_2$ и $x_4$) являются свободными. Нам нужно выразить базисные переменные через свободные.

Я предпочитаю работать с системой в матричной форме записи. Для начала очистим полученную матрицу $left( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 5\
0 & 0 & 3 & 4 & -6 \
0 & 0 & 0 & 0 & 0
end{array}right)$ от нулевой строки:

$$
left( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 5\
0 & 0 & 3 & 4 & -6
end{array}right)
$$

Свободным переменным, т.е. $x_2$ и $x_4$, соответствуют столбцы №2 и №4. Перенесём эти столбцы за черту. Знак всех элементов переносимых столбцов изменится на противоположный:

Почему меняются знаки? Что вообще значит это перенесение столбцов? показатьскрыть

А теперь продолжим решение обычным методом Гаусса. Наша цель: сделать матрицу до черты единичной. Для начала разделим вторую строку на 3, а потом продолжим преобразования обратного хода метода Гаусса:

$$
left( begin{array} {cc|ccc}
1 & 2 & 5 & 2 & -3\
0 & 3 & -6 & 0 & -4
end{array}right)
begin{array} {l} phantom{0} \ 1/3cdot{r_2} end{array} rightarrow
left( begin{array} {cc|ccc}
1 & 2 & 5 & 2 & -3\
0 & 1 & -2 & 0 & -4/3
end{array}right)
begin{array} {l} r_1-2r_2 \ phantom{0} end{array} rightarrow \

rightarrow left(begin{array} {cc|ccc}
1 & 0 & 9 & 2 & -1/3\
0 & 1 & -2 & 0 & -4/3
end{array}right).
$$

Матрица до черты стала единичной, метод Гаусса завершён. Общее решение найдено, осталось лишь записать его. Если вспомнить, что четвёртый столбец соответствует переменной $x_2$, а пятый столбец – переменной $x_4$, то получим:

$$
left{begin{aligned}
& x_1=9+2x_2-frac{1}{3}x_4;\
& x_2in R;\
& x_3=-2-frac{4}{3}x_4;\
& x_4 in R.
end{aligned}right.
$$

Нами получено общее решение заданной СЛАУ. Чтобы найти базисное решение, нужно все свободные переменные приравнять к нулю. Т.е. полагая $x_2=0$ и $x_4=0$, будем иметь:

$$
left{begin{aligned}
& x_1=9;\
& x_2=0;\
& x_3=-2;\
& x_4=0.
end{aligned}right.
$$

Решение $x_1=9$, $x_2=0$, $x_3=-2$, $x_4=0$ и является базисным решением данной СЛАУ. В принципе, задавая свободным переменным иные значения, можно получить иные частные решения данной системы. Таких частных решений бесконечное количество. Например, принимая $x_2=-4$ и $x_4=1$, получим такое частное решение: $left{begin{aligned}
& x_1=frac{2}{3};\
& x_2=-4;\
& x_3=-frac{10}{3};\
& x_4=1.
end{aligned}right.$. Базисное решение, которые мы нашли ранее – лишь одно из бесконечного множества частных решений заданной СЛАУ.

Если есть желание, то полученное решение можно проверить. Например, подставляя $x_1=9+2x_2-frac{1}{3}x_4$ и $x_3=-2-frac{4}{3}x_4$ в левую часть первого уравнения, получим:

$$
3x_1-6x_2+9x_3+13x_4=3cdot left(9+2x_2-frac{1}{3}x_4right)-6x_2+9cdot left(-2-frac{4}{3}x_4right)+13x_4=9.
$$

Проверка первого уравнения увенчалась успехом; точно так же можно проверить второе и третье уравнения.

Ответ: Общее решение: $left{begin{aligned}
& x_1=9+2x_2-frac{1}{3}x_4;\
& x_2in R;\
& x_3=-2-frac{4}{3}x_4;\
& x_4 in R.
end{aligned}right.$, базисное решение: $
left{begin{aligned}
& x_1=9;\
& x_2=0;\
& x_3=-2;\
& x_4=0.
end{aligned}right.$.

Пример №2

Решить СЛАУ

$$left{begin{aligned}
& x_1-2x_2+4x_3+2x_5=0;\
& 4x_1-11x_2+21x_3-2x_4+3x_5=-1; \
& -3x_1+5x_2-13x_3-4x_4+x_5=-2.
end{aligned}right.$$

Если система является неопределённой, указать базисное решение.

Решение

Похожий пример уже был решен в теме “метод Крамера” (пример №4). Переменные $x_4$ и $x_5$ были перенесены в правые части, а дальше применялись стандартные операции метода Крамера. Однако такой метод решения не гарантирует достижения результата. Например, мы переносим некие переменные в правую часть, а оставшийся определитель оказывается равным нулю, – что тогда? Решать перебором? 🙂 Поэтому гораздо удобнее применять преобразования метода Гаусса, как и в предыдущем примере.

$$
left( begin{array} {ccccc|c}
1 & -2 & 4 & 0 & 2 & 0\
4 & -11 & 21 & -2 & 3 & -1\
-3 & 5 & -13 & -4 & 1 & -2
end{array} right)
begin{array} {l} phantom{0} \r_2-4r_1\r_3+3r_1end{array} rightarrow

left( begin{array} {ccccc|c}
1 & -2 & 4 & 0 & 2 & 0\
0 & -3 & 5 & -2 & -5 & -1\
0 & -1 & -1 & -4 & 7 & -2
end{array} right) rightarrow \

rightarrow left|begin{aligned}
& text{поменяем местами вторую и третью}\
& text{строки, чтобы диагональным элементом}\
& text{второй строки стало число (-1).}
end{aligned}right|rightarrow

left( begin{array} {ccccc|c}
1 & -2 & 4 & 0 & 2 & 0\
0 & -1 & -1 & -4 & 7 & -2\
0 & -3 & 5 & -2 & -5 & -1
end{array} right)
begin{array} {l} phantom{0} \ phantom{0}\r_3-3r_1end{array} rightarrow \

rightarrow left( begin{array} {ccccc|c}
1 & -2 & 4 & 0 & 2 & 0\
0 & -1 & -1 & -4 & 7 & -2\
0 & 0 & 8 & 10 & -26 & 5
end{array} right).
$$

Матрица системы и расширенная матрица системы приведены к трапециевидной форме. Ранги этих матриц равны между собой и равны числу 3, т.е. $rang A=rangwidetilde{A} = 3$. Так как ранги равны между собой и меньше, чем количество переменных, то согласно следствию из теоремы Кронекера-Капелли данная система имеет бесконечное количество решений.

Количество неизвестных $n=5$, ранги обеих матриц $r=3$, поэтому нужно выбрать три базисных переменных и $n-r=2$ свободных переменных. Применяя тот же метод “ступенек”, что и в предыдущем примере, выберем в качестве базисных переменных $x_1$, $x_2$, $x_3$, а в качестве свободных переменных – $x_4$ и $x_5$.

Столбцы №4 и №5, которые соответствуют свободным переменным, перенесём за черту. После этого разделим третью строку на 8 и продолжим решение методом Гаусса:

$$
left( begin{array} {ccc|ccc}
1 & -2 & 4 & 0 & 0 & -2\
0 & -1 & -1 & -2 & 4 & -7\
0 & 0 & 8 & 5 & -10 & 26
end{array} right)
begin{array} {l} phantom{0} \ phantom{0}\1/8cdot{r_3}end{array} rightarrow

left( begin{array} {ccc|ccc}
1 & -2 & 4 & 0 & 0 & -2\
0 & -1 & -1 & -2 & 4 & -7\
0 & 0 & 1 & 5/8 & -5/4 & 13/4
end{array} right)
begin{array} {l}r_1-4r_3 \r_2+r_3\ phantom{0}end{array} rightarrow \

left( begin{array} {ccc|ccc}
1 & -2 & 0 & -5/2 & 5 & -15\
0 & -1 & 0 & -11/8 & 11/4 & -15/4\
0 & 0 & 1 & 5/8 & -5/4 & 13/4
end{array} right)
begin{array} {l} phantom{0} \ -1cdot{r_2}\ phantom{0}end{array} rightarrow

left( begin{array} {ccc|ccc}
1 & -2 & 0 & -5/2 & 5 & -15\
0 & 1 & 0 & 11/8 & -11/4 & 15/4\
0 & 0 & 1 & 5/8 & -5/4 & 13/4
end{array} right)
begin{array} {l}r_1+2r_2 \ phantom{0}\ phantom{0}end{array} rightarrow\

rightarrowleft( begin{array} {ccc|ccc}
1 & 0 & 0 & 1/4 & -1/2 & -15/2\
0 & 1 & 0 & 11/8 & -11/4 & 15/4\
0 & 0 & 1 & 5/8 & -5/4 & 13/4
end{array} right)
$$

Из последней матрицы имеем общее решение заданной СЛАУ: $left{begin{aligned}
& x_1=frac{1}{4}-frac{1}{2}x_4-frac{15}{2}x_5;\
& x_2=frac{11}{8}-frac{11}{4}x_4+frac{15}{4}x_5;\
& x_3=frac{5}{8}-frac{5}{4}x_4+frac{13}{4}x_5;\
& x_4 in R;\
& x_5 in R.
end{aligned}right.$. Базисное решение получим, если приравняем свободные переменные к нулю, т.е. $x_4=0$, $x_5=0$:

$$
left{begin{aligned}
& x_1=frac{1}{4};\
& x_2=frac{11}{8};\
& x_3=frac{5}{8};\
& x_4=0;\
& x_5=0.
end{aligned}right.
$$

Ответ: Общее решение: $left{begin{aligned}
& x_1=frac{1}{4}-frac{1}{2}x_4-frac{15}{2}x_5;\
& x_2=frac{11}{8}-frac{11}{4}x_4+frac{15}{4}x_5;\
& x_3=frac{5}{8}-frac{5}{4}x_4+frac{13}{4}x_5;\
& x_4 in R;\
& x_5 in R.
end{aligned}right.$, базисное решение: $left{begin{aligned}
& x_1=frac{1}{4};\
& x_2=frac{11}{8};\
& x_3=frac{5}{8};\
& x_4=0;\
& x_5=0.
end{aligned}right.$.

Продолжение этой темы рассмотрим во второй части, где разберём ещё два примера с нахождением общего решения.

Источник

1. Базисные решения системы линейных уравнений

Рассмотрим
систему m
линейных уравнений, содержащую n
переменных

(1)

Эту
систему можно записать короче в виде:

Или
в матричной форме: Ax
= B.

В
задачах линейного программирования
рассматриваются неопределенные системы
уравнений, т.е. имеющие бесконечное
множество решений. Тогда ранг r
матрицы системы ,меньше числа
переменных: rn.
Это означает, что максимальное число
линейно независимых уравнений в (1) равно
r.
Будем считать, что в системе (1) число
линейно независимых уравнений равно
m,
т.е. r
= m.
Из алгебры известно, что в этом случае
найдутся m
переменных, коэффициенты
у которых в системе (1) образуют матрицу
с определителем, отличным от нуля. Такой
определитель называется базисным
минором, а соответствующие переменные
– базисными. Остальные n
– m
переменных называются свободными
переменными. Базисные переменные можно
выразить через свободные переменные с
помощью уравнений системы (1), присвоить
свободным переменным произвольные
значения и найти значения базисных
переменных по формулам Крамера. Получится
одно из решений системы (1).

Определение
1. Решение
системы линейных уравнений (1), полученное
при нулевых значениях свободных
переменных, называется базисным решением.

Базисные переменные,
а поэтому и ненулевые компоненты
базисного решения соответствуют линейно
независимым столбцам матрицы коэффициентов
системы линейных уравнений. Это позволяет
дать другое определение базисного
решения системы линейных уравнений.

Определение
2. Базисным
решением системы линейных уравнений
называется решение этой системы,
ненулевые компоненты которого
соответствуют линейно независимым
столбцам матрицы коэффициентов этой
системы.

В
качестве базисных переменных могут
быть разные группы, содержащие m
переменных из заданных в (1) n
переменных. Максимальное возможное
число способов выбора m
переменных из множества, содержащего
n
переменных, равно числу сочетаний
.
Однако могут встретиться случаи, когда
соответствующий определитель матрицы,
составленной из коэффициентов при
выбранныхm
переменных в системе (1), равен нулю.
Поэтому число групп базисных переменных
не превосходит
.
Для каждой группы базисных переменных
можно найти соответствующее базисное
решение системы (1). Из приведенных выше
рассуждений вытекает теорема:

Теорема.
Число базисных решений неопределенной
системы (1), в которой ранг матрицы системы
r
= m
< n
не превосходит

Пример.
Найти все базисные решения системы
уравнений (2):

(2)

Решение.
Очевидно r=m=2,
n=4.
Общее число групп базисных переменных
не более чем
=
6. Однако первый, второй и четвертый
столбцы коэффициентов у переменных в
матрице системы – пропорциональные,
поэтому определители второго порядка,
составленные из коэффициентов любых
двух из этих трех столбцов, равны нулю.
Остаются наборы:,
и .

Для
набора переменных
определитель, составленный из их
коэффициентов d
==
–2
0. Следовательно, эти переменные можно
считать базисными переменными, –
свободными. Присвоим свободным переменным
нулевые значения:
Решаем систему:

(3), откуда .

Получили
первое базисное решение: Б=
(2, 0, 1, 0).

Аналогично
докажем, что наборы переменных
и являются базисными
наборами. Присваивая соответствующим
свободным переменным нулевые значения,
найдем еще два базисных решения системы
(1): Б=
(0, –1, 1, 0) и Б=
(0, 0, 1,).

В
задачах линейного программирования
особый интерес представляют допустимые
(т.е. неотрицательные) базисные решения.
В рассмотренном примере из трех базисных
решений только два ( первое и третье)
являются допустимыми базисными решениями.
Очевидно, число допустимых базисных
решений системы (1) не превосходит
.

Базисное
решение, в котором хотя бы одна базисная
переменная равна нулю, называется
вырожденным. В рассмотренном примере
вырожденных базисных решений нет.

Соседние файлы в папке лекции рогов

Источник

Базисные (основные) и свободные (неосновные) переменные. Общее и базисное решения системы линейных алгебраических уравнений. Первая часть.

Во всех изложенных ниже примерах матрицу системы будем обозначать буквой $A$, а расширенную матрицу системы – буквой $widetilde$.

Решить СЛАУ $ left < begin& 3x_1-6x_2+9x_3+13x_4=9\ & -x_1+2x_2+x_3+x_4=-11;\ & x_1-2x_2+2x_3+3x_4=5. end right.$. Если система является неопределённой, указать базисное решение.

$$ left( begin 3 & -6 & 9 & 13 & 9 \ -1 & 2 & 1 & 1 & -11 \ 1 & -2 & 2 & 3 & 5 end right) rightarrow left|begin & text<поменяем местами первую и третью>\ & text<строки, чтобы первым элементом>\ & text <первой строки стала единица.>endright| rightarrow \ rightarrowleft( begin 1 & -2 & 2 & 3 & 5\ -1 & 2 & 1 & 1 & -11 \ 3 & -6 & 9 & 13 & 9 end right) begin phantom <0>\ II+I\ III-3cdot Iend rightarrow left( begin 1 & -2 & 2 & 3 & 5\ 0 & 0 & 3 & 4 & -6 \ 0 & 0 & 3 & 4 & -6 endright) begin phantom <0>\ phantom<0>\ III-IIend rightarrow \ rightarrowleft( begin 1 & -2 & 2 & 3 & 5\ 0 & 0 & 3 & 4 & -6 \ 0 & 0 & 0 & 0 & 0 endright) $$

Почему можно принять переменные $x_1$ и $x_3$ в качестве базисных? Для ответа на этот вопрос давайте вспомним, что ранг матрицы системы равен числу $r=2$. Это говорит о том, что все миноры данной матрицы, порядок которых выше 2, либо равны нулю, либо не существуют. Ненулевые миноры есть только среди миноров второго порядка. Выберем какой-либо ненулевой минор второго порядка. Мы можем выбирать его как в исходной матрице системы $A$, т.е. в матрице $left( begin 3 & -6 & 9 & 13 \ -1 & 2 & 1 & 1 \ 1 & -2 & 2 & 3 end right)$, так и в преобразованной матрице системы, т.е. в $left( begin 1 & -2 & 2 & 3 \ 0 & 0 & 3 & 4 \ 0 & 0 & 0 & 0 endright)$. Так как в преобразованной матрице системы побольше нулей, то будем работать именно с нею.

Итак, давайте выберем минор второго порядка, элементы которого находятся на пересечении строк №1 и №2, и столбцов №1 и №2:

$$ M_<2>^<(1)>=left| begin 1 & -2 \ 0 & 0 endright|=1cdot 0-(-2)cdot 0=0. $$

Вывод: выбранный нами минор второго порядка не является базисным, ибо он равен нулю. Так как элементы этого минора взяты из столбца №1 (он соответствует переменной $x_1$) и столбца №2 (он соответствует переменной $x_2$), то пара переменных $x_1$ и $x_2$ не могут быть базисными переменными.

Осуществим вторую попытку, взяв минор второго порядка, элементы которого лежат на пересечении строк №1, №2 и столбцов №3 и №4:

$$ M_<2>^<(2)>=left| begin 2 & 3\ 3 & 4 endright|=2cdot 4-3cdot 3=-1. $$

Вывод: выбранный нами минор второго порядка является базисным, ибо он не равен нулю. Так как элементы этого минора взяты из столбца №3 (он соответствует переменной $x_3$) и столбца №4 (он соответствует переменной $x_4$), то пару переменных $x_3$ и $x_4$ можно принять в качестве базисных.

Сделаем и третью попытку, найдя значение минора, элементы которого расположены на пересечении строк №1, №2 и столбцов №1 и №3:

Вывод: выбранный нами минор второго порядка является базисным, ибо он не равен нулю. Так как элементы этого минора взяты из столбца №1 (он соответствует переменной $x_1$) и столбца №3 (он соответствует переменной $x_3$), то пару переменных $x_1$ и $x_3$ можно принять в качестве базисных.

Как видите, выбор базисных переменных не является однозначным. На самом деле количество вариантов выбора не превышает количество размещений из $n$ элементов по $r$, т.е. не больше чем $C_^$.

В рассматриваемом примере в качестве баисных были приняты переменные $x_1$ и $x_3$ – сугубо из соображений удобства дальнейшего решения. В чём это удобство состоит, будет видно чуток позже.

Я предпочитаю работать с системой в матричной форме записи. Для начала очистим полученную матрицу $left( begin 1 & -2 & 2 & 3 & 5\ 0 & 0 & 3 & 4 & -6 \ 0 & 0 & 0 & 0 & 0 endright)$ от нулевой строки:

$$ left( begin 1 & -2 & 2 & 3 & 5\ 0 & 0 & 3 & 4 & -6 endright) $$

Почему меняются знаки? Что вообще значит это перенесение столбцов? показатьскрыть

Давайте обратимся к расширенной матрице системы, которая после преобразований имеет вид $left( begin 1 & -2 & 2 & 3 & 5\ 0 & 0 & 3 & 4 & -6 endright)$. Перейдём от матрицы к уравнениям. Первая строка соответствует уравнению $x_1-2x_2+2x_3+3x_4=5$, а вторая строка соответствует уравнению $3x_3+4x_4=-6$. Теперь перенесём свободные переменные $x_2$ и $x_4$ в правые части уравнений. Естественно, что когда мы переносим выражение $4x_4$ в правую часть уравнения, то знак его изменится на противоположный, и в правой части появится $-4x_4$.

Если опять записать полученную систему в виде матрицы, то мы и получим матрицу с перенесёнными за черту столбцами.

$$ left( begin 1 & 2 & 5 & 2 & -3\ 0 & 3 & -6 & 0 & -4 endright) begin phantom <0>\ II:3 end rightarrow left( begin 1 & 2 & 5 & 2 & -3\ 0 & 1 & -2 & 0 & -4/3 endright) begin I-2cdot II \ phantom <0>end rightarrow \ rightarrow left(begin 1 & 0 & 9 & 2 & -1/3\ 0 & 1 & -2 & 0 & -4/3 endright). $$

Решение $x_1=9$, $x_2=0$, $x_3=-2$, $x_4=0$ и является базисным решением данной СЛАУ. В принципе, задавая свободным переменным иные значения, можно получить иные частные решения данной системы. Таких частных решений бесконечное количество. Например, принимая $x_2=-4$ и $x_4=1$, получим такое частное решение: $left <begin& x_1=frac<2><3>;\ & x_2=-4;\ & x_3=-frac<10><3>;\ & x_4=1. endright.$. Базисное решение, которые мы нашли ранее – лишь одно из бесконечного множества частных решений заданной СЛАУ.

Если есть желание, то полученное решение можно проверить. Например, подставляя $x_1=9+2x_2-frac<1><3>x_4$ и $x_3=-2-frac<4><3>x_4$ в левую часть первого уравнения, получим:

$$ 3x_1-6x_2+9x_3+13x_4=3cdot left(9+2x_2-frac<1><3>x_4right)-6x_2+9cdot left(-2-frac<4><3>x_4right)+13x_4=9. $$

Проверка первого уравнения увенчалась успехом; точно так же можно проверить второе и третье уравнения.

Если система является неопределённой, указать базисное решение.

$$ left( begin 1 & -2 & 4 & 0 & 2 & 0\ 4 & -11 & 21 & -2 & 3 & -1\ -3 & 5 & -13 & -4 & 1 & -2 end right) begin phantom <0>\ II-4cdot I\ III+3cdot Iend rightarrow left( begin 1 & -2 & 4 & 0 & 2 & 0\ 0 & -3 & 5 & -2 & -5 & -1\ 0 & -1 & -1 & -4 & 7 & -2 end right) rightarrow \ rightarrow left|begin & text<поменяем местами вторую и третью>\ & text<строки, чтобы диагональным элементом>\ & text <второй строки стало число (-1).>endright|rightarrow left( begin 1 & -2 & 4 & 0 & 2 & 0\ 0 & -1 & -1 & -4 & 7 & -2\ 0 & -3 & 5 & -2 & -5 & -1 end right) begin phantom <0>\ phantom<0>\ III-3cdot Iend rightarrow \ rightarrow left( begin 1 & -2 & 4 & 0 & 2 & 0\ 0 & -1 & -1 & -4 & 7 & -2\ 0 & 0 & 8 & 10 & -26 & 5 end right). $$

Матрица системы и расширенная матрица системы приведены к трапециевидной форме. Ранги этих матриц равны между собой и равны числу 3, т.е. $rang A=rangwidetilde = 3$. Так как ранги равны между собой и меньше, чем количество переменных, то согласно следствию из теоремы Кронекера-Капелли данная система имеет бесконечное количество решений.

$$ left( begin 1 & -2 & 4 & 0 & 0 & -2\ 0 & -1 & -1 & -2 & 4 & -7\ 0 & 0 & 8 & 5 & -10 & 26 end right) begin phantom <0>\ phantom<0>\ III:8end rightarrow left( begin 1 & -2 & 4 & 0 & 0 & -2\ 0 & -1 & -1 & -2 & 4 & -7\ 0 & 0 & 1 & 5/8 & -5/4 & 13/4 end right) begin I-4cdot III \ II+III\ phantom<0>end rightarrow \ left( begin 1 & -2 & 0 & -5/2 & 5 & -15\ 0 & -1 & 0 & -11/8 & 11/4 & -15/4\ 0 & 0 & 1 & 5/8 & -5/4 & 13/4 end right) begin phantom <0>\ IIcdot (-1)\ phantom<0>end rightarrow left( begin 1 & -2 & 0 & -5/2 & 5 & -15\ 0 & 1 & 0 & 11/8 & -11/4 & 15/4\ 0 & 0 & 1 & 5/8 & -5/4 & 13/4 end right) begin I+2cdot II \ phantom<0>\ phantom<0>end rightarrow\ rightarrowleft( begin 1 & 0 & 0 & 1/4 & -1/2 & -15/2\ 0 & 1 & 0 & 11/8 & -11/4 & 15/4\ 0 & 0 & 1 & 5/8 & -5/4 & 13/4 end right) $$

Продолжение этой темы рассмотрим во второй части, где разберём ещё два примера с нахождением общего решения.

Метод Жордана-Гаусса онлайн

Данный онлайн калькулятор находит общее решение системы линейных уравнений методом Жордана-Гаусса. Дается подробное решение. Для вычисления выбирайте количество уравнений и количество переменных. Затем введите данные в ячейки и нажимайте на кнопку “Вычислить.” Теоретическую часть нахождения решения системы линейных уравнений методом Жордана-Гаусса смотрите ниже.

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Метод Жордана-Гаусса

Метод Жордана-Гаусса − это метод для решения систем линейных уравнений а также метод нахождения обратной матрицы. Данный метод является модификацией метода Гаусса.

Первый этап метода Жордана-Гаусса аналогична методу Гаусса (прямой ход Гаусса), который подробно можно посмотреть на странице “Метод Гаусса онлайн”. Второй этап (обратный ход) метода Жордана-Гаусса заключается в обнулении всех элементов матрицы коэффициентов системы линейных уравнений, выше ведущих элементов. Отметим, что мы здесь рассматриваем произвольную систему линейных уравнений, где число переменных может быть не равным числу ограничений.

Рассмотрим следующую систему линейных уравнений:

(1)

Запишем систему (1) в матричном виде:

A-называется матрица коэффициентов системы, b − правая часть ограничений, x− вектор переменных, которую нужно найти. Пусть rang(A)=p.

Построим расшренную матрицу системы:

(4)

После прямого хода Гаусса (подробнее о прямом ходе Гаусса посмотрите на странице “Метод Гаусса онлайн”) получим следующую расширенную матрицу:

(5)

Если . равны нулю, то система линейных уравнений имеет решение, если же хотя бы один из этих чисел отлично от нуля, то система несовместна. Иными словами, система (2) совместна тогда и только тогда, когда ранг матрицы A навен рангу расширенной матрицы (A|b).

Пусть . Тогда в обратном порядке, начиная с ведущего элемента применяем обратный ход Гаусса. Суть обратного хода заключается в обнулении всех элементов расширенной матрицы, стоящих выше ведущих элементов.

Итак, обнуляем все элементы, стоящие в столбце p, выше элемента . Так как ≠0, то сложим строки 1,2. p−1 со строкой p, умноженной на соответственно.

Расширенная матрица примет следующий вид:

Аналогичным методом обнуляем элементы столбцов p−1, p−2, . 2 выше ведущих элементов .

Расширенная матрица примет следующий вид:

Делим каждую строку на соответствующий ведущий элемент (если ведущий элемент существует):

Тогда решение можно записать так:

где − произвольные вещественные числа.

Отметим, что при m=n и rangA=n система линейных уравнений (2) имеет единственное решение.

Рассмотрим численные примеры.

Примеры решения системы линейных уравнений методом Жордана-Гаусса

Пример 1. Найти решение системы линейных уравнений методом Жордана-Гаусса:

Матричный вид записи: Ax=b, где

Для решения системы, построим расширенную матрицу:

Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Первый этап. Прямой ход Гаусса

Исключим элементы 1-го столбца матрицы ниже элемента a₁₁. Для этого сложим строки 2,3 со строкой 1, умноженной на 1/2,-3/2 соответственно:

Исключим элементы 2-го столбца матрицы ниже элемента a2 2. Для этого сложим строку 3 со строкой 2, умноженной на 1/5:

Второй этап. Обратный ход Гаусса

Исключим элементы 3-го столбца матрицы выше элемента a₃₃. Для этого сложим строки 1, 2 со строкой 3, умноженной на -3/2, -5/4 соответственно:

Исключим элементы 2-го столбца матрицы выше элемента a₂₂. Для этого сложим строку 1 со строкой 2, умноженной на -2/5:

Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

Векторный вариант решения:

Пример 2. Найти решение системы линейных уравнений методом Жордана-Гаусса:

Матричный вид записи: Ax=b, где

Для решения системы, построим расширенную матрицу:

Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Первый этап. Прямой ход Гаусса.

Исключим элементы 1-го столбца матрицы ниже элемента a₁₁. Для этого сложим строки 2,3 со строкой 1, умноженной на 4/3, 5/3 соответственно:

Исключим элементы 2-го столбца матрицы ниже элемента a2 2. Для этого сложим строку 3 со строкой 2, умноженной на -2:

Второй этап. Обратный ход Гаусса

Исключим элементы 2-го столбца матрицы выше элемента a₂₂. Для этого сложим строку 1 со строкой 2, умноженной на -3/10:

Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

Выразим переменные x₁, x₂ относительно остальных переменных.

x₃− произвольное действительное число.

Векторный вариант решения:

Запишем вышеизложенное решение, представив свободные переменные в виде тождеств:

Тогда векторное решение можно представить так:

x₃− произвольное действительное число.

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Решение систем линейных алгебраических уравнений (СЛАУ)
Метод Гаусса, матричный метод, метод Крамера, исследование на совместность (теорема Кронекера-Капелли), определение количества решений, нахождение нормальной фундаментальной системы решений.

С помощью данной математической программы вы можете решить и исследовать систему линейных алгебраических уравнений (СЛАУ).

Программа не только даёт ответ задачи, но и приводит подробное решение с пояснениями шагов решения.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Ввод дробного числа в виде десятичной дроби.
При вводе десятичной дроби, целую часть от дробной части можно отделять точкой или запятой :
Ввод: -2.34
Результат: ( -2<,>34 )

Ввод: -1,15
Результат: ( -1<,>15 )

Ввод дробного числа в виде обыкновенной дроби.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: $$ -frac<2> <3>$$

Целая часть отделяется от дроби знаком амперсанд: &
Ввод: 5&8/3
Результат: $$ 5frac<8> <3>$$
Помните, что на ноль делить нельзя!

RND CFracNum Fill RND int Fill Start MathJax
Сюда ввести строку с GET параметрами :

Немного теории.

Системы линейных алгебраических уравнений

Основные определения

Система (m) линейных алгебраических уравнений с (n) неизвестными (сокращенно СЛАУ) представляет собой систему вида
( left< begin a_<11>x_1 + a_<12>x_2 + cdots + a_<1n>x_n = b_1 \ a_<21>x_1 + a_<22>x_2 + cdots + a_<2n>x_n = b_2 \ cdots \ a_x_1 + a_x_2 + cdots + a_x_n = b_m end right. tag <1>)

Уравнения системы называют алгебраическими потому, что левая часть каждого из них есть многочлен от (n) переменных ( x_1 , ldots x_n ), а линейными потому, что эти многочлены имеют первую степень.

Числа (a_ in mathbb ) называют коэффициентами СЛАУ. Их нумеруют двумя индексами: номером уравнения (i) и номером неизвестного (j). Действительные числа ( b_1 , ldots b_m ) называют свободными членами уравнений.

СЛАУ называют однородной, если ( b_1 = b_2 = ldots = b_m = 0 ). Иначе её называют неоднородной.

Решением СЛАУ, да и вообще всякой системы уравнений, называют такой набор значений неизвестных ( x_1^circ, ldots , x_n^circ ), при подстановке которых каждое уравнение системы превращается в тождество. Любое конкретное решение СЛАУ также называют её частным решением.

Решить СЛАУ — значит решить две задачи:
— выяснить, имеет ли СЛАУ решения;
— найти все решения, если они существуют.

СЛАУ называют совместной, если она имеет какие-либо решения. В противном случае её называют несовместной. Однородная СЛАУ всегда совместна, поскольку нулевой набор значений её неизвестных всегда является решением.

Если СЛАУ (1) имеет решение, и притом единственное, то её называют определенной, а если решение неединственное — то неопределенной. При (m=n), т.е. когда количество уравнений совпадает с количеством неизвестных, СЛАУ называют квадратной.

Формы записи СЛАУ

Кроме координатной формы (1) записи СЛАУ часто используют и другие её представления.

Рассматривая коэффициенты (a_) СЛАУ при одном неизвестном (x_j) как элементы столбца, а (x_j) как коэффициент, на который умножается столбец, из (1) получаем новую форму записи СЛАУ:
( begin a_ <11>\ a_ <21>\ vdots \ a_ end x_1 + begin a_ <12>\ a_ <22>\ vdots \ a_ end x_2 + ldots + begin a_ <1n>\ a_ <2n>\ vdots \ a_ end x_n = begin b_1 \ b_2 \ vdots \ b_m end )
или, обозначая столбцы соответственно ( a_1 , ldots , a_n , b ),
( x_1 a_1 + x_2 a_2 + ldots + x_n a_n = b tag <2>)

Таким образом, решение СЛАУ (1) можно трактовать как представление столбца (b) в виде линейной комбинации столбцов ( a_1, ldots, a_n ). Соотношение (2) называют векторной записью СЛАУ.

Поскольку (A ;,; X) и (B) являются матрицами, то запись СЛАУ (1) в виде (AX=B) называют матричной. Если (B=0), то СЛАУ является однородной и в матричной записи имеет вид (AX=0).

Приведенные рассуждения показывают, что задачи :
а) решения СЛАУ (1)
б) представления столбца в виде линейной комбинации данных столбцов
в) решения матричных уравнений вида (AX=B)
являются просто различной формой записи одной и той же задачи.

Критерий совместности СЛАУ

“Триединство” форм записи СЛАУ позволяет легко получить критерий совместности СЛАУ. Напомним, что содержательный смысл это понятие имеет для неоднородных СЛАУ (однородные СЛАУ всегда совместны).

Матрицу
( A = begin a_ <11>& a_ <12>& cdots & a_ <1n>\ a_ <21>& a_ <22>& cdots & a_ <2n>\ vdots & vdots & ddots & vdots \ a_ & a_ & cdots & a_ end )
называют матрицей (коэффициентов) СЛАУ (1), а матрицу
( (A|B) = left( begin a_ <11>& a_ <12>& cdots & a_ <1n>& b_1 \ a_ <21>& a_ <22>& cdots & a_ <2n>& b_2 \ vdots & vdots & ddots & vdots & vdots \ a_ & a_ & cdots & a_ & b_m end right) )
расширенной матрицей СЛАУ (1). Расширенная матрица полностью характеризует СЛАУ. Это означает, что по этой матрице однозначно (если сохранить обозначения для неизвестных) восстанавливается сама СЛАУ.

Теорема Кронекера-Капелли. Для совместности СЛАУ (AX=B) необходимо и достаточно, чтобы ранг её матрицы (A) был равен рангу её расширенной матрицы ( (A|B) ).

Формулы Крамера

Теорема. СЛАУ с квадратной невырожденной матрицей имеет решение, и притом единственное, которое определяется по формулам Крамера :
$$ x_i = frac<Delta_i> <|A|>;,quad i=overline <1,n>tag <3>$$
где (Delta_i) — определитель матрицы, получающейся из матрицы (A) заменой (i)-го столбца на столбец свободных членов.

Следствие. Однородная СЛАУ с квадратной невырожденной матрицей имеет единственное решение — нулевое.

Если матрица СЛАУ не является квадратной невырожденной, то формулы Крамера не работают и приходится использовать другие методы нахождения решений.

Однородные системы

Теорема. Если столбцы ( X^<(1)>, X^<(2)>, ldots , X^ <(s)>) — решения однородной СЛАУ (AX=0), то любая их линейная комбинация также является решением этой системы.

Следствие. Если однородная СЛАУ имеет ненулевое решение, то она имеет бесконечно много решений.

Естественно попытаться найти такие решения ( X^<(1)>, ldots , X^ <(s)>) системы (AX=0), чтобы любое другое решение этой системы представлялось в виде их линейной комбинации и притом единственным образом. Оказывается, что это всегда возможно и приводит к следующему определению.

Определение. Любой набор из (k=n-r) линейно независимых столбцов, являющихся решениями однородной СЛАУ (AX=0), где (n) — количество неизвестных в системе, а (r) — ранг её матрицы (A), называют фундаментальной системой решений этой однородной СЛАУ.

При исследовании и решении однородных систем линейных алгебраических уравнений будем использовать следующую терминологию. Если в матрице (A) однородной СЛАУ (AX=0) фиксировать базисный минор, то ему соответствуют базисные столбцы и, следовательно, набор неизвестных, отвечающих этим столбцам. Указанные неизвестные называют базисными, или зависимыми, а остальные неизвестные — свободными, или независимыми.

Теорема. Пусть дана однородная СЛАУ (AX=0) с (n) неизвестными и ( textA = r ). Тогда существует набор из (k=n-r) решений ( X^<(1)>, ldots , X^ <(k)>) этой СЛАУ, образующих фундаментальную систему решений.

Если в фундаментальной системе решений все значения независимых неизвестных равны нулю, кроме одного, которое равно единице, то такую систему решений называют фундаментальной нормальной системой решений.

Следствие. С помощью нормальной фундаментальной системы решений однородной СЛАУ множество всех решений можно описать формулой :
$$ X = c_1X^ <(1)>+ ldots + c_kX^ <(k)>$$
где постоянные ( c_i ;, quad i=overline <1,k>), принимают произвольные значения.

Следствие. Для существования ненулевого решения у однородной квадратной СЛАУ необходимо и достаточно, чтобы её матрица была вырождена.

Неоднородные системы

Рассмотрим произвольную СЛАУ (AX=B). Заменив столбец (B) свободных членов нулевым, получим однородную СЛАУ (AX=0), соответствующую неоднородной СЛАУ (AX=B). Справедливо следующее утверждение о структуре произвольного решения неоднородной СЛАУ.

Теорема. Пусть столбец (X^circ) — некоторое решение СЛАУ (AX=B). Произвольный столбец (X) является решением этой СЛАУ тогда и только тогда, когда он имеет представление (X = X^circ + Y ), где (Y) — решение соответствующей однородной СЛАУ (AY=0).

Следствие. Пусть (X’) и (X”) — решения неоднородной системы (AX=B). Тогда их разность ( Y = X’ – X” ) является решением соответствующей однородной системы (AY=0).

Эта теорема сводит проблему решения СЛАУ к случаю однородной системы: чтобы описать все решения неоднородной СЛАУ, достаточно энать одно её решение (частное решение) и все решения соответствующей однородной СЛАУ.

Чтобы решить неоднородную систему, надо, во-первых, убедиться, что она совместна (например, по теореме Кронекера-Капелли), а во-вторых, найти частное решение (X^circ) этой системы, чтобы свести её к однородной системе.

Теорема о структуре общего решения СЛАУ. Пусть (X^circ) — частное решение СЛАУ (AX=B) и известна фундаментальная система решений ( X^<(1)>, ldots , X^ <(k)>) соответствующей однородной системы (AX=0). Тогда любое решение СЛАУ (AX=B) можно представить в виде $$ X = X^circ + c_1 X^ <(1)>+ c_2 X^ <(2)>+ ldots + c_k X^ <(k)>$$
где ( c_i in mathbb ;, quad i=overline <1,k>).
Эту формулу называют общим решением СЛАУ.

[spoiler title=”источники:”]

http://matworld.ru/calculator/gauss-jordan-method-online.php

http://www.math-solution.ru/math-task/slau

[/spoiler]

Источник

Содержание:

Базисные и свободные переменные:

Пусть задана система

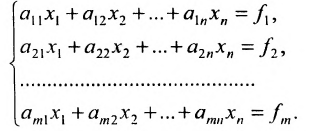
Элементарными преобразованиями системы линейных уравнений называются следующие преобразования:

исключение из системы уравнения вида
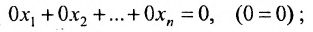
умножение обеих частей одного из уравнений системы на любое действительное число ;
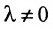перестановка местами уравнений системы;
прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число не равное нулю.

Элементарные преобразования преобразуют данную систему уравнений в эквивалентную систему, т.е. в систему, которая имеет те же решения, что и исходная.

Для решения системы т линейных уравнений с т неизвестными удобно применять метод Гаусса, называемый методом последовательного исключения неизвестных, который основан на применении элементарных преобразований системы. Рассмотрим этот метод.

Предположим, что в системе (6.1.1)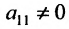. Если это не так, то переставим уравнения системы так, чтобы .

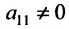На первом шаге метода Гаусса исключим неизвестное 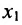из всех уравнений системы (6.1.1), начиная со второго. Для этого последовательно умножим первое уравнение системы на множители

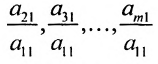и вычтем последовательно преобразованные уравнения из второго, третьего, …, последнего уравнения системы (6.1.1). В результате получим эквивалентную систему:

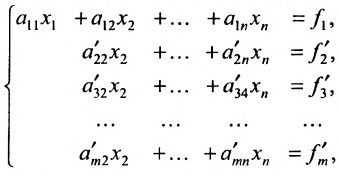(6.1.2)

в которой коэффициенты 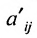вычислены по формулам:

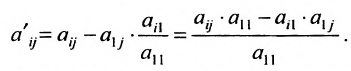На втором шаге метода Гаусса исключим неизвестное 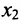из всех уравнений системы (6.1.2) начиная с третьего, предполагая, что 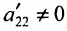(в противном случае, переставим уравнения системы (6.1.2)

чтобы это условие было выполнено). Для исключения неизвестного последовательно умножим второе уравнение системы (6.1.2) на множетели 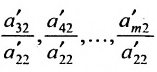и вычтем последовательно преобразованные уравнения из третьего, четвёртого, последнего,…,уравнения системы (6.1.2). В результате получим эквивалентную систему:

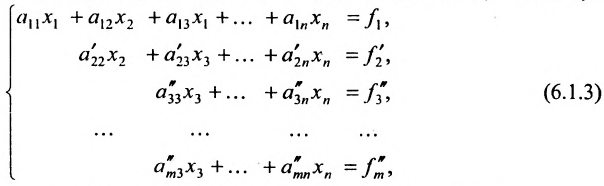
в которой коэффициенты 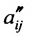вычислены по формулам:

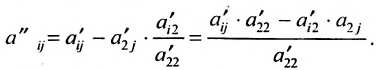
Продолжая аналогичные преобразования, систему (6.1.1) можно привести к одному из видов:

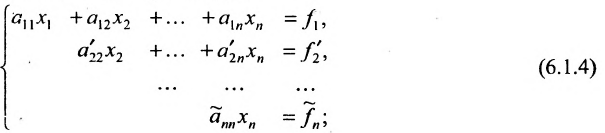
или

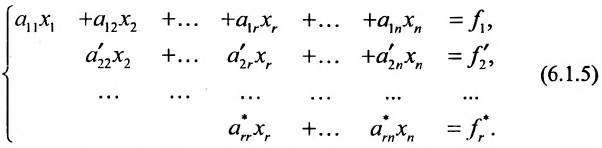
Совокупность элементарных преобразований, приводящих систему (6.1.1) к виду (6.1.4) или (6.1.5) называется прямым ходом метода Гаусса.

Отметим, что если на каком-то шаге прямого хода метода Гаусса получим уравнение вида:

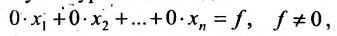, то это означает, что система (6.1.1) несовместна.

Итак, предположим, что в результате прямого хода метода Гаусса мы получили систему (6.1.4), которая называется системой треугольного вида. Тогда из последнего уравнения находим значение 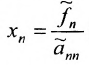подставляем найденное значение 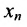в предпоследнее уравнение системы (6.1.4) и находим значение 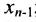; и т.д. двигаясь снизу вверх в системе (6.1.4) находим единственные значения неизвестных 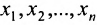которые и определяют единственное решение системы (6.1.1). Построение решения системы (6.1.4) называют обратным ходом метода Гаусса.

Если же в результате прямого хода метода Гаусса мы получим систему (6.1.5), которая называется системой ступенчатого вида, то из последнего уравнения этой системы находим значение неизвсстного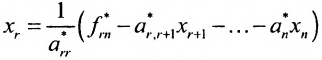 которое выражается через неизвестные 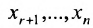. Найденное выражение подставляем в предпоследнее уравнение системы (6.1.5) и выражаем неизвестное 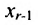через неизвестные 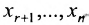и т.д. Двигаясь снизу вверх в системе (6.1.5) находим выражения неизвестных 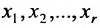через неизвестные 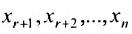При этом неизвестные 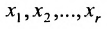называются базисными неизвестными, а неизвестные 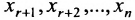– свободными. Так как свободным неизвестным можно придавать любые значения и получать соответствующие значения базисных неизвестных, то система (6.1.5), а, следовательно, и система (6.1.1) в этом случае имеет бесконечное множество решений. Полученные выражения базисных неизвестных через свободные неизвестные называются общим решением системы уравнений (6.1.1).

Таким образом, если система (6.1.1) путём элементарных преобразований приводится к треугольному виду (6.1.4), то она имеет единственное решение, если же она приводится к системе ступенчатого вида (6.1.5), то она имеет бесконечное множество решений. При этом неизвестные 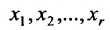, начинающие уравнения ступенчатой системы, называются базисными, а остальные неизвестные – свободными.

Практически удобнее преобразовывать не саму систему уравнений (6.1.1), а расширенную матрицу системы, соединяя последовательно получающиеся матрицы знаком эквивалентности.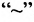

Формализовать метод Гаусса можно при помощи следующего алгоритма.

Алгоритм решения системы m линейных уравнений с n неизвестными методом Гаусса

1. Составьте расширенную матрицу коэффициентов системы уравнений так, чтобы 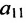было не равно нулю:

2. Выполните первый шаг метода Гаусса: в первом столбце начиная со второй строки, запишите нули, а все другие элементы вычислите по формуле

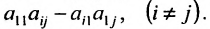
Матрица после первого шага примет вид

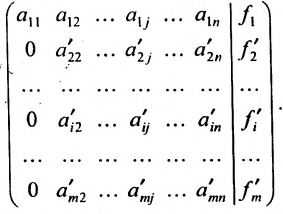
3. Выполните второй шаг метода Гаусса, предполагая, что 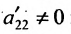: во втором столбце начиная с третьей строки, запишите нули, а все другие элементы вычислите по формуле

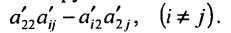
После второго шага матрица примет вид

4. Продолжая аналогичные преобразования, придёте к одному из двух случаев:

а) либо в ходе преобразований получим уравнение вида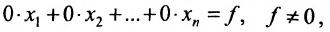

тогда данная система несовместна;

б) либо придём к матрице вида:

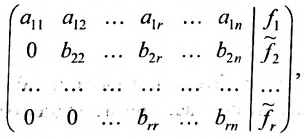
где 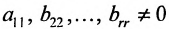. Возможное уменьшение числа строк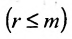

связано с тем, что в процессе преобразований матрицы исключаются строки, состоящие из нулей.

5. Использовав конечную матрицу, составьте систему, при этом возможны два случая:

5.1. r=n:

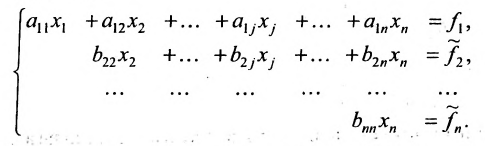
Система имеет единственное,решение 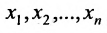, которое находим из системы обратным ходом метода Гаусса. Из последнего уравнения находите 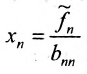. Из предпоследнего уравнения находите 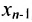затем из третьего от конца – 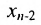и т.д., двигаясь снизу вверх, найдём все неизвестные .

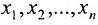5.2. :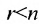

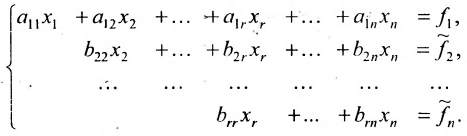
Тогда r неизвестных будут базисными, а остальные (n-r) – свободными. Из последнего уравнения выражаете неизвестное 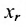через 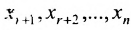. Из предпоследнего уравнения находите 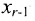и т.д.

Система имеет в этом случае бесконечное множество решений.

Приведенный алгоритм можно несколько видоизменить и получить алгоритм полного исключения, состоящий в выполнении следующих шагов. На первом шаге:

составляется расширенная матрица;
выбирается разрешающий элемент расширенной матрицы 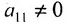(если 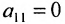, строки матрицы можно переставить так, чтобы выполнялось условие );
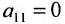элементы разрешающей строки (строки, содержащей разрешающий элемент) оставляем без изменения; элементы разрешающего столбца (столбца, содержащего разрешающий элемент), кроме разрешающего элемента, заменяем нулями;
все другие элементы вычисляем по правилу прямоугольника: преобразуемый элемент равен разности произведений элементов главной диагонали (главную диагональ образует разрешающий элемент и преобразуемый) и побочной диагонали (побочную диагональ образуют элементы, стоящие в разрешающей строке и разрешающем столбце): 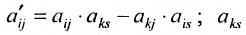– разрешающий элемент (см. схему).

Последующие шаги выполняем по правилам:

1) выбирается разрешающий элемент 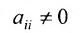(диагональный элемент матрицы);

2) элементы разрешающей строки оставляем без изменения;

3) все элементы разрешающего столбца, кроме разрешающего элемента, заменяем нулями; • •

4) все другие элементы матрицы пересчитываем по правилу прямоугольника.

На последнем шаге делим элементы строк на диагональные элементы матрицы, записанные слева от вертикальной черты, и получаем решение системы.

Пример:

Решить систему уравнений:

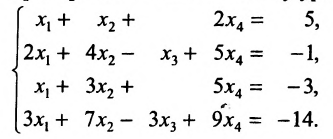
Решение:

Составим расширенную матрицу системы, и применим алгоритм полного исключения, обозначая разрешающий элемент символом

Из последней матрицы находим следующее решение системы

уравнении: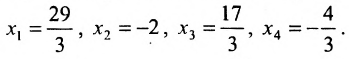

Ответ: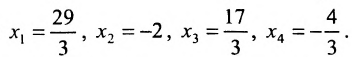

Пример:

Решить систему уравнений:

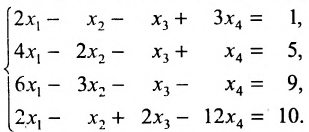
Решение:

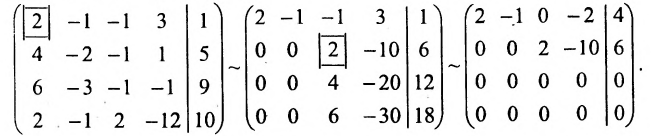
Система привелась к ступенчатому виду (трапециевидной форме):

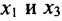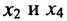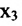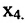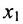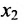в которой неизвестные – базисные, а – свободные. Из второго уравнения системы (6.1.6) находим выражение через . Из первого уравнений найдём выражение через и 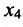. Система имеет бесконечное множество решений. Общее решение системы имеет вид:

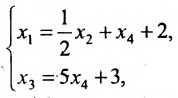
в котором 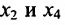принимают любые значения из множества действительных чисел.

Если в общем решении положить 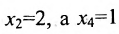, то получим решение 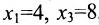, которое называется частным решением заданной системы.

Ответ: система имеет бесконечное множество решений, общее решение которой записывается в виде: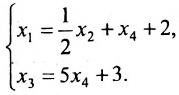

Пример:

Решить систему уравнений:

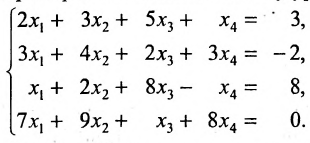
Решение:

Составим расширенную матрицу системы, и применим алгоритм полного исключения, обозначая разрешающий элемент символом 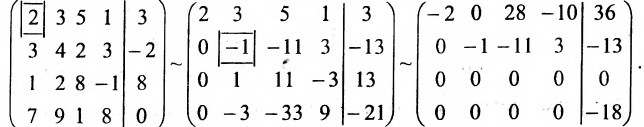В последней матрице мы получили четвёртую строку, которая равносильна уравнению 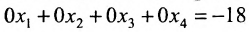. Это означает, что заданная система не имеет решений.

Ответ: система несовместна.

Замечание 1. Если дана система уравнений (6.1.1), в которой число уравнений m равно числу неизвестных n (m=n) и определитель этой системы 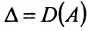не равен нулю 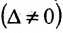, то система имеет единственное решение, которое можно найти по формулам Крамера: 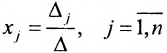, где определитель 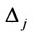получен из определи-теля 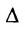заменой j-ro столбца столбцом свободных членов.

Если же такую систему (m-n) записать в матричной форме AX=F, то её решение можно найти по формуле 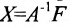и оно является единственным.

Замечание 2. Используя метод Гаусса, тем самым и алгоритм полного исключения, можно находить обратную матрицу. Для этого составляется расширенная матрица, в которой слева от вертикальной черты записана матрица А, а справа – единичная матрица. Реализовав алгоритм полного исключения, справа от вертикальной черты получаем обратную матрицу, а слева – единичную.

Пример:

Найти обратную матрицу для матрицы: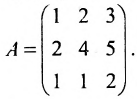

Решение:

Так как

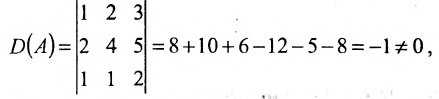
то обратная матрица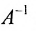 существует. Составим расширенную мат-рицу и применим алгоритм полного исключения:

тогда

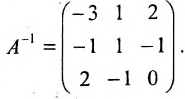
Покажем, что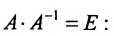

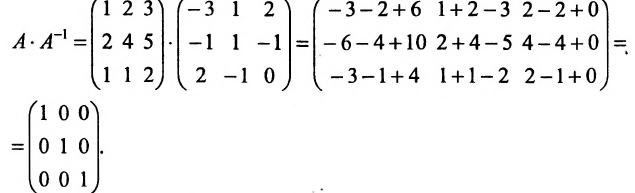
ответ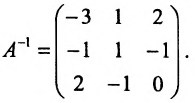

Исследование совместности и определённости системы. Теорема Кронекера-Капелли

Рассмотрим систему (6.1.1) m линейных уравнений с n неизвестными при любых m и n (случай m=n не исключается). Вопрос о совместности системы решается следующим критерием.

Теорема 6.2.1. (критерий Кронкера-Капелли). Для того, чтобы система линейных уравнений(6.1.1) была совместна, необходимо и достаточно, чтобы ранг матрицы А системы был равен рангу расширенной матрицы .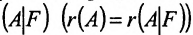

Доказательство и Необходимость:

Предположим, что система (6.1.1) совместна и 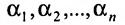– какое-либо её решение (возможно единственное). По определению решения системы получаем:

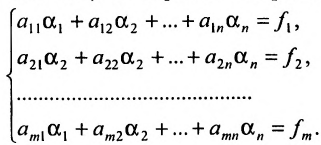
Из этих равенств следует, что последний столбец матрицы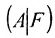 есть линейная комбинация остальных ее столбцов с коэффициентами 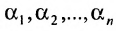, то есть система вектор-столбцов матрицы 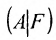линейно зависима (свойство 3 п.2.5) и значит последний столбец матрицы 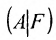не изменяет ранга матрицы А, т.е.

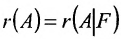Достаточность. Пусть 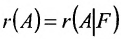. Рассмотрим r базисных

столбцов матрицы А, которые одновременно будут базисными столбцами и матрицы 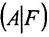. В этом случае последний столбец матрицы 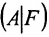можно представить как линейную комбинацию базисных столбцов, а следовательно, и как линейную комбинацию всех столбцов матрицы А, то есть

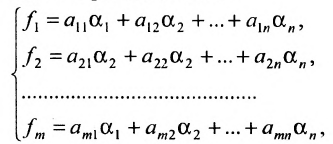
где 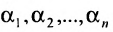– коэффициенты линейных комбинаций. А это означает, что 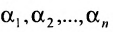– решение системы (6.1.1), следовательно,

эта система совместна.

Совместная система линейных уравнений (6.1.1) может быть либо определенной, либо неопределенной.

Следующая теорема даст критерий определенности.

Теорема 6.2.2. Совместная система линейных уравнений имеет единственное решение тогда и только тогда, когда ранг матрицы А системы равен числу п ее неизвестных.

Таким образом, если число уравнений m системы (6.1.1) меньше числа ее неизвестных n и система совместна, то ранг матрицы системы 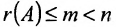. Значит система неопределенная.

В случае 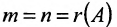по теореме 6.2.2 получаем, что система имеет единственное решение. Так как 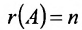, то определитель 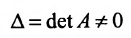и квадратная матрица А имеет обратную x матрицу 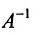и её решение можно найти по формуле: 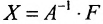, где Х- столбец неизвестных, F— столбец свободных членов, или по формулам Крамера.

Следует отметить, что, решая систему (6.1.1) методом Гаусса, мы определяем и совместность, и определённость системы.

Пример:

Исследовать на совместность и определённость следующую систему линейных уравнений:

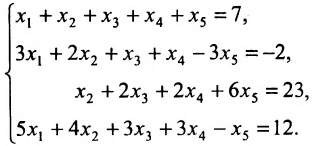
Решение:

Составим расширенную матрицу заданной системы. Определяя её ранг, находим тем самым и ранг матрицы системы. Для нахождения ранга матрицы применим алгоритм метода Гаусса.

Из последней матрицы следует, что ранг расширенной матрицы 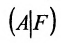не может быть больше ранга матрицы А системы. Так как

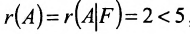, то заданная система совместная и неопределённая.

Заказать решение задач по высшей математике

Однородные системы линейных уравнений

Система линейных уравнений (6.1.1) называется однородной, если все свободные члены 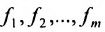равны нулю, то есть система имеет следующий вид:

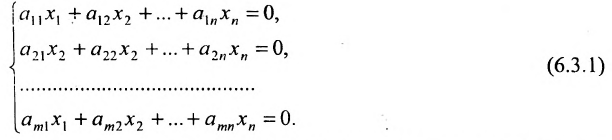
Эта система всегда совместна, так как очевидно, что она имеет нулевое решение

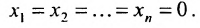
Для однородной системы важно установить, имеет ли она ненулевые решения. Этот факт устанавливается следующей теоремой.

Теорема 6.3.1. Для того, чтобы однородная система имела ненулевые решения, необходимо и достаточно, чтобы ранг г матрицы А системы был меньше числа неизвестных n (r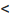n).

Доказательство. Необходимость. Пусть система (6.3.1) имеет ненулевое решение. Тогда она неопределённая, т.к. имеет еще и нулевое решение. В силу теоремы 6.2.2 ранг матрицы неопределённой системы не может равняться n потому что при r(А)=n система определённая. Следовательно, 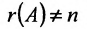и так как он не может быль больше n то .

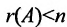Достаточность. Если 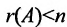, то в силу теоремы 6.2.2 система (6.3.1) имеет бесчисленное множество решений. А так как только одно решение является нулевым, то все остальные решения ненулевые.

Следствие 1. Если число неизвестных в однородной системе больше числа уравнений, то однородная система имеет ненулевые решения.

Доказательство. Действительно, ранг матрицы системы (6.3.1) не может превышать m. Но так как по условию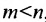, то и 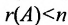. Следовательно, в силу теоремы 6.3.1 система имеет ненулевые решения.

Следствие 2. Для того, чтобы однородная система с квадрат-ной матрицей имела ненулевые решения, необходимо и достаточно, чтобы её определитель 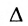равнялся нулю.

Доказательство. Рассмотрим однородную систему с квадратной матрицей:

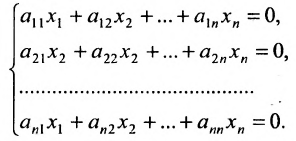(6.3.2)

Если определитель матрицы системы 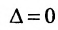, то ранг матрицы 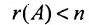, тогда в силу теоремы 6.3.1 система (6.3.2) имеет ненулевое решение, так как условие 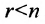является необходимым и достаточным условием для существования ненулевого решения. Заметим, что если определитель матрицы системы (6.3.2) не равен нулю, то 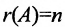в силу теоремы 6.3.1 она имеет только нулевое решение.

Пример:

Решить систему однородных линейных уравнений:

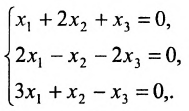
Решение:

Составим матицу системы и применим алгоритм полного исключения: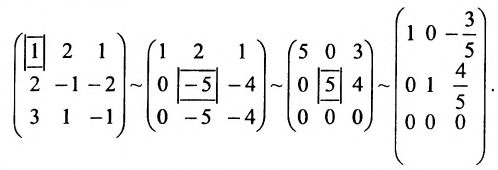

Из последней матрицы следует, что 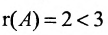и система имеет бесчисленное множество решений.

Используя последнюю матрицу, последовательно находим общее решение: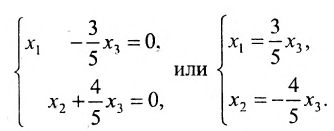

Неизвестные 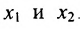– базисные, 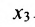– свободная неизвестная, .

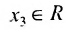Фундаментальная система решений. Общее решение неоднородной системы линейных уравнений

Рассмотрим систему однородных линейных уравнений

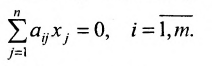(6.4.1)

Любое решение

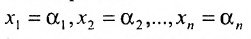
системы m линейных однородных уравнений с n неизвестными можно рассматривать как вектор-строку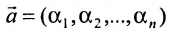 или как вектор-столбец 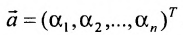. Поэтому имеют смысл такие понятия, как сумма двух решений, произведение решения на число, линейная комбинация решений, линейная зависимость или независимость системы решений. Непосредственной подстановкой в систему (6.4.1) можно показать, что:

1) сумма двух решений также является решением системы, т.е.

если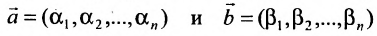 – решения системы

(6.4.1), то и 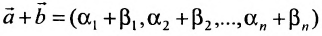– решение системы (6.4.1);

2) произведение решений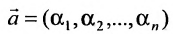на любое число 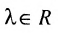есть решение системы, т.е. 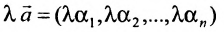– решение системы.

Из приведенных свойств следует, что

3) линейная комбинация решений системы (6.4.1) является решением этой системы.

В частности, если однородная система (6.4.1) имеет хотя бы одно ненулевое решение, то из него умножением на произвольные числа, можно получить бесконечное множество решений.

Определение 6.4.1. Фундаментальной системой решений для системы однородных линейных уравнений (6.4.1) называется линейно независимая система решений, через которую линейно выражается любое решение системы (6.4.1).

Заметим, что если ранг матрицы системы (6.4.1) равен числу неизвестных n (r(А)=n), то эта система не имеет фундаментальной системы решений, так как единственным решением будет нулевое решение, составляющее линейно зависимую систему. Существование и число фундаментальных решений определяется следующей теоремой.

Теорема 6.4.1. Если ранг матрицы однородной системы уравнений (6.4.1) меньше числа неизвестных (r(А)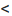n), то система (6.4.1) имеет бесконечное множество фундаментальных систем решений, причём каждая из них состоит из n-r решений и любые n-r линейно независимые решения составляют фундаментальную систему.

Сформулируем алгоритм построения фундаментальной системы решений:

Выбираем любой определитель 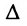порядка n-r, отличный от нуля, в частности, определитель порядка n-r, у которого элементы главной диагонали равны единице, а остальные – нули.
Свободным неизвестным придаём поочерёдно значения, равные элементам первой, второй и т.д. строк определителя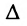, и каждый раз из общего решения находим соответствующие значения базисных неизвестных.
Из полученных n-r решений составляют фундаментальную систему решений.

Меняя произвольно определитель 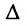, можно получать всевозможные фундаментальные системы решений.

Пример:

Найти общее решение и фундаментальную систему решений для однородной системы уравнений:

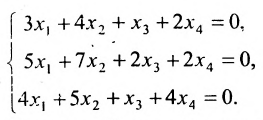
Решение:

Составим матрицу системы и применим алгоритм полного исключения.

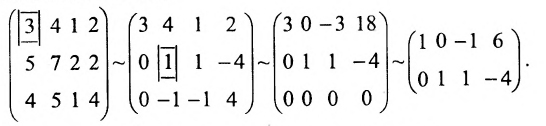
Для последней матрицы составляем систему:

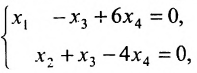, из которой находим общее решение:

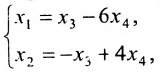
в котором 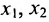— базисные неизвестные, а 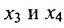– свободные неизвестные.

Построим фундаментальную систему решений. Для этого выбираем определитель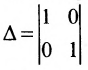 и свободным неизвестным придаём поочерёдно значения, равные элементам первой, а затем второй строк, т.е. положим вначале 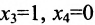и получим из общего решения 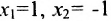; затем полагаем 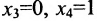, из общего решения находим: .

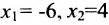Таким образом, построенные два решения (1; -1; 1; 0) и (-6; 4; 0; 1) составляют фундаментальную систему решений.

Если ранг матрицы системы однородных линейных уравнений (6.4.1) на единицу меньше числа неизвестных: 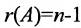то 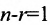, и значит, фундаментальная система состоит из одного решения. Следовательно, любое ненулевое решение образует фундаментальную систему. В этом случае любые два решения различаются между собой лишь числовыми множителями.

Рассмотрим теперь неоднородную систему m линейных уравнений с n неизвестными (6.1.1). Если в системе (6.1.1) положить 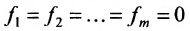, то полученная однородная система называется приведенной для системы (6.1.1).

Решения системы (6.1.1) и её приведенной системы удовлетворяют свойствам:

Сумма и разность любого решения системы (6.1.1) и любого решения её приведенной системы является решением неоднородной системы.
Все решения неоднородной системы можно получить, прибавляя к одному (любому) её решению поочерёдно все решения её приведенной системы.

Из этих свойств следует теорема.

Теорема 6.4.2. Общее решение неоднородной системы (6.1.1.) определяется суммой любого частного решения этой системы и общего решения её приведенной системы.

Пример:

Найти общее решение системы:

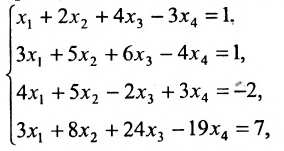
Решение:

Составим расширенную матрицу (A|F) заданной системы и применим алгоритм полного исключения:

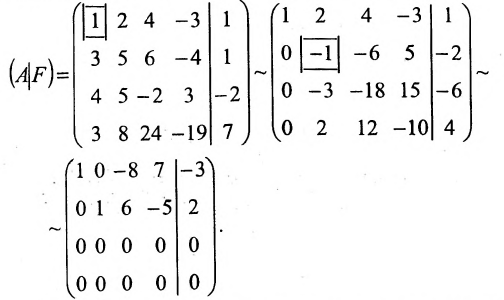Преобразованной матрице соответствует система уравнений:

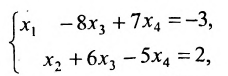
из которой находим общее решение системы:

, где 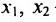— базисные неизвестные, а 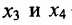– свободные неизвестные.

Покажем, что это общее решение определяется суммой любого частного решения заданной системы и общего решения приведенной системы.

Подставляя вместо свободных неизвестных 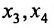в общее решение системы нули, получаем частное решение исходной системы: .

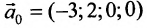Очевидно, что общее решение приведенной системы имеет вид:

Суммируя частное решение заданной системы и общее решение приведенной системы, получим общее решение (6.4.2) исходной системы.

Отметим, что общее решение системы (6.1.1) можно представить в векторном виде:

где 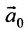– • некоторое решение (вектор-строка) системы (6.1.1);

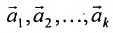– фундаментальная система решений системы (6.4.1);

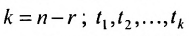– любые действительные числа.

Формула (6.4.4) называется общим решением системы (6.1.1) в векторной форме.

Запишем общее решение системы примера 6.4.1 в векторной форме. Для этого определим фундаментальную систему решений приведенной системы. Возьмём определитель 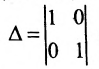и придадим поочерёдно свободным неизвестным значения, равные элементам строк. Пусть 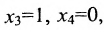тогда из общего решения (6.4.3) приведенной системы находим 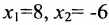; если же 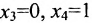, то 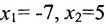. Следовательно, фундаментальную систему решений образуют решения: 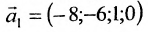и 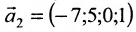. Тогда общее решение заданной системы в векторной форме имеет вид: 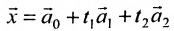, где 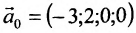– частное решение заданной системы; .

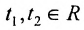Определение метода Гаусса

Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.

Пример:

Решить систему уравнений методом Гаусса:

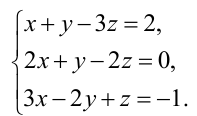
Решение:

Выпишем расширенную матрицу данной системы 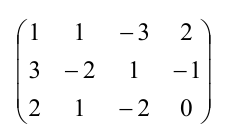и произведем следующие элементарные преобразования над ее строками:

а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2: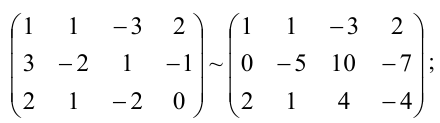

б) третью строку умножим на (-5) и прибавим к ней вторую: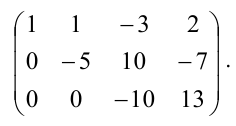

В результате всех этих преобразований данная система приводится к треугольному виду: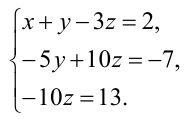

Из последнего уравнения находим 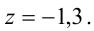Подставляя это значение во второе уравнение, имеем 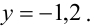Далее из первого уравнения получим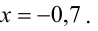

Вычисление метода Гаусса

Этот метод основан на следующей теореме.

Теорема:

Элементарные преобразования не изменяют ранга матрицы.

К элементарным преобразованиям матрицы относят:

перестановку двух параллельных рядов;
умножение какого-нибудь ряда на число, отличное от нуля;
прибавление к какому-либо ряду матрицы другого, параллельного ему ряда, умноженного на произвольное число.

Путем элементарных преобразований исходную матрицу можно привести к трапециевидной форме

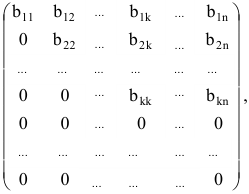
где все диагональные элементы 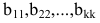отличны от нуля. Тогда ранг полученной матрицы равен рангу исходной матрицы и равен k.

Пример:

Найти ранг матрицы

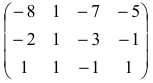
1) методом окаймляющих миноров;

2 ) методом Гаусса.

Указать один из базисных миноров.

Решение:

1. Найдем ранг матрицы методом окаймляющих миноров. Выберем минор второго порядка, отличный от нуля. Например,

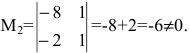Существуют два минора третьего порядка, окаймляющих минор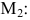

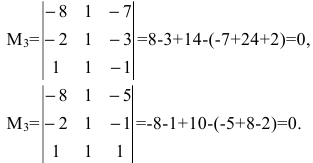Т.к. миноры третьего порядка равны нулю, ранг матрицы равен двум. Базисным минором является, например, минор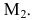

2. Найдем ранг матрицы методом Гаусса. Производя последовательно элементарные преобразования, получим: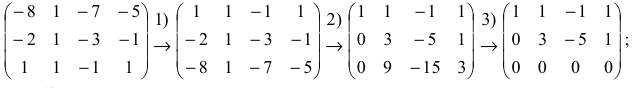

переставили первую и третью строки;
первую строку умножили на 2 и прибавили ко второй, первую строку умножили на 8 и прибавили к третьей;
вторую строку умножили на -3 и прибавили к третьей.

Последняя матрица имеет трапециевидную форму и ее ранг равен двум. Следовательно, ранг исходной матрицы также равен двум.

Прямая линия на плоскости и в пространстве
Плоскость в трехмерном пространстве
Функция одной переменной
Производная функции одной переменной
Дифференциальные уравнения с примерами
Обратная матрица – определение и нахождение
Ранг матрицы – определение и вычисление
Определители второго и третьего порядков и их свойства

Источник

Как определить количество базисных решений и как их найти

Анастасия Козлова

Ученик

(219),
закрыт

1 год назад

Как в системе линейных уравнений с помощью метода Гаусса найти базисные решения? Что это вообще такое, как определить их количество в системе?

Павел Коржов (который А.)

Гений

(96179)

2 года назад

Количество базисных решегий равняется n – rk A. (число ур-й минус ранг). Нахождение – проводить матрицу к ступенчатому виду. Тае вот, число базисных решений это кол-во нулевых строк в полученной матрице! Пнрвые rk A координат находятся однозначно, а остальные – могут быть любыми! Можно их задать ортами (1,0,…0), (0,1,..,0) и т. д.

Источник

Базисные (основные) и свободные (неосновные) переменные. Общее и базисное решения системы линейных алгебраических уравнений. Первая часть.

1. Базисные решения системы линейных уравнений

Базисные (основные) и свободные (неосновные) переменные. Общее и базисное решения системы линейных алгебраических уравнений. Первая часть.

Метод Жордана-Гаусса онлайн

Предупреждение

Метод Жордана-Гаусса

Примеры решения системы линейных уравнений методом Жордана-Гаусса

Решение задач по математике онлайн

Немного теории.

Системы линейных алгебраических уравнений

Основные определения

Формы записи СЛАУ

Критерий совместности СЛАУ

Формулы Крамера

Однородные системы

Неоднородные системы

Алгоритм решения системы m линейных уравнений с n неизвестными методом Гаусса

Исследование совместности и определённости системы. Теорема Кронекера-Капелли

Однородные системы линейных уравнений

Фундаментальная система решений. Общее решение неоднородной системы линейных уравнений

Определение метода Гаусса

Вычисление метода Гаусса

Как определить количество базисных решений и как их найти

Вам также может понравиться

Internal error 0x06 system error как исправить total war rome 2

Как исправить поврежденные сектора на жестком диске в linux

Как найти компанию друзей паре

Добавить комментарий Отменить ответ