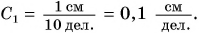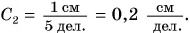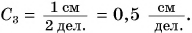Как найти число делений между этими значениями

Содержание:

При измерении разных физических величин мы получаем их числовые значения с определенной точностью. Например, при определении размеров листа бумаги (длины, ширины) мы можем указать их с точностью до миллиметра; размеры стола – с  точностью до сантиметра, размеры дома, стадиона – с точностью до метра.

Нет необходимости указывать размеры стола с точностью до миллиметра, а размеры стадиона с точностью до сантиметра или миллиметра. Мы сами в каждой ситуации, опыте и эксперименте определяем, с какой точностью нам нужны данные физические величины. Однако очень важно оценивать, насколько точно мы определяем физическую величину, какую ошибку (погрешность) в ее измерении допускаем.

При измерении мы не можем определить истинное значение измеряемой величины, а только пределы, в которых она находится.

Пример:

Измерим ширину стола рулеткой с сантиметровыми и миллиметровыми делениями на ней (рис. 5.1). Значение наименьшего деления шкалы называют ценой деления и обозначают буквой С. Видно, что цена деления рулетки С = 1 мм (или 0,1 см).

Совместим нулевое деление рулетки с краем стола и посмотрим, с каким значением 
шкалы линейки совпадает второй край стола  (рис. 5.1). Видно, что ширина стола составляет чуть больше 70 см и 6 мм, или 706 мм. Но результат наших измерений мы запишем с точностью до 1 мм, то есть L = 706 мм.

Абсолютная погрешность измерения ∆ (ДЕЛЬТА)

Из рис. 5.1 видно, что мы допускаем определенную погрешность и определить ее «на глаз» достаточно трудно. Эта погрешность составляет не более половины цены деления шкалы рулетки. Эту погрешность называют погрешностью измерения и помечают ∆L («дельта эль»). В данном эксперименте ее можно записать

Сам результат измерения принято записывать таким образом: ширина стола L = (706,0 ± 0,5) мм, читают: 706 плюс-минус 0,5 мм. Эти 0,5 мм в нашем примере называют абсолютной погрешностью. Значения измеряемой величины (706,0 мм) и абсолютной погрешности (0,5 мм) должны иметь одинаковое количество цифр после запятой, то есть нельзя записывать 706 мм ± 0,5 мм.  

Такая запись результата измерения означает, что истинное значение измеряемой величины находится между 705,5 мм и 706,5 мм, то есть 705,5 мм ≤ L ≤ 706,5 мм.

Относительная погрешность измерения ε (ЭПСИЛОН)

Иногда важно знать, какую часть составляет наша погрешность от значения 
измеряемой величины. Для этого разделим 0,5 мм на 706 мм. В результате получим: .  То есть наша ошибка составляет 0,0007 долю ширины стола, или 0,0007 · 100% = 0,07%. Это свидетельствует о достаточно высокой точности измерения. Эту погрешность называют относительной и обозначают греческой буквой  (эпсилон): 

     (5.1)

Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения –  плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.

Стандартная запись результата измерений и выводы

Таким образом, абсолютная погрешность в примере 5.1. составляет ∆L = 0,5 мм, а результат измерений следует записать в стандартном виде: L = (706,0 0,5) мм – Опыт выполнен с относительной погрешностью 0,0007 или 0,07%.

На точность измерения влияет много факторов, в частности:

1. При совмещении края стола с делением шкалы рулетки мы неминуемо допускаем погрешность, поскольку делаем это «на глаз» – смотреть можно под разными углами.
2. Не вполне ровно установили рулетку.
3. Наша рулетка является копией эталона и может несколько отличаться от оригинала.

Все это необходимо учитывать при проведении измерений.

Итоги:

• Измерения в физике всегда неточны, и надо знать пределы погрешности измерений, чтобы понимать, насколько можно доверять результатам.
• Абсолютную погрешность измерения можно определить как половину цены деления шкалы измерительного прибора. 
• Относительная погрешность есть частное от деления абсолютной погрешности на значение измеряемой величины:   и указывает на качество измерения. Ее можно выразить в процентах.

Измерительные приборы

Устройства, с помощью которых измеряют физические величины, называют измерительными приборами.

Простейший и хорошо известный вам измерительный прибор — линейка с делениями. На ее примере вы видите, что у измерительного прибора есть шкала, на которой нанесены деления, причем возле некоторых делений написано соответствующее значение физической величины. Так, значения длины в сантиметрах нанесены на линейке возле каждого десятого деления (рис. 3.11). Значения же, соответствующие «промежуточным» делениям шкалы, можно найти с помощью простого подсчета.

Разность значений физической величины, которые соответствуютближайшим делениям шкалы, называют ценой деления прибора. Ёе находят так: берут ближайшие деления, возле которых написаны значения величины, и делят разность этих значений на количество промежутков между делениями, расположенными между ними.

Например, ближайшие сантиметровые деления на линейке разделены на десять промежутков. Значит, цена деления линейки равна 0,1 см = 1 мм.

Как определяют единицы длины и времени

В старину мерами длины служили большей частью размеры человеческого тела и его частей. Дело в том, что собственное тело очень удобно как «измерительный прибор», так как оно всегда «рядом». И вдобавок «человек есть мера всех вещей»: мы считаем предмет большим или малым, сравнивая его с собой.

Так, длину куска ткани измеряли «локтями», а мелкие предметы — «дюймами» (это слово происходит от голландского слова, которое означает «большой палец»).

Однако человеческое тело в качестве измерительного прибора имеет существенный недостаток: размеры тела и его частей у разных людей заметно отличаются. Поэтому ученые решили определить единицу длины однозначно и точно. Международным соглашением было принято, что один метр равен пути, который проходит свет в вакууме за 1/299792458 с. А секунду определяют с помощью атомных часов, которые сегодня являются самыми точными.

Можно ли расстояние измерять годами

Именно так и измеряют очень большие расстояния — например, расстояния между звездами! Но при этом речь идет не о годах как промежутках времени, а о «световых годах». А один световой год — это расстояние, которое проходит свет за один земной год. По нашим земным меркам это очень большое расстояние — чтобы убедиться в этом, попробуйте выразить его в километрах! А теперь вообразите себе, что расстояние от Солнца до ближайшей к нему звезды составляет больше четырех световых лет! И по астрономическим масштабам это совсем небольшое расстояние: ведь с помощью современных телескопов астрономы тщательно изучают звезды, расстояние до которых составляет много тысяч световых лет!

Что надо знать об измерительных приборах

Приступая к измерениям, необходимо, прежде всего, подобрать приборы. Что надо знать об измерительных приборах?

Минимальное (нижний предел) и максимальное (верхний предел) значения шкалы прибора — это пределы измерения. Чаще всего предел измерения один, но может быть и два. Например, линейка имеет один предел — верхний. У линейки на рисунке 32 он равен 25 см. У термометра на рисунке 33 два предела: верхний предел измерения температуры равен +50 °С; нижний -40 °С.

На рисунке 34 изображены три линейки с одинаковыми верхними пределами (25 см). По эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 7, наименее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала понятие цена деления шкалы прибора.

Цена деления — это значение наименьшего деления шкалы прибора.

Как определить цену деления шкалы? Для этого необходимо:

1. выбрать на шкале линейки два соседних значения, например 3 см и 4 см;
2. подсчитать число делений (не штрихов!) между этими значениями; например, на линейке 1 (см. рис. 34) число делений между значениями 3 см и 4 см равно 10;
3. вычесть из большего значения меньшее (4 см – 3 см = 1 см) и результат разделить на число делений.

Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.

• Для линейки 1: 
• Для линейки 2: 
• Для линейки 3: 

Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 35). Цена деления шкалы мензурки 1:

Цена деления шкалы мензурки 2: 

А какими линейкой и мензуркой можно измерить точнее?

Измерим один и тот же объем мензуркой 1 и мензуркой 2. Но показаниям шкал в мензурке 1 объем воды V = 35 мл; в мензурке 2 — V = 37 мл.

Понятно, что точнее измерен объем воды мензуркой 2, цена деления которой меньше  Значит, чем меньше цена деления шкалы, тем точнее можно измерить данным прибором. Говорят: мензуркой 1 мы измерили объем с точностью до 5 мл (сравните с ценой деления шкалы ), мензуркой 2 – с точностью до 1 мл (сравните с ценой деления ). Точность измерения температуры термометрами 1 и 2 (рис. 36) определите самостоятельно.

Итак, любым прибором, имеющим шкалу, измерить физическую величину можно с точностью, не превышающей цены деления шкалы.

Линейкой 1 (см. рис. 34) можно измерить длину с точностью до 1 мм. Точность измерения длины линейками 2 и 3 определите самостоятельно.

Главные выводы:

1. Верхний и нижний пределы измерения — это максимальное и минимальное значения шкалы прибора.
2. Цена деления шкалы равна значению наименьшего деления шкалы.
3. Чем меньше цена деления шкалы, тем точнее будут проведены измерения данным прибором.

Для любознательных:

В истории науки есть немало случаев, когда повышение точности измерений давало толчок к новым открытиям. Более точные измерения плотности азота, выделенного из воздуха, позволили в 1894 г. открыть новый инертный газ — аргон. Повышение точности измерений плотности воды привело к открытию в 1932 г. одной из разновидностей тяжелых атомов водорода — дейтерия. Позже дейтерий вошел в состав ядерного горючего. Оценить расстояния до звезд и создать их точные каталоги ученые смогли благодаря повышению точности при измерении положения ярких звезд на небе.

• Заказать решение задач по физике

Пример решения задачи

Для измерения величины угла используют транспортир. Определите: 1) цену деления каждой шкалы транспортира, изображенного на рисунке 38; 2) значение угла BАС, используя каждую шкалу; укажите точность измерения угла ВАС в каждом случае.

Решение:

1) Цена деления нижней шкалы:

Цена деления средней шкалы: 

Цена деления верхней шкалы:

2) Определенный но нижней шкале с точностью до 10° определенный по средней шкале с точностью до 5° определенный по верхней шкале с точностью до 1°

Нахождение всех делителей числа

• Все делители числа
• Калькулятор нахождения всех делителей

Все делители числа

Все делители, на которые данное число делится нацело, можно получить из разложения числа на простые множители.

Нахождение всех делителей числа выполняется следующим образом:

1. Сначала нужно разложить данное число на простые множители.
2. Выписываем каждый полученный простой множитель (без повторов, если какой-то множитель повторяется).
3. Далее, находим всевозможные произведения всех полученных простых множителей между собой и добавляем их к выписанным простым множителям.
4. В конце добавляем в качестве делителя единицу.

Например, найдём все делители числа  40.  Раскладываем число  40  на простые множители:

40 = 2³ · 5.

Выписываем (без повторов) каждый полученный простой множитель — это  2  и  5.

Далее находим всевозможные произведения всех полученных простых множителей между собой:

2 · 2 = 4,

2 · 2 · 2 = 8,

2 · 5 = 10,

2 · 2 · 5 = 20,

2 · 2 · 2 · 5 = 40.

Добавляем в качестве делителя  1.  В итоге получаем все делители, на которые число  40  делится без остатка:

1,  2,  4,  5,  8,  10,  20,  40.

Других делителей у числа  40  нет.

Калькулятор нахождения всех делителей

Данный калькулятор поможет вам получить все делители числа. Просто введите число и нажмите кнопку “Вычислить”.

Как определить цену деления амперметра и вольтметра? Школьный вопрос. Запомнила еще с 7 класса, когда нам объяснял физик. Теперь пользуюсь всегда, даже когда готовлю что-нибудь и нужно понять, какова цена деления, например, измерительного пластикового контейнера в мультиварке. Из большего значения вычитаю меньшее, а после делю на количество промежутков между “черточками”. Например, здесь. 120 мл минус 60 мл = 60 мл. Делим на три и получаем 20 мл. То есть цена одного деления равняется 20 мл. автор вопроса выбрал этот ответ лучшим Есть что-то общее между всеми измерительными приборами – это шкала, которая разбита делениями. Например обычные ручные часы, мы привыкли, что на циферблате показаны шестьдесят делений, каждое из которых равно одной минуте. Но что делать если на современных часах всего четыре деления? Пятнадцать, тридцать, сорок пять и шестьдесят. Чему тогда равно деление? Все очень, мы отнимаем от большего меньшее, например от 45 отнимем 15 и получим разность между делениями – 30. Теперь чтобы узнать цену деления мы должны эту разность поделить на 2 – число взятых делений. Получаем на таких часах цена деления равна 15 минутам. Аналогично решаем задачу с любым измерительным прибором, амперметров или вольтметром. Отнимаем от большего обозначенного на шкале значения меньшее, и делим на количество необозначенных черточек-делений между ними. Azama­tik [55.3K] 6 лет назад  Цену деления как амперметра, так и вольтметра будем определять по следующей формуле: Ч2 – Ч1/n, где Ч2 и Ч1 – это соседние значения (числа), которые написаны на приборе; а n – это количество делений между ними. Определим цену деления приборов, изображенных на рисунке: Амперметр: Ч2 – это, к примеру, три, а Ч1 – два. Отнимаем от большего меньшее и получаем единицу. Единицу делим на есть и поучаем 0,2. Цена деления апмерметра 0,2. Вольтметр: от ста (Ч2) отнимаем пятьдесят (Ч1) и делим на десять (n). Получаем результат 5. Цена деления вольтметра равна 5. Nelli­4ka [114K] 6 лет назад  Давайте разберемся на конкретном примере. Берем пару любых соседних чисел – будь то 0 и 2, 2 и 4, 4 и 6 и т.д. Находим разницу между этими числами. В нашем случае это 2. Затем нужно посчитать, сколько делений находится между этими цифрами. Деления – это не сами полоски, а пространство между ними. У нас получается 4. Далее мы делим на это число получившуюся ранее разницу: 2:4 = получаем 0,5. Таким образом, цена деления – 0,5. Чтобы определить цену деления какого-то прибора (амперметра, вольтметра и т.д.), нужно найти два соседних числа, отнять от большего меньшее и поделить получившееся число на количество промежутков между делениями (которые расположены между двумя этими числами). Пример из фото: 10-5=5 5:5=1 Цена деления=1. Сахар­ный имбир­ь [3.6K] 4 года назад  Возьмем, допустим, мерный стакан. На нем указаны следующие числа: 0, 50, 100, 150, 200. Между этими числами расположено четыре черточки, плюс напротив самих чисел они также имеются. То есть между числами у нас есть пять делений, и нам нужно понять, чему они соответствуют. Берем любые два соседних числа и отнимаем от большего меньшее. Например, от 150 отнимаем 100, получается 50. Потом это число делим на количество делений между “соседями”, то есть в нашем случае на 5. Получается 10 – это и есть цена деления на нашем мерном стакане. Werte­p75 [1.5K] 4 года назад  Первое действие – вычитание. Естественно, вычитать нужно меньшее из большего, а не наоборот, нам нужно найти положительное значение. Второе действие – деление. Делить нужно то число, что стало результатом первого действия. Делить надо на число, соответствующее количеству промежутков (не чёрточек!) между двумя значениями. MMM DANON­E [27.1K] 4 года назад  Цену деления данных приборов найти легко, пригодятся элементарные знания с уроков физики. Посчитайте, сколько делений у вас находятся между соседними числами. Затем произведите разность между соседними числами на шкале (от большего вычесть меньшее), полученную цифру поделите на высчитанное заранее число делений. Нужно из максимального значения шкалы прибора, вычесть минимальное (начальное) Полученный результат разделить на количество самых маленьких делений имеющихся на шкале. Полученный результат и будет ценой каждого деления в отдельности. Нэпэй­шни [18.2K] 6 лет назад  Цена деления амперметраа и вольтметра? вычисляется по простой формуле.Число1-Число2/n(число делений у шкалы.Например амперметр (число делений5):Ч1 это 4 Ч2 это 2.Отнимает и получаем 2.Двойку делим на n выходит единица. Чтобы определить цену деления нужно посчитать количество делений между двумя соседними числами.Затем вычесть из большего числа меньшее и разделить на количество делений. Знаете ответ?

Для измерения физических величин используют измерительные приборы. Например, для измерения высоты мы будем использовать такой измерительный прибор как линейка, для измерения массы тела – весы, для измерения температуры – термометр, а для измерения времени – часы и т.д..

Многие измерительные приборы имеют шкалу. Шкала измерительного прибора представляет собой совокупность отметок (точек, штрихов) вместе со связанной с ними нумерацией (числами). Для того, чтобы определить с какой точностью может измерить тот или иной прибор, необходимо знать его цену деления.

Ценой деления шкалы прибора называет расстояние между двумя ближайшими штрихами на шкале прибора. Для того чтобы определить цену деления (С) надо найти два ближайших штриха шкалы, возле которых написаны значения величины;

вычесть из большего значения меньшее и полученное число разделить на число делений, находящихся между ними.

Например, рассмотрим такой измерительный прибор как шприц. Шприц нужен для измерения такой физической величины как объем (V). Рассмотрим шкалу шприца и определить ее цену деления (см.рис.).

Для того, чтобы определить цену деления данной шкалы мы возьмем два ближайших штриха, возле которых написаны значения, например 7 и 8.

Далее выполним вычитание, как указано в инструкции выше: 8-7=1. Затем, посчитаем сколько делений между большими штрихами (на рисунке отмечены зелеными черточками и подписаны цифрами снизу). У нас получилось 5 делений.

Разделим получившуюся разницу на 5: 1/5=0,2. Значит цена деления шкалы нашего измерительного прибора равна 0,2 мл.

Запишем наши вычисления формулой: С=(8-7)/5=0,2 мл.

Пример с мензуркой

С = 40 – 30/2 = 5 мл.

Если данную мензурку наполнить полностью жидкостью, то ее объем будет равен 50 мл. А если на­лить жидкость до первого значения, отличного от нуля, то её объем будет равен 5 мл. Между штрихами 40 и 30 вмещается 10 мл жидкости. Между самыми близкими штрихами объем налитой жидкости будет равен 5 мл. Эта величина и будет являться ценой деления мензурки.

Для основных и производных единиц измерения в системе СИ используют дольные и кратные десятичные приставки для удобной записи чисел. Например: 6000000000=10М (приставки обозначают числа).

Задание. Приведите примеры известных Вам внесистемных единиц и соотношение их с единицами системы СИ.

В большинстве задач, где не дано обратное, желательно переводить скорость в метры/секунду (м/с). Для этого вспоминаем, что

1 км = 1000 м = 100 000 см = 1 000 000 мм

1 ч = 60 мин = 3600 с

Допустим, нам необходимо перевести 72 км/ч в метры в секунду.

Километры у нас находятся в числителе, часы в знаменателе, поэтому

72 км/ч * 1000 (домножаем на 1000, чтобы получить метры)

= 72000 м/ч / 3600 (делим на количество секунд в часе, чтобы получить из часов секунды; делим, поскольку часы у нас в знаменателе (снизу дроби), а не в числителе) = 20 м/с

Преобразовать – сначала перевести величину измерения в систему СИ, а потом преобразовать в стандартный вид.

Для того, чтобы определить, что такое миллисекунда, нужно понять, что представляет собой приставка “милли”. С помощью данной приставки образуются дольные единицы измерения в системе СИ. Приставка “милли” имеет латинское происхождение и означает “mille” – тысяча. Таким образом, единица измерения, образованная с помощью “милли” будет равна 0,001 от исходной единицы. Итак, миллисекунда – это одна из единиц измерения времени, она равна тысячной доле от 1 секунды.

Обозначается: мс (русский язык), ms (английский язык).

Чтобы перевести миллисекунды в секунды и наоборот, нужно помнить, что:

1 секунда = 1000 миллисекунд.

1 миллисекунда = 0,001 секунды.

Если нужно перевести миллисекунды в секунды, то достаточно заданное количество миллисекунд разделить на 1000. Например:

20 миллисекунд = 20 / 1000 = 0,02 секунды.

2000 миллисекунд = 2000 / 1000 = 2 секунды.

Если наоборот нужно перевести секунды в миллисекунды, то умножаем имеющееся число секунд на 1000. Например:

3 секунды = 3 * 1000 = 3000 миллисекунд.

0,05 секунды = 0,05 * 1000 = 50 миллисекунд.

0,15 : 1000=0,00015

Физические величины при измерениях и вычислениях обычно выражают числами. Они могут значительно отличаться друг от друга и выражаться как чрезвычайно малыми, так и гигантскими числами. Например, размеры различных тел лежат в пределах от микроскопических до космических масштабов и различаются в 1000000000000000000000000000000… раз (всего надо написать 60 нулей) – такое число даже сложно прочитать!

Как же записать очень малое или очень большое число, чтобы сэкономить бумагу и чтобы легко оперировать этими числами – складывать, вычитать, умножать, делить, да и вообще быстро прочитать и понять записанное?

Наиболее удобный способ записи малых и больших чисел заключается в использовании множителя 10 в некоторой степени. Например, число 2000 можно записать как 2·1000 или 2·10^3. Степень десяти (в данном случае «3») показывает, сколько нулей нужно приписать справа за первым множителем (в нашем примере «2»). Это называют записью числа в стандартной форме. Если число содержит более, чем одну значащую цифру, например 21500, то его можно записать как 21500·10^0 или 2150·10^1 или 215·10^2 или 21,5·10^3 или 2,15·10^4 или 0,215·10^5 или 0,0215·10^6 и так далее.

Запомним: в стандартной форме числа до запятой всегда оставляют только одну цифру, отличную от нуля, а остальные цифры записывают после запятой. Например, в стандартной форме число 21500 = 2,15·10^4.

math-prosto@mail.ru

Материал взят с инета.

Как найти цену деления шкалы

Приборы, в которых для измерений используется шкала, имеют большое количество делений, не все из которых пронумерованы. Определение цены деления шкалы необходимо для повышения точности измерений, если измеряемая величина находится между пронумерованными делениями.

Вам понадобится

• – прибор со шкалой;
• – калькулятор;
• – тонкий предмет для отсчета делений (игла).

Инструкция

Возьмите прибор со шкалой, цену деления которой необходимо определить. Внимательно осмотрите ее, она должна равномерно делить поле для измерений и не быть поврежденной. Если каждое деление шкалы пронумеровано, то для того, чтобы найти цену деления, возьмите два ближайших числовых значения и от большего вычтите меньшее.

Например, если каждая риска (черточка) на шкале пронумерована числами 0, 100, 200, 300, 400. То возьмите любые два рядом стоящие числа, подходят 200 и 300, и из большего вычтите меньшее 300-200=100. Это и будет цена деления такой шкалы. Обратите внимание, в каких единицах измеряются величины, такая же размерность будет и у цены деления.

Если у прибора между основными пронумерованными делениями есть более мелкие, не пронумерованные, заметьте два ближайших числовых значения. После этого подсчитайте количество делений, которые заключены между этими числовыми значениями. В случае, если шкала мелкая, воспользуйтесь иголкой. Обязательно считайте деления между рисками шкалы, а не сами риски (черточки), поскольку их будет на одну больше.

Для расчета цены деления, возьмите два замеченных ранее числовых значения, отнимите от большего значения меньшее. Полученный результат поделите на количество раннее подчитанных делений, которые находились между числовыми значениями на шкале, полученный результат и будет ценой деления данной шкалы.

Например, если шкала состоит из числовых делений 0, 20, 40, 60, 80, 100, возьмите два ближайших числовых значения. Для этого подойдут числа 60 и 80. Тщательно подсчитайте между ними количество делений. Предположим, что между ними 10 делений. Для того чтобы подсчитать цену деления от большего числа вычтите меньшее 80-60=20. Полученный результат поделите на количество делений 20/10=2. Если прибор измеряет, например, напряжение в вольтах, то его цена деления равна 2 В.

Видео по теме