В данной публикации мы рассмотрим, каким образом можно найти дробь от целого числа и наоборот – как найти число, если известно, чему равна определенная дробь от него. Также разберем примеры решения задач для лучшего понимания и закрепления теоретического материала.
- Нахождение дроби от числа
- Нахождение числа по значению дроби
Нахождение дроби от числа
Чтобы найти часть от целого числа n, которая представлена дробью, нужно умножить эту дробь (например, a/b) на данное число n.
Дробь от числа = n ⋅
a/b
=
n ⋅ a/b
Пример 1
Решение
5/12
⋅ 24 =
5 ⋅ 24/12
=
120/12
= 10
Пример 2
Решение
4/9
⋅ 7 =
4 ⋅ 7/9
=
28/9
=3
1/9
Таким образом, результат нахождения дроби числа не всегда бывает целым числом.
Примечание: если дробь является смешанной, сперва ее следует представить в виде неправильной и только потом выполнять умножение.
Нахождение числа по значению дроби
Если известно сколько число n занимает в числе m, и эта доля выражена в виде дроби, то для нахождения числа m используется формула:
Пример:
Один ряд кинозала вмещает 20 кресел, что составляет
2/5
от всей вместимости зала. Определите, сколько всего посадочных мест в зале.
Решение
Общее количество кресел равняется:
20 :
2/5
= 20 ⋅
5/2
=
20 ⋅ 5/2
= 50
Правило нахождения числа по его дроби:
Чтобы найти число по данному значению его дроби, нужно это значение разделить на дробь.
Рассмотрим, как найти число по его дроби, на конкретных примерах.
Примеры.
1) Найти число, 3/4 которого равны 12.
Решение:
![Rendered by QuickLaTeX.com [12:frac{3}{4} = 12 cdot frac{4}{3} = frac{{mathop {12}limits^4 cdot 4}}{{mathop 3limits_1 }} = frac{{4 cdot 4}}{1} = 16.]](https://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-36511d1819111c033089ca3273acc85f_l3.png)
Чтобы найти число по его дроби, это число делим на эту дробь. Чтобы разделить число на дробь, надо данное число умножить на число, обратное к дроби (то есть на перевернутую дробь). Чтобы умножить дробь на число, надо числитель умножить на это число, а знаменатель оставить без изменения. Сокращаем 12 и 3 на 3. Так как в знаменателе получили единицу, ответ — целое число.
2) Найти число, если 9/10 его равняются 3/5.
Решение:
![Rendered by QuickLaTeX.com [frac{3}{5}:frac{9}{{10}} = frac{3}{5} cdot frac{{10}}{9} = frac{{mathop 3limits^1 cdot mathop {10}limits^2 }}{{mathop 5limits_1 cdot mathop 9limits_3 }} = frac{{1 cdot 2}}{{1 cdot 3}} = frac{2}{3}.]](https://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-bf84912aa20ee4de9b744cbdba8d5218_l3.png)
Чтобы найти число по данному значению его дроби, это значение делим на эту дробь. Чтобы разделить дробь на дробь, первую дробь умножаем на обратную ко второй (перевернутую). Чтобы умножить дробь на дробь, числитель умножаем на числитель, знаменатель — на знаменатель. Сокращаем 10 и 5 на 5, 3 и 9 — на 3. В результате получили правильную несократимую дробь, значит это — окончательный результат.
3) Найти число, 9/7 которого равны
![]()
Решение:
![Rendered by QuickLaTeX.com [7frac{1}{{14}}:frac{9}{7} = frac{{99}}{{14}} cdot frac{7}{9} = frac{{mathop {99}limits^{11} cdot mathop 7limits^1 }}{{mathop {14}limits_2 cdot mathop 9limits_1 }} = ]](https://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-b33fab4d662914875c6a6b923654f611_l3.png)
![]()
Чтобы найти число по значению его дроби, это значение делим на эту дробь. Смешанное число переводим в неправильную дробь и умножаем его на число, обратное ко второму (перевернутую дробь). Сокращаем 99 и 9 на 9, 7 и 14 — на 7. Поскольку получили неправильную дробь, необходимо выделить из нее целую часть.
Как найти число дробь которого равна числу?
Вы открыли страницу вопроса Как найти число дробь которого равна числу?. Он относится к категории
Математика. Уровень сложности вопроса – для учащихся 5 – 9 классов.
Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие
ответы по интересующей теме. Чтобы получить наиболее развернутый ответ,
можно просмотреть другие, похожие вопросы в категории Математика,
воспользовавшись поисковой системой, или ознакомиться с ответами других
пользователей. Для расширения границ поиска создайте новый вопрос, используя
ключевые слова. Введите его в строку, нажав кнопку вверху.
Существует ряд задач, в которых необходимо найти часть или дробь
некоторого числа. Такие задачи решаются умножением на основании следующего правила:
Чтобы найти дробь от заданного числа, нужно это число умножить на дробь.
Пример
Задание. Найти
$frac{7}{20}$ от 40.
Решение. В рассматриваемом примере 40 – это заданное число, $frac{7}{20}$ – дробь, задающая искомую часть.
Тогда, согласно правилу, имеем:
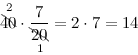
Итак, получили, что $frac{7}{20}$ от 40 равно 14 – искомая часть данного числа.
Ответ. $frac{7}{20}$ от 40 равно 14.
Иногда требуется по известной части числа и дроби, которая выражает эту часть, определить все число. Подобные задачи решаются делением.
Чтобы найти число, по известной величине его дроби, надо заданную величину поделить на дробь.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. В классе 12 мальчиков, что составляет $frac{4}{5}$ части всех учеников класса.
Сколько всего человек учится в классе?
Решение. Искомое количество учеников
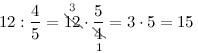
Ответ. Всего в классе учится 15 человек.
Читать следующую тему: десятичные дроби.
Если известно сколько составляет часть от целого, то по известной части можно “восстановить”
целое.
Для этого пользуемся правилом нахождения целого (числа)
по его дроби (части).
Запомните!
![]()
Чтобы найти число по его части, выраженной дробью, нужно данное число
разделить на дробь.
Пример. Рассмотрим задачу.
Поезд прошёл 240 км, что составило
всего пути.
Какой путь должен пройти поезд?
Решение. 240 км — часть всего пути. Эти же километры
выражены дробью 15/23
от всего пути. Знаменатель дроби говорит о том, что весь путь разделён на 23 части,
и 15 таких частей составляют 240 км
(числитель дроби равен 15).
Значит, можно найти, сколько составляет
часть пути.
240 : 15 = 16 (км)
Весь путь (целое) всегда обозначаем за единицу, которую можно выразить дробью
.
Значит, чтобы найти весь путь (23 части, каждая из которых по
16 км) нужно:
16 · 23 = 368 (км)
Кратко запись решения такой задачи можно сделать следующим образом.
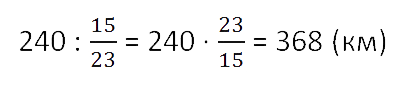
Ответ: поезд должен пройти 368 км.
Сложные задачи на нахождение числа по его части
Часто задачи данного типа сложнее, чем рассмотренная задача выше, и более сложные задачи приходиться решать в
несколько действий.
Рассмотрим задачу.
При подготовке к диктанту по английскому языку Оля
выучила четверть всех слов, заданных учителем.
Если бы она выучила ещё 4 слова, то была
бы выучена треть всех слов.
Сколько всего слов надо было выучить Оле?
Решение. Как обычно подчеркнём в условии задачи все важные данные.
Как видно из условия, четыре невыученных слова — это часть от всех слов, которую можно найти в виде
разности дробей.
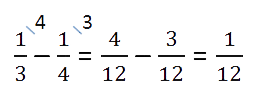
Такую часть всех слов составляют 4 слова.
Итак, 4 слова — это
от всех слов (целого). Теперь по правилу нахождения
числа по его части данное числовое значение разделим на соответствующую ему дробь
.
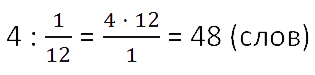
Ответ: всего 48 слов надо было выучить к диктанту.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
