Нам известно, как
находят объединение двух конечных
непересекающихся множеств. Например,
если А = {х, у, z}, а В = {k,l,m,p},
то А∪В ={х,
у,z,k,l,m,p}. Чтобы
ответить на вопрос: «Сколько элементов
в полученном множестве?», достаточно
пересчитать их.
А как определить
число элементов в объединении конечных
множеств, не образуя его и не обращаясь
к пересчету элементов?
Условимся предложение
«Множество А содержит а элементов»
записывать в таком виде: n(А)
= а. Например, если А = {х, у,z},
то утверждение «Множество А содержит
три элемента можно записать так:n(А)
= 3.
Можно доказать,
что в множестве А содержится а элементов,
а в множестве В – bэлементов
и множества А и В не пересекаются, то в
объединении множеств А и В содержится
а +bэлементов, т.е.
n(А∪В)
= n(А) + n(В)
= в + b.(1)
Это правило
нахождения числа элементов в объединении
двух конечных непересекающихся множеств,
его можно обобщить на случай tпопарно непересекающихся множеств,
т.е. если множества А₁,
А₂, …, Аtпопарно не пересекаются, тоn(А₁
∪ А₂ ∪ …∪
Аt) =n(А₁)
+ n(А₂)
+ … + n(Аt).
Для выше описанных
множеств n(А) = 3,n(В)
= 4. Видим, что А∩
В =∅. Тогдаn(А∪В)
=n(А) +n(В) =
3 + 4 = 7.
Нетрудно убедиться
в том, что если В ⊂
А, то n
(В´А)
= n(А)
– n(В),т.е. число
элементов дополнения подмножества В
до конечного множества А равно разности
численностей этих множеств.
Пусть, например,
А = {х, у, z,p,t}, а В = { х,p,t}. Получаемn(А)
= 5,n(В) = 3. Тогдаn(В´А)
=n(А) -n(В)
= 5 – 3 = 2.
Формула (1) позволяет
находить число элементов в объединении
конечных непересекающихся множеств. А
если множества А и В имеют общие элементы,
то как найти число элементов в их
объединении?
Пусть, например,
А = {х, у, z}, а В = {х,z,
р,s,k}. Тогда
А∪ В = {х,
у,z, р,s,k},
т.е.n(А) = 3,n(В)
= 5, аn(А∩
В) = 2 и, значит, общие элементы множеств
А и В в объединении этих множеств записаны
только один раз.
В общем виде правило
подсчета элементов в объединении двух
конечных множеств может быть представлено
в виде формулы:
n(А∪В)
= n(А) + n(В)
– n(А ∩
В).(2)
Полученные формулы
для подсчета числа элементов в объединении
двух и более множеств можно использовать
для решения текстовых задач следующего
вида.
Задача. Из 40
студентов курса 32 изучают английский
язык, 21 – немецкий язык, а 15 – английский
и немецкий языки. Сколько студентов
курса не изучает ни английский, ни
немецкий языки?
Решение. Пусть А
– множество студентов курса, изучающих
английский язык, В – множество студентов
курса, изучающих немецкий язык, С –
множество всех студентов курса. По
условию задачи: n(А) = 32,n(В) = 21,n(А∩ В) = 15,n(С) = 40. Требуется найти
число студентов курса, не изучающих ни
английского, ни немецкого языка.
1 способ.
1) Найдем число
элементов в объединении данных множеств
А и В. Для этого воспользуемся формулой
(2):
n(А∪В)
=n(А) +n(В) -n(А∩
В) = 32 + 21 – 15 = 38.
2) Найдем число
студентов курса, которые не изучают ни
английский, ни немецкий языки: 40 – 38 =
2.
2 способ.
1) Изобразим данные
множества при помощи кругов Эйлера и
определим число элементов в каждом из
непересекающихся подмножеств (рисунок).
Так как в пересечении
множеств А и В содержится 15 элементов,
то студентов, изучающих только английский
язык, будет 32 – 15 = 17, а студентов, изучающих
только немецкий язык, 21 – 15 = 6. Тогда
n(А∪В)
= 17 + 15 + 6 = 38, и, следовательно, число
студентов курса, которые не изучают ни
английский, ни немецкий языки, будет 40
– 38 = 2.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Тип урока: изучение нового материала.
Цели:
- формирование знаний о пересечении и объединении множеств;
- развитие умений и нахождение числа элементов пересечения и объединения множеств, выявлять закономерность, обобщать и делать выводы, воспитание ответственного отношения к учебе.
Ход урока
1. Организационный момент.
2. Повторение изученного по теме «Множества».
Вопросы для учащихся:
- Что такое множество?
- Что такое элементы множества?
- Какое множество конечно и бесконечно?
- Какое множество называется пустым?
3. Изучение нового материала «Пересечение множеств».
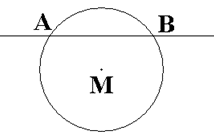
Учитель. Рассмотрим следующие два множества: М – множество всех точек круга, N – множество точек прямой, пересекающей круг. Каждый видит, что пересечение круга с прямой – это отрезок; обозначим его концы буквами А и В. Задумаемся: каким свойством обладают точки этого отрезка по отношению к множествам М и N? Ответ ясен: точки отрезка АВ – это в точности те точки, которые принадлежат и множеству М, и множеству N. Так что множество всех точек отрезка АВ естественно назвать пересечением множеств М и N.
Точно так же можно определить пересечение любых двух множеств М и N. Пересечением множеств М и N называется множество, состоящее из всех элементов, принадлежащих каждому из множеств М и N. Пересечение множеств М и N обозначают М ∩ N. Читают: «пересечение М и N» или «М пересечение N». Знак ∩ называется знаком пересечения.
Обсудим несколько примеров.
Пример 1. М – множество всех учениц какой-то школы, N – множество всех учащихся данного класса этой школы. Тогда М ∩ N – это множество всех девочек из данного класса.
Пример 2. М – множество всех квартир на 1-м этаже в каком-то доме, N – множество всех квартир в данном подъезде этого дома. Тогда М ∩ N – это множество всех квартир на 1-м этаже в данном подъезде.
Пересечение множеств точек двух фигур на плоскости легче представить, если нарисовать эти фигуры. Сделаем это, например, для двух кругов. Множество всех точек первого круга обозначим М, второго – N. Для пересечения М ∩ Nмогут быть три варианта; они изображены на рисунке.
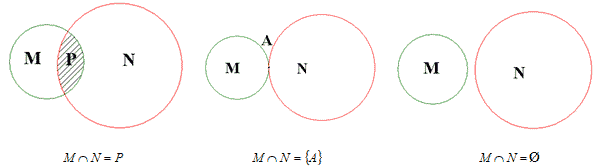
Если конечные множества записаны при помощи фигурных скобок списками своих элементов, то легко записать их пересечение.
Примеры:
Пересечение можно образовывать не только для двух множеств, но и для любого их числа. Определяется это точно так же, как и для двух множеств: пересечением данных множеств называется множество, состоящее из всех элементов, принадлежащих каждому из этих множеств. Пересечение множеств М, N и Р обозначается М ∩N ∩ Р.
Вопрос для учащихся:
Что обозначает запись Р ∩ Q ∩ R ∩ S? Какому множеству равно это пересечение, если
4. Первичное закрепление понятия пересечения множеств.
Вопросы:
- Что такое пересечение двух множеств; нескольких множеств?
- Что значит, что два множества не пересекаются? Приведите 2-3 примера непересекающихся множеств.
- Какое множество обозначается знаком ?
Практические задания:
1. Для каждой пары множеств М и Nзапишите их пересечение:
N – множество всех неправильных дробей.
2. Для каждой пары множеств М и N укажите их пересечение:
- М – множество всех нечетных чисел, N – множество всех натуральных чисел, делящихся на 4;
- М – множество всех правильных дробей, N – множество всех десятичных дробей;
- М – множество всех натуральных чисел, делящихся на 3, N – множество всех натуральных чисел, делящихся на 5.
3. Дан многоугольник. Каждую его сторону будем рассматривать как множество всех точек, принадлежащих этой стороне. Для каждой пары сторон многоугольника укажите множество, равное пересечению этих двух сторон, если многоугольник – это:
а) треугольник АВС;
б) прямоугольник KLMN.
4. Рассмотрите три множества {1, 2}, {2, 3}, и {3, 1}. Убедитесь, что их пересечение пусто, а пересечение любых двух из этих множеств не пусто.
5. Пусть М – множество всех букв слова СЛОН, N – множество всех букв слова СТОН, Р – множество всех букв слова СТОГ, S – множество всех букв слова СЛОГ.
- Запишите всевозможные попарные пересечения этих множеств. Имеются ли среди них равные?
- Запишите всевозможные пересечения троек этих множеств. Имеются ли среди них равные?
- Запишите пересечение всех этих множеств. Равно ли оно какому-то из множеств, найденных вами в пунктах а) и б)?
5. Изучение нового материала «Объединение множеств».
Учитель. Объединением множеств М и N называется множество всех элементов, принадлежащих хотя бы одному из множеств М и N.
Объединение множеств М и N обозначают М N. Читают: «объединение М и N» или «М объединение N». Знак
называется знаком объединения.
Разберем несколько примеров. Обдумайте каждый из них.
Пример 1. М – множество всех учеников данного класса, получивших на сегодняшний день пятерку по какому-нибудь предмету, N – множество всех учеников того же класса, получивших в этот день четверку по какому-нибудь предмету. Тогда М N – это множество всех учеников данного класса, получивших за сегодняшний день повышенные отметки.
Пример 2. М – множество всех правильных дробей, N – множество всех неправильных дробей. Тогда М N – это множество всех обыкновенных дробей.
Пример 3. М – множество всех букв слова КОШКА, N – множество всех букв слова МЫШКА. Тогда М N = {А, К, М, О, Ш, Ы}.
Задание для учащихся: Приведите сами какой-нибудь пример объединения двух множеств.
Учитель. Как и пересечение, объединение можно образовать не только для двух множеств, но и для любого их числа: объединением данных множеств называется множество, состоящее…
Закончите определение. Догадайтесь, как записать объединение трех множеств М, N и Р.
Если конечные множества записаны при помощи фигурных скобок списками своих элементов, то, как и для пересечения, легко записать их объединения.
Для любых множеств М и N можно образовать их пересечение М ∩ N и объединение М N. Это похоже на то, что происходит при действиях над числами: для любых двух чисел m и n можно образовать их произведение m n и сумму m+n. Так получаются действия, которые назвали умножением и сложением. Поэтому образование пересечения и образование объединения можно назвать действиями над множествами.
Выполняются ли те же законы для пересечения и объединения множеств? Давайте рассуждать. Начнем с переместительного закона.
Повторим, что такое пересечение двух множеств: множество М ∩ N состоит из всех элементов, принадлежащих каждому из множеств М и N, а множество N ∩М состоит из всех элементов, принадлежащих каждому из множеств Nи М. Но сказать «каждому из множеств М и N» или «каждому из множеств N и М» – значит сказать одно и то же: ведь ясно, что неважно, в каком порядке перечислять здесь множества. Значит, множества М ∩N и N ∩М состоят из одних и тех же элементов, т.е.
М ∩ N = N ∩М.
Данное равенство и означает, что переместительный закон для пересечения верен.
Чтобы проверить сочетательный закон, надо убедиться, что для любых трех множеств М, N и Р выполняется равенство
М ∩(N ∩Р)= (М ∩N) ∩Р
Легко понять, что в левой и правой частях этого равенства записаны множества, состоящие из всех элементов, принадлежащих каждому из множеств М, N и Р, т.е. состоящие из одних и тех же элементов. Это и означает, что требуемое равенство выполняется.
6. Первичное закрепление изученного понятия объединения множеств.
Вопросы:
- Что такое объединение двух множеств; нескольких множеств?
- О выполнении каких законов для действий пересечения и объединения множеств идет речь в объяснительном тексте этого параграфа?
- Каким множеством – конечным или бесконечным – будет объединение: а) двух конечных множеств; б) двух бесконечных множеств; в) конечного и бесконечного множеств?
Практические задания:
1. Для каждой пары множеств М и N запишите их объединение:
2. Для каждой пары множеств М и N укажите их объединение:
- М – множество всех нечетных чисел, N – множество всех четных чисел;
- М – множество всех квадратов на плоскости, N – множество всех прямоугольников на той же плоскости, четырехугольников;
- М – множество всех натуральных чисел, делящихся на 3, N – множество всех натуральных чисел, делящихся на 15.
3. Пусть М – множество всех букв слова СЛОН, N – множество всех букв слова СТОН, Р – множество всех букв слова СТОГ, S – множество всех букв слова СЛОГ.
- Запишите всевозможные попарные объединения этих множеств. Имеются ли среди них равные?
- Запишите всевозможные объединения троек этих множеств. Имеются ли среди них равные?
- Запишите объединение всех этих множеств. Равно ли оно какому-то из множеств, найденных вами в пунктах а) и б)?
7. Изучение нового – вывод правила подсчета числа элементов объединения и пересечения множеств.
Учитель. Чтобы вывести правило давайте разберем конкретный пример. Пусть М = {Вася, Валя, Вера, Игорь}, т.е. m=4;
N = {Валя, Гриша, Игорь}, т.е. n=3.
Запишем объединение этих множеств:
М N = {Вася, Валя, Вера, Гриша, Игорь}.
В множестве МN пять элементов, а m+n=4+3=7. Вот мы и видим, что в М
N элементов меньше чем 7.
Почему так получилось? Да потому, что в данном примере можно указать учеников, которые в этот день получили и пятерку, и четверку. Другими словами здесь пересечение М ∩N не пусто: М ∩ N = {Валя, Игорь}. Но в объединении-то МN каждый элемент пересечения М ∩N присутствует (и подсчитывается) только один раз, а не два раза.
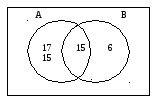
Давайте-ка изобразим ситуацию нашего примера на рисунке.
Если бы подсчитали здесь сумму m+n (т.е. 4+3), то каждый элемент пересечения (в данном примере Валя и Игорь, т.е. 2 элемента) оказался бы подсчитанным дважды. Значит, чтобы узнать число элементов объединения, надо из суммы m+n вычесть число лишний раз сосчитанных элементов пересечения. В данном примере получаем 4+3-2=5.
Данная задача была решена с помощью рисунка, этот способ называется «Круги Эйлера». Леонард Эйлер – швейцарский математик, который в 18 веке работал в Российской академии наук и сделал много открытий для нашей науки.
Итак, если мы возьмем сумму m+n, то в ней элементы пересечения М ∩N будут сосчитаны дважды. Значит, чтобы определить число элементов объединения, надо из суммы m+n вычесть число лишний раз сосчитанных элементов из М ∩N, т.е. число р. Получим такую формулу: q=m+n-p.
Сформулируем правило для нахождения числа элементов объединения множеств:
Чтобы найти число элементов объединения двух множеств, надо сложить числа элементов этих множеств и вычесть из полученной суммы число элементов их пересечения.
Сформулируем правило для нахождения числа элементов пересечения множеств:
Чтобы найти число элементов пересечения двух множеств, надо сложить числа элементов этих множеств и вычесть из полученной суммы число элементов их объединения.
8. Первичное закрепление изученного.
Практические задания (устно):
1. Вычислите число элементов в объединении множеств М и N, если:
- М содержит 10 элементов, N – 15 элементов, а М ∩N – 7 элементов;
- М содержит 27 элементов, N – 18 элементов, а М ∩N – 13 элементов;
- М содержит 45 элементов, N – 57 элементов, а М ∩N – 1 элемент.
2. Вычислите число элементов в пересечении множеств М и N, если:
- М содержит 10 элементов, N – 15 элементов, а М ∩N – 17 элементов;
- М содержит 27 элементов, N – 18 элементов, а М ∩ N – 45 элементов;
- М содержит 45 элементов, N – 57 элементов, а М ∩N – 100 элементов.
Решение задач с помощью кругов Эйлера:
№1. В классе 28 учеников. Каждый из них начертил у себя в тетради один из двух четырехугольников – прямоугольник или ромб. При проверке прямоугольников оказалось 17, а ромбов – 15. Как такое могло случиться?
№2. В осенние каникулы 12 учеников класса участвовали в междугородных экскурсиях в Москву и Санкт-Петербург, при этом 8 из них посетили Санкт-Петербург, а 6 – Москву. Сколько из этих учеников побывало и в Москве, и в Санкт-Петербурге?
Задание на дом:
№1. Найдите пересечение множеств учителей, которые вели уроки в вашем классе: а) вчера и сегодня; б) вчера и позавчера. Оказалось ли какое-то из этих двух пересечений пустым?
№2. Вася, рассматривая свой дневник погоды, обнаружил, что в сентябре 17 раз отмечен дождь и 19 раз – сильный ветер. При этом дней, когда одновременно шел дождь и дул сильный ветер, оказалось 7. Был ли хоть один день, когда не было ни дождя, ни сильного ветра?
Объединение A и B
Объедине́ние мно́жеств (тж. су́мма или соедине́ние) в теории множеств — множество, содержащее в себе все элементы исходных множеств. Объединение двух множеств 




Содержание
- 1 Определения
- 1.1 Объединение двух множеств
- 1.2 Объединение семейства множеств
- 2 Свойства
- 3 Примеры
- 4 Примечания
- 5 См. также
Определения[править | править код]
Объединение двух множеств[править | править код]
Пусть даны два множества 

Объединение семейства множеств[править | править код]
Пусть дано семейство множеств 
Свойства[править | править код]
- Объединение множеств является бинарной операцией на произвольном булеане
- Операция объединения множеств коммутативна:
- Операция объединения множеств ассоциативна:
- Операция объединения множеств дистрибутивна относительно операции пересечения:[1]
- Пустое множество
является нейтральным элементом операции объединения множеств:
- Таким образом булеан вместе с операцией объединения множеств является моноидом;
- Операция объединения множеств идемпотентна:
Примеры[править | править код]
- Пусть
Тогда
Примечания[править | править код]
- ↑ В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 2. Вещественные числа // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. 1. — С. 66. — 672 с. — ISBN 5-482-00445-7.
См. также[править | править код]
- Дизъюнктное объединение
- Операции над множествами
Теория множеств |
||
|---|---|---|
| Обзор |
|
|
| Аксиомы |
|
|
| Операции |
|
|
|
|
|
| Типы множеств |
|
|
| Теории |
|
|
|
|
|
| Теоретики множеств |
|
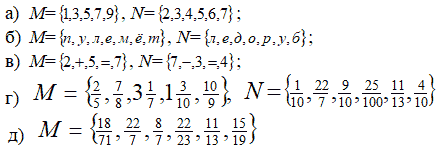
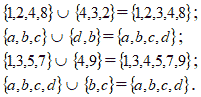
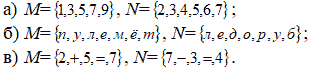












![{displaystyle bigcup limits _{nin mathbb {Z} }[n,n+1]=mathbb {R} .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3835f4db48045c5a8bebe8bf50c998c384adab7c)

