На чтение 3 мин Просмотров 192к. Опубликовано 27.05.2022
Содержание
- Введение
- Числа Фибоначчи циклом while
- Числа Фибоначчи циклом for
- Числа Фибоначчи рекурсией
- Заключение
Введение
В статье разберём 3 способа получения ряда Фибоначчи на Python. Первые два способа будут с использованием циклов, а третий – рекурсивный.
Числа Фибоначчи – бесконечная последовательность чисел, каждое из которых является суммой двух предыдущих и так до бесконечности.
Формула:

Числа Фибоначчи циклом while
Для начала создадим переменную, в которую будет вводиться длина ряда:
n = int(input('Введите длину ряда: '))Далее создадим две переменные (f1 и f2), которые будут равняться начальным единицам и выведем их:
f1 = f2 = 1
print(f1, f2, end=' ')Создадим переменную i, которая будет равняться двум:
Добавим цикл, который не закончится, пока переменная i будет меньше переменной n:
while i < n:
f1, f2 = f2, f1 + f2 # f1 приравнивается к f2, f2 приравнивается к f1 + f2
print(f2, end=' ') # Выводится f2
i += 1
print()Числа Фибоначчи на Python:
n = int(input('Введите длину ряда: '))
f1 = f2 = 1
print(f1, f2, end=' ')
i = 2
while i < n:
f1, f2 = f2, f1 + f2 # f1 приравнивается к f2, f2 приравнивается к f1 + f2
print(f2, end=' ') # Выводится f2
i += 1
print()Числа Фибоначчи циклом for
Создадим переменную, в которую будет вводиться длина ряда:
n = int(input('Введите длину ряда: '))Далее создадим две переменные (f1 и f2), которые будут равняться начальным единицам и выведем их:
f1 = f2 = 1
print(f1, f2, end=' ')Добавим цикл, который начинается с 2, и заканчивается на n:
for i in range(2, n):
f1, f2 = f2, f1 + f2 # f1 приравнивается к f2, f2 приравнивается к f1 + f2
print(f2, end=' ') # Выводится f2Числа Фибоначчи на Python:
n = int(input('Введите длину ряда: '))
f1 = f2 = 1
print(f1, f2, end=' ')
for i in range(2, n):
f1, f2 = f2, f1 + f2
print(f2, end=' ')Числа Фибоначчи рекурсией
Для начала создадим рекурсивную функцию, назовём её fibonacci и добавим ей параметр n:
Добавим условие, что если n = 1, или n = 2, то возвращается единица, так как первый и второй элементы ряда Фибоначчи равны единице. Если же условие не срабатывает, то элементы складываются:
def fibonacci(n):
if n == 1 or n == 2: # Если n = 1, или n = 2, вернуть в вызывающую ветку единицу, так как первый и второй элементы ряда Фибоначчи равны единице.
return 1
return fibonacci(n - 1) + fibonacci(n - 2)Числа Фибоначчи на Python:
def fibonacci(n):
if n == 1 or n == 2:
return 1
return fibonacci(n - 1) + fibonacci(n - 2)
n = int(input())
print(fibonacci(n))Заключение
В данной статье мы научились вычислять n-ное число ряда Фибоначчи на Python. Надеюсь Вам понравилась статья, удачи! 🙂
Watch Now This tutorial has a related video course created by the Real Python team. Watch it together with the written tutorial to deepen your understanding: Exploring the Fibonacci Sequence With Python
The Fibonacci sequence is a pretty famous sequence of integer numbers. The sequence comes up naturally in many problems and has a nice recursive definition. Learning how to generate it is an essential step in the pragmatic programmer’s journey toward mastering recursion. In this tutorial, you’ll focus on learning what the Fibonacci sequence is and how to generate it using Python.
In this tutorial, you’ll learn how to:
- Generate the Fibonacci sequence using a recursive algorithm
- Optimize the recursive Fibonacci algorithm using memoization
- Generate the Fibonacci sequence using an iterative algorithm
To get the most out of this tutorial, you should know the basics of Big O notation, object-oriented programming, Python’s special methods, conditional statements, functions, and basic data structures like lists, queues, and stacks. Having some familiarity with these concepts will greatly help you understand the new ones you’ll be exploring in this tutorial.
Let’s dive right in!
Getting Started With the Fibonacci Sequence
Leonardo Fibonacci was an Italian mathematician who was able to quickly produce an answer to this question asked by Emperor Frederick II of Swabia: “How many pairs of rabbits are obtained in a year, excluding cases of death, supposing that each couple gives birth to another couple every month and that the youngest couples are able to reproduce already at the second month of life?”
The answer was the following sequence:
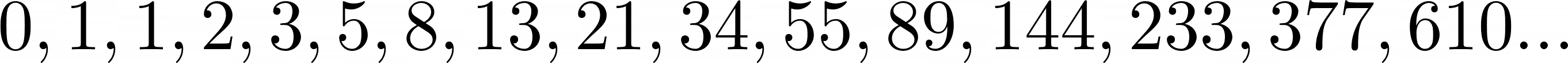
The pattern begins after the first two numbers, 0 and 1, where each number in the sequence is always the sum of the two numbers before it. Indian mathematicians had known about this sequence since the sixth century, and Fibonacci leveraged it to calculate the growth of rabbit populations.
F(n) is used to indicate the number of pairs of rabbits present in month n, so the sequence can be expressed like this:
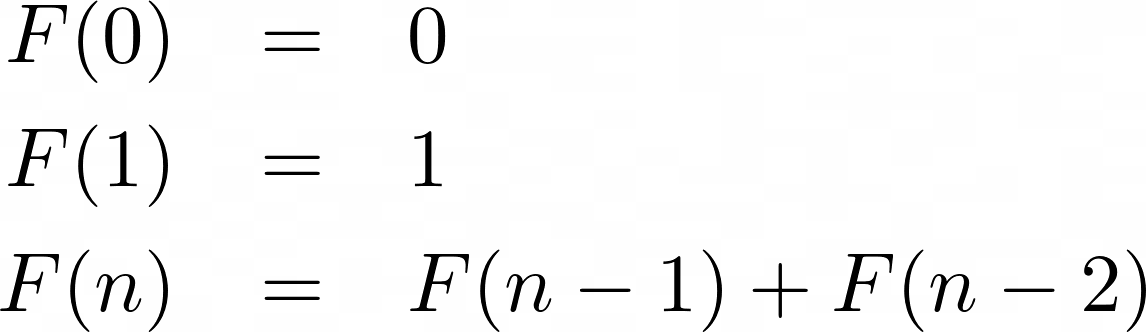
In mathematical terminology, you’d call this a recurrence relation, meaning that each term of the sequence (beyond 0 and 1) is a function of the preceding terms.
There’s also a version of the sequence where the first two numbers are both 1, like so:
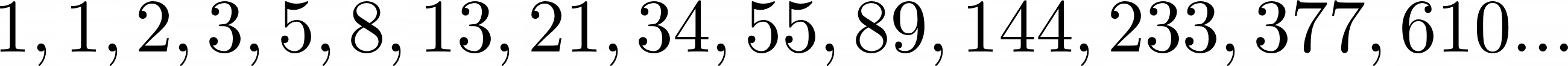
In this alternative version, F(0) is still implicitly 0, but you start from F(1) and F(2) instead. The algorithm remains the same because you’re always summing the previous two numbers to get the next number in the sequence.
For the purposes of this tutorial, you’ll use the version of the sequence that starts with 0.
Examining the Recursion Behind the Fibonacci Sequence
Generating the Fibonacci sequence is a classic recursive problem. Recursion is when a function refers to itself to break down the problem it’s trying to solve. In every function call, the problem becomes smaller until it reaches a base case, after which it will then return the result to each intermediate caller until it returns the final result back to the original caller.
If you wanted to calculate the F(5) Fibonacci number, you’d need to calculate its predecessors, F(4) and F(3), first. And in order to calculate F(4) and F(3), you would need to calculate their predecessors. The breakdown of F(5) into smaller subproblems would look like this:
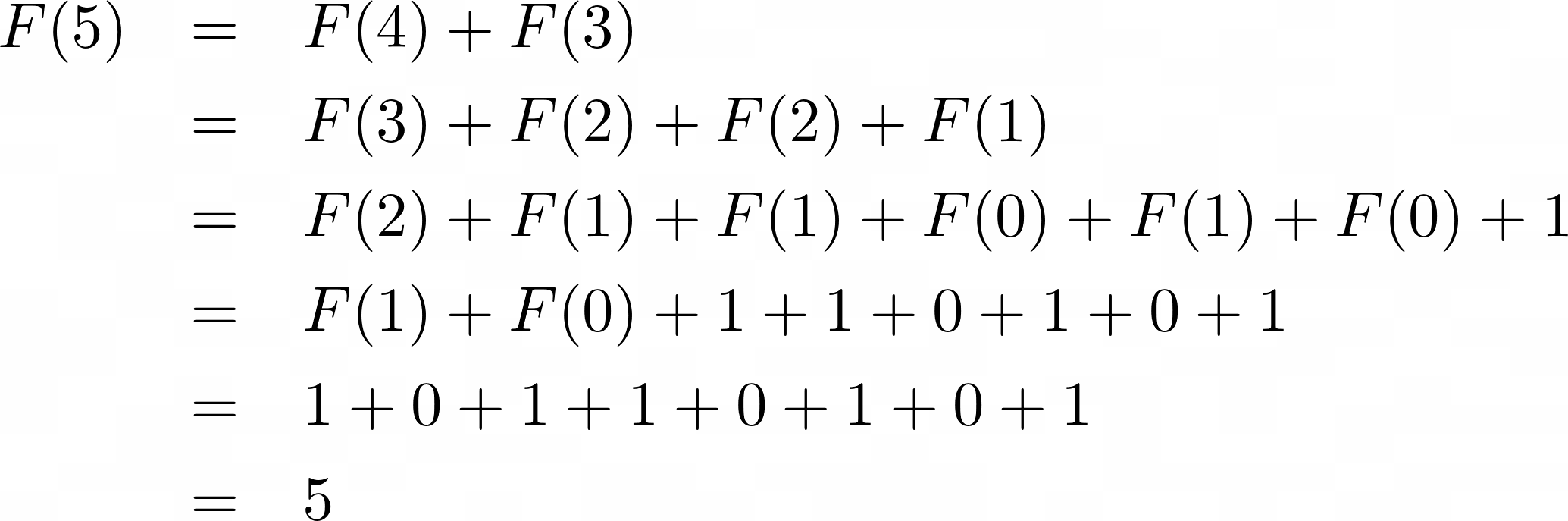
Each time the Fibonacci function is called, it gets broken down into two smaller subproblems because that’s how you defined the recurrence relation. When it reaches the base case of either F(0) or F(1), it can finally return a result back to its caller.
In order to calculate the fifth number in the Fibonacci sequence, you solve smaller but identical problems until you reach the base cases, where you can start returning a result:
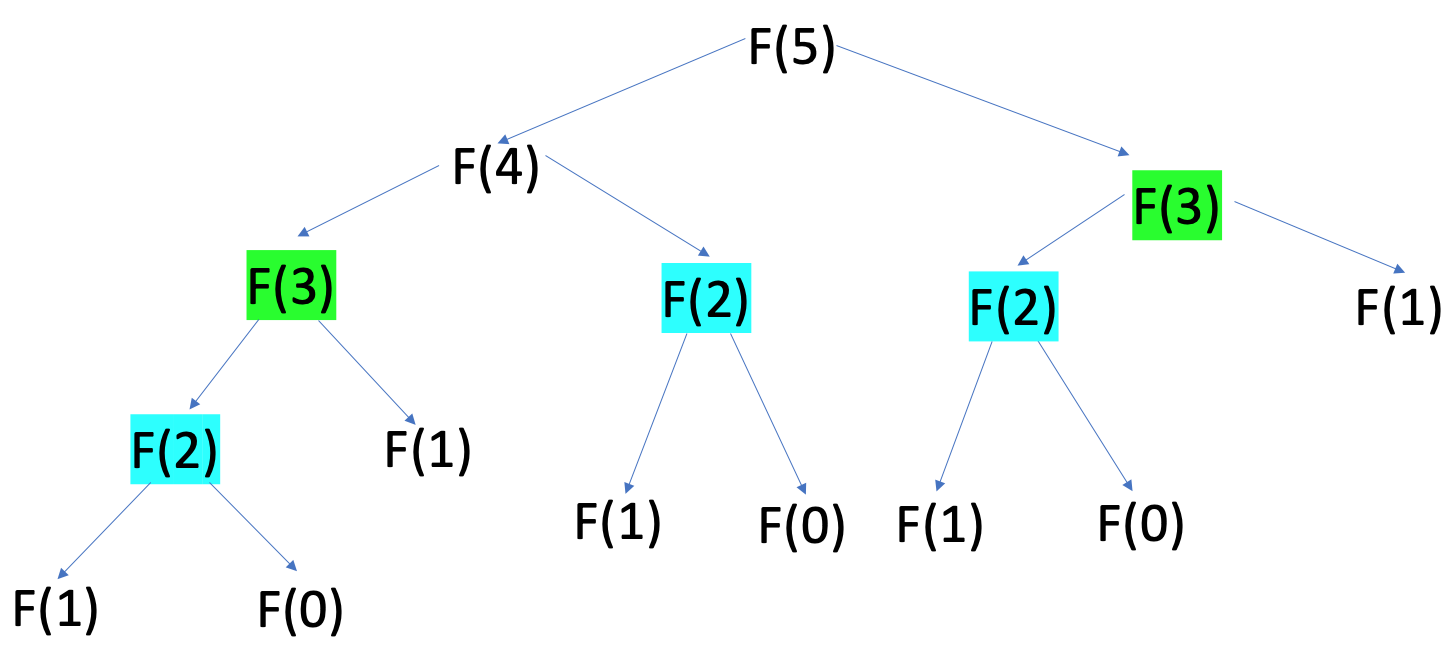
The colored subproblems on this diagram represent repetitive solutions to the same problem. If you go further up the tree, you’ll find more of these repetitive solutions. This means that to generate a Fibonacci sequence recursively, you have to calculate many intermediate numbers over and over. This is one of the fundamental issues in the recursive approach to the Fibonacci sequence.
Generating the Fibonacci Sequence Recursively in Python
The most common and minimal algorithm to generate the Fibonacci sequence requires you to code a recursive function that calls itself as many times as needed until it computes the desired Fibonacci number:
>>>
>>> def fibonacci_of(n):
... if n in {0, 1}: # Base case
... return n
... return fibonacci_of(n - 1) + fibonacci_of(n - 2) # Recursive case
...
>>> [fibonacci_of(n) for n in range(15)]
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377]
Inside fibonacci_of(), you first check the base case. You then return the sum of the values that results from calling the function with the two preceding values of n. The list comprehension at the end of the example generates a Fibonacci sequence with the first fifteen numbers.
This function quickly falls into the repetition issue you saw in the above section. The computation gets more and more expensive as n gets bigger. The required time grows exponentially because the function calculates many identical subproblems over and over again.
To calculate F(5), fibonacci_of() has to call itself fifteen times. To calculate F(n), the maximum depth of the call tree is n, and since each function call produces two additional function calls, the time complexity of this recursive function is O(2n).
Most of those calls are redundant because you’ve already calculated their results. F(3) appears twice, and F(2) appears three times. F(1) and F(0) are base cases, so it’s fine to call them multiple times. You may want to avoid this wasteful repetition, which is the topic of the following sections.
Optimizing the Recursive Algorithm for the Fibonacci Sequence
There are at least two techniques you can use to make the algorithm to generate the Fibonacci sequence more efficient—in other words, to make it take less time to compute. These techniques ensure that you don’t keep computing the same values over and over again, which is what made the original algorithm so inefficient. They’re called memoization and iteration.
Memoizing the Recursive Algorithm
As you saw in the code above, the Fibonacci function calls itself several times with the same input. Instead of a new call every time, you can store the results of previous calls in something like a memory cache. You can use a Python list to store the results of previous computations. This technique is called memoization.
Memoization speeds up the execution of expensive recursive functions by storing previously calculated results in a cache. This way, when the same input occurs again, the function just has to look up the corresponding result and return it without having to run the computation again. You can refer to these results as cached or memoized:
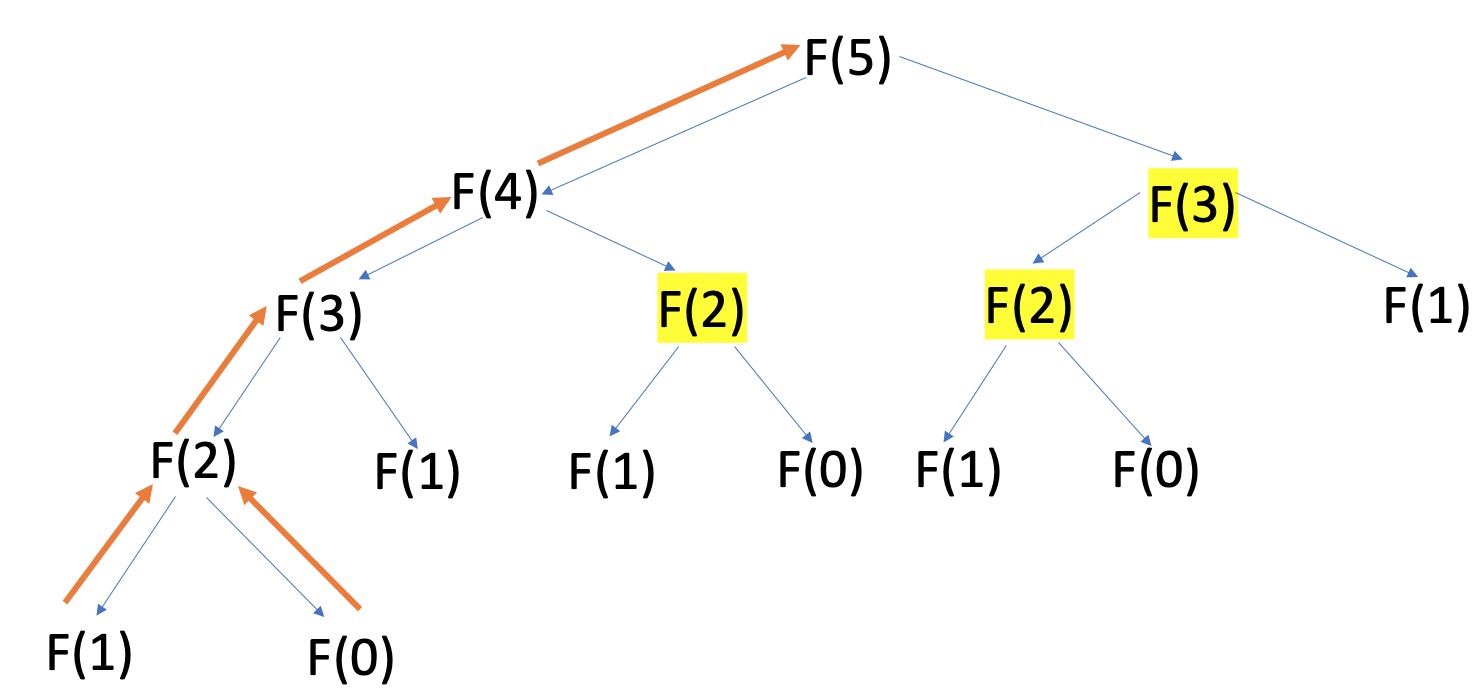
With memoization, you just have to traverse up the call tree of depth n once after returning from the base case, as you retrieve all the previously calculated values highlighted in yellow, F(2) and F(3), from the cache earlier.
The orange path shows that no input to the Fibonacci function is called more than once. This significantly reduces the time complexity of the algorithm from exponential O(2n) to linear O(n).
Even for the base cases, you can replace calling F(0) and F(1) with just retrieving the values directly from the cache at indices 0 and 1, so you end up calling the function just six times instead of fifteen!
Here’s a possible translation of this optimization into Python code:
>>>
>>> cache = {0: 0, 1: 1}
>>> def fibonacci_of(n):
... if n in cache: # Base case
... return cache[n]
... # Compute and cache the Fibonacci number
... cache[n] = fibonacci_of(n - 1) + fibonacci_of(n - 2) # Recursive case
... return cache[n]
>>> [fibonacci_of(n) for n in range(15)]
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377]
In this example, you use a Python dictionary to cache the computed Fibonacci numbers. Initially, cache contains the starting values of the Fibonacci sequence, 0 and 1. Inside the function, you first check if the Fibonacci number for the current input value of n is already in cache. If so, then you return the number at hand.
If there is no Fibonacci number for the current value of n, then you compute it by calling fibonacci_of() recursively and updating cache. The final step is to return the requested Fibonacci number.
Exploring an Iterative Algorithm
What if you don’t even have to call the recursive Fibonacci function at all? You can actually use an iterative algorithm to compute the number at position n in the Fibonacci sequence.
You know that the first two numbers in the sequence are 0 and 1 and that each subsequent number in the sequence is the sum of its previous two predecessors. So, you can just create a loop that adds the previous two numbers, n - 1 and n - 2, together to find the number at position n in the sequence.
The bolded purple numbers in the diagram below represent the new numbers that need to be calculated and added to cache in each iterative step:

To calculate the Fibonacci number at position n, you store the first two numbers of the sequence, 0 and 1, in cache. Then, calculate the next numbers consecutively until you can return cache[n].
Generating the Fibonacci Sequence in Python
Now that you know the basics of how to generate the Fibonacci sequence, it’s time to go deeper and further explore the different ways to implement the underlying algorithm in Python. In the following sections, you’ll explore how to implement different algorithms to generate the Fibonacci sequence using recursion, Python object-oriented programming, and also iteration.
Using Recursion and a Python Class
Your first approach to generating the Fibonacci sequence will use a Python class and recursion. An advantage of using the class over the memoized recursive function you saw before is that a class keeps state and behavior (encapsulation) together within the same object. In the function example, however, cache is a completely separate object, so you don’t have control over it.
Below is the code that implements your class-based solution:
1# fibonacci_class.py
2
3class Fibonacci:
4 def __init__(self):
5 self.cache = [0, 1]
6
7 def __call__(self, n):
8 # Validate the value of n
9 if not (isinstance(n, int) and n >= 0):
10 raise ValueError(f'Positive integer number expected, got "{n}"')
11
12 # Check for computed Fibonacci numbers
13 if n < len(self.cache):
14 return self.cache[n]
15 else:
16 # Compute and cache the requested Fibonacci number
17 fib_number = self(n - 1) + self(n - 2)
18 self.cache.append(fib_number)
19
20 return self.cache[n]
Here’s a breakdown of what’s happening in the code:
-
Line 3 defines the
Fibonacciclass. -
Line 4 defines the class initializer,
.__init__(). It’s a special method that you can use to initialize your class instances. Special methods are sometimes referred to as dunder methods, short for double underscore methods. -
Line 5 creates the
.cacheinstance attribute, which means that whenever you create aFibonacciobject, there will be a cache for it. This attribute initially contains the first numbers in the Fibonacci sequence. -
Line 7 defines another special method,
.__call__(). This method turns the instances ofFibonacciinto callable objects. -
Lines 9 and 10 validate the value of
nby using a conditional statement. Ifnis not a positive integer number, then the method raises aValueError. -
Line 13 defines a conditional statement to check for those Fibonacci numbers that were already calculated and are available in
.cache. If the number at indexnis already in.cache, then line 14 returns it. Otherwise, line 17 computes the number, and line 18 appends it to.cacheso you don’t have to compute it again. -
Line 20 returns the requested Fibonacci number.
To try this code, go ahead and save it into fibonacci_class.py. Then run this code in your interactive shell:
>>>
>>> from fibonacci_class import Fibonacci
>>> fibonacci_of = Fibonacci()
>>> fibonacci_of(5)
5
>>> fibonacci_of(6)
8
>>> fibonacci_of(7)
13
>>> [fibonacci_of(n) for n in range(15)]
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377]
Here, you create and then call an instance of the Fibonacci class named fibonacci_of. The first call uses 5 as an argument and returns 5, which is the sixth Fibonacci number because you’re using zero-based indices.
This implementation of the Fibonacci sequence algorithm is quite efficient. Once you have an instance of the class, the .cache attribute holds the already computed numbers from call to call.
Visualizing the Memoized Fibonacci Sequence Algorithm
You can effectively understand how each call to a recursive Fibonacci function is handled using a call stack representation. The way each call is pushed onto the stack and popped off reflects exactly how the program runs. It clearly demonstrates how calculating large numbers will take a long time if you don’t optimize the algorithm.
In a call stack, whenever a function returns a result, a stack frame representing the function call is popped off the stack. Whenever you call a function, you add a new stack frame to the top of the stack. In general, this operation has a space complexity of O(n) because there are no more than n stack frames on the call stack at a single time.
To visualize the memoized recursive Fibonacci algorithm, you’ll use a set of diagrams representing the call stack. The step number is indicated by the blue label below each call stack.
Say you want to compute F(5). To do this, you push the first call to the function onto the call stack:

To compute F(5), you must compute F(4) as outlined by the Fibonacci recurrence relation, so you add that new function call to the stack:
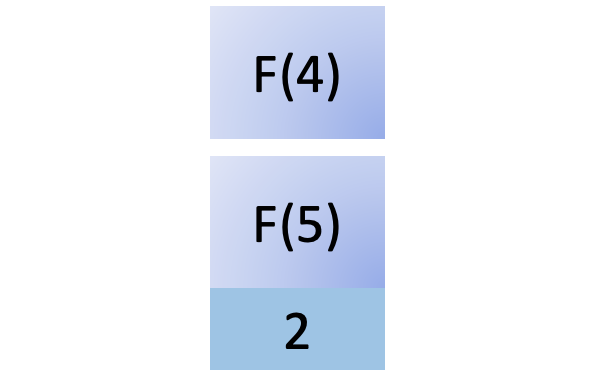
To compute F(4), you must compute F(3), so you add another function call to the stack:
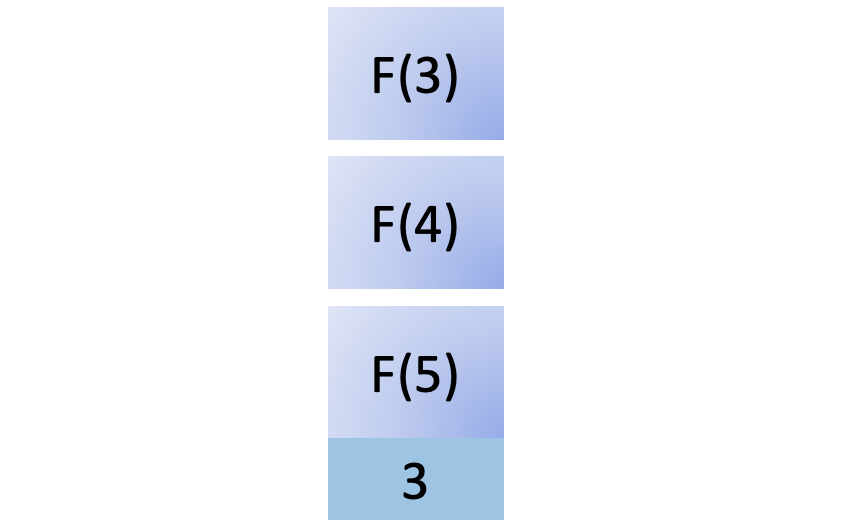
To compute F(3), you must compute F(2), so you add yet another function call to the call stack:
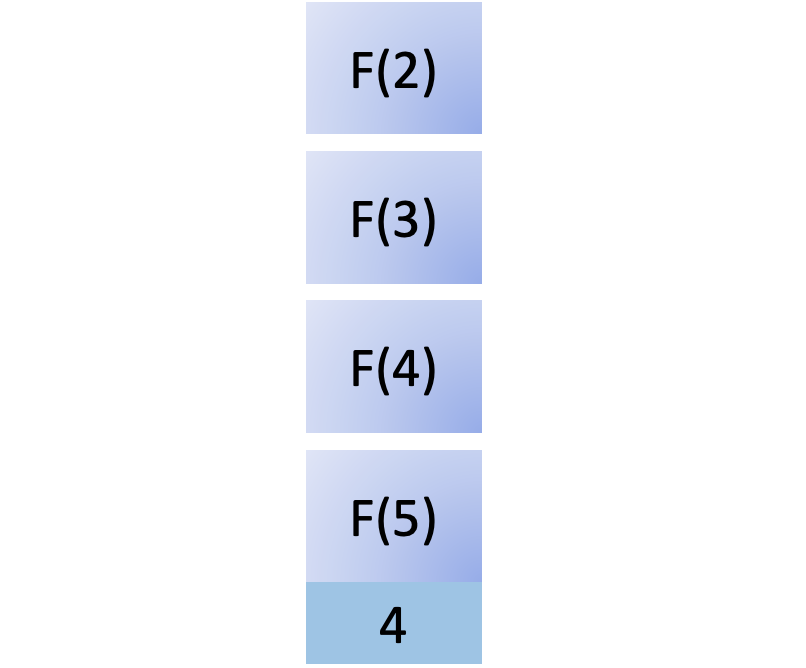
To compute F(2), you must compute F(1), so you add that to the stack. As F(1) is a base case, it returns immediately with 1, and you remove this call from the stack:
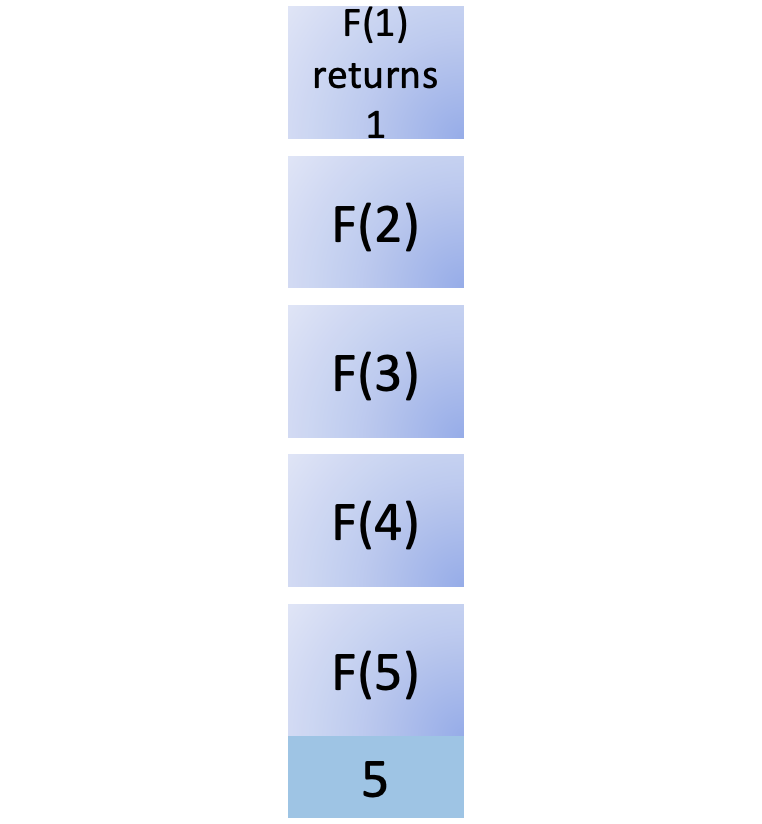
Now you start to unwind the results recursively. F(1) returns the result back to its calling function, F(2). To compute F(2), you also need to compute F(0):
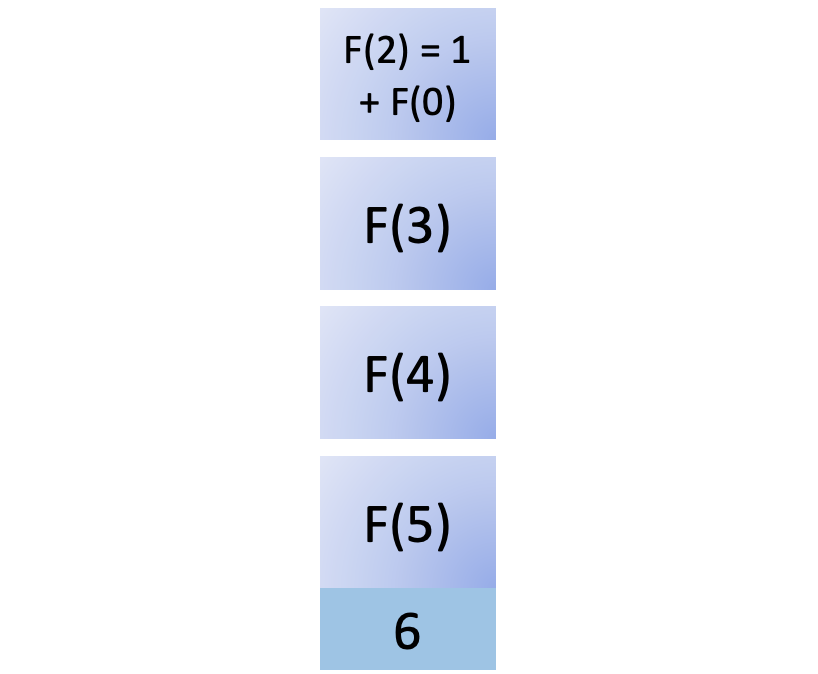
You add F(0) to the stack. Since F(0) is a base case, it returns immediately, giving you 0. Now you can remove it from the call stack:
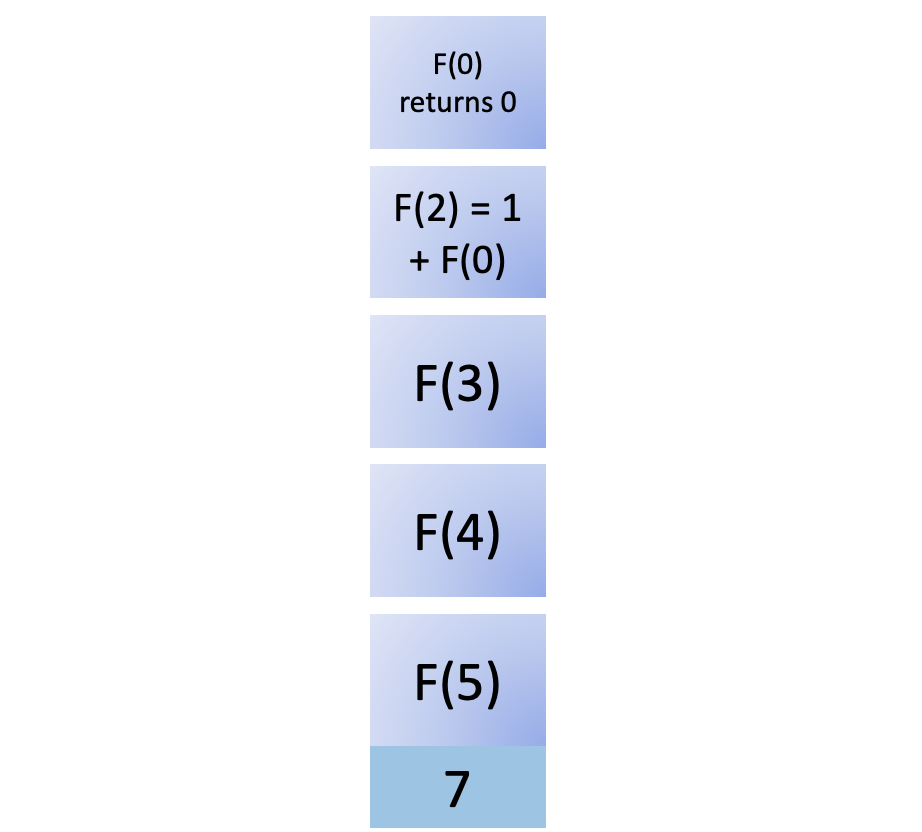
This result of calling F(0) is returned to F(2). Now you have what you need to compute F(2) and remove it from the stack:
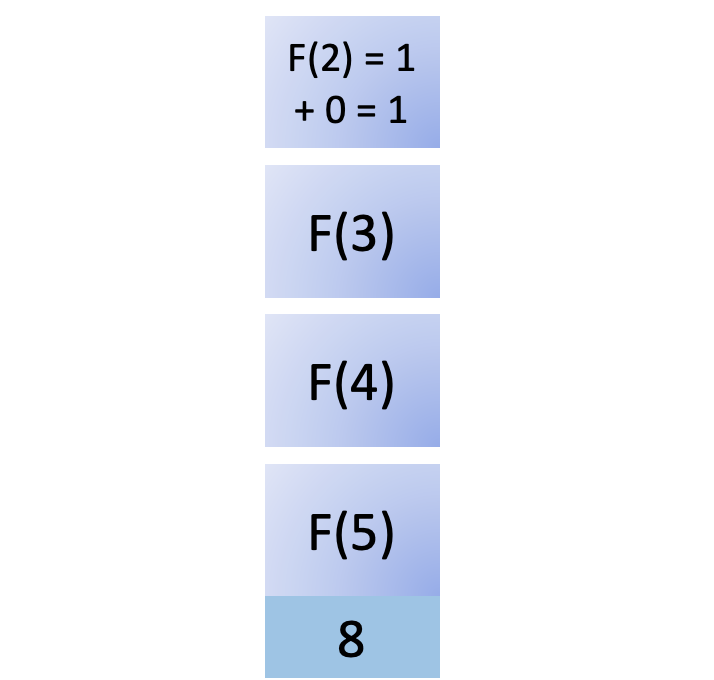
The result of F(2) is returned to its caller, F(3). F(3) also needs the results of F(1) to complete its calculation, so you add it back to the stack:
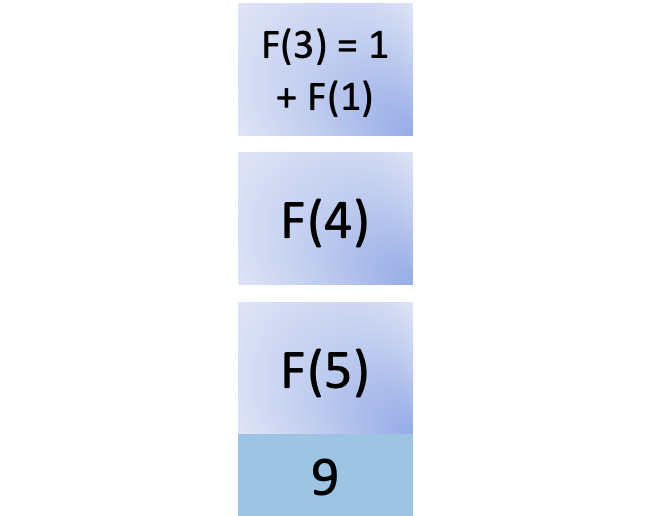
F(1) is a base case and its value is available in the cache, so you can return the result immediately and remove F(1) from the stack:
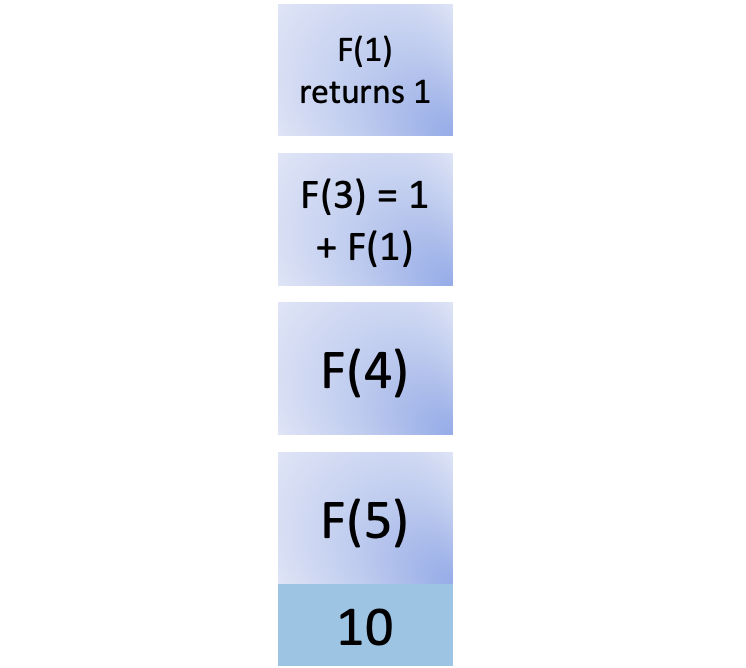
You can complete the calculation for F(3), which is 2:
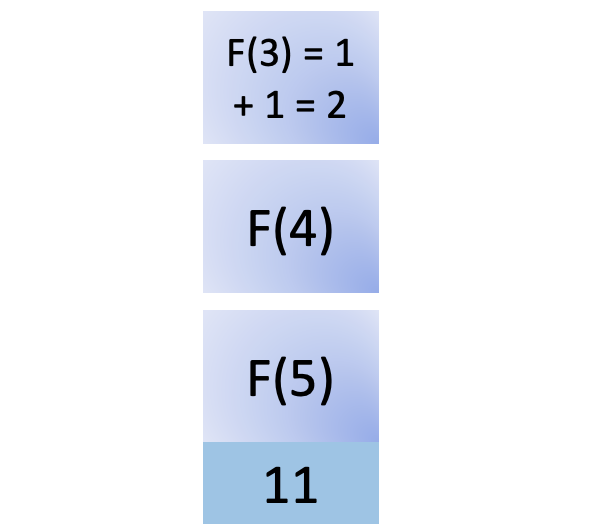
You remove F(3) from the stack after completing its calculation and return the result to its caller, F(4). F(4) also needs the result of F(2) to compute its value:

You push the call to F(2) onto the stack. This is where the nifty cache comes in. You have calculated it before, so you can just retrieve the value from the cache, avoiding a recursive call to compute the result of F(2) again. The cache returns 1, and you remove F(2) from the stack:
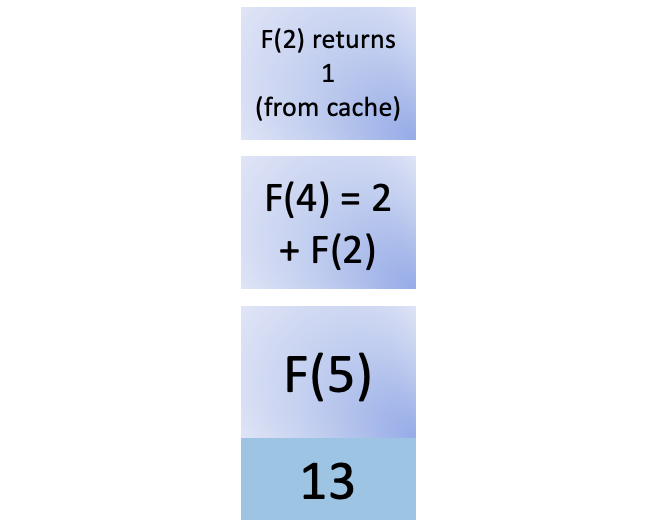
F(2) is returned to its caller, and now F(4) has all it needs to compute its value, which is 3:

Next, you remove F(4) from the stack and return its result to the final and original caller, F(5):

F(5) now has the result of F(4) and also the result of F(3). You push an F(3) call onto the stack, and the nifty cache comes into play again. You previously calculated F(3), so all you need to do is retrieve it from the cache. There’s no recursive process to compute F(3). It returns 2, and you remove F(3) from the stack:
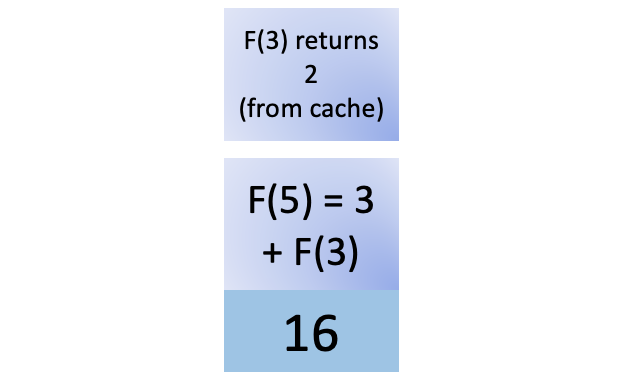
Now F(5) has all the values it needs to calculate its own value. You get 5 by adding 3 and 2, and that’s the final step before you pop the F(5) call off the stack. This action ends your sequence of recursive function calls:

The call stack is empty now. You’ve completed the final step to compute F(5):

Representing recursive function calls using a call stack diagram helps you understand all the work that takes place behind the scenes. It also allows you to see how many resources a recursive function can take up.
Putting all these diagrams together allows you to visualize how the whole process looks:
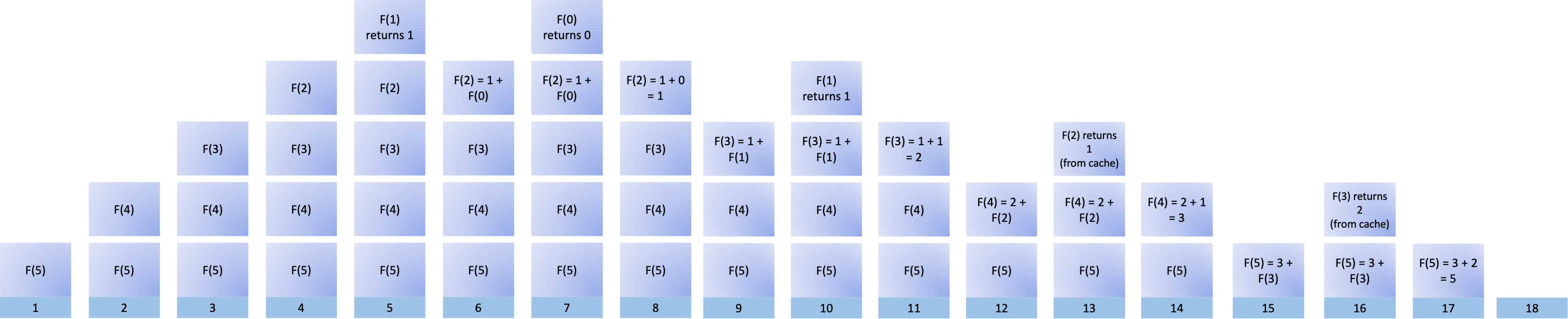
You can click the image above to zoom in on individual steps. If you don’t cache previously computed Fibonacci numbers, some of the stack stages in this diagram would be way taller, which means that they would take longer to return a result to their respective callers.
Using Iteration and a Python Function
The example in the previous sections implements a recursive solution that uses memoization as an optimization strategy. In this section, you’ll code a function that uses iteration. The code below implements an iterative version of your Fibonacci sequence algorithm:
1# fibonacci_func.py
2
3def fibonacci_of(n):
4 # Validate the value of n
5 if not (isinstance(n, int) and n >= 0):
6 raise ValueError(f'Positive integer number expected, got "{n}"')
7
8 # Handle the base cases
9 if n in {0, 1}:
10 return n
11
12 previous, fib_number = 0, 1
13 for _ in range(2, n + 1):
14 # Compute the next Fibonacci number, remember the previous one
15 previous, fib_number = fib_number, previous + fib_number
16
17 return fib_number
Now, instead of using recursion in fibonacci_of(), you’re using iteration. This implementation of the Fibonacci sequence algorithm runs in O(n) linear time. Here’s a breakdown of the code:
-
Line 3 defines
fibonacci_of(), which takes a positive integer,n, as an argument. -
Lines 5 and 6 perform the usual validation of
n. -
Lines 9 and 10 handle the base cases where
nis either 0 or 1. -
Line 12 defines two local variables,
previousandfib_number, and initializes them with the first two numbers in the Fibonacci sequence. -
Line 13 starts a
forloop that iterates from2ton + 1. The loop uses an underscore (_) for the loop variable because it’s a throwaway variable and you won’t be using this value in the code. -
Line 15 computes the next Fibonacci number in the sequence and remembers the previous one.
-
Line 17 returns the requested Fibonacci number.
To give this code a try, get back to your interactive session and run the following code:
>>>
>>> from fibonacci_func import fibonacci_of
>>> fibonacci_of(5)
5
>>> fibonacci_of(6)
8
>>> fibonacci_of(7)
13
>>> [fibonacci_of(n) for n in range(15)]
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377]
This implementation of fibonacci_of() is quite minimal. It uses iterable unpacking to compute the Fibonacci numbers during the loops, which is quite efficient memory-wise. However, every time you call the function with a different value of n, it has to recompute the sequence over again. To fix this, you can use closures and make your function remember the already computed values between calls. Go ahead and give it a try!
Conclusion
The Fibonacci sequence can help you improve your understanding of recursion. In this tutorial, you’ve learned what the Fibonacci sequence is. You’ve also learned about some common algorithms to generate the sequence and how to translate them into Python code.
The Fibonacci sequence can be an excellent springboard and entry point into the world of recursion, which is a fundamental skill to have as a programmer.
In this tutorial, you learned how to:
- Generate the Fibonacci sequence using a recursive algorithm
- Optimize your recursive Fibonacci algorithm using memoization
- Generate the Fibonacci sequence using an iterative algorithm
You’ve also visualized the memoized recursive algorithm to get a better understanding of how it works behind the scenes. To do that, you used a call stack diagram.
Once you master the concepts in this tutorial, your Python programming skills will improve along with your recursive algorithmic thinking.
Watch Now This tutorial has a related video course created by the Real Python team. Watch it together with the written tutorial to deepen your understanding: Exploring the Fibonacci Sequence With Python
В этой статье вы узнаете, как определить пользовательский тип последовательности в Python и как реализовать последовательность Фибоначчи с помощью кастомного типа Sequence.
Иногда полезно реализовать собственный тип последовательности, у которого есть функции, аналогичные встроенным функциям для кортежей или списков.
Как вы уже знаете, последовательность может быть изменяемой или неизменяемой. В этой статье мы сосредоточимся на создании пользовательского неизменяемого типа последовательности.
У неизменяемой последовательность должно быть две основные возможности:
- Возвращать количество элементов последовательности.
- Возвращать элемент по заданному индексу или вызывать ошибку IndexError, если индекс выходит за границы последовательности.
Если объект удовлетворяет вышеуказанным требованиям, получится производить следующие действия:
- Использовать синтаксис квадратных скобок [] для получения элемента по индексу.
- Перебирать элементы последовательности: например, с помощью цикла for.
Чтобы реализовать перечисленные выше возможности, нужно создать следующие методы:
__getitem__— возвращает элемент по заданному индексу.__len__— возвращает длину последовательности.
1) Метод __getitem__
У метода __getitem__ должен быть аргумент index, который является целым числом. Метод __getitem__ должен вернуть элемент из последовательности на основе указанного индекса.
Диапазон значений index: от нуля до length - 1. Если индекс выходит за границы, метод __getitem__ должен выдать исключение IndexError.
Метод __getitem__ может принимать объект среза для слайсинга.
2) The __len__ method
Если у пользовательской последовательности есть метод __len__, вы можете использовать встроенную функцию len(), чтобы получить количество элементов последовательности.
Последовательность Фибоначчи
Последовательность Фибоначчи примерно в 1170 году открыл Леонардо Фибоначчи, итальянский математик.
В последовательности Фибоначчи каждое число является суммой двух предшествующих ему чисел. Например:
1, 1, 2, 3, 5, 8 , 13, 21, …
Последовательность Фибоначии можно задать следующей формулой:
f(1) = 1
f(2) = 1
f(n) = f(n-1) + f(n-2) если n > 2
В некоторые источниках сказано, что последовательность Фибоначчи начинается с нуля, а не с 1, как сейчас. То есть вот так:
0, 1, 1, 2, 3, 5, 8 , 13, 21, ...
Но мы будем придерживаться исходной последовательности Фибоначчи, которая начинается с единицы.
Чтобы вычислить число Фибоначчи в Python, нужно создать такую рекурсивную функцию:
def fib(n):
if n < 2:
return 1
return fib(n-2) + fib(n-1) В этой рекурсивной функции fib(1) и fib(2) всегда возвращают 1. А когда n больше 2, fib(n) = fib(n-2) – fib(n-1).
Добавим print() в начало функции, чтобы посмотреть, как она работает, и вызовем функцию fib() с аргументом 6.
def fib(n):
print(f'Считаю {n} число Фибоначчи')
if n < 2:
return 1
return fib(n-2) + fib(n-1)
fin(6)Вывод
Считаю 6 число Фибоначчи
Считаю 4 число Фибоначчи
Считаю 2 число Фибоначчи
Считаю 0 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 3 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 2 число Фибоначчи
Считаю 0 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 5 число Фибоначчи
Считаю 3 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 2 число Фибоначчи
Считаю 0 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 4 число Фибоначчи
Считаю 2 число Фибоначчи
Считаю 0 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 3 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 2 число Фибоначчи
Считаю 0 число Фибоначчи
Считаю 1 число Фибоначчи
Как вы видите, функция fib() часто повторяется.
Например, ей приходится трижды вычислять 3 число Фибоначчи. Это неэффективно.
Чтобы решить эту проблему, в Python есть декоратор под названием lru_cache из модуля functools.
lru_cache позволяет кэшировать результат работы функции. Когда вы передаете тот же аргумент функции, функция просто получает результат из кэша вместо того, чтобы пересчитывать его.
Ниже показано, как использовать декоратор lru_cache для ускорения работы функции fib():
from functools import lru_cache
@lru_cache
def fib(n):
print(f'Считаю {n} число Фибоначчи')
if n < 2:
return 1
return fib(n-2) + fib(n-1)
fib(6)Вывод
Считаю 6 число Фибоначчи
Считаю 4 число Фибоначчи
Считаю 2 число Фибоначчи
Считаю 0 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 3 число Фибоначчи
Считаю 5 число Фибоначчи
Как вы видите, количество вычислений значительно уменьшилось.
Создаем последовательность Фибоначии
1. Сначала определим класс, реализующий последовательность Фибоначчи:
class Fibonacci:
def __init__(self, n):
self.n = nМетод __init__ принимает целое число n, которое задает длину последовательности.
2. Теперь определим статический метод, который вычисляет значение определенного числа Фибоначчи:
@staticmethod
@lru_cache(2**16)
def fib(n):
if n < 2:
return 1
return Fibonacci.fib(n-2) + Fibonacci.fib(n-1)3. Реализуем метод __len__, чтобы мы могли использовать встроенную функцию len() для получения количества элементов из последовательности Фибоначчи:
def __len__(self):
return self.n 4. Реализуем метод __getitem__ для поддержки индексации с помощью синтаксиса квадратных скобок []:
def __getitem__(self, index):
if isinstance(index, int):
if index < 0 or index > self.n - 1:
raise IndexError
return Fibonacci.fib(index)Метод __getitem__ принимает целое число index. Метод __getitem__ проверяет, является ли индекс целым числом, используя функцию isinstance().
Если index выходит за границы последовательности, __getitem__ вызовет исключение IndexError. В противном случае он вернет число Фибоначчи индекса.
Соединим все вместе:
from functools import lru_cache
class Fibonacci:
def __init__(self, n):
self.n = n
def __len__(self):
return self.n
def __getitem__(self, index):
if isinstance(index, int):
if index < 0 or index > self.n - 1:
raise IndexError
return Fibonacci.fib(index)
@staticmethod
@lru_cache(2**16)
def fib(n):
if n < 2:
return 1
return Fibonacci.fib(n-2) + Fibonacci.fib(n-1)Кастомная последовательность Фибоначчи в виде Python-класса готова. Однако вы не сможете просто сохранить этот код в модуле fibonacci.py и использовать его в другом скрипте.
Давайте разберемся, как использовать созданную последовательность.
Используем последовательность Фибоначии
Ниже показано, как использовать последовательность Фибоначчи из модуля fibonacci.py:
from fibonacci import Fibonacci
fibonacci = Fibonacci(10)
# используем []
print('Используем последовательность Фибоначчи с помощью []:')
print(fibonacci[0])
print(fibonacci[1])
print(fibonacci[2])
print('Используем последовательность Фибоначчи с помощью цикла for:')
# используем for
for f in fibonacci:
print(f)Вывод
Используем последовательность Фибоначии с помощью []:
1
1
2
Используем последовательность Фибоначчи с помощью цикла for:
1
1
2
3
5
8
13
21
34
55
Как это работает
- Создаем новый экземпляр последовательности Фибоначчи, в котором содержится 10 элементов.
- Получаем доступ к элементам последовательности Фибначчи с помощью квадратных скобок [].
- Используем последовательность Фибоначии в цикле for.
Добавляем поддержку срезов
Чтобы можно было делать срезы нашей последовательности, как показано ниже,
fibonacci[1:5]… нужно добавить соответсвующую логику, которая будет обрабатывать объект среза.
В fibonacci[1:5] аргументом index метода __getitem__ является объект среза, начало которого равно 1, а конец — 5.
Вы можете использовать метод indices() объекта среза, чтобы получить индексы элементов для возврата из последовательности:
indices = index.indices(self.n)self.n — это длина последовательности, которая будет «нарезана». В данном случае это количество элементов в последовательности Фибоначчи.
Чтобы вернуть список Фибоначчи из среза, вы можете передать индексы в функцию range() и сделать вот так:
[Fibonacci.fib(k) for k in range(*indices)]
Соберем все вместе:
from functools import lru_cache
class Fibonacci:
def __init__(self, n):
self.n = n
def __len__(self):
return self.n
def __getitem__(self, index):
if isinstance(index, int):
if index < 0 or index > self.n - 1:
raise IndexError
return Fibonacci.fib(index)
else:
indices = index.indices(self.n)
return [Fibonacci.fib(k) for k in range(*indices)]
@staticmethod
@lru_cache
def fib(n):
if n < 2:
return 1
return Fibonacci.fib(n-2) + Fibonacci.fib(n-1)Теперь можно сделать срез последовательности следующим образом:
from fibonacci import Fibonacci
fibonacci = Fibonacci(10)
print(fibonacci[1:5])Вывод
[1, 2, 3, 5]
Что нужно запомнить
- Для создания кастомной последовательно нужно реализовать методы
__len__и__getitem__. - Метод
__getitem__должен возвращать элемент по заданному индексу или вызывать ошибку IndexError, если индекс выходит за границы последовательности.
In this python tutorial, you will learn about the Python Fibonacci series, we will see the Python program to print Fibonacci series and also we will check:
- fibonacci series in python
- Python program to print fibonacci series using recursion
- fibonacci series in python using for loop
- Python program to print fibonacci series up to n terms
- Python program to print fibonacci series between 0 to 50
- Python program to print fibonacci series using iteration
- Python program to print fibonacci series without using recursion
- Python program to print fibonacci series until ‘n’ value using recursion
- print fibonacci series in python using while loop
- Python program to print fibonacci series using function
- Program to print first 50 fibonacci numbers in python
- Python program to print fibonacci series in python using a list
- fibonacci series in python using function
Now, we will see python program to print fibonacci series.
- In this example, I have used the function def fib(n)
- We have initialized the first term to 0 and the second term to 1.
- The for loop is used to iterate the values till the given number
- At last, it will print fibonacci series
Example:
def fib(n):
a = 0
b = 1
if n == 1:
print(a)
else:
print(a)
print(b)
for i in range(2,n):
c = a + b
a = b
b = c
print(c)
fib(10)To get the output, I have used print(c) to get the Fibonacci series. You can refer to the below screenshot for the output.

The above code, we can use to print fibonacci series in Python.
You may like, How to create a variable in python and Comment lines in Python.
Python program to print fibonacci series using recursion
Here, we will see python program to print fibonacci series using recursion.
- In this example, I have used the function def Fibonacci(number)
- Here, if (number == 0) check whether the given number is 0 or not. If it is true, the function returns the value zero.
- elif (number == 1) check whether the given number is 1 or not. If it is true, the function returns the value one.
- A recursive function Fibonacci() is used to calculate the n term sequence.
- A for loop is used to iterate and calculate each term recursively.
- We will take the input from the user
Example:
def Fibonacci(number):
if(number == 0):
return 0
elif(number == 1):
return 1
else:
return (Fibonacci(number - 2)+ Fibonacci(number - 1))
number = int(input("Enter the Range Number: "))
for n in range(0, number):
print(Fibonacci(n))To get the output, I have used print(Fibonacci(n)) to get the fibonacci series using recursion. You can refer to the below screenshot for the output.

The above code we can use to print fibonacci series using recursion in Python.
You may like, Python dictionary append with examples and Check if a list is empty in Python.
Fibonacci series in python using for loop
Let’s see python program to print fibonacci series using for loop
- Firstly, we will allow the user to enter any positive integer.
- We have initialized the First_val to 0 and the second_val to 1.
- Here, for loop is used to iterate the number from 0 to user-specified number.
- At last, print(next) is used to get the fibonacci series in Python
Example:
Below is an example of fibonacci series in python using for loop.
num = int(input("Enter the Range Number: "))
First_val = 0
Second_val = 1
for n in range(0, num):
if(n <= 1):
next = n
else:
next = First_val + Second_val
First_val = Second_val
Second_val = next
print(next)To get the output, I have used print(next) to get the fibonacci series using for loop. You can refer to the below screenshot for the output.

The above code, we can use to print fibonacci series using for loop in Python.
Also read, Python Program to Check Leap Year.
Python program to print fibonacci series up to n terms
Here, we will see python program to print fibonacci series up to n terms
- Firstly, we will allow the user to enter n terms
- We have initialized n1 to 0 and n2 to 1.
- If the number of terms is more than 2, we will use a while loop to find the next term in the sequence by adding the preceding two terms.
- After that, we interchange the variable and continue with the process.
Example:
n = int(input("Enter the n terms: "))
n1, n2 = 0, 1
count = 0
if n <= 0:
print("Please enter a positive integer")
elif n == 1:
print("Fibonacci sequence upto",n,":")
print(n1)
else:
print("Fibonacci sequence:")
while count < n:
print(n1)
r = n1 + n2
n1 = n2
n2 = r
count += 1To get the output, I have used print(Fibonacci sequence) to get the fibonacci series up to n terms. You can refer to the below screenshot for the output

This is the Python program to print fibonacci series up to n terms.
Also, read, How to convert list to string in Python and Python square a number.
Python program to print fibonacci series between 0 to 50
Now, we will see python program to print fibonacci series between 0 to 50
- We have initialized n1 to 0 and n2 to 1.
- Every next number is found by adding up the two numbers before it.
Example:
n1,n2 = 0,1
print(n1)
while n2<50:
print(n2)
n1,n2 = n2, n1+n2To get the output, I have used print to get the fibonacci series between 0 to 50. You can refer to the below screenshot for the output.

The above Python code, we can use to print fibonacci series between 0 to 50 in Python.
Python program to print fibonacci series using iteration
Now, we will see python program to print fibonacci series using iteration.
- In this example, I have used the function def fib(number).
- We have initialized first as 0 and second as 1.
- The while loop is used to find the next term in the sequence by adding the preceding two terms.
- And then update the value of the first and second.
Example:
def fib(number):
count = 0
first = 0
second = 1
temp = 0
while count <= number:
print(first)
temp = first + second
first = second
second = temp
count = count + 1
fib(6)To get the output, I have used print to get the fibonacci series using iteration. You can refer to the below screenshot for the output.

The above Python code, we can use to print fibonacci series using iteration in Python.
You may like to read, What is a Python Dictionary and Python print without newline.
Python program to print Fibonacci series without using recursion
Let’s see python program to print fibonacci series without using recursion.
- Firstly, the user will enter the first two numbers of the series and the number of terms to be printed from the user.
- Then print the first two numbers
- The while loop is used to find the sum of the first two numbers and then the fibonacci series
- Now, print the fibonacci series till n-2 is greater than 0.
Example:
n1=int(input("Enter the first number of the series: "))
n2=int(input("Enter the second number of the series: "))
n=int(input("Enter the number of terms needed: "))
print(n1,n2,end=" ")
while(n-2):
t=n1+n2
n1=n2
n2=t
print(n2,end=" ")
n=n-1To get the output, I have used print to get the fibonacci series without using recursion. You can refer to the below screenshot for the output.

The above Python code we can use to print fibonacci series without using recursion in Python.
You may like, Python zip() Function.
Python program to print fibonacci series until ‘n’ value using recursion
Let see python program to print fibonacci series until ‘n’ value using recursion.
- In this example, I have used the function def recursion_fib(num)
- Here, if num <= 1 then return num
- The other terms are obtained by adding the preceding two terms. The n term is the sum of (num-1) and (num-2) terms.
- A recursive function recursion_fib is used to calculate the n term sequence.
- A for loop is used to iterate and calculate each term recursively.
Example:
def recursion_fib(num):
if num <= 1:
return num
else:
return(recursion_fib(num-1) + recursion_fib(num-2))
n = 9
if n <= 0:
print("Plese enter a positive integer")
else:
print("Fibonacci sequence:")
for i in range(n):
print(recursion_fib(i))To get the output, I have used print(recursion_fib(i)) to get the fibonacci series until ‘n’ value using recursion. You can refer to the below screenshot for the output.

The above code we can use to print fibonacci series until ‘n’ value using recursion in Python.
print fibonacci series in python using while loop
Now, we will see python program to print fibonacci series using while loop.
- Firstly, the user will enter any positive integer.
- We have initialized F_val as 0 and S_val as 1.
- We have declared three integer variables like i, F_val, and S_val.
- The while loop makes sure that the loop starts from 0 and is less than the user given number.
- Within the while loop, we have used if and else.
- And at last fibonacci series will get printed in the output.
Example:
Num = int(input("Enter the Range Number: "))
i = 0
F_val = 0
S_val = 1
while(i < Num):
if(i <= 1):
Next = i
else:
Next = F_val + S_val
F_val = S_val
S_val = Next
print(Next)
i = i + 1To get the output, I have used print(Next) to get the fibonacci series using a while loop. You can refer to the below screenshot for the output.

The above code, we can use to print fibonacci series using while loop in Python.
Also read, Python For Loop with Examples and Python While Loop Example.
fibonacci series in python using function
Here, we will see python program to print fibonacci series using function
- In this example, we have used the function as def fib(n)
- We have initialized the n1 to 0 and n2 to 1.
- if n == 1 then print(n1)
- The for loop is used to iterate the values till the given number
- At last, it will print fibonacci series
Example:
def fib_series(n):
n1 = 0
n2 = 1
if n == 1:
print(n1)
else:
print(n1)
print(n2)
for i in range(2,n):
t = n1 + n2
n1 = n2
n2 = t
print(t)
fib_series(5)To get the output, I have used print(t) to get the fibonacci series using function. You can refer to the below screenshot for the output.

Program to print first 50 fibonacci numbers in python
Is anyone asking you to write a python program to get the fibonacci series between 0 to 50? Let’s see the program to print the first 50 fibonacci numbers in python.
- In this example, I have used the function def FibonacciNum(n)
- We have initialized the n1 to 0 and n2 to 1.
- Here, if n < 1 then return
- The for loop is used to iterate the values till the given number.
- At last, call the function FibonacciNum(50) to get the first 50 fibonacci numbers in the output.
Example:
def FibonacciNum(n):
n1 = 0
n2 = 1
if (n < 1):
return
print(n1, end=" ")
for i in range(1, n):
print(n2, end=" ")
next = n1 + n2
n1 = n2
n2 = next
FibonacciNum(50)You can refer to the below screenshot for the output of first 50 fibonacci numbers in python.

Python program to print fibonacci series in python using a list
Now, we will see python program to print fibonacci series in python using a list
- Firstly, the user will enter any positive integer.
- The for loop is used to iterate the values till the given number
- At last, print(fib) to get the fibonacci series in the list.
Example:
n = int(input("Enter the number:"))
if n==0:
fib=[0]
elif n==1:
fib=[0,1]
else:
fib=[0,1]
for i in range(2,n):
fib.append(fib[i-1]+fib[i-2])
print(fib)To get the output, I have used print(fib) to get the fibonacci series using function. You can refer to the below screenshot for the output.

The above code we can use to to print fibonacci series using function in Python.
You may like the following tutorials:
- How to subtract two numbers in Python
- How to divide two numbers in Python
- How to add two variables in Python
In this Python tutorial, we have learned about the Python program to print Fibonacci series or Fibonacci Series in Python. Also, we covered these below topics:
- Python program to print fibonacci series
- Fibonacci series in python using recursion
- Python program to print fibonacci series using for loop
- Python program to print fibonacci series up to n terms
- Python program to print fibonacci series between 0 to 50
- Python program to print fibonacci series using iteration
- Fibonacci series in python without recursion
- Python program to print fibonacci series until ‘n’ value using recursion
- Python program to print fibonacci series using while loop
- Python program to print fibonacci series using function
- Program to print first 50 fibonacci numbers in python
- Python program to print fibonacci series in python using a list

Python is one of the most popular languages in the United States of America. I have been working with Python for a long time and I have expertise in working with various libraries on Tkinter, Pandas, NumPy, Turtle, Django, Matplotlib, Tensorflow, Scipy, Scikit-Learn, etc… I have experience in working with various clients in countries like United States, Canada, United Kingdom, Australia, New Zealand, etc. Check out my profile.
Числа Фибоначчи: циклом и рекурсией
Числа Фибоначчи – это ряд чисел, в котором каждое следующее число равно сумме двух предыдущих.
1, 1, 2, 3, 5, 8, 13, …
Иногда ряд начинают с нуля.
0, 1, 1, 2, 3, 5, 8, …
В данном случае мы будем придерживаться первого варианта.
Вычисление n-го числа ряда Фибоначчи с помощью цикла while
Присвоим переменным fib1 и fib2 значения двух первых элементов ряда, то есть единицы.
Получим от пользователя номер элемента, значение которого требуется вычислить. Присвоим номер элемента переменной n.
Поскольку значения первых двух элементов ряда Фибоначчи нам уже известны и вычисления начинаем с третьего, количество проходов по телу цикла должно быть на 2 меньше значения n, то есть n - 2.
Если пользователь вводит 1 или 2, тело цикла ни разу не выполняется, на экран выводится исходное значение fib2.
В теле цикла выполнять следующие действия:
- Сложить fib1 и fib2, присвоив результат переменной для временного хранения данных, например, fib_sum.
- Переменной fib1 присвоить значение fib2.
- Переменной fib2 присвоить значение fib_sum.
После окончания работы цикла вывести значение fib2 на экран.
fib1 = 1 fib2 = 1 n = input("Номер элемента ряда Фибоначчи: ") n = int(n) i = 0 while i < n - 2: fib_sum = fib1 + fib2 fib1 = fib2 fib2 = fib_sum i = i + 1 print("Значение этого элемента:", fib2)
Пример выполнения программы:
Номер элемента ряда Фибоначчи: 10 Значение этого элемента: 55
Компактный вариант кода:
fib1 = fib2 = 1 n = input("Номер элемента ряда Фибоначчи: ") n = int(n) - 2 while n > 0: fib1, fib2 = fib2, fib1 + fib2 n -= 1 print("Значение этого элемента:", fib2)
Вывод ряда чисел Фибоначчи с помощью цикла for
В данном случае выводится не только значение искомого элемента ряда Фибоначчи, но и все числа до него включительно. Для этого вывод значения fib2 помещен в цикл.
fib1 = fib2 = 1 n = int(input()) print(fib1, fib2, end=' ') for i in range(2, n): fib1, fib2 = fib2, fib1 + fib2 print(fib2, end=' ')
Пример выполнения:
10 1 1 2 3 5 8 13 21 34 55
Рекурсивное вычисление n-го числа ряда Фибоначчи
- Если n = 1 или n = 2, вернуть в вызывающую ветку единицу, так как первый и второй элементы ряда Фибоначчи равны единице.
- Во всех остальных случаях вызвать эту же функцию с аргументами n – 1 и n – 2. Результат двух вызовов сложить и вернуть в вызывающую ветку программы.
def fibonacci(n): if n in (1, 2): return 1 return fibonacci(n - 1) + fibonacci(n - 2) print(fibonacci(10))
Допустим, n = 4. Тогда произойдет рекурсивный вызов fibonacci(3) и fibonacci(2). Второй вернет единицу, а первый приведет к еще двум вызовам функции: fibonacci(2) и fibonacci(1). Оба вызова вернут единицу, в сумме будет два. Таким образом, вызов fibonacci(3) возвращает число 2, которое суммируется с числом 1 от вызова fibonacci(2). Результат 3 возвращается в основную ветку программы. Четвертый элемент ряда Фибоначчи равен трем: 1 1 2 3.
Больше задач в PDF
