Как найти число фотонов падающих на поверхность

Формула
Эйнштейна h
= A
+ (m²_max)/2,

где

= h
– энергия фотона, падающего на поверхность
металла; А
– работа выхода электрона из металла;
(m²_max
)/2 – максимальная кинетическая энергия
фотоэлектрона.

Красная
граница фотоэффекта _о
= А
/ h
или _о
= сh
/ A
,

где
_о
– минимальная частота (_о
–
максимальная длина волны), при которой
еще возможен фотоэффект.

Условие
наблюдения фотоэффекта h

A
.

Примеры решения задач

Задача
18. Фотон с
энергией 10 эВ падает на серебряную
пластину и вызывает фотоэффект. Определить
импульс, полученный пластиной, если
принять, что направления движения фотона
и фотоэлектрона лежат на одной прямой,
перпендикулярной поверхности пластин.

электрона,

– импульс, полученный пластиной.

Импульс
электрона найдем из уравнения Эйнштейна

h
= A_в
+ ( m²_max
)/2 ,

откуда

.

Импульс,
полученный пластинкой

Задача
19. Электроны,
вылетевшие из некоторого металла при
облучении его светом с длиной волны
600 нм, задерживаются напряжением U
= 0,69 В.
При уменьшении длины волны падающего
света в два раза, скорость фотоэлектронов
увеличивается в два раза. Определить
из этих данных постоянную Планка.

Скорость

электрона определим из условия, что при
облучении металла светом с длиной волны
,
фотоэлектроны задерживаются напряжением
U,
то есть

(m
²)
/2 = e
U,
откуда ²
= (2еU)/m
.

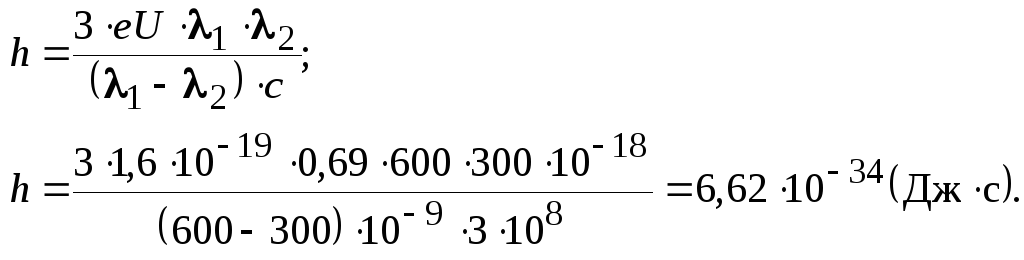
6. Давление света Основные формулы:

Давление,
производимое светом при нормальном
падении

где
J
– интенсивность света (энергия,
переносимая волной через единичную
поперечную площадку в единицу времени);

– коэффициент отражения; с
– скорость света в вакууме.

Для
абсолютно черной поверхности 
= 0.

Для
абсолютно белой поверхности 
= 1.

где
N
– число фотонов, падающих на поверхность
площадью S
за единицу времени; 
– частота света.

Примеры решения задач

Задача
20. Спутник
в форме шара движется вокруг Земли на
такой высоте, что поглощением солнечного
света в атмосфере можно пренебречь.
Диаметр спутника 10 м. Считая, что
поверхность спутника полностью отражает
свет, определить силу давления солнечного
света на спутник.

где
P
– давление солнечного света на поверхность
спутника, S
– площадь поверхности спутника, причем
мы учли, что спутник повернут к солнцу
только половиной поверхности.

Так
как поверхность спутника полностью
отражает свет, то 
= 1 и давление света P
= (J/c)
^.2,

откуда
сила давления F=
(J
^. S)/c
.

Для
расчета интенсивности солнечного света
J
воспользуемся результатом решения
задачи № 15 из раздела «Тепловое
излучение»: J = E_э = 1380
Вт/м².

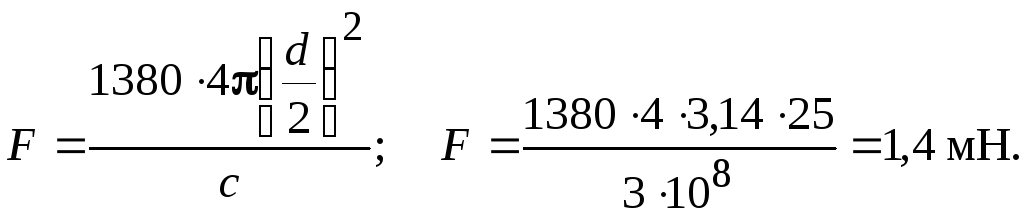
Ответ:
F
= .

Задача
21. Параллельный
пучок монохроматического света с длиной
волны =0,663
мкм падает на зачерненную поверхность
и производит на нее давление P = 0,3 мкПа.
Определить концентрацию фотонов в
световом пучке.

где
N
– общее число фотонов в пучке, t
– время, S
– площадь поверхности.

Если
принять, что свет распространяется в
виде цилиндрического пучка, то c·t·S
– объем светового пучка, а N/V
– концентрация фотонов, тогда

Ответ:
n=10¹².

Список
литературы

1. Савельев
   И.В. Курс
   общей физики. Кн.4. – М.: Наука, 1999.

2. Трофимова
   Т.И. Курс
   физики. – М.: Высшая школа, 1998.

3. Детлаф
   А.А., Яворский
   Б.М. Курс
   физики. – М.: Высшая школа, 1998.

4. Волькенштейн
   В.С. Сборник
   задач по общему курсу физики. – СПб.:
   СпецЛит, 2001.

5. Чертов
   А.Г.,
   Воробьев
   А.А. Задачник
   по физике. – М.: Интеграл–пресс,1997.

3

Соседние файлы в папке FIZIKA

• #
• #
• #
• #
• #
• #
• #

Давление света можно объяснить с помощью электромагнитной теории Максвелла. Свет — это электромагнитная волна. Электрическое поле разгоняет электроны вещества. Из-за присутствия магнитного поля на движущиеся электроны действует сила Лоренца, которая направлена внутрь вещества.
В (1873) году с помощью своей теории Максвелл доказал, что давление света вычисляется по формуле:
(P=frac{2W}{c}).  ((1))
Давление света можно объяснить и с точки зрения квантовой теории, то есть рассматривая свет как поток частиц с энергией (E=hnu) и импульсом (p=hnu/c). Если энергетическая освещённость поверхности (W), то можно определить число фотонов, падающих на поверхность площадью (S) за время (Delta t):
(boxed{n=frac{W}{SDelta t hnu}}).  ((2))
Коэффициент отражения (R) показывает отношение количества отражённых фотонов к количеству падающих, поэтому в среднем фотон передаёт импульс:
(Delta p=p-R(-p)=(1+R)p=(1+R)frac{h}{c}.)  ((3))
Используя закон изменения импульса, можно записать, что:
(F=n frac{Delta p}{Delta t}).  ((4))
Если поверхность чёрная ((R=0)), то давление света выразится как:
(boxed{P_{черн}=frac{W}{SDelta t hnu} cdot frac{h}{c Delta t}=frac{W}{c}}).  ((5))
Зеркало можно представить как поверхность с коэффициентом отражения (R=1). В этом случае давление света определяется как:
(boxed{P_{зерк}=frac{W}{SDelta t hnu} cdot frac{2 h}{c Delta t}=frac{W}{c} =frac{2W}{c}}).  ((6))
Формула для подсчёта давления света в теории Максвелла ((1)) является частным случаем формулы ((6)) корпускулярной (квантовой) теории. Результаты, предсказанные формулами ((5)) и ((6)), с высокой точностью (погрешность (2) (%)) подтверждаются экспериментальными данными.

В этой статье будем определять концентрацию фотонов в световом луче, и количество фотонов, падающих за определенное время на поверхность известной площади.

Задача 1.

Рубиновый лазер дает импульс монохроматического излучения с длиной волны А. Определить концентрацию фотонов в пучке, если мощность излучения лазера МВт, а площадь сечения луча м.

Концентрация – это количество фотонов в объеме. Объем найдем как . Количество фотонов определим как

Определим теперь концентрацию:

Ответ: 1/м.

Задача 2.  Сколько квантов излучения падает за время с на поверхность площадью см, если ее облучают потоком гамма-лучей с длиной волны см, мощность которого на площадь см составляет Вт?

Число фотонов можно найти как:

Число фотонов, падающих на единицу поверхности:

Мощность на площадь можно выразить как , тогда

Ответ:

Задача 3.

Сколько гамма-квантов падает ежесекундно на поверхность, которую облучают гамма-лучами мощностью Вт и длиной волны  м?

Число фотонов, падающих на единицу поверхности:

Число фотонов можно найти как:

А за время :

Ответ: 1/см с

Задача 4.

Точечный источник света мощностью испускает свет с длиной волны . Сколько фотонов падает за время на маленькую площадку площадью , расположенную перпендикулярно к падающим лучам, на расстоянии от источника?

Число фотонов, падающих на единицу поверхности:

Но источник излучает во все стороны, то есть лучи образуют сферу, а площадь площадки относится к площади сферы как , тогда количество квантов, попавших «в  нужное место» равно

Ответ:

Задача 5.

Мощность точечного источника монохроматического излучения с длиной волны мкм Вт. Определить число фотонов, падающих за 1 с на см площади, расположенной перпендикулярно лучам на расстоянии м.

По аналогии с предыдущей задачей

Ответ: .

Глава7. Квантово-оптические явления. Физика атома (§ 34-39) >> §36 Давление света. Фотоны >> задача – 36.10

0 Пользователей и 1 Гость просматривают эту тему.