Содержание
Характеристический полином, собственные числа, собственные векторы матрицы
§
В настоящем разделе $ n_{} $ означает порядок квадратной матрицы $ A_{} $.
Характеристический полином
определяется для произвольной квадратной матрицы $ A_{} $ как1)
$ det (A_{}-lambda E) $, где $ E_{} $ – единичная матрица одинакового с $ A_{} $ порядка.
П
Пример. Для $ n=2_{} $:
$$ det (A-lambda E)=
begin{vmatrix}
a_{11}-lambda & a_{12}\
a_{21}& a_{22}-lambda
end{vmatrix}=
$$
$$
=lambda^2-(a_{11}+a_{22})lambda + (a_{11}a_{22}-a_{12}a_{21}) ;
$$
для $ n=3_{} $:
$$
det (A-lambda E)=
begin{vmatrix}
a_{11}-lambda & a_{12} & a_{13}\
a_{21}& a_{22}-lambda & a_{23} \
a_{31}& a_{32} & a_{33}-lambda
end{vmatrix}=
$$
$$
=-lambda^3+(a_{11}+a_{22}+a_{33})lambda^2 –
$$
$$
-left {
begin{vmatrix}
a_{11}& a_{12}\
a_{21}& a_{22}
end{vmatrix}
+begin{vmatrix}
a_{22}& a_{23}\
a_{32}& a_{33}
end{vmatrix}+
begin{vmatrix}
a_{11}& a_{13}\
a_{31}& a_{33}
end{vmatrix}
right }lambda+
det A .
$$
Т
Теорема 1.
$$ det (A-lambda E)=
(-1)^nBigg(
lambda^n – lambda^{n-1}sum_{1le jle n} a_{jj}
+ lambda^{n-2}sum_{1le j_1< j_2 le n} left|begin{array}{ll}
a_{j_1j_1}& a_{j_1j_2}\
a_{j_2j_1}& a_{j_2j_2}
end{array}right| – dots +
$$
$$
+(-1)^k lambda^{n-k}
sum_{1le j_1< j_2 < dots < j_kle n} left|begin{array}{llll}
a_{j_1j_1}& a_{j_1j_2} & dots & a_{j_1j_k}\
a_{j_2j_1}& a_{j_2j_2} & dots & a_{j_2j_k}\
vdots & & & vdots \
a_{j_kj_1}& a_{j_kj_2} & dots & a_{j_kj_k}
end{array}right|+ dots + (-1)^n det A
Bigg) .
$$
Образно говоря, коэффициент при $ (-1)^{k}lambda^{n-k} $ получается
суммированием всех миноров $ k_{} $-го порядка матрицы $ A_{} $, построенных на
элементах, стоящих в строках и столбцах с одинаковыми номерами..
Такой минор матрицы
$$
left|begin{array}{cccc}
a_{j_1j_1} & a_{j_1j_2} & dots & a_{j_1j_k} \
a_{j_2j_1} & a_{j_2j_2} & dots & a_{j_2j_k} \
vdots & & ddots & vdots \
a_{j_kj_1} & a_{j_kj_2} & dots & a_{j_kj_k}
end{array}
right|
, quad 1le j_1<j_2< dots < j_k le n
$$
в настоящем ресурсе называется ведущим минором ($k$-го порядка). См. замечание о терминологии
☞
ЗДЕСЬ.
Результат теоремы имеет исключительно теоретическое значение: практическое вычисление характеристического полинома матрицы большого порядка по этой теореме обычно крайне неэффективно. Методы практического вычисления характеристического полинома разбираются
☟
НИЖЕ.
П
Пример. Характеристический полином матрицы Фробениуса
$$
mathfrak F=
left( begin{array}{lllllll}
0 & 1 & 0 & 0 & dots & 0 & 0 \
0 & 0 & 1 & 0 & dots & 0 & 0 \
0 & 0 & 0 & 1 & dots & 0 & 0 \
vdots& &&&ddots & & vdots \
0 & 0 & 0 & 0 & dots & 0 & 1 \
a_n & a_{n-1} & a_{n-2} & & dots & a_2 & a_1
end{array} right)_{n times n}
$$
равен $ (-1)^n(lambda^n-a_1lambda^{n-1}-dots-a_{n}) $.
Характеристический полином линейного оператора
определяется как характеристический полином матрицы этого оператора в произвольном базисе линейного пространства, в котором этот оператор задан. Подробнее
☞
ЗДЕСЬ.
Характеристический полином линейного однородного разностного уравнения
$ n_{} $-го порядка
$$
x_{n+K}=a_1 x_{n+K-1}+ dots+ a_n x_K, quad a_n ne 0,
$$
определяется как
$$ lambda^n – a_1 lambda^{n-1} – dots – a_n . $$
Подробнее
☞
ЗДЕСЬ.
Свойства
Т
Теорема 2. Характеристический полином матрицы не меняется
1.
при ее транспонировании:
$$ det (A-lambda E) = det (A^{top}-lambda E_{}) , ;$$
2.
при переходе к подобной матрице: если $ B=C^{-1}AC^{} $ при произвольной неособенной матрице $ C_{} $, то
$$ det (A-lambda E) equiv det (B-lambda E_{}) , . $$
Т
Теорема 3. Пусть матрица $ A_{} $ имеет порядок $ mtimes n_{} $, а $ B_{} $ — порядок $ ntimes m_{} $. Тогда эти матрицы допускают умножение в любом порядке, т.е. определены $ AB_{} $ и $ BA_{} $ и оба произведения будут квадратными матрицами — порядков $ m_{} $ и $ n_{} $ соответственно. Тогда характеристические полиномы этих произведений различаются лишь на степень $ lambda_{} $:
$$
lambda^n det (AB – lambda E_{m times m})equiv lambda^m det (BA – lambda E_{n times n}) .
$$
=>
Если матрицы $ A_{} $ и $ B_{} $ — квадратные одинакового порядка, то характеристические полиномы матриц $ AB_{} $ и $ BA_{} $ тождественны.
Т
Теорема 4. Если характеристический полином матрицы $ A_{} $ равен
$$ f(lambda)=(-1)^n lambda^n+a_1lambda^{n-1}+dots+a_{n-1}lambda+a_n $$
и $ a_{n} ne 0 $, то характеристический полином матрицы $ A^{-1}_{} $ равен
$$ f^{ast}(lambda)=frac{(-lambda)^n}{a_n} f(1/lambda) = frac{(-1)^n}{a_n} left[ (-1)^n+a_1 lambda + dots+
a_{n-1}lambda^{n-1}+a_nlambda^{n} right] . $$
Теорема Гамильтона-Кэли
Т
Теорема 5. Результатом подстановки в характеристический полином $ det (A_{}-lambda E) $ самой матрицы $ A_{} $ будет нулевая матрица:
$$
det (A-lambda E)= (-1)^n lambda^n +a_1 lambda^{n-1}+dots+a_{n-1}lambda+ a_n Rightarrow
$$
$$
Rightarrow
(-1)^n A^n +a_1 A^{n-1}+dots+a_{n-1}A+ a_n E = {mathbb O}_{ntimes n} .
$$
В литературе эта теорема обычно приводится в иной формулировке:
матрица является корнем своего характеристического полинома.
Доказательство
☞
ЗДЕСЬ.
П
Пример. Для $ n_{}=2 $:
$$
left(begin{array}{ll} a_{11} & a_{12} \ a_{21} & a_{22}
end{array} right)^2 – (a_{11}+a_{22})left(begin{array}{ll} a_{11} & a_{12} \ a_{21} & a_{22}
end{array} right) +
(a_{11}a_{22}-a_{12}a_{21})
left(begin{array}{ll} 1 & 0 \ 0 & 1
end{array} right) = left(begin{array}{ll} 0 & 0 \ 0 & 0
end{array} right) .
$$
Собственное число
Собственное (или характеристическое) число2) определяется для квадратной матрицы $ A_{} $ как произвольный корень ее характеристического полинома $ det (A_{}-lambda E) $. Уравнение
$$
det(A-lambda E)=0
$$
называется характеристическим уравнением матрицы $ A $.
И
Понятие характеристического уравнения было введено Коши в 1840 г. В литературе XIX века известно также как вековое уравнение.
Набор всех собственных чисел матрицы $ A_{} $ (с учетом их кратностей) называется спектром матрицы3) (таким образом спектр матрицы $ A_{} $ порядка $ n_{} $ всегда состоит из $ n_{} $ чисел, часть из которых могут быть одинаковыми). Максимальный из модулей собственных чисел матрицы $ A_{} $ называется ее спектральным радиусом4), он иногда обозначается $ rho(A) $.
П
Пример. Найти спектр матрицы
$$
A=
left(begin{array}{rrrr}
0&1&2&3\
-1&0&4&7\
-2&-4&0&2\
-3&-7&-2&0
end{array}right).
$$
Решение. Характеристический полином
$$ det (A-lambda E)=left|begin{array}{rrrr}
-lambda&1&2&3\
-1&-lambda&4&7\
-2&-4&-lambda&2\
-3&-7&-2&-lambda
end{array}right|=lambda^4+
83lambda^2
$$
имеет корни $ lambda_1=0, lambda_2 = {mathbf i}sqrt{83}, lambda_3 = – {mathbf i} sqrt{83} $, причем $ lambda_{1} $ — второй кратности.
Ответ. Спектр матрицы $ A_{} $:
$ {0,0, {mathbf i} sqrt{83},- {mathbf i} sqrt {83} } $. Спектральный радиус матрицы $ A_{} $: $ rho(A)= sqrt {83} $.
Т
Теорема 6. Если $ {lambda_{1},lambda_{2},dots,lambda_{n} } $ — спектр матрицы $ A_{} $, то
$$ lambda_1+lambda_{2}+dots+lambda_n = operatorname{Sp}(A)=a_{11}+a_{22}+dots+a_{nn}, $$
$$ lambda_1cdotlambda_{2}times dots times lambda_n = (-1)^ndet (A) . $$
Доказательство следует из представления характеристического полинома через миноры матрицы и формул Виета.
♦
Можно, разумеется, привести еще $ n-2 $ зависимостей между собственными числами матрицы и ее минорами, но они редко нужны — а вот равенства из теоремы полезно запомнить.
=>
Для того, чтобы матрица $ A_{} $ была неособенной необходимо и достаточно, чтобы среди ее собственных чисел не было нулевого.
Т
Теорема 7. Пусть $ g(x)=b_{0}x^m+dots+b_m in {mathbb C}[x] $ — произвольный полином. Вычислим полином от матрицы $ A_{} $:
$$ g(A)=b_{0}A^m+dots+b_m E , . $$
Тогда если $ {lambda_{1},dots,lambda_{n} } $ — спектр матрицы $ A_{} $, то $ {g(lambda_{1}),dots,g(lambda_n) } $ — спектр матрицы $ g(A_{}) $.
=>
Результат теоремы обобщается и на более широкий класс функций $ g_{}(x) $ — фактически на любую функцию, которая, вместе со своими производными, может быть определена на спектре матрицы $ A_{} $. В частности, если $ det A_{} ne 0 $, то спектр матрицы $ A^{-1}_{} $ совпадает с $ {1/lambda_j}_{j=1}^n $.
=>
Имеет место следующее равенство, связывающее степени матрицы $ A_{} $ с суммами Ньютона ее характеристического полинома:
$$ operatorname{Sp}(A^k)=lambda_1^k+dots+lambda_n^k . $$
Здесь $ operatorname{Sp}_{} $ обозначает след матрицы (т.е. сумму ее диагональных элементов). Утверждение остается справедливым и для отрицательных показателей $ k_{} $ при условии, что $ det A_{} ne 0 $.
=>
Имеет место следующее равенство:
$$ det g(A) = (-1)^{mn} {mathcal R}(f,g_{}) , $$
где $ {mathcal R}(f,g_{}) $ означает результант полиномов $ f(x) =det (A-x_{} E) $ и $ g_{}(x) $.
Т
Теорема 8. Собственные числа вещественной симметричной матрицы $ A_{} $ все вещественны.
Доказательство
☞
ЗДЕСЬ.
Т
Теорема 9. Собственные числа вещественной кососимметричной матрицы $ A_{} $ все мнимы, за исключением, возможно, $ lambda_{} = 0 $.
Доказательство
☞
ЗДЕСЬ.
Т
Теорема 10. Собственные числа вещественной ортогональной матрицы все равны $ 1_{} $ по абсолютной величине (модулю). Характеристический полином ортогональной матрицы является возвратным если $ +1 $ не является его корнем или является корнем четной кратности. Хотя бы одно собственное число ортогональной матрицы нечетного порядка равно $ +1 $ или $ (-1) $.
Доказательство
☞
ЗДЕСЬ.
Т
Теорема 11. Спектр циклической матрицы
$$
left(begin{array}{lllll}
a_1 & a_2 & a_3 & dots & a_n \
a_n & a_1 & a_2 & dots & a_{n-1} \
a_{n-1} & a_n & a_1 & dots & a_{n-2} \
vdots & & & & vdots \
a_2 & a_3 & a_4 & dots & a_1
end{array}
right) .
$$
совпадает с набором чисел
$$ {f(1),f(varepsilon_1), dots, f(varepsilon_{n-1}) } ,$$
при
$$ f(x)=a_{1}+a_2x+a_3x^2+dots+a_nx^{n-1} $$
и
$$
varepsilon_k=cos frac{2,pi k}{n} + {mathbf i} sin frac{2,pi k}{n}
$$
— корне n-й степени из единицы.
Доказательство
☞
ЗДЕСЬ.
Локализация собственных чисел
Т
Теорема 12. [1]. Собственные числа матрицы являются непрерывными функциями ее элементов. Иначе: пусть
$$A=left[a_{jk} right]_{j,k=1}^n quad , quad B=left[b_{jk} right]_{j,k=1}^n
.
$$
Обозначим
$$M= max_{j,kin{1,dots,n}} left{|a_{jk} |, |b_{jk} | right} quad ,
quad delta = frac{1}{nM}sum_{j,k=1}^n |a_{jk} – b_{jk} | . $$
Тогда любому собственному числу $ lambda_{ast}^{} $ матрицы $ A_{} $ можно поставить
в соответствие такое собственное число $ mu_{ast}^{} $ матрицы $ B_{} $, что
$$ |lambda_{ast}-mu_{ast} | le (n+2) M sqrt[n]{delta} . $$
Собственно факт непрерывной зависимости собственных чисел от элементов матрицы следует из представления характеристического полинома из теоремы
☞
ПУНКТА — коэффициенты этого полинома полиномиально (и, следовательно, непрерывно) зависят от элементов матрицы.
Далее используем теорему о непрерывной зависимости корней полинома от его коэффициентов.
Выясним теперь на примере, насколько малым может быть возмущение элементов матрицы чтобы сохранились хотя бы количество вещественных корней ее характеристического полинома.
П
Пример [Уилкинсон] [2]. Найти собственные числа матрицы
$$
A=
left(
begin{array}{cccccc}
20 & 20 & & & & \
& 19 & 20 & & & \
& & 18 & 20 & & \
& & & ddots & ddots & \
& & & & 2 & 20 \
{color{Red} varepsilon } & & & & & 1 \
end{array}
right)_{20times 20}
$$
при $ {color{Red} varepsilon }=10^{-10} $
(все неуказанные элементы матрицы считаются равными нулю).
Решение. Характеристический полином
$$
det(A-lambda E) = prod_{j=1}^{20} (j-lambda) – 20^{19} {color{Red} varepsilon } =
$$
$$
=lambda^{20}-{scriptstyle 210},lambda^{19}+{scriptstyle 20615},lambda^{18}-{scriptstyle 1256850}, lambda^{17}
+{scriptstyle 53327946}, lambda^{16}-{scriptstyle 1672280820}, lambda^{15}+
{scriptstyle 40171771630}, lambda^{14}-{scriptstyle 756111184500}, lambda^{13}+
$$
$$
+{scriptstyle 11310276995381}, lambda^{12} –
{scriptstyle 135585182899530}, lambda^{11}
+{scriptstyle 1307535010540395}, lambda^{10}-{scriptstyle 10142299865511450}, lambda^9 +
$$
$$
+{scriptstyle 63030812099294896}, lambda^8 –
{scriptstyle 311333643161390640}, lambda^7+{scriptstyle 1206647803780373360}, lambda^6 -{scriptstyle 3599979517947607200}, lambda^5
+{scriptstyle 8037811822645051776}, lambda^4-
$$
$$
-{scriptstyle 12870931245150988800}, lambda^3
+{scriptstyle 13803759753640704000}, lambda^2
-{scriptstyle 8752948036761600000},lambda +{scriptstyle 2432377720176640000}
$$
очень похож на полином из другого
☞
ПРИМЕРА Уилкинсона. Он имеет корни
$$
lambda_1=0.995754, lambda_2=2.109241, lambda_3=2.574881,
$$
$$
lambda_{4,5}=3.965331pm 1.087735, mathbf i, lambda_{6,7}=5.893977pm 1.948530 , mathbf i,
$$
$$
lambda_{8,9}=8.118073 pm
2.529182 , mathbf i,
lambda_{10,11}=10.5pm 2.733397 , mathbf i,
$$
$$
lambda_{12,13}=12.881926pm 2.529182 , mathbf i, lambda_{14,15}=15.106022 pm 1.948530
, mathbf i, $$
$$
lambda_{16,17}=17.034669pm 1.087735 , mathbf i,
$$
$$
lambda_{18}=18.425118, lambda_{19}=18.890758, lambda_{20}=20.004245 .
$$
Итак, нановозмущение5) в одном-единственном элементе матрицы приводит к существенному изменению спектра: из $ 20 $ вещественных собственных чисел «остаются в живых» только $ 6_{} $; кроме того, у образовавшихся мнимых корней оказываются достаточно большими мнимые части. В данном примере допустимые возмущения для $ {color{Red} varepsilon } $, т.е. такие, при
которых сохранится
свойство вещественности всех корней характеристического полинома, находятся в пределах6)
$$ -8.636174times 10^{-14} < {color{Red} varepsilon } le frac{685872258640569}{8796093022208000000000000000} approx +7.797464 times 10^{-14} .$$
♦
Т
Теорема 13 [Гершгорин].7) Обозначим $ mathbb D_{j} $ круг на комплексной
плоскости $ mathbb C_{} $ с центром в точке $ a_{jj}^{} $ и радиуса
$$ r_j=sum_{ell=1 atop ellne j}^n left|a_{j ell}right| .$$
Тогда спектр матрицы $ A_{} $ лежит внутри объединения этих кругов:
$$ {lambda_1,dots, lambda_n } subset bigcup_{j=1}^n mathbb D_j . $$
Иными словами: любое собственное число матрицы должно удовлетворять хотя бы одному из
неравенств
$$ |z- a_{jj} | < r_j . $$
Доказательство
☞
ЗДЕСЬ
П
Пример. Построить круги Гершгорина для матрицы
$$ A=left(
begin{array}{crr}
-1+3,{mathbf i} & 2- {mathbf i} & 3+2, {mathbf i} \
-1+{mathbf i} & 4+ {mathbf i} & 3, {mathbf i} \
-1& 2-2,{mathbf i}& -2-3, {mathbf i}
end{array}
right) . $$
Решение.
$$|lambda + 1 – 3,{mathbf i} |le | 2-{mathbf i} |+| 3+2,{mathbf i} |=sqrt{5}+sqrt{13}, $$
$$|lambda – 4 – {mathbf i} |le 3+sqrt{2}, $$
$$ |lambda + 2+ 3, {mathbf i} |le 1 + 2sqrt{2} . $$

Проверка. Собственные числа матрицы $ A_{} $ (на рисунке обозначены красными крестиками):
$$ { -2.509081750-3.442241533,{mathbf i} , -1.041999986+2.655757676,{mathbf i} , 4.551081736+1.786483857, {mathbf i} } .$$
Локализация вещественных собственных чисел
Симметричная матрица
Т
Теорема 14 [Коши].
Для вещественной симметричной матрицы $ A_{} $ число ее собственных чисел, лежащих на интервале $ ]a,b_{}[ $, определяется по формуле:
$$operatorname{nrr} { det (A-lambda E) =0 | a< lambda<b }= $$
$$= {mathcal P}(1, H_1(a), H_2(a),dots, H_n(a))-
{mathcal P}(1, H_1(b), H_2(b),dots, H_n(b)) . $$
Здесь $ H_1(lambda), H_2(lambda),dots, H_n(lambda) $ —
главные миноры матрицы $ A-lambda, E $, а $ {mathcal P}_{} $ — число знакопостоянств.
Доказательство
☞
ЗДЕСЬ.
Согласно этой теореме, главные миноры матрицы $ A-lambda, E $ играют роль системы
полиномов Штурма для характеристического полинома симметричной матрицы $ A_{} $.
=>
Если все главные миноры $ A_1,A_2,dots,A_{n} $ симметричной матрицы $ A_{} $ отличны от нуля, то
число положительных собственных чисел матрицы $ A_{} $ равно числу знакопостоянств, а число отрицательных собственных чисел — числу знакоперемен в ряду $ 1,A_1,dots,A_n $:
$$ operatorname{nrr} { det (A-lambda E) =0 | lambda>0 } = {mathcal P}(1,A_1,dots,A_n),
$$
$$
operatorname{nrr} { det (A-lambda E) =0 | lambda<0 }={mathcal V}(1,A_1,dots,A_n) .
$$
П
Пример. Локализовать собственные числа матрицы
$$
left(
begin{array}{rrr}
11 & 2 & -8 \
2 & 2 & 10 \
-8 & 10 & 5
end{array}
right)
$$
Решение.
$$ H_1(lambda)=11- lambda, H_2(lambda)=lambda^2-13, lambda+18,
$$
$$
f(lambda)= H_3(lambda)=-lambda^3+18, lambda^2 +81, lambda -1458
.
$$
| $ lambda $ | $ 1_{} $ | $ H_1(lambda) $ | $ H_2(lambda) $ | $ H_3(lambda) $ | $ {mathcal P} $ | Комментарии |
|---|---|---|---|---|---|---|
| $ 0_{} $ | $ + $ | $ + $ | $ + $ | $ – $ | 2 | число положительных =2 |
| $ -10 $ | $ + $ | $ + $ | $ + $ | $ + $ | 3 | собственное число |
| $ -5 $ | $ + $ | $ + $ | $ + $ | $ – $ | 2 | лежит на $ ]-10,-5[ $ |
| $ 5 $ | $ + $ | $ + $ | $ – $ | $ – $ | 2 | собственное число |
| $ 10 $ | $ + $ | $ + $ | $ – $ | $ + $ | 1 | лежит на $ ]5,10[ $ |
| $ 15 $ | $ + $ | $ – $ | $ – $ | $ + $ | 1 | собственное число |
| $ 20 $ | $ + $ | $ – $ | $ + $ | $ – $ | 0 | лежит на $ ]15,20[ $ |
Проверка. Спектр матрицы: $ {-9,9,18 } $.
П
Пример. Локализовать собственные числа матрицы
$$
left(
begin{array}{rrr}
1 & -2 & 2 \
-2 & -2 & 4 \
2 & 4 & -2
end{array}
right) .
$$
Решение.
$$H_1(lambda)=1- lambda, H_2(lambda)=lambda^2+, lambda-6,
f(lambda)=H_3(lambda)=-lambda^3-3, lambda^2 +24, lambda -28
.
$$
| $ lambda_{} $ | $ 1_{} $ | $ H_1(lambda) $ | $ H_2(lambda) $ | $ H_3(lambda) $ | $ {mathcal P} $ | Комментарии |
|---|---|---|---|---|---|---|
| $ 0_{} $ | $ + $ | $ + $ | $ – $ | $ – $ | 2 | число положительных =2 |
| $ -8 $ | $ + $ | $ + $ | $ + $ | $ + $ | 3 | собственное число |
| $ -6 $ | $ + $ | $ + $ | $ + $ | $ – $ | 2 | лежит на $ ]-8,-6[ $ |
| $ 1.5 $ | $ + $ | $ – $ | $ – $ | $ – $ | 2 | два собственных числа |
| $ 3_{} $ | $ + $ | $ – $ | $ + $ | $ – $ | 0 | лежат на $ ]1.5,3[ $ |
Никаким дроблением интервала $ ]1.5, , , 3[ $ не удается отделить
два вещественных собственных числа. Вывод: имеется кратное собственное
число.
Проверка. Спектр матрицы: $ {-7,2,2 } $.
Произвольная матрица
Собственный вектор
Собственный вектор матрицы8) $ A_{} $, принадлежащий (или соответствующий) ее собственному собственному числу $ lambda_{ast}^{} $, определяется как ненулевой столбец
$$
X_{ast}= left(
begin{array}{c} x_{1}^{ast} \ vdots \ x_{n}^{ast}
end{array} right)
in mathbb{C}^n
$$
такой, что
$$ AX_{ast}=lambda_{ast} X_{ast} quad iff quad (A -lambda_{ast}E) X_{ast} = mathbb O_{ntimes 1} . $$
По определению собственного числа, $ det (A^{} -lambda_{ast}E) = 0 $ и, следовательно,
система однородных уравнений $ (A -lambda_{ast}E) X^{} = mathbb O $ всегда имеет нетривиальное решение; более того, этих решений бесконечно много. Таким образом, одному и тому же собственному числу матрицы принадлежит бесконечное множество собственных векторов. Эту бесконечность можно описать с помощью фундаментальной системы решений (ФСР).
Строго говоря, только что введено определение правого собственного вектора матрицы $ A $. Потому как для
этой же матрицы определяется и левый собственный вектор — как строка $ Y_{ast}=(y_1^{ast},dots, y_n^{ast}) ne mathbb O $, такая, что
$$ Y_{ast} A= mu_{ast} A quad mbox{ при некотором } mu_{ast} in mathbb C , . $$
Очевидно, что $ Y_{ast} $ является левым собственным вектором $ A $ тогда и только тогда, когда столбец $ Y_{ast}^{top} $ является правым собственным вектором матрицы $ A^{^{top}} $. Кроме того, поскольку спектры матриц $ A $ и $ A^{^{top}} $ совпадают, то все результаты, полученные для правых собственных векторов, автоматически переносятся и на левые. Традиционно принято рассматривать правые собственные векторы; в этом случае слово «правый» опускают.
П
Пример. Найти собственные векторы матрицы
$$
A=
left(begin{array}{rrrr}
0&1&2&3\
-1&0&4&7\
-2&-4&0&2\
-3&-7&-2&0
end{array}right).
$$
Решение. Спектр матрицы найден выше.
$$(A-0 cdot E)X=mathbb O quad Longrightarrow mbox{ ФСР}=
left{
{mathfrak X}_1=left(begin{array}{r}
4 \ -2 \ 1 \ 0 end{array}right),
{mathfrak X}_2=left(begin{array}{r}
7 \ -3 \ 0 \ 1 end{array} right) right}.$$
Любой вектор вида $ alpha_{1} {mathfrak X}_1 + alpha_2 {mathfrak X}_2 $ будет собственным,
принадлежащим $ lambda_{}=0 $.
$$ begin{array}{c}
(A- mathbf i, sqrt {83} E)X=mathbb O \ \ Downarrow \ \ {mathfrak X}_3=
left(begin{array}{c}
1- mathbf i , sqrt {83} \ 8-2, mathbf i , sqrt {83} \ 12 \ 17+mathbf i , sqrt {83}
end{array}right)
end{array}
qquad
begin{array}{c}
(A+mathbf i sqrt {83} E)X=mathbb O \ \ Downarrow \ \ {mathfrak X}_4=
left(begin{array}{c}
1+mathbf i , sqrt {83} \ 8+2mathbf i , sqrt {83} \ 12 \ 17- mathbf i ,sqrt {83}
end{array}right)
end{array} .
$$
♦
Еще один способ нахождения собственного вектора основан на теореме Гамильтона-Кэли.
Т
Теорема 15. Пусть $ lambda_{ast}^{} $ — собственное число матрицы $ A_{} $. Обозначим частное от деления характеристического полинома на линейный множитель $ lambda_{} – lambda_{ast} $ через $ f_{ast}(lambda)^{} $:
$$ f_{ast}(lambda) equiv f(lambda) / (lambda-lambda_{ast}) . $$
Тогда любой ненулевой столбец матрицы $ f_{ast}(A)^{} $ является собственным вектором, принадлежащим $ lambda_{ast}^{} $.
Доказательство следует из равенства
$$(A-lambda_{ast} E)f_{ast}(A)=mathbb O_{ntimes n} . $$
На основании определения любой ненулевой столбец $ f_{ast}(A)^{} $ должен быть
собственным вектором матрицы $ A_{} $.
♦
П
Пример. Найти собственные векторы матрицы
$$
A=left( begin{array}{rrr}
9 & 22 & -6 \ -1 &-4 & 1 \ 8 & 16 & -5
end{array}
right) .
$$
Решение.
$$ det (A-lambda E)=-lambda^3+ 7, lambda + 6 equiv -(lambda_{}-3) (lambda+2)(lambda+1) , .$$
Пренебрегая знаком – , имеем:
$$
begin{matrix}
f_1(lambda)=lambda^2+3lambda+2 & u & f_1(A)=
left( begin{array}{rrr}
40 & 80 & -20 \ 0 &0 & 0 \ 40 & 80 & -20
end{array}
right) , \
f_2(lambda)=lambda^2-2lambda-3 & u & f_2(A)=
left( begin{array}{rrr}
-10 & -30 & 10 \ 5 &15 & -5 \ 0 & 0 & 0
end{array}
right) , \
f_3(lambda)=lambda^2-lambda-6 & u & f_3(A)=
left( begin{array}{rrr}
-4 & -8 & 4 \ 4 & 8 & -4 \ 8 & 16 & -8
end{array}
right) .
end{matrix}
$$
Ответ. $ {mathfrak X}_{1}=[1,0,1]^{^{top}} $ принадлежит $ lambda_{1}^{}=3 $,
$ {mathfrak X}_{2}=[-2,1,0]^{^{top}} $ принадлежит $ lambda_{2}^{}=-2 $,
$ {mathfrak X}_{3}=[-1,1,2]^{^{top}} $ принадлежит $ lambda_{3}^{}=-1 $.
=>
Если $ lambda_{ast}^{} $ является простым корнем характеристического полинома9), то ненулевые столбцы $ f_{ast}(A)^{} $ будут пропорциональными. Или, что то же, $ operatorname{rank} f_{ast}(A)^{} = 1 $.
Тогда очевидно, что и строки матрицы $ f_{ast}(A)^{} $ тоже должны быть пропорциональны!
На практике вычисление полинома $ f_{ast}(lambda)^{} $ может быть осуществлено с помощью схемы Хорнера.
П
Пример. Вычислить собственный вектор матрицы
$$
A=left( begin{array}{rrr}
23 & 75 & -92 \ 6 & 74 & 72 \ 37 & -23 & 87
end{array}
right) ,
$$
принадлежащий ее вещественному собственному числу.
Решение. Характеристический полином
$$ f(lambda)= -lambda^3+184,lambda^2-14751,lambda+611404 $$
имеет единственное вещественное собственное число $ lambda_{ast} approx 96.8817 $. Составляем схему Хорнера
$$
begin{array}{c|cccc}
& -1 & 184 & -14751 & 611404 \
hline
96.8817 & -1 & 87.1183 & -6310.8310 & -0.0352
end{array}
$$
За счет ошибок округления мы получили ненулевое значение для $ f(lambda_{ast}) $. В качестве частного от деления $ f(lambda) $ на $ lambda-lambda_{ast} $ берем
$$
f_{ast}(lambda)= -lambda^2 + 87.1183, lambda – 6310.8310 .
$$
Подставляем в него матрицу $ A_{} $ и вычисляем первый столбец матрицы
$$ -A^2+87.1183,A -6310, E =
left( begin{array}{rrr}
-1882.1101 & * & * \ -2723.2902 & * & * \ -708.6229 & * & *
end{array}
right) .$$
Проверяем:
$$
left( begin{array}{rrr}
23 & 75 & -92 \ 6 & 74 & 72 \ 37 & -23 & 87
end{array}
right)
left( begin{array}{r}
-1882.1101 \ -2723.2902 \ -708.6229
end{array}
right) – 96.8817 left( begin{array}{r}
-1882.1101 \ -2723.2902 \ -708.6229
end{array}
right)= left( begin{array}{r}
0.0356 \ 0 \ -0.0002
end{array}
right) .
$$
♦
Можно развить последний метод далее: найти универсальную формулу для собственного вектора как функции ее собственного числа. Действительно, найдем частное от деления характеристического полинома
$$ f(lambda) =a_0lambda^n+a_0lambda^{n-1}+dots+ a_n, quad a_0=(-1)^n $$
на линейный полином $ lambda- lambda_{ast} $, где $ lambda_{ast} $ — произвольное число из $ mathbb C $. С помощью той же схемы Хорнера, получаем
$$ q(lambda)= $$
$$
=a_0lambda^{n-1}+(a_0lambda_{ast}+a_1)lambda^{n-2}+(a_0lambda_{ast}^2+a_1lambda_{ast}+a_2)lambda^{n-3}+dots+ (a_0lambda_{ast}^{n-1}+a_1lambda_{ast}^{n-2}+dots+a_{n-1}) , .
$$
Если $ lambda_{ast} $ является собственным числом матрицы $ A_{} $, то любой ненулевой столбец матрицы
$$ q(A)= $$
$$
=a_0A^{n-1}+(a_0lambda_{ast}+a_1)A^{n-2}+(a_0lambda_{ast}^2+a_1lambda_{ast}+a_2)A^{n-3}+dots+ (a_0lambda_{ast}^{n-1}+a_1lambda_{ast}^{n-2}+dots+a_{n-1})E
$$
будет собственным вектором, принадлежащим $ lambda_{ast} $.
П
Пример. Найти представление всех собственных векторов матрицы
$$
A=left( begin{array}{rrr}
9 & 22 & -6 \ -1 &-4 & 1 \ 8 & 16 & -5
end{array}
right)
$$
в виде функции ее собственных чисел.
Решение. Характеристический полином матрицы был вычислен выше: $ f(lambda)=-lambda^3+ 7, lambda + 6 $. Имеем,
$$
q(lambda)=-lambda^2-lambda_{ast}lambda+(7-lambda_{ast}^2)
$$
и
$$
q(A)=-A^2-lambda_{ast}A+(7-lambda_{ast}^2)E=
left(begin{array}{ccc} -lambda_{ast}^2-9lambda_{ast}-4 & -22lambda_{ast}-14 & 6lambda_{ast}+2 \
lambda_{ast}-3 & -lambda_{ast}^2+4lambda_{ast}-3 & -lambda_{ast}+3 \
-8lambda_{ast}-16 & -16lambda_{ast}-32 & -lambda_{ast}^2+5lambda_{ast}+14
end{array} right) , .
$$
Берем произвольный столбец этой матрицы, например, первый:
$$
X_{ast}(lambda_{ast})=
left(begin{array}{c}
-lambda_{ast}^2-9lambda_{ast}-4 \
lambda_{ast}-3 \ -8lambda_{ast}-16
end{array} right) , .
$$
Утверждается, что $ X_{ast} (lambda_{ast}) $ — универсальное представление всех собственных векторов матрицы. Действительно,
$$
X_{ast}(-1)
=
left(begin{array}{r}
4 \
-4 \
-8
end{array} right),
X_{ast}(-2)
=
left(begin{array}{r}
10 \
-5 \ 0
end{array} right),
X_{ast}(3)
=
left(begin{array}{r}
-40 \
0 \
-40
end{array} right) , .
$$
♦
Матрица $ q(A) $, которую мы построили для нахождения универсального представления собственного вектора, может быть получена другим способом. В самом деле, поскольку
$$ f(lambda)equiv q(lambda)(lambda-lambda_{ast})+ f(lambda_{ast}), $$
то имеем справедливость матричного равенства:
$$ f(A)equiv q(A)(A-lambda_{ast}E)+ f(lambda_{ast})E , . $$
Откуда, на основании теоремы Гамильтона-Кэли, получаем равенство
$$ q(A)(A-lambda_{ast}E) = – E det (A-lambda_{ast}E) , . $$
Это равенство означает, что матрица $ (- q(A)) $ является взаимной матрице $ A-lambda_{ast}E $:
$$ – q(A)=operatorname{adj}(A-lambda_{ast}E) , . $$
Следовательно, ее выражение (а нам, собственно, нужно только выражение для какого-то ее столбца)
может быть получено с помощью алгебраических дополнений элементов матрицы $ A-lambda_{ast}E $. Именно такой способ вычисления взаимной матрицы использовался при доказательстве теоремы Гамильтона-Кэли.
Т
Теорема 16. Пусть $ g(x)=b_0x^m+dots+b_{m} in {mathbb C}[x] $ – произвольный полином. Если $ X_{ast}in mathbb C^{n} $ — собственный вектор матрицы $ A_{} $,
соответствующий собственному числу $ lambda_{ast}^{} $, то он же будет собственным и для матрицы $ g(A)^{} $, принадлежащим собственному числу $ g(lambda_{ast})^{} $.
Доказательство. Домножим равенство $ A{mathfrak X}_{ast}=lambda_{ast}^{}{mathfrak X}_{ast} $ слева
на матрицу $ A_{} $:
$$ A^2{mathfrak X}_{ast}=lambda_{ast}A{mathfrak X}_{ast}=lambda_{ast}^2{mathfrak X}_{ast} .$$
По индукции доказывается и общее равенство:
$$ A^k{mathfrak X}_{ast}=lambda_{ast}^k{mathfrak X}_{ast} .$$
Домножим его на $ b_{m-k}^{} $ и просуммируем по $ k_{} $ от $ 0_{} $ до $ m_{} $:
$$ g(A){mathfrak X}_{ast}=g(lambda_{ast}){mathfrak X}_{ast} ,$$
что и доказывает утверждение теоремы.
♦
=>
Если матрица $ A $ невырождена, то теорема остается справедливой и для произвольного полинома от $ A^{-1} $. В частности, собственные векторы $ A^{-1} $ совпадают с собственными векторами матрицы $ A $.
Т
Теорема 17. Собственные векторы, принадлежащие различным собственным числам матрицы $ A_{} $, линейно независимы.
Т
Теорема 18. Собственные векторы, принадлежащие различным собственным числам вещественной симметричной матрицы $ A_{} $, ортогональны, т.е. если $ mathfrak X_1 $ принадлежит собственному числу $ lambda_{1} $, а $ mathfrak X_2 $ принадлежит собственному числу $ lambda_{2} $ и $ lambda_1 ne lambda_2 $, то
$$ langle mathfrak X_1, mathfrak X_2 rangle =0 , $$
где $ langle , rangle $ означает скалярное произведение, определяемое стандартным образом: $ langle X,Y rangle =x_1y_1+dots+x_ny_n $.
Доказательство
☞
ЗДЕСЬ.
Теорема Перрона-Фробениуса
Т
Теорема 19 [Перрон, Фробениус]. Для положительной матрицы $ A_{} $ существует положительное собственное число $ lambda_{+} $ такое, что все остальные собственные числа этой матрицы меньше $ lambda_{+} $ по абсолютной величине (модулю). Соответствующий этому собственному числу собственный вектор может быть выбран положительным:
$$ exists mathfrak X_{+} > mathbb O: quad A mathfrak X_{+} = lambda_{+} mathfrak X_{+} . $$
Число $ lambda_{+} $ из теоремы называется собственным числом Перрона или собственным числом Перрона-Фробениуса матрицы $ A_{} $, а соответствующий ему произвольный положительный собственный вектор —
собственным вектором Перрона-Фробениуса матрицы $ A_{} $.
=>
Спектральный радиус положительной матрицы $ A_{} $ совпадает с ее собственным числом Перрона-Фробениуса:
$$ rho(A)=lambda_{+} . $$
П
Пример. Найти собственное число и вектор Перрона-Фробениуса для матрицы
$$
A=
left(begin{array}{rrrr}
2 & 7 & 18 & 28 \
1 & 8 & 2 & 8 \
3 & 1 & 4 & 1 \
5 & 9 & 26 & 5
end{array}
right) , .
$$
Решение. Характеристический полином матрицы $ A_{} $
$$
det(A-lambda E)=lambda^4-19, lambda^3-175, lambda^2-285, lambda+10390
$$
имеет корнями
$$
lambda_{1,2} approx -6.260463 pm 5.452465 mathbf i, lambda_3 approx 5.878976, lambda_4 approx 25.641950 .
$$
Числом Перрона-Фробениуса является $ lambda_4 $, а соответствующий ему собственный вектор Перрона-Фробениуса можно взять равным
$$
left(
begin{array}{c}
1 \
0.365240 \ 0.184802 \ 0.634244
end{array}
right) quad mbox{ или } quad
left(
begin{array}{c}
2.737922 \ 1 \ 0.505974 \ 1.736510
end{array}
right) quad mbox{ или }
left(
begin{array}{c}
5.411185 \ 1.976383 \ 1 \ 3.432010
end{array}
right) quad mbox{ или } quad
left(
begin{array}{c}
1.576681 \ 0.575868 \ 0.291374 \ 1
end{array}
right) quad mbox{ или } quad
left(
begin{array}{r}
0.798133 \
0.291510 \
0.147496\
0.506210
end{array}
right) quad mbox{ или } dots
$$
(напоминаю: собственный вектор определяется с точностью до ненулевого сомножителя!). Последний вектор имеет длину равную $ 1_{} $.
♦
Свойства.
1.
Собственное число Перрона-Фробениуса всегда простое для характеристического полинома матрицы $ A_{} $. Отсюда следует, что собственный вектор Перрона-Фробениуса определяется единственным образом — с точностью до домножения на положительный скаляр.
2.
Любой собственный вектор положительной матрицы $ A_{} $, не соответствующий собственному числу Перрона-Фробениуса, не может состоять исключительно только из положительных элементов. Иными словами, хотя бы одна компонента такого вектора должна быть либо отрицательной либо мнимой.
3.
Для собственного числа Перрона-Фробениуса справедливо неравенство
$$ min_{jin{1,dots,n}} sum_{k=1}^n a_{jk} le lambda_{+} le max_{jin{1,dots,n}} sum_{k=1}^n a_{jk} . $$
4.
Собственное число Перрона-Фробениуса матрицы $ A_{} $ совпадает с собственным числом Перрона-Фробениуса матрицы $ A^{top} $.
Какие из перечисленных свойств можно распространить на случай неотрицательных матриц ? Каждую такую матрицу можно рассматривать как предел последовательности (строго)
положительных матриц.
Воспользовавшись теоремой о непрерывной зависимости собственных чисел матрицы от ее элементов, можем сделать вывод, о том, что для неотрицательной матрицы $ A_{} $ всегда найдется вещественное неотрицательное собственное число, которое будет являться максимальным по модулю среди всех собственных чисел матрицы. Другое дело, что в данном случае — в отличие от случая положительных матриц — такое мажорирующее собственное число может оказаться не единственным.
П
Пример. Спектр неотрицательной матрицы
$$ A=left( begin{array}{cc} 0 & 1 \ 1 & 0 end{array} right) $$
состоит из чисел $ lambda_1=+1 $ и $ lambda_1=-1 $ одинакового модуля.
♦
Однако, по-прежнему, хотя бы одно неотрицательное вещественное число $ lambda_{+} $ со свойством $ rho(A) = lambda_{+} $ существовать будет; более того, ему будет соответствовать неотрицательный собственный вектор $ mathfrak X ge mathbb O $. Это число (вектор) по-прежнему называются числом (вектором) Перрона-Фробениуса10) матрицы $ A_{} $.
Частным случаем неотрицательных матриц являются стохастические матрицы, т.е. неотрицательные матрицы, в которых сумма элементов
каждой строки равна $ 1_{} $:
$$
mathfrak P=left[p_{jk}right]_{j,k=1}^n, {p_{jk}ge 0 }_{j,k=1}^n, sum_{k=1}^n p_{jk} = 1 npu quad j in {1,2,dots,n} .
$$
Т
Теорема 20. Собственное число Перрона-Фробениуса стохастической матрицы равно $ 1_{} $. Этому собственному числу соответствует собственный вектор $ X=[1,1,dots,1]^{top} $.
Доказательство существования собственного числа равного $ 1_{} $ и соответствующего ему собственного вектора $ X=[1,1,dots,1]^{top} $ следует из равенства
$$mathfrak P left(
begin{array}{c}
1 \
1 \ vdots \ 1
end{array}
right) =
left(
begin{array}{c}
1 \ 1 \ vdots \ 1
end{array}right) .
$$
Далее, из теоремы Гершгорина следует, что любое собственное
число $ lambda_{}in mathbb C $ стохастической матрицы должно удовлетворять неравенству
$$|lambda – p_{jj}|le sum_{kne j} |p_{jk}|=1-p_{jj} $$
хотя бы при одном $ j_{} $. Воспользовавшись следствием к неравенству треугольника получаем:
$$|lambda| – |p_{jj}|le |lambda – p_{jj}| le 1-p_{jj} Rightarrow
|lambda| le 1 . $$
♦
Численное нахождение собственного числа и собственного вектора Перрона-Фробениуса возможно по методу, разобранному в пункте
☞
ЧАСТИЧНАЯ ПРОБЛЕМА СОБСТВЕННЫХ ЧИСЕЛ.
Методы вычисления характеристического полинома
Вычисление коэффициентов характеристического полинома матрицы $ A_{} $
непосредственным разложением определителя $ det (A-lambda_{} E) $ на $ n!_{} $ слагаемых — крайне неэффективно. Элементами этого разложения являются выражения, полиномиально зависящие от параметра $ lambda_{} $. На каждом этапе вычислений мы получаем проблему символьных вычислений: хранения таких полиномов и действий над ними.
Основной метод вычисления числовых определителей — метод Гаусса — также неэффективен в приложении к вычислению определителя, элементы которого зависят от параметра.
Источником вычислительных проблем является неудобное расположение переменной $ lambda_{} $ — на главной диагонали матрицы. Первый же шаг метода Гаусса приводит к делению на элемент $ a_{11} – lambda $, и, в дальнейшем, элементы преобразованной матрицы будут уже не полиномами, а рациональными функциями относительно $ lambda_{} $. Следующие шаги метода приводят к возрастанию степеней знаменателей. Необходимость в организации хранения рациональных функций и программировании действий с ними кажется тем более неоправданной, если вспомнить, что окончательный ответ — выражение для $ det (A-lambda_{} E) $ — должно быть полиномом по $ lambda_{} $; т.е. знаменатели дробей в конечном ответе сократятся.
А в качестве усугубляющего положение обстоятельства «на заднем плане» маячит проблема точности вычислений коэффициентов характеристического полинома — чувствительность его корней к возмущению его коэффициентов бывает весьма высокой.
Какой выход предлагается? — Предварительно преобразовать определитель $ det (A-lambda_{} E) $ к виду, когда переменная $ lambda_{} $ оказывается «выметенной» с диагонали на крайний ряд (в столбец или в строку). При этом допускается увеличение размеров (порядка) определителя. Такое представление дает возможность разложения определителя по этому исключительному ряду, и, тем самым, позволяет свести задачу к вычислению числовых
определителей — а уж для этой задачи применение метода Гаусса вполне эффективно.
Метод Леверье
Метод основан на формуле (см. следствие к теореме $ 7 $
☞
ЗДЕСЬ ):
$$ operatorname{Sp} (A^k)=lambda_1^k+dots+lambda_n^k=s_k , $$
т.е. след $ k_{} $-й степени матрицы $ A_{} $ равен $ k_{} $-й сумме Ньютона ее характеристического полинома $ f(lambda)=det (A-lambda E ) $.
Вычисляем последовательные степени матрицы $ A_{} $:
$$s_1=operatorname{Sp} (A), s_2=operatorname{Sp} (A^2), dots, s_n=operatorname{Sp} (A^n) .$$
Неизвестные коэффициенты $ f(lambda)=(-1)^n(lambda^n+a_1lambda^{n-1}+
dots+a_n) $ находим по рекурсивным формулам Ньютона:
$$
a_1=-s_1, a_2=-(s_2+a_1s_1)/2,
$$
$$
a_k=-(s_{k}+a_1s_{k-1}+a_2s_{k-2}+dots+a_{k-1}s_1)/k npu k le n.
$$
Очевидно, что не имеет смысла вычислять все элементы матрицы $ A^{n} $ — достаточно обойтись лишь элементами ее главной диагонали.
П
Пример [Леверье]. Найти характеристический полином матрицы
$$
A=left(begin{array}{rrrr}
-5.509882&1.870086&0.422908&0.008814 \
0.287865&-11.811654&5.711900&0.058717 \
0.049099&4.308033&-12.970687&0.229326 \
0.006235&0.269851&1.397369&-17.596207
end{array}
right) .
$$
Решение.
$$
A^2=left(begin{array}{rrrr}
30.91795128&-30.56848188&2.878480155&0.0031325713\
-4.705449283&164.6764010&-141.3504639&-0.4143169528\
0.3341843103&-106.6094396&193.1869924& -6.756396001\
0.0022236138&-1.904168948&-41.16923134& 309.9628536
end{array}
right),
$$
$$
A^3=left(begin{array}{rrrr}
-179.0125092&431.2849919&-198.8601505& -0.9173897610\
66.38829278&-2562.954533& 2771.458834& -15.49709921\
-23.08728044&2090.291485&-3124.010318& 156.9329019\
-0.649145142&-71.21907809&956.2502143& -5463.723497
end{array}
right),
$$
$$
A^4=left(begin{array}{cccc}
1100.720103& ast& ast& ast \
ast& 42332.23816& ast& ast \
ast& ast& 52669.62534& ast \
ast& ast& ast& 96355.91518
end{array}
right) .
$$
Вычисляем следы матриц:
$$s_1=-47.888430, s_2=698.7441983, s_3=-11329.70086, s_4= 192458.4988 ,$$
и по формулам Ньютона получаем:
$$a_1= 47.888430, a_2 = 797.278764_{displaystyle 8}
, a_3 = 5349.45551_{displaystyle 3},
a_4 = 12296.550_{displaystyle 68} . $$
♦
После нахождения коэффициентов характеристического полинома можно найти его корни каким-либо11) методом. Если $ lambda_{ast}^{} $ — одно
из собственных чисел, то для нахождения соответствующего собственного
вектора воспользуемся алгоритмом из
☞
ПУНКТА. Предположив дополнительно, что это собственное число простое12), обозначим
$$
f_{ast}(lambda)= f(lambda)/(lambda-lambda_{ast})=(-1)^n(lambda^{n-1}
+p_1lambda^{n-2}+dots+p_{n-2}lambda+p_{n-1})
$$
т.е. частное от деления $ f(lambda_{}) $ на $ lambda-lambda_{ast} $. Тогда любой ненулевой столбец матрицы $ f_{ast}(A)^{} $ будет собственным вектором, принадлежащим $ lambda_{ast}^{} $. Как правило, собственным вектором можно взять комбинацию

Степени матрицы $ A_{} $ уже нами посчитаны при вычислении коэффициентов характеристического полинома.
П
Пример. Для приведенного выше примера находим собственные числа:
$$
lambda_1=-17.86326,
lambda_2=-17.15242, lambda_3=-7.57404,
lambda_4= -5.29869 .
$$
Коэффициенты $ f_1(lambda) $ можно определить по схеме Хорнера:
$$
begin{array}{r|r|r|r|r|r}
&1 & 47.888430 & 797.2787648 & 5349.455513 & 12296.55068 \ hline
-17.86326 & 1 & underbrace{30.025170}_{p_{_1}}&
underbrace{260.9313465}_{p_{_2}} &underbrace{688.371028}_{p_{_3}}&
approx 0 \
end{array}
$$
Собственным вектором, принадлежащим $ lambda_{1} $, будет
$$left[ -0.0256_{displaystyle 67},
0.21938_{displaystyle 0},
-0.24187_{displaystyle 1},
1.044526 right]^{^{top}} .$$
♦
Т
Теорема 21. Характеристический полином явно выражается через суммы Ньютона с помощью следующего представления:
$$
f(lambda)=frac{1}{n!}left|
begin{array}{llllll}
s_1 &1 & & & &\
s_2&s_1& 2 & &mathbb O & \
s_3&s_2&s_1&3& & \
vdots& & & ddots &ddots & \
s_n&s_{n-1}& s_{n-2} & dots &s_1&n \
lambda^n&lambda^{n-1}&lambda^{n-2}& dots &lambda&1
end{array}
right|_{(n+1)times (n+1)} .
$$
Этот определитель имеет порядок больший, чем исходный $ det (A_{}-lambda E) $, однако в нем все включения переменной $ lambda_{} $ локализованы в одной строке — именно такое размещение трактовалось как «хорошее» в смысле вычисления определителя
☝
ВЫШЕ.
И
Биографические заметки о Леверье
☞
ЗДЕСЬ.
Существует модификация метода Леверье, позволяющая организовать одновременное вычисление как самого характеристического полинома матрицы $ A_{} $, так и матрицы взаимной к матрице $ A_{}-lambda E $ (что делает возможным получение универсальной формулы для всех собственных векторов матрицы $ A_{} $); этот метод известен как метод Леверье-Фаддеева.
Метод Крылова
Рассмотрим произвольный ненулевой столбец $ Y_0=left[ y_{1}^{[0]},dots,y_{n}^{[0]} right]^{^{top}} in mathbb C^n $. Cоставим итерационную векторную
последовательность
$$
Y_1=Acdot Y_0, Y_2=Acdot Y_1, dots, Y_{n}=Acdot Y_{n-1} .
$$
Т
Теорема 22. Определитель
$$
det left[begin{array}{c|c|c|c|c}
Y_0&Y_{1}&dots&Y_{n-1}&Y_{n}\
1& lambda&dots&lambda^{n-1}&lambda^n
end{array}
right]_{(n+1)times (n+1)}
$$
совпадает — с точностью до постоянного множителя — с характеристическим полиномом матрицы $ A_{} $. Здесь $ |_{} $ означает конкатенацию.
Доказательство. Легко видеть, что
$$ Y_K=A^KY_0 quad npu quad K in {1,dots,n} . $$
Если
$$ f(lambda)=det(A-lambda E) =(-1)^n lambda^n+a_1 lambda^{n-1}+a_2 lambda^{n-2}+dots+a_n , $$
то по теореме Гамильтона-Кэли:
$$
(-1)^n A^n+a_1A^{n-1}+dots+a_nE=mathbb O_{n times n} .
$$
Это равенство останется справедливым и после умножения его на произвольный вектор, в том числе на $ Y_{0} $:
$$
(-1)^n A^ncdot Y_0+a_1A^{n-1} cdot Y_0 +dots+a_ncdot Y_0=mathbb O_{n times 1} iff
$$
$$
iff quad (-1)^n Y_n+a_1Y_{n-1} +dots+a_nY_0=mathbb O .
$$
Последнее равенство представляет линейную систему относительно неизвестных коэффициентов характеристического полинома. Можно решать ее по формулам Крамера, но мы пойдем другим путем. Дополним эту систему тождеством $ f(lambda)=(-1)^n lambda^n+a_1 lambda^{n-1}+a_2 lambda^{n-2}+dots+a_n $. Рассмотрим получившуюся систему как линейную однородную относительно столбца $ left[ a_n,a_{n-1},dots,a_1,1right]^{top} $. Поскольку эта система имеет нетривиальное решение, то ее определитель должен равняться нулю:
$$
0=det left[begin{array}{c|c|c|c|c}
Y_0&Y_{1}&dots&Y_{n-1}&(-1)^nY_{n}\
1& lambda&dots&lambda^{n-1}&(-1)^nlambda^n-f(lambda)
end{array}
right]=
$$
(представляем последний столбец в виде суммы двух столбцов и используем свойство
5
определителя)
$$
=det left[begin{array}{c|c|c|c|c}
Y_0&Y_{1}&dots&Y_{n-1}&(-1)^nY_{n}\
1& lambda&dots&lambda^{n-1}&(-1)^nlambda^n
end{array}
right]-f(lambda)
det left[begin{array}{c|c|c|c}
Y_0&Y_{1}&dots&Y_{n-1}
end{array}
right] .
$$
Таким образом,
$$ f(lambda)=(-1)^n frac{det left[begin{array}{c|c|c|c|c}
Y_0&Y_{1}&dots&Y_{n-1}&Y_{n}\
1& lambda&dots&lambda^{n-1}&lambda^n
end{array}
right]}{det left[begin{array}{c|c|c|c}
Y_0&Y_{1}&dots&Y_{n-1}
end{array}
right]} ,
$$
если только знаменатель в этой дроби не обратится в нуль.
♦
П
Пример. Найти характеристический полином матрицы примера Леверье
$$
A=left(begin{array}{rrrr}
-5.509882&1.870086&0.422908&0.008814 \
0.287865&-11.811654&5.711900&0.058717 \
0.049099&4.308033&-12.970687&0.229326 \
0.006235&0.269851&1.397369&-17.596207
end{array}
right) .
$$
Решение. Возьмем $ Y_0=left[ 1,0,0,0 right]^{top} $. Имеем
$$
begin{array}{cccc}
Y_1=A Y_0= & Y_2=AY_1= & Y_3=AY_2= & Y_4=AY_3= \
left(begin{array}{r}
-5.509882\
0.287865 \
0.049099 \
0.006235
end{array}
right), &
left(begin{array}{r}
30.917951\
-4.705449 \
0.334184 \
0.002223
end{array}
right), &
left(begin{array}{r}
-179.012509\
66.388293 \
-23.087280\
-0.649145
end{array}
right), &
left(begin{array}{r}
1100.720101\
-967.597333\
576.522644\
-4.040153
end{array}
right) .
end{array}
$$
$$
det left[begin{array}{c|c|c|c|c}
Y_0&Y_{1}&Y_2& Y_{3}& Y_{4}\
1& lambda&lambda^2 &lambda^{3}&lambda^4
end{array}
right]=
left| begin{array}{rrrrr}
1 & -5.509882 & 30.917951 & -179.012509 & 1100.720101 \
0 & 0.287865 & -4.705449 & 66.388293 & -967.597333\
0 & 0.049099 & 0.334184 & -23.087280 & 576.522644\
0 & 0.006235 & 0.002223 & -0.649145 & -4.040153 \
1 & lambda & lambda^2 & lambda^3 & lambda^4
end{array}
right|=
$$
$$
=0.348621 lambda^4+16.694915lambda^3+277.948166lambda^2+1864.932835lambda+4286.836454 =
$$
$$
=0.348621 left(lambda^4+47.888430lambda^3+797.27876_{displaystyle 3}lambda^2+5349.4555_{displaystyle 0}lambda+12296.550_{displaystyle 5} right) .
$$
♦
После нахождения характеристического полинома можно найти его корни каким-либо13) методом. Пусть $ lambda_{ast}^{} $ — одно из собственных чисел, и оно —
простое; тогда для нахождения соответствующего собственного вектора можно воспользоваться тем же приемом, что был задействован в предыдущем ПУНКТЕ. Вычислим14) частное от деления $ f(lambda_{}) $ на $ lambda-lambda_{ast} $
$$
f_{ast}(lambda)= f(lambda)/(lambda-lambda_{ast})=(-1)^n(lambda^{n-1}
+p_1lambda^{n-2}+dots+p_{n-2}lambda+p_{n-1}) .
$$
Тогда любой ненулевой столбец матрицы $ f_{ast}(A)^{} $ будет собственным вектором, принадлежащим $ lambda_{ast}^{} $. Но тогда и произвольная комбинация столбцов этой матрицы тоже будет собственным вектором (если только не обратится в нулевой вектор). В частности, это относится и к комбинации, записываемой в матричном виде
$$ (-1)^n f_{ast}(A) Y_0 = A^{n-1}Y_0 +p_1A^{n-2}Y_0+dots+p_{n-1}Y_0=Y_{n-1}+p_1Y_{n-2}+dots+p_{n-1}Y_0 . $$
А комбинируемые векторы уже посчитаны.
Теперь обсудим исключительные случаи. При неудачном выборе $ Y_{0} $ определитель
$$
det left[begin{array}{c|c|c|c}
Y_0&Y_{1}&dots&Y_{n-1}
end{array}
right]
$$
может обратиться в нуль. Эта неприятность обязательно произойдет если, например, наш выбор пал на вектор $ Y_0 $, совпадающий с собственным вектором матрицы $ A_{} $. Вероятность такого события — нулевая. В общем же случае, трудно ожидать, чтобы $ n_{} $ почти произвольных столбцов
$ Y_0,Y_{1},dots,Y_{n-1} $ оказались линейно зависимыми — если только сама матрица $ A_{} $ не обладает «скрытым дефектом» — типа рассмотренного в следующем примере.
П
Пример. Найти характеристический полином матрицы
$$A=left( begin{array}{ccc}
2&1&1 \
1&2&1 \
1&1&2
end{array}
right) .
$$
Решение. При любом выборе $ Y_0 $ векторы $ {Y_0,Y_1,Y_2 } $ оказываются линейно зависимыми:
$$
Y_0=
left(begin{array}{r}
1\
0\
0
end{array}
right),
Y_1=
left(begin{array}{r}
2\
1\
1
end{array}
right),
Y_2=
left(begin{array}{r}
6\
5\
5
end{array}
right),dots ;
Y_0=
left(begin{array}{r}
1\
1\
1
end{array}
right),
Y_1=
left(begin{array}{r}
4\
4\
4
end{array}
right),dots
$$
Объяснение этого феномена состоит в том, что для матрицы $ A_{} $ ее аннулирующий полином имеет степень меньшую ее порядка:
$$ A^2-5 A+4 E = mathbb O . $$
Домножение этого равенства на произвольный столбец $ Y_0 $ и доказывает линейную зависимость системы $ {Y_0,Y_1,Y_2} $.
♦
Такая ситуация возможна только в случае, когда характеристический полином матрицы $ A_{} $ имеет кратные корни (в рассмотренном выше примере $ lambda_{}=1 $ являлся двойным корнем $ det (A-lambda_{} E) $); она исключительно редко встречается на практике.
Поиск всех собственных чисел
Существуют методы нахождения спектра матрицы, не требующие предварительного построения характеристического полинома.
QR-алгоритм
Этот алгоритм основан на QR-разложении матрицы $ A $.
Т
Теорема 23. Спектр матрицы $ A $ совпадает со спектром матрицы $ P^{top} A P $ при произвольной ортогональной матрице $ P $.
Доказательство.
$$ det (P^{top} A P-lambda E)=det (P^{top} A P- lambda P^{top} E P)=det P^{top} (A -lambda E ) P =
det (A -lambda E ) P P^{top} = det (A -lambda E ) , .
$$
♦
Пусть QR-разложение матрицы $ A $ имеет вид
$$ A=Q_1R_1 , , $$
где $ Q_1 $ — ортогональная, а $ R_1 $ — верхнетреугольная матрицы. Тогда матрица
$$ A_2=R_1Q_1 $$
имеет тот же спектр, что и матрица $ A $. Действительно, поскольку
$$ A_2=Q_1^{top} A Q_1 , $$
то сработает предыдущая теорема. Вычислим QR-разложение матрицы $ A_2 $
$$ A_2=Q_2R_2 $$
и переставим местами матрицы этого произведения:
$$ A_3=R_2Q_2 , . $$
Матрица
$$ A_3= Q_2^{top} A_2 Q_2=Q_2^{top} Q_1^{top} A Q_1 Q_2 $$
продолжаем иметь те же собственные числа, что и матрица $ A $. Утверждается, что бесконечная последовательность матриц
$$ {A_j=R_{j-1}Q_{j-1}}_{j=1}^{infty} $$
как правило, сходится к матрице $ A_{infty} $, которая будет верхнетреугольной.
Т
Теорема 24 [4]. Если все собственные числа матрицы $ A $ различны по модулю, то матрица $ A_{infty} $ является верхнетреугольной и на ее главной диагонали стоят собственные числа матрицы $ A $.
П
Пример. Найти все собственные числа матрицы
$$
A=left(begin{array}{rrr}
2 & 3 &-1\
7 & 3 & 3 \
-1 & -2 & 4
end{array}
right) , .
$$
Решение.
$$
A_1=Aapprox
underbrace{left(begin{array}{rrr}
0.272165 & 0.759752 & 0.590511 \
0.952579 & -0.299517 & -0.053683 \
-0.136083& -0.577119 & 0.805242
end{array}
right)}_{Q_1}
underbrace{left(begin{array}{rrr}
7.348469 & 3.946400 & 2.041241\
0 & 2.534941 & -3.966781 \
0 & 0 & 2.469409
end{array}
right)}_{R_1}
$$
Теперь переставляем матрицы произведения местами и строим QR-разложение получившейся матрицы:
$$
quad Rightarrow quad A_2 = R_1Q_1approx
left(begin{array}{rrr}
5.481481 & 3.222957 & 5.771191 \
2.954542 & 1.530046 & -3.3303021 \
-0.336044 & -1.425143 & 1.988472
end{array}
right)approx
$$
$$
approxunderbrace{left(begin{array}{rrr}
-0.878992 & 0.022595 & 0.476300\
0.473781 & -0.154267 & -0.867026 \
0.053886 & -0.987771 & 0.146304
end{array}
right)}_{Q_2}
underbrace{left(begin{array}{rrr}
-6.236096& -3.634658 & -3.387848\
0 & 1.244502 & -1.319999\
0 & 0 & 5.927198
end{array}
right)}_{R_2}
$$
Продолжим процесс:
$$
quad Rightarrow quad A_3 = R_2Q_2approx
left(begin{array}{rrr}
7.020952& 3.766220 & -0.314568\
-0.660752 & 1.111870 & -1.272137\
0.319398 & -5.854713 & 0.867177
end{array}
right) approx
$$
$$
approx
underbrace{left(begin{array}{rrr}
-0.994581 & -0.065879 & 0.080426 \
0.093601 & -0.230749 & 0.968501 \
-0.045246 & 0.970780 & 0.235665
end{array}
right)}_{Q_3}
underbrace{left(begin{array}{rrr}
-7.059205 & -3.376839 & 0.154554 \
0 & -6.188319 & 1.156106 \
0 & 0 & -1.053002
end{array}
right)}_{R_3}
$$
Замечаем тенденцию убывания элементов матриц $ {A_j} $, стоящих под главной диагональю.
$$
Rightarrow dots Rightarrow A_{10} approx
left(begin{array}{rrr}
mathbf{6.}_{246022} & 2.758769 & -2.160057\
-0.0467437 & mathbf{4.4}_{09292} & -5.341014\
0.000018 &-0.005924 & mathbf{-1.6}_{55314}
end{array}
right) approx
$$
$$
underbrace{left(begin{array}{rrr}
-0.999972 & -0.007483 & 0.000007 \
0.007483 & -0.999971 & 0.001339 \
-0.000003 & 0.001339 & 0.999999
end{array}
right)}_{Q_{10}}
underbrace{left(begin{array}{rrr}
-6.246197 & -2.725694 & 2.120031\
0 & -4.429817 & 5.354807 \
0 & 0 & -1.662479
end{array}
right)}_{R_{10}} , .
$$
Матрица $ Q_j $ уже близка к диагональной (с элементами $ pm 1 $), верхнетреугольность матрицы $ A_j $ также заметна, но точность приближения еще не достаточна.
$$
Rightarrow dots Rightarrow A_{20} approx
left(begin{array}{rrr}
mathbf{6.17}_{5608} & 2.805821 & -2.020513 \
-0.001776 & mathbf{4.48}_{4917} & -5.388407\
0 & 0 & -mathbf{1.660525}
end{array}
right) approx
$$
Точность приближения минимильного собственного числа существенно выше точностей приближения остальных чисел.
$$
Rightarrow dots Rightarrow A_{30} approx
left(begin{array}{rrr}
mathbf{6.172}_{778} & 2.807524 & -2.015076\
-0.000073 & mathbf{4.487}_{747} & -5.390442\
0 & 0 & -mathbf{1.660525}
end{array}
right) , .
$$
♦
К сожалению условие теоремы достаточно ограничительно: собственные числа вещественной матрицы $ A $ могут оказаться и мнимыми, но тогда они одинаковы по модулю.
§
Как это обстоятельство сказывается на структуре матрицы $ A_{infty} $ и дальнейшее развитие метода
☞
ЗДЕСЬ
Частичная проблема собственных чисел
Задача. Найти максимальное по модулю собственное число матрицы $ A_{} $.
Предположение
. Будем считать сначала, что максимальное по модулю собственное число матрицы единственно.
Излагаемый ниже метод поиска этого собственного числа называется методом степенны́х итераций15).
Рассмотрим произвольный ненулевой столбец $ Y_0=left[ y_{1}^{[0]},dots,y_{n}^{[0]} right]^{^{top}} in mathbb C^n $. Cоставим такую же итерационную векторную
последовательность, как и в методе Крылова
$$
Y_1=Acdot Y_0, Y_2=Acdot Y_1, dots, Y_{K}=Acdot Y_{K-1},dots ,
$$
(только теперь, в отличие от метода Крылова, считаем ее неограниченно продолжающейся) и выделим последовательность первых элементов этих векторов:
$$y_{1}^{[1]},y_{1}^{[2]},dots,y_{1}^{[K]},dots $$
Т
Теорема 25. Как правило, предел
$$
lim_{Kto +infty}frac{y_{1}^{[K+1]}}{y_{1}^{[K]}}
$$
существует и он равен максимальному по модулю собственному числу матрицы $ A_{} $.
Доказательство. Перенумеруем собственные числа $ lambda_{1},dots,lambda_n $ матрицы $ A_{} $ так, чтобы $ lambda_{1} $ обозначило максимальное по модулю:
$$|lambda_1|= max_{jin {1,dots,n}} |lambda_j| , quad |lambda_1|>|lambda_j| quad npu quad jin {2,dots,n} . $$
Очевидно,
$$
Y_{K}=A^Kcdot Y_0 ;
$$
отсюда следует, что любой элемент столбца $ Y_{K} $ может быть линейно выражен через $ lambda_{1}^K,dots,lambda_n^K $.
В частности, это справедливо и для первого элемента:
$$
y_{1}^{[K]}=C_1lambda_1^K+C_2lambda_2^K+dots+C_nlambda_n^K .
$$
В этом представлении $ {C_j}_{j=1}^n $ — будут константами из $ mathbb C_{} $ в случае если все собственные числа являются простыми, и полиномами из $ mathbb C[K] $ в случае, если имеются кратные собственные числа. Действительно, в первом случае существует базис пространства $ mathbb C^n $, состоящий из собственных векторов матрицы $ A_{} $:
$$ A{mathfrak X}_j=lambda_j{mathfrak X}_j quad npu quad jin {1,dots,n} . $$
Вектор $ Y_0 $ можно разложить по этому базису:
$$Y_0=alpha_1{mathfrak X}_1+dots+alpha_n{mathfrak X}_n .$$
Тогда последовательным домножением на матрицу $ A_{} $ получаем :
$$begin{matrix}
Y_1=AY_0&=& alpha_1 lambda_1{mathfrak X}_1+dots+alpha_nlambda_n{mathfrak X}_n, \
dots & & dots \
Y_K=A^KY_0&=& alpha_1 lambda_1^K{mathfrak X}_1+dots+alpha_nlambda_n^K{mathfrak X}_n
end{matrix}
$$
откуда и следует доказываемое равенство.
Во втором случае — когда имеются кратные собственные числа матрицы $ A_{} $ — придется применять «тяжелую артиллерию» в виде жордановой нормальной формы; см. теорему $ 5 $
☞
ЗДЕСЬ. Для простоты рассуждений, будем в оставшейся части доказательства считать все собственные числа матрицы различными. Имеем тогда
$$
lim_{K to +infty} frac{y_{1}^{[K+1]}}{y_{1}^{[K]}}=
lim_{K to +infty} frac{lambda_1^{K+1} left[C_1+
C_2(lambda_2/lambda_1)^{K+1}+dots+
C_n(lambda_n/lambda_1)^{K+1} right]}
{lambda_1^{K} left[C_1+C_2(lambda_2/lambda_1)^{K}+dots+
C_n(lambda_n/lambda_1)^{K} right]}
=lambda_1
$$
поскольку
$$
lim_{K to +infty} left| frac{lambda_j}{lambda_1} right|^K = 0 quad
npu quad jin {2,dots,n} .
$$
Исключительным случаем является ситуация $ C_1=0 $, в этом случае утверждение теоремы может оказаться несправедливым16).
♦
=>
Как правило, вектор
$$
left[1, lim_{Kto +infty}frac{y_{2}^{[K]}}{y_{1}^{[K]}},dots,
lim_{Kto +infty}frac{y_{n}^{[K]}}{y_{1}^{[K]}}right]^{^{top}}
$$
будет собственным, принадлежащим максимальному по модулю собственному числу матрицы $ A_{} $.
П
Пример. Для матрицы
$$
A=left(begin{array}{rrr}
2 & 3 &-1\
7 & 3 & 3 \
-1 & -2 & -4
end{array}
right)
$$
найти максимальное по модулю собственное число и принадлежащий ему собственный вектор.
Решение. Возьмем в качестве стартового столбца $ Y_0=[1,0,0]^{^{top}} $. Имеем:
$$
Y_1=AY_0=left( begin{array}{r} 2 \ 7 \ -1 end{array} right),
Y_2=AY_1=left( begin{array}{r} 26 \ 32 \ -12 end{array} right),
Y_3=AY_2=left( begin{array}{r} 160 \ 242 \ -42 end{array} right),dots,
$$
$$
Y_{19}=left( begin{array}{r}
{scriptstyle 4259667747238636} \ {scriptstyle 6435097324667832} \ {scriptstyle -1571397155909260}
end{array} right), Y_{20}=AY_{19}=left( begin{array}{r}
{scriptstyle 29396024624390028} \ {scriptstyle 44408774736946168} \ {scriptstyle -10844273772937260}
end{array} right)
$$
Смотрим на отношения первых элементов векторов:
$$
begin{array}{c|c|c|c|c|c|c|c|c|c}
K & 1 & 2 & 3 & 4 & 5 & dots & 15 & dots & 19 \
hline
y_{1}^{[K+1]}/y_{1}^{[K]} & 2 & 13 & 6.153846 & 6.8 & 7.180147 & dots & 6.900726 & dots & mathbf{6.90101}_{displaystyle 3}
end{array}
$$
Далее, в соответствии со следствием, собственный вектор, принадлежащий найденному числу
$$
approx left[1, frac{y_{2}^{[20]}}{y_{1}^{[20]}},frac{y_{3}^{[20]}}{y_{1}^{[20]}}right]^{^{top}} approx left[1, 1.51070_{displaystyle 6}, -0.368902 right]^{^{top}}
$$
♦
Результат теоремы представляет собой обобщение метода Бернулли поиска максимального по модулю корня полинома. Если в качестве матрицы $ A_{} $ взять матрицу Фробениуса
$$
mathfrak F=
left( begin{array}{lllllll}
0 & 1 & 0 & 0 & dots & 0 & 0 \
0 & 0 & 1 & 0 & dots & 0 & 0 \
0 & 0 & 0 & 1 & dots & 0 & 0 \
vdots& &&&ddots & & vdots \
0 & 0 & 0 & 0 & dots & 0 & 1 \
a_n & a_{n-1} & a_{n-2} & & dots & a_2 & a_1
end{array} right)_{n times n} ,
$$
то равенство
$$ X_K=mathfrak F X_{K-1} npu Kin {1,2,dots } $$
определяет — при задании (произвольным образом) чисел $ x_0,x_1,dots,x_{n-1} $ — линейную рекуррентную последовательность порядка $ n_{} $:
$$
x_{n+K}=a_1 x_{n+K-1}+ dots+ a_n x_K .
$$
Здесь столбцы $ X_K $ определяются формулами
$$
X_0=left( begin{array}{l}
x_0 \ x_1 \ vdots \ x_{n-1}
end{array}
right), X_1=left( begin{array}{l}
x_1 \ x_2 \ vdots \ x_{n}
end{array}
right), X_2=left( begin{array}{l}
x_2 \ x_3 \ vdots \ x_{n+1}
end{array}
right), dots,
X_K=left( begin{array}{l}
x_K \ x_{K+1} \ vdots \ x_{K+n-1}
end{array}
right),dots ;
$$
Характеристический полином последовательности совпадает с характеристическим полиномом матрицы $ mathfrak F $, т.е. с $ lambda^n-a_1 lambda^{n-1} -a_2 lambda^{n-2} -dots – a_n $.
Метод степенных итераций используется в поисковике Google для вычисления PageRank.
Теперь обсудим исключительные случаи алгоритма.
1.
Нарушение сходимости итерационного процесса за счет неудачного выбора стартового вектора. Если в качестве $ Y_{0} $ оказался случайно взят собственный вектор $ mathfrak X_{ast} $ матрицы $ A_{} $, принадлежащий произвольному ее собственному числу $ lambda_{*} $, то предел последовательности из теоремы будет равен именно этому числу; если при этом $ |lambda_{*} | ne max_{1le j le n} | lambda_j | $, то мы выйдем за пределы смысла выражения «как правило». Понятно, что вероятность настолько плохого выбора нулевая, но и выбор $ Y_0 $ вблизи $ mathfrak X_{ast} $ также может существенно замедлить скорость сходимости. Поэтому если возникает ситуация медленной «стабилизации» значащих цифр в десятичном приближении собственного числа, попробуйте сменить начальный вектор.
2.
Нарушение условия
предположения
,
выдвинутого в начале пункта: максимальное по модулю собственное число неединственно.
П
Пример. Найти максимальное по модулю собственное число матрицы примера Леверье
$$
A=left(begin{array}{rrrr}
-5.509882&1.870086&0.422908&0.008814 \
0.287865&-11.811654&5.711900&0.058717 \
0.049099&4.308033&-12.970687&0.229326 \
0.006235&0.269851&1.397369&-17.596207
end{array}
right) .
$$
Решение. Для столбца $ Y_0=[1,0,0,0]^{^{top}} $ имеем
$$y_{1}^{[100]}/y_{1}^{[99]}=-17.8_{displaystyle 3113} ,$$
т.е. на $ 100 $-й итерации получаем лишь $ 3_{} $ истинные десятичные цифры в представлении собственного числа. При этом
компонентами векторов $ Y_{K} $ являются числа порядка $ 10^{123} $. Если мы
посмотрим на ответ примера Леверье, то увидим, что имеются два собственных числа матрицы, близких по модулю.
♦
К сожалению, вероятность того факта, что у случайно выбранной матрицы два ее собственных числа будут иметь одинаковый модуль становится ненулевой если эта матрица выбирается из множества вещественных матриц. Дело в том, что в этом случае ее характеристический полином будет иметь вещественные коэффициенты, а мнимые корни такого полинома всегда пáрные — для любого невещественного корня $ lambda_{ast}^{} $ полинома, комплексно сопряженное к нему число $ overline{lambda_{ast}} $ также будет корнем. При этом $ |lambda_{ast}|= |overline{lambda_{ast}} | $.
П
Пример. Для матрицы
$$
A=left(begin{array}{rrr}
3 & 2 &7\
-2 & -8 & 2 \
5 & -3 & -2
end{array}
right)
$$
итерационная последовательность из теоремы ведет себя хаотически: при выборе $ Y_0=[1,0,0]^{top} $ получим
$$
left{frac{y_{1}^{[K+1]}}{y_{1}^{[K]}}right}_{K=1}^{infty} = 3; 13.3333; 5.9250;
4.6455; 15.9273; 0.8546; 68.0186;
$$
$$
0.4543; 91.7873; dots
$$
Спектр матрицы: $ { 6.9363, -6.9682pm 3.0186 mathbf i} $, и максимальное по модулю собственное число неединственно.
♦
Существуют приемы, позволяющие модифицировать метод на случай когда два числа спектра матрицы близки по модулю к максимальному; они подробно обсуждаются в [3].
Предположение 2
. Пусть два максимальных по модулю собственных числа матрицы разнесены по величине, например
$$ |lambda_1| > | lambda_2 | > | lambda_ j | quad npu j in {2,dots, n } . $$
Обобщение степенного метода основывается на использовании последовательностей из каких-то двух компонент векторов $ Y_{K+1}=AY_K $, например, наряду с уже использованной выше последовательностью первых компонент
$$y_{1}^{[1]},y_{1}^{[2]},dots,y_{1}^{[K]},dots $$
возьмем еще и аналогичную для вторых:
$$y_{2}^{[1]},y_{2}^{[2]},dots,y_{2}^{[K]},dots $$
Т
Теорема 26 [Эйткен]. При практически любом выборе стартового вектора $ Y_0 ne mathbb O $ для последовательности
$$
Y_1=Acdot Y_0, Y_2=Acdot Y_1, dots, Y_{K}=Acdot Y_{K-1},dots ,
$$
имеет место равенство
$$
lambda_1 lambda_2 = lim_{Kto +infty} frac{left|begin{array}{ll} y_1^{[K+1]} & y_1^{[K+2]} \ y_2^{[K+1]} & y_2^{[K+2]} end{array} right|}
{left|begin{array}{ll} y_1^{[K]} & y_1^{[K+1]} \ y_2^{[K]} & y_2^{[K+1]} end{array} right|} , .
$$
Доказательство. Построим квадратное уравнение
$$ p_0x^2+p_1x+p_2 = 0 $$
имеющее корнями $ lambda_1 $ и $ lambda_2 $.
Если существует базис рпостранства $ mathbb C^n $
$$Y_0=alpha_1{mathfrak X}_1+alpha_2{mathfrak X}_2+dots+alpha_n{mathfrak X}_n .$$
Тогда последовательным домножением на матрицу $ A_{} $ получаем :
$$begin{array}{llll}
Y_K=& alpha_1 lambda_1^K{mathfrak X}_1 &+alpha_2 lambda_2^K{mathfrak X}_2+dots &+alpha_nlambda_n^K{mathfrak X}_n, \
Y_{K+1}=& alpha_1 lambda_1^{K+1}{mathfrak X}_1 &+alpha_2 lambda_2^{K+1}{mathfrak X}_2+dots &+alpha_nlambda_n^{K+1}{mathfrak X}_n,\
Y_{K+2}=& alpha_1 lambda_1^{K+2}{mathfrak X}_1 & +alpha_2 lambda_2^{K+2}{mathfrak X}_2+dots &+alpha_nlambda_n^{K+2}{mathfrak X}_n.
end{array}
$$
Отбрасываем из правых частей равенств слагаемые порядков возрастания ниже, чем $ lambda_2^K, lambda_2^{K+1}, lambda_2^{K+2} $ соответственно, домножаем получившиеся приближенные равенства
$$begin{array}{lll|l}
Y_K & approx alpha_1 lambda_1^K{mathfrak X}_1 &+alpha_2 lambda_2^K{mathfrak X}_2, & color{Red} times p_2 \
Y_{K+1}& approx alpha_1 lambda_1^{K+1}{mathfrak X}_1 &+alpha_2 lambda_2^{K+1}{mathfrak X}_2, & color{Red} times p_1\
Y_{K+2} & approx alpha_1 lambda_1^{K+2}{mathfrak X}_1 & +alpha_2 lambda_2^{K+2}{mathfrak X}_2, & color{Red} times p_0
end{array}
$$
и складываем:
$$ p_2 Y_K + p_1Y_{K+1} + p_0 Y_{K+2} approx mathbb O , . $$
В получившемся векторном равенстве выбираем первые две компоненты:
$$
left{
begin{array}{ll}
p_2 y_1^{[K]} + p_1 y_1^{[K+1]} + p_0 y_1^{[K+2]} approx 0 , , \
p_2 y_2^{[K]} + p_1 y_2^{[K+1]} + p_0 y_2^{[K+2]} approx 0 , ,
end{array}
right.
$$
которые и позволят определить приближенное значение набора $ p_0,p_1,p_2 $. С точностью до числового сомножителя, искомый полином можно представить в виде определителя
$$
p_0x^2+p_1x+p_2 approx
left|begin{array}{lll}
y_1^{[K]} & y_1^{[K+1]} & y_1^{[K+2]} \
y_2^{[K]} & y_2^{[K+1]} & y_2^{[K+2]} \
1 & x & x^2
end{array}
right| , .
$$
Формулы Виета завершат доказательство.
♦
=>
При выполнении условия
предположения 2
имеет место равенство
$$ lambda_2 =
lim_{Kto +infty} frac{left|begin{array}{ll} y_1^{[K+1]} & y_1^{[K+2]} \ y_2^{[K+1]} & y_2^{[K+2]} end{array} right| y_{1}^{[K+1]}}
{left|begin{array}{ll} y_1^{[K]} & y_1^{[K+1]} \ y_2^{[K]} & y_2^{[K+1]} end{array} right| y_{1}^{[K+2]} } , .
$$
П
Пример. Для матрицы
$$
A=left(begin{array}{rrr}
2 & 3 &-1\
7 & 3 & 3 \
-1 & -2 & 4
end{array}
right)
$$
найти первые два по порядку убывания модулей собственных числа.
Решение. Для $ Y_0= [1,0,0]^{top} $ имеем:
$$
Y_1=left( begin{array}{r} 2 \ 7 \ -1 end{array} right),
Y_2=left( begin{array}{r} 26 \ 32 \ -20 end{array} right), dots,
$$
$$
Y_{18}=left( begin{array}{r} {scriptstyle 164983395620948} \ {scriptstyle 156537857759336} \ -{scriptstyle 219402049179956} end{array} right),
Y_{19}=left( begin{array}{r} {scriptstyle 1018982413699860} \ {scriptstyle 966291195084776} \ -{scriptstyle 1355667307859444} end{array} right),
Y_{20}=left( begin{array}{r} {scriptstyle 6292505720513492} \ {scriptstyle 5964748557575016} \ -{scriptstyle 8374234035307188} end{array} right), .
$$
Таким образом,
$$
lambda_1 approx frac{y_1^{[20]}}{y_1^{[19]}}= frac{1573126430128373}{254745603424965} approx mathbf{6.17}_5 ,
$$
$$
lambda_2 approx
frac{left|begin{array}{ll} y_1^{[19]} & y_1^{[20]} \ y_2^{[19]} & y_2^{[20]} end{array} right| y_{1}^{[19]}}
{left|begin{array}{ll} y_1^{[18]} & y_1^{[19]} \ y_2^{[18]} & y_2^{[19]} end{array} right| y_{1}^{[20]} }=
frac{300892177677465751832368453246033765185}{67074186846991590001957412392957971737 }
approx mathbf{4.48}_5
$$
♦
Обобщение этого подхода для поиска следующих по убыванию модулей собственных чисел проводится по аналогии с деления-вычитания вычисления корня полинома. Кстати, теоретически можно довести этот метод и до построения характеристического (точнее, минимального аннулирующего) полинома матрицы: при любом $ K in {0,1,2,dots } $ определитель
$$
left|begin{array}{llll}
y_1^{[K]} & y_1^{[K+1]} & dots & y_1^{[K+n]} \
y_2^{[K]} & y_2^{[K+1]} & dots & y_2^{[K+n]} \
vdots & vdots & & vdots \
y_n^{[K]} & y_n^{[K+1]} & dots & y_n^{[K+n]} \
1 & lambda & dots & lambda^n
end{array}
right|=
det left[begin{array}{c|c|c|c|c}
Y_K&Y_{K+1}&dots&Y_{K+n-1}&Y_{K+n}\
1& lambda&dots&lambda^{n-1}&lambda^n
end{array}
right]
$$
совпадает — с точностью до числового сомножителя — с $ det (A-lambda E) $. И мы вернулись к
☝
методу Крылова вычисления характеристического полинома!
Для случая симметричной матрицы альтернативное обобщение степенного метода для поиска ранжированных по убыванию модулей собственных чисел и соответствующих им собственных векторов разбирается
☞
ЗДЕСЬ.
Задачи
Источники
[1]. Островский А.М. Решение уравнений и систем уравнений. М. ИЛ, 1963, c. 137-142
[2]. Уилкинсон Дж.Х. Алгебраическая проблема собственных значений. М.Наука. 1970, с.93-94
[3]. Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. М.ГИФМЛ. 1960
[4]. Хорн Р., Джонсон Ч. Матричный анализ. М.Мир.1989
In matrix theory, the Perron–Frobenius theorem, proved by Oskar Perron (1907) and Georg Frobenius (1912), asserts that a real square matrix with positive entries has a unique largest real eigenvalue and that the corresponding eigenvector can be chosen to have strictly positive components, and also asserts a similar statement for certain classes of nonnegative matrices. This theorem has important applications to probability theory (ergodicity of Markov chains); to the theory of dynamical systems (subshifts of finite type); to economics (Okishio’s theorem,[1] Hawkins–Simon condition[2]);
to demography (Leslie population age distribution model);[3]
to social networks (DeGroot learning process); to Internet search engines (PageRank);[4] and even to ranking of football
teams.[5] The first to discuss the ordering of players within tournaments using Perron–Frobenius eigenvectors is Edmund Landau.[6][7]
Statement[edit]
Let positive and non-negative respectively describe matrices with exclusively positive real numbers as elements and matrices with exclusively non-negative real numbers as elements. The eigenvalues of a real square matrix A are complex numbers that make up the spectrum of the matrix. The exponential growth rate of the matrix powers Ak as k → ∞ is controlled by the eigenvalue of A with the largest absolute value (modulus). The Perron–Frobenius theorem describes the properties of the leading eigenvalue and of the corresponding eigenvectors when A is a non-negative real square matrix. Early results were due to Oskar Perron (1907) and concerned positive matrices. Later, Georg Frobenius (1912) found their extension to certain classes of non-negative matrices.
Positive matrices[edit]
Let 



- There is a positive real number r, called the Perron root or the Perron–Frobenius eigenvalue (also called the leading eigenvalue or dominant eigenvalue), such that r is an eigenvalue of A and any other eigenvalue λ (possibly complex) in absolute value is strictly smaller than r , |λ| < r. Thus, the spectral radius
is equal to r. If the matrix coefficients are algebraic, this implies that the eigenvalue is a Perron number.
- The Perron–Frobenius eigenvalue is simple: r is a simple root of the characteristic polynomial of A. Consequently, the eigenspace associated to r is one-dimensional. (The same is true for the left eigenspace, i.e., the eigenspace for AT, the transpose of A.)
- There exists an eigenvector v = (v1,…,vn)T of A with eigenvalue r such that all components of v are positive: A v = r v, vi > 0 for 1 ≤ i ≤ n. (Respectively, there exists a positive left eigenvector w : wT A = r wT, wi > 0.) It is known in the literature under many variations as the Perron vector, Perron eigenvector, Perron-Frobenius eigenvector, leading eigenvector, or dominant eigenvector.
- There are no other positive (moreover non-negative) eigenvectors except positive multiples of v (respectively, left eigenvectors except w), i.e., all other eigenvectors must have at least one negative or non-real component.
, where the left and right eigenvectors for A are normalized so that wTv = 1. Moreover, the matrix v wT is the projection onto the eigenspace corresponding to r. This projection is called the Perron projection.
- Collatz–Wielandt formula: for all non-negative non-zero vectors x, let f(x) be the minimum value of [Ax]i / xi taken over all those i such that xi ≠ 0. Then f is a real valued function whose maximum over all non-negative non-zero vectors x is the Perron–Frobenius eigenvalue.
- A “Min-max” Collatz–Wielandt formula takes a form similar to the one above: for all strictly positive vectors x, let g(x) be the maximum value of [Ax]i / xi taken over i. Then g is a real valued function whose minimum over all strictly positive vectors x is the Perron–Frobenius eigenvalue.
- Birkhoff–Varga formula: Let x and y be strictly positive vectors. Then
[8]
- Donsker–Varadhan–Friedland formula: Let p be a probability vector and x a strictly positive vector. Then
[9][10]
- Fiedler formula:
[11]
- The Perron–Frobenius eigenvalue satisfies the inequalities
All of these properties extend beyond strictly positive matrices to primitive matrices (see below). Facts 1-7 can be found in Meyer[12] chapter 8 claims 8.2.11–15 page 667 and exercises 8.2.5,7,9 pages 668–669.
The left and right eigenvectors w and v are sometimes normalized so that the sum of their components is equal to 1; in this case, they are sometimes called stochastic eigenvectors. Often they are normalized so that the right eigenvector v sums to one, while 
Non-negative matrices[edit]
There is an extension to matrices with non-negative entries. Since any non-negative matrix can be obtained as a limit of positive matrices, one obtains the existence of an eigenvector with non-negative components; the corresponding eigenvalue will be non-negative and greater than or equal, in absolute value, to all other eigenvalues.[13][14] However, for the example 

However, Frobenius found a special subclass of non-negative matrices — irreducible matrices — for which a non-trivial generalization is possible. For such a matrix, although the eigenvalues attaining the maximal absolute value might not be unique, their structure is under control: they have the form 

The eigenvector corresponding to r has strictly positive components (in contrast with the general case of non-negative matrices, where components are only non-negative). Also all such eigenvalues are simple roots of the characteristic polynomial. Further properties are described below.
Classification of matrices[edit]
Let A be a n × n square matrix over field F.
The matrix A is irreducible if any of the following equivalent properties
holds.
Definition 1 : A does not have non-trivial invariant coordinate subspaces.
Here a non-trivial coordinate subspace means a linear subspace spanned by any proper subset of standard basis vectors of Fn. More explicitly, for any linear subspace spanned by standard basis vectors ei1 , …,
eik, 0 < k < n its image under the action of A is not contained in the same subspace.
Definition 2: A cannot be conjugated into block upper triangular form by a permutation matrix P:
where E and G are non-trivial (i.e. of size greater than zero) square matrices.
Definition 3: One can associate with a matrix A a certain directed graph GA. It has n vertices labeled 1,…,n, and there is an edge from vertex i to vertex j precisely when aij ≠ 0. Then the matrix A is irreducible if and only if its associated graph GA is strongly connected.
If F is the field of real or complex numbers, then we also have the following condition.
Definition 4: The group representation of 




A matrix is reducible if it is not irreducible.
A real matrix A is primitive if it is non-negative and its mth power is positive for some natural number m (i.e. all entries of Am are positive).
Let A be real and non-negative. Fix an index i and define the period of index i to be the greatest common divisor of all natural numbers m such that (Am)ii > 0. When A is irreducible, the period of every index is the same and is called the period of A. In fact, when A is irreducible, the period can be defined as the greatest common divisor of the lengths of the closed directed paths in GA (see Kitchens[15] page 16). The period is also called the index of imprimitivity (Meyer[12] page 674) or the order of cyclicity. If the period is 1, A is aperiodic. It can be proved that primitive matrices are the same as irreducible aperiodic non-negative matrices.
All statements of the Perron–Frobenius theorem for positive matrices remain true for primitive matrices. The same statements also hold for a non-negative irreducible matrix, except that it may possess several eigenvalues whose absolute value is equal to its spectral radius, so the statements need to be correspondingly modified. In fact the number of such eigenvalues is equal to the period.
Results for non-negative matrices were first obtained by Frobenius in 1912.
Perron–Frobenius theorem for irreducible non-negative matrices[edit]
Let 



Then the following statements hold.
where 
- The Perron–Frobenius eigenvalue satisfies the inequalities
The example 
Further properties[edit]
Let A be an irreducible non-negative matrix, then:
- (I+A)n−1 is a positive matrix. (Meyer[12] claim 8.3.5 p. 672). For a non-negative A, this is also a sufficient condition.[16]
- Wielandt’s theorem.[17][clarification needed] If |B|<A, then ρ(B)≤ρ(A). If equality holds (i.e. if μ=ρ(A)eiφ is eigenvalue for B), then B = eiφ D AD−1 for some diagonal unitary matrix D (i.e. diagonal elements of D equals to eiΘl, non-diagonal are zero).[18]
- If some power Aq is reducible, then it is completely reducible, i.e. for some permutation matrix P, it is true that:
, where Ai are irreducible matrices having the same maximal eigenvalue. The number of these matrices d is the greatest common divisor of q and h, where h is period of A.[19]
- If c(x) = xn + ck1 xn-k1 + ck2 xn-k2 + … + cks xn-ks is the characteristic polynomial of A in which only the non-zero terms are listed, then the period of A equals the greatest common divisor of k1, k2, … , ks.[20]
- Cesàro averages:
where the left and right eigenvectors for A are normalized so that wTv = 1. Moreover, the matrix v wT is the spectral projection corresponding to r, the Perron projection.[21]
- Let r be the Perron–Frobenius eigenvalue, then the adjoint matrix for (r–A) is positive.[22]
- If A has at least one non-zero diagonal element, then A is primitive.[23]
- If 0 ≤ A < B, then rA ≤ rB. Moreover, if B is irreducible, then the inequality is strict: rA < rB.
A matrix A is primitive provided it is non-negative and Am is positive for some m, and hence Ak is positive for all k ≥ m. To check primitivity, one needs a bound on how large the minimal such m can be, depending on the size of A:[24]
- If A is a non-negative primitive matrix of size n, then An2 − 2n + 2 is positive. Moreover, this is the best possible result, since for the matrix M below, the power Mk is not positive for every k < n2 − 2n + 2, since (Mn2 − 2n+1)11 = 0.
Applications[edit]
Numerous books have been written on the subject of non-negative matrices, and Perron–Frobenius theory is invariably a central feature. The following examples given below only scratch the surface of its vast application domain.
Non-negative matrices[edit]
The Perron–Frobenius theorem does not apply directly to non-negative matrices. Nevertheless, any reducible square matrix A may be written in upper-triangular block form (known as the normal form of a reducible matrix)[25]
-
-
-
- PAP−1 =
- PAP−1 =
-
-
where P is a permutation matrix and each Bi is a square matrix that is either irreducible or zero. Now if A is
non-negative then so too is each block of PAP−1, moreover the spectrum of A is just the union of the spectra of the
Bi.
The invertibility of A can also be studied. The inverse of PAP−1 (if it exists) must have diagonal blocks of the form Bi−1 so if any
Bi isn’t invertible then neither is PAP−1 or A.
Conversely let D be the block-diagonal matrix corresponding to PAP−1, in other words PAP−1 with the
asterisks zeroised. If each Bi is invertible then so is D and D−1(PAP−1) is equal to the
identity plus a nilpotent matrix. But such a matrix is always invertible (if Nk = 0 the inverse of 1 − N is
1 + N + N2 + … + Nk−1) so PAP−1 and A are both invertible.
Therefore, many of the spectral properties of A may be deduced by applying the theorem to the irreducible Bi. For example, the Perron root is the maximum of the ρ(Bi). While there will still be eigenvectors with non-negative components it is quite possible
that none of these will be positive.
Stochastic matrices[edit]
A row (column) stochastic matrix is a square matrix each of whose rows (columns) consists of non-negative real numbers whose sum is unity. The theorem cannot be applied directly to such matrices because they need not be irreducible.
If A is row-stochastic then the column vector with each entry 1 is an eigenvector corresponding to the eigenvalue 1, which is also ρ(A) by the remark above. It might not be the only eigenvalue on the unit circle: and the associated eigenspace can be multi-dimensional. If A is row-stochastic and irreducible then the Perron projection is also row-stochastic and all its rows are equal.
Algebraic graph theory[edit]
The theorem has particular use in algebraic graph theory. The “underlying graph” of a nonnegative n-square matrix is the graph with vertices numbered 1, …, n and arc ij if and only if Aij ≠ 0. If the underlying graph of such a matrix is strongly connected, then the matrix is irreducible, and thus the theorem applies. In particular, the adjacency matrix of a strongly connected graph is irreducible.[26][27]
Finite Markov chains[edit]
The theorem has a natural interpretation in the theory of finite Markov chains (where it is the matrix-theoretic equivalent of the convergence of an irreducible finite Markov chain to its stationary distribution, formulated in terms of the transition matrix of the chain; see, for example, the article on the subshift of finite type).
Compact operators[edit]
More generally, it can be extended to the case of non-negative compact operators, which, in many ways, resemble finite-dimensional matrices. These are commonly studied in physics, under the name of transfer operators, or sometimes Ruelle–Perron–Frobenius operators (after David Ruelle). In this case, the leading eigenvalue corresponds to the thermodynamic equilibrium of a dynamical system, and the lesser eigenvalues to the decay modes of a system that is not in equilibrium. Thus, the theory offers a way of discovering the arrow of time in what would otherwise appear to be reversible, deterministic dynamical processes, when examined from the point of view of point-set topology.[28]
Proof methods[edit]
A common thread in many proofs is the Brouwer fixed point theorem. Another popular method is that of Wielandt (1950). He used the Collatz–Wielandt formula described above to extend and clarify Frobenius’s work.[29] Another proof is based on the spectral theory[30] from which part of the arguments are borrowed.
Perron root is strictly maximal eigenvalue for positive (and primitive) matrices[edit]
If A is a positive (or more generally primitive) matrix, then there exists a real positive eigenvalue r (Perron–Frobenius eigenvalue or Perron root), which is strictly greater in absolute value than all other eigenvalues, hence r is the spectral radius of A.
This statement does not hold for general non-negative irreducible matrices, which have h eigenvalues with the same absolute eigenvalue as r, where h is the period of A.
Proof for positive matrices[edit]
Let A be a positive matrix, assume that its spectral radius ρ(A) = 1 (otherwise consider A/ρ(A)). Hence, there exists an eigenvalue λ on the unit circle, and all the other eigenvalues are less or equal 1 in absolute value. Suppose that another eigenvalue λ ≠ 1 also falls on the unit circle. Then there exists a positive integer m such that Am is a positive matrix and the real part of λm is negative. Let ε be half the smallest diagonal entry of Am and set T = Am − εI which is yet another positive matrix. Moreover, if Ax = λx then Amx = λmx thus λm − ε is an eigenvalue of T. Because of the choice of m this point lies outside the unit disk consequently ρ(T) > 1. On the other hand, all the entries in T are positive and less than or equal to those in Am so by Gelfand’s formula ρ(T) ≤ ρ(Am) ≤ ρ(A)m = 1. This contradiction means that λ=1 and there can be no other eigenvalues on the unit circle.
Absolutely the same arguments can be applied to the case of primitive matrices; we just need to mention the following simple lemma, which clarifies the properties of primitive matrices.
Lemma[edit]
Given a non-negative A, assume there exists m, such that Am is positive, then Am+1, Am+2, Am+3,… are all positive.
Am+1 = AAm, so it can have zero element only if some row of A is entirely zero, but in this case the same row of Am will be zero.
Applying the same arguments as above for primitive matrices, prove the main claim.
Power method and the positive eigenpair[edit]
For a positive (or more generally irreducible non-negative) matrix A the dominant eigenvector is real and strictly positive (for non-negative A respectively non-negative.)
This can be established using the power method, which states that for a sufficiently generic (in the sense below) matrix A the sequence of vectors bk+1 = Abk / | Abk | converges to the eigenvector with the maximum eigenvalue. (The initial vector b0 can be chosen arbitrarily except for some measure zero set). Starting with a non-negative vector b0 produces the sequence of non-negative vectors bk. Hence the limiting vector is also non-negative. By the power method this limiting vector is the dominant eigenvector for A, proving the assertion. The corresponding eigenvalue is non-negative.
The proof requires two additional arguments. First, the power method converges for matrices which do not have several eigenvalues of the same absolute value as the maximal one. The previous section’s argument guarantees this.
Second, to ensure strict positivity of all of the components of the eigenvector for the case of irreducible matrices. This follows from the following fact, which is of independent interest:
- Lemma: given a positive (or more generally irreducible non-negative) matrix A and v as any non-negative eigenvector for A, then it is necessarily strictly positive and the corresponding eigenvalue is also strictly positive.
Proof. One of the definitions of irreducibility for non-negative matrices is that for all indexes i,j there exists m, such that (Am)ij is strictly positive. Given a non-negative eigenvector v, and that at least one of its components say j-th is strictly positive, the corresponding eigenvalue is strictly positive, indeed, given n such that (An)ii >0, hence: rnvi =
Anvi ≥
(An)iivi
>0. Hence r is strictly positive. The eigenvector is strict positivity. Then given m, such that (Am)ij >0, hence: rmvj =
(Amv)j ≥
(Am)ijvi >0, hence
vj is strictly positive, i.e., the eigenvector is strictly positive.
Multiplicity one[edit]
This section proves that the Perron–Frobenius eigenvalue is a simple root of the characteristic polynomial of the matrix. Hence the eigenspace associated to Perron–Frobenius eigenvalue r is one-dimensional. The arguments here are close to those in Meyer.[12]
Given a strictly positive eigenvector v corresponding to r and another eigenvector w with the same eigenvalue. (The vectors v and w can be chosen to be real, because A and r are both real, so the null space of A-r has a basis consisting of real vectors.) Assuming at least one of the components of w is positive (otherwise multiply w by −1). Given maximal possible α such that u=v- α w is non-negative, then one of the components of u is zero, otherwise α is not maximum. Vector u is an eigenvector. It is non-negative, hence by the lemma described in the previous section non-negativity implies strict positivity for any eigenvector. On the other hand, as above at least one component of u is zero. The contradiction implies that w does not exist.
Case: There are no Jordan cells corresponding to the Perron–Frobenius eigenvalue r and all other eigenvalues which have the same absolute value.
If there is a Jordan cell, then the infinity norm
(A/r)k∞ tends to infinity for k → ∞ ,
but that contradicts the existence of the positive eigenvector.
Given r = 1, or A/r. Letting v be a Perron–Frobenius strictly positive eigenvector, so Av=v, then:
So Ak∞ is bounded for all k. This gives another proof that there are no eigenvalues which have greater absolute value than Perron–Frobenius one. It also contradicts the existence of the Jordan cell for any eigenvalue which has absolute value equal to 1 (in particular for the Perron–Frobenius one), because existence of the Jordan cell implies that Ak∞ is unbounded. For a two by two matrix:
hence Jk∞ = |k + λ| (for |λ| = 1), so it tends to infinity when k does so. Since Jk = C−1 AkC, then Ak ≥ Jk/ (C−1 C ), so it also tends to infinity. The resulting contradiction implies that there are no Jordan cells for the corresponding eigenvalues.
Combining the two claims above reveals that the Perron–Frobenius eigenvalue r is simple root of the characteristic polynomial. In the case of nonprimitive matrices, there exist other eigenvalues which have the same absolute value as r. The same claim is true for them, but requires more work.
No other non-negative eigenvectors[edit]
Given positive (or more generally irreducible non-negative matrix) A, the Perron–Frobenius eigenvector is the only (up to multiplication by constant) non-negative eigenvector for A.
Other eigenvectors must contain negative or complex components since eigenvectors for different eigenvalues are orthogonal in some sense, but two positive eigenvectors cannot be orthogonal, so they must correspond to the same eigenvalue, but the eigenspace for the Perron–Frobenius is one-dimensional.
Assuming there exists an eigenpair (λ, y) for A, such that vector y is positive, and given (r, x), where x – is the left Perron–Frobenius eigenvector for A (i.e. eigenvector for AT), then
rxTy = (xT A) y = xT (Ay) = λxTy, also xT y > 0, so one has: r = λ. Since the eigenspace for the Perron–Frobenius eigenvalue r is one-dimensional, non-negative eigenvector y is a multiple of the Perron–Frobenius one.[31]
Collatz–Wielandt formula[edit]
Given a positive (or more generally irreducible non-negative matrix) A, one defines
the function f on the set of all non-negative non-zero vectors x such that f(x) is the minimum value of [Ax]i / xi taken over all those i such that xi ≠ 0. Then f is a real-valued function, whose maximum is the Perron–Frobenius eigenvalue r.
For the proof we denote the maximum of f by the value R. The proof requires to show R = r. Inserting the Perron-Frobenius eigenvector v into f, we obtain f(v) = r and conclude r ≤ R. For the opposite inequality, we consider an arbitrary nonnegative vector x and let ξ=f(x). The definition of f gives 0 ≤ ξx ≤ Ax (componentwise). Now, we use the positive right eigenvector w for A for the Perron-Frobenius eigenvalue r, then ξ wT x = wT ξx ≤ wT (Ax) = (wT A)x = r wT x . Hence f(x) = ξ ≤ r, which implies
R ≤ r.[32]
Perron projection as a limit: Ak/rk[edit]
Let A be a positive (or more generally, primitive) matrix, and let r be its Perron–Frobenius eigenvalue.
- There exists a limit Ak/rk for k → ∞, denote it by P.
- P is a projection operator: P2 = P, which commutes with A: AP = PA.
- The image of P is one-dimensional and spanned by the Perron–Frobenius eigenvector v (respectively for PT—by the Perron–Frobenius eigenvector w for AT).
- P = vwT, where v,w are normalized such that wT v = 1.
- Hence P is a positive operator.
Hence P is a spectral projection for the Perron–Frobenius eigenvalue r, and is called the Perron projection. The above assertion is not true for general non-negative irreducible matrices.
Actually the claims above (except claim 5) are valid for any matrix M such that there exists an eigenvalue r which is strictly greater than the other eigenvalues in absolute value and is the simple root of the characteristic polynomial. (These requirements hold for primitive matrices as above).
Given that M is diagonalizable, M is conjugate to a diagonal matrix with eigenvalues r1, … , rn on the diagonal (denote r1 = r). The matrix Mk/rk will be conjugate (1, (r2/r)k, … , (rn/r)k), which tends to (1,0,0,…,0), for k → ∞, so the limit exists. The same method works for general M (without assuming that M is diagonalizable).
The projection and commutativity properties are elementary corollaries of the definition: MMk/rk = Mk/rk M ; P2 = lim M2k/r2k = P. The third fact is also elementary: M(Pu) = M lim Mk/rk u = lim rMk+1/rk+1u, so taking the limit yields M(Pu) = r(Pu), so image of P lies in the r-eigenspace for M, which is one-dimensional by the assumptions.
Denoting by v, r-eigenvector for M (by w for MT). Columns of P are multiples of v, because the image of P is spanned by it. Respectively, rows of w. So P takes a form (a v wT), for some a. Hence its trace equals to (a wT v). Trace of projector equals the dimension of its image. It was proved before that it is not more than one-dimensional. From the definition one sees that P acts identically on the r-eigenvector for M. So it is one-dimensional. So choosing (wTv) = 1, implies P = vwT.
Inequalities for Perron–Frobenius eigenvalue[edit]
For any non-negative matrix A its Perron–Frobenius eigenvalue r satisfies the inequality:
This is not specific to non-negative matrices: for any matrix A with an eigenvalue 
that 
Gershgorin circle theorem. However another proof is more direct:
Any matrix induced norm satisfies the inequality 





Another inequality is:
This fact is specific to non-negative matrices; for general matrices there is nothing similar. Given that A is positive (not just non-negative), then there exists a positive eigenvector w such that Aw = rw and the smallest component of w (say wi) is 1. Then r = (Aw)i ≥ the sum of the numbers in row i of A. Thus the minimum row sum gives a lower bound for r and this observation can be extended to all non-negative matrices by continuity.
Another way to argue it is via the Collatz-Wielandt formula. One takes the vector x = (1, 1, …, 1) and immediately obtains the inequality.
Further proofs[edit]
Perron projection[edit]
The proof now proceeds using spectral decomposition. The trick here is to split the Perron root from the other eigenvalues. The spectral projection associated with the Perron root is called the Perron projection and it enjoys the following property:
The Perron projection of an irreducible non-negative square matrix is a positive matrix.
Perron’s findings and also (1)–(5) of the theorem are corollaries of this result. The key point is that a positive projection always has rank one. This means that if A is an irreducible non-negative square matrix then the algebraic and geometric multiplicities of its Perron root are both one. Also if P is its Perron projection then AP = PA = ρ(A)P so every column of P is a positive right eigenvector of A and every row is a positive left eigenvector. Moreover, if Ax = λx then PAx = λPx = ρ(A)Px which means Px = 0 if λ ≠ ρ(A). Thus the only positive eigenvectors are those associated with ρ(A). If A is a primitive matrix with ρ(A) = 1 then it can be decomposed as P ⊕ (1 − P)A so that An = P + (1 − P)An. As n increases the second of these terms decays to zero leaving P as the limit of An as n → ∞.
The power method is a convenient way to compute the Perron projection of a primitive matrix. If v and w are the positive row and column vectors that it generates then the Perron projection is just wv/vw. The spectral projections aren’t neatly blocked as in the Jordan form. Here they are overlaid and each generally has complex entries extending to all four corners of the square matrix. Nevertheless, they retain their mutual orthogonality which is what facilitates the decomposition.
Peripheral projection[edit]
The analysis when A is irreducible and non-negative is broadly similar. The Perron projection is still positive but there may now be other eigenvalues of modulus ρ(A) that negate use of the power method and prevent the powers of (1 − P)A decaying as in the primitive case whenever ρ(A) = 1. So we consider the peripheral projection, which is the spectral projection of A corresponding to all the eigenvalues that have modulus ρ(A). It may then be shown that the peripheral projection of an irreducible non-negative square matrix is a non-negative matrix with a positive diagonal.
Cyclicity[edit]
Suppose in addition that ρ(A) = 1 and A has h eigenvalues on the unit circle. If P is the peripheral projection then the matrix R = AP = PA is non-negative and irreducible, Rh = P, and the cyclic group P, R, R2, …., Rh−1 represents the harmonics of A. The spectral projection of A at the eigenvalue λ on the unit circle is given by the formula 
Counterexamples[edit]
The matrices L = 



Terminology[edit]
A problem that causes confusion is a lack of standardisation in the definitions. For example, some authors use the terms strictly positive and positive to mean > 0 and ≥ 0 respectively. In this article positive means > 0 and non-negative means ≥ 0. Another vexed area concerns decomposability and reducibility: irreducible is an overloaded term. For avoidance of doubt a non-zero non-negative square matrix A such that 1 + A is primitive is sometimes said to be connected. Then irreducible non-negative square matrices and connected matrices are synonymous.[33]
The nonnegative eigenvector is often normalized so that the sum of its components is equal to unity; in this case, the eigenvector is the vector of a probability distribution and is sometimes called a stochastic eigenvector.
Perron–Frobenius eigenvalue and dominant eigenvalue are alternative names for the Perron root. Spectral projections are also known as spectral projectors and spectral idempotents. The period is sometimes referred to as the index of imprimitivity or the order of cyclicity.
See also[edit]
- Min-max theorem
- Z-matrix (mathematics)
- M-matrix
- P-matrix
- Hurwitz matrix
- Metzler matrix (Quasipositive matrix)
- Positive operator
- Krein–Rutman theorem
Notes[edit]
- ^ Bowles, Samuel (1981-06-01). “Technical change and the profit rate: a simple proof of the Okishio theorem”. Cambridge Journal of Economics. 5 (2): 183–186. doi:10.1093/oxfordjournals.cje.a035479. ISSN 0309-166X.
- ^ Meyer 2000, pp. 8.3.6 p. 681 “Archived copy” (PDF). Archived from the original (PDF) on March 7, 2010. Retrieved 2010-03-07.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ Meyer 2000, pp. 8.3.7 p. 683 “Archived copy” (PDF). Archived from the original (PDF) on March 7, 2010. Retrieved 2010-03-07.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ Langville & Meyer 2006, p. 15.2 p. 167 Langville, Amy N.; Langville, Amy N.; Meyer, Carl D. (2006-07-23). Google’s PageRank and Beyond: The Science of Search Engine Rankings. ISBN 978-0691122021. Archived from the original on July 10, 2014. Retrieved 2016-10-31.
{{cite book}}: CS1 maint: bot: original URL status unknown (link) - ^ Keener 1993, p. p. 80
- ^ Landau, Edmund (1895), “Zur relativen Wertbemessung der Turnierresultaten”, Deutsches Wochenschach, XI: 366–369
- ^ Landau, Edmund (1915), “Über Preisverteilung bei Spielturnieren”, Zeitschrift für Mathematik und Physik, 63: 192–202
- ^ Birkhoff, Garrett and Varga, Richard S., 1958. Reactor criticality and nonnegative matrices. Journal of the Society for Industrial and Applied Mathematics, 6(4), pp.354-377.
- ^ Donsker, M.D. and Varadhan, S.S., 1975. On a variational formula for the principal eigenvalue for operators with maximum principle. Proceedings of the National Academy of Sciences, 72(3), pp.780-783.
- ^ Friedland, S., 1981. Convex spectral functions. Linear and multilinear algebra, 9(4), pp.299-316.
- ^ Miroslav Fiedler; Charles R. Johnson; Thomas L. Markham; Michael Neumann (1985). “A Trace Inequality for M-matrices and the Symmetrizability of a Real Matrix by a Positive Diagonal Matrix”. Linear Algebra and Its Applications. 71: 81–94. doi:10.1016/0024-3795(85)90237-X.
- ^ a b c d Meyer 2000, pp. chapter 8 page 665 “Archived copy” (PDF). Archived from the original (PDF) on March 7, 2010. Retrieved 2010-03-07.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ Meyer 2000, pp. chapter 8.3 page 670. “Archived copy” (PDF). Archived from the original (PDF) on March 7, 2010. Retrieved 2010-03-07.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ Gantmacher 2000, p. chapter XIII.3 theorem 3 page 66
- ^ Kitchens, Bruce (1998), Symbolic dynamics: one-sided, two-sided and countable state markov shifts., Springer, ISBN 9783540627388
- ^ Minc, Henryk (1988). Nonnegative matrices. New York: John Wiley & Sons. p. 6 [Corollary 2.2]. ISBN 0-471-83966-3.
- ^ Gradshtein, Izrailʹ Solomonovich (18 September 2014). Table of integrals, series, and products. ISBN 978-0-12-384934-2. OCLC 922964628.
- ^ Meyer 2000, pp. claim 8.3.11 p. 675 “Archived copy” (PDF). Archived from the original (PDF) on March 7, 2010. Retrieved 2010-03-07.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ Gantmacher 2000, p. section XIII.5 theorem 9
- ^ Meyer 2000, pp. page 679 “Archived copy” (PDF). Archived from the original (PDF) on March 7, 2010. Retrieved 2010-03-07.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ Meyer 2000, pp. example 8.3.2 p. 677 “Archived copy” (PDF). Archived from the original (PDF) on March 7, 2010. Retrieved 2010-03-07.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ Gantmacher 2000, p. section XIII.2.2 page 62
- ^ Meyer 2000, pp. example 8.3.3 p. 678 “Archived copy” (PDF). Archived from the original (PDF) on March 7, 2010. Retrieved 2010-03-07.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ Meyer 2000, pp. chapter 8 example 8.3.4 page 679 and exercise 8.3.9 p. 685 “Archived copy” (PDF). Archived from the original (PDF) on March 7, 2010. Retrieved 2010-03-07.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ Varga 2002, p. 2.43 (page 51)
- ^ Brualdi, Richard A.; Ryser, Herbert J. (1992). Combinatorial Matrix Theory. Cambridge: Cambridge UP. ISBN 978-0-521-32265-2.
- ^ Brualdi, Richard A.; Cvetkovic, Dragos (2009). A Combinatorial Approach to Matrix Theory and Its Applications. Boca Raton, FL: CRC Press. ISBN 978-1-4200-8223-4.
- ^ Mackey, Michael C. (1992). Time’s Arrow: The origins of thermodynamic behaviour. New York: Springer-Verlag. ISBN 978-0-387-97702-7.
- ^ Gantmacher 2000, p. section XIII.2.2 page 54
- ^ Smith, Roger (2006), “A Spectral Theoretic Proof of Perron–Frobenius” (PDF), Mathematical Proceedings of the Royal Irish Academy, 102 (1): 29–35, doi:10.3318/PRIA.2002.102.1.29
- ^ Meyer 2000, pp. chapter 8 claim 8.2.10 page 666 “Archived copy” (PDF). Archived from the original (PDF) on March 7, 2010. Retrieved 2010-03-07.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ Meyer 2000, pp. chapter 8 page 666 “Archived copy” (PDF). Archived from the original (PDF) on March 7, 2010. Retrieved 2010-03-07.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ For surveys of results on irreducibility, see Olga Taussky-Todd and Richard A. Brualdi.
References[edit]
- Perron, Oskar (1907), “Zur Theorie der Matrices”, Mathematische Annalen, 64 (2): 248–263, doi:10.1007/BF01449896, hdl:10338.dmlcz/104432, S2CID 123460172
- Frobenius, Georg (May 1912), “Ueber Matrizen aus nicht negativen Elementen”, Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften: 456–477
- Frobenius, Georg (1908), “Über Matrizen aus positiven Elementen, 1”, Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften: 471–476
- Frobenius, Georg (1909), “Über Matrizen aus positiven Elementen, 2”, Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften: 514–518
- Gantmacher, Felix (2000) [1959], The Theory of Matrices, Volume 2, AMS Chelsea Publishing, ISBN 978-0-8218-2664-5 (1959 edition had different title: “Applications of the theory of matrices”. Also the numeration of chapters is different in the two editions.)
- Langville, Amy; Meyer, Carl (2006), Google page rank and beyond, Princeton University Press, doi:10.1007/s10791-008-9063-y, ISBN 978-0-691-12202-1, S2CID 7646929
- Keener, James (1993), “The Perron–Frobenius theorem and the ranking of football teams”, SIAM Review, 35 (1): 80–93, doi:10.1137/1035004, JSTOR 2132526
- Meyer, Carl (2000), Matrix analysis and applied linear algebra (PDF), SIAM, ISBN 978-0-89871-454-8, archived from the original (PDF) on 2010-03-07
- Minc, Henryk (1988), Nonnegative matrices, John Wiley&Sons,New York, ISBN 0-471-83966-3
- Romanovsky, V. (1933), “Sur les zéros des matrices stocastiques”, Bulletin de la Société Mathématique de France, 61: 213–219, doi:10.24033/bsmf.1206
- Collatz, Lothar (1942), “Einschließungssatz für die charakteristischen Zahlen von Matrizen”, Mathematische Zeitschrift, 48 (1): 221–226, doi:10.1007/BF01180013, S2CID 120958677
- Wielandt, Helmut (1950), “Unzerlegbare, nicht negative Matrizen”, Mathematische Zeitschrift, 52 (1): 642–648, doi:10.1007/BF02230720, hdl:10338.dmlcz/100322, S2CID 122189604
Further reading[edit]
- Abraham Berman, Robert J. Plemmons, Nonnegative Matrices in the Mathematical Sciences, 1994, SIAM. ISBN 0-89871-321-8.
- Chris Godsil and Gordon Royle, Algebraic Graph Theory, Springer, 2001.
- A. Graham, Nonnegative Matrices and Applicable Topics in Linear Algebra, John Wiley&Sons, New York, 1987.
- R. A. Horn and C.R. Johnson, Matrix Analysis, Cambridge University Press, 1990
- Bas Lemmens and Roger Nussbaum, Nonlinear Perron-Frobenius Theory, Cambridge Tracts in Mathematics 189, Cambridge Univ. Press, 2012.
- S. P. Meyn and R. L. Tweedie, Markov Chains and Stochastic Stability London: Springer-Verlag, 1993. ISBN 0-387-19832-6 (2nd edition, Cambridge University Press, 2009)
- Seneta, E. Non-negative matrices and Markov chains. 2nd rev. ed., 1981, XVI, 288 p., Softcover Springer Series in Statistics. (Originally published by Allen & Unwin Ltd., London, 1973) ISBN 978-0-387-29765-1
- Suprunenko, D.A. (2001) [1994], “Perron–Frobenius theorem”, Encyclopedia of Mathematics, EMS Press (The claim that Aj has order n/h at the end of the statement of the theorem is incorrect.)
- Varga, Richard S. (2002), Matrix Iterative Analysis (2nd ed.), Springer-Verlag.
Для любой неотрицательной матрицы А=>0
существует собственное значение λА=>0
(называемое числом Фробениуса) такое,
что λА=>|λ| для любого собственного
значения λ матрицы А. Кроме того,
существует неотрицательный собственный
вектор
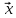
соответствующий собственному значению
λА и называемый вектором Фробениуса.
Причём, если А>0, то λА>0 и
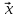
2. Докажите следующее утверждение: если
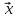
– собственный вектор неотрицательной
матрицы, то он является ее вектором
Фробениуса.
Обозначим через α собственное значение,
которому принадлежит вектор
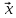
следовательно, выполнено равенство
A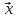
Умножая его слева на
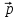
и учитывая, что
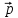
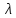
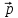
имеем:
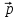
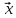
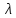
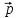
так что,
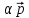
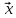

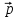
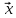
Поскольку по условию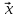
то
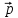
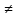
так что α= λА, ч.т.д.
3. Докажите следующее утверждение. Пусть s и s – минимальная и максимальная суммы элементов столбцов матрицы а. Тогда число Фробениуса λА матрицы а удовлетворяет неравенству s
Док-во: выберем в качестве вектора
Фробениуса
вектор, сумма координат которого равна
1, т.е.
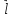
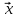
= 1
По определению имеем A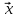
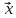
Умножая это равенство слева на
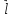
и учитывая, что
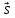
получим
= λА(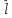
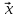
поэтому λА =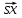
= s1x1+s2x2+…+snxn
отсюда следует, что s(x1+…+xn)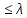
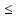
Учитывая, что сумма координат вектора
xA
равна 1, из неравенства получаем s
4. Запишите структурную таблицу и
уравнение межотраслевого баланса
Леонтьева для трехотраслевой модели
экономики; укажите экономический смысл
входящих в уравнение величин. Запишите
формулу вычисления элементов матрицы
Л. Через известные эл-ты струт. Табл.
Межотр. Баланса.
|
Произв. |
Конечное |
Валовой |
|
X11 |
Y1 |
X1 |
|
X21 |
Y2 |
X2 |
|
… |
… |
… |
|
X1n |
Yn |
Xn |
– уравнение межотраслевого баланса
(уравнение Леонтьева). Межотраслевой
баланс — экономико-математическая
балансовая модель, характеризующая
межотраслевые производственные
взаимосвязи в экономике страны. Основная
задача межотраслевого баланса состоит
в нахождении такого вектора валового
выпуска
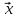
который при известной матрице прямых
затрат A обеспечивает заданный вектор
конечного продукта
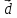
Зная матрицу А и вектор
остаётся решить уравнение
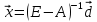
5. Сформулируйте и докажите первый критерий продуктивности
Матрица А=>0 продуктивна тогда и только
тогда, когда матрица
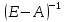
и неотрицательна. Пусть существует
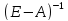
тогда x=(E-A)-1y,
где оба множителя >0, следовательно,
x=>0, значит матрица
продуктивна. Пусть А продуктивна.
(E-A)x=e1,
значит с1=>0, (E-A)x=e2,
значит с2=>0, следовательно,
(с1,с2,cn)=C=>0.
(E-A)C=E=>C=(E-A)-1=>0
6. Докажите, что если неотрицательная квадратная матрица продуктивна, то ее число Фробениуса меньше 1
Матрица А≥0 называется продуктивной,
если для любого вектора
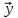
существует решение
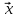
уравнения
Пусть матрица А – неотрицательна и
продуктивна.
Тогда для любого неотрицательного
вектора
существует решение
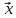
уравнения
Пусть
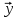
тогда, очевидно,
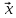
Умножив
слева еа левый вектор Фробениуса
и учитывая, что
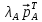
то получим
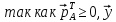
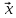
то
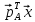
>0. Поэтому из последнего равенства
вытекает, что
<1.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
-
-
May 28 2018, 08:04
- Наука
- Cancel
Норма Фробениуса
Норма Фробениуса или, как её ещё называют Евклидова норма, — это квадратный корень сумм квадратов модулей элементов матрицы размера m × n:
Простой пример. Есть матрица размера 3 × 3:
Она же, но с элементами, возведёнными в квадрат:
Сумма элементов этой матрицы будет равна 60. Квадратный корень из 60 примерно равен 7,746. Это число и есть норма Фробениуса для нашей матрицы.
Есть иной способ вычисления нормы Фробениуса: как квадратный корень произведения следа этой матрицы и эрмитово-сопряжённой матрицы:
https://ru.wikipedia.org/wiki/Норма_матрицы#Норма_Фробениуса
Пусть positiveи в качестве неотрицательный соответственно описывают матрицы исключительно положительными действительными числами в элементах и матриц. с исключительно неотрицательными действительными числами в качестве элементов. собственные значения реальная квадратная матрица A – это комплексные числа, которые составляют спектр. экспоненциальный рост степеней матрицы A при k → ∞ управляется значение A с наибольшим абсолютным значением (модулем ). Теорема неотъемлемых свойств главного значения и соответствующих собственных векторов, когда A –рицательная вещественная квадратная матрица. Первые результаты были связаны с Оскаром Перроном (1907) и касались положительных матриц. Позже Георг Фробениус (1912) нашел их распространение на классы неотрицательных матриц.
Положительные матрицы
Пусть A = (aij) { displaystyle A = (a_ {ij})}



- Существует положительное действительное число r, называемое корнем Перрона или собственным уровнем Перрона – Фробениуса (также называется ведущим величиной положения или доминантным определенным значением ), так что r области значения A и любого другого значения длины λ (возможно, комплексным ) в абсолютное значение строго меньше, чем r, | λ | спектральный радиус ρ (A) { displaystyle rho (A)}
равно г. Если матричные коэффициенты являются алгебраическими, это означает, что собственное значение – это Перронное число.
- Собственное значение Перрона – Фробениуса простое: r является основным корнем типического многочлена от A. Следовательно, собственное подпространство, связанное с r, одномерно. (То же самое верно для левого собственного подпространства, т. Е. Собственного подпространства для A, транспонированной A.)
- Существует собственное v = (v 1,…, v n) оператора A с числом r таким, что все компоненты v положительны: A v = rv, v i>0 для 1 ≤ i ≤ n. (Соответственно, существует положительный левый собственный вектор w: w A = rw, w i>0.) Он известен в литературе во многих вариантах как Вектор Перрона, Собственный вектор Перрона, Собственный вектор Перрона-Фробениуса, ведущий собственный вектор или доминантный собственный вектор .
- Других положительных (тем более неотрицательных) собственных векторов, кроме положительных, нет кратные v (соответственно, левые собственные конструкции, кроме w), т. е. все остальные конструктивные элементы должны иметь хотя бы один отрицательный компонент.
- lim k → ∞ A k / rk = vw T { displaystyle lim _ {k rightarrow infty} A ^ {k} / r ^ {k} = vw ^ {T}}
, где левый и правый собственный дизайн для A нормированы так, что wv = 1. Кроме того, матрица vw – это проекция на собственное подпространство, соответствующее r. Эта проекция называется проекцией Перрона .
- Формула Коллатца –Виландта : для всех неотрицательных ненулевых векторов x пусть f (x) будет минимальным размером [Ax] i / x i, взятый по всем тем i таким, что x i ≠ 0. Тогда f вещественная функция, максимум по всем не -отрицательные ненулевые стандарты x надлежащего уровня Перрона – Фробениуса.
- Формула «Min-max» Коллатца – Виландта принимает форму, аналогичную приведенной выше: для всех строго положительных векторов x пусть g (x) – максимальное значение [Ax] i / x i, взятое по i. Тогда g – вещественная функция, минимум которой по всем строго положительным вещественным веществом x является собственное Перрона – Фробениуса.
- Формула Биркгофа – Варга : Пусть x и y – строго положительные рекомендации. Тогда r = sup x>0 inf y>0 y ⊤ A xy ⊤ x = inf x>0 sup y>0 y ⊤ A xy ⊤ x = inf x>0 sup y>0 ∑ i, j = 1 nxi A ijyj / ∑ i = 1 nyixi. { displaystyle r = sup _ {x>0} inf _ {y>0} { frac {y ^ { top} Ax} {y ^ { top} x}} = inf _ {x>0} sup _ {y>0} { frac {y ^ { top} Ax} {y ^ { top} x}} = inf _ {x>0} sup _ {y>0} sum _ {i, j = 1} ^ {n} x_ {i} A_ {ij} y_ {j} / sum _ {i = 1} ^ {n} y_ {i} x_ {i}.}
- Донскер – Варадхан – Тогда Варадхан – <>Формула Фридланда : Пусть p – вектор вероятности, а x – строго положительный вектор. r = sup p inf x>0 ∑ i = 1 npi [A x ] i / xi. { Displaystyle r = sup _ {p} inf _ {x>0} sum _ {i = 1} ^ {n} p_ {i} [Ax] _ {i} / x_ { i}.}
- Формула Фидлера : r = sup z>0 inf x>0, y>0, x ∘ y = zy ⊤ A xy ⊤ x = sup z>0 inf x>0, y>0, x ∘ y = z ∑ i, j = 1 nxi A ijyj / ∑ i = 1 nyixi. { Displaystyle г = sup _ {z>0} inf _ {x>0, y>0, x circ y = z} { frac {y ^ { top} Ax} {y ^ { top} x}} = sup _ {z>0} inf _ {x>0, y>0, x circ y = z} sum _ {i, j = 1} ^ { n} x_ {i} A_ {ij} y_ {j} / sum _ {i = 1} ^ {n} y_ {i} x_ {i}.}
- Собственное значение Перрона – Фробениуса удовлетворяет неравенствам
-
- min i ∑ jaij ≤ r ≤ max i ∑ jaij. { displaystyle} j min _ sum. { displaystyle} j min _ sum. } a_ {ij} leq r leq max _ {i} sum _ {j} a_ {ij}.}
- min i ∑ jaij ≤ r ≤ max i ∑ jaij. { displaystyle} j min _ sum. { displaystyle} j min _ sum. } a_ {ij} leq r leq max _ {i} sum _ {j} a_ {ij}.}
Все эти свойства выходят за рамки строго положительных матриц до примитивных матриц ( см. Ниже). Факты 1-7 можно найт и в Мейере глава 8 утверждает 8.2.11–15 стр. 667 и упражнениях 8.2.5,7,9 стр. 668–669.
Левый и правый построенный w и v таковы, что времена нормированы так, чтобы сумма их компонентов была равна 1; в этом случае их иногда называют стохастическими собственными руками . Как w T v = 1 { displaystyle w ^ {T} v = 1}
неотрицательные матрицы
Имеется расширение матриц. с неотрицательными элементами. Так как любая неотрицательная матрица может быть получена как предел положительных матриц, получается существование собственного вектора с неотрицательными компонентами; соответствующее собственное значение будет неотрицательным и больше или равно по модулю всем остальным собственным значениям. Однако для <пример294>A = (0 1 1 0) { displaystyle A = left ({ begin {smallmatrix} 0 1 \ 1 0 end {smallmatrix}} right)}

Однако Фробениус обнаружил особый подкласс неотрицательных матриц – неприводимых матриц, возможно нетривиальное обобщение. Для таких матрицы, хотя собственные значения, достигают абсолютного значения, их структура находится под контролем: они имеют вид ω r { displaystyle omega r}

Классификация матриц
Пусть A – квадратная матрица (не обязательно положительная или даже действительная). Матрица A неприводима, выполняется любое из следующих эквивалентных свойств.
Определение 1: A не имеет нетривиальных инвариантных координатных подпространств. Здесь нетривиальное координатное подпространство означает линейное подпространство , натянутое на любое собственное подмножество базисных векторов R n { displaystyle mathbb {R} ^ {n}}
Эквивалентно, представление группы из (R, +) { displaystyle ( mathbb {R}, +)}


Определение 2: Не может быть сопряжен в блок верхняя треугольная форма с помощью матрицы перестановок P:
- PAP – 1 ≠ (EF 0 G), { displaystyle PAP ^ {- 1} neq { begin {pmatrix} EF \ 0 G end {pmatrix}},}
где E и G – нетривиальные (т.е. размером больше нуля) квадратные матрицы.
Если A неотрицательно, имеет другое определение:
Определение 3: Можно связать с матрицей A некий ориентированный граф GA. Он имеет ровно n вершин, где n – размер A, и есть ребро от вершины i до вершины j именно тогда, когда A ij>0. Тогда матрица A неприводима тогда и только тогда, когда связанная с ней граф G A является Матрица приводима, если она не является неприводимой.
Матрица A является примитивной, если она неотрицательна и ее степень m положительна для некоторого натурального числа m (т.е. все элементы матрицы A положительны).
Пусть А неотрицательно. Зафиксируйте индекс i и определите период индекс i как наибольший общий делитель всех натуральных чисел m, что (A) ii>0. Когда A неприводима, каждый период одинаков и называется периодом A. Фактически, когда A неприводимо, период может быть определен как наибольший общий делитель замкнутые границы пути в G A (см. Кухни) на стр. 16). Период также называется индексом импримитивности (стр. 674 Мейера) или порядком цикличности. Если период равен 1, A является апериодическим . Можно доказать, что примитивные матрицы – это то же самое, что и неприводимые апериодические неотрицательные матрицы.
Все утверждение теоремы Перрона – Фробениуса для положительных матриц остаются верными для примитивных матриц. Те же справедливы и для неотрицательной неприводимой матрицы, за исключением того, что она может иметь несколько значений. Фактически количество таких значений равно периоду.
Результаты для неотрицательных матриц были впервые получены Фробениусом в 1912 году.
Теорема Перрона – Фробениуса для неприводимых неотрицательных матриц
Пусть A – неприводимая неотрицательная матрица. Матрица размера n × n с периодом h и спектральным радиусом ρ (A) = r. Тогда верны следующие утверждения.
- Число r – положительное действительное и собственное значение матрицы A, называемое собственное число Перрона – Фробениуса .
- Собственное значение Перрона – Фробениуса r простое. Правое и левое собственные подпространства, связанные с r, одномерны.
- A имеет правый собственный вектор v с соответствующим значением r, все компоненты которого положительны.
- Аналогично, A левый собственный вектор с собственным значением r, все компоненты которого положительны.
- Единственные собственные компоненты положительны, связанные с определением r.
- Матрица A имеет ровно h (где h – период ) комплексные собственные значения с модулем r. Каждый из них является основным корнем характерного особенности и является произведением его на h-й корень из единицы.
- . Пусть ω = 2π / h. Тогда матрица A аналогична матрице eA, следовательно, матрица спектра A инвариантен относительно умножения на e (соответствующий повороту комплексной плоскости на угол ω).
- Если h>1, то существует матрица перестановок P такая, что
-
- PAP – 1 = (0 A 1 0 0… 0 0 0 A 2 0… 0 ⋮ ⋮ ⋮ ⋮ 0 0 0 0… A h – 1 A h 0 0 0… 0), { displaystyle PAP ^ {- 1} = { begin {pmatrix} 0 A_ {1} 0 0 ldots 0 \ 0 0 A_ {2} 0 ldots 0 \ vdots vdots vdots vdots vdots \ 0 0 0 0 ldots A_ {h-1} \ A_ { h} 0 0 0 ldots 0 end {pmatrix}},}
- где блоки вдоль главной диагонали представляют собой нулевые квадратные матрицы.
- PAP – 1 = (0 A 1 0 0… 0 0 0 A 2 0… 0 ⋮ ⋮ ⋮ ⋮ 0 0 0 0… A h – 1 A h 0 0 0… 0), { displaystyle PAP ^ {- 1} = { begin {pmatrix} 0 A_ {1} 0 0 ldots 0 \ 0 0 A_ {2} 0 ldots 0 \ vdots vdots vdots vdots vdots \ 0 0 0 0 ldots A_ {h-1} \ A_ { h} 0 0 0 ldots 0 end {pmatrix}},}
- 9. Формула Коллатца –Виландта : для всех неотрицательных ненулевых векторов x пусть f (x) будет минимальным значением [Ax] i / x i взято по всем таким образом, что x i ≠ 0. Тогда f вещественной функцией, максимум является единиц величиной Перрона – Фробениуса.
- 10. Собственное значение Перрона – Фробениуса удовлетворяет неравенствам
- min i ∑ j a i j ≤ r ≤ max i ∑ j a i j. { displaystyle min _ {i} sum _ {j} a_ {ij} leq r leq max _ {i} sum _ {j} a_ {ij}.}
- min i ∑ j a i j ≤ r ≤ max i ∑ j a i j. { displaystyle min _ {i} sum _ {j} a_ {ij} leq r leq max _ {i} sum _ {j} a_ {ij}.}
Пример A Знак равно (0 0 1 0 0 1 1 1 0) { displaystyle A = left ({ begin {smallmatrix} 0 0 1 \ 0 0 1 \ 1 1 0 end {smallmatrix} } right)}
Дополнительные свойства
Пусть A – неприводимая неотрицательная матрица, тогда:
- (I + A) – положительная матрица. (Мейер п. 8.3.5 с. 672 ).
- Теорема Виландта. Если | B |
- Если некоторая степень A приводима, то она полностью приводима, т.е. для некоторой матрицы перестановок P она верно, что: PA q P – 1 = (A 1 0 0… 0 0 A 2 0… 0 ⋮ ⋮ ⋮ ⋮ 0 0 0… A d) { displaystyle PA ^ {q} P ^ {- 1 } = { begin {pmatrix} A_ {1} 0 0 dots 0 \ 0 A_ {2} 0 dots 0 \ vdots vdots vdots vdots 0 0 0 dots A_ {d} \ end {pmatrix}}}
, где A i – неприводимые матрицы, имеющие одинаковое максимальное собственное значение. эти матриц d является наибольшим общим делителем q и h, где h равно период A.
- Если c (x) = x + c k1x + c k2x +… + c ksx является характерным многочленом A, в котором только не -перечисляются нулевые члены, тогда период A равен наибольшему общему делителю k 1, k 2,…, k s.
- Cesàro средние значения : lim k → ∞ 1 / k ∑ i = 0,…, k A i / ri = (vw T), { displaystyle lim _ {k rightarrow infty} 1 / k sum _ {я = 0,…, k} A ^ {i} / r ^ {i} = (vw ^ {T}),}
где левый и правый построенный для A нормированы так, что wv = 1. Кроме того, матрица vw является спектральной проекцией, проекцией на r, проекцию Перрона.
- Пусть r – собственное значение Перрона – Фробениуса, тогда сопряженная матрица для (rA) положительна.
- Если A имеет хотя бы один ненулевой диагональный элемент, то A примитивна.
- Если 0 ≤ A < B, then rA≤ r B. Более того, если B неприводима, то неравенство строгое: r A< rB.
Матрица A является примитивен при условии, что он неотрицателен и A положителен для некоторого m, и, следовательно, A положительно для всех k ≥ m. Чтобы проверить примитивность, нужно определить, насколько большим может быть минимальное такое m, в зависимости от размера A:
- Если A – неотрицательная примитивная матрица размера n, то A положительна. Более того, это наилучший возможный результат, поскольку для матрицы M ниже степень M не является положительной для любого k < n − 2n + 2, since (M)11 = 0.
- M = (0 1 0 0 ⋯ 0 0 0 1 0 ⋯ 0 0 0 0 1 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 0 ⋯ 1 1 1 0 0 ⋯ 0) { displaystyle M = left ({ begin {smallmatrix} 0 1 0 0 cdots 0 \ 0 0 1 0 cdots 0 \ 0 0 0 1 cdots 0 \ vdots vdots vdots vdots vdots \ 0 0 0 0 cdots 1 \ 1 1 0 0 cdots 0 end {smallmatrix}} right)}
Приложения
На тему неотрицательных матриц было написано множество книг, и теория Перрона – Фробениуса неизменно является центральной особенностью. Следующие ниже примеры, приведенные ниже, лишь поверхностно касаются ее обширной области применения.
Неотрицательные матрицы
Теорема Перрона – Фробениуса не применяется непосредственно к неотрицательным матрицам. Тем не менее, любая приводимая квадратная матрица A может быть записана в виде верхнетреугольного блока (известная как нормальная форма приводимой матрицы )
-
-
-
- PAP = (B 1 ∗ ∗ ⋯ ∗ 0 B 2 ∗ ⋯ ∗ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ ∗ 0 0 0 ⋯ B h) { displaystyle left ({ begin {smallmatrix} B_ {1} * * cdots * \ 0 B_ {2} * cdots * \ vdots vdots vdots vdots \ 0 0 0 cdots * \ 0 0 0 cdots B_ {h} end {smallmatrix}} right)}
- PAP = (B 1 ∗ ∗ ⋯ ∗ 0 B 2 ∗ ⋯ ∗ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ ∗ 0 0 0 ⋯ B h) { displaystyle left ({ begin {smallmatrix} B_ {1} * * cdots * \ 0 B_ {2} * cdots * \ vdots vdots vdots vdots \ 0 0 0 cdots * \ 0 0 0 cdots B_ {h} end {smallmatrix}} right)}
-
-
где P – это матрица перестановок, и каждый B i является квадратной матрицей, которая либо неприводима, либо равна нулю. Теперь, если A неотрицательна, то также и каждый блок PAP, более того, спектр A является просто объединением спектры B i.
Обратимость A также может быть изучена. Инверсия PAP (если она существует) должна иметь диагональные блоки формы B i, поэтому, если любой B i не является обратимым, то ни PAP, ни A. И наоборот, пусть D будет блочно-диагональной матрицей, соответств ующей PAP, другими словами PAP со звездочками, обнуленными. Если каждый B i обратим, то D тоже. а также D (PAP) равно единице плюс нильпотентная матрица. Но такая матрица всегда обратима (если N = 0, обратное к 1 – N равно 1 + N + N +… + N), поэтому PAP и A обратимы.
Следовательно, многие из спектральных свойств A можно вывести, применяя теорему к неприводимому B i. Например, корень Перрона – это максимум ρ (B i). Хотя все еще будут собственные векторы с неотрицательными компонентами, вполне возможно, что ни один из них не будет положительным.
Стохастические матрицы
Строка (столбец) стохастическая матрица – это квадратная матрица, каждая из строк (столбцов) которой состоит из неотрицательных действительных чисел, сумма которых равна единице. Теорема не может быть применена непосредственно к таким матрицам, потому что они не обязательно должны быть неприводимыми.
Если A является стохастическим по строкам, то вектор-столбец с каждой записью 1 является собственным вектором, соответствующим собственному значению 1, которое также является ρ (A) согласно замечанию выше. Это может быть не единственное собственное значение на единичной окружности: и соответствующее собственное подпространство может быть многомерным. Если A является стохастическим по строкам и неприводимым, то проекция Перрона также является стохастической по строкам и все ее строки равны.
Алгебраическая теория графов
Эта теорема находит особое применение в алгебраической теории графов. «Базовый граф» неотрицательной n-квадратной матрицы – это граф с вершинами, пронумерованными 1,…, n и дугой ij тогда и только тогда, когда A ij ≠ 0. Если базовый граф такой матрицы матрица сильно связна, то матрица неприводима, и поэтому теорема применима. В частности, матрица смежности сильно связного графа неприводима.
Конечные цепи Маркова
Теорема имеет естественную интерпретацию в теории конечных цепей Маркова (где это теоретико-матричный эквивалент сходимости неприводимой конечной цепи Маркова к ее стационарному распределению, сформулированный в терминах матрицы переходов цепи; см., например, статья о субсдвиге конечного типа ).
Компактные операторы
В более общем смысле его можно распространить на случай неотрицательных компактных операторов, которые во многом напоминают конечномерные матрицы. Их обычно изучают в физике под названием операторов переноса, а иногда и операторов Рюэля – Перрона – Фробениуса (после Дэвида Руэля ). В этом случае главное собственное значение соответствует термодинамическому равновесию динамической системы, а меньшие собственные значения – режимам распада системы, которая не находится в равновесии. Таким образом, теория предлагает способ обнаружить стрелу времени в том, что в противном случае могло бы показаться обратимым, детерминированным динамическим процессом, если рассматривать его с точки зрения топологии множества точек.
Методы доказательства
Общей чертой многих доказательств является теорема Брауэра о неподвижной точке. Другой популярный метод – это Wielandt (1950). Он использовал описанную выше формулу Коллатца -Виландта, чтобы расширить и прояснить работу Фробениуса. Другое доказательство основано на спектральной теории, часть аргументов которой заимствована.
Корень Перрона является строго максимальным собственным значением для положительных (и примитивных) матриц
Если A является положительной (или, в более общем смысле, примитивной) матрицей, то существует действительное положительное собственное значение r (Перрон – Фробениус собственное значение или корень Перрона), который строго больше по модулю, чем все другие собственные значения, следовательно, r – это спектральный радиус числа A.
Это утверждение не выполняется для общих неотрицательных неприводимых матриц, которые имеют h собственных значений с тем же абсолютным собственным значением, что и r, где h – период A.
Доказательство для положительных матриц
Пусть A – положительная матрица, предположим, что ее спектральный радиус ρ (A) = 1 (иначе рассмотрим A / ρ (A)). Следовательно, существует собственное значение λ на единичной окружности, а все остальные собственные значения меньше или равны 1 по модулю. Предположим, что на единичную окружность также попадает другое собственное значение λ ≠ 1. Тогда существует натуральное число m такое, что A – положительная матрица, а действительная часть λ отрицательна. Пусть ε – половина наименьшего диагонального элемента матрицы A, и положим T = A – εI, которая является еще одной положительной матрицей. Более того, если Ax = λx, то Ax = λx, таким образом, λ – ε является собственным значением T. Из-за выбора m эта точка лежит вне единичного круга, следовательно, ρ (T)>1. С другой стороны, все элементы в T положительны и меньше или равны элементам в A, поэтому по формуле Гельфанда ρ (T) ≤ ρ (A) ≤ ρ (A) = 1. Это противоречие означает, что λ = 1 и других собственных значений на единичной окружности быть не может.
Абсолютно те же аргументы могут быть применены к случаю примитивных матриц; нам просто нужно упомянуть следующую простую лемму, разъясняющую свойства примитивных матриц.
Лемма
Для неотрицательного A, предположим, что существует m такое, что A положительно, тогда все A, A, A,… положительны.
A = AA, поэтому он может иметь нулевой элемент только в том случае, если некоторая строка A полностью равна нулю, но в этом случае та же строка A будет нулем.
Применяя те же аргументы, что и выше для примитивных матриц, докажите основное утверждение.
Степенной метод и положительная собственная пара
Для положительной (или, в более общем смысле, неприводимой неотрицательной) матрицы A доминирующий собственный вектор является действительным и строго положительным (для не- отрицательный A, соответственно неотрицательный.)
Это может быть установлено с помощью метода степени, который утверждает, что для достаточно общей (в смысле ниже) матрицы A последовательность векторов b k + 1 = Ab k / | Ab k | сходится к собственному вектору с максимальным собственным значением. (Начальный вектор b 0 может быть выбран произвольно, за исключением некоторой установки нуля меры). Начиная с неотрицательного вектора b 0, получается последовательность неотрицательных векторов b k. Следовательно, предельный вектор также неотрицателен. По степенному методу этот предельный вектор является доминирующим собственным вектором для A, что доказывает утверждение. Соответствующее собственное значение неотрицательно.
Для доказательства требуются два дополнительных аргумента. Во-первых, степенной метод сходится для матриц, у которых нет нескольких собственных значений, имеющих то же абсолютное значение, что и максимальное. Аргумент предыдущего раздела гарантирует это.
Во-вторых, чтобы гарантировать строгую положительность всех компонент собственного вектора для случая неприводимых матриц. Это следует из следующего факта, представляющего самостоятельный интерес:
- Лемма: учитывая положительную (или, в более общем смысле, неприводимую неотрицательную) матрицу A и v как любой неотрицательный собственный вектор для A, тогда она обязательно строго положительна и соответствующее собственное значение также строго положительно.
Доказательство. Одно из определений неприводимости неотрицательных матриц состоит в том, что для всех индексов i, j существует m такое, что (A) ij строго положительно. Для неотрицательного собственного вектора v и того, что по крайней мере один из его компонентов утверждает, что j-й строго положителен, соответствующее собственное значение строго положительно, действительно, если n такое, что (A) ii>0, отсюда: rv i = Av i ≥ (A) iivi>0. Следовательно, r строго положительно. Собственный вектор – строгая положительность. Тогда для m, такого что (A) ij>0, следовательно: rv j = (Av) j ≥ (A) ijvi>0, следовательно, v j строго положительно, т. е. собственный вектор строго положителен.
Кратность один
Этот раздел доказывает, что собственное значение Перрона – Фробениуса является простым корнем характеристического полинома матрицы. Следовательно, собственное подпространство, связанное с собственным значением Перрона – Фробениуса r, одномерно. Аргументы здесь близки к аргументам Мейера.
Дан строго положительный собственный вектор v, соответствующий r, и другой собственный вектор w с тем же собственным значением. (Векторы v и w могут быть выбраны действительными, поскольку оба A и r действительны, поэтому нулевое пространство Ar имеет базис, состоящий из действительных векторов.) Предполагая, что хотя бы один из компонентов w положителен (в противном случае умножьте w на −1). Если задано максимально возможное α такое, что u = v- α w неотрицательно, то одна из компонент u равна нулю, иначе α не является максимальным. Вектор u – это собственный вектор. Оно неотрицательно, поэтому по лемме, описанной в предыдущем разделе, неотрицательность подразумевает строгую положительность для любого собственного вектора. С другой стороны, как указано выше, по крайней мере, одна компонента u равна нулю. Противоречие означает, что w не существует.
Случай: нет жордановых ячеек, соответствующих собственному значению Перрона – Фробениуса r и всем другим собственным значениям, имеющим такое же абсолютное значение.
Если есть жорданова клетка, то бесконечная норма (A / r) ∞ стремится к бесконечности при k → ∞, но это противоречит существованию положительный собственный вектор.
Дано r = 1 или A / r. Пусть v – строго положительный собственный вектор Перрона – Фробениуса, поэтому Av = v, тогда:
‖ v ‖ ∞ = ‖ A kv ‖ ∞ ≥ ‖ A k ‖ ∞ min i (vi), ⇒ ‖ A k ‖ ∞ ≤ ‖ V ‖ / мин я (vi) { displaystyle | v | _ { infty} = | A ^ {k} v | _ { infty} geq | A ^ {k} | _ { infty} min _ {i} (v_ {i}), ~~ Rightarrow ~~ | A ^ {k} | _ { infty} leq | v | / min _ {i } (v_ {i})}
- J k = (λ 1 0 λ) k = (λ kk λ k – 1 0 λ k), { displaystyle J ^ {k} = { begin {pmatrix} lambda 1 \ 0 lambda end {pmatrix}} ^ {k} = { begin {pmatrix} lambda ^ {k} k lambda ^ {k-1} \ 0 lambda ^ {k} end { pmatrix}},}
, следовательно, J ∞ = | k + λ | (для | λ | = 1), поэтому при k стремится к бесконечности. Поскольку J = C AC, то A ≥ J / (C C), поэтому оно также стремится к бесконечности. Полученное противоречие означает, что для соответствующих собственных значений нет жордановых клеток.
Объединение двух приведенных выше утверждений показывает, что собственное значение Перрона – Фробениуса r является простым корнем характеристического многочлена. В случае непримитивных матриц существуют другие собственные значения, которые имеют то же абсолютное значение, что и r. То же самое верно и для них, но требует дополнительной работы.
Никаких других неотрицательных собственных векторов
Для положительной (или, в более общем смысле, неприводимой неотрицательной матрицы) A, собственный вектор Перрона – Фробениуса является единственным (с точностью до умножения на константу) неотрицательным eigenvector for A.
Other eigenvectors must contain negative or complex components since eigenvectors for different eigenvalues are orthogonal in some sense, but two positive eigenvectors cannot be orthogonal, so they must correspond to the same eigenvalue, but the eigenspace for the Perron–Frobenius is one-dimensional.
Assuming there exists an eigenpair (λ, y) for A, such that vector y is positive, and given (r, x), where x – is the left Perron–Frobenius eigenvector for A (i.e. eigenvector for A), then rxy = (x A) y = x (Ay) = λxy, also x y>0, so one has: r = λ. Since the eigenspace for the Perron–Frobenius eigenvalue r is one-dimensional, non-negative eigenvector y is a multiple of the Perron–Frobenius one.
Collatz–Wielandt formula
Given a positive (or more generally irreducible non-negative matrix) A, one defines the function f on the set of all non-negative non-zero vectors x such th at f (x) – минимальное значение [Ax] i / x i, взятое для всех тех i, что x i ≠ 0. Тогда f равно действительная функция, максимум которой является собственным значением Перрона – Фробениуса r.
Для доказательства мы обозначим максимум f значением R. Доказательство требует показать R = r. Подставляя собственный вектор Перрона-Фробениуса v в f, получаем f (v) = r и заключаем, что r ≤ R. Для противоположного неравенства рассмотрим произвольный неотрицательный вектор x и положим ξ = f (x). Определение f дает 0 ≤ ξx ≤ Ax (покомпонентно). Теперь мы используем положительный правый собственный вектор w для A для собственного значения Перрона-Фробениуса r, тогда ξ w x = w ξx ≤ w (Ax) = (w A) x = r w x. Следовательно, f (x) = ξ ≤ r, что подразумевает R ≤ r.
проекция Перрона как предел: A / r
Пусть A будет положительной (или, в более общем смысле, примитивной) матрицей, и пусть r его собственное значение Перрона – Фробениуса.
- Существует предел A / r для k → ∞, обозначим его через P.
- P – оператор проекции : P = P, который коммутирует с A: AP = PA.
- Изображение P одномерно и натянуто на собственный вектор Перрона – Фробениуса v (соответственно для P – на собственный вектор Перрона – Фробениуса w для A).
- P = vw, где v, w нормированы так, что wv = 1.
- Следовательно, P – положительный оператор.
Следовательно, P является a для собственного значения Перрона – Фробениуса r и называется проекцией Перрона. Сказанное выше утверждение неверно для общих неотрицательных неприводимых матриц.
Фактически приведенная выше формула (кроме формулы 5) действительна для любой матрицы M, такой что существует собственное значение r, которое строго больше других собственных значений по модулю и является простым корнем характеристики многочлен. (Эти требования выполняются для примитивных матриц, как указано выше).
Учитывая, что M диагонализуема, M сопряжена с диагональной матрицей с собственными значениями r 1,…, r n на диагонали (обозначим r 1 = г). Матрица M / r будет сопряженной (1, (r 2 / r),…, (r n / r)), которая стремится к (1,0, 0,…, 0) при k → ∞, поэтому предел существует. Тот же метод работает для общего M (без предположения, что M диагонализуема).
Свойства проекции и коммутативности являются элементарными следствиями определения: MM / r = M / r M; P = lim M / r = P. Третий факт также элементарен: M (Pu) = M lim M / ru = lim rM / ru, поэтому переход к пределу дает M (Pu) = r (Pu), так что образ P лежит в собственном r-подпространстве для M, которое по предположениям одномерно.
Обозначение v, r-собственный вектор для M (w для M). Столбцы P кратны v, потому что ими покрывается образ P. Соответственно, строки w. Итак, P принимает форму (a v w) для некоторого a. Следовательно, его след равен (a w v). След проектора равен размеру его изображения. Ранее было доказано, что он не более чем одномерный. Из определения видно, что P одинаково действует на r-собственный вектор для M. Значит, он одномерный. Таким образом, выбор (wv) = 1 влечет P = vw.
Неравенства для собственного значения Перрона – Фробениуса
Для любой неотрицательной матрицы A ее собственное значение Перрона – Фробениуса r удовлетворяет неравенству:
- r ≤ max i ∑ j A i j. { displaystyle r ; leq ; max _ {i} sum _ {j} A_ {ij}.}
Это не относится к неотрицательным матрицам: для любой матрицы A с собственным значением λ { displaystyle scriptstyle lambda}

Любая матрица , индуцированная норма удовлетворяет неравенству ‖ A ‖ ≥ | λ | { Displaystyle scriptstyle | А | geq | lambda |}





Другое неравенство:
- min i ∑ j A ij ≤ r. { Displaystyle мин _ {я} сумма _ {j} A_ {ij} ; leq ; r.}
Этот факт характерен для неотрицательных матриц; для общих матриц ничего подобного нет. Учитывая, что A положительно (а не только неотрицательно), тогда существует положительный собственный вектор w такой, что Aw = rw и наименьшая компонента w (скажем, w i) равна 1. Тогда r = (Aw) i ≥ чисел сумма в строке i матрицы A. Таким образом, минимальная сумма строки дает нижнюю границу для r, и это наблюдение можно распространить на все неотрицательные матрицы по непрерывности.
Другой способ аргументировать это – использовать формулу Коллатца -Виландта. Берется вектор x = (1, 1,…, 1) и сразу получается неравенство.
Дальнейшие доказательства
Проекция Перрона
Теперь доказательство проводится с использованием спектрального разложения. Уловка здесь состоит в том, чтобы отделить корень Перрона от других значений. Спектральная проекция, связанная с корнем Перрона, называется Перрона, и она проекционным следующим своим:
Проекция Перрона неприводимой неотрицательной квадратной матрицы является положительной матрицей.
Выводы Перрона, а также (1) – (5) теоремы являются следствиями этого результата. Ключевым моментом является то, что положительная проекция всегда имеет первый ранг. Это означает, что если A – неприводимая неотрицательная квадратная матрица, то алгебраическая и геометрическая кратности ее корня Перронаны единице. Также, если P – его проекция Перрона, то AP = PA = ρ (A) P, так что каждый столбец P является положительным правым собственным вектором A, каждая строка является положительным левым собственным вектором. Более того, если Ax = λx, то PAx = λPx = ρ (A) Px, что означает Px = 0, если λ ≠ ρ (A). Таким образом единственными положительными собственными руками являются те, которые связаны с ρ (A). Если A – примитивная матрица с ρ (A) = 1, то ее можно разложить как P ⊕ (1 – P) A, так что A = P + (1 – P) A. По мере увеличения n второй из членов этих убывает до нуля, оставляя P как предел для A при n → ∞.
Степенной метод – удобный способ вычислить проекцию Перрона примитивной матрицы. Если v и w – положительные элементы строк и столбцов, которые он генерирует, то проекция Перрона равна просто wv / vw. Спектральные проекции не заблокированы аккуратно, как в форме Джордана. Здесь наложены друг на друга, и каждый, как правило, сложные элементы, распространяющиеся на все четыре угла квадратной матрицы. Тем не менее, они сохраняют взаимную ортогональность, что облегчает разложение.
Периферийная проекция
Анализ, когда A является несократимым и неотрицательным, в целом. Проекция Перрона по-прежнему положительна, но теперь могут быть другие собственные значения модуля ρ (A), которые исключают использование методов степеней и предотвращают убывание степеней (1 – P) A, как в примитивном случае, когда ρ (A) = 1. Итак, мы рассматриваем периферийную проекцию, которая является спектральной проекцией A, которая является всем собственным значением, имеющим модуль ρ (A). Затем можно показать, что периферийная проекция неприводимой неотрицательной квадратной матрицы является неотрицательной матрицей с положительной диагональю.
Цикличность
Предположим также, что ρ (A) = 1 и A имеет h собственных значений на единичной окружности. Если P – периферийная проекция, тогда матрица R = AP = PA неотрицательна и неприводима, R = P, а циклическая группа P, R, R,…., R представляет гармоники матрицы A. Спектральная проекция матрицы A в собственном значении λ на единичной окружности задается формулой h – 1 ∑ 1 h λ – k R k { displaystyle scriptstyle h ^ {- 1} sum _ {1} ^ {h} lambda ^ {- k} R ^ {k }}
Контрпримеры
Матрицы L = (1 0 0 1 0 0 1 1 1) { displaystyle left ({ begin {smallmatrix} 1 0 0 \ 1 0 0 \ 1 1 1 end {smallmatrix}} right)}


Терминология
Проблема, которая вызывает путаницу, заключается в отсутствии стандартизации в определениях. Например, некоторые используют термины строго положительный и положительный для обозначения>0 и ≥ 0 соответственно. В этой статье положительное означает>0, неотрицательное означает ≥ 0. Еще одна неприятная область касается разложимости и сводимости: неприводимый – это перегруженный термин. Во избежание такой ненулевую неотрицательную квадратную матрицу A, что 1 + A примитивно, иногда называют связной. Тогда неприводимые неотрицательные квадратные матрицы и связанные матрицы являются синонимами.
Неотрицательный собственный вектор часто регулируется, чтобы сумма его компонентов была равна единице; в этом случае собственный вектор является вектором распределения вероятностей и иногда называется стохастическим собственным вектором.
Собственное значение Перрона – Фробениуса и доминирующее собственное значение – альтернативные названия корня Перрона. Спектральные проекции также известны как спектральные проекторы и спектральные идемпотенты. Период иногда называют индексом импримитивности или порядком цикличности.
См. Также
Примечания
Ссылки
Исходные статьи
- Перрон, Оскар (1907), «Теория Цура Матрицы» «, Mathematische Annalen, 64(2): 248–263, doi : 10.1007 / BF01449896, hdl : 10338.dmlcz / 104432
- Фробениус, Георг (май 1912 г.), «Ueber Matrizen aus nicht negativen Elementen», Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften : 456–477,
- Георг (1908), «Über Matrizen aus positiven Elementen, 1», Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften: 471–476
- Frobenius, Georg (1909), «Uber Matrizen aus Positiven Elementen, «berchen» Akademie der Wissenschaften: 514–518
- Гантмахер, Феликс (2000) [1959], Теория матриц, Том 2, A MS Chelsea Publishing, ISBN 978-0-8218-2664-5 (издание 1959 года имело другое название: «Приложения теории матриц». Также нумерация глав в двух изданиях разная.)
- Лэнгвилл, Эми; Мейер, Карл (2006), рейтинг страницы Google и выше, Princeton University Press, doi : 10.1007 / s10791-008-9063-y, ISBN 978-0-691-12202-1
- Кинер, Джеймс (1993), «Теорема Перрона – Фробениуса и рейтинг футбольных команд», SIAM Review, 35 (1): 80– 93, doi : 10.1137 / 1035004, JSTOR 2132526
- Мейер, Карл (2000), Матричный анализ и прикладная линейная алгебра (PDF), SIAM, ISBN 978-0-89871-454-8, заархивировано из оригинала (PDF) на 07.03.2010
- Романовский В. (1933), “Sur les zéros des matrices stocastiques”, Bulletin de la Société Mathématique de France, 61 : 213–219, doi : 10.24033 / bsmf.1206
- Коллатц, Лотар (1942), «Einschließungssatz für die charakteristischen Zahlen von Matrizen», Mathematische Zeitschrift, 48 (1): 221–226, doi : 10.1007 / BF01180013
- Виландт, Гельмут (1950), «Unzerlegbare, nicht negative Matrizen», Mathematische Zeitschrift, 52 (1): 642–648, doi : 10.1007 / BF02230720, hdl : 10338.dmlcz / 100322
Дополнительная литература
- Абрахам Берман, Роберт Дж. Племмонс, Неотрицательные матрицы в математических науках, 1994, SIAM. ISBN 0-89871-321-8.
- Крис Годсил и Гордон Ройл, Алгебраическая теория графов, Springer, 2001.
- А. Грэм, Неотрицательные матрицы и применимые темы в линейной алгебре, John Wiley Sons, Нью-Йорк, 1987.
- R. А. Хорн и К.Р. Джонсон, Матричный анализ, Cambridge University Press, 1990
- Бас Лемменс и Роджер Нуссбаум, Нелинейная теория Перрона-Фробениуса, Кембриджские трактаты по математике 189, Кембриджский университет. Press, 2012.
- С. П. Мейн и Р.Л. Твиди, Цепи Маркова и стохастическая стабильность Лондон: Springer-Verlag, 1993. ISBN 0-387-19832-6 (2-е издание, Cambridge University Press, 2009)
- Хенрик Минк, неотрицательные матрицы, John Wiley Sons, Нью-Йорк, 1988, ISBN 0-471-83966-3
- Сенета, Э. Неотрицательные матрицы и цепи Маркова. 2-е изд. изд., 1981, XVI, 288 стр., Серия Springer в мягкой обложке по статистике. (Первоначально опубликовано Allen Unwin Ltd., Лондон, 1973 г.) ISBN 978-0-387-29765-1
- Супруненко, Д.А. (2001) [1994], Энциклопедия математики, EMS Press (Утверждение, что A j имеет порядок н / ч в конце утверждения Теорема неверна.)
- Варга, Ричард С. (2002), Матричный итерационный анализ (2-е изд.), Springer-Verlag.



![{displaystyle r=sup _{p}inf _{x>0}sum _{i=1}^{n}p_{i}[Ax]_{i}/x_{i}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45dd8fd197c0aedebf82064d1d0c2276fc7e8866)











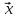
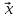
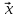
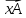
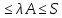
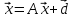
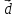
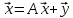
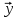
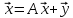
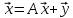
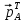
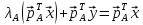
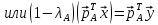
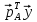
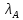




![{displaystyle r=sup _{p}inf _{x>0} sum _ {i = 1} ^ {n} p_ {i} [Ax] _ {i} / x_ {i}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45dd8fd197c0aedebf82064d1d0c2276f%20c7e8866)



 , где A i – неприводимые матрицы, имеющие одинаковое максимальное собственное значение. эти матриц d является наибольшим общим делителем q и h, где h равно период A.
, где A i – неприводимые матрицы, имеющие одинаковое максимальное собственное значение. эти матриц d является наибольшим общим делителем q и h, где h равно период A.

