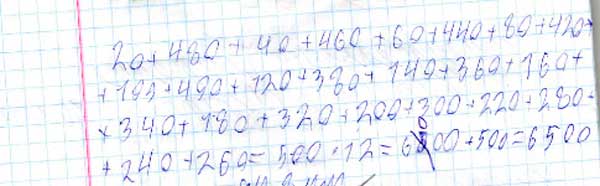Га́уссовы це́лые чи́сла (гауссовы числа, целые комплексные числа) — это комплексные числа, у которых как вещественная, так и мнимая часть — целые числа[1].
Примеры: 
Впервые введены Гауссом в монографии «Теория биквадратичных вычетов» (1828—1832)[2] [3]. Множество гауссовых целых чисел принято обозначать ![{mathbb {Z}}[i],](https://wikimedia.org/api/rest_v1/media/math/render/svg/59ada2ccab5ac1f61c1a433445d58dea97a0c69d)


Общие свойства[править | править код]
Определение и классификация[править | править код]
Формальное определение:
.
Множество ![{mathbb {Z}}[i]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ffa94e9e2e6d9e5e5373d5fafb954b902743fde)

Сопряжённое к гауссовому числу 

Каждое гауссово число 
Поэтому гауссово число есть целое алгебраическое число.
Норма[править | править код]
Норма для гауссова числа 
.
Свойства нормы[7]:
Норма, как и модуль, обладает важным свойством мультипликативности[7]:
Отсюда следует[8], что обратимыми элементами кольца (делителями единицы) являются те элементы, у которых норма равна 1, то есть 
Два гауссовых числа называются ассоциированными, если одно получается из другого умножением на делитель единицы. Легко видеть, что ассоциированность — отношение эквивалентности[8]. Пример: гауссовы числа 

.
У каждого ненулевого гауссова числа есть три ассоциированных с ним. Нормы всех четырёх ассоциированных между собой чисел совпадают.
Теория делимости[править | править код]
Деление нацело[править | править код]
Деление нацело гауссовых чисел определяется обычным образом[7]:
Произношение: один из трёх равносильных вариантов.
Используются традиционные термины: делимое или кратное (


Пример: число 2 делится нацело на 

Все гауссовы числа делятся на делители единицы, поэтому любое гауссово число, отличное от делителей единицы, имеет как минимум 8 делителей: 4 делителя единицы и 4 их произведения на само это число. Эти делители называются тривиальными[9].
Деление нацело в ![{mathbb {Z}}[i]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ffa94e9e2e6d9e5e5373d5fafb954b902743fde)
- Если гауссово число
делится нацело на обычное целое число, то на это целое число делятся как вещественная, так и мнимая часть
.
- Если
и
, то эти числа ассоциированы.
- Если
, то любое из 3 чисел, ассоциированных с
, делится на любое из 3 чисел, ассоциированных с
.
- Если
делится на
, то сопряжённое к делимому число
делится на сопряжённое к делителю
.
- Все делители гауссова числа
являются также делителями его нормы
.
- Норма гауссова числа чётна тогда и только тогда, когда это число делится на
.
- Если
, то и норма делимого, в силу мультипликативности, делится нацело на норму делителя. При этом:
Решётка кратных для
Геометрическое представление делимости[править | править код]
У каждого гауссова числа 



Но умножение на 






Пример: на рисунке одним из узлов решётки является число 

.
Простые гауссовы числа[править | править код]
Распределение гауссовых простых чисел на комплексной плоскости
Распределение гауссовых простых вблизи нуля
Простое гауссово число — это ненулевое число, не имеющее других делителей, кроме тривиальных. Число, не являющееся простым, называется составным. При этом делители единицы, подобно натуральной единице, не считаются ни простыми, ни составными числами[10].
Некоторые свойства простых гауссовых чисел:
Натуральное простое число может не быть гауссовым простым числом. Например, числа 2 и 5 в ![{mathbb {Z}}[i]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ffa94e9e2e6d9e5e5373d5fafb954b902743fde)
Разложение гауссовых чисел с нормой от 2 до 100 на простые гауссовы множители см. в таблице Факторизация гауссовых чисел.
Взаимно простые числа[править | править код]
Если гауссово число 


Отметим, что если нормы гауссовых чисел 



Укажем два свойства, аналогичные свойствам целых чисел.
Критерий Гаусса[править | править код]
Гаусс указал определяющие признаки простого числа в ![{mathbb {Z}}[i]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ffa94e9e2e6d9e5e5373d5fafb954b902743fde)
Примеры простых гауссовых чисел:
- к первой части критерия:
;
- ко второй части критерия:
.
Некоторые источники для большей ясности разделяют вторую часть критерия на две[14]:
- Числа, ассоциированные с
. Их норма равна 2.
- Числа, норма которых есть простое натуральное число вида
.
Сам Гаусс такого разделения не делал[15].
Следствия:
Разложение на простые множители[править | править код]
В ![{mathbb {Z}}[i]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ffa94e9e2e6d9e5e5373d5fafb954b902743fde)
Пример: 

Чтобы практически разложить гауссово число 

Таким образом, начать следует с разложения нормы числа 
- Множитель 2, если он присутствует в разложении нормы, разлагается как
. Следует включить в результирующее разложение те из этих множителей (в соответствующей степени), на которые
делится нацело.
- Кроме 2, остальные множители нормы — нечётные. Множитель вида
является простым гауссовым числом, поэтому он делит не только норму
, но и само
. Но тогда этот множитель делит и сопряжённое число
. Отсюда вытекает, что множитель вида
входит в разложение нормы всегда в чётной степени, а в разложение самого
— в степени, вдвое меньшей.
- Множитель вида
можно разложить на произведение сопряжённых простых гауссовых чисел (или, что то же самое, на сумму квадратов натуральных чисел). И здесь следует делением выяснить, какой из сомножителей относится к исходному числу, а какой — к сопряжённому.
Например, для разложения на простые множители 








.
Теория сравнений[править | править код]
Сравнения по гауссовому модулю[править | править код]
Понятие сравнения по модулю определяется в ![{mathbb {Z}}[i]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ffa94e9e2e6d9e5e5373d5fafb954b902743fde)
Свойства сравнений в ![{mathbb {Z}}[i]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ffa94e9e2e6d9e5e5373d5fafb954b902743fde)
![{mathbb {Z}}[i]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ffa94e9e2e6d9e5e5373d5fafb954b902743fde)
Пример. Возьмём в качестве модуля сравнения 
![{mathbb {Z}}[i]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ffa94e9e2e6d9e5e5373d5fafb954b902743fde)



У гауссова сравнения имеются некоторые особенности. Например, если для целых чисел по модулю 3 существуют 3 класса вычетов с представителями 
Как обнаружил Гаусс, кольцо вычетов по модулю 








На том же примере с 

Назовём класс вычетов по модулю 






![{mathbb {Z}}[i]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ffa94e9e2e6d9e5e5373d5fafb954b902743fde)

Функция Эйлера для гауссовых чисел[править | править код]
Введём аналог функции Эйлера для гауссовых чисел. Определение для целых чисел не годится хотя бы потому, что содержащееся в нём выражение «от 

Определённая таким образом функция, как и её прототип для целых чисел, мультипликативна, поэтому достаточно знать её значения для простых чисел и их натуральных степеней. Если 
Пример: 
Теперь можно обобщить приведённую в предыдущем разделе малую теорему Ферма на случай произвольного (не обязательно простого) модуля сравнения, то есть привести аналог теоремы Эйлера[20]:
Сравнение по модулю
Геометрическое представление сравнения по модулю[править | править код]
Рассмотрим для примера сравнения по модулю 


Каждый квадрат решётки получается из любого другого квадрата сдвигом (переносом) на величину, кратную 

Гауссовы числа сравнимы по модулю 
Например, сравнимы все центры квадратов, или все середины их соответствующих сторон и т. п.
Деление с остатком[править | править код]
Определение[править | править код]
В кольце ![{mathbb {Z}}[i]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ffa94e9e2e6d9e5e5373d5fafb954b902743fde)
Несложно показать, что в качестве частного от деления с остатком можно взять гауссово число, ближайшее к частному от обычного деления комплексных чисел[22].
Необходимо отметить, что условия «норма остатка меньше нормы делителя» недостаточно для того, чтобы гарантировать однозначность остатка от деления, поэтому в ![{mathbb {Z}}[i]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ffa94e9e2e6d9e5e5373d5fafb954b902743fde)


Можно гарантировать только то, что все остатки попадают в один класс вычетов по модулю делителя. Впрочем, похожая ситуация имеет место и для обычных целых чисел — например, разделить с остатком 8 на 3 можно двумя способами: 

Пример. Для деления с остатком 

Ближайшее к результату гауссово число есть 

Для гауссовых чисел имеет место аналог китайской теоремы об остатках, поскольку она доказывается с помощью алгоритма Евклида.
Геометрическое представление[править | править код]
Из определения деления с остатком 







Распределение числа решений задачи деления с остатком
В вышеприведённом примере деления 

Все они находятся от делимого на расстоянии меньше, чем 


В общем случае, проведя из вершин квадрата 


Наибольший общий делитель[править | править код]
Кольцо гауссовых чисел является евклидовым, и в нём всегда можно определить наибольший общий делитель, определённый однозначно с точностью до делителей единицы[23].
Эквивалентное определение: НОД

- Свойства НОД
- Если известен некоторый НОД, то любое из трёх чисел, ассоциированных с ним, также будет НОД. В частности. если один из НОД — делитель единицы, то такими же будут и остальные три НОД.
- Гауссовы числа взаимно просты тогда и только тогда, когда их НОД есть делитель единицы.
- Имеет место аналог соотношения Безу[25]:
-
- Другими словами, наибольший общий делитель двух гауссовых чисел можно всегда представить как линейную комбинацию этих чисел с гауссовыми коэффициентами.
Алгоритм Евклида и практическое вычисление НОД[править | править код]
Для определения НОД в ![{mathbb {Z}}[i]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ffa94e9e2e6d9e5e5373d5fafb954b902743fde)

Пример 1. Найдём НОД для 

- Шаг 1:
(разделили с остатком первое число на второе)
- Шаг 2:
(разделили с остатком предыдущий делитель на остаток предыдущего шага)
- Шаг 3:
(то же действие)
- Шаг 4:
(то же действие, деление выполнилось нацело)
Отметим, что на каждом шаге норма остатка монотонно уменьшается. Последний ненулевой остаток равен 
Пример 2. Найдём НОД для 

- Шаг 1:
- Шаг 2:
- Шаг 3:
(деление выполнилось нацело)
Последний ненулевой остаток равен 
Некоторые приложения[править | править код]
Гаусс использовал открытую им алгебраическую структуру для глубокого исследования биквадратичных вычетов. Можно указать и другие области успешного применения гауссовых чисел[27]. Примечательно, что значительная их часть относится к теории не комплексных, а натуральных чисел.
Разложение натуральных чисел на сумму двух квадратов[править | править код]
Из критерия Гаусса[⇨] вытекает, что простое натуральное число вида 

Разложение натуральных чисел другого вида не всегда возможно — например, 



Пример: 


Подсчёт числа представлений в виде суммы двух квадратов[править | править код]
Число представлений 



Здесь 



- Если хотя бы один показатель степени
нечётный, число
не может быть представлено в виде суммы квадратов.
- Пусть все
чётные. Окончательная формула зависит от чётности
. Если все они тоже чётные, то формула имеет вид:
- Если не все
чётные, то формула немного отличается:
Теория пифагоровых троек[править | править код]
Пифагорова тройка — это одно из целочисленных решений уравнения:
.
Общее решение уравнения зависит от двух целых параметров 
.
Для генерации пифагоровых троек можно использовать такой приём. Пусть 



Пример: для исходного числа 

Решение диофантовых уравнений[править | править код]
Решение многих диофантовых уравнений удаётся найти, если привлечь аппарат гауссовых чисел. Например, для уравнения 

В 1850 году Виктор Лебег, используя гауссовы числа, исследовал уравнение 

Нерешённые проблемы[править | править код]
- Найти количество гауссовых чисел, норма которых меньше заданной натуральной константы
. В эквивалентной формулировке эта тема известна как «проблема круга Гаусса» в геометрии чисел[30][31].
- Найти прямые на комплексной плоскости, содержащие бесконечно много простых гауссовых чисел. Две такие прямые очевидны — это координатные оси; неизвестно, существуют ли другие[32].
- Вопрос, известный под названием «ров Гаусса»: можно ли дойти до бесконечности, переходя от одного простого гауссова числа к другому скачками заранее ограниченной длины? Задача поставлена в 1962 году и до сих пор не решена[33].
Вариации и обобщения[править | править код]
Треугольная решётка чисел Эйзенштейна
Ещё одним исторически важным евклидовым кольцом, похожим по свойствам на целые числа, стали «целые числа Эйзенштейна».
Гауссовы рациональные числа, обозначаемые 


История[править | править код]
В 1820-х годах Карл Фридрих Гаусс исследовал биквадратичный закон взаимности, результатом стала монография «Теория биквадратичных вычетов» (1828—1832). Именно в этом труде целые комплексные числа доказали свою полезность для решения задач теории чисел, хотя формулировка этих задач никак не связана с комплексными числами. Гаусс писал, что «естественный источник общей теории следует искать в расширении области арифметики»[3].
Карл Фридрих Гаусс в 1828 году
В книге Гаусса было показано, что новые числа по своим свойствам во многом напоминают обычные целые числа. Автор описал четыре делителя единицы, определил отношение ассоциированности, понятие простого числа, дал критерий простоты и доказал аналоги основной теоремы арифметики, малой теоремы Ферма. Далее Гаусс подробно рассмотрел вычеты по комплексному модулю, индексы и первообразные корни. Главным достижением построенной теории стал биквадратичный закон взаимности, который Гаусс обещал доказать в следующем томе; этот том так и не был опубликован, но в рукописях Гаусса была обнаружена подробная схема строгого доказательства[3].
Гаусс использовал введённые им числа также и в других своих трудах, например, по алгебраическим уравнениям[34]. Идеи Гаусса были развиты в трудах Карла Густава Якоба Якоби и Фердинанда Готтхольда Эйзенштейна. В середине XIX века Эйзенштейн, Дирихле и Эрмит ввели и исследовали обобщённое понятие целого алгебраического числа.
Кольцо гауссовых целых чисел было одним из первых примеров алгебраической структуры с непривычными свойствами. Со временем было открыто большое количество структур такого типа, а в конце XIX века появилась абстрактная алгебра, изучающая алгебраические свойства отдельно от объектов-носителей этих свойств.
Примечания[править | править код]
- ↑ 1 2 Математическая энциклопедия, 1977.
- ↑ Гаусс К. Ф., 1959, с. 655—754.
- ↑ 1 2 3 Математика XIX века. Том I: Математическая логика, алгебра, теория чисел, теория вероятностей, 1978, с. 88—92.
- ↑ Кузьмин Р. О., Фаддеев Д. К., 1939, с. 146.
- ↑ Айерлэнд К., Роузен М., 1987, с. 23.
- ↑ Окунев Л. Я., 1941, с. 27—28.
- ↑ 1 2 3 4 Кузьмин Р. О., Фаддеев Д. К., 1939, с. 147—149.
- ↑ 1 2 3 Окунев Л. Я., 1941, с. 29.
- ↑ Окунев Л. Я., 1941, с. 32.
- ↑ Кузьмин Р. О., Фаддеев Д. К., 1939, с. 150.
- ↑ 1 2 Кузьмин Р. О., Фаддеев Д. К., 1939, с. 155.
- ↑ Кузьмин Р. О., Фаддеев Д. К., 1939, с. 156.
- ↑ Окунев Л. Я., 1941, с. 41, 44.
- ↑ A classification of gaussian primes, с. 10.
- ↑ Гаусс К. Ф., 1959, с. 698.
- ↑ Кузьмин Р. О., Фаддеев Д. К., 1939, с. 158.
- ↑ 1 2 3 Conrad, Keith, Глава 9.
- ↑ Окунев Л. Я., 1941, с. 33—34.
- ↑ Conrad, Keith, Глава 6.
- ↑ 1 2 3 4 5 6 7 8 9 Conrad, Keith, Глава 7.
- ↑ Conrad, Keith, Глава 3.
- ↑ Окунев Л. Я., 1941, с. 30—31.
- ↑ Окунев Л. Я., 1941, с. 35—36.
- ↑ Conrad, Keith, Глава 4.
- ↑ 1 2 Conrad, Keith, Глава 5.
- ↑ Кузьмин Р. О., Фаддеев Д. К., 1939, с. 153—155.
- ↑ 1 2 3 4 Conrad, Keith, Глава 8.
- ↑ Кузьмин Р. О., Фаддеев Д. К., 1939, с. 164—166.
- ↑ Кузьмин Р. О., Фаддеев Д. К., 1939, с. 162—163.
- ↑ Conway J. H., Sloane N. J. A. Sphere Packings, Lattices and Groups. — Springer-Verlag. — P. 106.
- ↑ последовательность A000328 в OEIS
- ↑ Ribenboim, Paulo. The New Book of Prime Number Records, Ch.III.4.D Ch. 6.II, Ch. 6.IV. — 3rd ed. — New York: Springer, 1996. — ISBN 0-387-94457-5.
- ↑ Guy Richard K. Unsolved problems in number theory. — 3rd ed. — New York: Springer, 2004. — P. 55—57. — ISBN 978-0-387-20860-2.
- ↑ Hardy G. H., Wright E. M., 1968, с. 189.
Литература[править | править код]
- Айерлэнд К., Роузен М. Классическое введение в современную теорию чисел. — М.: Мир, 1987. — 416 с.
- Алфутова Н. Б, Устинов А. В. Алгебра и теория чисел. Сборник задач для математических школ. — 3-е изд., испр. и доп. — М.: МЦНМО, 2009. — 336 с. — ISBN 978-5-94057-550-4.
- Гаусс К. Ф. Труды по теории чисел. — М.: Изд-во АН СССР, 1959. — С. 695—754.
- Гауссово число // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1977. — Т. 1.
- Калужнин Л. А. Основная теорема арифметики. — М.: Наука, 1969. — 32 с. — (Популярные лекции по математике).
- Колмогоров А. Н., Юшкевич А. П. (ред.). Математика XIX века. Математическая логика, алгебра, теория чисел, теория вероятностей. — М.: Наука, 1978. — Т. I.
- Кузьмин Р. О., Фаддеев Д. К. Алгебра и арифметика комплексных чисел. Пособие для учителей. — М.: Учпедгиз, 1939. — 187 с.
- Окунев Л. Я. Целые комплексные числа. — М.: Гос. уч.-пед. изд-во Наркомпроса РСФСР, 1941. — 56 с.
- Сендеров В., Спивак А. Суммы квадратов и целые гауссовы числа // Квант. — 1999. — № 3. — С. 14—22.
- Hardy G. H., Wright E. M. An introduction to the theory of numbers (англ.). — 4th edition. — Oxford.: Oxford University Press, 1968. — 421 p.
Ссылки[править | править код]
- Complex Gaussian Integers for ‘Gaussian Graphics’ (англ.). Дата обращения: 11 сентября 2013. Архивировано из оригинала 14 июня 2006 года.
- Butler, Lee A. A classification of gaussian primes (англ.). Дата обращения: 16 января 2017.
- Conrad, Keith. The gaussian integers (англ.). Дата обращения: 11 сентября 2013.
In number theory, a Gaussian integer is a complex number whose real and imaginary parts are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as ![mathbf {Z} [i]](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0a617cf5867f951fefb72f3ab7278e0f6f1eedd)
![{displaystyle mathbb {Z} [i].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03900897cdf515bbbc52879377653a871b9efc06)
Gaussian integers share many properties with integers: they form a Euclidean domain, and have thus a Euclidean division and a Euclidean algorithm; this implies unique factorization and many related properties. However, Gaussian integers do not have a total ordering that respects arithmetic.
Gaussian integers are algebraic integers and form the simplest ring of quadratic integers.
Gaussian integers are named after the German mathematician Carl Friedrich Gauss.
Basic definitions[edit]
The Gaussian integers are the set[1]
In other words, a Gaussian integer is a complex number such that its real and imaginary parts are both integers.
Since the Gaussian integers are closed under addition and multiplication, they form a commutative ring, which is a subring of the field of complex numbers. It is thus an integral domain.
When considered within the complex plane, the Gaussian integers constitute the 2-dimensional integer lattice.
The conjugate of a Gaussian integer a + bi is the Gaussian integer a – bi.
The norm of a Gaussian integer is its product with its conjugate.
The norm of a Gaussian integer is thus the square of its absolute value as a complex number. The norm of a Gaussian integer is a nonnegative integer, which is a sum of two squares. Thus a norm cannot be of the form 4k + 3, with k integer.
The norm is multiplicative, that is, one has[2]
for every pair of Gaussian integers z, w. This can be shown directly, or by using the multiplicative property of the modulus of complex numbers.
The units of the ring of Gaussian integers (that is the Gaussian integers whose multiplicative inverse is also a Gaussian integer) are precisely the Gaussian integers with norm 1, that is, 1, –1, i and –i.[3]
Euclidean division[edit]
Visualization of maximal distance to some Gaussian integer
Gaussian integers have a Euclidean division (division with remainder) similar to that of integers and polynomials. This makes the Gaussian integers a Euclidean domain, and implies that Gaussian integers share with integers and polynomials many important properties such as the existence of a Euclidean algorithm for computing greatest common divisors, Bézout’s identity, the principal ideal property, Euclid’s lemma, the unique factorization theorem, and the Chinese remainder theorem, all of which can be proved using only Euclidean division.
A Euclidean division algorithm takes, in the ring of Gaussian integers, a dividend a and divisor b ≠ 0, and produces a quotient q and remainder r such that
In fact, one may make the remainder smaller:
Even with this better inequality, the quotient and the remainder are not necessarily unique, but one may refine the choice to ensure uniqueness.
To prove this, one may consider the complex number quotient x + iy = a/b. There are unique integers m and n such that –1/2 < x – m ≤ 1/2 and –1/2 < y – n ≤ 1/2, and thus N(x – m + i(y – n)) ≤ 1/2. Taking q = m + in, one has
with
and
The choice of x – m and y – n in a semi-open interval is required for uniqueness.
This definition of Euclidean division may be interpreted geometrically in the complex plane (see the figure), by remarking that the distance from a complex number ξ to the closest Gaussian integer is at most √2/2.[4]
Principal ideals[edit]
Since the ring G of Gaussian integers is a Euclidean domain, G is a principal ideal domain, which means that every ideal of G is principal. Explicitly, an ideal I is a subset of a ring R such that every sum of elements of I and every product of an element of I by an element of R belong to I. An ideal is principal if it consists of all multiples of a single element g, that is, it has the form
In this case, one says that the ideal is generated by g or that g is a generator of the ideal.
Every ideal I in the ring of the Gaussian integers is principal, because, if one chooses in I a nonzero element g of minimal norm, for every element x of I, the remainder of Euclidean division of x by g belongs also to I and has a norm that is smaller than that of g; because of the choice of g, this norm is zero, and thus the remainder is also zero. That is, one has x = qg, where q is the quotient.
For any g, the ideal generated by g is also generated by any associate of g, that is, g, gi, –g, –gi; no other element generates the same ideal. As all the generators of an ideal have the same norm, the norm of an ideal is the norm of any of its generators.
In some circumstances, it is useful to choose, once for all, a generator for each ideal. There are two classical ways for doing that, both considering first the ideals of odd norm. If the g = a + bi has an odd norm a2 + b2, then one of a and b is odd, and the other is even. Thus g has exactly one associate with a real part a that is odd and positive. In his original paper, Gauss made another choice, by choosing the unique associate such that the remainder of its division by 2 + 2i is one. In fact, as N(2 + 2i) = 8, the norm of the remainder is not greater than 4. As this norm is odd, and 3 is not the norm of a Gaussian integer, the norm of the remainder is one, that is, the remainder is a unit. Multiplying g by the inverse of this unit, one finds an associate that has one as a remainder, when divided by 2 + 2i.
If the norm of g is even, then either g = 2kh or g = 2kh(1 + i), where k is a positive integer, and N(h) is odd. Thus, one chooses the associate of g for getting a h which fits the choice of the associates for elements of odd norm.
Gaussian primes[edit]
As the Gaussian integers form a principal ideal domain they form also a unique factorization domain. This implies that a Gaussian integer is irreducible (that is, it is not the product of two non-units) if and only if it is prime (that is, it generates a prime ideal).
The prime elements of Z[i] are also known as Gaussian primes. An associate of a Gaussian prime is also a Gaussian prime. The conjugate of a Gaussian prime is also a Gaussian prime (this implies that Gaussian primes are symmetric about the real and imaginary axes).
A positive integer is a Gaussian prime if and only if it is a prime number that is congruent to 3 modulo 4 (that is, it may be written 4n + 3, with n a nonnegative integer) (sequence A002145 in the OEIS). The other prime numbers are not Gaussian primes, but each is the product of two conjugate Gaussian primes.
A Gaussian integer a + bi is a Gaussian prime if and only if either:
- one of a, b is zero and the absolute value of the other is a prime number of the form 4n + 3 (with n a nonnegative integer), or
- both are nonzero and a2 + b2 is a prime number (which will not be of the form 4n + 3).
In other words, a Gaussian integer is a Gaussian prime if and only if either its norm is a prime number, or it is the product of a unit (±1, ±i) and a prime number of the form 4n + 3.
It follows that there are three cases for the factorization of a prime number p in the Gaussian integers:
- If p is congruent to 3 modulo 4, then it is a Gaussian prime; in the language of algebraic number theory, p is said to be inert in the Gaussian integers.
- If p is congruent to 1 modulo 4, then it is the product of a Gaussian prime by its conjugate, both of which are non-associated Gaussian primes (neither is the product of the other by a unit); p is said to be a decomposed prime in the Gaussian integers. For example, 5 = (2 + i)(2 − i) and 13 = (3 + 2i)(3 − 2i).
- If p = 2, we have 2 = (1 + i)(1 − i) = i(1 − i)2; that is, 2 is the product of the square of a Gaussian prime by a unit; it is the unique ramified prime in the Gaussian integers.
Unique factorization[edit]
As for every unique factorization domain, every Gaussian integer may be factored as a product of a unit and Gaussian primes, and this factorization is unique up to the order of the factors, and the replacement of any prime by any of its associates (together with a corresponding change of the unit factor).
If one chooses, once for all, a fixed Gaussian prime for each equivalence class of associated primes, and if one takes only these selected primes in the factorization, then one obtains a prime factorization which is unique up to the order of the factors. With the choices described above, the resulting unique factorization has the form
where u is a unit (that is, u ∈ {1, –1, i, –i}), e0 and k are nonnegative integers, e1, …, ek are positive integers, and p1, …, pk are distinct Gaussian primes such that, depending on the choice of selected associates,
- either pk = ak + ibk with a odd and positive, and b even,
- or the remainder of the Euclidean division of pk by 2 + 2i equals 1 (this is Gauss’s original choice[5]).
An advantage of the second choice is that the selected associates behave well under products for Gaussian integers of odd norm. On the other hand, the selected associate for the real Gaussian primes are negative integers. For example, the factorization of 231 in the integers, and with the first choice of associates is 3 × 7 × 11, while it is (–1) × (–3) × (–7) × (–11) with the second choice.
Gaussian rationals[edit]
The field of Gaussian rationals is the field of fractions of the ring of Gaussian integers. It consists of the complex numbers whose real and imaginary part are both rational.
The ring of Gaussian integers is the integral closure of the integers in the Gaussian rationals.
This implies that Gaussian integers are quadratic integers and that a Gaussian rational is a Gaussian integer, if and only if it is a solution of an equation
with c and d integers. In fact a + bi is solution of the equation
and this equation has integer coefficients if and only if a and b are both integers.
Greatest common divisor[edit]
As for any unique factorization domain, a greatest common divisor (gcd) of two Gaussian integers a, b is a Gaussian integer d that is a common divisor of a and b, which has all common divisors of a and b as divisor. That is (where | denotes the divisibility relation),
- d | a and d | b, and
- c | a and c | b implies c | d.
Thus, greatest is meant relatively to the divisibility relation, and not for an ordering of the ring (for integers, both meanings of greatest coincide).
More technically, a greatest common divisor of a and b is a generator of the ideal generated by a and b (this characterization is valid for principal ideal domains, but not, in general, for unique factorization domains).
The greatest common divisor of two Gaussian integers is not unique, but is defined up to the multiplication by a unit. That is, given a greatest common divisor d of a and b, the greatest common divisors of a and b are d, –d, id, and –id.
There are several ways for computing a greatest common divisor of two Gaussian integers a and b. When one knows the prime factorizations of a and b,
where the primes pm are pairwise non associated, and the exponents μm non-associated, a greatest common divisor is
with
Unfortunately, except in simple cases, the prime factorization is difficult to compute, and Euclidean algorithm leads to a much easier (and faster) computation. This algorithm consists of replacing of the input (a, b) by (b, r), where r is the remainder of the Euclidean division of a by b, and repeating this operation until getting a zero remainder, that is a pair (d, 0). This process terminates, because, at each step, the norm of the second Gaussian integer decreases. The resulting d is a greatest common divisor, because (at each step) b and r = a – bq have the same divisors as a and b, and thus the same greatest common divisor.
This method of computation works always, but is not as simple as for integers because Euclidean division is more complicated. Therefore, a third method is often preferred for hand-written computations. It consists in remarking that the norm N(d) of the greatest common divisor of a and b is a common divisor of N(a), N(b), and N(a + b). When the greatest common divisor D of these three integers has few factors, then it is easy to test, for common divisor, all Gaussian integers with a norm dividing D.
For example, if a = 5 + 3i, and b = 2 – 8i, one has N(a) = 34, N(b) = 68, and N(a + b) = 74. As the greatest common divisor of the three norms is 2, the greatest common divisor of a and b has 1 or 2 as a norm. As a gaussian integer of norm 2 is necessary associated to 1 + i, and as 1 + i divides a and b, then the greatest common divisor is 1 + i.
If b is replaced by its conjugate b = 2 + 8i, then the greatest common divisor of the three norms is 34, the norm of a, thus one may guess that the greatest common divisor is a, that is, that a | b. In fact, one has 2 + 8i = (5 + 3i)(1 + i).
Congruences and residue classes[edit]
Given a Gaussian integer z0, called a modulus, two Gaussian integers z1,z2 are congruent modulo z0, if their difference is a multiple of z0, that is if there exists a Gaussian integer q such that z1 − z2 = qz0. In other words, two Gaussian integers are congruent modulo z0, if their difference belongs to the ideal generated by z0. This is denoted as z1 ≡ z2 (mod z0).
The congruence modulo z0 is an equivalence relation (also called a congruence relation), which defines a partition of the Gaussian integers into equivalence classes, called here congruence classes or residue classes. The set of the residue classes is usually denoted Z[i]/z0Z[i], or Z[i]/⟨z0⟩, or simply Z[i]/z0.
The residue class of a Gaussian integer a is the set
of all Gaussian integers that are congruent to a. It follows that a = b if and only if a ≡ b (mod z0).
Addition and multiplication are compatible with congruences. This means that a1 ≡ b1 (mod z0) and a2 ≡ b2 (mod z0) imply a1 + a2 ≡ b1 + b2 (mod z0) and a1a2 ≡ b1b2 (mod z0).
This defines well-defined operations (that is independent of the choice of representatives) on the residue classes:
With these operations, the residue classes form a commutative ring, the quotient ring of the Gaussian integers by the ideal generated by z0, which is also traditionally called the residue class ring modulo z0 (for more details, see Quotient ring).
Examples[edit]
- There are exactly two residue classes for the modulus 1 + i, namely 0 = {0, ±2, ±4,…,±1 ± i, ±3 ± i,…} (all multiples of 1 + i), and 1 = {±1, ±3, ±5,…, ±i, ±2 ± i,…}, which form a checkerboard pattern in the complex plane. These two classes form thus a ring with two elements, which is, in fact, a field, the unique (up to an isomorphism) field with two elements, and may thus be identified with the integers modulo 2. These two classes may be considered as a generalization of the partition of integers into even and odd integers. Thus one may speak of even and odd Gaussian integers (Gauss divided further even Gaussian integers into even, that is divisible by 2, and half-even).
- For the modulus 2 there are four residue classes, namely 0, 1, i, 1 + i. These form a ring with four elements, in which x = –x for every x. Thus this ring is not isomorphic with the ring of integers modulo 4, another ring with four elements. One has 1 + i2 = 0, and thus this ring is not the finite field with four elements, nor the direct product of two copies of the ring of integers modulo 2.
- For the modulus 2 + 2i = (i − 1)3 there are eight residue classes, namely 0, ±1, ±i, 1 ± i, 2, whereof four contain only even Gaussian integers and four contain only odd Gaussian integers.
Describing residue classes[edit]
All 13 residue classes with their minimal residues (blue dots) in the square Q00 (light green background) for the modulus z0 = 3 + 2i. One residue class with z = 2 − 4i ≡ −i (mod z0) is highlighted with yellow/orange dots.
Given a modulus z0, all elements of a residue class have the same remainder for the Euclidean division by z0, provided one uses the division with unique quotient and remainder, which is described above. Thus enumerating the residue classes is equivalent with enumerating the possible remainders. This can be done geometrically in the following way.
In the complex plane, one may consider a square grid, whose squares are delimited by the two lines
with s and t integers (blue lines in the figure). These divide the plane in semi-open squares (where m and n are integers)
The semi-open intervals that occur in the definition of Qmn have been chosen in order that every complex number belong to exactly one square; that is, the squares Qmn form a partition of the complex plane. One has
This implies that every Gaussian integer is congruent modulo z0 to a unique Gaussian integer in Q00 (the green square in the figure), which its remainder for the division by z0. In other words, every residue class contains exactly one element in Q00.
The Gaussian integers in Q00 (or in its boundary) are sometimes called minimal residues because their norm are not greater than the norm of any other Gaussian integer in the same residue class (Gauss called them absolutely smallest residues).
From this one can deduce by geometrical considerations, that the number of residue classes modulo a Gaussian integer z0 = a + bi equals its norm N(z0) = a2 + b2 (see below for a proof; similarly, for integers, the number of residue classes modulo n is its absolute value |n|).
Proof
The relation Qmn = (m + in)z0 + Q00 means that all Qmn are obtained from Q00 by translating it by a Gaussian integer. This implies that all Qmn have the same area N = N(z0), and contain the same number ng of Gaussian integers.
Generally, the number of grid points (here the Gaussian integers) in an arbitrary square with the area A is A + Θ(√A) (see Big theta for the notation). If one considers a big square consisting of k × k squares Qmn, then it contains k2N + O(k√N) grid points. It follows k2ng = k2N + Θ(k√N), and thus ng = N + Θ(√N/k), after a division by k2. Taking the limit when k tends to the infinity gives ng = N = N(z0).
Residue class fields[edit]
The residue class ring modulo a Gaussian integer z0 is a field if and only if 
If z0 is a decomposed prime or the ramified prime 1 + i (that is, if its norm N(z0) is a prime number, which is either 2 or a prime congruent to 1 modulo 4), then the residue class field has a prime number of elements (that is, N(z0)). It is thus isomorphic to the field of the integers modulo N(z0).
If, on the other hand, z0 is an inert prime (that is, N(z0) = p2 is the square of a prime number, which is congruent to 3 modulo 4), then the residue class field has p2 elements, and it is an extension of degree 2 (unique, up to an isomorphism) of the prime field with p elements (the integers modulo p).
Primitive residue class group and Euler’s totient function[edit]
Many theorems (and their proofs) for moduli of integers can be directly transferred to moduli of Gaussian integers, if one replaces the absolute value of the modulus by the norm. This holds especially for the primitive residue class group (also called multiplicative group of integers modulo n) and Euler’s totient function. The primitive residue class group of a modulus z is defined as the subset of its residue classes, which contains all residue classes a that are coprime to z, i.e. (a,z) = 1. Obviously, this system builds a multiplicative group. The number of its elements shall be denoted by ϕ(z) (analogously to Euler’s totient function φ(n) for integers n).
For Gaussian primes it immediately follows that ϕ(p) = |p|2 − 1 and for arbitrary composite Gaussian integers
Euler’s product formula can be derived as
where the product is to build over all prime divisors pm of z (with νm > 0). Also the important theorem of Euler can be directly transferred:
- For all a with (a,z) = 1, it holds that aϕ(z) ≡ 1 (mod z).
Historical background[edit]
The ring of Gaussian integers was introduced by Carl Friedrich Gauss in his second monograph on quartic reciprocity (1832).[6] The theorem of quadratic reciprocity (which he had first succeeded in proving in 1796) relates the solvability of the congruence x2 ≡ q (mod p) to that of x2 ≡ p (mod q). Similarly, cubic reciprocity relates the solvability of x3 ≡ q (mod p) to that of x3 ≡ p (mod q), and biquadratic (or quartic) reciprocity is a relation between x4 ≡ q (mod p) and x4 ≡ p (mod q). Gauss discovered that the law of biquadratic reciprocity and its supplements were more easily stated and proved as statements about “whole complex numbers” (i.e. the Gaussian integers) than they are as statements about ordinary whole numbers (i.e. the integers).
In a footnote he notes that the Eisenstein integers are the natural domain for stating and proving results on cubic reciprocity and indicates that similar extensions of the integers are the appropriate domains for studying higher reciprocity laws.
This paper not only introduced the Gaussian integers and proved they are a unique factorization domain, it also introduced the terms norm, unit, primary, and associate, which are now standard in algebraic number theory.
Unsolved problems[edit]
The distribution of the small Gaussian primes in the complex plane
Most of the unsolved problems are related to distribution of Gaussian primes in the plane.
- Gauss’s circle problem does not deal with the Gaussian integers per se, but instead asks for the number of lattice points inside a circle of a given radius centered at the origin. This is equivalent to determining the number of Gaussian integers with norm less than a given value.
There are also conjectures and unsolved problems about the Gaussian primes. Two of them are:
- The real and imaginary axes have the infinite set of Gaussian primes 3, 7, 11, 19, … and their associates. Are there any other lines that have infinitely many Gaussian primes on them? In particular, are there infinitely many Gaussian primes of the form 1 + ki?[7]
- Is it possible to walk to infinity using the Gaussian primes as stepping stones and taking steps of a uniformly bounded length? This is known as the Gaussian moat problem; it was posed in 1962 by Basil Gordon and remains unsolved.[8][9]
See also[edit]
- Algebraic integer
- Cyclotomic field
- Eisenstein integer
- Eisenstein prime
- Hurwitz quaternion
- Proofs of Fermat’s theorem on sums of two squares
- Proofs of quadratic reciprocity
- Quadratic integer
- Splitting of prime ideals in Galois extensions describes the structure of prime ideals in the Gaussian integers
- Table of Gaussian integer factorizations
Notes[edit]
- ^ a b Fraleigh (1976, p. 286)
- ^ Fraleigh (1976, p. 289)
- ^ Fraleigh (1976, p. 288)
- ^ Fraleigh (1976, p. 287)
- ^ Gauss (1831, p. 546)
- ^ Kleiner (1998)
- ^ Ribenboim, Ch.III.4.D Ch. 6.II, Ch. 6.IV (Hardy & Littlewood’s conjecture E and F)
- ^ Gethner, Ellen; Wagon, Stan; Wick, Brian (1998). “A stroll through the Gaussian primes”. The American Mathematical Monthly. 105 (4): 327–337. doi:10.2307/2589708. JSTOR 2589708. MR 1614871. Zbl 0946.11002.
- ^ Guy, Richard K. (2004). Unsolved problems in number theory (3rd ed.). Springer-Verlag. pp. 55–57. ISBN 978-0-387-20860-2. Zbl 1058.11001.
References[edit]
- Gauss, C. F. (1831), “Theoria residuorum biquadraticorum. Commentatio secunda.”, Comm. Soc. Reg. Sci. Göttingen, 7: 89–148; reprinted in Werke, Georg Olms Verlag, Hildesheim, 1973, pp. 93–148. A German translation of this paper is available online in ″H. Maser (ed.): Carl Friedrich Gauss’ Arithmetische Untersuchungen über höhere Arithmetik. Springer, Berlin 1889, pp. 534″.
- Fraleigh, John B. (1976), A First Course In Abstract Algebra (2nd ed.), Reading: Addison-Wesley, ISBN 0-201-01984-1
- Kleiner, Israel (1998). “From Numbers to Rings: The Early History of Ring Theory”. Elem. Math. 53 (1): 18–35. doi:10.1007/s000170050029. Zbl 0908.16001.
- Ribenboim, Paulo (1996). The New Book of Prime Number Records (3rd ed.). New York: Springer. ISBN 0-387-94457-5. Zbl 0856.11001.
- Henry G. Baker (1993). “Complex Gaussian Integers for “Gaussian Graphics”“. ACM SIGPLAN Notices. 28 (11): 22–27. doi:10.1145/165564.165571. S2CID 8083226.
External links[edit]
- IMO Compendium text on quadratic extensions and Gaussian Integers in problem solving
- Keith Conrad, The Gaussian Integers.
Цикл «Занимательная математика» посвящен деткам увлекающимся математикой и родителям, которые уделяют время развитию своих детей, «подкидывая» им интересные и занимательные задачки, головоломки.
Первая статья из этого цикла посвящена правилу Гаусса.
Немного истории
Известный немецкий математик Карл Фридрих Гаусс (1777-1855) с раннего детства отличался от своих сверстников. Несмотря на то, что он был из небогатой семьи, он достаточно рано научился читать, писать, считать. В его биографии есть даже упоминание того, что в возрасте 4-5 лет он смог скорректировать ошибку в неверных подсчетах отца, просто наблюдая за ним.

Найти сумму всех натуральных чисел от 1 до 100.
Юный Гаусс справился с этим заданием достаточно быстро, найдя интересную закономерность, которая получила большое распространение и применяется по сей день при устном счете.
Давайте попробуем решить эту задачку устно. Но для начала возьмем числа от 1 до 10:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10
Посмотрите внимательно на эту сумму и попробуйте догадаться, что же необычного смог разглядеть Гаусс? Для ответа необходимо хорошо представлять себе состав чисел.
Гаусс сгруппировал числа следующим образом:
(1+10) + (2+9) + (3+8) + (4+7) + (5+6)
Таким образом маленький Карл получил 5 пар чисел, каждая из которых в отдельности в сумме дает 11. Тогда, чтобы вычислить сумму натуральных чисел от 1 до 10 необходимо
5 * 11 = 55
Вернемся к первоначальной задаче. Гаусс заметил, что перед суммированием необходимо группировать числа в пары и тем самым изобрел алгоритм, благодаря которому можно быстро сложить числа от 1 до100:
1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100
-
Находим количество пар в ряде натуральных чисел. В данном случае их 50.
-
Суммируем первое и последнее числа данного ряда. В нашем примере — это 1 и 100. Получаем 101.
-
Умножаем полученную сумму первого и последнего члена ряда на количество пар этого ряда. Получаем 101 * 50 = 5050
Следовательно, сумма натуральных чисел от 1 до 100 равна 5050.
Задачи на использование правила Гаусса
А сейчас вашему вниманию предлагаются задачи, в которых в той или иной степени используется правило Гаусса. Эти задачки вполне способен понять и решить четвероклассник.
Можно дать возможность ребенку порассуждать самому, чтобы он сам «изобрел» это правило. А можно разобрать вместе и посмотреть как он сможет его применить. Среди ниже приведенных задач есть примеры, в которых нужно понять как модифицировать правило Гаусса, чтобы его применить к данной последовательности.
В любом случае, чтобы ребенок мог оперировать этим в своих вычислениях необходимо понимание алгоритма Гаусса, то есть умение разбить правильно по парам и посчитать.
Важно! Если будет заучена формула без понимания, то это очень быстро будет забыто.
Задача 1
Найти сумму чисел:
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10;
- 1 + 2 + 3 + … + 14 + 15 + 16;
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9;
- 1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100.
Решение.
Вначале можно дать возможность ребенку самому решить первый пример и предложить найти способ, при котором это сделать легко в уме. Далее разобрать этот пример вместе с ребенком и показать как это сделал Гаусс. Лучше всего для наглядности записать ряд и соединить линиями пары чисел, дающие в сумме одинаковое число. Важно, чтобы ребенок понял как образуются пары — берем самое маленькое и самое большое из оставшихся чисел при условии, что количество чисел в ряду четно.
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = (1 + 10) + (2 + 9) + (3 + 8) + (4 + 7) + (5 + 6) = (1 + 10) * 5;
- 1 + 2 + 3 + … + 14 + 15 + 16 = (1 + 16) + (2 + 15) + (3 + 14) + (4 + 13) + (5 + 12) + (6 + 11) + (7 + 10) + (8 + 9) = (1 + 16) * 8 = 136;
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = (1 + 8) + (2 + 7) + (3 + 6) + (4 + 5) + 9 = (1+ 8) * 4 + 9 = 45;
- 1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100 = (1 + 100) * 50 = 5050
Задача 2
Имеется 9 гирь весом 1г, 2г, 3г, 4г, 5г, 6г, 7г, 8г, 9г. Можно ли разложить эти гири на три кучки с равным весом?
Решение.
С помощью правила Гаусса находим сумму всех весов:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = (1 + 8) * 4 + 9 = 45 (г)
Далее смотрим, можно ли этот вес разбить на три равных веса:
45 : 3 = 15 (г)
Значит, если мы сможем сгруппировать гири так, чтобы в каждой кучке были гири суммарным весом 15г, то задача решена.
Один из вариантов:
- 9г, 6г
- 8г, 7г
- 5г, 4г, 3г, 2г, 1г
Другие возможные варианты найдите сами с ребенком.
Обратите внимание ребенка на то, что когда решаются подобные задачи лучше всегда начинать группировать с большего веса (числа).
Задача 3
Можно ли разделить циферблат часов прямой линией на две части так, чтобы суммы чисел в каждой части были равны?
Решение.
Для начала к ряду чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 применим правило Гаусса: найдем сумму и посмотрим, делится ли она на 2:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = (1 + 12) * 6 = 78
Значит разделить можно. Теперь посмотрим как.
По правилу Гаусса у нас получается 6 пар чисел, каждая из которых в сумме дает 13:
1 и 12, 2 и 11, 3 и 10, 4 и 9, 5 и 8, 6 и 7.
Следовательно, надо провести линию на циферблате так, чтобы 3 пары попали в одну половину, а три в другую.
Ответ: линия пройдет между числами 3 и 4, а затем между числами 9 и 10.
Задача 4
Можно ли провести на циферблате часов две прямые линией так, чтобы в каждой части сумма чисел была одинаковой?
Решение.
Для начала к ряду чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 применим правило Гаусса: найдем сумму и посмотрим делиться ли она на 3:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = (1 + 12) * 6 = 78
78 делиться на 3 без остатка, значит разделить можно. Теперь посмотрим как.
По правилу Гаусса у нас получается 6 пар чисел, каждая из которых в сумме дает 13:
1 и 12, 2 и 11, 3 и 10, 4 и 9, 5 и 8, 6 и 7.
Следовательно, надо провести линии на циферблате так, чтобы в каждую часть попали по 2 пары.
Ответ: первая линия пройдет между числами 2 и 3, а затем между числами 10 и 11; вторая линия — между числами 4 и 5, а затем между 8 и 9.
Задача 5
Летит стая птиц. Впереди одна птица (вожак), за ней две, потом три, четыре и т. д. Сколько птиц в стае, если в последнем ряду их 20?
Решение.
Получаем, что нам необходимо сложить числа от 1 до 20. А к вычислению такой суммы можно применить правило Гаусса:
1 + 2 + 3 + 4 + 5 + … + 15 + 16 + 17 + 18 + 19 + 20 = (20 + 1) * 10 = 210.
Задача 6
Как рассадить 45 кроликов в 9 клеток так, чтобы во всех клетках было разное количество кроликов?
Решение.
Если ребенок решил и с пониманием разобрал примеры из задания 1, то тут же вспоминается, что 45 это сумма чисел от 1 до 9. Следовательно, сажаем кроликов так:
- первая клетка — 1,
- вторая — 2,
- третья — 3,
- …
- восьмая — 8,
- девятая — 9.
Но если ребенок сразу не может сообразить, то попробуйте натолкнуть его на мысль о том, что подобные задачи можно решить перебором и надо начинать с минимального числа.
Задача 7
Вычислить сумму, используя прием Гаусса:
- 31 + 32 + 33 + … + 40;
- 5 + 10 + 15 + 20 + … + 100;
- 91 + 81 + … + 21 + 11 + 1;
- 1 + 2 + 3 + 4 + … + 18 + 19 + 20;
- 1 + 2 + 3 + 4 + 5 + 6;
- 4 + 6 + 8 + 10 + 12 + 14;
- 4 + 6 + 8 + 10 + 12;
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11.
Решение.
- 31 + 32 + 33 + … + 40 = (31 + 40) * 5 = 355;
- 5 + 10 + 15 + 20 + … + 100 = (5 + 100) * 10 = 1050;
- 91 + 81 + … + 21 + 11 + 1 = (91 + 1) * 5 = 460;
- 1 + 2 + 3 + 4 + … + 18 + 19 + 20 = (1 + 20) * 10 =210;
- 1 + 2 + 3 + 4 + 5 + 6 = (1 + 6) * 3 = 21;
- 4 + 6 + 8 + 10 + 12 + 14 = (4 + 14) * 3 = 54;
- 4 + 6 + 8 + 10 + 12 = (4 + 10) * 2 + 12 = 40;
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 = (1 + 10) * 5 + 11 = 66.
Задача 8
Имеется набор из 12 гирек массой 1г, 2г, 3г, 4г, 5г, 6г, 7г, 8г, 9г, 10г, 11г, 12г. Из набора убрали 4 гирьки, общая масса которых равна трети общей массы всего набора гирек. Можно ли оставшиеся гирьки расположить на двух чашках весов по 4 штуки на каждой чашке так, чтобы они оказались в равновесии?
Решение.
Применяем правило Гаусса, чтобы найти общую массу гирек:
1 + 2 + 3 + … + 10 + 11 + 12 = (1 + 12) * 6 = 78 (г)
Вычисляем массу гирек, которые убрали:
78 : 3 = 26 (г)
Следовательно, оставшиеся гирьки (общей массой 78-26 = 52г) надо расположить по 26 г на каждую чашу весов, чтобы они оказались в равновесии.
Нам не известно какие гирьки были убраны, значит мы должны рассмотреть все возможные варианты.
Применяя правило Гаусса можно разбить гирьки на 6 пар с равным весом (по 13г):
1г и 12г, 2г и 11г, 3г и 10, 4г и 9г, 5г и 8г, 6г и 7г.
Тогда лучший вариант, когда при убирании 4 гирек уберутся две пары из приведенных выше. В этом случае у нас останутся 4 пары: 2 пары на одну чашу весов и 2 пары на другую.
Худший вариант — это когда 4 убранные гирьки разобьют 4 пары. У нас останутся 2 неразбитые пары общим весом 26г, значит их помещаем на одну чашу весов, а оставшиеся гирьки можно поместить на другую чашу весов и они тоже будут 26г.
Удачи в развитии Ваших детей.
Карл Фридрих Гаусс, величайший математик долгое время колебался, выбирая между философией и математикой. Возможно, именно такой склад ума позволил ему столь заметно «наследить» в мировой науке. В частности, создав «Метод Гаусса» …
… Почти 4 года статьи этого сайта касались школьного образования, в основном, со стороны философии, принципов (не)понимания, внедряемых в сознание детей. Приходит время бОльшей конкретики, примеров и методов … Я верю, что именно такой подход к привычным, запутанным и важным областям жизни дает лучшие результаты.
… Мы, люди так устроены, что сколько ни говори об абстрактном мышлении, но понимание всегда происходит через примеры. Если примеры отсутствуют, то принципы уловить невозможно … Как невозможно оказаться на вершине горы иначе, как пройдя весь ее склон от подножия.
Тоже и со школой: пока живых историй недостаточно мы инстинктивно продолжаем считать ее местом, где детей учат понимать.
Например, обучая методу Гаусса …
Метод Гаусса в 5 классе школы
Оговорюсь сразу: метод Гаусса имеет гораздо более широкое применение, например, при решении систем линейных уравнений. То, о чем мы будем говорить, проходят в 5 классе. Это начала, уяснив которые, гораздо легче разобраться в более «продвинутых вариантах». В этой статье мы говорим о методе (способе) Гаусса при нахождении суммы ряда
Вот пример, который принес из школы мой младший сын, посещающий 5 класс московской гимназии.
Школьная демонстрация метода Гаусса
… Учитель математики с использованием интерактивной доски (современные методы обучения ) показал детям презентацию истории «создания метода» маленьким Гауссом.
… Школьный учитель выпорол маленького Карла (устаревший метод, нынче в школах не применяется) за то, что тот,
вместо того, чтобы последовательно складывая числа от 1 до 100 найти их сумму
заметил
, что пары чисел, равно отстоящие от краев арифметической прогрессии, в сумме дают одно и то же число. например, 100 и 1, 99 и 2. Посчитав количество таких пар, маленький Гаусс почти моментально решил предложенную учителем задачу. За что и был подвергнут экзекуции на глазах изумленной публики. Чтобы остальным думать было неповадно.
Что сделал маленький Гаусс, развивший чувство числа? Заметил некоторую особенность числового ряда с постоянным шагом (арифметической прогрессии). И именно это сделало его впоследствии великим ученым, умеющим замечать, обладающим чувством, инстинктом понимания.
… Этим и ценна математика, развивающая способность видеть общее в частном — абстрактное мышление. Поэтому большинство родителей и работодателей инстинктивно считают математику важной дисциплиной …
«Математику уже затем учить надо, что она ум в порядок приводит.
М.В.Ломоносов».
Однако, последователи тех, кто порол розгами будущих гениев, превратили Метод в нечто противоположное. Как 35 лет назад говорил мой научный руководитель: «Занаучили вопрос». Или как сказал вчера о методе Гаусса мой младший сын: «Может не стоит из этого большую науку делать-то, а?»
Последствия творчества «ученых» видны по уровню нынешней школьной математики, уровню ее преподавания и понимания «Царицы наук» большинством.
Однако, продолжим …
Методы объяснения метода Гаусса в 5 классе школы
Учитель математики московской гимназии, объясняя метод Гаусса по-Виленкину, усложнил задание.
Что, если разность (шаг) арифметической прогрессии будет не единица, а другое число? Например, 20.
Задача, которую он дал пятиклассникам:
посчитать сумму ряда чисел:
20+40+60+80+ … +460+480+500
Прежде, чем познакомиться с гимназическим методом, заглянем в Сеть: как это делают школьные учителя — репетиторы по математике?..
Метод Гаусса: объяснение №1
Известный репетитор на своем канале YOUTUBE приводит следующие рассуждения:
«запишем числа от 1 до 100 следующим образом:
сначала ряд чисел от 1 до 50, а строго под ним другой ряд чисел от 50 до 100, но в обратной последовательности»
1, 2, 3, … 48, 49, 50
100, 99, 98 … 53, 52, 51
«Обратите внимание: сумма каждой пары чисел из верхнего и нижнего рядов одинакова и равняется 101 ! Посчитаем количество пар, оно составляет 50 и умножим сумму одной пары на количество пар! Вуаля: Ответ готов!».
«Если вы не смогли понять — не расстраивайтесь!», — три раза в процессе объяснения повторил учитель. «Этот метод вы будете проходить в 9 классе!»
Метод Гаусса: объяснение №2
Другой репетитор, менее известный (судя по числу просмотров) использует более научный подход, предлагая алгоритм решения из 5 пунктов, которые необходимо выполнить последовательно.
Для непосвященных: 5 это одно из чисел Фибоначчи, традиционно считающееся магическим. Метод из 5 шагов всегда более научен, чем метод, например, из 6 шагов. … И это вряд ли случайность, скорее всего, Автор — скрытый приверженец теории Фибоначчи
Дана арифметическая прогрессия: 4, 10, 16 … 244, 250, 256.
Алгоритм нахождения суммы чисел ряда методом Гаусса:
4, 10, 16 … 244, 250, 256
256, 250, 244 … 16, 10, 4
При этом нужно помнить о правиле «Плюс один»: к полученному частному необходимо прибавить единицу: иначе мы получим результат, меньший на единицу, чем истинное число пар: 42 + 1 = 43.
Это и есть искомая сумма арифметической прогрессии от 4 до 256 с разницей 6 !
Метод Гаусса: объяснение в 5 классе московской гимназии
А вот как требовалось решить задачу нахождения суммы ряда:
20+40+60+ … +460+480+500
в 5 классе московской гимназии, учебник Виленкина (со слов моего сына).
… Показав презентацию, учительница математики показала пару примеров по методу Гаусса и дала классу задачу по нахождению суммы чисел ряда с шагом 20.
При этом требовалось следующее:
Как видим, это более компактная и эффективная методика: число 3 — также член последовательности Фибоначчи
Мои комментарии к школьной версии метода Гаусса
Великий математик определенно выбрал бы философию, если бы предвидел, во что превратят его «метод» последователи немецкого учителя, выпоровшего Карла розгами. Он узрел бы и символизм, и диалектическую спираль и неумирающую глупость «учителей», пытающихся измерить алгеброй непонимания гармонию живой математической мысли ….
Между прочим: знаете ли вы. что наша система образования уходит корнями в немецкую школу 18 — 19 веков?
Но Гаусс выбрал математику.
В чем суть его метода?
В упрощении. В наблюдении и схватывании простых закономерностей чисел. В превращении сухой школьной арифметики в интересное и увлекательное занятие, активизирующее в мозге желание продолжать, а не блокирующее высокозатратную умственную деятельность.
Разве возможно одной из приведенных «модификаций метода» Гаусса посчитать сумму чисел арифметической прогрессии почти моментально? По «алгоритмам» маленький Карл гарантированно избежал бы порки, воспитал отвращение к математике и подавил на корню свои творческие импульсы.
Почему репетитор так настойчиво советовал пятиклассникам «не бояться непонимания» метода, убеждая, что «такие» задачи они будут решать аж в 9 классе? Психологически безграмотное действие. Удачным приемом было отметить: «Видите? Вы уже в 5 классе можете решать задачи, которые будете проходить только через 4 года! Какие вы молодцы!».
Для использования метода Гаусса достаточно уровня 3 класса, когда нормальные дети уже умеют складывать, умножать и делить 2 -3 значные числа. Проблемы возникают из-за неспособности взрослых учителей, «не въезжающих», как объяснить простейшие вещи нормальным человеческим языком, не то что математическим … Не способных заинтересовать математикой и напрочь отбивающих охоту даже у «способных».
… Или, как прокомментировал мой сын: «делающих из этого большую науку».
Метод Гаусса, мои объяснения
Нашему ребенку мы с супругой объясняли этот «метод», кажется, еще до школы …
Простота вместо усложнения или игра в вопросы — ответы
«»Посмотри, вот числа от 1 до 100. Что ты видишь?»
Дело не в том, что именно увидит ребенок. Фокус в том, чтобы он стал смотреть.
«Как можно их сложить?» Сын уловил, что такие вопросы не задаются «просто так» и нужно взглянуть на вопрос «как-то по-другому, иначе, чем он делает обычно»
Не важно, увидит ли ребенок решение сразу, это маловероятно. Важно, чтобы он перестал бояться смотреть, или как я говорю: «шевелил задачу». Это начало пути к пониманию
«Что легче: сложить, например, 5 и 6 или 5 и 95?» Наводящий вопрос … Но ведь любое обучение и сводится к «наведению» человека на «ответ» — любым приемлемым для него способом.
На этом этапе уже могут возникнуть догадки о том, как «сэкономить» на вычислениях.
Все, что мы сделали — намекнули: «лобовой, линейный» метод счета — не единственно возможный. Если ребенок это усек, то впоследствии он выдумает еще много таких методов, ведь это интересно!!! И он точно избежит «непонимания» математики, не будет испытывать к ней отвращение. Он получил победу!
Если ребенок обнаружил, что сложение пар чисел, дающих в сумме сотню, плевое занятие, то «арифметическая прогрессия с разницей 1» — довольно муторная и неинтересная для ребенка вещь — вдруг для него обрела жизнь. Из хаоса возник порядок, а это всегда вызывает энтузиазм: так мы устроены!
Вопрос на засыпку: зачем после полученного ребенком озарения вновь загонять его в рамки сухих алгоритмов, к тому же функционально бесполезных в этом случае?!
Зачем заставлять тупо переписывать числа последовательности в тетрадь: чтобы даже у способных не возникло и единого шанса на понимание? Статистически, конечно, а ведь массовое образование заточено на «статистику» …
Куда делся ноль?
И все-таки складывать числа, дающие в сумме 100 для ума гораздо более приемлемо, чем дающие 101 …
«Школьный метод Гаусса» требует именно этого: бездумно складывать равноотстоящие от центра прогрессии пары чисел, несмотря ни на что.
А если посмотреть?
Все-таки ноль — величайшее изобретение человечества, которому более 2 000 лет. А учителя математики продолжают его игнорировать.
Гораздо проще преобразовать ряд чисел, начинающийся с 1, в ряд, начинающийся с 0. Сумма ведь не изменится, не правда ли?
Нужно перестать «думать учебниками» и начать смотреть …
И увидеть, что пары с суммой 101 вполне можно заменить парами с суммой 100 !
0 + 100, 1 + 99, 2 + 98 … 49 + 51
Как упразднить «правило плюс 1»?
Если честно, то я о таком правиле впервые услышал от того ютубовского репетитора …
Как я до сих пор поступаю, когда требуется определить количество членов какого-нибудь ряда?
Упрощаю.
Смотрю на последовательность:
1, 2, 3, .. 8, 9, 10
а когда совсем устал, то на более простой ряд:
1, 2, 3, 4, 5
и прикидываю: если вычесть из 5 единицу, то получится 4, но я совершенно ясно вижу 5 чисел! Следовательно, нужно прибавить единицу! Чувство числа, развитое в начальной школе, подсказывает: даже если членов ряда будет целый гугл (10 в сотой степени), закономерность останется той же.
На фиг правила?..
Чтобы через пару — тройку лет заполнить все пространство между лбом и затылком и перестать соображать? А зарабатывать на хлеб с маслом как? Ведь мы ровными шеренгами движемся в эпоху цифровой экономики!
Еще о школьном методе Гаусса: «зачем науку-то из этого делать?..»
Я не зря разместил скриншот из тетрадки сына…
«Что там было, на уроке?»
«Ну, я сосчитал сразу, поднял руку, но она не спросила. Поэтому, пока остальные считали я стал делать ДЗ по русскому языку, чтобы не тратить время. Потом, когда остальные дописали (???), она вызвала меня к доске. Я сказал ответ.»
«Правильно, покажи, как ты решал», — сказала учительница. Я показал. Она сказала: «Неправильно, нужно считать так, как я показала!»
«Хорошо, что двойку не поставила. И заставила написать в тетради «ход решения» по-ихнему. Зачем науку-то большую из этого делать?..»
Главное преступление учителя математики
Вряд ли после того случая Карл Гаусс испытал высокое чувство уважения по отношению к школьному учителю математики. Но если бы он знал, как последователи того учителя извратят самую суть метода … он взревел бы от негодования и через Всемирную организацию интеллектуальной собственности ВОИС добился запрета на использование своего честного имени в школьных учебниках!..
В чем главная ошибка школьного подхода? Или, как я выразился — преступление школьных учителей математики против детей?
Алгоритм непонимания
Что делают школьные методисты, абсолютное большинство которых думать не умеет ни фига?
Создают методики и алгоритмы (см. статью об этом). Это защитная реакция, предохраняющая учителей от критики («Все делается согласно …»), а детей — от понимания. И таким образом — от желания критиковать учителей! (Вторая производная чиновничьей «мудрости», научный подход к проблеме ). Человек не улавливая смысл скорее будет пенять на собственное непонимание, а не на тупость школьной системы.
Что и происходит: родители пеняют на детей, а учителя … то же на детей, «не понимающих математику!..
Смекаете?
Что сделал маленький Карл?
Абсолютно нешаблонно подошел к шаблонной задаче. Это квинтэссенция Его подхода. Это главное, чему следует учить в школе: думать не учебниками, а головой. Конечно, есть и инструментальная составляющая, которую вполне можно использовать … в поисках более простых и эффективных методов счета.
Метод Гаусса по-Виленкину
В школе учат, что метод Гаусса состоит в том, чтобы
Но:
что, если число элементов ряда окажется нечетным, как в задаче, которую задали сыну?..
«Подвох» состоит в том, что в этом случае следует обнаружить «лишнее» число ряда и прибавить его к сумме пар. В нашем примере это число 260.
Как обнаружить? Переписывая все пары чисел в тетрадь! (Именно почему учительница заставила детей делать эту тупую работу, пытаясь научить «творчеству» методом Гаусса … И именно поэтому такой «метод» практически неприменим к большим рядам данных, И именно поэтому он не является методом Гаусса).
Немного творчества в школьной рутине …
Сын же поступил иначе.
(20 + 500, 40 + 480 …).
0+500, 20+480, 40+460 …
Несложно, правда?
А практически делается еще легче, что и позволяет выкроить 2-3 минуты на ДЗ по русскому, пока остальные «считают». К тому же сохраняет количество шагов методики: 5, что не позволяет критиковать подход за антинаучность.
Явно этот подход проще, быстрее и универсальнее, в стиле Метода. Но … учительница не то, что не похвалила, но и заставила переписать «правильным образом» (см. скриншот). То есть предприняла отчаянную попытку задушить творческий импульс и способность понимать математику на корню! Видимо, чтобы потом наняться репетитором … Не на того напала …
Все, что я так долго и нудно описал можно объяснить нормальному ребенку максимум за полчаса. Вместе с примерами.
Причем так, что он это никогда не забудет.
И это будет шаг к пониманию … не только математики.
Признайтесь: сколько раз в жизни вы складывали методом Гаусса? И я ни разу!
Но инстинкт понимания, который развивается (или гасится) в процессе изучения математических методов в школе … О!.. Это поистине незаменимая вещь!
Особенно в век всеобщей цифровизации, в который мы незаметно вошли под чутким руководством Партии и Правительства.
Несколько слов в защиту учителей …
Несправедливо и неправильно всю ответственность за такой стиль обучения сваливать исключительно на школьных учителей. Действует система.
Некоторые учителя понимают абсурдность происходящего, но что делать? Закон об образовании, ФГОСы, методики, технологические карты уроков … Все должно делаться «в соответствии и на основании» и все должно быть задокументировано. Шаг в сторону — встал в очередь на увольнение. Не будем ханжами: зарплата московских учителей ну очень неплохая … Уволят — куда идти?..
Поэтому сайт этот не об образовании. Он об индивидуальном образовании, единственно возможном способе выбраться из толпы поколения Z …
Комплексное число, действительная и мнимая части которого являются целыми числами
В теории чисел Гауссовское целое число – это комплексное число, действительная и мнимая части которого являются целыми числами. Целые числа Гаусса с обычным сложением и умножением комплексных чисел образуют область целостности, обычно записываемую как Z [я]. Эта область целостности является частным случаем коммутативного кольца из целых квадратичных чисел. У него нет общего упорядочивания, учитывающего арифметику.

Содержание
- 1 Основные определения
- 2 Евклидово деление
- 3 Главные идеалы
- 4 Гауссовские простые числа
- 5 Уникальная факторизация
- 6 Гауссовские рациональные числа
- 7 Наибольший общий делитель
- 8 Конгруэнции и классы остатков
- 8.1 Примеры
- 8.2 Описание классов остатков
- 8.3 Поля классов остатков
- 9 Примитив группа классов остатков и общая функция Эйлера
- 10 Историческая справка
- 11 Нерешенные проблемы
- 12 См. также
- 13 Примечания
- 14 Ссылки
- 15 Внешние ссылки
Основные определения
Целые числа Гаусса – это множество
- Z [i] = {a + bi ∣ a, b ∈ Z}, где i 2 = – 1. { displaystyle mathbf {Z} [i] = {a + bi mid a, b in mathbf {Z} }, qquad { text {where}} i ^ {2} = – 1.}
Другими словами, целое число Гаусса – это комплексное число такое, что его действительная и мнимая части являются целыми числами. Поскольку гауссовские целые числа замкнуты относительно сложения и умножения, они образуют коммутативное кольцо , которое является подкольцом поля комплексных чисел. Таким образом, это область целостности.
Если рассматривать в пределах комплексной плоскости, гауссовские целые числа составляют двумерную целочисленную решетку.
Сопряжение гауссовского целого числа a + bi – целое гауссовское число a – bi.
норма гауссовского целого числа – это его произведение с его сопряженным.
- N (a + b i) = (a + b i) (a – b i) = a 2 + b 2. { displaystyle N (a + bi) = (a + bi) (a-bi) = a ^ {2} + b ^ {2}.}
Таким образом, нормой гауссовского целого числа является квадрат его абсолютное значение как комплексное число. Норма гауссовского целого числа – неотрицательное целое число, которое представляет собой сумму двух квадратов . Таким образом, норма не может иметь вид 4k + 3 с целым числом k.
Нормой является мультипликативный, то есть один имеет
- N (zw) = N (z) N (w), { displaystyle N (zw) = N (z) N (w),}
для каждой пары целых гауссовских чисел z, w. Это можно показать напрямую или с помощью мультипликативного свойства модуля комплексных чисел.
единицы кольца гауссовских целых чисел (то есть гауссовские целые числа, мультипликативная обратная величина также является гауссовским целым числом) в точности являются гауссовскими целыми числами с нормой 1, то есть 1, –1, i и –i.
Евклидово деление

Гауссовские целые числа имеют евклидово деление (деление на остаток) аналогично целым числам и многочленам. Это делает гауссовские целые числа евклидовой областью и подразумевает, что гауссовские целые числа разделяют с целыми числами и многочленами многие важные свойства, такие как существование алгоритма Евклида для вычисления наибольших общих делителей, тождество Безу, свойство главного идеала, лемма Евклида, теорема разложения на множители и китайская теорема об остатке, все из которых можно доказать, используя только евклидово деление.
Алгоритм евклидова деления берет в кольце гауссовских целых чисел делимое a и делитель b 0 и производит частное q и остаток r, такие что
- a = bq + r и N (r) < N ( b). {displaystyle a=bq+rquad {text{and}}quad N(r)
Фактически, можно уменьшить остаток:
- a = bq + r и N (r) ≤ N (b) 2. { displaystyle a = bq + r quad { text {and}} quad N (r) leq { frac {N (b)} {2}}.}
Даже с этим лучшим неравенством частное и остаток не обязательно уникальны, но можно уточнить выбор, чтобы гарантировать уникальность.
Чтобы доказать это, можно рассмотреть комплексное число как частное x + iy = a / b. Существуют уникальные целые числа m и n такие, что –1/2 < x – m ≤ 1/2 and –1/2 < y – n ≤ 1/2, and thus N(x – m + i(y – n)) ≤ 1/2. Taking q = m + in, one has
- a = bq + r, { displaystyle a = bq + r,}
с
- r = b (x – m + i (y – n)), { displaystyle r = b { bigl (} x-m + i (yn) { bigr)},}
и
- N (r) ≤ N (b) 2. { displaystyle N (r) leq { frac {N (b)} {2}}.}
Выбор x – m и y – n в полуоткрытом интервале равен требуется для уникальности. Это определение евклидова деления можно интерпретировать геометрически в комплексной плоскости (см. Рисунок), отметив, что расстояние от комплексного числа ξ до ближайшего гауссовского целого не превышает √2 / 2.
Основные идеалы
Поскольку кольцо G гауссовских целых чисел является евклидовой областью, G является областью главных идеалов, что означает, что каждый идеал группы G является главным. Явно идеал I – это подмножество кольца R такое, что каждая сумма элементов I и каждое произведение элемента I на элемент R принадлежит I. Идеал является главным, если он состоит из всех кратных одного элемента g, то есть имеет вид
- {gx ∣ x ∈ G}. { displaystyle {gx mid x in G }.}
В этом случае говорят, что идеал порождается g или что g является генератором идеала.
Каждый идеал I в кольце целых гауссовских чисел является главным, потому что, если выбрать в I ненулевой элемент g минимальной нормы для каждого элемента x из I, остаток евклидова деления x на g принадлежит также I и имеет меньшую норму, чем у g; из-за выбора g эта норма равна нулю, и, следовательно, остаток также равен нулю. То есть x = qg, где q – частное.
Для любого g идеал, порожденный g, также порождается любым ассоциатом g, то есть g, gi, –g, –gi; никакой другой элемент не порождает такого же идеала. Поскольку все образующие идеала имеют одинаковую норму, норма идеала – это норма любого из его образующих.
В некоторых обстоятельствах полезно раз и навсегда выбрать генератор для каждого идеала. Для этого есть два классических способа, каждый из которых рассматривает сначала идеалы нечетной нормы. Если g = a + bi имеет нечетную норму a + b, то один из a и b нечетный, а другой четный. Таким образом, g имеет ровно один ассоциированный элемент с нечетной и положительной действительной частью a. В своей оригинальной статье Гаусс сделал другой выбор, выбрав такой уникальный ассоциированный объект, что остаток от его деления на 2 + 2i равен единице. Фактически, поскольку N (2 + 2i) = 8, норма остатка не больше 4. Поскольку эта норма нечетная, а 3 не является нормой гауссовского целого числа, норма остатка равна единице, т.е. есть, остаток – единица. Умножая g на обратную единицу, можно найти ассоциата, у которого есть единица в качестве остатка при делении на 2 + 2i.
Если норма g четная, то либо g = 2h, либо g = 2h (1 + i), где k – целое положительное число, а N (h) – нечетное. Таким образом, выбирается ассоциат g для получения h, который соответствует выбору ассоциатов для элементов нечетной нормы.
Гауссовы простые числа
Поскольку целые числа Гаусса образуют область главного идеала, они также образуют уникальную область факторизации. Это означает, что гауссовское целое число неприводимо (то есть не является произведением двух неединиц ) тогда и только тогда, когда оно является простым (что есть, он порождает простой идеал ).
простые элементы из Z [i] также известны как простые числа Гаусса . Ассоциированный элемент гауссовского простого числа также является гауссовским простым числом. Сопряжение гауссовского простого числа также является гауссовым простым числом (это означает, что гауссовы простые числа симметричны относительно действительной и мнимой осей).
Положительное целое число является гауссовским простым числом тогда и только тогда, когда оно является простым числом, которое конгруэнтно 3 по модулю 4 (то есть может быть записано 4n + 3 с n неотрицательным целым числом) (последовательность A002145 в OEIS ). Остальные простые числа не являются гауссовыми простыми числами, но каждое из них является произведением двух сопряженных гауссовских простых чисел.
Гауссовское целое число a + bi является гауссовским простым числом тогда и только тогда, когда:
- одно из a, b равно нулю и абсолютное значение другого является простым числом форма 4n + 3 (с na неотрицательное целое число) или
- оба ненулевые, а a + b – простое число (которое не будет иметь форму 4n + 3).
Другими словами, a Гауссовское целое число является гауссовским простым числом тогда и только тогда, когда либо его норма является простым числом, либо оно является произведением единицы (± 1, ± i) и простого числа вида 4n + 3.
Отсюда следует, что существует три случая факторизации простого числа p в гауссовских целых числах:
- Если p конгруэнтно 3 по модулю 4, то это гауссовское простое число; на языке теории алгебраических чисел, p называется инертным в целых гауссовских числах.
- Если p сравнимо с 1 по модулю 4, то это произведение гауссовского простого числа на его сопряженное, оба из которых являются неассоциированными гауссовскими простыми числами (ни одно из них не является произведением другого на единицу); p называется разложенным простым числом в гауссовских целых числах. Например, 5 = (2 + i) (2 – i) и 13 = (3 + 2i) (3 – 2i).
- Если p = 2, мы имеем 2 = (1 + i) ( 1 – i) = i (1 – i); то есть 2 – произведение квадрата гауссовского простого числа на единицу; это уникальное разветвленное простое число в гауссовых целых числах.
Уникальная факторизация
Что касается каждой уникальной области факторизации, каждое гауссовское целое число может быть разложено на множители единицы и гауссовских простых чисел, и эта факторизация уникальна до порядка множителей и замены любого простого числа любым из его ассоциированных (вместе с соответствующим изменением единичного множителя).
Если выбрать один раз и навсегда фиксированное простое число Гаусса для каждого класса эквивалентности связанных простых чисел, и если при факторизации используются только эти выбранные простые числа, то получается факторизация простых чисел который уникален в зависимости от порядка факторов. С вариантами, описанными выше, результирующая уникальная факторизация имеет вид
- u (1 + i) e 0 p 1 e 1 ⋯ pkek, { displaystyle u (1 + i) ^ {e_ { 0}} {p_ {1}} ^ {e_ {1}} cdots {p_ {k}} ^ {e_ {k}},}
где u – единица (то есть u ∈ {1, –1, i, –i}), e 0 и k – неотрицательные целые числа, e 1,…, e k – положительные целые числа, а p 1,…, p k – разные гауссовские простые числа, такие что, в зависимости от выбора выбранных ассоциатов,
- либо p k = a k + ib k с нечетным и положительным числом и b четным,
- или остаток от евклидова деления p k на 2 + 2i равен 1 (это первоначальный выбор Гаусса).
Преимущество второго выбора состоит в том, что выбранные партнеры хорошо себя ведут при произведениях для гауссовских целых чисел нечетной нормы. С другой стороны, выбранный ассоциированный элемент для вещественных гауссовских простых чисел – отрицательные целые числа. Например, факторизация 231 в целых числах и при первом выборе ассоциатов составляет 3 × 7 × 11, в то время как это (–1) × (–3) × (–7) × (–11) со вторым выбор.
гауссовские рациональные числа
Поле из гауссовских рациональных чисел является полем дробей кольца гауссовых целых чисел. Оно состоит из комплексных чисел, действительная и мнимая части которых являются рациональными.
Кольцо гауссовских целых чисел – это интегральное замыкание целых чисел в гауссовых рациональных числах.
Это означает, что гауссовские целые числа являются квадратичными целыми и что гауссовское рациональное число является гауссовским целым числом, если и только если оно является решением уравнения
- x 2 + cx + d = 0, { displaystyle x ^ {2} + cx + d = 0,}
с целыми числами c и d. Фактически a + bi является решением уравнения
- x 2 – 2 ax + a 2 + b 2, { displaystyle x ^ {2} -2ax + a ^ {2} + b ^ {2},}
и это уравнение имеет целые коэффициенты тогда и только тогда, когда a и b оба являются целыми числами.
Наибольший общий делитель
Как и для любой уникальной области факторизации, наибольший общий делитель (НОД) двух целых гауссовских чисел a, b равен Гауссовское целое число d, которое является общим делителем a и b, которое имеет все общие делители a и b в качестве делителя. То есть (где | обозначает отношение делимости ),
- d | а и г | b и
- c | а и с | b влечет c | d.
Таким образом, наибольшее значение относится к отношению делимости, а не к порядку кольца (для целых чисел оба значения наибольшего совпадают).
С технической точки зрения, наибольший общий делитель a и b является генератором идеала , генерируемого a и b (эта характеристика действительна для принципала идеальные области, но не, в общем, для уникальных областей факторизации).
Наибольший общий делитель двух целых чисел Гаусса не уникален, но определяется с точностью до умножения на единицу. То есть, учитывая наибольший общий делитель d чисел a и b, наибольшие общие делители a и b равны d, –d, id и –id.
Существует несколько способов вычисления наибольшего общего делителя двух целых гауссовских чисел a и b. Если известно разложение на простые множители a и b,
- a = ik ∏ mpm ν m, b = in ∏ mpm μ m, { displaystyle a = i ^ {k} prod _ {m} {p_ {m} } ^ { nu _ {m}}, quad b = i ^ {n} prod _ {m} {p_ {m}} ^ { mu _ {m}},}
где простые числа p m попарно не ассоциированы, а показатели степени μ m не связаны, наибольший общий делитель равен
- ∏ mpm λ m, { displaystyle prod _ {m} { p_ {m}} ^ { lambda _ {m}},}
с
- λ m = min (ν m, μ m). { displaystyle lambda _ {m} = min ( nu _ {m}, mu _ {m}).}
К сожалению, за исключением простых случаев, разложение на простые множители трудно вычислить и Алгоритм Евклида приводит к гораздо более простым (и быстрым) вычислениям. Этот алгоритм состоит из замены входа (a, b) на (b, r), где r – остаток от евклидова деления a на b, и повторения этой операции до получения нулевого остатка, то есть пары (d, 0). Этот процесс завершается, потому что на каждом шаге норма второго гауссовского целого числа уменьшается. Результирующий d является наибольшим общим делителем, потому что (на каждом шаге) b и r = a – bq имеют те же делители, что и a и b, и, следовательно, один и тот же наибольший общий делитель.
Этот метод вычисления работает всегда, но он не так прост, как для целых чисел, потому что евклидово деление сложнее. Поэтому для рукописных вычислений часто предпочитают третий метод. Он состоит в том, чтобы отметить, что норма N (d) наибольшего общего делителя a и b является общим делителем N (a), N (b) и N (a + b). Когда наибольший общий делитель D этих трех целых чисел имеет несколько множителей, тогда легко проверить на общий делитель все гауссовские целые числа с нормой, делящей D.
Например, если a = 5 + 3i, и b = 2 – 8i, N (a) = 34, N (b) = 68 и N (a + b) = 74. Поскольку наибольший общий делитель трех норм равен 2, наибольший общий делитель a и b имеют 1 или 2 в качестве нормы. Поскольку гауссовское целое число нормы 2 необходимо связать с 1 + i, а поскольку 1 + i делит a и b, то наибольший общий делитель равен 1 + i.
Если b заменить его сопряженным b = 2 + 8i, то наибольший общий делитель трех норм равен 34, норма a, поэтому можно предположить, что наибольший общий делитель равен a, то есть, что а | б. Фактически, 2 + 8i = (5 + 3i) (1 + i).
Конгруэнции и классы остатков
Для данного целого гауссова числа z 0, называемого модулем, два целых гауссовских числа z 1,z2конгруэнтны по модулю z 0, если их разность кратна z 0, то есть если существует гауссовское целое число q такое, что z 1 – z 2 = qz 0. Другими словами, два гауссовских целых числа являются конгруэнтными по модулю z 0, если их разность принадлежит идеалу, сгенерированному с помощью z 0. Это обозначается как z 1 ≡ z 2 (mod z 0).
Сравнение по модулю z 0 является отношением эквивалентности (также называемым отношением конгруэнтности ), которое определяет разбиение гауссовских целых чисел в классы эквивалентности, называемые здесь классами конгруэнтности или классами вычетов. Набор классов остатков обычно обозначается Z [i] / z 0Z[i] или Z [i] / ⟨z 0 ⟩, или просто Z [i] / z 0.
Класс вычетов гауссовского целого числа a – это множество
- a ¯: = {z ∈ Z [i] ∣ z ≡ a (mod z 0)} { displaystyle { bar {a}}: = left {z in mathbf {Z} [i] mid z Equiv a { pmod {z_ {0}}} right } }
всех гауссовских целых чисел, конгруэнтных a. Отсюда следует, что a = b тогда и только тогда, когда a ≡ b (mod z 0).
Сложение и умножение совместимы со сравнениями. Это означает, что a 1 ≡ b 1 (mod z 0) и a 2 ≡ b 2 ( mod z 0) подразумевает a 1 + a 2 ≡ b 1 + b 2 (mod z 0) и a 1a2≡ b 1b2(mod z 0). Это определяет четко определенные операции (которые не зависят от выбора представителей) над классами вычетов:
- a ¯ + b ¯: = a + b ¯ и a ¯ ⋅ b ¯: = ab ¯. { displaystyle { bar {a}} + { bar {b}}: = { overline {a + b}} quad { text {and}} quad { bar {a}} cdot { bar {b}}: = { overline {ab}}.}
С помощью этих операций классы вычетов образуют коммутативное кольцо, кольцо частных гауссовского целые числа по идеалу, порожденному z 0, который также традиционно называют кольцом классов вычетов по модулю z 0 (для более подробной информации см. Quotient ring ).
Примеры
- Существует ровно два класса вычетов для модуля 1 + i, а именно 0 = {0, ± 2, ± 4,…, ± 1 ± i, ± 3 ± i,…} ( все кратные 1 + i), и 1 = {± 1, ± 3, ± 5,…, ± i, ± 2 ± i,…}, которые образуют узор шахматной доски в комплексной плоскости. Таким образом, эти два класса образуют кольцо с двумя элементами, которое, по сути, является полем , уникальным (с точностью до изоморфизма) полем с двумя элементами, и, таким образом, может быть отождествлено с целыми числами по модулю 2. Эти два класса можно рассматривать как обобщение разбиения целых чисел на четные и нечетные целые числа. Таким образом, можно говорить о четных и нечетных целых гауссовских числах (Гаусс разделил далее четные гауссовские целые числа на четные, которые делятся на 2, и половинные четные).
- Для модуля 2 существует четыре класса остатков, а именно 0, 1, я, 1 + я. Они образуют кольцо из четырех элементов, в котором x = –x для каждого x. Таким образом, это кольцо не изоморфно кольцу целых чисел по модулю 4, другому кольцу с четырьмя элементами. Одно имеет 1 + i = 0, и, следовательно, это кольцо не является ни конечным полем с четырьмя элементами, ни прямым произведением двух копий кольца целых чисел по модулю 2.
- Для модуля 2 + 2i = (i – 1) существует восемь классов вычетов, а именно 0, ± 1, ± i, 1 ± i, 2, из которых четыре содержат только четные целые гауссовы числа, а четыре – только нечетные гауссовы целые числа.
Описание классов остатков

Учитывая модуль z 0, все элементы Класс остатка имеет тот же остаток для евклидова деления на z 0, при условии, что используется деление с уникальным частным и остатком, которое описано выше. Таким образом, перечисление классов остатков эквивалентно перечислению возможных остатков. Геометрически это можно сделать следующим образом.
В комплексной плоскости можно рассмотреть квадратную сетку, квадраты которой разделены двумя линиями
- V s = {z 0 (s – 1 2 + ix) | x ∈ R} и H t = {z 0 (x + i (t – 1 2)) | Икс ∈ R}, { Displaystyle { begin {align} V_ {s} = left { left.z_ {0} left (s – { tfrac {1} {2}} + ix right) right vert x in mathbf {R} right } quad { text {and}} \ H_ {t} = left { left.z_ {0} left (x + i left (t – { tfrac {1} {2}} right) right) right vert x in mathbf {R} right }, end {align}}}
с s и t целые числа (синие линии на рисунке). Они делят плоскость на полуоткрытые квадраты (где m и n – целые числа)
- Q m n = {(s + i t) z 0 | s ∈ [m – 1 2, m + 1 2), t ∈ [n – 1 2, n + 1 2)}. { Displaystyle Q_ {mn} = left {(s + it) z_ {0} left vert s in left [м – { tfrac {1} {2}}, м + { tfrac {1} } {2}} right), t in left [n – { tfrac {1} {2}}, n + { tfrac {1} {2}} right) right. Right }. }
Полуоткрытые интервалы, которые встречаются в определении Q mn, были выбраны для того, чтобы каждое комплексное число принадлежало ровно одному квадрату; то есть квадраты Q mn образуют разбиение комплексной плоскости. Имеется
- Q m n = (m + i n) z 0 + Q 00 = {(m + i n) z 0 + z ∣ z ∈ Q 00}. { displaystyle Q_ {mn} = (m + in) z_ {0} + Q_ {00} = left {(m + in) z_ {0} + z mid z in Q_ {00} right }.}
Это означает, что каждое целое число Гаусса конгруэнтно по модулю z 0 уникальному целому числу Гаусса в Q 00 (зеленый квадрат на рисунке), остаток которого для деление на z 0. Другими словами, каждый класс вычетов содержит ровно один элемент в Q 00.
Целые гауссовские числа в Q 00 (или в его границе ) иногда называют минимальными вычетами, потому что их норма не больше нормы любого другого гауссовского целого числа в том же классе вычетов (Гаусс назвал их абсолютно наименьшими вычетами).
Из этого можно вывести геометрическими соображениями, что количество классов остатков по модулю гауссовского целого числа z 0 = a + bi равно его норме N (z 0) = a + b (см. ниже для доказательства; аналогично, для целых чисел количество классов вычетов по модулю n равно его абсолютному значению | n |).
Доказательство –
Соотношение Q mn = (m + in) z 0 + Q 00 означает, что все Q mn получаются из Q 00 посредством преобразования его в гауссовское целое число. Это означает, что все Q mn имеют одинаковую площадь N = N (z 0) и содержат одинаковое количество n g целых гауссовских чисел.
Как правило, количество точек сетки (здесь гауссовские целые числа) в произвольном квадрате с площадью A равно A + Θ (√A) (см. Big theta для обозначений). Если рассматривать большой квадрат, состоящий из k × k квадратов Q mn, то он содержит kN + O (k√N) узлов сетки. Отсюда следует kn g = kN + Θ (k√N) и, следовательно, n g = N + Θ (√N / k) после деления на k. Переход к пределу, когда k стремится к бесконечности, дает n g = N = N (z 0).
Поля класса остатка
Кольцо класса остатка по модулю целого гауссова числа z 0 является полем тогда и только тогда, когда z 0 { displaystyle z_ {0}}
Если z 0 является разложенным простым числом или разветвленным простым числом 1 + i (то есть, если его норма N (z 0) является простым числом, которое либо 2, либо простое число, сравнимое с 1 по модулю 4), тогда поле класса вычетов имеет простое число элементов (то есть N (z 0)). Таким образом, он изоморфен полю целых чисел по модулю N (z 0).
Если, с другой стороны, z 0 – инертное простое число (то есть N (z 0) = p – квадрат простого числа, что сравнимо с 3 по модулю 4), то поле классов вычетов имеет p элементов и является расширением степени 2 (уникальным с точностью до изоморфизма) простого поля с p элементами (целые числа по модулю p).
Группа классов примитивных вычетов и общая функция Эйлера
Многие теоремы (и их доказательства) для модулей целых чисел можно напрямую перенести на модули целых чисел Гаусса, если заменить абсолютное значение модуля по норме. Это особенно справедливо для группы классов примитивных вычетов (также называемой мультипликативной группой целых чисел по модулю n ) и функцией Эйлера. Группа примитивных классов вычетов модуля z определяется как подмножество его классов вычетов, которое содержит все классы вычетов a, взаимно простые с z, то есть (a, z) = 1. Очевидно, эта система строит мультипликативную группа. Число его элементов обозначим через ϕ (z) (аналогично функции Эйлера φ (n) для целых n).
Для простых чисел Гаусса сразу следует, что ϕ (p) = | p | – 1 и для произвольных составных целых чисел Гаусса
- z = ik ∏ mpm ν m { displaystyle z = i ^ {k} prod _ {m} {p_ {m}} ^ { nu _ {m}}}
Формула произведения Эйлера может быть выведена как
- ϕ (z) = m (ν m>0) | p m ν m | 2 (1 – 1 | p m | 2) = | z | 2 ∏ п м | z (1–1 | pm | 2) { displaystyle phi (z) = prod _ {m , ( nu _ {m}>0)} | {p_ {m}} ^ { nu _ { m}} | ^ {2} left (1 – { frac {1} {| p_ {m} | ^ {2}}} right) = | z | ^ {2} prod _ {p_ {m } | z} left (1 – { frac {1} {| p_ {m} | ^ {2}}} right)}
где продукт строится поверх всех простых делителей p m of z (с ν m>0). Также можно напрямую перенести важную теорему Эйлера :
- Для всех a с (a, z) = 1 выполняется ≡ 1 (mod z).
Историческая справка
Кольцо гауссовых целых чисел было введено Карлом Фридрихом Гауссом в его второй монографии о четверной взаимности (1832 г.) Теорема квадратичной взаимности (которую ему впервые удалось доказать в 1796 г.) связывает решенное способность сравнения x ≡ q (mod p) к таковой x ≡ p (mod q). Точно так же кубическая взаимность связывает разрешимость x ≡ q (mod p) с разрешимостью x ≡ p (mod q), а биквадратичная (или квартичная) взаимность – это связь между x ≡ q (mod p) и x ≡ p (mod q). Гаусс обнаружил, что закон биквадратной взаимности и его дополнения легче сформулировать и доказать как утверждения о «целых комплексных числах» (т.е. гауссовских целых числах), чем как утверждения об обычных целых числах (т.е. целых числах).
В сноске он отмечает, что целые числа Эйзенштейна являются естественной областью для формулирования и доказательства результатов по кубической взаимности, и указывает, что аналогичные расширения целых чисел являются подходящими домены для изучения высших законов взаимности.
Эта статья не только ввела гауссовские целые числа и доказала, что они являются уникальной областью факторизации, но также ввела термины норма, единица, примар и ассоциация, которые теперь являются стандартными в теории алгебраических чисел.
Нерешенные проблемы

Большинство нерешенных проблем связано с распределением гауссовых простых чисел на плоскости.
- Задача круга Гаусса не имеет отношения к гауссовым целым числам как таковым, а вместо этого запрашивает количество точек решетки внутри круга заданного радиуса с центром в начале координат. Это эквивалентно определению числа гауссовских целых чисел с нормой меньше заданного значения.
Есть также предположения и нерешенные проблемы относительно простых гауссовских чисел. Два из них:
- Реальная и мнимая оси имеют бесконечный набор гауссовских простых чисел 3, 7, 11, 19,… и их партнеров. Есть ли какие-нибудь другие линии, на которых есть бесконечно много гауссовских простых чисел? В частности, существует ли бесконечно много гауссовских простых чисел вида 1 + ki?
- Можно ли дойти до бесконечности, используя гауссовские простые числа как ступеньки и делая шаги равномерно ограниченной длины? Это известно как проблема гауссова рва ; оно было сформулировано в 1962 году Бэзилом Гордоном и остается нерешенным.
См. также
Примечания
Ссылки
- C. Ф. Гаусс (1831) «Theoria резидуум biquadraticorum. Commentatio secunda.», Comm. Soc. Рег. Sci. Гёттинген 7 : 89-148; перепечатано в Werke, Georg Olms Verlag, Hildesheim, 1973, стр. 93–148. Немецкий перевод этой статьи доступен в Интернете в ″ H. Мазер (ред.): Arithmetische Untersuchungen über höhere Arithmetik Карла Фридриха Гаусса. Springer, Berlin 1889, pp. 534 ″.
- Фрали, Джон Б. (1976), Первый курс абстрактной алгебры (2-е изд.), Чтение: Аддисон-Уэсли, ISBN 0-201-01984-1
- Кляйнер, Израиль (1998). «От чисел к кольцам: ранняя история теории колец». Elem. Математика. 53 (1): 18–35. doi : 10.1007 / s000170050029. Zbl 0908.16001.
- Рибенбойм, Пауло (1996). Новая книга рекордов простых чисел (3-е изд.). Нью-Йорк: Спрингер. ISBN 0-387-94457-5. Zbl 0856.11001.
- Генри Г. Бейкер (1993). “Комплексные гауссовские целые числа для” гауссовой графики “”. Уведомления ACM SIGPLAN. 28 (11): 22–27. doi : 10.1145 / 165564.165571.
Внешние ссылки
- Сборник IMO текст о квадратичных расширениях и гауссовых целых числах при решении задач
- Кейт Конрад, Целые числа Гаусса.
.
![{mathbb {Z}}[i]={a+bimid a,bin {mathbb {Z}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06a6015e9cdb49042c983729de21091662309627)











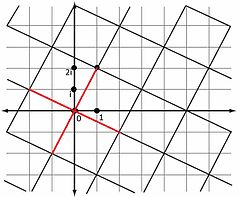
































![rho (m)={frac {1}{2}}[(lambda _{1}+1)(lambda _{2}+1)cdots (lambda _{r}+1)+1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/314ec8971ff4b885d497e781820afb4d745649b7)








![mathbf {Z} [i]={a+bimid a,bin mathbf {Z} },qquad {text{ where }}i^{2}=-1.](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1e23ae09a25e0fde987eb1f99eb41e838ce6537)


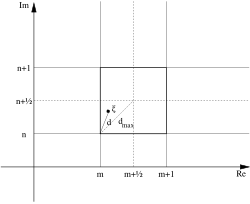












![{displaystyle {bar {a}}:=left{zin mathbf {Z} [i]mid zequiv a{pmod {z_{0}}}right}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fff8f7224fcd09a0b310e70c5211a2283725c677)