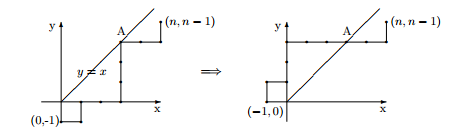Как найти число каталана формула

Числа Каталана

Несомненно, самым замечательным математическим фактом является тождество 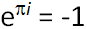. В нем удивительным образом сошлись, казалось бы, совершенно не связанные константы из разных областей математики. Доказать это тождество не так сложно, но объяснить его, понять глубинный смысл, удается немногим.
В качестве еще одного замечательного факта хотелось бы вспомнить числа Каталана, которые удивительным образом всплывают в самых разных комбинаторных задачах. К сожалению, они выпадают из рассмотрения типовой школьной программы, но уверен, что любой специалист компьютерных наук должен быть знаком с ними.

Само число Каталана выражается формулой C(n) = (2n)!/n!(n+1)!, где восклицательный знак, как обычно, обозначает факториал. Начало последовательности выглядит так: 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796…
Английская Википедия утверждает, что известно, как минимум 66 различных конструкций, которые приводят к появлению чисел Каталана. Вот некоторые из них:

• Правильные скобочные последовательности – наборы открывающихся и закрывающихся скобок, в которых каждой открывающейся скобке соответствует закрывающаяся. Число возможных последовательностей с фиксированным числом пар скобок выражается числом Каталана. Например, 14 правильных последовательностей из четырех пар скобок:
  (((()))), ((()())), ((())()), ((()))(), (()(())), (()()()), (()())(),
  (())(()), (())()(), ()((())), ()(()()), ()(())(), ()()(()), ()()()()
• Двоичные деревья – деревья, из каждого узла которых (кроме листьев) выходит ровно две ветки. Количество бинарных деревьев с заданным числом листьев – число Каталана. На рисунке представлены пять деревьев с 4 листьями в каждом.
  
  Такие деревья уже обсуждались на Хабре
• Любые деревья. Число неизоморфных деревьев с заданным числом вершин также равно числу Каталана. Такие деревья тоже обсуждались
• Монотонные пути в квадрате – маршруты из левого нижнего угла квадрата в правый верхний, которые идут по линиям сетки вверх или вправо и не заходят выше диагонали. На рисунке все такие пути для квадрата 3×3.
  
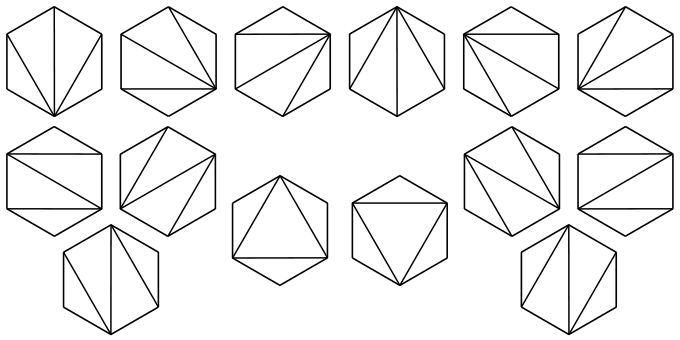
• Триангуляции многоугольника. Количество различных триангуляций выпуклого многоугольника диагоналями равно числу Каталана.
  
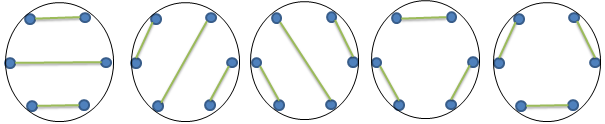
• Разбиение вершин многоугольника на пары. Четное число точек на окружности можно объединить в пары непересекающимися хордами. Число способов таких объединений также равно числу Каталана.
  
• Таблица Юнга – прямоугольник, заполненный последовательными числами так, чтобы они возрастали во всех строках и столбцах. Число таблиц Юнга размером 2xn также выражается числом Каталана.
  

Для каждой из этих конструкций можно либо по индукции, либо реккурентными соотношениями доказать, что число соответствующих объектов выражается числом Каталана. Не буду останавливаться на этих доказательствах – их можно найти в учебниках по дискретной математике. Также есть некоторые замечательные соотношения, которые можно получить, используя некоторые из упомянутых построений. Но это требует написания громоздких формул, чего хотелось бы избежать. Сейчас интереснее другое – неужели совпадение всех этих количеств для совершенно разных вещей случайность?
Конечно же, нет. Связь этих конструкций гораздо глубже. Можно построить взаимнооднозначное соответствие между этими объектами и некоторые из таких соответствий я попробую продемонстрировать. Помимо простого любопытства это имеет и некоторую практическую ценность. Например, задачу о генерации всех бинарных деревьев (решение которой в лоб неочевидно) можно свести к гораздо более простой задаче о генерации скобочных последовательностей.

Соответствие 1

Очень легко построить соответствие между скобочными последовательностями и монотонными путями в квадрате. Читая скобочную последовательность слева направо, будем строить путь, начав из левого нижнего угла, – для каждой открывающейся скобки нарисуем горизонтальный отрезок, для закрывающейся скобки – вертикальный.
Так как в последовательности было равное число открывающихся и закрывающихся скобок, то путь в итоге закончится в правом верхнем углу, а тот факт, что каждая открывающаяся скобка стоит раньше соответствующей ей закрывающейся скобки (ведь последовательность — правильная) гарантирует нам, что путь не перейдет в верхнюю половину квадрата. Очевидно, что это построение обратимо и из каждого монотонного пути можно получить скобочную последовательность.
На приведенном рисунке соответствующие скобки и отрезки отмечены одним цветом. Хорошо заметно, что отрезки, соответствующие одной паре скобок «видят друг друга»:

Соответствие 2

В качестве второй задачи построим соответствие между правильными скобочными последовательностями и таблицами Юнгам 2xn. Тут тоже все просто. Пронумеруем скобки слева направо. Если скобка открывающаяся, то соответствующее ей число пишем в верхнюю строку. Если закрывающаяся, то в – нижнюю. Так как i-ая открывающаяся скобка всегда стоит левее i-ой закрывающейся, то число соответствующее открывающейся скобке будет меньше числа, соответствующего закрывающей. А значит, верхнее число в таблице окажется меньше нижнего в той же колонке, то есть из правильной скобочной последовательности мы получили таблицу Юнга. Это построение также обратимо, а значит получено взаимно-однозначное соответствие.

Соответствие 3

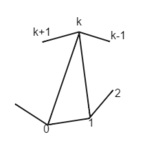
Теперь займемся бинарными деревьями. Очень легко увидеть соответствие между бинарными деревьями и расстановками скобок в выражении с однородными операциями, но это дает несколько другие последовательности. Для привязки бинарных деревьев к правильным скобочным последовательностям надо воспользоваться несколько другим подходом. Воспользуемся стандартным обходом дерева и пронумеруем вершины (корень примем за 0) в порядке обхода. Теперь, если при переходе к числу I мы спустились от родителя к ребенку, то на i-ое место ставим открывающуюся скобку. В противном случае ставим закрывающуюся.

Дерево – бинарное, поэтому у каждого узла есть сосед. А значит, спустившись к ребенку и поставив открывающуюся скобку, мы рано или поздно доберемся до его соседа и поставим закрывающуюся скобку. Это гарантирует правильность получившейся последовательности. Построение легко обратить и взяв за основу скобочную последовательность получить бинарное дерево.
Заметим, что если в скобочной последовательности n пар то соответствующее дерево имеет n+1 лист.

Соответствие 4

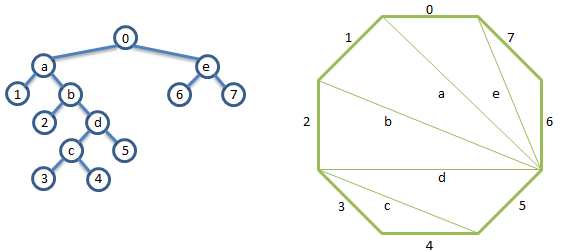
Для построения соответствия между триангуляциями многоугольника проще всего использовать бинарное дерево. На этот раз мы занумеруем в нем все листья слева направо (остальные узлы пометим буквами). Для триангуляции возьмем многоугольник, в котором вершин на одну больше, чем листьев в дереве. Одну из сторон этого многоугольника отметим, как стартовую, а остальные занумеруем (для наглядности – против часовой стрелки).
Далее выполняем следующую процедуру – если две вершины дерева соседние, то соответствующие стороны многоугольника «стянем» диагональю, которую пометим той буквой, которой помечен родитель этой пары узлов в дереве. Далее продолжаем процедуру «стягивания» пока от многоугольника не останется единственный стартовый отрезок.

Как можно заметить три стороны каждого треугольника в получившемся разбиении соответствуют одному родительскому узлу и двум его потомкам. Поэтому, если взять два разных дерева, то получится два разных разбиения.

Вместо эпилога

Ну и в заключение приведу табличку, в котором изображено соответствие объектов для третьего числа Каталана.

Числа Каталана

Первые несколько чисел Каталана:

Формулы вычисления чисел Каталана

Рекуррентная формула

Доказательство

Рекуррентную формулу легко вывести из задачи о правильных скобочных последовательностях.

Пусть — произвольная правильная скобочная последовательность длины . Она начинается с открывающейся скобки. Найдем парную ей закрывающуюся скобку и представим последовательность в виде: , где и — тоже правильные скобочные последовательности. Если длина последовательности равна , то последовательность можно составить способами. Тогда длина последовательности равна и последовательность можно составить способами. Комбинация любого способа составить последовательность с любым способом составить последовательность даст новую последовательность , а величина может меняться от до . Получили рекуррентное соотношение: . Так как , то последовательность совпадает с числами Каталана.

Аналитическая формула

Доказательство

Правильной скобочной структуре из открывающих и закрывающих скобок мы поставим в соответствие путь в квадрате . Путь начинается в точке и заканчивается в точке . Открывающей скобке мы сопоставляем горизонтальный отрезок длины , а закрывающей — вертикальный.
Если путь сопоставлен правильной структуре, то ни одна его точка не может лежать выше главной диагонали квадрата. Обратно, такому пути (“правильному пути”) сопоставляется правильная скобочная структура.
Геометрическое представление правильных скобочных структур позволяет найти выражение для чисел Каталана.

Сместим правильный путь на одну клетку вниз. Теперь правильный путь начинается в точке
, заканчивается в точке и не имеет общих точек с прямой — биссектрисой первого квадранта. Нам нужно найти количество правильных путей. Для этого мы найдем количество неправильных, и из общего числа путей вычтем количество неправильных. Мы рассматриваем пути из точки в точку . Длина такого пути равна и он содержит вертикальных сегментов и горизонтальных. Количество всех таких путей равно числу способов выбрать вертикальных сегментов из общего числа сегментов, т.е. равно .

Рассмотрим неправильный путь и его первую точку на прямой (точка ). Отрезок пути от точки до точки заменим симметричным относительно прямой . Мы получим путь длины , идущий из точки в точку (Смотри рис.).

Такой путь обязательно пересекает прямую . Обратно, пусть нам дан путь длины из точки в точку и пусть — первая точка этого пути, лежащая на прямой . Заменив участок пути от точки до точки на симметричный относительно прямой , мы получим неправильный путь из точки в точку . Следовательно, неправильных путей из точки в точку столько же, сколько путей из точки в
точку . Такой путь длины содержит горизонтальных и вертикальных участков. Поэтому, количество таких путей равно . Значит, количество правильных путей (т.е. число Каталана ) равно

Задача разбиения выпуклого —угольника на треугольники не пересекающимися диагоналями

Доказательство

Пусть — число триангуляций выпуклого -угольника при . Положим . Пронумеруем вершины многоугольника, начиная с произвольной против часовой стрелки. Рассмотрим произвольную триангуляцию и выделим треугольник, примыкающий к стороне (см. рис.).

Пусть — номер третьей вершины этого треугольника. Выделенный треугольник разбивает — угольник на — угольник и — угольник, каждый из которых триангулирован диагоналями. Перенумеруем вершины этих многоугольников против часовой стрелки так, чтобы нумерация вершин в каждом из них начиналась с 0. В результате получим пару триангуляций -угольника и — угольника. Наоборот, каждая пара триангуляций — угольника и — угольника
определяет триангуляцию исходного многоугольника. Поэтому

и поскольку , последовательность чисел совпадает с последовательностью Каталана.

Пример

Ответ на задачу при тривиален: никаких
диагоналей проводить не надо. В четырёхугольнике можно провести любую из
двух диагоналей, так что способов два. В пятиугольнике — из любой вершины две
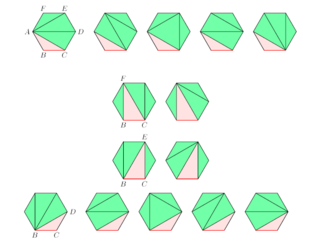
диагонали, способов. При — первый не вполне очевидный ответ: способов (см. рис.); чтобы
не запутаться, сторона BC выделена и отдельно нарисованы разрезания, в которых
к ней примыкают соответственно треугольники и .

Для семиугольника можно выделить одну из сторон и расклассифицировать разрезания в зависимости от того, какой треугольник к этой стороне примыкает. Имеем разных случаев. В первом и последнем из них количество разбиений равно ,
ибо после отрезания треугольника остаётся шестиугольник. Во втором и четвёртом
случаях при вырезании треугольника семиугольник распадается на треугольник и
пятиугольник. В третьем случае семиугольник распадается на два четырёхугольника. Поскольку каждый из них можно разбить двумя способами, получаем

варианта. Итак, семиугольник можно разбить всего

способами. Рассматривая восьмиугольник, аналогично получаем

способа.Такие вычисления можно проводить и дальше.

Подсчет чисел Каталана

Числа Каталана просто посчитать с помощью рекуррентной формулы. Для этого понадобится памяти и времени. За времени их можно посчитать, если использовать аналитическую формулу. Также из аналитической формулы можно выразить простую реккурентную формулу:

.

Вычисление производящей функции чисел Каталана

Задача:

Вычислить производящую функцию чисел Каталана

Пусть мы имеем последовательность чисел Каталана .

Будем искать её производящую функцию в виде

Как известно, рекуррентное соотношение для чисел Каталана имеет вид

Домножаем на , получая

Суммируя по всем от до , получаем:

(так как по определению чисел Каталана).

Получили, что

Распишем произведение по определению произведения формальных степенных рядов.

В последнем выражении выполним сдвиг индексации, положив . Тогда имеем: . Кроме того, . преобразуется в (так как ). Тогда, преобразуя предыдущее выражение, получаем:

Домножая это произведение на , получаем

Тогда

Из и получаем:

Преобразуя, получаем квадратное уравнение на

Из этого квадратного уравнения находим два варианта

Выберем из двух корней тот, который удовлетворяет определению как производящей функции чисел Каталана.

Домножая обе части на , получаем

Выберем нужный из двух корней, посчитав значение обеих частей при

Из определения производящей функции для чисел Каталана известно, что , тогда

Тогда при выражение принимает вид , или .

Тогда очевидно, нужно выбрать знак в выражении, чтобы при левая и правая части были равны.

Тогда

Проверим, что действительно является производящей функцией чисел Каталана. Для этого разложим в ряд.

Тогда коэффициент при в разложении равен , что совпадает с аналитической формулой для чисел Каталана. () Поэтому , поэтому является производящей функцией чисел Каталана.

Смотри также

• Производящая функция

• Числа Стирлинга первого рода

• Числа Стирлинга второго рода

• Числа Эйлера первого и второго рода

Источники информации

• MAXimal :: algo :: Числа Каталана

• Числа Каталана / Хабрахабр

• Википедия — Числа Каталана

• Журнал “Квант”

• Глава 5. Комбинаторика

Числа Катала́на — числовая последовательность, встречающаяся во многих задачах комбинаторики.

Последовательность названа в честь бельгийского математика Эжена Шарля Каталана, хотя была известна ещё Леонарду Эйлеру.

Числа Каталана для образуют последовательность:

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, … (последовательность A000108 в OEIS)

Определения[править | править код]

n-е число Каталана можно определить несколькими эквивалентными способами, такими как^[1]:

• Количество разбиений выпуклого (n+2)-угольника на треугольники непересекающимися диагоналями.
• Количество способов соединения 2n точек на окружности n непересекающимися хордами.
• Количество правильных скобочных последовательностей длины 2n, то есть таких последовательностей из n левых и n правых скобок, в которых количество открывающих скобок равно количеству закрывающих, и в любом её префиксе открывающих скобок не меньше, чем закрывающих.
  • Например, для n = 3 существует 5 таких последовательностей:

    ((())), ()(()), ()()(), (())(), (()())

    то есть .

Свойства[править | править код]

Это соотношение легко получается из того, что любая непустая правильная скобочная последовательность однозначно представима в виде w = (w₁)w₂, где w₁, w₂ — правильные скобочные последовательности.

• Есть ещё одно рекуррентное соотношение:

и .

• Ещё одна рекуррентная формула:

и . Если положить , то получается удобная для вычислений рекурсия , .

Отсюда следует: .

• Производящая функция чисел Каталана равна:

  

• Числа Каталана можно выразить через биномиальные коэффициенты:

  

Другими словами, число Каталана равно разности центрального биномиального коэффициента и соседнего с ним в той же строке треугольника Паскаля.

• Асимптотически

См. также[править | править код]

• Размещение
• Сочетание
• Перестановка

Примечания[править | править код]

Ссылки[править | править код]

• С. К. Ландо. Лекции по комбинаторике. — МЦНМО, 1994.
• А. Шень. Разделы 2.6 и 2.7 // Программирование: теоремы и задачи. — M.: МЦНМО, 2017.
• Stanley, Richard P. (2013), Catalan addendum to Enumerative Combinatorics, Volume 2, <http://www-math.mit.edu/~rstan/ec/catadd.pdf>
• Weisstein, Eric W. Catalan Number (англ.) на сайте Wolfram MathWorld.

Рекуррентная формула для чисел Каталана.

В
действительности числа Каталана C(n)
определяются так: нулевое число Каталана
равно единице. Число с номером n
равно сумме следующих произведений:
нулевого числа на (n-1)–е,
первого числа на (n-2)–e,
второго на (n-3)–е,
…, (n-1)–го
на нулевое, так чтобы сумма номеров двух
перемножаемых чисел была равна n-1.
Более строго это можно записать так:

(1)

Так,
для малых значений n
получаем:

Покажем,
что именно такая рекуррентная формула
соответствует решениям всех трех
предложенных задач.

Рассмотрим
сначала случай правильных скобочных
структур (расстановок скобок). Пусть
дана некоторая правильная расстановка
n
пар скобок. Понятно, что начальная скобка
a
будет открывающей. Следовательно,
ей соответствует какая–то закрывающая
скобка b.
Между этими двумя скобками находится
другой набор скобок, возможно пустой,
который, очевидно, является правильной
скобочной структурой. Кроме того,
последовательность скобок, стоящая
после скобки b,
также правильная. Таким образом, внутри
нашей структуры есть еще две правильные
структуры, суммарное количество пар
скобок в которых равно n-1.
Эти две структуры полностью определяют
изначальную расстановку скобок: для ее
получения достаточно заключить в скобки
первую структуру, а затем справа приписать
к ней вторую.

Пример.В
структуре (
( ) ( ) )
( ( ) ) из пяти пар скобок скобки, отмеченные
красным, отделяют правильную структуру
из двух пар скобок от правильной структуры
из двух пар скобок.

Таким
образом, становится понятен смысл
формулы (1): для того, чтобы посчитать
количество правильных структур из пяти
пар скобок нужно рассмотреть зафиксировать
первую пару скобок, а затем поставить
две правильные структуры, суммарное
количество скобок в которых равно
четырем.

Аналогичная
ситуация имеет место и в случае с
многоугольниками: мы фиксируем некоторое
ребро и рассматриваем треугольник,
примыкающий к этому ребру, см. рис. 2. Он
разбивает (n+2)–угольник
на (p+2)–угольник
и (q+2)–угольник,
где p+q=n-1.
Эти два многоугольника должны быть
разбиты на треугольники своими
непересекающимися диагоналями, которые
являются диагоналями исходного
многоугольника. Любое такое разбиение
двух “маленьких” многоугольников
порождает разбиение изначального
многоугольника.

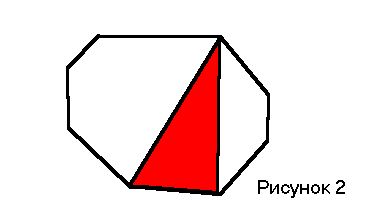
На
рисунке 2 изображен восьмиугольник
(8=6+2),
разбиение которого на треугольники
непересекающимися диагоналями порождается
такими разбиениями для четырехугольника
(4=2+2)
и пятиугольника (5=3+2).
При этом 6-1=2+3.

Таким
образом, для количества разбиений
(n+2)–угольника
непересекающимися диагоналями на
треугольники имеет место та же рекуррентная
формула, что и для скобочных структур.

Перейдем,
наконец, к описанию задачи про билеты
в театр. Для каждого возможного случая
распределения пятирублевых и десятирублевых
банкнот у стоящих в очереди можно
построить правильную скобочную структуру.
Действительно, каждому следующему
стоящему в очереди будем приписывать
скобку, которая будет открывающей, если
у него на руках пятирублевая купюра, и
закрывающей, если десятирублевая.
Условие того, что у кассира всегда будет
достаточно пятирублевых купюр означает,
что по ходу написания слова из скобок
количество открывающих будет всегда
не меньше количества закрывающих, а то,
что эти купюры иссякнут после обслуживания
последнего покупателя, значит, что во
всем слове количество открывающих
скобок будет равно
количеству закрывающих. Это и означает,
что каждой открывающей скобке будет
однозначно соответствовать закрывающая.
Для этого человеку, давшему пять рублей,
после чего у кассира стало m
пятирублевых банкнот, нужно сопоставить
человека, давшего десять рублей и
стоящего после первого, после чего у
кассира осталась (m-1)
пятирублевая
банкнота, причем между первым и вторым
человеком у кассира должно всегда быть
не меньше n
пятирублевых
банкнот.

Пример.
Для скобочной структуры ( ) ( ( ) ( ( ) ) ) из
пяти пар скобок поставим в соответствие
такое распределение банкнот: 5, 10, 5, 5,
10, 5, 5, 10, 10, 10. При этом количество
пятирублевых банкнот у кассира после
продажи очередного билета будет
изменяться следующим образом:

1,
0, 1, 2, 1, 2, 3, 2, 1, 0

(
) ( ( ) ( ( ) ) )

Из
сказанного выше следует, что правильные
скобочные структуры из n
скобок
однозначно соответствуют “хорошим”
распределениям пяти– и десятирублевых
банкнот у стоящих в очереди.

Таким
образом, количество правильных очередей
из 2n
человек
равно C(n)
и ответ на третью задачу, как и на первые
две, связан с числами Каталана.

При
этом у нас остается открытым еще один
вопрос: как считать числа Каталана, т.е.
найти формулу для C(n)
не рекуррентную, а в явном виде.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Муниципальное
общеобразовательное учреждение

«Средняя
общеобразовательная школа №19 г. Новоалтайска»

Способы
получения чисел Каталана и доказательства их эквивалентности

Выполнил: Керимова Сабина

ученица 10э класса

Руководитель: С.В. Куличенко

учитель математики,

высшей квалификационной категории

2021

Оглавление

Введение

Основная
часть

1.     
Теоретические аспекты исследования чисел
Каталана

1.1.
Определения чисел Каталана исходя из способов их получения

1.2.Формулы
определения чисел Каталана

2.     
Эмпирическое исследование идентичности
способов определения числа Каталана

2.1.
Взаимнооднозначное соответствие междускобочными последовательностями и
монотонными путями в квадрате

2.2.
Соответствие между правильными скобочными последовательностями и таблицами
Юнгам 2xn

2.3.
Соответствие между бинарными деревьями и расстановками скобок в выражении с
однородными операциями

2.4.Соответствие
между триангуляциями многоугольника и многоугольного дерева

Заключение

Список
используемой литературы

Приложение

Введение

Любому
математику (и ученому вообще) часто приходится сталкиваться с бесконечными
последовательностями целых положительных чисел. Если последовательность
простая, как например, последовательность удваивающихся чисел (1,2,4,8,16…) или
последовательность квадратов (1,4,9,16,25…), то она распознается сразу же.
Редкий математик не сможет узнать числа Фибоначчи (1,1,2,3,5,8..) или
треугольные числа (1,3,6,10,15,21…). Если же последовательность не столь
известна, то можно потратить много времени в поисках задающего ее рекуррентного
(если вычисление следующего члена требует знания предыдущих членов) или нерекуррентного
закона (нереккурентная формула дает n-ый
член, не требуя знания предыдущих). Данная работа посвящена числам Каталана, которые
появляются в самых разных комбинаторных задачах. Эта последовательность названа
в честь бельгийского математика Каталана (Catalan), жившего в 19 веке, хотя на
самом деле она была известна ещё Эйлеру (Euler), жившему за век до Каталана.

Актуальность темы
состоит в том, что числа Каталана, являясь специальными числами натурального
ряда, возникая из комбинаторных задач, порождают своим существованием целый ряд
других комбинаторных проблем, требующих решения.

Цель исследования: доказать
эквивалентность способов определения числа Каталана на конкретных примерах.

Для
достижения цели в работе поставлены следующие задачи:

–       
раскрыть различные определения чисел
Каталана

–       
рассмотреть рекуррентную и аналитическую
формулы определения чисел Каталана;

–       
выстроить взаимнооднозначное соответствие
между способами определения числа Каталана.

Гипотеза: различные
способы получения чисел Каталана эквивалентны друг другу.

Для
решения поставленных задач и подтверждения гипотезы были использованы
следующие методы:

–
теоретические: изучение и анализ научно-публицистической, и учебной литературы,
изучение и анализ публикаций периодической печати и сборников по теме
исследования;

–
эмпирические: решение комбинаторных задач.

Исследовательская
работа состоит из введения, двух глав, заключения и списка литературы.

1. Теоретические
аспекты исследования чисел Каталана

1.1    Определения чисел Каталана исходя из способов их получения

Числа
Каталана которые обозначаются c0, c1, c2, c3 . . . . Вот некоторые значения
чисел Каталана (таблица 1):

Таблица
1 – Некоторые значения чисел Каталана[1]

n	n 0	n1	n2	n3	n 4	n5	n 6	n 7	n 8	n 9	n 10	n 11	n 12	n 13
cn	1	1	2	5	14	42	132	429	1430	4862	16796	58786	208012	742900

Имеется огромное количество разных определений чисел Каталана.
Рассмотрим некоторые из них.

1.
Количество плоских корневых деревьев с n рёбрами.

Вот
полные списки при n ≤ 3 (рис.1)

Рисунок
1 – Полные списки плоских корневых деревьев с n рёбрами при
n ≤ 3

2.     
Количество триангуляций (n + 2)-угольника
с выделенной стороной.

Полная
запись чисел Каталана при n ≤ 3 (рис. 2):

Рисунок
2 – Полная запись чисел Каталана по определению триангуляций, при n ≤ 3

Исходя
из рисунка 2, при n = 0 приходится иметь дело с пустой триангуляцией
двуугольника.

3.
Количество правильных скобочных слов с n
парами скобок.

Представим
себе все правильно записанные алгебраические выражения, в которых скобки
используются так, как учат в школе. Потом мысленно сотрём все знаки, кроме
скобок. То, что останется, и называется правильными скобочными словами. Скобки
окажутся разбитыми на пары: каждой открывающейся скобке соответствует
закрывающаяся. При n = 0 нам придётся работать с пустым словом, которое будет
обозначаться прочерком. – Полные списки (рис.3):

Рисунок
3 – Полная запись чисел Каталана по определению скобочных слов с n
парами скобок, при n ≤ 3

4. Монотонные пути в квадрате.

Это
маршруты из левого нижнего угла квадрата в правый верхний, которые идут по
линиям сетки вверх или вправо и не заходят выше диагонали. На рисунке все такие
пути для квадрата 3×3.

Рисунок
4 – Полная запись чисел Каталана по способу монотонных путей   в квадрате, для
квадрата 3×3

5.
Разбиение вершин многоугольника на пары.

Четное
число точек на окружности можно объединить в пары непересекающимися хордами.
Число способов таких объединений также равно числу Каталана.

Рисунок
5 – Полная запись чисел Каталана по способу разбиения вершин многоугольника на
пары

6. Таблица Юнга

Таблица Юнга – прямоугольник, заполненный
последовательными числами так, чтобы они возрастали во всех строках и столбцах.
Число таблиц Юнга размером 2xn также выражается числом Каталана.

Рисунок
5 – Полная запись чисел Каталана по способу таблиц Юнга

Для каждой из этих конструкций можно либо по
индукции, либо реккурентными соотношениями доказать, что число соответствующих
объектов выражается числом Каталана.

1.2 Формулы определения чисел Каталана

Числа
Каталана удовлетворяют рекуррентному соотношению (то есть соотношению,
выражающему очередной член последовательности через предыдущие)[2]:

с₀
= 1,

 (1)

при
n=
0,1,2,3…

Это
соотношение легко получается из того, что любая непустая правильная скобочная
последовательность однозначно представима в виде w = (w ₁) w ₂ ,
где w ₁ , w ₂ — правильные
скобочные последовательности.

Есть
еще одно реккурентное соотношение: . (2)

Здесь
используется обозначение для биномиальных коэффициентов  , фигурирующее в
современной математической литературе наряду с .

Данную
формулу также называют аналитической, где  обозначен, как
биномиальный коэффициент.

Кроме
того, числа Каталана определяются реккурентным соотношением:

с₀
= 1,

 (3)

при
n = 0, 1, 2, 3….

В
последнем определении даётся просто формула для чисел Каталана.

  (4)

Приводимый
ряд можно рассматривать либо как формальный (для его понимания достаточно знать
формулу Тейлора-Маклорена f(x)
= f(0)
+  Или формулу Ньютона (1+t)
^α=1+at+…), либо как сходящийся
при .[3]

Вывод по 1 главе:
Известно много определений числа Каталана, которые
исходят из способов их появления чисел: правильные скобочные
последовательности, двоичные деревья, монотонные пути в квадрате, триангуляции
многоугольника, разбиение вершин многоугольника на пары. таблица Юнга. Имеется
две формулы для чисел Каталана: рекуррентная и аналитическая.

2. Эмпирическое исследование идентичности способов
определения числа Каталана

2.1 Взаимнооднозначное соответствие между скобочными
последовательностями и монотонными путями в квадрате

Очень легко построить соответствие между
скобочными последовательностями и монотонными путями в квадрате. Читая
скобочную последовательность слева направо, будем строить путь, начав из левого
нижнего угла, – для каждой открывающейся скобки нарисуем горизонтальный
отрезок, для закрывающейся скобки – вертикальный.

Преобразуем скобочную структуру ((()())())[4].

((()())()) ⇒ (((∗(∗ ∗ (∗∗ ⇒ (((∗. ∗ (∗∗

Здесь точка указывает, что в этом месте в
выражении будет стоять (a ∗ a).

Продолжаем. (((∗. ∗ (∗∗ ⇒ ((.. ∗ (∗∗

Здесь две точки указывают, что в выражении в этом
месте будет стоять (a ∗ (a ∗ a)). Продолжаем. ((.. ∗ (∗∗ ⇒ ((.. ∗ .∗ ⇒ (…∗

Здесь три точки указывают, что в выражении в э
том месте будет стоять фрагмент ((a ∗ (a ∗ a)) ∗ (a ∗ a)).

Окончательно получаем (((a ∗ (a ∗ a)) ∗ (a ∗ a)) ∗ a).

Обратное преобразование (((a ∗ (a ∗ a)) ∗ (a ∗ a)) ∗ a) ⇒ ((()())()) дает нам исходную скобочную
структуру. Если же в строке нет двух знаков ∗ подряд, то строка имеет вид (∗(∗(∗ · · · и ей отвечает выражение (a ∗ (a ∗ (a ∗ (a ∗ · · · .

Правильной скобочной структуре из 2n открывающих
и 2n закрывающих скобок мы поставим в соответствие путь в квадрате [0, n]×[0,
n]. Путь начинается в точке (0,0) и заканчивается в точке (n, n). Открывающей
скобке мы сопоставляем горизонтальный отрезок длины 1, а закрывающей —
вертикальный. На рисунке 6 представлены соответствующие скобкам отрезки:

Рисунок
6 – Соответствие между скобочными последовательностями и монотонными путями в
квадрате

Если
путь сопоставлен правильной структуре, то ни одна его точка не может лежать
выше главной диагонали квадрата. Обратно, такому пути („правильному пути“)
сопоставляется правильная скобочная структура. Геометрическое представление
правильных скобочных структур позволяет найти выражение для чисел Каталана.

2.2 Соответствие между правильными скобочными
последовательностями и таблицами Юнгам 2xn

В качестве второй задачи построим соответствие
между правильными скобочными последовательностями и таблицами Юнгам 2xn. Тут
тоже все просто. Пронумеруем скобки слева направо. Если скобка открывающаяся,
то соответствующее ей число пишем в верхнюю строку. Если закрывающаяся, то в –
нижнюю. Так как i-ая открывающаяся скобка всегда стоит левее i-ой
закрывающейся, то число, соответствующее открывающейся скобке будет меньше
числа, соответствующего закрывающей. А значит, верхнее число в таблице окажется
меньше нижнего в той же колонке, то есть из правильной скобочной
последовательности мы получили таблицу Юнга. Это построение также обратимо, а
значит получено взаимно-однозначное соответствие (рисунок 7).

Рисунок
7 – Соответствие между правильными скобочными последовательностями и таблицами
Юнгам 2xn

2.3 Соответствие между бинарными деревьями и
расстановками скобок в выражении с однородными операциями

Теперь рассмотрим бинарные деревья. Очень легко
увидеть соответствие между бинарными деревьями и расстановками скобок в
выражении с однородными операциями, но это дает несколько другие
последовательности. Для привязки бинарных деревьев к правильным скобочным
последовательностям надо воспользоваться несколько другим подходом.
Воспользуемся стандартным обходом дерева и пронумеруем вершины (корень примем
за 0) в порядке обхода. Теперь, если при переходе к числу I мы спустились от
родителя к ребенку, то на i-ое место ставим открывающуюся скобку. В противном
случае ставим закрывающуюся, как показано на рисунке 8.

Рисунок
8 – Соответствие между бинарными деревьями и расстановками скобок в выражении с
однородными операциями[5]

Дерево
– бинарное, поэтому у каждого узла есть сосед. А значит, спустившись к ребенку
и поставив открывающуюся скобку, мы рано или поздно доберемся до его соседа и
поставим закрывающуюся скобку. Это гарантирует правильность получившейся
последовательности. Построение легко обратить и взяв за основу скобочную последовательность
получить бинарное дерево.
Заметим, что если в скобочной последовательности n пар то соответствующее
дерево имеет n+1 лист.

2.4 Соответствие между триангуляциями
многоугольника и многоугольного дерева

Для построения соответствия между триангуляциями
многоугольника проще всего использовать бинарное дерево. На этот раз мы
занумеруем в нем все листья слева направо (остальные узлы пометим буквами). Для
триангуляции возьмем многоугольник, в котором вершин на одну больше, чем
листьев в дереве[6]. Одну из сторон
этого многоугольника отметим, как стартовую, а остальные занумеруем (для
наглядности – против часовой стрелки).
Далее выполняем следующую процедуру
– если две вершины дерева соседние, то соответствующие стороны многоугольника
«стянем» диагональю, которую пометим той буквой, которой помечен родитель этой
пары узлов в дереве. Далее продолжаем процедуру «стягивания» пока от
многоугольника не останется единственный стартовый отрезок (рисунок 9).

Рисунок 9 – Соответствия между триангуляциями многоугольника и
многоугольного дерева

Как
можно заметить три стороны каждого треугольника в получившемся разбиении
соответствуют одному родительскому узлу и двум его потомкам. Поэтому, если
взять два разных дерева, то получится два разных разбиения.

В
качестве примера соответствие объектов для третьего числа Каталана приведено в
Приложении 1.

Вывод по 2 главе:
различные
способы получения чисел Каталана эквивалентны друг другу

3. Пример решения комбинаторной задачи с помощью чисел Каталана

Как
было сказано выше, числа Каталана используются при решении комбинаторных задач.
Рассмотрим пример решения такой задачи.

Задача 1.

У
театральной кассы стоит очередь за билетами из 2n
человек. Билет стоит пять рублей, а в наличии у каждого из стоящих в очереди
есть ровно одна банкнота — либо пять, либо десять рублей, причем каждый из двух
видов банкнот встречается ровно у n
человек. У кассира в начальный момент нет пятирублевых банкнот. Каждый, стоящий
в очереди, покупая билет, если дает десятирублевую банкноту, должен получить
сдачу. Какова вероятность того, что на протяжении всей очереди у кассира всегда
будет достаточный запас пятирублевых банкнот для сдачи, а в конце у него не останется
пятирублевых купюр?

Решение:

Легко
видеть, что всего существует  возможных
ситуаций (ровно столько есть способов распределить среди 2n
любителей театра n
человек, у которых на руках десятирублевая купюра и n
человек с пятирублевыми купюрами на руках). Следовательно, для решения задачи
нужно посчитать, в скольких случаях у кассира на протяжении всей очереди будут
иметься в достаточном количестве пятирублевые купюры, причем в последний момент
они у него закончатся. Полученное число случаев нужно разделить  число случаев
на .

Подсчет
таких случаев для малых значений числа n
приводит нас к знакомой последовательности: при n=1
это число равно единице, при n=2
— двум, далее пяти, четырнадцати, и т.д.

Заключение

Известно
множество различных конструкций, которые приводят к появлению чисел Каталана. В
данном исследовании были рассмотрены некоторые из них:

–       
правильные скобочные последовательности;

–       
двоичные деревья;

–       
монотонные пути в квадрате;

–       
триангуляции многоугольника;

–       
разбиение вершин многоугольника на пары;

–       
таблица Юнга.

Для
каждой из этих конструкций можно либо по индукции, либо реккурентными
соотношениями доказать, что число соответствующих объектов выражается числом
Каталана. Таким образом доказана гипотеза о том, что различные способы
получения чисел Каталана эквивалентны друг другу.

 В
работе построено взаимнооднозначное соответствие между этими объектами. Помимо
интереса это имеет и некоторую практическую ценность. Например, задачу о
генерации всех бинарных деревьев (решение которой в лоб неочевидно) можно
свести к гораздо более простой задаче о генерации скобочных
последовательностей.

Список  используемой литературы

1.       
Доценко В. В. Числа Каталана и
естественные отображения // Летние конференции Турнира городов: Избранные
материалы. Вып. 1 / Под общ. ред. Н. Н. Константинова. Сост. Б. Р. Френкин. —
М.: МЦНМО, С. 139-166.

2.       
Лекция 2. Числа Каталана [электронный
ресурс]//Режим доступа: https://nnov.hse.ru/data/2016/10/19/1107972447/Числа%20Каталана-2.pdf

3.       
Лекция 2: перечслительная комбинаторика
Дискретная математика, ВШЭ, факультет компьютерных наук [Электронный
ресурс]//Режим доступа: http://www.mi-ras.ru/~podolskii/files/lecture2.pdf

4.       
Специальные числа: многоуровневая
система творческих задач : учебно-методическое пособие / А.С. Ростовцев, Е.И.
Деза, Т.А. Немкина, А.В. Эргешовав. – Москва : Белый ветер, 2020. – С.8.

5.       
Числа Каталана [Электронный ресурс]//
Режим доступа: http://www.e-maxx-ru.1gb.ru/algo/catalan_numbers

6.       
Числа Каталана [электронный ресурс]//
Режим доступа: https://habr.com/ru/post/165295/

Приложение 1

Соответствие объектов для третьего числа
Каталана