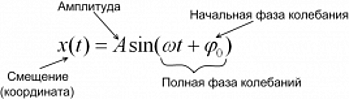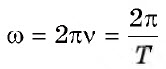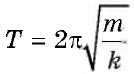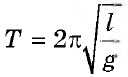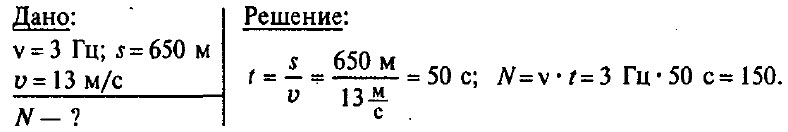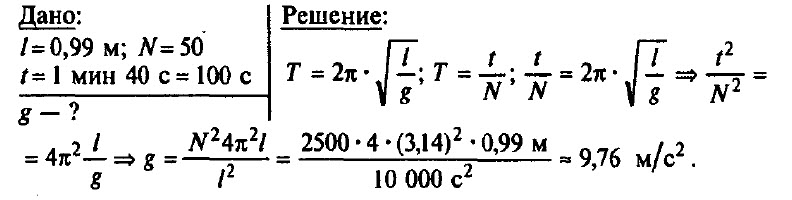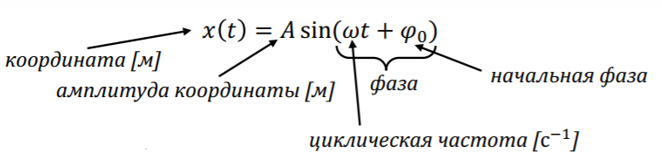Как найти число колебаний если известно время

Колебания ― это процесс, при котором состояние системы изменяется, повторяясь во времени, и смещаясь то в одну, то в другую сторону относительно состояния равновесия.

Период ― это время, через которое повторяются показатели системы, т. е. система совершает одно полное колебание. Период изменяется в секундах.

Частота ― величина обратная периоду: число полных колебаний за единицу времени. Частота измеряется в герцах [Гц] = [c-1]. Частота равна v = $frac{1}{T}$ , где

v ― частота [Гц];

T ― период [c].

Если известно, что тело совершает N колебаний за время t, то частоту его колебаний можно определить как v = $frac{N}{t}$ , где

ν ― частота [Гц];

N ― количество колебаний;

t - время [с].

Для описания колебательных систем, совершающих круговые процессы, удобно использовать круговую (циклическую) частоту. Циклическая частота показывает количество полных колебаний, которые происходят за 2π секунд и равна ω = 2πvили ω = $frac{2pi}{T}$ , где

ω ― циклическая частота [рад/с];

ν ― частота [Гц];

T ― период [c].

Гармонические колебания ― колебания, в которых физические величины изменяются по закону синуса или косинуса. Кинематическое уравнение гармонических колебаний имеет вид:

x(t) = Asin(ωt + φ0) или x(t) = Acos(ωt + φ0), где

x ― смещение [м];

t ― время, [с];

A ― амплитуда колебаний [м];

ω ― циклическая частота [рад/с];

φ0 ― начальная фаза колебаний, [рад];

(ωt + φ0) ― полная фаза колебаний [рад].

Смещение (x) ― это отклонение тела от положения равновесия. Смещение также является координатой тела, если отсчитывать ее от положения равновесия.

Амплитуда колебаний (A) ― максимальное отклонение колеблющейся величины от положения равновесия, т. е. максимальное смещение равно амплитуде колебаний xmax = A.

Начальная фаза колебаний (φ0) определяет смещение в начальный момент времени, выраженное в радианах.

Фаза колебаний (φ) или полная фаза колебаний, определяет смещение в данный момент времени, выраженное в радианах. Фаза колебаний равна φ = ωt + φ0, где

φ ― полная фаза колебаний [рад];

φ0 ― начальная фаза колебаний, [рад];

ω ― циклическая частота [рад/с];

t ― время, [с].

Пример анализа гармонических колебаний точки

Рассмотрим гармонические колебания, в которых уравнение движения точки имеет вид x(t) = Asin(ωt), где

x ― смещение [м];

t ― время, [с];

A — амплитуда колебаний [м];

ω ― циклическая частота [рад/с].

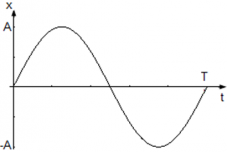
Из уравнения x(t) = Asin(ωt) следует, что начального смещения нет (φ0 = 0) и колебания начинаются из положения равновесия. Смещение x достигает максимального значения xmax и равно амплитуде xmax = A, в тот момент, когда модуль синуса равен единице |sin(ωt)| = 1. Когда x = A фаза колебаний равна φ = $frac{pi}{2} +2pi n$ когда x = –A фаза колебаний принимает значения φ = $frac{3pi}{2} +2pi n$ , где n = 0, 1 , 2, … N.

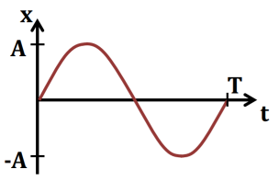
График колебания координаты точки имеет вид:

Определим уравнение и график колебания скорости. Скорость ― это производная координаты по времени: v = xt‘, где

v ― скорость движения точки [м/с];

x ― координата точки [м];

t ― время, [с].

Так как закон изменения координаты нам известен x(t) = Asin(ωt), скорость движения колеблющейся точки: v = xt‘ = |Asin(ωt)|’t = Acos(ωt).

Уравнение скорости точки равно v(t) = Acos(ωt), где

v ― скорость движения точки [м/с];

A — амплитуда колебаний [м];

ω ― циклическая частота [рад/с];

t ― время, [с].

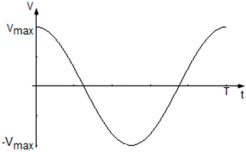
Сравнив уравнение v(t) = Aωcos(ωt) с кинематическим уравнением гармонических колебаний, легко заметить, что Aω ― амплитуда изменения скорости, а ωt ― фаза колебаний скорости. Таким образом, максимальное значение скорости равно vmax = Aω, и оно достигается при | cos(ωt) | = 1, т. е. тогда, когда фаза колебаний скорости равна φ = πn, где n = 0, 1, 2, … N.

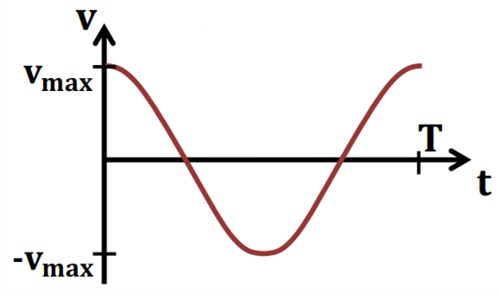
График колебания скорости точки имеет вид:

Аналогично определяются уравнение и график колебания ускорения точки, которая движется по гармоническому закону.

Ускорение ― это производная скорости по времени: a = vt‘, где

a ― ускорение движения точки [м/с2];

v ― скорость движения точки [м/с];

t ― время, [с].

Так как закон изменения скорости был определен выше v(t) = Aωcos(ωt), определим ускорения движения колеблющейся точки: a = vt‘ = [Aωcos(ωt)]t‘ = –Aω2sin(ωt).

Уравнение ускорения точки равно a(t) = –Aω2sin(ωt), где

a ― ускорение движения точки [м/с2];

A — амплитуда колебаний [м];

ω ― циклическая частота [рад/с];

t ― время, [с].

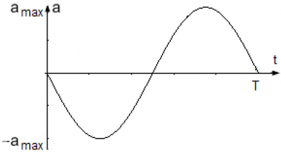
Модуль ускорения точки максимален, когда |sin(ωt)| = 1 ― тогда же, когда достигает максимума смещение точки. Максимальное ускорение, т. е. амплитуда ускорения точки равна amax = Aω2.

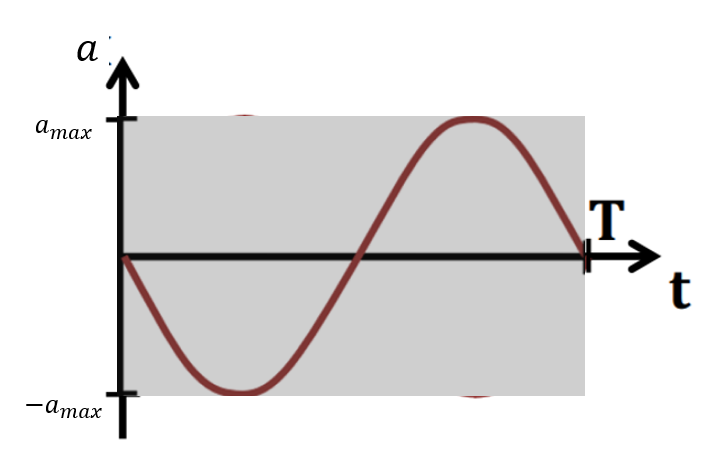
График колебания ускорения точки имеет вид:

Во время гармонических колебаний, формы энергии колебательной системы все время находятся в процессе взаимной трансформации. В механической колебательной системе преобразуется механическая энергия: потенциальная энергия ― в кинетическую, а затем кинетическая энергия ― вновь в потенциальную. Полная механическая энергия колеблющейся системы постоянна, и в любой момент времени справедлив закон сохранения энергии E = EП + EK, где

E ― полная механическая энергия системы, E = const, [Дж];

EП ― потенциальная энергия системы, изменяющаяся во времени, [Дж];

EK ― кинетическая энергия системы, изменяющаяся во времени, [Дж].

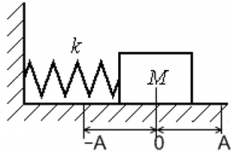
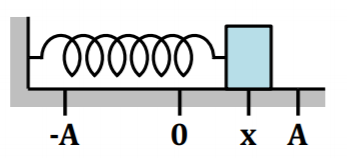
Рассмотрим изменение потенциальной энергии пружинного маятника, который колеблется по гармоническому уравнению x(t) = Asin(ωt).

Потенциальная энергия деформированной пружины равна EП = $frac{kx^2}{2}$ , где

EП ― потенциальная энергия деформированной пружины, [Дж];

k ― коэффициент упругости пружины [Н/м];

x ― деформация пружины (величина ее удлинения или сжатия) [м].

У пружинного маятника деформация пружины ― переменная величина, которая зависит от времени. Кинематическое уравнение движения точки, принадлежащей этому маятнику ― x(t) = Asin(ωt). Следовательно, потенциальную энергию пружинного маятника можно записать как EП = $frac{k(x(t))^2}{2}$ = $frac{k(Asin(omega t))^2}{2}$ = $frac{k}{2} cdot A^2 sin^2 (omega t)$ .

Уравнение потенциальной энергии пружинного маятника EП = $frac{k}{2} cdot A^2 sin^2 (omega t)$ , где

EП ― потенциальная энергия пружинного маятника, [Дж];

k ― коэффициент упругости пружины [Н/м];

A — амплитуда колебаний [м];

ω ― циклическая частота [рад/с];

t ― время, [с].

Амплитуда потенциальной энергии пружинного маятника равна EПmax = $frac{k}{2}A^2$ , где

EПmax ― максимальная потенциальная энергия пружинного маятника, [Дж];

k ― коэффициент упругости пружины [Н/м];

A — амплитуда колебаний [м].

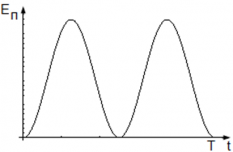
Потенциальная энергия пружинного маятника равна нулю, когда sin(ωt) = 0 ― когда маятник проходит положение равновесия, и максимальна, когда sin(ωt) = 1 ― когда маятник находится в крайних положениях, т. е. когда его смещение равно амплитуде.

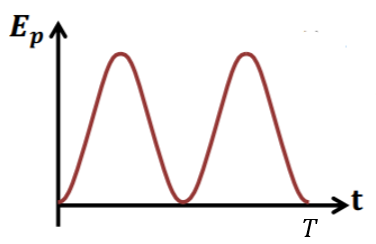
График колебаний потенциальной энергии пружинного маятника:

Рассмотрим изменение кинетической энергии маятника. Кинетическая энергия тела равна Eк = $frac{mv^2}{2}$ , где

Eк ― кинетическая энергия тела, [Дж];

m ― масса тела, [кг];

v ― скорость движения тела, [м/с].

У тела, которое совершает колебательные движения, скорость ― переменная величина.

Выше было показано, что если уравнение движения точки имеет вид x(t) = Asin(ωt), то уравнение скорости точки v(t) = Aωcos(ωt). Таким образом, кинетическая энергия маятника равна Eк = $frac{m(v(t))^2}{2}$ = $frac{m}{2} cdot (Aomegacos(omega t))^2$ = $frac{m}{2} cdot A^2 omega^2 cos^2 (omega t)$ .

Уравнение кинетической энергии маятника Eк = $frac{m}{2} cdot A^2 omega^2 cos^2 (omega t)$ , где

Eк ― кинетическая энергия маятника, [Дж];

m ― масса тела, [кг];

A — амплитуда колебаний [м];

ω ― циклическая частота [рад/с];

t ― время, [с].

Амплитуда кинетической энергии маятника равна EКmax = $frac{m}{2} cdot A^2 omega^2$ , где

EКmax ― максимальная кинетическая энергия маятника, [Дж];

m ― масса тела, [кг];

A — амплитуда колебаний [м];

ω ― циклическая частота [рад/с].

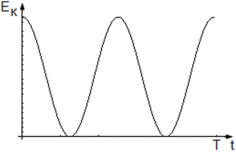
Максимальная кинетическая энергия маятника достигается тогда, когда cos2(ωt) = 1 ― маятник проходит положение равновесия, и она равна нулю, когда маятник находится в крайнем положении.

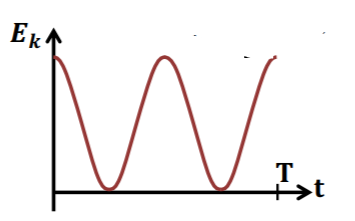
График колебаний кинетической энергии маятника:

Математический маятник ― это колебательная система, состоящая из материальной точки, подвешенной на нерастяжимой нити или стержне.

Период колебаний математического маятника равен T = $2pi sqrt{frac{l}{g}}$ , где

T ― период колебаний [с];

l ― длина нити математического маятника [м];

g ― ускорение свободного падения [м/с2].

Период колебаний пружинного маятника равен T = $2pi sqrt{frac{m}{k}}$ , где

T ― период колебаний [с];

m ― масса груза [кг];

k ― жесткость пружины [Н/м].

Существует особый тип колебаний ― вынужденные колебания. Вынужденные колебания происходят только под постоянным периодическим внешним воздействием и их характеристики зависят от характеристик этого воздействия.

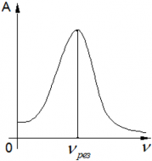
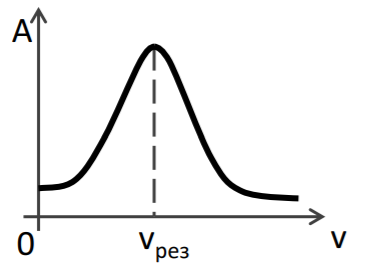
Если частота внешнего воздействия, которое вызывает вынужденные колебания, совпадает с собственной внутренней частотой колебательной системы ― возникает явление резонанса. При резонансе резко возрастает амплитуда колебаний системы. Частота, при которой возникает явление резонанса, называется резонансной частотой.

На рисунке показан график резонансной кривой ― увеличение амплитуды при совпадении частоты внешнего воздействия с внутренней частотой системы.

Задачи на Механические колебания с решениями

Формулы, используемые на уроках «Задачи на Механические колебания».

Название величины	Обозначение	Единица измерения	Формула
Амплитуда колебаний	A	м
Период колебаний	T	с	T = 1 / v ; T = t / N
Частота колебаний	v	Гц	v = 1 / T ; v = N / t
Число колебаний за какое-то время	N		N = t /T ; N = vt
Время	t	с	t = NT ; t = N / v
Циклическая частота колебаний	ω	Гц
Период колебаний пружинного маятника	T	c
Период колебаний математического маятника	T	c
Уравнение гармонических колебаний			x(t) = Asin(ωt+φ0)

---

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

---

Задача № 1.
 Шарик на нити совершил 60 колебаний за 2 мин. Определите период и частоту колебаний шарика.

---

Задача № 2.
 На рисунке изображен график зависимости координаты от времени колеблющегося тела.

По графику определите: 1) амплитуду колебаний; 2) период колебаний; 3) частоту колебаний; 4) запишите уравнение координаты.

---

Задача № 3.
 Амплитуда незатухающих колебаний точки струны 2 мм, частота колебаний 1 кГц. Какой путь пройдет точка струны за 0,4 с? Какое перемещение совершит эта точка за один период колебаний?

---

Задача № 4.
 Пользуясь графиком изменения координаты колеблющегося тела от времени, определить амплитуду, период и частоту колебаний. Записать уравнение зависимости x(t) и найти координату тела через 0,1 и 0,2 с после начала отсчета времени.

---

Задача № 5.
 Какова длина математического маятника, совершающего гармонические колебания с частотой 0,5 Гц на поверхности Луны? Ускорение свободного падения на поверхности Луны 1,6 м/с².

---

Задача № 6.
 Груз массой 400 г совершает колебания на пружине с жесткостью 250 Н/м. Амплитуда колебаний 15 см. Найти полную механическую энергию колебаний и наибольшую скорость движения груза.

---

Задача № 7.
 Частота колебаний крыльев вороны в полете равна в среднем 3 Гц. Сколько взмахов крыльями сделает ворона, пролетев путь 650 м со скоростью 13 м/с?

---

Задача № 8.
 Гармоническое колебание описывается уравнением 
 Чему равны циклическая частота колебаний, линейная частота колебаний, начальная фаза колебаний?

---

Задача № 9.
 Математический маятник длиной 0,99 м совершает 50 полных колебаний за 1 мин 40 с. Чему равно ускорение свободного падения в данном месте на поверхности Земли? (Можно принять π² = 9,87.)

---

Задача № 10.
  ОГЭ
 Как и во сколько раз изменится период колебаний пружинного маятника, если шарик на пружине заменить другим шариком, радиус которого вдвое меньше, а плотность — в два раза больше?

---

Задача № 11.
   ЕГЭ
 Два математических маятника за одно и то же время совершают — первый N₁ = 30, а второй — N₂ = 40 колебаний. Какова длина каждого из них, если разность их длин Δl = 7 см?

---

Краткая теория для решения Задачи на Механические колебания.

---

Это конспект по теме «ЗАДАЧИ на Механические колебания». Выберите дальнейшие действия:

• Перейти к теме: ЗАДАЧИ на 
• Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
• Вернуться к списку конспектов по Физике.
• Проверить свои знания по Физике.

Последние вопросы

• 
  Литература

  6 минут назад

  Художественные выразительные средства в произведении джека лондона любовь к жизни

  можно пару штук хотя бы =_

• 
  Русский язык

  37 минут назад

  Письмён на писька содержание своей любимой книге перед началом работы составь план в последнем абзаце своего текста напиши почему это книга

  твоя любимая

• 
  Другие предметы

  2 часа назад

  Что делать если скучно???

• 
  Геометрия

  2 часа назад

  № 1. Две стороны параллелограмма равны 3 см и 4√2 см, а угол между ними – 135°. Найдите: 1) большую диагональ параллелограмма; 2) площадь параллелограмма.

  № 2. В треугольнике DEF известно, что EF = 10√3 см, DE = 10 см, ∠F = 30°. Найдите угол D.

  С ПОДРОБНЫМ РЕШЕНИЕМ

• 
  Геометрия

  2 часа назад

  № 1. Две стороны параллелограмма равны 8 см и 3 см, а угол между ними – 120°. Найдите: 1) большую диагональ параллелограмма; 2) площадь параллелограмма.

  № 2 В треугольнике DEF известно, что DF = 8√2 см, EF = 8√3 см, ∠E = 45°. Найдите угол D.

  С ПОДРОБНЫМ РЕШЕНИЕМ

• 
  Геометрия

  2 часа назад

  № 1. Две стороны параллелограмма равны 4 см и 4√3 см, а угол между ними – 30°. Найдите: 1) большую диагональ параллелограмма; 2) площадь параллелограмма

  № 2. В треугольнике ABC известно, что AC = 3√2 см, BC = 3 см, ∠A = 30°. Найдите угол B.

  С ПОДРОБНЫМ РЕШЕНИЕМ

• 
  Геометрия

  4 часа назад

  один из углов трапеций вписанной в окружность равен 29, 4 Найдите остальные углы

• 
  Экономика

  12 часов назад

  На фото

• 
  Математика

  14 часов назад

  Спростіть вираз -3(2x-1) і знайдіть його значення, якщо х=-2

• 
  Математика

  17 часов назад

  Люди помогите!

  Постройте треугольник АBC, по данным:

  Угол А = 35°

  ВС = 5 см

  АС = 4 см

  Мне не нужен ответ с другого сайта!

  Скажите пожалуйста, как сделать это с помощью циркуля, кто учится в 7 классе.

• 
  Математика

  18 часов назад

  (x-1)^8*(2x+3)^2*(x-7)^4*(3x-5)*(x+6)^3>0

• 
  Математика

  23 часов назад

  помогите решить пожалуйста задачу

• 
  Литература

  1 день назад

  пересказ повести мелентьева одни сутки войны пересказ всего текста

• 
  Право

  1 день назад

  у rauf.bakirov нет прав

  кто тоже так считает +

• 
  Математика

  1 день назад

  кто даун?

Механические колебания

Частота измеряется в герцах [Гц] = [c^-1]. Частота равна

(nu = frac{1}{T}) , где

v ― частота [Гц];

T ― период [c].

Если известно, что тело совершает N колебаний за время t, то частоту его колебаний можно определить как

(nu = frac{N}{T}) , где

ν ― частота [Гц];

N ― количество колебаний;

t — время [с].

Для описания колебательных систем, совершающих круговые процессы, удобно использовать круговую (циклическую) частоту.

Циклическая частота показывает количество полных колебаний, которые происходят за 2π секунд и равна:

ω = 2πv или (omega = frac{2pi}{T})

ω ― циклическая частота [рад/с];

ν ― частота [Гц];

T ― период [c].

Кинематическое уравнение гармонических колебаний имеет вид:

Фаза колебаний равна

φ = ωt + φ₀, где

φ ― полная фаза колебаний [рад];

φ0 ― начальная фаза колебаний, [рад];

ω ― циклическая частота [рад/с];

t ― время, [с].

Пример анализа гармонических колебаний точки

Рассмотрим гармонические колебания, в которых уравнение движения точки имеет вид

x(t) = Asin(ωt), где

x ― смещение [м];

t ― время, [с];

A — амплитуда колебаний [м];

ω ― циклическая частота [рад/с].

Из уравнения x(t) = Asin(ωt) следует, что начального смещения нет (φ₀ = 0) и колебания начинаются из положения равновесия. Смещение x достигает максимального значения Х_max и равно амплитуде Х_max = A, в тот момент, когда модуль синуса равен единице |sin(ωt)| = 1. Когда x = A фаза колебаний равна (varphi = frac{pi}{2} + 2pi n) , когда x = –A фаза колебаний принимает значения (varphi = frac{3pi}{2} + 2pi n) , где n = 0, 1 , 2, … N.

График колебания координаты точки имеет вид:

Определим уравнение и график колебания скорости.

Скорость ― это производная координаты по времени: v = xt‘, где:

v ― скорость движения точки [м/с];

x ― координата точки [м];

t ― время, [с].

Так как закон изменения координаты нам известен x(t) = Asin(ωt), скорость движения колеблющейся точки: v = xt‘ = |Asin(ωt)|’t = Acos(ωt).

Сравнив уравнение v(t) = Aωcos(ωt) с кинематическим уравнением гармонических колебаний, легко заметить, что Aω ― амплитуда изменения скорости, а ωt ― фаза колебаний скорости. Таким образом, максимальное значение скорости равно v_max = Aω, и оно достигается при | cos(ωt) | = 1, т. е. тогда, когда фаза колебаний скорости равна φ = πn, где n = 0, 1, 2, … N.

График колебания скорости точки имеет вид:

Аналогично определяются уравнение и график колебания ускорения точки, которая движется по гармоническому закону.

Так как закон изменения скорости был определен выше v(t) = Aωcos(ωt), определим ускорения движения колеблющейся точки: a = vt‘ = [Aωcos(ωt)]t‘ = –Aω²sin(ωt).

График колебания ускорения точки имеет вид:

Во время гармонических колебаний, формы энергии колебательной системы все время находятся в процессе взаимной трансформации. В механической колебательной системе преобразуется механическая энергия: потенциальная энергия ― в кинетическую, а затем кинетическая энергия ― вновь в потенциальную. Полная механическая энергия колеблющейся системы постоянна, и в любой момент времени справедлив закон сохранения энергии

E = E_П + E_K, где:

E ― полная механическая энергия системы, E = const, [Дж];

E_П ― потенциальная энергия системы, изменяющаяся во времени, [Дж];

E_K ― кинетическая энергия системы, изменяющаяся во времени, [Дж].

Рассмотрим изменение потенциальной энергии пружинного маятника, который колеблется по гармоническому уравнению x(t) = Asin(ωt).

Потенциальная энергия деформированной пружины равна (E_{n} = frac{kx^{2}}{2}) . У пружинного маятника деформация пружины ― переменная величина, которая зависит от времени. Кинематическое уравнение движения точки, принадлежащей этому маятнику ― x(t) = Asin(ωt). Следовательно, потенциальную энергию пружинного маятника можно записать как (E_{n} = frac{k{(x(t))}^{2}}{2} = frac{kleft( Asin{(omega t)} right)^{2}}{2} = frac{k}{2}A^{2}sin^{2}{(omega t)})

Уравнение потенциальной энергии пружинного маятника

(E_{n} = frac{k}{2}A^{2}sin^{2}{(omega t)}) , где

E_П ― потенциальная энергия пружинного маятника, [Дж];

k ― коэффициент упругости пружины [Н/м];

A — амплитуда колебаний [м];

ω ― циклическая частота [рад/с];

t ― время, [с].

Амплитуда потенциальной энергии пружинного маятника равна

(E_{text{n.max}} = frac{k}{2}A^{2}), где

E_Пmax ― максимальная потенциальная энергия пружинного маятника, [Дж];

k ― коэффициент упругости пружины [Н/м];

A — амплитуда колебаний [м].

Потенциальная энергия пружинного маятника равна нулю, когда sin(ωt) = 0 ― когда маятник проходит положение равновесия, и максимальна, когда sin(ωt) = 1 ― когда маятник находится в крайних положениях, т. е. когда его смещение равно амплитуде.

График колебаний потенциальной энергии пружинного маятника:

Рассмотрим изменение кинетической энергии маятника. Кинетическая энергия тела равна (E_{k} = frac{mv^{2}}{2}) .У тела, которое совершает колебательные движения, скорость ― переменная величина.

Выше было показано, что если уравнение движения точки имеет вид x(t) = Asin(ωt), то уравнение скорости точки v(t) = Aωcos(ωt). Таким образом, кинетическая энергия маятника равна (E_{k} = frac{m{(v(t))}^{2}}{2} = frac{mleft( text{Aω}cosleft( text{ωt} right) right)^{2}}{2} = frac{m}{2}A^{2}omega^{2}cos^{2}left( text{ωt} right))

Уравнение кинетической энергии маятника

(E_{k} = frac{m}{2}A^{2}omega^{2}cos^{2}left( text{ωt} right)) , где

E_к ― кинетическая энергия маятника, [Дж];

m ― масса тела, [кг];

A — амплитуда колебаний [м];

ω ― циклическая частота [рад/с];

t ― время, [с].

Амплитуда кинетической энергии маятника равна

(E_{text{k.max}} = frac{m}{2}A^{2}omega^{2}) , где

E_Кmax ― максимальная кинетическая энергия маятника, [Дж];

m ― масса тела, [кг];

A — амплитуда колебаний [м];

ω ― циклическая частота [рад/с].

Максимальная кинетическая энергия маятника достигается тогда, когда cos2(ωt) = 1 ― маятник проходит положение равновесия, и она равна нулю, когда маятник находится в крайнем положении.

График колебаний кинетической энергии маятника:

Период колебаний математического маятника равен

(T = 2pisqrt{frac{l}{g}}) , где

T ― период колебаний [с];

l ― длина нити математического маятника [м];

g ― ускорение свободного падения [м/с²].

Период колебаний пружинного маятника равен

(T = 2pisqrt{frac{m}{k}}) , где

T ― период колебаний [с];

m ― масса груза [кг];

k ― жесткость пружины [Н/м].

Вынужденные колебания

Существует особый тип колебаний ― вынужденные колебания. Вынужденные колебания происходят только под постоянным периодическим внешним воздействием и их характеристики зависят от характеристик этого воздействия.

Если частота внешнего воздействия, которое вызывает вынужденные колебания, совпадает с собственной внутренней частотой колебательной системы ― возникает явление резонанса. При резонансе резко возрастает амплитуда колебаний системы. Частота, при которой возникает явление резонанса, называется резонансной частотой.

На рисунке показан график резонансной кривой ― увеличение амплитуды при совпадении частоты внешнего воздействия с внутренней частотой системы.