Как найти число квантово механических состояний

Соотношение
неопределенностей Гейзенберга ∆x∆p≥h
устанавливает различия в описании
состояния систем в квантовой и классической
механике. Состояние частицы в классической
механике описывается с помощью координат
и импульсов (точка в фазовом
-пространстве).
Квантовая же частица в состоянии с
определенными координатами (x,
y,
z)
не обладает определенным импульсом. То
есть, для квантовой частицы не существует
состояний, в которые ее координаты и
импульсы имели бы одновременно точные
значения. Состояние квантовой системы
описывает главная величина в квантовой
механике – волновая
функция

(x,
y,
z,
t).
Шредингер установил соответствующее
уравнение для волновой функции. Его
следует понимать как один из постулатов
квантовой механики, и оно играет в ней
такую же роль, как 2-ой закон Ньютона в
классической механике. Для стационарных
состояний,
в которых вероятности измерения
физических величин не зависят от времени,
уравнение Шредингера имеет вид
Для
нахождения волновой функции должны
быть еще заданы граничные условия,
которые сводятся к требованию однозначности
и непрерывности волновой функции и ее
первой производной. Как и в любой теории,
дающей вероятностное описание, в
квантовой механике сопоставление с
опытом производится для средних значений
физических величин.

Рассмотрим
общие свойства решений уравнения
Шредингера на простом примере движения
электрона в прямоугольной бесконечно
глубокой потенциальной яме,

Видно,
что уравнение Шредингера имеет решения,
удовлетворяющие граничным условиям
только при дискретных значениях квантовых
чисел. n1,
n2
и n3
образуют фазовое пр-во.

ЧИСЛО
СОСТОЯНИЙ ОПРЕДЕЛЯЕТСЯ ФАЗОВЫМ ОБЪЕМОМ.
ТОГДА ЭТА ЗАДАЧА СВОДИТСЯ К НАХОЖДЕНИЮ
ФАЗОВОГО ОБЪЕМА ОБЛАСТИ E÷E+dE.
Объем
слоя
dE=dV=4pi*R^2/8dR=4*pi(n1^2+n2^2+n3^2)

Значит

24.26.
РАСПРЕДЕЛЕНИЯ В КВАНТОВОЙ СТАТИСТИКЕ.
ЧАСТИЦА В ПРЯМОУГОЛЬНОМ ЯЩИКЕ.
ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР. МАТРИЦА
ПЛОТНОСТИ.Квантовая
статистика – это применение статистического
метода Гиббса для описания квантовых
систем. Суть статистического метода
одинакова и для классических, и для
квантовых систем: необходимо определить
вероятность того, что система находится
в данном микросостоянии. Для классической
статистики микросостояние – это
одновременное задание координат и
импульсов (q,
p)
всех частиц системы. Для квантовой
системы это невозможно из-за принципа
неопределенности. Квантовая система
может иметь только определенный набор
дискретных значений энергий, называемый
ее энергетическим спектром. Каждому
значению энергии E_n
соответствует одно или несколько
различных квантовых состояний. Под n
понимается совокупность квантовых
чисел, которые и определяют состояние
системы. Так что микросостояние квантовой
системы – это задание полного набора
квантовых чисел n
(n₁,
n₂,
…) или соответствующих значений энергий
E_n
(E₁,
E₂,
…) системы. Пусть квантовая система
находится в контакте с термостатом
(окружающей средой) при температуре Т
(заданы число частиц N,
объем системы V
и температура Т).
Тогда, можно показать, что выражение
для вероятности _n
того, что система находится в квантовом
состоянии с энергией E_n,
определяется соотношением, подобным
каноническое
распределение Гиббса в квантовой
статистике.
Z
называется
статистической суммой
системы
Она
заменяет в квантовой статистике
статистический интеграл. Важно отметить,
что_n
– это именно вероятность данного
состояния системы, а не вероятность
системы иметь определенное значение
энергии Е_n,
потому что при вырождении данной энергии
может соответствовать не одно, а несколько
различных состояний. С помощью
распределения Гиббса можно вычислить
среднее по ансамблю (статистическое
среднее) любой физической величины,
зависящей от состояния системы. Если
L
(E_n)
– значение этой величины для состояний
с энергией E_n,
то по определению среднего значения
.
Матрица плотности (оператор плотности)один
из способов описания состояния
квантовомеханической системы. В отличие
от волновой функции, пригодной лишь для
описания чистых состояний, оператор
плотности в равной мере может задавать
как чистые, так и смешанные состояния.
Гармонический осциллятор в квантовой
механике представляет собой квантовый
аналог простого гармонического
осциллятора, при этом рассматривают не
силы, действующие на частицу, а
гамильтониан, то есть полную энергию
гармонического осциллятора, причём
потенциальная энергия предполагается
квадратично зависящей от координат.
Гамильтониан квантового осциллятора
массы m, собственная частота которого
ω, выглядит так:

Частица может двигаться по оси х
в обоих направлениях, но не может
находиться вне ящика, где U=∞,
а ψ=0..
Уравнение Шредингера для одномерного
движения внутри ящика
Граничные условия:ψ(0)= ψ(α)=0. Общее решение
ψ(x)=Asin(k*x)+Bcos(k*x)
приВидно, что уравнение Шредингера имеет
решения, удовлетворяющие граничным
условиям только при дискретных значениях
квантового числаn.
Таким образом, энергия частицы в потенц.
яме оказывается квантованной. Причем
дискретность энергии возникла естественным
образом, без каких-либо дополнительных
предположений, как следствие граничных
условий, налагаемых на волновую функцию.
Оказывается, что состояние квантовой
системы (электрон в потенциальной яме
в нашем примере) определяется квантовым
числом n.

27,28.
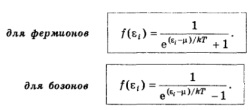
РАСПРЕДЕЛЕНИЕ ФЕРМИ И БОЗЕ.
Согласно квантовой теории все микрочастицы
подразделяют на два класса, которым
соответствуют две квантовые статисти­ки:1)
частицы с полуцелым
спином, их
называют фермионами;
они
подчиняются статистике
Ферми-Дирака; 2)
частицы с целым
спином —
бозоны;
они
подчиняются статистике
Бозе-Эйнштейна. Во
всех трех статистиках (классической,
Бозе-Эинштеина и Ферми-Дирака) допустимые
микросостояния считаются равно­вероятными.
Но
различие их — в способах определения
мик­росостояний и статистических
весов. В статистике Больцмана считается,
что даже тождественные частицы
принципиально
различимы. В
квантовых же статистиках, наоборот,
считается, что тождественные частицы
принципиально
неразличимы.

В
статистике Ферми-Дирака в каждом
квантовом состоянии может находиться
не более одной частицы (принцип
Паули), а
в статистике Бозе-Эйнштейна — любое
число частиц.

Для
описания состояния системы частиц
рассматривают во­ображаемое шестимерное
пространство, каждая точка которого

характеризуется
шестью координатами: х,
у, z,
p_x
,p_y
,p_z.
Это
так называемое фазовое
пространство.
Состояние
системы определяется тем, как распределены
в этом пространстве точ­ки, изображающие
состояния всех N
частиц
системы. При этом нужно учесть присущий
частицам корпускулярно-волновой
ду­ализм, согласно которому
неопределенности координаты х
и
со­ответствующей проекции импульса
р_х
могут
быть определены только с неопределенностью,
произведение
которых, согласно принципу
неопределенностей Гейзенберга, δxδp_x≥h
.
Аналогично и для других пар: у
и
p_y
, z
и
р_г.
Поэтому
естественно считать, что данному
состоянию части­цы в фазовом пространстве
соответствует не точка, а фазовая
ячейка,
объем
которой

Распределение
частиц по таким фазовым ячейкам есть
пре­дельно
подробное квантовое описание состояния
системы.

Квантовые
распределения. Эти распределения
представля­ют собой функции
определяющие
средние числа частицв
одной фазовой
ячейке с энергией
или функции заполнения ячеек:

Здесь
μ — так называемый химический
потенциал (некоторая
характерная энергия, значение которой
можно найти из усло­вия нормировки:
суммарное число частиц во всех фазовых
ячейках должно быть равно полному числу
N
частиц
макроси­стемы).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 6 апреля 2022 года; проверки требует 1 правка.

У этого термина существуют и другие значения, см. Состояние.

Квантовая механика
Введение[en] История[en] Математические основы
Основа Классическая механика Постоянная Планка Интерференция Бра и кет Гамильтониан Старая квантовая теория
Фундаментальные понятия Квантовое состояние Квантовая наблюдаемая Волновая функция Квантовая суперпозиция Квантовая запутанность Смешанное состояние Измерение Неопределённость Принцип Паули Дуализм Декогеренция Симметрия Теорема Эренфеста Туннельный эффект
Эксперименты Опыт Дэвиссона — Джермера Опыт Франка — Герца Опыт Штерна — Герлаха Опыт Юнга Квантовый ластик Квантовый ластик с отложенным выбором Проверка неравенств Белла Фотоэффект Эффект Комптона
Формулировки Представление Шрёдингера Представление Гейзенберга Представление взаимодействия Представление фазового пространства Матричная квантовая механика Интегралы по траекториям Диаграммы Фейнмана
Уравнения Шрёдингера Паули Клейна — Гордона Дирака Швингера — Томонаги фон Неймана Блоха Линдблада Гейзенберга
Интерпретации Копенгагенская Теория скрытых параметров Локальная[en] Многомировая Теория де Бройля — Бома
Развитие теории Квантовая теория поля Квантовая электродинамика Теория Глэшоу — Вайнберга — Салама Квантовая хромодинамика Стандартная модель Квантовая гравитация
Сложные темы Релятивистская квантовая механика Квантовая теория поля Квантовая гравитация Теория всего
Известные учёные Планк Эйнштейн Шрёдингер Гейзенберг Йордан Бор Паули Дирак Фок Борн де Бройль Ландау Фейнман Бом Эверетт
См. также История возникновения Глоссарий[en] ЭПР-парадокс
См. также: Портал:Физика

Квантовое состояние — любое возможное состояние, в котором может находиться квантовая система. Чистое квантовое состояние может быть описано:

• В волновой механике — волновой функцией,
• В матричной механике — вектором состояния, или полным набором квантовых чисел для определённой системы.

Эти описания математически равнозначны. В общем случае квантовое состояние (смешанное) принципиально не может быть описано волновой функцией и должно быть описано матрицей плотности, являющейся неотрицательным самосопряжённым оператором с единичным следом. Квантовые состояния можно интерпретировать как статистические ансамбли с некоторыми фиксированными квантовыми числами.

Векторы состояний[править | править код]

Для описания возможных состояний заданной квантовой системы применяется математический аппарат гильбертова пространства , позволяющий практически полностью описать всё, что может происходить с системой.

Для описания квантового состояния в этом случае вводится так называемый вектор состояния (амплитуда состояния), представляющий собой множество математических величин, которое полностью описывает квантовую систему. К примеру, множество 4 чисел {, , , } определяет состояние электрона в атоме водорода, и называются квантовыми числами электрона.

Подобная конструкция оказывается возможной благодаря принципу суперпозиции для квантовых систем. Он проявляется в том, что если существуют два возможных состояния квантовой системы, причём в первом состоянии некоторая наблюдаемая величина может принимать значения p₁, p₂, …, а во втором — q₁, q₂,… , то существует и состояние, называемое их суперпозицией, в котором эта величина может принимать любое из значений p₁, p₂, …, q₁, q₂,…. Количественное описание этого явления приведено ниже.

Обозначения бра-кет[править | править код]

Будем обозначать вектор состояния, соответствующий состоянию , как . Сопряжённый вектор, соответствующий состоянию , будем обозначать как . Скалярное произведение векторов и будем обозначать как , а образ вектора под действием оператора будем обозначать . Символ называется бра (англ. bra), а символ , как  — кет (англ. ket). Подобные обозначения в целом согласуются с обозначениями обычной линейной алгебры, но более удобны в квантовой механике, так как позволяют более наглядно и коротко называть используемые векторы. Такие обозначения были впервые введены Дираком. Названия векторов образованы разбиением слова bracket (скобка) на две звучные части — bra и ket.

Математический формализм[править | править код]

Всякий ненулевой вектор из пространства соответствует некому чистому состоянию. Однако векторы, различающиеся лишь умножением на ненулевое комплексное число, отвечают одному физическому состоянию.
Иногда полагают, что вектор состояния обязан быть «нормирован на единицу»:  — любой ненулевой вектор приобретает это свойство, если разделить его на свою норму .

Если мы рассмотрим два различных состояния, то суперпозиции (всевозможные линейные комбинации) пары соответствующих им векторов дадут двумерное линейное комплексное пространство.
Соответственное множество физических состояний будет представлять двумерную поверхность — сферу Римана.

При рассмотрении квантовой системы, состоящей из двух подсистем, пространство состояний строится в виде тензорного произведения. Подобные системы, помимо комбинаций состояний своих подсистем, имеют также и сцепленные (запутанные) состояния.

«Количество состояний»[править | править код]

Если система имеет хотя бы два физически различных состояния, то мощность множества возможных векторов состояния (даже с точностью до умножения на комплексное число), разумеется, бесконечна. Однако под количеством состояний квантовой системы подразумевают количество линейно независимых состояний, то есть размерность пространства .
Это вполне соответствует интуиции, поскольку описывает количество возможных исходов измерения; к тому же при тензорном произведении (то есть построении составной системы) размерности пространств перемножаются.

В контексте рассмотрения замкнутой квантовой системы (то есть решения уравнения Шрёдингера) под состояниями могут пониматься только стационарные состояния — собственные векторы гамильтониана, отвечающие различным уровням энергии. В случае конечномерного пространства и при отсутствии вырождения число уровней энергии (и соответствующих им состояний) будет равно размерности пространства.

Чистое состояние[править | править код]

Чистое состояние — это полностью указанное квантовое состояние. Если данный квантовый объект (например, какая-то элементарная частица) находится в чистом состоянии, это означает, что у нас есть вся информация о ней. Только чистые состояния полностью можно описать волновыми функциями.

См. также[править | править код]

• Плотность состояний
• Квантовая наблюдаемая

Литература[править | править код]

• Березин Ф. А., Шубин М. А. Уравнение Шрёдингера. М.: Изд-во МГУ, 1983. 392 с.
• Боум А. Квантовая механика: основы и приложения. М.: Мир, 1990. — 720 c. Глава IV.
• Дирак П. Принципы квантовой механики. 2-е изд. М.: Наука, 1979. — 480 с. Архивная копия от 11 ноября 2007 на Wayback Machine
• Ландау Л. Д., Лифшиц Е. М. Квантовая механика (нерелятивистская теория). — Издание 4-е. — М.: Наука, 1989. — 768 с. — («Теоретическая физика», том III). — ISBN 5-02-014421-5.
• Isham, Chris J. Lectures on Quantum Theory: Mathematical and Structural Foundations. — Imperial College Press, 1995.
• Bratteli, Ola. Operator Algebras and Quantum Statistical Mechanics 1 / Ola Bratteli, Robinson, Derek W. — Springer, 1987. — ISBN 2nd edition.
• Bengtsson I. Geometry of Quantum States / Bengtsson I, Życzkowski K. — Cambridge : Cambridge University Press, 2006.

В простейшем из атомов – атоме водорода – потенциальная энергия электрона определяется его кулоновским притяжением к ядру. Поскольку в атомных единицах заряды электрона и ядра равны -1 и +1 соответственно, то:

Если подставить в гамильтониан данное выражение для потенциальной энергии и решить уравнение Шредингера, то можно найти, что распределение электрона по энергиям и в пространстве атома
водорода определяется волновой функцией ψ, зависящей от сферических координат (r, θ, φ) электрона и от трех параметров (n, l, m_l),
принимающих целочисленные значения. Последние три параметра называют квантовыми числами:

• n – главное квантовое число;
• l – орбитальное квантовое число;
• m_l – магнитное квантовое число;
• m_s – спиновое квантовое число.

В простейших приложениях квантовой механики иногда удобнее вместо самой волновой функции пользоваться квантовыми числами, представляющими ее. Такой подход часто применяется для объяснения свойств
многоэлектронных атомов.

Главное квантовое число

В многоэлектронных атомах конкретный электрон находится в поле ядра, экранированном полем остальных электронов. С физической точки зрения это можно представить так, что данный электрон «видит» не все
ядро атома, а лишь некоторую, его часть. Данный заряд ядра, действующий на электрон конкретной орбитали с учетом экранирования ядра другими электронами, называется эффективным зарядом ядра данной
орбитали (z*). В этом случае:

Подставляя данное выражение для Е_п в уравнение Шредингера, можно найти, что уравнение имеет решения не при любых, а только при определенных значениях энергии. Таким образом,
квантованность энергетических состояний электрона в атоме оказывается следствием присущих электрону волновых свойств. При этом полная энергия электрона в многоэлектронном атоме рассчитывается с помощью
выражения:

включающего главное квантовое число. Таким образом, главное квантовое число характеризует энергию электрона в атоме. Оно принимает положительные целочисленные значения от 1 до бесконечно больших
чисел:

n = 1, 2, 3, …, ∞

Значения главного квантового числа определяют:

• номер энергетического уровня (в теории Бора – номер орбиты);
• интервал энергий электронов, находящихся на этом уровне;
• размеры орбиталей (в теории Бора-радиусы орбит);
• число подуровней данного энергетического уровня (первый уровень состоит из одного подуровня, второй – из двух, третий – из трех и т. д.);
• в Периодической системе Д. И. Менделеева значению главного квантового числа соответствует номер периода.

Иногда пользуются буквенными обозначениями главного квантового числа, т.е. каждому численному значению n соответствует определенное буквенное обозначение:

Численное значение n		1	2	3	4	5	6	7
Буквенное обозначение n		K	L	M	N	O	P	Q

Наименьшей энергией электрон обладает при n = 1; с увеличением n энергия электрона возрастает. Поэтому состояние электрона, характеризующееся определенным значением главного квантового
числа, принято называть энергетическим уровнем электрона в атоме: при n = 1 электрон находится на первом энергетическом уровне, при n = 2 – на втором и т. д. Увеличение значения n
ведет к повышению энергии электрона, достигая в пределе нулевого значения. При этом электрон оказывается бесконечно далеко удаленным от ядра и не испытывает к нему какого-либо притяжения. Поэтому, чем
меньше значение n, тем отрицательнее энергия электрона, тем более он связан, т. е. испытывает притяжение к ядру, находится в устойчивом состоянии связи с ядром.

При малых значениях n разность энергий ближайших электронных оболочек относительно велика, а при больших значениях n мала. На рисунке изображена энергетическая диаграмма атома, на которой
положение энергетического уровня отображается горизонтальной чертой при соответствующем значении энергии. Энергетические уровни с n = 5 и выше настолько близки друг к другу по энергии, что они
практически сливаются.

Если электрон атома характеризуется определенным значением энергии:

то говорят, что он «находится» на энергетическом уровне Е_i. Состояние атома, когда его электроны находятся на таких энергетических уровнях, что их суммарная энергия в атоме является
минимальной из возможных значений энергии, называется основным состоянием. Соответствующие состояния электронов также называют основными. Состояния с более высокими значениями энергии называют
возбужденными, а сам процесс или результат повышения энергии атома (или электрона) – возбуждением.

Главное квантовое число также определяет характер радиальной зависимости орбитали, т.е. размеры электронного облака. Чем больше n, тем дальше от ядра атома располагается область наиболее
вероятного нахождения электрона. Другими словами, n определяет средний радиус нахождения электрона в атоме.

Приближенно средний радиус нахождения электрона в атоме может быть рассчитан по формуле:

Для атома водорода в основном состоянии n = 1 и z* = 1, тогда r_m = 1 а. е. При переходе атома в возбужденное состояние величина n принимает значения больше, чем 1.
Поэтому средний радиус нахождения электрона (или средний радиус атома водорода) будет увеличиваться: при n = 2, r_m = 4 а. е.; n = 3, r_m = 9 а. е. и т.д.
При очень больших значениях n, например n = 1000, r_m = 10⁶ а. е. ≈ 0,53·10 ^-2 см, размер атомов становится макроскопической величиной.
При таких высоких степенях возбуждения у атома резко меняются и другие свойства: энергия ионизации (которая уменьшается), время жизни возбужденного состояния (которое увеличивается) и др. Такие атомы,
находящиеся в высоковозбужденных состояниях, называются ридберговскими.

О нескольких электронах атома, имеющих одно и то же значение n, говорят, что они относятся к некоторой общей электронной оболочке, энергетическому уровню или квантовому слою.

Орбитальное (азимутальное) квантовое число

В отличие от главного, орбитальное квантовое число определяет не радиальную, а угловую зависимость волновой функции, т.е. форму электронного облака. Возможные значения данного числа зависят от
значения главного квантового числа и, не превышая значения (n – 1), изменяются в ряду:

l = 0, 1, 2, …, (n-1)

причем каждому значению главного квантового числа n соответствует n значений орбитального квантового числа l. Например, если n = 1, то l принимает только одно значение
(l = 0) при n = 2 величина l принимает два значения: 0 и 1 и т. д. Каждому численному значению l соответствует определенная геометрическая форма орбиталей и приписывается
буквенное обозначение. Первые четыре буквенных обозначения имеют историческое происхождение и связаны с характером спектральных линий, соответствующих электронным переходам между этими подуровнями: s, p,
d, f – первые буквы английских слов, использованных для названия спектральных линий sharp (резкий), principal (главный), diffuse (диффузный), fundamental (основной). Обозначения
других подуровней идут в алфавитном порядке: g,h,….

Значение n		1	2	3	4	5
Значение l		0	0	1	0	1	2	0	1	2	3	0	1	2	3	4
Буквенное обозначение l		s	s	p	s	p	d	s	p	d	f	s	p	d	f	g
Число подуровней		1	2	3	4	5

Электроны с орбитальным квантовым числом 0, называются s-электронами. Орбитали и соответственно электронные облака имеют сферическую форму.

Электроны с орбитальным квантовым числом 1 называются р-электронами. Орбитали и соответственно электронные облака имеют форму, напоминающую гантель.

Электроны с орбитальным квантовым числом 2 называют d-электронами. Орбитали имеют более сложную форму, чем р-орбитали.

Электроны с орбитальным квантовым числом 3 получили название f-электронов. Форма их орбиталей еще сложнее, чем форма d-орбиталей.

Состояние электрона в атоме, отвечающее определенным значениям n и l, записывается следующим образом: сначала цифрой указывается значение главного квантового числа, а затем буквой –
орбитального квантового числа. Так, обозначение 2р относится к электрону, у которого n = 2 и l = 1, обозначение 3d – к электрону, у которого n = 3 и l = 2.

В одной и той же оболочке (уровне) энергия подоболочек (подуровней) возрастает в ряду:

В первой оболочке (n = 1) может быть одна (s-), во второй (n = 2) – две (s-, р-), в третьей (n = 3) – три (s-, р-, d-), в четвертой (n = 4) – четыре
(s-, р-, d-, f-) – подоболочки.

Если несколько электронов имеют одинаковые значения и главного, и орбитального квантовых чисел (комбинацию (n; l), то говорят, что они относятся к одной электронной подоболочке,
энергетическому подуровню, квантовому подслою.

Магнитное квантовое число

Вращение электрона вокруг ядра можно сравнить с движением тока по замкнутому контуру. При этом возникает магнитное поле, напряженность которого направлена перпендикулярно плоскости вращения электрона.
Если атом находится во внешнем магнитном поле, то, согласно квантовомеханическим представлениям, его электроны должны расположиться так, чтобы проекции их магнитных моментов на направление этого поля
были целочисленными. При этом они могут принимать как отрицательные, так и положительные значения, включая нулевое.

Численное значение проекции магнитного момента и является магнитным квантовым числом. Если значение орбитального квантового числа равно l, то магнитное квантовое число будет принимать значения
от – l до + l, включая ноль. Общее количество значений будет равно 2l+1.

Число орбиталей на подуровне

n	1	2	3	…
l	0	0	1	0	1	2	…
ml	0	0	-1,0,+1	0	-1,0,+1	-2,-1,0,+1,+2	…
Число орбиталей на подуровне	1	1	3	1	3	5	…

Квантовое число m_l получило название магнитного, поскольку от его значения зависит взаимодействие магнитного поля, создаваемого электроном, с внешним магнитным полем. В отсутствие
внещнего магнитного поля энергия электрона в атоме не зависит от значения m_l. В этом случае электроны с одинаковыми значениями n и l, но с разными значениями
m_l обладают одинаковой энергией. Однако при действии на электрон внешнего магнитного поля энергия электрона в атоме изменяется, так что состояния электрона, различающиеся значением
m_l, различаются и по энергии. Это происходит потому, что энергия взаимодействия магнитного поля электрона с внешним магнитным полем зависит от величины магнитного квантового числа.
Именно поэтому в магнитном поле происходит расщепление некоторых атомных спектральных линий: вместо одной линии в спектре атома появляются несколько (эффект Зеемана).

Таким образом, магнитное квантовое число определяет расположение орбиталей в пространстве относительно выбранной системы координат. Общее число возможных значений m_l, показывает,
сколькими способами можно расположить орбитали данного подуровня в пространстве, т.е. общее число орбиталей на подуровне.

Атомная орбиталь

Волновая функция, описывающая состояние электрона в атоме, и полностью характеризуемая конкретными значениями квантовых чисел n, l и m_l, называется пространственной
атомной орбиталью или просто атомной орбиталью.

Орбитальному квантовому числу l = 0 соответствует единственное значение магнитного квантового числа m_l = 0. Эти значения характеризуют все s-орбитали, которые имеют
форму сферы. Т.к. в этом случае магнитное квантовое число принимает только одно значение, каждый s-подуровень состоит только из одной орбитали.

Рассмотрим любой p-подуровень: при l = 1 орбитали имеют форму гантелей (объемные «восьмерки»), магнитное квантовое число принимает следующие значения m_l = – 1, 0, +1
(три значения), следовательно, p-подуровень состоит из трех орбиталей, и эти орбитали располагаются вдоль трех осей координат и, соответственно, обозначаются р_х, р_y,
р_z.

Для d-подуровня l = 2, m_l = – 2, -1, 0, +1, +2 (5 значений), и любой d-подуровень состоит из пяти орбиталей, которые определенным образом расположены в пространстве
и соответственно обозначаются d_xy, d_xz, d_zy, d_z² и d_x²-y². Четыре из пяти
d-орбиталей имеют форму четырехлепестковых розеток, каждая из которых образована двумя гантелями, пятая орбиталь представляет собой гантель с тором в экваториальной плоскости
(d_z²-орбиталь) и расположена вдоль оси z. «Лепестки» орбитали d_x²-y². расположены вдоль осей х и у. Орбитали d_xy,
d_xz и d_zy, расположены между соответствующими осями.

Четвертый энергетический уровень состоит из четырех подуровней – s, р, d и f Первые три из них аналогичны рассмотренным выше, а четвертый – f-подуровень состоит уже из семи орбиталей,
пространственные конфигурации которых достаточно сложны.

Для атомной орбитали принято сокращенное обозначение – АО, которым пользуются повсеместно при обсуждении свойств и строения атомов и молекул. Состояние, описываемое АО, условно обозначают в виде
квадрата (квантовой ячейки) в виде окружности или черты. Последний способ обозначения используется, как наименее громоздкий и позволяющий одновременно указывать относительное значение энергии выбранного
состояния. Данный способ в настоящее время почти всегда используется при описании свойств молекул.

Спиновое квантовое число

Теоретически было показано Дираком, а экспериментально подтверждено в 1926 г. Уленбеком и Голдсмитом, что помимо квантовых чисел n, l и m_l,
электрон характеризуется еще одной квантованной величиной, не связанной с движением электрона вокруг ядра, а определяющей его собственное состояние. Эта величина получила название спинового квантового
числа или просто спина (от английского spin – кручение, вращение); спин обычно обозначают буквой m_s.

Спиновое квантовое число отражает наличие у электрона собственного момента движения. Проекция собственного момента количества движения электрона на избранное направление (например, на ось z) и
называется спином. Спиновое квантовое число принимает два значения:

При записи формул и составлении энергетических диаграмм, отражающих состояние электронов в атомах и молекулах, наличие того или иного значения спинового квантового числа указывают стрелкой ↑ или
↓.

Волновая функция, описывающая состояние электрона в атоме конкретными значениями квантовых чисел n, l, m_l и m_s, называется спин-орбиталью.
Спин-орбиталь с одним направлением спина называется α-спин-орбиталью, а с другим – β-спин-орбиталью.

Четыре квантовых числа – n, l, m_l и m_s – полностью определяют состояние электрона в атоме.

Математические основы механики квантов созданы:

• Л. де Бройлем, открывшим волны материи;
• В. Гейзенбергом (автором принципа неопределенности и матричной механики);
• Э. Шредингером (уравнение Шредингера);
• Н. Бором (им сформулирован принцип дополнительности).

Завершил создание математических основ механики квантов, придав им современную форму, П. Дирак. Отличительным признаком математических уравнений для квантовой механики считается наличие в них символа постоянной Планка.

Векторы состояний и наблюдаемые величины

С целью описания физических систем, в квантовой механике в качестве основных характеристик применяются наблюдаемые величины и состояния.

Радиусу-вектору частицы $x$, например, будет соответствовать оператор умножения $x$. Соответствием для импульса частицы выступает оператор:

$hat {p}=-i bar{h} nabla$

Соответствием для момента импульса является оператор:

$bar{h} hat {L}=hat {x}hat {p}$

«Математические основы квантовой механики» 👇

Волновые функции соответствуют квантовому принципу суперпозиции. Он заключается в следующем: в случае, если два возможных состояния изображают волновые функции $psi_1$ и $psi_2$, может существовать третье состояние:

$psi=c_1psi_1+c_2psi_2$

Здесь $c_1$ и $c_2$ – произвольные амплитуды.

В качестве результата точного измерения физической величины $A$ могут выступатьтолько собственные значения указанного оператора: $widehat {A}$.

Для вычисления математического ожидания $bar{A}$ значений величины $A$ в состоянии $psi$ применима формула:

$bar{A}=(psi,widehat {A},psi)$

В вышеприведенной формуле круглые скобки будут означать скалярное произведение векторов (диагональный матричный элемент). Векторы состояний $psi_1$ и $psi_2$ могут описывать одно и то же состояние только если $psi_2=cpsi_1$

Где $c$ будет произвольным комплексным числом.

Каждая наблюдаемая величина однозначно сопоставляется с линейным самосопряженным оператором. Распределение вероятности для возможных значений наблюдаемой величины $A$ в состоянии $psi$ определяется формулой:

$dm_widehat {A}, psi (a)=d(E_a psi, psi)$,

Где $widehat {A}$ будет самосопряженным оператором, отвечающим наблюдаемой величине $a$, $psi$ – это вектор состояния, $E_a$ – спектральная функция оператора $widehat {A}$, круглые скобки здесь означают скалярное произведение векторов.

Уравнения Гамильтона в квантовой механике

Математические основы в квантовой механике представляет уравнение Гамильтона. Матричные элементы операторов существуют для:

• декартовых координат $widehat {x_i}$;
• операторов импульсов $widehat {p_i}$.

Они аналогичны уравнениям Гамильтона в классической механике:

$frac{d}{dt}(f,widehat {p_i},g)=-(f,frac{partialwidehat {H}}{partialwidehat {x_i}},g)$

$frac{d}{dt}(f,widehat {x_i},g)= (f,frac{partialwidehat {H}}{partialwidehat {p_i}},g)$

Где $widehat {H} представляет оператор, соответствующий функции Гамильтона в классической механике.widehat {H} представляет оператор, соответствующий функции Гамильтона в классической механике.

Уравнение Шредингера

В математических основах квантовой механики эволюцию чистого состояния системы Гамильтона во времени определяет нестационарное уравнение Шредингера:

$ibar{h}frac {partialpsi}{partial t}=hat{H}psi$

здесь $hat {H}$ это гамильтониан:

$hat {H}=- frac {bar{h}^2}{2m} left( frac{partial^2}{partial x^2}+frac {partial^2}{partial y^2}+frac {partial^2}{partial z^2}right)+hat {E_pot}$

Стационарные (не изменяющиеся со временем состояния) будут определяться стационарным уравнением Шредингера:

$hat {H} psi=E psi$

При этом, существует предположение, что эволюция квантовой системы представляет марковский процесс, а число частиц является постоянным. Такие положения способствуют созданию математического аппарата с целью описания разнообразного спектра задач в квантовой механике для гамильтоновых систем в чистых состояниях. Дальнейшему развитию этого аппарата способствует квантовая теория поля. Она описывает квантовые процессы с переменным числом частиц.