Как найти число линейно независимых векторов

Линейно зависимые и линейно независимые вектора.

Навигация по странице:

• Определение линейной комбинации векторов
• Определение линейно независимой комбинации векторов
• Определение линейно зависимой комбинации векторов
• Свойства линейно зависимых векторов
• Примеры задач на линейную зависимость и линейную независимость векторов

Определение. Линейной комбинацией векторов a₁, …, a_n с коэффициентами x₁, …, x_n называется вектор

x₁a₁ + … + x_na_n.

Определение. Линейная комбинация x₁a₁ + … + x_na_n называется тривиальной, если все коэффициенты x₁, …, x_n равны нулю.

Определение. Линейная комбинация x₁a₁ + … + x_na_n называется нетривиальной, если хотя быбы один из коэффициентов x₁, …, x_n не равен нулю.

Определение. Вектора a₁, …, a_n называются линейно независимыми, если не существует нетривиальной комбинации этих векторов равной нулевому вектору.

То есть вектора a₁, …, a_n линейно независимы если x₁a₁ + … + x_na_n = 0 тогда и только тогда, когда x₁ = 0, …, x_n = 0.

Определение. Вектора a₁, …, a_n называются линейно зависимыми, если существует нетривиальная комбинация этих векторов равная нулевому вектору.

Свойства линейно зависимых векторов:

• Для 2-х и 3-х мерных векторов.

  Два линейно зависимые вектора – коллинеарные. (Коллинеарные вектора – линейно зависимы.)
  .

• Для 3-х мерных векторов.

  Три линейно зависимые вектора – компланарные. (Три компланарные вектора – линейно зависимы.)

• Для n -мерных векторов.

  n + 1 вектор всегда линейно зависимы.

Примеры задач на линейную зависимость и линейную независимость векторов:

Пример 1. Проверить будут ли вектора a = {3; 4; 5}, b = {-3; 0; 5}, c = {4; 4; 4}, d = {3; 4; 0} линейно независимыми.

Решение:

Вектора будут линейно зависимыми, так как размерность векторов меньше количества векторов.

Пример 2. Проверить будут ли вектора a = {1; 1; 1}, b = {1; 2; 0}, c = {0; -1; 1} линейно независимыми.

Решение: Найдем значения коэффициентов при котором линейная комбинация этих векторов будет равна нулевому вектору.

x₁a + x₂b + x₃c₁ = 0

Это векторное уравнение можно записать в виде системы линейных уравнений

	x1 + x2 = 0
x1 + 2x2 – x3 = 0
x1 + x3 = 0

Решим эту систему используя метод Гаусса

1100
12-10
1010

~

из второй строки вычтем первую; из третей строки вычтем первую:

1100
1 – 12 – 1-1 – 00 – 0
1 – 10 – 11 – 00 – 0

~

1100
01-10
0-110

~

из первой строки вычтем вторую; к третей строке добавим вторую:

1 – 01 – 10 – (-1)0 – 0
01-10
0 + 0-1 + 11 + (-1)0 + 0

~

1010
01-10
0000

Данное решение показывает, что система имеет множество решений, то есть существует не нулевая комбинация значений чисел x₁, x₂, x₃ таких, что линейная комбинация векторов a, b, c равна нулевому вектору, например:

–a + b + c = 0

а это значит вектора a, b, c линейно зависимы.

Ответ: вектора a, b, c линейно зависимы.

Пример 3. Проверить будут ли вектора a = {1; 1; 1}, b = {1; 2; 0}, c = {0; -1; 2} линейно независимыми.

Решение: Найдем значения коэффициентов при котором линейная комбинация этих векторов будет равна нулевому вектору.

x₁a + x₂b + x₃c₁ = 0

Это векторное уравнение можно записать в виде системы линейных уравнений

	x1 + x2 = 0
x1 + 2x2 – x3 = 0
x1 + 2x3 = 0

Решим эту систему используя метод Гаусса

1100
12-10
1020

~

из второй строки вычтем первую; из третей строки вычтем первую:

1100
1 – 12 – 1-1 – 00 – 0
1 – 10 – 12 – 00 – 0

~

1100
01-10
0-120

~

из первой строки вычтем вторую; к третей строке добавим вторую:

1 – 01 – 10 – (-1)0 – 0
01-10
0 + 0-1 + 12 + (-1)0 + 0

~

1010
01-10
0010

~

из первой строки вычтем третью; к второй строке добавим третью:

1 – 00 – 01 – 10 – 0
0 + 01 + 0-1 + 10 + 0
0010

~

1010
0100
0010

Данное решение показывает, что система имеет единственное решение x₁ = 0, x₂ = 0, x₃ = 0, а это значит вектора a, b, c линейно независимые.

Ответ: вектора a, b, c линейно независимые.

Определение 1. Система векторов
{a₁,…,a_n}
называетсялинейно зависимой, если
найдутся коэффициентыλ₁,…,λ_nне все равные нулю, линейная комбинация
с которыми равна нулю, т.е.

Определение 2. Система векторов
{a₁,…,a_n}
называетсялинейно независимой,если ее линейная

комбинация равна нулю толькос
нулевыми коэффициентами:.

Имеют место несколько простых
утверждений.

Теорема 1 (необходимое и достаточное
условие линейной зависимости). Векторыа₁,…,a_n– линейно зависимыкогда хотя бы один из них является
линейной комбинацией остальных.

{1.(необходимость: {a_k}
– л.з. ):Пусть, для определенности,

,
т.е.а₁− линейная комбинация
остальных.

2.(достаточность: a_m– л.к.):
система лин. зав.}

Теорема 2. Если один из векторов
системы равен нулю, то вся система
линейно зависима.

{0a₁+ … + 0a_n–1+}

Теорема 3.Если подсистема линейно
зависима, то и вся система линейно
зависима.

{}

Примеры.

1)
.
2)они компланарны.

Отсюда следует, что три вектора на
плоскости всегда линейно зависимы.

3) Четыре вектора в пространстве всегда
линейно зависимы.

4) {f₁ = 1, f₂
= x, f₃
= x² } –
линейно независимы.

5) {sin²x,cos²x,
1} − линейно зависимы.

§5. Базис. Координаты. Размерность.

Определение 1. Базисомвекторного
пространстваLназывается система элементов,

удовлетворяющая двумусловиям:

1) система {e₁,…,e_n} линейно независима.

2) Любой вектор L линейно выражается через базисные (т.е.
является линейной комбинацией элементове₁,е₂, … ,е_n):.

Примеры. Базис на плоскости (V₂– 2 неколлинеарных вектора), в пространстве
(V₃– 3 некомпланарных
вектора), в пространстве многочленов
степени ≤n :
(1,х,х²,…,хⁿ).

Теорема 1. Коэффициенты разложения
по базису – единственны.

{Пусть
}

Определение 2. Координатами вектора
в некотором базисе называются коэффициенты
разложения по этому базису:а= ()
или.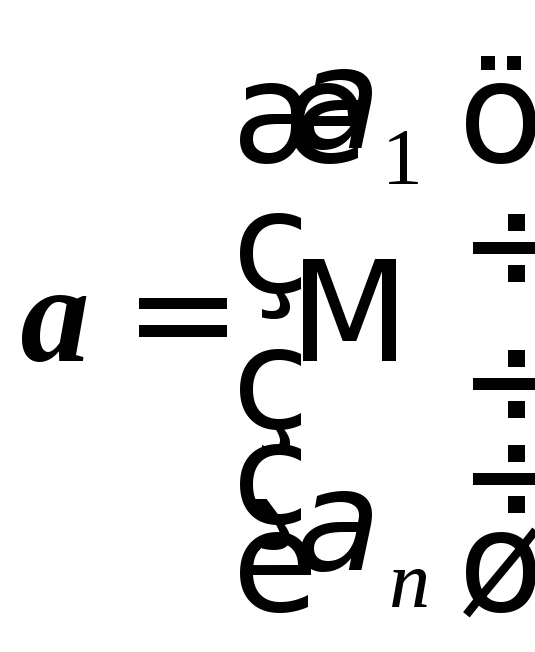

Замечания.1. В силуТ.1 данное
определение – корректно.

1. В качестве стандарта можно рассматривать
   как векторы – строки , так и векторы –
   столбцы.

2. Координаты базисных векторов е₁,е₂,е₃(в пространстве) в собственном базисе
   равны:

е₁= (1,0,0),е₂= (0,1,0),е₃= (0,0,1).

Определение 3. Размерностью
векторного пространстваL
(обозначаетсяdimL)
называется максимальное число линейно
независимых векторов этого пространства.

Если такого числа не существует –
пространство называется бесконечномерным.

Теорема 2. Размерность линейного
пространства равна числу базисных
векторов. {б/д}

Отсюда, в частности, следует, что все
базисы одного пространства состоят из
одинакового числа векторов.

Примеры.V₂; V₃; Rⁿ;
C[a,b].

Результаты линейных операций легко
вычисляются в координатной форме.

Теорема 3. При сложении векторов их
соответствующие координаты складываются:

.

{}

Теорема 4. При умножении вектора на
число его координаты умножаются на это
число:

λа = (λα₁,…,λα_n).
{д – во аналогично}

В заключение рассмотрим пример базиса,
который используется наиболее часто.

Определение 4. Ортонормированным
базисом в пространстве называется
базис, состоящий из трех взаимно
ортогональных векторов единичной длины
(на плоскости – из двух).

Эти векторы
обозначают буквами i,
j и
k и
называют

базисными
ортами.Таким образом, выполняются
соотношения

аa₃k, а произвольный вектора

ka₂jможет быть представлен в
следующем виде (рис.10):

j
a
= a₁
i
+ a₂
j +
a₃
k =
( a₁,
a₂,
a₃
).

a₁i
i

рис.10

10. Линейная зависимость и независимость векторов

Рассмотрим далее основополагающие в линейной алгебре понятие о линейной зависимости и независимости векторов, а также определение базиса системы векторов.

Любую конечную последовательность векторов Будем называть системой векторов, а любую ее подпоследовательность – подсистемой векторов. Линейной комбинацией векторов назовем вектор , равный сумме произведений произвольных чисел на векторы системы, т. е. .

Система векторов называется линейно независимой, если их линейная комбинация равна нулевому вектору только в том случае, когда все числа равны нулю. В обратном случае система векторов называется линейно зависимой. Отсюда, система векторов является линейно зависимой в том случае, когда линейная комбинация векторов равна нулевому вектору, а хотя бы один числовой коэффициент отличен от нуля.

Линейная зависимость и независимость есть свойства системы векторов. Однако часто соответствующие прилагательные относят и к самим векторам. Поэтому вместо «линейно независимая система векторов» допустимо говорить «линейно независимые векторы».

Например, двумерные арифметические векторы И Линейно независимы. Их линейная комбинация равна вектору , который обращается в нулевой вектор Только тогда, когда и .

Если взять векторы И , то они являются линейно зависимыми, так как их линейная комбинация равна нулевому вектору при И , не равных нулю.

Из определения линейной зависимости (независимости) системы векторов вытекают следующие утверждения.

1) Если некоторая система векторов содержит нулевой вектор, то она является линейно зависимой.

Пусть для определенности первый вектор системы является нулевым, т. е.

Тогда линейная комбинация векторов вида равна нулевому вектору, что и доказывает наше утверждение.

2) Если среди векторов системы есть такие, которые сами образуют линейно зависимую подсистему, то вся система также линейно зависима.

Так как исходная подсистема линейно зависима, то среди коэффициентов линейной комбинации векторов подсистемы имеется хотя бы один отличный от нуля. Добавим к этой линейной комбинацию линейную комбинацию векторов, не вошедших в исходную подсистему, с числовыми коэффициентами, равными нулю. Мы получим линейную комбинацию из векторов полной системы, которая равна нулевому вектору, причем имеется хотя бы один коэффициент отличный от нуля. Таким образом, наше утверждение доказано.

3) Если система векторов линейно независима, то и любая ее подсистема также линейно независима.

Если предположить обратное, т. е. существование некоторой линейно зависимой подсистемы, то по предыдущему утверждению отсюда следует зависимость исходной системы, что противоречит условию доказываемой теоремы. Полученное противоречие доказывает сформулированное утверждение.

4) Для того чтобы система из 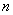Ненулевых векторов была линейно зависима необходимо и достаточно, чтобы хотя бы один из векторов системы мог быть представлен как линейная комбинация предшествующих векторов.

Необходимость. Пусть система векторов линейно зависима. Тогда равенство выполняется при том условии, что хотя бы одно из чисел в левой части равенства отлично от нуля. Будем перебирать эти числа, начиная с большего номера, и остановимся на некотором номере таком, что соответствующий коэффициент отличен от нуля, т. е. . Номер не может быть равен единице, так как иначе из условий И теоремы о нулевом произведении следовало бы равенство , что противоречит правилу выбора номера и условию теоремы. Таким образом , и справедливо равенство. Отсюда находим вектор Таким образом, чтобы он является линейной комбинацией предшествующих ему векторов, а именно .

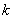
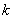
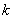
Достаточность. Пусть имеется некоторый вектор , который представлен в виде линейной комбинации предшествующих ему векторов . Тогда выполняется условие , что по определению означает линейную независимость исходной системы векторов.

По аналогичной схеме доказывается следующее утверждение.

5) Система векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов системы может быть представлен в виде линейной комбинации остальных векторов.

Как найти подсистему системы векторов

Определение 1. Система векторов 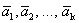называется линейно зависимой, если один из векторов системы можно представить в виде линейной комбинации остальных векторов системы, и линейно независимой – в противном случае.

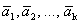
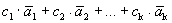
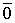
Определение 1´. Система векторов называется линейно зависимой, если найдутся числа с ₁ , с ₂ , …, с _k , не все равные нулю, такие, что линейная комбинация векторов с данными коэффициентами равна нулевому вектору: = , в противном случае система называется линейно независимой.

Покажем, что эти определения эквивалентны.

Пусть выполняется определение 1, т.е. один из векторов системы равен линейной комбинации остальных:

,

.

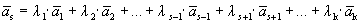
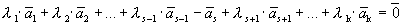
Линейная комбинация системы векторов равна нулевому вектору, причем не все коэффициенты этой комбинации равны нулю, т.е. выполняется определение 1´.

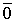
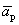
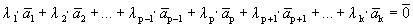
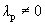
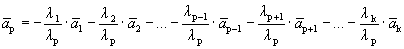
Пусть выполняется определение 1´. Линейная комбинация системы векторов равна , причем не все коэффициенты комбинации равны нулю, например, коэффициенты при векторе .

,

,

.

Один из векторов системы мы представили в виде линейной комбинации остальных, т.е. выполняется определение 1.

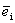
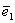
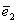
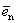
Определение 2. Единичным вектором, или ортом, называется n -мерный вектор , у которого i -я координата равна единице, а остальные – нулевые.

. (1, 0, 0, …, 0),

(0, 1, 0, …, 0),

(0, 0, 0, …, 1).

Теорема 1. Различные единичные векторы n -мерного пространства линейно независимы.

Доказательство. Пусть линейная комбинация этих векторов с произвольными коэффициентами равна нулевому вектору.

= .

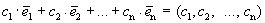
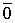
Из этого равенства следует, что все коэффициенты равны нулю. Получили противоречие.

Каждый вектор n -мерного пространства ā(а ₁ , а ₂ , . а _n ) может быть представлен в виде линейной комбинации единичных векторов с коэффициентами, равными координатам вектора

.

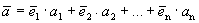
Теорема 2. Если системы векторов содержит нулевой вектор, то она линейно зависима.

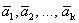
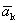
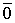
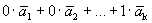
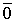
Доказательство. Пусть дана система векторов и один из векторов является нулевым, например = . Тогда с векторами данной системы можно составить линейную комбинацию, равную нулевому вектору, причем не все коэффициенты будут нулевыми:

= .

Следовательно, система линейно зависима.

Теорема 3. Если некоторая подсистема системы векторов линейно зависима, то и вся система линейно зависима.

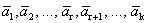
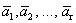
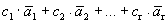
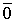
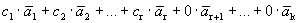
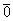
Доказательство. Дана система векторов . Предположим, что система линейно зависима, т.е. найдутся числа с ₁ , с ₂ , …, с _r , не все равные нулю, такие, что = . Тогда

= .

Получилось, что линейная комбинация векторов всей системы равна 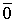, причем не все коэффициенты этой комбинации равны нулю. Следовательно, система векторов линейно зависима.

Следствие. Если система векторов линейно независима, то и любая ее подсистема также линейно независима.

Предположим противное, т.е. некоторая подсистема линейно зависима. Из теоремы следует, что вся система линейно зависима. Мы пришли к противоречию.

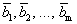
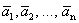
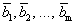
Теорема 4 (теорема Штейница). Если каждый из векторов является линейной комбинацией векторов и m > n , то система векторов линейно зависима.

Следствие. В любой системе n -мерных векторов не может быть больше чем n линейно независимых.

Доказательство. Каждый n -мерный вектор выражается в виде линейной комбинации n единичных векторов. Поэтому, если система содержит m векторов и m > n , то, по теореме, данная система линейно зависима.

Как найти подсистему системы векторов

1.4. РАНГ СИСТЕМЫ ВЕКТОРОВ

Рассмотрим систему векторов (1.1), где . Максимальной линейно независимой подсистемой системы векторов (1.1) называется любой набор векторов последней, удовлетворяющий следующим условиям: векторы этого набора линейно независимы; всякий вектор из системы (1.1) линейно выражается через векторы этого набора. В общем, система векторов (1.1) может иметь несколько разных максимальных линейно независимых подсистем.

Теорема 1. 6. Все максимальные линейно независимые подсистемы данной системы векторов содержат одно и то же число векторов.

Число векторов в максимальной линейно независимой подсистеме системы векторов (1.1) называется рангом последней. Системы векторов (1.1) и (1.2) называются эквивалентными, если векторы системы (1.1) линейно выражаются через систему векторов (1.2) и наоборот.

Теорема 1. 7. Ранги эквивалентных систем векторов равны.

Операции, переводящие систему векторов (1.1) в систему, ей эквивалентную, следующие:

1) изменение нумерации векторов в системе;

2) удаление нулевого вектора;

3) удаление вектора, являющегося линейной комбинацией остальных векторов системы;

4) умножение произвольного вектора системы на любое, не равное нулю число;

5) прибавление к одному из векторов системы линейной комбинации остальных векторов системы.

[spoiler title=”источники:”]

http://lms2.sseu.ru/courses/eresmat/course1/razd8z1/par8_5z1.htm

http://www.math.mrsu.ru/text/courses/method/rang_sist_vect.htm

[/spoiler]

Понятие линейной зависимости и линейной независимости векторов

Для элементов линейного пространства были введены операции умножения вектора на число (из некоторого числового поля) и сложения векторов. При помощи этих операций можно составлять алгебраические выражения.

Вектор называется линейной комбинацией векторов , если

где – некоторые числа. В этом случае говорят, что вектор разложен по векторам (вектор линейно выражается через векторы , а числа называют коэффициентами разложения. Линейная комбинация с нулевыми коэффициентами называется тривиальной.

Набор векторов из пространства называется системой векторов, а любая часть системы векторов – подсистемой.

Система из векторов называется линейно зависимой, если существуют такие числа не все равные нулю одновременно, что справедливо равенство

т.е. линейная комбинация является нулевым вектором.

Система из векторов называется линейно независимой, если равенство (8.2) возможно только при , т.е. когда линейная комбинация в левой части (8.2) тривиальная.

---

Замечания 8.2

1. Один вектор тоже образует систему: при — линейно зависимую, а при — линейно независимую.

2. Понятия линейной зависимости и линейной независимости для векторов определяются также, как для столбцов матриц. Поэтому все свойства, рассмотренные для столбцов матриц, переносятся на векторы. Применение свойств, доказанных для векторов, к столбцам, можно делать без обоснования, так как множество столбцов является линейным пространством (см. пункт 3 в примерах линейных пространств).

3. Рангом системы векторов называется максимальное число линейно независимых векторов этой системы и обозначается .

---

Пример 8.1. Установить необходимые и достаточные условия линейной зависимости двух, трех, четырех ненулевых векторов пространства где — множество векторов (направленных отрезков) пространства (см. пункт 2 в примерах линейных пространств).

Решение. Из элементарной геометрии известно, что два ненулевых вектора и коллинеарны тогда и только тогда, когда существует такое число , что . Это равенство можно представить в виде , т.е. в виде нетривиальной линейной комбинации векторов и , равной нулевому вектору. Следовательно, условие коллинеарности необходимо и достаточно для линейной зависимости двух ненулевых векторов.

Рассмотрим три ненулевых вектора , и . Они компланарны (принадлежат или параллельны одной плоскости) тогда и только тогда, когда один из них может быть разложен по другим, т.е. когда существуют такие числа аир, что . Записав это равенство в виде равной нулевому вектору нетривиальной линейной комбинации:

делаем вывод, что три ненулевых вектора пространства линейно зависимы тогда и только тогда, когда они компланарны.

Покажем, что любые четыре ненулевых вектора линейно зависимы. Если три вектора компланарны, то . От сюда получаем равенство , т.е. векторы линейно зависимы. Если же векторы не компланарны, то вектор может быть разложен по ним, т.е. представлен в виде , где — некоторые числа. Отсюда получаем равенство: . Значит, векторы линей но зависимы.

---

Свойства линейно зависимых и независимых n-мерных векторов

1. Если в систему векторов входит нулевой вектор, то она линейно зависима.

2. Если в системе векторов имеется два равных вектора, то она линейно зависима.

3. Если в системе векторов имеется два пропорциональных (коллинеарных) вектора , то она линейно зависима.

4. Система из векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов есть линейная комбинация остальных.

5. Любые векторы, входящие в линейно независимую систему, образуют линейно независимую подсистему.

6. Система векторов, содержащая линейно зависимую подсистему, линейно зависима.

7. Если система векторов — линейно независима, а после присоединения к ней вектора — оказывается линейно зависимой, то вектор можно разложить по векторам и притом единственным образом, т.е. коэффициенты разложения (8.1) находятся однозначно.

8. Пусть каждый вектор системы может быть разложен по векторам системы , т.е. (говорят, что система векторов линейно выражается через систему векторов ). Тогда, если , то система векторов — линейно зависима.

Докажем, например, последнее свойство. Составим линейную комбинацию векторов с коэффициентами и приравняем ее нулевому вектору:

Надо показать, что эта линейная комбинация может быть нетривиальной, т.е. среди коэффициентов , можно взять числа, не равные нулю. Действительно, подставим в линейную комбинацию (8.3) разложения векторов по векторам системы

Чтобы это равенство выполнялось, достаточно потребовать, чтобы . Таким образом, получили однородную систему линейных уравнений с неизвестными . Матрица системы имеет размеры , т.е. количество уравнений меньше количества неизвестных, так как . Поэтому , т.е. система имеет бесконечно много решений, в том числе и ненулевых (см. структуру общего решения системы уравнений). Таким образом, линейная комбинация в (8.3) может быть нетривиальной, т.е. система векторов линейно зависима.

---

Аффинные, неотрицательные и выпуклые комбинации векторов

Пусть дана система векторов вещественного линейного пространства (т.е. над полем ). Множество линейных комбинаций векторов называется их линейной оболочкой и обозначается:

Векторы называются образующими линейной оболочки .

Линейная комбинация векторов называется аффинной, если сумма ее коэффициентов равна единице. Множество аффинных комбинаций векторов называется их аффинной оболочкой и обозначается:

Линейная комбинация векторов называется неотрицательной, если все ее коэффициенты — неотрицательные числа. Множество неотрицательных комбинаций векторов называется их конической оболочкой и обозначается:

Линейная комбинация векторов называется выпуклой, если все ее коэффициенты — неотрицательные числа, а их сумма равна единице. Множество выпуклых комбинаций векторов называется их выпуклой оболочкой и обозначается:

Аналогично определению образующих линейной оболочки, векторы называют образующими множеств , , соответственно.

Понятия линейной, аффинной, конической и выпуклой оболочек, определенные для конечной системы векторов, можно обобщить.

Линейной оболочкой непустого подмножества линейного пространства называется множество всевозможных линейных комбинаций векторов из

Аналогично определяются аффинная, коническая и выпуклая оболочки непустого подмножества

Если множество пустое , то по определению считается, что

Из определений следуют включения:

и равенство .

---

Пример 8.2. В пространстве радиус-векторов на плоскости (см. пункт 3 в [url=http://mathhelpplanet.com/static.php?p=linyeinye-prostranstva]примерах линейных пространств[/ur]) даны два неколлинеарных вектора и (рис.8.1).

Найти .

Решение. . Любой радиус-вектор плоскости можно разложить по двум неколлинеарным векторам этой плоскости, т.е. представить в виде линейной комбинации , где и . Следователь но, множество всевозможных линейных комбинаций векторов и сов падает со всем пространством радиус-векторов на плоскости, т.е. .

. Заметим, что точка — конец вектора при условии принадлежит прямой , так как (при )

т.е. радиус-вектор получается в результате прибавления к вектору некоторого вектора, параллельного прямой . Следовательно, — множество радиус-векторов, концы которых лежат на прямой, проходящей через точки и (см. рис.8.1).

. При умножении вектора на положительное число его на правление не изменяется. Поэтому вектор при можно рассматривать как сумму двух векторов, принадлежащих лучам и соответственно. По правилу сложения векторов заключаем, Что радиус-вектор лежит либо между этими лучами, либо на одном из них. Следовательно, множество образуют радиус-векторы, концы которых принадлежат углу (заштрихованное множество на рис. 8.1).

. Конец радиус-вектора при принадлежит прямой и углу одновременно. Следовательно, точка принадлежит отрезку . Поэтому — множество радиус-векторов, концы которых принадлежат отрезку (см. рис.8.1). Этот вывод соответствует указанному выше равенству .

---

Замечания 8.3

1. Свойство 7 линейно зависимых и линейно независимых векторов можно сформулировать (без указания единственности разложения) следующим образом: если система векторов линейно независима, а после присоединения к ней вектора — оказывается линейно зависимой, то вектор .

2. Свойство 8 линейно зависимых и линейно независимых векторов можно сформулировать так: если каждый вектор системы принадлежит линейной оболочке и , то система векторов — линейно зависима.

3. Свойства аффинных оболочек будут рассматриваться в линейных многообразиях. Свойства конических и выпуклых оболочек относятся к выпуклому анализу и применяются в теории оптимизации.

4. В некоторых источниках для линейной оболочки векторов используется обозначение .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.