История
Археологи нашли свидетельства того, что волшебные таблицы были известны еще древним грекам и китайцам. «Магическими» эти фигуры назвали арабы, которые наделяли их сверхъестественными защитными свойствами.
В середине XVI в. европейские математики занялись исследованиями загадочных таблиц, положив начало их новой жизни. Они искали общий метод построения магических квадратов и пытались описать все возможные их варианты.
На уроках математики в школе
Решение магических квадратов на уроках математики и внеклассных занятиях вызывает интерес, способствует развитию мышления. Дети учатся планировать и контролировать свою работу. В клетки магических квадратов можно записывать не только числа, но и выражения. Все зависит от изучаемой темы. Задания с магическими квадратами часто дают как дополнительные или олимпиадные уже в начальной школе.
Один из способов решения магического квадрата
Нетрудно решить магический квадрат третьего порядка (у которого по три столбца и строки). Можно воспользоваться тем фактом, что число (выражение), стоящее на пересечении его диагоналей, всегда равно ⅓ волшебной суммы. Отсюда следует алгоритм построения:
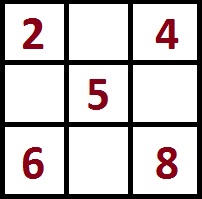
- Вписываем в первую строку или столбец 3 любых числа.
- Вычисляем магическую сумму (0 + 2 + 4 = 6).
- Ищем ее третью часть (6/3 = 2).
- Полученное число записываем на пересечении диагоналей.
- Подбираем остальные числа и заполняем ими пустые клеточки квадрата.

- Презентация “Магические квадраты”; 2 класс
- Презентация “Магические квадрат”; 2-3 класс
- Сценарий мероприятия “Магические квадраты и фокусы”; 5 класс
- Серия “Гимнастика для ума”. Магические квадраты; 3-4 класс
Как рассчитать магический квадрат Пифагора самому?
Пифагор — математик, заложивший основы нумерологии. Ученый верил, что миром правят числа. Даже человеческая сущность зависит от них, ведь дата рождения не что иное, как число.
Магический квадрат Пифагора — фигура третьего порядка, клетки которой заполнены числами от 1 до 9. Он делится на 3 уровня: материальный, души и разума.
Цифры даты рождения вписываются в определенном порядке. Полученная комбинация рассказывает о заложенных природой способностях человека.
Материал может быть использован на занятии математического кружка, на внеклассном мероприятии. Цель — развить и расширить познавательный кругозор и логическое мышление.
Решаем магический квадрат Пифагора: пример
Дата рождения: 17.09.2005 г. Складываем эти цифры, не учитывая нули: 1 + 7 + 9 + 2 + 5 = 24. Аналогично поступаем с цифрами результата: 2 + 4 = 6.
Из первой суммы вычитаем удвоенную первую цифру дня рождения: 24 -2 = 22. Снова складываем: 2 + 2 = 4. Полученные числа: 17; 9; 25; 24; 6; 22; 4.
Цифры вписываем в магический квадрат так, чтобы все единицы оказались в первой клеточке, двойки — во второй и так далее. Нули не учитываем.
Результат:
Значение:
|
Клетка 1 – волевые качества, эгоизм. |
|
|
1 |
Очень эгоистичные люди. |
|
11 |
Эгоизм — яркая, но не преобладающая черта характера. |
|
111 |
Спокойные, покладистые люди. |
|
1111 |
Сильный, волевой человек. |
|
11111 |
Люди с замашками диктатора. |
|
111111 |
Жестокость. |
|
Клетка 2 — биоэнергетика. |
|
|
— |
Воспитанность, природное благородство. |
|
2 |
Люди с повышенной чувствительностью к атмосферным изменениям. |
|
22 |
Человек с хорошим запасом биоэнергетики. |
|
222 |
Экстрасенсы. |
|
Клетка 3 — организованность, любовь к точности, конкретности, скрупулезность, скупость. |
|
|
Чем больше троек, тем сильнее выражены вышеперечисленные качества. |
|
|
Клетка 4 — здоровье. |
|
|
4 |
Среднее, требуется закаливание. |
|
44 |
Все в норме. |
|
444 и более |
Очень крепкое здоровье. |
|
Клетка 5 — интуиция, экстрасенсорные способности |
|
|
Чем больше пятерок, тем более выражена связь с космосом. |
|
|
Клетка 6 — материализм. |
|
|
— |
Люди с неординарным воображением, которым необходим физический труд. |
|
6 |
Могут посвятить время и творчеству, и точным наукам. Физические нагрузки обязательны. |
|
66 |
Заземленные личности, тянущиеся к физическому труду. |
|
666 |
Повышенная темпераментность. |
|
6666 |
Очень много заземленности. |
|
Клетка 7 — талант. |
|
|
Чем больше семерок, тем талантливее человек. |
|
|
Клетка 8 — судьба, отношение к обязанностям. |
|
|
— |
Чувства долга нет. |
|
8 |
Добросовестные личности. |
|
88 |
Люди, которые всегда спешат помочь другим. |
|
888 |
Признак служения народу. |
|
8888 |
Парапсихологические способности. |
|
Клетка 9 — умственные способности |
|
|
Полное отсутствие девяток означает очень низкий уровень умственной деятельности. Чем больше количество девяток, тем умнее человек. |
Задачи на составление магических квадратов часто включаются в сборники нестандартных заданий. Они встречаются на олимпиадах. Увлеченным математикой школьникам будет полезно узнать об этом классе задач.
Об авторе: Филиппова Оксана, учитель математики, физики и информатики.
Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Маги́ческий, или волше́бный квадра́т — квадратная таблица 




Нормальные магические квадраты существуют для всех порядков 


Сумма чисел в каждой строке, столбце и на диагоналях называется магической константой, M. Магическая константа нормального волшебного квадрата зависит только от n и определяется формулой
Первые значения магических констант приведены в следующей таблице (последовательность A006003 в OEIS):
Порядок 
|
3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|

|
15 | 34 | 65 | 111 | 175 | 260 | 369 | 505 | 671 | 870 | 1105 |





Исторически значимые магические квадраты[править | править код]
Квадрат Ло Шу[править | править код]
Изображение Ло Шу в книге эпохи Мин
Ло Шу (кит. трад. 洛書, упр. 洛书, пиньинь luò shū) Единственный нормальный магический квадрат 3×3. Был известен ещё в Древнем Китае, первое изображение на черепаховом панцире датируется 2200 г. до н. э.
В Западноевропейской традиции этот квадрат называется «Печать Сатурна» (Sigillum Saturni). Параметры квадрата: 3, 9, 15, 45 (3х3, 9 ячеек, сумма по всем направлениям 15, сумма всех чисел в квадрате — 45).[1]
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45
45 : 3 = 15
Квадрат, найденный в Кхаджурахо (Индия)[править | править код]
Самый ранний уникальный магический квадрат обнаружен в надписи XI века в индийском городе Кхаджурахо:
| 7 | 12 | 1 | 14 |
| 2 | 13 | 8 | 11 |
| 16 | 3 | 10 | 5 |
| 9 | 6 | 15 | 4 |
Это первый магический квадрат, относящийся к разновидности так называемых «дьявольских» квадратов[2].
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15 + 16 = 136
136 : 4 = 34
Магический квадрат Ян Хуэя (Китай)[править | править код]
В XIII в. математик Ян Хуэй занялся проблемой методов построения магических квадратов. Его исследования были потом продолжены другими китайскими математиками. Ян Хуэй рассматривал магические квадраты не только третьего, но и больших порядков. Некоторые из его квадратов были достаточно сложны, однако он всегда давал правила для их построения. Он сумел построить магический квадрат шестого порядка, причем последний оказался почти ассоциативным (в нем только две пары центрально противолежащих чисел не дают сумму 37)[3]:
| 27 | 29 | 2 | 4 | 13 | 36 |
| 9 | 11 | 20 | 22 | 31 | 18 |
| 32 | 25 | 7 | 3 | 21 | 23 |
| 14 | 16 | 34 | 30 | 12 | 5 |
| 28 | 6 | 15 | 17 | 26 | 19 |
| 1 | 24 | 33 | 35 | 8 | 10 |
Сумма всех 36 чисел равна 666
666 : 6 = 111
Квадрат Альбрехта Дюрера[править | править код]
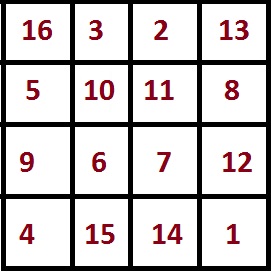
Магический квадрат 4×4, изображённый на гравюре Альбрехта Дюрера «Меланхолия I», считается самым ранним в европейском искусстве[4]. Два средних числа в нижнем ряду указывают дату создания гравюры (1514).
| 16 | 3 | 2 | 13 |
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| 4 | 15 | 14 | 1 |
Сумма чисел на любой горизонтали, вертикали и диагонали равна 34. Эта сумма также встречается во всех угловых квадратах 2×2, в центральном квадрате (10+11+6+7), в квадрате из угловых клеток (16+13+4+1), в квадратах, построенных «ходом коня» (2+12+15+5 и 3+8+14+9), в вершинах прямоугольников, параллельных диагоналям (2+8+15+9 и 3+12+14+5), в прямоугольниках, образованных парами средних клеток на противоположных сторонах (3+2+15+14 и 5+8+9+12). Большинство дополнительных симметрий связано с тем, что сумма любых двух центрально симметрично расположенных чисел равна 17.
Данный квадрат является «Печатью Юпитера» (Sigillum Iouis), имеет параметры: 4, 16, 34, 136 (размер 4х4, 16 ячеек, сумма по направлениям — 34, сумма всех чисел равна 136).[1]
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15 + 16 = 136
136 : 4 = 34
Магические квадраты Афанасия Кирхера[1][править | править код]
Квадрат Марса[править | править код]
Квадрат или печать Марса (Sigillum Martis) имеет параметры: 5, 25, 65, 325 (размер 5х5, 25 ячеек, сумма по направлениям — 65, сумма всех чисел равна 325).
| 12 | 25 | 8 | 21 | 4 |
| 5 | 13 | 26 | 9 | 17 |
| 18 | 6 | 14 | 22 | 10 |
| 11 | 19 | 2 | 15 | 23 |
| 24 | 7 | 20 | 3 | 16 |
325 : 5 = 65
Квадрат Солнца[править | править код]
Печать Солнца (Sigillum Solis) имеет параметры: 6, 36, 111, 666 (размер 6х6, 36 ячеек, сумма по направлениям — 111, сумма всех чисел равна 666).
| 6 | 32 | 3 | 34 | 35 | 1 |
| 7 | 11 | 27 | 28 | 8 | 30 |
| 19 | 14 | 16 | 15 | 23 | 24 |
| 18 | 20 | 22 | 21 | 17 | 13 |
| 25 | 29 | 10 | 9 | 26 | 12 |
| 36 | 5 | 33 | 4 | 2 | 31 |
666 : 6 = 111
Квадрат Венеры[править | править код]
Печать Венеры (Sigillum Veneris) имеет параметры: 7, 49, 175, 1225 (размер 7х7, 49 ячеек, сумма по направлениям — 175, сумма всех чисел — 1225).
| 22 | 47 | 16 | 41 | 10 | 35 | 4 |
| 5 | 23 | 48 | 17 | 42 | 11 | 29 |
| 30 | 6 | 24 | 49 | 18 | 36 | 12 |
| 13 | 31 | 7 | 25 | 43 | 19 | 37 |
| 38 | 14 | 32 | 1 | 26 | 44 | 20 |
| 21 | 39 | 8 | 33 | 2 | 27 | 45 |
| 46 | 15 | 40 | 9 | 34 | 3 | 28 |
1225 : 7 = 175
Квадрат Меркурия[править | править код]
Печать Меркурия (Sigillum Mercurio) имеет параметры: 8, 64, 260, 2080 (размер 8х8, 64 ячейки, сумма по направлениям — 260, сумма всех чисел — 2080).
| 8 | 58 | 59 | 5 | 4 | 62 | 63 | 1 |
| 49 | 15 | 14 | 52 | 53 | 11 | 10 | 56 |
| 41 | 23 | 22 | 44 | 45 | 19 | 18 | 48 |
| 32 | 34 | 35 | 29 | 28 | 38 | 39 | 25 |
| 40 | 26 | 27 | 37 | 36 | 30 | 31 | 33 |
| 17 | 47 | 46 | 20 | 21 | 43 | 42 | 24 |
| 9 | 55 | 54 | 12 | 13 | 51 | 50 | 16 |
| 64 | 2 | 3 | 61 | 60 | 6 | 7 | 57 |
2080 : 8 = 260
Квадрат Луны[править | править код]
Печать Луны (Sigillum Lune) имеет параметры: 9, 81, 369, 3321 (размер 9х9, 81 ячейка, сумма по направлениям — 369, сумма всех чисел — 3321).
| 37 | 78 | 29 | 70 | 21 | 62 | 13 | 54 | 5 |
| 6 | 38 | 79 | 30 | 71 | 22 | 63 | 14 | 46 |
| 47 | 7 | 39 | 80 | 31 | 72 | 23 | 55 | 15 |
| 16 | 48 | 8 | 40 | 81 | 32 | 64 | 24 | 56 |
| 57 | 17 | 49 | 9 | 41 | 73 | 33 | 65 | 25 |
| 26 | 58 | 18 | 50 | 1 | 42 | 74 | 34 | 66 |
| 67 | 27 | 59 | 10 | 51 | 2 | 43 | 75 | 35 |
| 36 | 68 | 19 | 60 | 11 | 52 | 3 | 44 | 76 |
| 77 | 28 | 69 | 20 | 61 | 12 | 53 | 4 | 45 |
3321 : 9 = 369
Квадраты Генри Э. Дьюдени и Аллана У. Джонсона-мл.[править | править код]
Если в квадратную матрицу n × n заносится не строго натуральный ряд чисел, то данный магический квадрат — нетрадиционный. Ниже представлены два таких магических квадрата, заполненные простыми числами (хотя 1 в современной теории чисел не считается простым числом). Первый имеет порядок n=3 (квадрат Дьюдени); второй (размером 4×4) — квадрат Джонсона. Оба они были разработаны в начале двадцатого столетия[5]:
|
Есть еще несколько подобных примеров:
| 17 | 89 | 71 |
| 113 | 59 | 5 |
| 47 | 29 | 101 |
| 1 | 823 | 821 | 809 | 811 | 797 | 19 | 29 | 313 | 31 | 23 | 37 |
| 89 | 83 | 211 | 79 | 641 | 631 | 619 | 709 | 617 | 53 | 43 | 739 |
| 97 | 227 | 103 | 107 | 193 | 557 | 719 | 727 | 607 | 139 | 757 | 281 |
| 223 | 653 | 499 | 197 | 109 | 113 | 563 | 479 | 173 | 761 | 587 | 157 |
| 367 | 379 | 521 | 383 | 241 | 467 | 257 | 263 | 269 | 167 | 601 | 599 |
| 349 | 359 | 353 | 647 | 389 | 331 | 317 | 311 | 409 | 307 | 293 | 449 |
| 503 | 523 | 233 | 337 | 547 | 397 | 421 | 17 | 401 | 271 | 431 | 433 |
| 229 | 491 | 373 | 487 | 461 | 251 | 443 | 463 | 137 | 439 | 457 | 283 |
| 509 | 199 | 73 | 541 | 347 | 191 | 181 | 569 | 577 | 571 | 163 | 593 |
| 661 | 101 | 643 | 239 | 691 | 701 | 127 | 131 | 179 | 613 | 277 | 151 |
| 659 | 673 | 677 | 683 | 71 | 67 | 61 | 47 | 59 | 743 | 733 | 41 |
| 827 | 3 | 7 | 5 | 13 | 11 | 787 | 769 | 773 | 419 | 149 | 751 |
Последний квадрат, построенный в 1913 г. Дж. Н. Манси, примечателен тем, что он составлен из 143 последовательных простых чисел за исключением двух моментов: привлечена единица, которая не является простым числом, и не использовано единственное чётное простое число 2.
Квадраты с дополнительными свойствами[править | править код]
Пандиагональный магический квадрат[править | править код]
Пандиагональный или дьявольский квадрат — магический квадрат, в котором также с магической константой совпадают суммы чисел по ломаным диагоналям[en] (диагонали, которые образуются при сворачивании квадрата в тор) в обоих направлениях.
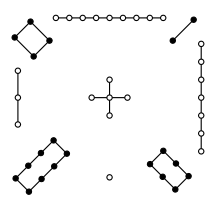
Существует 48 дьявольских квадратов 4×4 в стандартной форме Френикля[fr] — с точностью до поворотов и отражений. Пандиагональный квадрат сохраняет свойства при параллельном переносе строк или столбцов. Поэтому единицу можно переместить в левый верхний угол. Таких пандиагональных квадратов на плоскости 12. Они приведены ниже:
|
|
|
|
|
|
|
|
|
|
|
|
На торе каждой четвёрке таких квадратов соответствует один квадрат. Это происходит потому, что если разрезать тор, начиная с единичной клетки как угловой, то это можно сделать четырьмя способами, сопоставляя каждому из четырёх углов единичной клетки угол плоского квадрата. Поэтому пандиагональных квадратов на торе всего 3. Для изображения торического квадрата на плоскости можно использовать любой из соответствующей ему четвёрки.
Пандиагональные квадраты существуют для нечётного порядка n>3, для любого порядка двойной чётности n=4k (k=1,2,3…) и не существуют для порядка одинарной чётности 

Пандиагональные квадраты четвёртого порядка обладают рядом дополнительных свойств, за которые их называют совершенными. Совершенных квадратов нечётного порядка не существует. Среди пандиагональных квадратов двойной чётности выше 4 имеются совершенные[6].
С учётом торических параллельных переносов имеется 144 различных пандиагональных квадратов. Один из них показан ниже.
| 1 | 15 | 24 | 8 | 17 |
| 9 | 18 | 2 | 11 | 25 |
| 12 | 21 | 10 | 19 | 3 |
| 20 | 4 | 13 | 22 | 6 |
| 23 | 7 | 16 | 5 | 14 |
Разломанные диагонали пандиагонального квадрата
Если пандиагональный квадрат ещё и ассоциативный, то он носит название идеальный[7]. Пример идеального магического квадрата:
| 21 | 32 | 70 | 26 | 28 | 69 | 22 | 36 | 65 |
| 40 | 81 | 2 | 39 | 77 | 7 | 44 | 73 | 6 |
| 62 | 10 | 51 | 58 | 18 | 47 | 57 | 14 | 52 |
| 66 | 23 | 34 | 71 | 19 | 33 | 67 | 27 | 29 |
| 4 | 45 | 74 | 3 | 41 | 79 | 8 | 37 | 78 |
| 53 | 55 | 15 | 49 | 63 | 11 | 48 | 59 | 16 |
| 30 | 68 | 25 | 35 | 64 | 24 | 31 | 72 | 20 |
| 76 | 9 | 38 | 75 | 5 | 43 | 80 | 1 | 42 |
| 17 | 46 | 60 | 13 | 54 | 56 | 12 | 50 | 61 |
Известно, что не существует идеальных магических квадратов порядка n = 4k+2 и квадрата порядка n = 4. В то же время существуют идеальные квадраты порядка n = 8.
Методом построения составных квадратов можно построить на базе данного квадрата восьмого порядка идеальные квадраты порядка n = 8k, k=5,7,9…и порядка n = 8^p, p=2,3,4… В 2008 г. разработан комбинаторный метод построения идеальных квадратов порядка n = 4k, k = 2, 3, 4,…
Построение магических квадратов[править | править код]
Метод террас[править | править код]
Описан Ю. В. Чебраковым в «Теории магических матриц».
Для заданного нечетного n начертим квадратную таблицу размером n на n. Пристроим к этой таблице со
всех четырех сторон террасы (пирамидки). В результате получим ступенчатую симметричную фигуру.
Начиная с левой вершины ступенчатой фигуры, заполним её диагональные ряды последовательными натуральными числами от 1 до 
После этого для получения классической матрицы N-го порядка числа, находящиеся в террасах, поставим на те места таблицы размером NxN, в которых они оказались бы, если перемещать их вместе с террасами до того момента, пока основания террас не примкнут к противоположной стороне таблицы.
| 3 | 16 | 9 | 22 | 15 |
| 20 | 8 | 21 | 14 | 2 |
| 7 | 25 | 13 | 1 | 19 |
| 24 | 12 | 5 | 18 | 6 |
| 11 | 4 | 17 | 10 | 23 |
Кроме того, данный способ является верным и в том случае, если магический квадрат нужно составить не из чисел от 1 до N, но и от K до N, где 1 <= K< N.
Прочие способы[править | править код]
Правила построения магических квадратов делятся на три категории в зависимости от того, каков порядок квадрата: нечетен, равен удвоенному нечетному числу или равен учетверенному нечетному числу. Общий метод построения всех квадратов неизвестен, хотя широко применяются различные схемы.[8][9]
Найти все магические квадраты порядка 







Ещё проще построение выполнить следующим образом. Берётся матрица n x n . Внутри её строится ступенчатый ромб. В нём ячейки слева вверх по диагоналям заполняются последовательным рядом нечётных чисел. Определяется значение центральной ячейки C. Тогда в углах магического квадрата значения будут такими: верхняя правая ячейка C-1 ; нижняя левая ячейка C+1 ; нижняя правая ячейка C-n; верхняя левая ячейка C+n. Заполнение пустых ячеек в ступенчатых угловых треугольниках ведётся с соблюдением простых правил: 1)по строкам числа слева направо увеличиваются с шагом n + 1; 2) по столбцам сверху вниз числа увеличиваются с шагом n-1.
Также разработаны алгоритмы построения пандиагональных квадратов[10][11]
и идеальных магических квадратов 9×9.[12]
[13] Эти результаты позволяют строить идеальные магические квадраты порядков 


[16]
Разработаны методы построения идеальных магических квадратов порядка n=8k, k=1,2,3…[17] и совершенных магических квадратов.[18]
Пандиагональные и идеальные квадраты четно-нечётного порядка удаётся скомпоновать лишь в том случае, если они нетрадиционные.[19][20]
[21] Тем не менее, можно находить почти пандиагональные квадраты[22] Найдена особая группа идеально-совершенных магических квадратов (традиционных и нетрадиционных)[23].
Примеры более сложных квадратов[править | править код]
Методически строго отработаны магические квадраты нечётного порядка и порядка двойной чётности.[24] Формализация квадратов порядка одинарной чётности намного труднее, что иллюстрируют следующие схемы:
|
|
|
Существуют несколько десятков других методов построения магических квадратов
Шахматный подход[править | править код]
Известно, что шахматы, как и магические квадраты, появились десятки веков назад в Индии. Поэтому не случайно возникла идея шахматного подхода к построению магических квадратов. Впервые эту мысль высказал Эйлер. Он попытался получить полный магический квадрат непрерывным обходом коня. Однако, это сделать ему не удалось, поскольку в главных диагоналях суммы чисел отличались от магической константы. Тем не менее шахматная разбивка позволяет создавать любой магический квадрат. Цифры заполняются регулярно и построчно с учётом цвета ячеек.
Изображение схем построения магических квадратов
См. также[править | править код]
- Математическая магия
- Латинский квадрат
- Магический граф
- Магический куб
- Магический шестиугольник
- Чисугвимундо
- Палиндром
- Рамочный магический квадрат
- Судоку
- Супермагический квадрат
- Супермагический куб
Примечания[править | править код]
Литература[править | править код]
- Я. В. Успенский. Избранные математические развлечения. — Сеятель, 1924.
- Б. А. Кордемский. Математическая смекалка. — М.: ГИФМЛ, 1958. — 576 с.
- М. М. Постников. Магические квадраты. — М.: Наука, 1964.
- Н. М. Рудин. От магического квадрата к шахматам. — М.: Физкультура и спорт, 1969.
- Е. Я. Гуревич. Тайна древнего талисмана. — М.: Наука, 1969.
- М. Гарднер. Математические досуги. — М.: Мир, 1972.
- Энциклопедический словарь юного математика / Сост. А. П. Савин. — М. : Педагогика, 1989. — 352 с. — ISBN 5-7155-0218-7.
- Ю. В. Чебраков. Магические квадраты. Теория чисел, алгебра, комбинаторный анализ. — СПб.: СПб гос. техн. ун-т, 1995.
- Ю. В. Чебраков. Теория магических матриц. — СПб., 2008.
- М. Гарднер. Глава 17. Магические квадраты и кубы // Путешествие во времени. — М.: Мир, 1990. (недоступная ссылка)
- Чирказов Д. Буквенные магические квадраты как симметричные текстовые массивы. // Современные научные исследования и инновации. — № 11 Ноябрь 2012
Ссылки[править | править код]
- Магические квадраты (недоступная ссылка) (англ.)
- последовательность A164843 в OEIS
- М. Гарднер »Рецензия на книгу Кэтлин Оллереншоу и Дэвида Бри”
- H. Heinz Magic Squares, Magic Stars & Other Patterns (англ.)
- Н. Скрябина, В.Дубовской Магические квадраты
- Шахматный подход
- Нетрадиционные магические квадраты из простых чисел
- Наименьшие магические квадраты из простых чисел
- «Общие формулы магических квадратов.»
- Магические квадраты // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Загрузить PDF
Загрузить PDF
Магические квадраты обрели популярность наряду с появлением математических игр, таких как судоку. Магический квадрат — это таблица, заполненная целыми числами таким образом, чтобы сумма чисел по горизонтали, вертикали и диагонали была одинакова (так называемая магическая константа). Эта статья расскажет вам, как построить квадрат нечетного порядка, квадрат порядка одинарной четности и квадрат порядка двойной четности.
-
1
Вычислите магическую константу.[1]
Это можно сделать при помощи простой математической формулы [n * (n2 + 1)] / 2, где n – количество строк или столбцов в квадрате. Например, в квадрате 3×3 n=3, а его магическая константа:- Магическая константа = [3 * (32 + 1)] / 2
- Магическая константа = [3 * (9 + 1)] / 2
- Магическая константа = (3 * 10) / 2
- Магическая константа = 30/2
- Магическая константа квадрата 3х3 равна 15.
- Сумма чисел в любой строке, столбце и по диагонали должна быть равна магической константе.
-
2
Напишите 1 в центральной ячейке верхней строки. Строить любой нечетный квадрат нужно именно с этой ячейки. Например, в квадрате 3х3 напишите 1 во второй ячейке верхней строки, а в квадрате 15х15 напишите 1 в восьмой ячейке верхней строки.
-
3
Следующие числа (2,3,4 и так далее по возрастанию) записывайте в ячейки по правилу: одна строка – вверх, один столбец – вправо. Но, например, чтобы записать 2, нужно “выйти” за пределы квадрата, поэтому существуют три исключения из данного правила:
- Если вы вылезли за верхний предел квадрата, напишите цифру в самой нижней ячейке соответствующего столбца.
- Если вы вылезли за правый предел квадрата, напишите цифру в самой дальней (левой) ячейке соответствующей строки.
- Если вы попали на ячейку, которая занята другой цифрой, напишите цифру непосредственно под предыдущей записанной цифрой.
Реклама
-
1
Существуют различные методики для построения квадратов порядка одинарной четности и двойной четности.
- Число строк или столбцов в квадрате порядка одинарной четности делится на 2, но не на 4.[2]
- Наименьшим квадратом порядка одинарной четности является квадрат 6х6 (квадрат 2×2 построить нельзя).
- Число строк или столбцов в квадрате порядка одинарной четности делится на 2, но не на 4.[2]
-
2
Вычислите магическую константу. Это можно сделать при помощи простой математической формулы [n * (n2 + 1)] / 2, где n – количество строк или столбцов в квадрате. Например, в квадрате 6×6 n=6, а его магическая константа:
- Магическая константа = [6 * (62 + 1)] / 2
- Магическая константа = [6 * (36 + 1)] / 2
- Магическая константа = (6 * 37) / 2
- Магическая константа = 222/2
- Магическая константа квадрата 6х6 равна 111.
- Сумма чисел в любой строке, столбце и по диагонали должна быть равна магической константе.
-
3
Разделите магический квадрат на четыре квадранта одинакового размера. Обозначьте квадранты через А (сверху слева), C (сверху справа), D (снизу слева) и B (снизу справа). Чтобы выяснить размер каждого квадранта, разделите n на 2.
- Таким образом, в квадрате 6х6 размер каждого квадранта равен 3×3.
-
4
В квадранте А напишите четвертую часть всех чисел; в квадранте В напишите следующую четвертую часть всех чисел; в квадранте С напишите следующую четвертую часть всех чисел; в квадранте D напишите заключительную четвертую часть всех чисел.
- В нашем примере квадрата 6х6 в квадранте А напишите числа 1-9; в квадранте В – числа 10-18; в квадранте С – числа 19-27; в квадранте D – числа 28-36.
-
5
Числа в каждом квадранте записывайте так, как вы строили нечетный квадрат. В нашем примере квадрант А начните заполнять числами с 1, а квадранты С, B, D – с 10, 19, 28, соответственно.
- Число, с которого вы начинаете заполнение каждого квадранта, всегда пишите в центральной ячейке верхней строки определенного квадранта.
- Заполняйте каждый квадрант числами так, как будто это отдельный магический квадрат. Если при заполнении квадранта доступна пустая ячейка из другого квадранта, игнорируйте этот факт и пользуйтесь исключениями из правила заполнения нечетных квадратов.
-
6
Выделите определенные числа в квадрантах А и D.[3]
На данном этапе сумма чисел в столбцах, строках и по диагонали не будет равна магической константе. Поэтому вы должны поменять местами числа в определенных ячейках верхнего левого и нижнего левого квадрантов.- Начиная с первой ячейки верхней строки квадранта А, выделите количество ячеек, равное медиане количества ячеек во всей строке. Таким образом, в квадрате 6×6 выделите только первую ячейку верхней строки квадранта А (в этой ячейке написано число 8); в квадрате 10х10 вам нужно выделить первые две ячейки верхней строки квадранта А (в этих ячейках написаны числа 17 и 24).
- Образуйте промежуточный квадрат из выделенных ячеек. Так как в квадрате 6х6 вы выделили только одну ячейку, то промежуточный квадрат будет состоять из одной ячейки. Назовем этот промежуточный квадрат как A-1.
- В квадрате 10х10 вы выделили две ячейки верхней строки, поэтому необходимо выделить две первые ячейки второй строки, чтобы образовать промежуточный квадрат 2х2, состоящий из четырех ячеек.
- В следующей строке пропустите число в первой ячейке, а затем выделите столько чисел, сколько вы выделили в промежуточном квадрате A-1. Полученный промежуточный квадрат назовем A-2.
- Получение промежуточного квадрата А-3 аналогично получению промежуточного квадрата A-1.
- Промежуточные квадраты А-1, А-2, А-3 образуют выделенную область А.
- Повторите описанный процесс в квадранте D: создайте промежуточные квадраты, которые образуют выделенную область D.
-
7
Поменяйте местами числа из выделенных областей А и D (числа из первой строки квадранта А с числами из первой строки квадранта D и так далее). Теперь сумма чисел в любой строке, столбце и по диагонали должна быть равна магической константе.
Реклама
-
1
Число строк или столбцов в квадрате порядка двойной четности делится на 4.[4]
- Наименьшим квадратом порядка двойной четности является квадрат 4х4.
-
2
Вычислите магическую константу. Это можно сделать при помощи простой математической формулы [n * (n2 + 1)] / 2, где n – количество строк или столбцов в квадрате. Например, в квадрате 4×4 n=4, а его магическая константа:
- Магическая константа = [4 * (42 + 1)] / 2
- Магическая константа = [4 * (16 + 1)] / 2
- Магическая константа = (4 * 17) / 2
- Магическая константа = 68/2
- Магическая константа квадрата 4х4 равна 34.
- Сумма чисел в любой строке, столбце и по диагонали должна быть равна магической константе.
-
3
Создайте промежуточные квадраты А-D. В каждом углу магического квадрата выделите промежуточный квадрат размером n/4, где n – количество строк или столбцов в магическом квадрате.[5]
Обозначьте промежуточные квадраты как A, B, C, D (в направлении против часовой стрелки).- В квадрате 4×4 промежуточные квадраты будут состоять из угловых ячеек (по одной в каждом промежуточном квадрате).
- В квадрате 8х8 промежуточные квадраты будут иметь размер 2×2.
- В квадрате 12х12 промежуточные квадраты будут иметь размер 3×3 (и так далее).
-
4
Создайте центральный промежуточный квадрат. В центре магического квадрата выделите промежуточный квадрат размером n/2, где n – количество строк или столбцов в магическом квадрате. Центральный промежуточный квадрат не должен пересекаться с угловыми промежуточными квадратами, но должен касаться их углов.
- В квадрате 4×4 центральный промежуточный квадрат имеет размер 2×2.
- В квадрате 8×8 центральный промежуточный квадрат имеет размер 4×4 (и так далее).
-
5
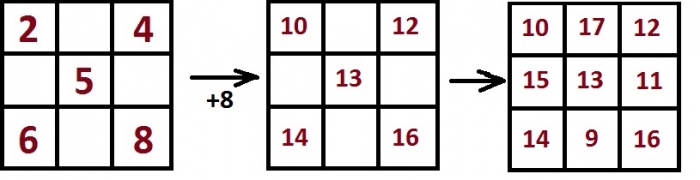
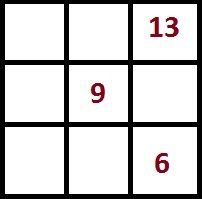
Начните строить магический квадрат (слева направо), но числа записывайте только в ячейки, расположенные в выделенных промежуточных квадратах. Например, квадрат 4×4 вы заполните так:
- Напишите 1 в первой строке первом столбце; напишите 4 в первой строке четвертом столбце.
- Напишите 6 и 7 в центре второй строки.
- Напишите 10 и 11 в центре третьей строки.
- Напишите 13 в четвертой строке первого столбца; напишите 16 в четвертой строке четвертого столбца.
-
6
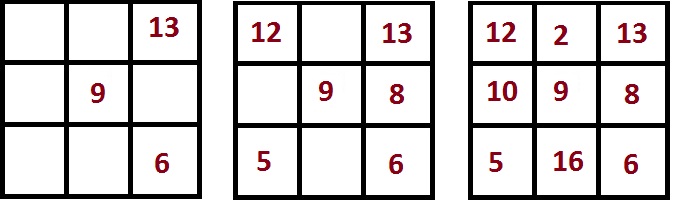
Оставшиеся ячейки квадрата заполняются аналогичным образом (слева направо), но числа нужно записывать в порядке убывания и только в ячейки, расположенные вне выделенных промежуточных квадратов. Например, квадрат 4×4 вы заполните так:
- Напишите 15 и 14 в центре первой строки.
- Напишите 12 во второй строке первого столбца; напишите 9 во второй строке четвертого столбца.
- Напишите 8 в третьей строке первого столбца; напишите 5 в третьей строке четвертого столбца.
- Напишите 3 и 2 в центре четвертой строки.
- Теперь сумма чисел в любой строке, столбце и по диагонали должна быть равна магической константе.
Реклама
Советы
- Воспользуйтесь описанными методами и найдите свой способ решения магических квадратов.
Реклама
Что вам понадобится
- Карандаш
- Бумага
- Ластик
Похожие статьи
Об этой статье
Эту страницу просматривали 352 055 раз.
Была ли эта статья полезной?
Download Article
What makes magic squares special and how to fill them in
Download Article
- What is a magic square?
- Solving a 3 x 3
- Solving a 4 x 4
- Singly Even Magic Square
- Video
- Q&A
|
|
|
|
|
If you’re a fan of math and logic puzzles like Sudoku or Kenken, then trying to solve a magic square is the perfect little challenge to try out. A magic square is a grid of numbers where each row, column, and diagonal add up to the same sum. How you solve your magic square depends on the size of the puzzle, but they each have easy instructions for filling them in. Keep reading and we’ll walk through our solving strategies step by step to finish any odd- or even-numbered magic square.
Things You Should Know
- A magic square is a square grid of numbers where each row, column, and diagonal add up to the same total.
- Find the “magic constant” sum of each row, column, and diagonal with
where n is the number of squares in each row.
- Use a solving technique based on the size of the magic square and how many boxes are in each row or column.
-
Magic squares have rows, columns, and diagonals that total the same sum. Each number in a magic square fits into a cell on a grid. The number of rows or columns determines the order, so an “order 3” magic square is one with a 3 x 3 grid. When you add up the numbers in a column, the value is called the “magic constant,” and all the other columns, rows, and diagonals will add up to that number.[1]
- A normal magic square has consecutive numbers from 1 to
(where n equals the order). A normal order 3 magic square with a magic constant of 15 would be:
8 – 1 – 6
3 – 5 – 7
4 – 9 – 2 - On a non-normal magic square, the lowest number may be higher than 1. A non-normal order 4 magic square with a magic constant of 87 could be:
21 – 24 – 28 – 14
27 – 15 – 20 – 25
16 – 30 – 22 – 19
23 – 18 – 17 – 29
- A normal magic square has consecutive numbers from 1 to
Advertisement
-
1
Calculate the magic constant. To find the magic constant (S) for a normal magic square use the formula
where
equals the order, or number of rows, in the magic square. So for a 3×3 magic square, the formula would be:[2]
-
2
Place the number 1 in the center box on the top row. The placement is the same for any normal magic square with an odd number of columns or rows. Find the center square in the top row and write down the number 1 to get started.[3]
- Example: If you have a 3 x 3 magic square, put 1 in the second box in the top row.
- Example: For a 15 x 15 magic square, put the 1 in the eighth box of the row.
-
3
Follow an up-one, right-one pattern to fill in the remaining numbers. Start at the middle box in the top row where you placed the 1. Move up one row and to the right one column and write in the next number sequentially. Whenever a move takes you above the top row (like the first move will), go to the bottom row instead. If you need to move a square to the right but are already in the rightmost column, move to the leftmost column instead. Continue filling in the square following the pattern until it’s complete.[4]
- Example: In a normal 3 x 3 square, the 2 goes in the bottom right corner and the 3 goes in the left column in the center row.
- If the movement takes you to a box that is already occupied, go back to the last box that has been filled in, and place the next number directly below it. For example, when you place the 4 in a 3 x 3 magic square, it fits in the bottom left corner below the 3. Then, following the same up-one, right-one pattern, place the 5 in the center of the puzzle to continue.
Advertisement
-
1
Recognize a doubly even square if the sides are divisible by 4. Count the number of squares in a single row or column of your magic square. If the magic square is an order 4 square or the number is evenly divisible by 4 (8, 12, 16, etc.), then you’re working with a doubly even square.[5]
-
2
Calculate the magic constant. Use the formula
, where
equals the order, or the number of boxes per row in your magic square. So, for a 4 x 4 square, the magic constant calculation becomes:[6]
-
3
Create Highlights A–D in the corners of the magic square. Form a mini square in each corner that has a length of
on each side, where
is the magic square’s order. Start in the top left corner and label the mini squares A, B, C, and D going clockwise around the magic square.[7]
- In a 4 x 4 square, only mark the 4 corner boxes as your highlights.
- For an 8 x 8 magic square, the Highlights become 2 x 2 mini squares in the corners.
- In a 12 x 12 square, each Highlight is a 3 x 3 area.
-
4
Create the Central Highlight. Mark all the boxes in the center of the magic square in a square area of length
, where
is the magic square’s order. The Central highlight will touch a 1 corner each from Highlights A–D, but it shouldn’t overlap them at all.[8]
- In a 4 x 4 square, the Central Highlight would be a 2 x 2 area in the center.
- In an 8 x 8 square, the Central Highlight would be a 4 x 4 area in the center.
-
5
Fill in the highlighted areas of your magic square. Start in the top left corner of your magic square. Place 1 in the top left corner and count the boxes across the top row. If a box is highlighted, fill it in with the number. Work down the entire magic square until all the highlighted areas are filled in. In an order 4 magic square, the boxes and their numbers are:[9]
- 1 in the top-left box and 4 in the top-right box
- 6 and 7 in the second and third boxes in Row 2
- 10 and 11 in the second and third boxes of Row 3
- 13 in the bottom-left box and 16 in the bottom-right box
-
6
Fill in the rest of the magic square by counting backward. Begin again with the top left box, but skip over all the boxes that you already filled in. Count down from the highest number in the magic square as you work across the row, and add the number to any empty box. Once you finish, your magic square is complete. In a 4×4 magic square, the boxes you fill in are:[10]
- 15 and 14 in the second and third boxes in Row 1
- 12 in the leftmost box and 9 in the rightmost box in Row 2
- 8 in the leftmost box and 5 in the rightmost box in Row 3
- 3 and 2 in the second and third boxes in Row 4
Advertisement
-
1
Check if the square’s sides are divisible by 2, but not 4. Singly even magic squares have an even number of boxes in their rows and columns. If you divide the magic square’s order by 2 and get an odd number as the result, you’re working with a singly even square.[11]
- The smallest possible singly even magic square is 6 x 6 since 2 x 2 magic squares are impossible to make.
-
2
Calculate the magic constant. Use the formula
, where n equals the magic square’s order, or the number of boxes per side. For a 6 x 6 square, your formula would look like:[12]
-
3
Divide the magic square into four quadrants of equal size. Divide the magic square’s order by 2 to find out how many boxes each side of the quadrant should be. Draw lines to separate the quadrants and label them A (top left), C (top right), D (bottom left), and B (bottom right).[13]
- For a 6 x 6 square, each quadrant is 3 x 3 boxes.
-
4
Assign each quadrant a number range. Count the number of boxes in a single quadrant to know how many numbers are in each section. Assign Quadrant A the first quarter of numbers, Quadrant B the second quarter, Quadrant C the third quarter, and Quadrant D the final quarter. That way, you know which numbers are going into specific quadrants without accidentally reusing them.[14]
- In a 6 x 6 square, Quadrant A contains the numbers 1-9, Quadrant B has 10-18, Quadrant C has 19-27, and Quadrant D ends with 28-36.
-
5
Solve each quadrant using a one-up, one-right pattern. In each quadrant, put the lowest value in the center box in the top row. Move up one row and to the right one column to place your next number. If you go above the top row of the quadrant, then move to the bottom row instead. When you go past the rightmost column, add the number to the leftmost column. If there’s already a number in the next square, put the next number directly below the last one.[15]
-
6
Create Highlights A and D. In Quadrant A, mark all the squares in the top row to the left of the quadrant’s center square. In the second row, skip the first column and highlight the center square and remaining boxes to the left of it. Then, mark the squares in the bottom row that share a column with the boxes in the top row to finish the A highlights. Then, repeat the same process in Quadrant D for the D highlights.[16]
- In a 6 x 6 square, Highlight A-1 is the top right box, Highlight A-2 is the center box in the middle row, and Highlight A-3 is the bottom right corner of Quadrant A. The D highlights are in the same position in Quadrant D.
- If you tried to add up your columns, rows, and diagonals right now, the square isn’t considered magic since they don’t add up to the same magic constant yet.
-
7
Swap the positions of Highlights A and D. Simply take the number from one square and swap it with the corresponding box between Quadrant A and Quadrant D. Once you’ve done this, all the rows, columns, and diagonals in a 6 x 6 magic square will add up to the magic constant you calculated.[17]
- Example: In a 6 x 6 magic square, 8 swaps positions with 35, 5 swaps with 32, and 4 swaps with 31.
-
8
Swap the right columns in B and C for magic squares larger than 6 x 6. Count the highlighted columns in the top row of Quadrant A and subtract 1. Count that number of columns in from the right side of Quadrants B and C and highlight all the squares. Move the values in Quadrant C into the corresponding squares in Quadrant B, and vice-versa to complete your magic square.[18]
- For a 10 x 10 magic square, only swap the rightmost column in quadrants B and C.
- For a 14 x 14 magic square, swap the 2 rightmost columns instead.
Advertisement
Add New Question
-
Question
How do you solve a 7×7 magic square?
This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.
wikiHow Staff Editor
Staff Answer
Place the first number of the magic square in the center box of the top row. Then, use an up-one, right-one pattern to add the numbers.
-
Question
How do I solve a magic square with no known sum?
This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.
wikiHow Staff Editor
Staff Answer
Magic squares with numbers that start at 1 and are in consecutive order always have the same sum. A 3 x 3 magic square always has the sum of 15 and a 4 x 4 has a sum of 34.
-
Question
How do you make a 4 x 4 magic square using only 0-9 digits?
This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.
wikiHow Staff Editor
Staff Answer
Typically, you can’t repeat digits in a magic square so making a 4 x 4 with the digits 0-9 isn’t possible unless you repeat them.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
Thanks for submitting a tip for review!
References
About This Article
Article SummaryX
To solve an odd-numbered magic square, start by using the formula n[(n^2+1)/2] to calculate the magic constant, or the number that all rows, columns, and diagonals must add up to. For example, in a 3 by 3 square where n=3, the magic constant is 15. Next, start your square by placing the number 1 in the center box of the top row. Then, arrange the rest of the numbers sequentially by moving up 1 row, then 1 column to the right. To learn more, including how to solve singly even magic squares and doubly even magic squares, read on.
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,003,587 times.
Did this article help you?
Магический квадрат
Магический, или волшебный квадрат — это квадратная таблица, заполненная числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова. Минимальный размер магического квадрата – 3×3. Задачи на магический квадрат часто встречаются на математических олимпиадах для 4 -6 классов.
Магическая константа M – сумма чисел в каждой строке, столбце и на диагоналях.
Для квадрата любой размерности n∙n минимальная магическая константа вычисляется по следующей формуле:
M = n(n2 + 1)/2
I. Магический квадрат 3×3
Для квадрата размера 3×3 минимально возможная магическая константа будет равна:
3(32 + 1)/2 = 3(9 + 1)/2 = 15
Подчеркнём, что 15 – это не единственно возможная магическая константа для квадрата 3×3, а константа, меньше которой других констант для этого квадрата быть не может.
Важное правило, которое вам пригодится при построении магического квадрата 3×3:
Число в центре квадрата 3×3 всегда в три раза меньше магической константы.
То есть, если у нас магическая константа M = 15, то в центре квадрата 3×3 будет стоять
15:3 = 5.
Для дальнейшего составления магического квадрата с магической константой M=15 расставьте по углам чётные числа 2,4,8,6.
Как видим, по сумма чисел на диагоналях квадрата равна 15, то есть магической константе.
Зная магическую константу и по два числа в ряду и столбце, мы можем вписать третье число в ряд и столбец. Определить это число очень просто – надо из магической константы вычесть два числа из ряда или столбца.
Применив этот метод, мы получим полностью заполненный магический квадрат:
Ещё одно важное правило построения магических квадратов:
Если у нас есть один магический квадрат, и мы все числа этого квадрата увеличим на одно и то же число или умножим на одно и то же число, то у нас опять получится квадрат. Это правило достаточно очевидно.
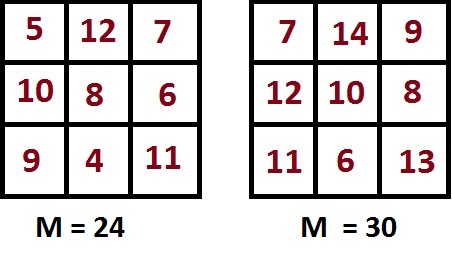
Пример 1. К числам в нашем магическом квадрате с M=15 прибавим 3 и 5
Как видим, у первого квадрата сумма чисел по вертикали, горизонтали и диагонали одинакова и составляет 24 (это и есть его магическая константа), а у второго квадрата магическая константа равна 30.
У этих двух квадратов число в центре по прежнему в три раза меньше, чем магическая константа (8 у первого квадрата и 10 у второго).
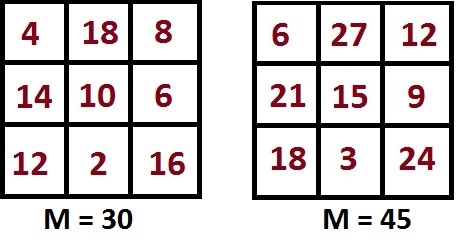
Пример 2. Числа нашего магического квадрата с M=15 умножим на 2 и на 3
Как видим, в первом случае, после умножения чисел на два, мы получили квадрат с магической константой 30 – та же самая константа, что и после того, как в первом примере мы увеличили все числа на 5. Но при этом, несмотря на то, что у этих двух магических квадратах одинаковые магические константы, числа при этом в клетках разные – а вот число в центральном квадрате одно и то же – это 10.
Так и должно быть, ведь, как было сказано выше, в магическом квадрате 3×3 число в центральной клетке должно быть в три раза меньше магической константы. Т.к. магическая константа у обеих магических квадратов одинаковая, то и центральное число одно и то же.
Задача 1.
Постройте магический квадрат с магической константой 39.
Зная магическую константу, мы легко найдём число, которое должно быть в центральной клетке – нужно магическую константу разделить на 3. 39:3 = 13.
Далее можно или подбирать числа (помня о том, что сумма чисел по диагонали, по горизонтали и по вертикали должна быть равна магической константе) или, для ускорения процесса, воспользоваться знанием чисел магического квадрата с минимальной магической константой M = 15.
Напомним этот квадрат:
В центре этого квадрата – число 5. В центре того квадрата, который мы должны построить – число 13.
Разница между этими числами составляет 8. И, как следует из правила, которое мы написали выше, если все числа одного магического квадрата увеличить на одно и то же число, то получится другой магический квадрат.
Достаточно запомнить, что в центре минимального магического квадрата – 5, а по углам – чётные числа 2, 4, 6, 8. Таким образом, нам надо увеличить эти числа на 8. Далее будет легко заполнить оставшиеся клетки (числа в них вычисляются как магическая константа минус числа в ряду или столбце).
В итоге получится вот такой квадрат:
Задача 2.
Достройте магический квадрат
В этом квадрате мы знаем число в центральной клетке (9), а, значит, мы знаем магическую константу, которая в 3 раза больше и равна 27. Ну а зная магическую константу и три первоначальных числа, вписать оставшиеся числа в клетки не составит труда.
Решение:
II. Магический квадрат 4×4
Мы не будем подробно останавливаться на магических квадратах 4×4 – они почти не встречаются на математических олимпиадах и вступительных экзаменах в физматшколы, но общее представление о них дадим.
Минимально возможная магическая константа вычисляется всё по той же формуле:
M = n(n2 + 1)/2
M = 4(42 + 1)/2 = 34.
У квадрата 4×4 обе стороны чётные, а это значит, что центральной клетки, в отличие от квадрата 3×3, у него нет, и нет соответствующей закономерности, с ним связанной.
Однако, у этого квадрата есть другие закономерности:
Помимо того, что у магического квадрата 4×4 равна сумма числе по диагонали, вертикали и горизонтали, у него сумма чисел в угловых квадратах 2×2 равна магической константе M, сумма чисел в центральном квадрате 2×2 также равна M, и сумма чисел в углах квадрата тоже равна M.
Сумма чисел в левом верхнем квадрате 2×2: 16+3+5+10 = 34. В трёх других угловых квадратах 2×2 сумма также равна магической константе, о чём и сказано выше.
Сумма чисел в центральном квадрате 2×2 также равна магической константе 34: 10+11+6+7 = 34.
Сумма чисел в углах магического квадрата тоже равна магической константе: 16+13+4+1 = 34





















![{displaystyle S=n[(n^{2}+1)/2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6645cd02ee35be03b0fc03e0e9c3dd8b3295d96)






![{displaystyle S=[n(n^{2}+1)]/2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d5a367b0a5dbe975df34131a0b5bd57332d05d5)