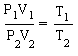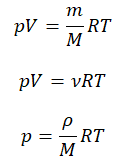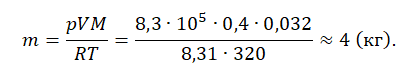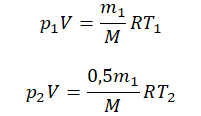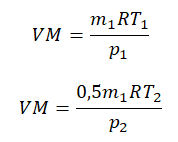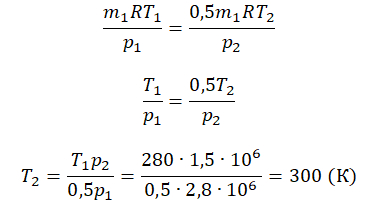Как подсчитать количество молей
Моль – это такое количество вещества, в котором находится 6,022*10^23 элементарных частиц (молекул, атомов, или ионов). Упомянутая величина носит название «число Авогадро» – по имени известного итальянского ученого. Масса моля любого вещества, выраженная в граммах, численно равна массе его молекулы в атомных единицах. Как можно подсчитать количество молей вещества?

Инструкция
Например, поставлена задача: определить, сколько молей содержится в 150 граммах натриевой селитры (то есть натрия азотнокислого). Прежде всего, напишите формулу этого вещества – NaNO3.
Определите его молекулярную массу, зная атомные массы элементов и с учетом индекса 3 у кислорода. Получится: 14+23+48=85 а.е.м. (атомных единиц массы). Следовательно, один моль азотнокислого натрия составит 85 грамм. А у вас 150 грамм вещества. Таким образом, находите: 150/85=1,765 моля. Задача решена.
А если, например, заданы такие условия: имеется 180 литров кислорода при комнатной температуре и атмосферном давлении. Сколько это будет молей? И тут нет ничего трудного. Надо лишь помнить, что 1 моль любого газа при нормальных условиях занимает объем, примерно равный 22,4 литра. Разделив 180 на 22,4, получите искомую величину: 180/22,4=8,036 моля.
Предположим, температура существенно превышала комнатную, а давление намного превосходило атмосферное. При этом вам известна масса кислорода, и объем сосуда, в который он был заключен. Как найти количество молей газа в таком случае?
Вот тут вам на помощь придет универсальное уравнение Менделеева-Клапейрона. Правда, оно выведено для описания состояний идеального газа, которым кислород, конечно же, не является. Но его можно использовать в расчетах: погрешность будет весьма незначительной. PVm = MRT, где Р – давление газа в паскалях, V – его объем в кубических метрах, m – молярная масса, M – масса в граммах, R – универсальная газовая постоянная, T – температура в градусах Кельвина.
Легко можно видеть, что M/m = PV/RT. А величина M/m как раз и является количеством молей газа при данных условиях. Подставив известные величины в формулу, вы получите ответ.
А если вы имеете дело со сплавом? Как тогда вычислить количество молей каждого компонента в образце? Для решения такой задачи, надо знать массу образца и точный состав сплава. Например: широко распространенный мельхиор – сплав меди с никелем. Предположим, у вас есть мельхиоровое изделие весом 1500 грамм, содержащее 55% меди и 45% никеля. Решение: 1500*0,55=825 грамм меди. То есть, 825/63,5=13 молей меди. Соответственно, 1500–825=675 грамм никеля. 675/58,7 = 11,5 молей никеля. Задача решена
Источники:
- как вычислить моль
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Газы
нередко бывают реагентами и продуктами
в химических реакциях. Не всегда удается
заставить их реагировать между собой
при нормальных условиях. Поэтому нужно
научиться определять число молей газов
в условиях, отличных от нормальных.
Для
этого используют уравнение
состояния идеального газа (его
также называют уравнением
Клапейрона-Менделеева):
PV
= nRT
где n –
число молей газа;
P
– давление газа (например, в атм;
V
– объем газа (в литрах);
T
– температура газа (в кельвинах);
R
– газовая постоянная (0,0821 л·атм/моль·K).
Например,
в колбе объемом 2,6 л находится кислород
при давлении 2,3 атм и
температуре 26 оС.
Вопрос: сколько молей O2 содержится
в колбе?
Из
газового закона найдем искомое число
молей n:
Не
следует забывать преобразовывать
температуру из градусов Цельсия в
кельвины: (273 оС
+ 26 оС)
= 299 K. Вообще говоря, чтобы не ошибиться
в подобных вычислениях, нужно внимательно
следить за размерностью величин,
подставляемых в уравнение
Клапейрона-Менделеева. Если давление
дается в мм ртутного столба, то нужно
перевести его в атмосферы, исходя из
соотношения: 1 атм =
760 мм рт. ст. Давление, заданное в паскалях
(Па), также можно перевести в атмосферы,
исходя из того, что 101325 Па = 1 атм.
**
Можно проводить вычисления и в системе
СИ, где объем измеряется в м3,
а давление – в Па. Тогда используется
значение газовой постоянной для системы
СИ: R = 8,314 Дж/K·моль. В этом параграфе мы
будем использовать объем в литрах и
давление в атм.
Решим
такую задачу: некоторое количество газа
гелия при 78 оС
и давлении 45,6 атм занимает объем 16,5 л.
Каков объем этого газа при нормальных
условиях? Сколько это молей гелия? Можно,
конечно, просто подставить данные нам
значения в уравнение Клапейрона-Менделеева
и сразу вычислить число молей n.
Но что делать, если на экзамене вы забыли
точное значение газовой постоянной R?
Газовую
постоянную не нужно запоминать – ее
можно легко вычислить в любой момент.
Действительно, 1 моль газа при нормальных
условиях (1 атм и 273 К) занимает объем
22,4 л. Тогда:
Другой
способ заключается в том, чтобы заставить
газовую постоянную R сократиться. Снова
вспомним, что нормальные условия – это
давление 1 атм и температура 0 оС
(273 K). Запишем все, что нам известно про
исходные (в задаче) и конечные (при н.у.)
значения P, V и T для нашего газа:
Исходные
значения: P1 =
45,6 атм, V1 =
16,5 л, T1 =
351 K;
Конечные
значения: P2 =
1 атм, V2 =
? T2 =
273 K.
Очевидно,
что уравнение Клапейрона-Менделеева
одинаково справедливо как для начального
состояния газа, так и для конечного:
P1V1 = nRT1
P2V2 = nRT2
Если
теперь почленно разделить верхнее
уравнение на нижнее, то при неизменном
числе молей n мы
получаем:
После
подстановки всех известных нам значений
получим объем газа при н.у.
V2 =
45,6·16,5·273 / 351 = 585 л
Итак,
объем гелия при н.у. составит 585 л. Поделив
это число на молярный объем газа при
н.у. (22,4 л/моль) найдем число молей гелия:
585/22,4 = 26,1 моль.
Некоторых
из вас, возможно, интересует вопрос,
каким образом удалось определить
постоянную Авогадро NA =
6,02·1023 ?
Действительно, ранее мы получили близкое
значение 6·1023 исходя
из массы протона и нейтрона 1,67·1024 г.
Но в 1811 году, когда Амедео Авогадро
высказал свою гипотезу, ничего не было
известно не только о массе протона или
нейтрона, но и о самом существовании
этих частиц!
Значение
числа Авогадро было экспериментально
установлено только в конце XIX – начале
XX века. Опишем один из таких экспериментов.
В
откачанный до глубокого вакуума сосуд
объемом V = 30 мл поместили навеску элемента
радия массой 0,5 г и выдержали там в
течение одного года. Было известно, что
за секунду 1 г радия испускает
3,7·1010 альфа-частиц.
Эти частицы представляют собой ядра
гелия, которые тут же принимают электроны
из стенок сосуда и превращаются в атомы
гелия. За год давление в сосуде выросло
до 7,95·10-4 атм
(при температуре 27 оС).
Изменением массы радия за год можно
пренебречь. Итак, чему равна NA?
Сначала
найдем, сколько альфа-частиц (то есть
атомов гелия) образовалось за один год.
Обозначим это число как N атомов:
N
= 3,7·1010 ·
0,5 г · 60 сек · 60 мин · 24 час · 365 дней =
5,83·1017 атомов.
Запишем
уравнение Клапейрона-Менделеева PV = nRT
и заметим, что число молей гелия n =
N/NA.
Отсюда:
В
начале XX века этот способ определения
постоянной Авогадро был самым точным.
Но почему так долго (в течение года)
длился эксперимент? Дело в том, что радий
добывается очень трудно. При его малом
количестве (0,5 г) радиоактивный распад
этого элемента дает очень мало гелия.
А чем меньше газа в замкнутом сосуде,
тем меньшее он создаст давление и тем
большей будет ошибка измерения. Понятно,
что ощутимое количество гелия может
образоваться из радия только за достаточно
долгое время.
О
других подходах к экспериментальному
определению постоянной Авогадро можно
прочитать в задаче к этому параграфу.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Молярный объем газа

4.3
Средняя оценка: 4.3
Всего получено оценок: 502.
4.3
Средняя оценка: 4.3
Всего получено оценок: 502.
Для того, чтобы узнать состав любых газообразных веществ необходимо уметь оперировать такими понятиями, как молярный объем, молярная масса и плотность вещества. В данной статье рассмотрим, что такое молярный объем, и как его вычислить?
Количество вещества
Количественные расчеты проводят с целью, чтобы в реальности осуществить тот или иной процесс или узнать состав и строение определенного вещества. Эти расчеты неудобно производить с абсолютными значениями массы атомов или молекул из-за того, что они очень малы. Относительные атомные массы также в большинстве случаев невозможно использовать, так как они не связаны с общепринятыми мерами массы или объема вещества. Поэтому введено понятие количество вещества, которое обозначается греческой буквой v (ню) или n. Количество вещества пропорционально числу содержащихся в веществе структурных единиц (молекул, атомных частиц).
Единицей количества вещества является моль.
моль – это такое количество вещества, которое содержит столько же структурных единиц, сколько атомов содержится в 12 г изотопа углерода.
Масса 1 атома равна 12 а. е. м., поэтому число атомов в 12 г изотопа углерода равно:
Na= 12г/12*1,66057*10в степени-24г=6,0221*10 в степени 23
Физическая величина Na называется постоянной Авогадро. Один моль любого вещества содержит 6,02*10 в степени 23 частиц.
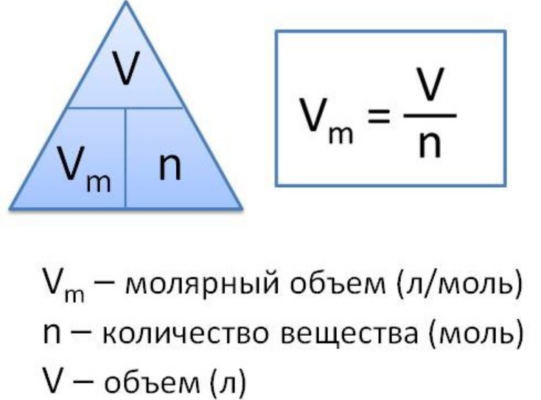
Молярный объем газа
Молярный объем газа – это отношение объема вещества к количеству этого вещества. Эту величину вычисляют при делении молярной массы вещества на его плотность по следующей формуле:
Vm=M/p,
где Vm – молярный объем, М – молярная масса, а p – плотность вещества.
В международной системе Си измерение молярного объема газообразных веществ осуществляется в кубических метрах на моль (м3 /моль)
Молярный объем газообразных веществ отличается от веществ, находящихся в жидком и твердом состоянии тем, что газообразный элемент количеством 1 моль всегда занимает одинаковый объем (если соблюдены одинаковые параметры).
Объем газа зависит от температуры и давления, поэтому при расчетах следует брать объем газа при нормальных условиях. Нормальными условиями считается температура 0 градусов и давление 101,325 кПа. Молярный объем 1 моля газа при нормальных условиях всегда одинаков и равен 22,41 дм3 /моль. Этот объем называется молярным объемом идеального газа. То есть, в 1 моле любого газа (кислород, водород, воздух) объем равен 22,41 дм3 /м.
Таблица «молярный объем газов»
В следующей таблице представлен объем некоторых газов:
| Газ | Молярный объем, л |
| H2 | 22,432 |
| O2 | 22,391 |
| Cl2 | 22,022 |
| CO2 | 22,263 |
| NH3 | 22,065 |
| SO2 | 21,888 |
| Идеальный | 22,41383 |
Что мы узнали?
Молярный объем газа, изучаемый по химии (8 класс) наряду с молярной массой и плотностью являются необходимыми величинами для определения состава того или иного химического вещества. Особенностью молярного газа является то, что в одном моле газа всегда содержится одинаковый объем. Этот объем называется молярным объемом газа.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-
Аэлита Коробка
5/5
-
Александр Котков
5/5
-
Настя Бабич
5/5
-
Александр Котков
5/5
Оценка доклада
4.3
Средняя оценка: 4.3
Всего получено оценок: 502.
А какая ваша оценка?
Моля́рный объём Vm — отношение объёма вещества к его количеству, численно равен объёму одного моля вещества. Термин «молярный объём» может быть применён к простым веществам, химическим соединениям и смесям. В общем случае он зависит от температуры, давления и агрегатного состояния вещества. Молярный объём также можно получить делением молярной массы M вещества на его плотность ρ: таким образом, Vm = V/n = M/ρ. Молярный объём характеризует плотность упаковки молекул в данном веществе. Для простых веществ иногда используется термин атомный объём[1].
В Международной системе единиц (СИ) единицей измерения молярного объёма является кубический метр на моль (русское обозначение: м3/моль; международное: m3/mol).
Молярный объём смеси[править | править код]
Для смеси веществ, при расчёте молярного объёма, количеством вещества считают сумму количеств всех веществ, составляющих смесь. Если известна плотность смеси ρc, мольные доли компонентов xi и их молярные массы Mi, молярный объём смеси можно найти как отношение средней молярной массы смеси (суммы молярных масс её компонентов, умноженных на их мольные доли) к плотности смеси.
Молярный объём газов[править | править код]
Согласно закону Авогадро, одинаковые количества газов при одинаковых условиях занимают одинаковый объём. Молярный объём идеального газа рассчитывается по формуле, выводящейся из уравнения состояния идеального газа
,
где T — термодинамическая температура, P — давление, R = 8,314 462 618 153 24 (точно) м3⋅Па⋅К−1⋅моль−1 — универсальная газовая постоянная.
При стандартных условиях (T = 273,15 K (0 °C), P = 101 325 Па) молярный объём идеального газа Vm = 22,413 969 545… л/моль[2][3]. Молярные объёмы идеального газа при других давлениях и температурах, часто принимаемых в качестве стандартных:
- Vm = 24,465 403 697… л/моль (T = 298,15 K (25 °C), P = 101 325 Па),
- Vm = 22,710 954 641… л/моль (T = 273,15 K (0 °C), P = 100 000 Па)[4],
- Vm = 24,789 570 296… л/моль (T = 298,15 K (25 °C), P = 100 000 Па).
| Газ | Vm, л/моль | Газ | Vm, л/моль |
|---|---|---|---|
| He | 22,426 | CO | 22,408 |
| Ne | 22,428 | CO2 | 22,262 |
| Ar | 22,394 | N2O | 22,260 |
| Kr | 22,388 | SO2 | 21,889 |
| Xe | 22,266 | CH4 | 22,376 |
| H2 | 22,430 | C2H6 | 22,176 |
| O2 | 22,393 | C2H4 | 22,255 |
| N2 | 22,404 | C2H2 | 22,157 |
Молярные объёмы реальных газов в той или иной степени отличаются от молярного объёма идеального газа, однако во многих случаях для практических вычислений отклонениями от идеальности можно пренебречь. Различие молярных объёмов идеального и реального газа связано в первую очередь с силами притяжения между молекулами и с конечным объёмом молекулы реального газа; в связи с этим, уравнение состояния реального газа с большей точностью описывается не формулой Менделеева — Клапейрона (уравнением состояния идеального газа), а формулой Ван-дер-Ваальса:
В таблице справа приведены молярные объёмы некоторых реальных газов (T = 273,15 K (0 °C), P = 101 325 Па)[5]. Видно, что для газов с относительно большими молекулами (двуокись серы, углеводороды) молярный объём несколько меньше молярного объёма идеального газа (22,414 л/моль в указанных условиях); для газов с маленькими молекулами (гелий, неон, водород) молярный объём несколько больше «идеального».
С молярным объёмом идеального газа связана постоянная Лошмидта NL — количество молекул идеального газа в единице объёма при стандартных условиях:
Молярный объём кристаллов[править | править код]
Объём Vя элементарной ячейки кристалла можно вычислить из параметров кристаллической структуры, которые определяются с помощью рентгеноструктурного анализа. Объём ячейки связан с молярным объёмом следующим образом:
- Vm = VяNA/Z,
где Z — количество формульных единиц в элементарной ячейке.
Значения молярного объёма химических элементов[править | править код]
Ниже приведены значения молярного (атомного) объёма простых веществ в см3/моль (10−6 м3/моль, 10−3 л/моль) при нормальных условиях либо (для элементов, газообразных при н.у.) при температуре конденсации и нормальном давлении.
| Группа | I A (1) | II A (2) | III B (3) | IV B (4) | V B (5) | VI B (6) | VII B (7) | VIII B (8) | VIII B (9) | VIII B (10) | I B (11) | II B (12) | III A (13) | IV A (14) | V A (15) | VI A (16) | VII A (17) | VIII A (18) |
| Период | ||||||||||||||||||
| 1 | H 14,0 |
He 31,8 |
||||||||||||||||
| 2 | Li 13,1 |
Be 5 |
B 4,6 |
C 5,3 |
N 17,3 |
O 14 |
F 17,1 |
Ne 16,8 |
||||||||||
| 3 | Na 23,7 |
Mg 14 |
Al 10 |
Si 12,1 |
P 17 |
S 15,5 |
Cl 18,7 |
Ar 24,2 |
||||||||||
| 4 | K 45,3 |
Ca 29,9 |
Sc 15 |
Ti 10,6 |
V 8,35 |
Cr 7,23 |
Mn 7,39 |
Fe 7,1 |
Co 6,7 |
Ni 6,6 |
Cu 7,1 |
Zn 9,2 |
Ga 11,8 |
Ge 13,6 |
As 13,1 |
Se 16,5 |
Br 23,5 |
Kr 32,2 |
| 5 | Rb 55,9 |
Sr 33,7 |
Y 19,8 |
Zr 14,1 |
Nb 10,8 |
Mo 9,4 |
Tc 8,5 |
Ru 8,3 |
Rh 8,3 |
Pd 8,9 |
Ag 10,3 |
Cd 13,1 |
In 15,7 |
Sn 16,3 |
Sb 18,4 |
Te 20,5 |
I 25,7 |
Xe 42,9 |
| 6 | Cs 70 |
Ba 39 |
* | Hf 13,6 |
Ta 10,9 |
W 9,53 |
Re 8,85 |
Os 8,43 |
Ir 8,54 |
Pt 9,1 |
Au 10,2 |
Hg 14,8 |
Tl 17,2 |
Pb 18,3 |
Bi 21,3 |
Po 22,7 |
At н/д |
Rn н/д |
| 7 | Fr н/д |
Ra 45 |
** | Rf н/д |
Db н/д |
Sg н/д |
Bh н/д |
Hs н/д |
Mt н/д |
Ds н/д |
Rg н/д |
Cn н/д |
Nh н/д |
Fl н/д |
Mc н/д |
Lv н/д |
Ts н/д |
Og н/д |
| Лантаноиды | * | La 22,5 |
Ce 21 |
Pr 20,8 |
Nd 20,6 |
Pm 19,96 |
Sm 19,9 |
Eu 28,9 |
Gd 19,9 |
Tb 19,2 |
Dy 19 |
Ho 18,7 |
Er 18,4 |
Tm 18,1 |
Yb 24,8 |
Lu 17,8 |
||
| Актиноиды | ** | Ac 22,54 |
Th 19,8 |
Pa 15 |
U 12,5 |
Np 21,1 |
Pu 12,12 |
Am 20,8 |
Cm 18,28 |
Bk 16,8 |
Cf 16,5 |
Es н/д |
Fm н/д |
Md н/д |
No н/д |
Lr н/д |
||
См. также[править | править код]
- Число Авогадро
- Удельный объём
- Молярная масса
- Молярная теплоёмкость
Примечания[править | править код]
- ↑ Для молекулярных кристаллов простых веществ молярный объём, определяемый через 1 моль молекул, не равен атомному объёму, поскольку количество атомов не равно количеству молекул. В этих случаях необходимо уточнять, относится ли указанная величина к молекулярному или к атомному молярному объёму. Так, атомный молярный объём иода (кристаллы, состоящие из двухатомных молекул I2) вдвое меньше молекулярного молярного объёма.
- ↑ CODATA Value: molar volume of ideal gas (273.15 K, 101.325 kPa). Дата обращения: 17 ноября 2022.
- ↑ После изменения определений основных единиц СИ в 2019 году универсальная газовая константа стала не измеряемой, а определяемой (точно фиксированной) величиной, будучи произведением точно фиксированных величин — постоянной Больцмана и постоянной Авогадро. Это же относится и к стандартному молярному объёму.
- ↑ CODATA Value: molar volume of ideal gas (273.15 K, 100 kPa). Дата обращения: 17 ноября 2022.
- ↑ 1 2 Battino R. The Ostwald coefficient of gas solubility (англ.) // Fluid Phase Equilibria. — 1984. — Vol. 15, no. 3. — P. 231—240. — ISSN 0378-3812. — doi:10.1016/0378-3812(84)87009-0. [исправить]; Table 2.
Уравнение состояния идеального газа
теория по физике 🧲 молекулярная физика, МКТ, газовые законы
Уравнение состояния идеального газа было открыто экспериментально. Оно носит название уравнения Клапейрона — Менделеева. Это уравнение устанавливает математическую зависимость между параметрами идеального газа, находящегося в одном состоянии. Математически его можно записать следующими способами:
Уравнение состояния идеального газа
Внимание! При решении задач важно все единицы измерения переводить в СИ.
Пример №1. Кислород находится в сосуде вместимостью 0,4 м 3 под давлением 8,3∙10 5 Па и при температуре 320 К. Чему равна масса кислорода? Молярная масса кислорода равна 0,032 кг/моль.
Из основного уравнения состояния идеального газа выразим массу:
Уравнение состояния идеального газа следует использовать, если газ переходит из одного состояния в другое и при этом изменяется его масса (количество вещества, число молекул) или молярная масса. В этом случае необходимо составить уравнение Клапейрона — Менделеева отдельно для каждого состояния. Решая систему уравнений, легко найти недостающий параметр.
Подсказки к задачам
Важна только та масса, что осталась в сосуде. Поэтому:
| Давление возросло на 15% | p2 = 1,15p1 |
| Объем увеличился на 2% | V2 = 1,02V1 |
| Масса увеличилась в 3 раза | m2 = 3m1 |
| Газ нагрелся до 25 о С | T2 = 25 + 273 = 298 (К) |
| Температура уменьшилась на 15 К (15 о С) | T2 = T1 – 15 |
| Температура уменьшилась в 2 раза | 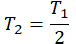 |
| Масса уменьшилась на 20% | m2 = 0,8m1 |
| Выпущено 0,7 начальной массы | |
| Какую массу следует удалить из баллона? | Нужно найти разность начальной и конечной массы: |
| Газ потерял половину молекул | 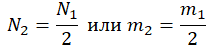 |
| Молекулы двухатомного газа (например, водорода), диссоциируют на атомы | 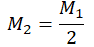 |
| Озон (трехатомный кислород) при нагревании превращается в кислород (двухатомный газ) | M (O3) = 3Ar (O)∙10 –3 кг/моль M (O2) = 2Ar (O)∙10 –3 кг/моль |
| Открытый сосуд | Объем V и атмосферное давление pатм остаются постоянными |
| Закрытый сосуд | Масса m, молярная масса M, количество вещества ν, объем V, число N и концентрация n частиц, плотность ρ— постоянные величины |
| Нормальные условия | Температура T0 = 273 К Давление p0 = 10 5 Па |
| Единицы измерения давления | 1 атм = 10 5 Па |
Пример №2. В баллоне содержится газ под давлением 2,8 МПа при температуре 280 К. Удалив половину молекул, баллон перенесли в помещение с другой температурой. Определите конечную температуру газа, если давление уменьшилось до 1,5 МПа.
2,8 МПа = 2,8∙10 6 Па
1,5 МПа = 1,5∙10 6 Па
Так как половина молекул была выпущена, m2 = 0,5m1. Объем остается постоянным, как и молярная масса. Учитывая это, запишем уравнение состояния идеального газа для начального и конечного случая:
Преобразим уравнения и получим:
Приравняем правые части и выразим искомую величину:

Алгоритм решения
Решение
График построен в координатах (V;Ek). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:
Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.
Запишем уравнение Менделеева — Клапейрона:
Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:
ν R = p 1 V 1 T 1 . . = p 2 V 2 T 2 . .
Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.
Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.
pазбирался: Алиса Никитина | обсудить разбор | оценить
На высоте 200 км давление воздуха составляет примерно 10 –9 от нормального атмосферного давления, а температура воздуха Т – примерно 1200 К. Оцените плотность воздуха на этой высоте.
Уравнение Клапейрона-Менделеева
Что такое уравнение Клапейрона-Менделеева
Идеальный газ — это газ, в котором пренебрегают взаимодействием молекул газа между собой.
Идеальными считают разреженные газы. Особенно близкими к идеальным считают гелий и водород.
Идеальный газ — это упрощенная математическая модель, которая широко применяется для описания свойств и поведения реальных газов при атмосферном давлении и комнатной температуре.
Давление, объем и температура — это основные параметры состояния системы, и они связаны друг с другом. Соотношение, при котором определяется данная связь, называется уравнением состояния данного газа.
Существует эквивалентная макроскопическая формулировка идеального газа — это такой газ, который одновременно будет подчиняться закону Бойля-Мариотта и Гей-Люссака, то есть:
p V = c o n s t * T
В представленном выше уравнении состоянии газа под const подразумевается количество молей.
Свойства классического и квазиклассического идеального газа описываются уравнением состояния идеального газа, которое называется уравнением Менделеева-Клапейрона, ниже представлена формула Менделеева-Клапейрона.
p V = m M R T = n R T , где m — масса газа, M — молярная масса газа, R = 8 , 314 Д ж / ( м о л ь * К ) — универсальная газовая постоянная, T — температура (К), n — количество молей газа.
Таким образом давление и объем прямо пропорциональны количеству молей и температуре.
Также уравнение Клапейрона-Менделеева можно записать в ином виде:
p V = N k T , где N — это количество молекул газа массой m , k = 1 , 38 * 10 — 23 Д ж / К — постоянная Больцмана, которая определяет «долю» газовой постоянной, приходящуюся на одну молекулу и определяется по формуле:
N = m N A M , где
N A = 6 . 02 * 10 23 м о л ь — 1 ; — это постоянная Авогадро.
Какое значение имеет универсальная газовая постоянная
Универсальная газовая постоянная (R) — это величина, которая является константой, численно равная работе расширения одного моля идеального газа в изобарном процессе при увеличении температуры на 1 K.
Значение данной константы находится как произведение постоянной Больцмана ( k = 1 , 38 * 10 — 23 Д ж / К ) на число Авогадро ( N A = 6 . 02 * 10 23 м о л ь — 1 ) . Таким образом универсальная газовая постоянная принимает следующее значение: R = 8 , 314 Д ж / ( м о л ь * К ) .
Постоянную Больцмана используют в формулах, описывающих изучаемое явление или поведение рассматриваемого объекта с микроскопической точки зрения, тогда как универсальная газовая постоянная более удобна при расчетах, касающихся макроскопических систем, когда число частиц задано в молях.
Связь с другими законами состояния идеального газа
С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса и один трех макропараметров (давление, температура или объем) — остаются неизменными.
Количественные зависимости между двумя параметрами газа при фиксированном третьем параметре называют газовыми законами, которые связывают эти параметры.
Изопроцессы — это термодинамические процессы, во время протекания которых количество вещества и один из макропараметров состояния: давление, объем, температура или энтропия — остается неизменным.
В зависимости от того, какой параметр остается неизменным различают разные процессы, которые выражаются законами, являющимися следствием уравнения состояния газа:
- изотермический процесс (T=const);
- изохорный процесс (V=const);
- изобарный процесс (p=const).
Изотермический процесс (T=const)
Процесс изменения состояния термодинамической системы при постоянной температуре называют изотермическим.
Для поддержания температуры газа постоянной необходимо, чтобы он мог обмениваться теплотой с большой системой — термостатом. Им может служить атмосферный воздух, если температура его заметно не меняется на протяжении всего процесса.
Согласно уравнению Клапейрона-Менделеева, в любом состоянии с неизменной температурой произведение давления газа на объем одно и то же, то есть постоянно:
Этот закон был открыт экспериментально английским ученым Бойлем и несколько позднее французским ученым Мариоттом. Именно поэтому он называется закон Бойля-Мариотта.
Закон Бойля-Мариотта справедлив для любых газов, а также для смеси газов (например, для воздуха).
Зависимость давления газа от объема при постоянной температуре изображается графической кривой — изотермой. Изотерма для различных температур представлена в координатах pV на рис.1. и представляет собой гиперболу.
Рис.1. Изотерма в pV — координатах.
Изохорный процесс (V=const)
Процесс изменения состояния термодинамической системы при постоянном объеме называют изохорным.
Из уравнения состояния следует, что отношение давлений газа данной массы при постоянно объеме равно отношению его абсолютных температур:
p 1 p 2 = T 1 T 2
Газовый закон был установлен экспериментально в 1787 г. французским физиком Ж. Шарлем и носит название закона Шарля: давление данной массы газа при постоянном объеме прямо пропорционально абсолютной температуре.
Так, если в качестве одного из состояний газа выбрать состояние газа при нормальных условиях, тогда
p = p 0 T T 0 = p 0 γ T
Коэффициент γ называют температурным коэффициентом давления газа. Он одинаков для всех газов.
Зависимость давления газа от температуры при постоянном объеме изображается графически прямой, которая называется изохорой (Рис.2).
Рис.2 Изображение изохоры в pT-координатах.
Изобарный процесс (p=const)
Процесс изменения состояния термодинамической системы при постоянном давлении называют изобарным.
Из уравнения Клапейрона-Менделеева вытекает, что отношение объемов газа данной массы при постоянном давлении равно отношению его абсолютных температур.
V 1 V 2 = T 1 T 2
Если в качестве второго состояния газа выбрать состояние при нормальных условиях (нормальном атмосферном давлении, температуре таяния льда) следует:
V = V 0 T T 0 = V 0 α T
Этот газовый закон был установлен экспериментально в 1802 г французским ученым Гей-Люссаком.
Закон Гей-Люссака: объем данной массы газа при постоянном давлении прямо пропорционален абсолютной температуре.
Коэффициент α называют температурным коэффициентом объемного расширения газов.
Зависимость объема газа от температуры при постоянном давлении изображается графической прямой, которая называется изобарой (Рис.3).
Рис. 3. Изобара в VT-координатах.
Использование универсального уравнения для решения задачи
В реальности проводятся различные физико-химические процессы. Рассмотрим каким образом уравнение состояния идеального газа и законы, связанные с ним находят применение для решения физических и химических задач.
Определить давление кислорода в баллоне объемом 1 м 3 при температуре t = 27 C o . Масса кислорода 1 кг.
Так как в уравнении даны объем и температура — два из трех макроскопических параметров, а третий (давление) нужно определить, то мы можем использовать уравнение Клапейрона-Менделеева:
p V = n R T = m M R T
Не забываем перевести температуру в Кельвины:
T = t + 273 = 27 + 273 = 300 K
Молярная масса кислорода известна из таблицы Менделеева:
M ( O 2 ) = 2 * 16 = 32 г / м о л ь = 32 * 10 — 3 к г / м о л ь
Выразим из уравнения состояния давления и поставим все имеющиеся данные:
p = n R T V = m R T M V = 1 * 8 . 31 * 300 32 * 10 — 3 * 1 = 77 . 906 П а = 78 к П а
Ответ: p = 78 кПа.
Каким может быть наименьший объем баллона, содержащего кислород массой 6,4 кг, если его стенки при t = 20 C o выдерживают p = 1568 Н / с м 2 ?
Используем уравнение Менделеева-Клапейрона, из которого выражаем объем кислорода, который нужно найти:
p = n R T V = m R T M V
Молярная масса кислорода предполагается равной:
M ( O 2 ) = 2 * 16 = 32 г / м 3
Не забываем перевести температуру в Кельвины:
T = t + 273 = 20 + 273 = 293 K
Переводим давление: p = 15680000 Па
Выражаем из уравнения Клапейрона-Менделеева объем и подставляем значения, данные в условиях задачи:
V = n R T p = m R T M p = 6 . 4 * 8 . 31 * 293 15680000 * 32 * 10 — 3 = 3 . 1 * 10 — 2 м 3 = 31 л .
Используя уравнение состояния идеального газа, доказать, что плотность любого газа равна половине плотности водорода ( ρ Н 2 ) , взятого при тех же условиях, умноженной на относительную молекулярную массу этого газа M_r, то есть ρ = ρ Н 2 * M r 2 .
Согласно уравнению Менделеева-Клапейрона:
p = n R T V = m R T M V
Плотность — это величина, характеризующая массу некоторого объема и находится по формуле:
ρ = m V и л и V = m ρ
Тогда p m ρ = n R T = m R T M
Откуда выражаем плотность газа:
Для водорода эта формула запишется следующим образом:
ρ H 2 = p M H 2 R T
По условию задачи водород и любой другой газ находятся при одинаковых условиях, откуда следует, что:
ρ H 2 M H 2 = p R T
Поставим последнее выражение в выражение для плотности любого газа:
ρ = M * ρ H 2 M H 2
Молярная масса водорода, исходя из таблицы Менделеева равна 2 г/моль и тогда. Молекулярная масса численно равная молярной и представляет собой массу молекулы в атомных единицах, поэтому в дальнейшем мы совершили переход к молекулярной массе.
ρ = M r * ρ H 2 2
Вывод: плотность любого газа равна половине плотности водорода ( ρ Н 2 ) , взятого при тех же условиях, умноженной на относительную молекулярную массу этого газа M_r, то есть ρ = ρ Н 2 * M r 2 .
Рассмотрим несколько задач на законы, связанные с уравнение Клапейрона-Менделеева, то есть на изотермические, изохорные, изобарные процессы.
При уменьшении давления газа в 2,5 раза его объем увеличился на 12 л. Какой объем занимал газ в начальном состоянии, если температура на протяжении всего процесса оставалась постоянной?
По условию задачи температура в ходе всего процесса оставалась постоянной, откуда следует, что у нас изотермический процесс, и мы можем воспользоваться для решения законом Бойля-Мариотта.
p 1 V 1 = p 2 V 2 , г д е p 1 – давление газа в начальном состоянии (до расширения), V 1 — объем газа в начальном состоянии, p 2 = p 1 2 . 5 — давление газа в конечном состоянии (после расширения), V 2 = V 1 + ∆ V — объем газа в конечном состоянии.
Откуда можем найти начальный объем:
p 1 V 1 = p 1 2 . 5 ( V 1 + ∆ V ) = p 1 2 . 5 V 1 + p 1 2 . 5 ∆ V
V 1 ( p 1 — p 1 2 . 5 ) = p 1 2 . 5 ∆ V
p 1 2 . 5 V 1 ( 2 . 5 — 1 ) = p 1 2 . 5 ∆ V
V 1 = ∆ V 1 , 5 = 8 л
Ответ: первоначальный объем газа был равен 8 л.
Газ находится в баллоне при температуре 400 К. До какой температуры нужно нагреть газ, чтобы его давление увеличилось в 1,5 раза?
Так как нагревание газа по условиям данной задачи происходит при постоянном объеме, значит перед нами изохорный процесс.
При изохорном процессе:
p 1 T 1 = p 2 T 2
T 2 = p 2 T 1 p 1
p 2 p 1 = 1 . 5 T 2 = 1 . 5 * T 1 = 1 . 5 * 400 = 600 K
При 27°C объем газа равен 600 мл. Какой объем займет газ при 57°C, если давление будет оставаться постоянным?
Так как давление по условию остается постоянным, то можем использовать закон Гей-Люссака.
V 1 V 2 = T 1 T 2
V_2 – искомый объем
Для правильного расчета необходимо перевести температуры из Цельсий в Кельвины:
T 1 = 273 + 27 = 300 K
T 2 = 273 + 57 = 330 K
T 2 V 1 T 1 = V 2
V 2 = ( 600 * 330 ) / 300 = 660 м л
Газ в трубе плавильной печи охлаждается от температуры t 1 = 1150 ° С д о t 2 = 200 ° С . Во сколько раз увеличивается плотность газа при этом? Давление газа не меняется.
Так как по условию задания давления газа не изменяется, значит перед нами изобарный процесс. Для решения воспользуемся законом Гей-Люссака:
V 1 V 2 = T 1 T 2
Перейдем к абсолютной температуре:
T 1 = 1150 + 273 = 1423 K
T 2 = 200 + 273 = 473 K
Масса газа: m = ρ 1 V 1 = ρ 2 V 2
Использование этих формул приводит к следующему:
Прменение уравнения Менделеева — Клапейрона в рассчетах объма и количества газообразных веществ
Задача 36.
Рассчитайте, какой объем (в литрах) занимают:
а) 1,2 кг водяного пара при 100 °С и 1,013· 10 5 Па;
б) 1,2 кг метана при 25 °С и 1,013· 10 5 Па.
Решение:
M[Н2О(пар)] = 18 кг/моль . 10 -3 ;
М(СН4) = 16 кг/моль . 10 -3 ;
T1 = 100 °С = (100 + 273) = 373 K;
T2 = (25 + 273 = 298 K);
P1 = P2 = 1,013· 10 5 Па.
Для решения задачи прменим уравнение Менделеева — Клапейрона:
PV = nRT = mRT/M, где
n – число молей газа;
P – давление газа (например, в атм или Па;
V – объем газа (в литрах);
T – температура газа (в кельвинах);
R – газовая постоянная [0,0821 л·атм/моль·K)] или [8,314 Дж/(моль . К)];
M — молярная масса вещества (в г/моль или кг/моль;
m — масса вещества (например, в г или кг).
Рассчитаем объемы газов:
а) объем 1,2 кг водяного пара:
PV = mRT/M, V(пар) = mRT1/MР = [1,2 . 8,314 Дж/(моль . К) . 373 К]/[(18 кг/моль . 10 -3 ) . 1,013· 10 5 Па] =
= 3721,3464/1823,4 = 2,04 м 3 = 2040 л.
б) объем 1,2 кг метана:
V(СН4) = mRT1/MР = [1,2 . 8,314 Дж/(моль . К) . 298 К]/[(16 кг/моль . 10 -3 ) * 1,013· 10 5 Па] =
= 2973,0864/1620,8 = 1,834 м 3 = 1834 л.
Ответ: V(пар) = 2040 л; V(СН4) = 1834 л.
Задача 37.
Некоторое количество газа гелия при 78 °С и давлении 15,6 атм занимает объем 26,5 л. Каков объем этого газа при нормальных условиях? Сколько это молей гелия?
Решение:
Для решения задачи прменим уравнение Менделеева — Клапейрона:
n – число молей газа;
P – давление газа (например, в атм или Па;
V – объем газа (в литрах);
T – температура газа (в кельвинах);
R – газовая постоянная [0,0821 л·атм/моль·K)] или [8,314 Дж/(моль . К)].
Уравнение Клапейрона-Менделеева одинаково справедливо как для начального состояния газа, так и для конечного:
Если почленно разделим верхнее уравнение на нижнее, то при неизменном числе молей n мы получаем:
Найдем число молей гелия:
n(Hе) = V/Vm = 321,5/22,4 = 14,35 моль.
Ответ: V2(He) = 321,5 л; n(Hе) = 14,35 моль.
Задача 38.
В стальном баллоне объемом 40 л находится водород под давлением 60 атм и температуре 25 °С. Сколько молей водорода в баллоне? Сколько граммов? Какой объем займет водород из баллона при н.у.?
Решение:
М(Н2) — 2 г/моль;
V1 = 40 л;
Р1 — 60 атм;
Т1 = Т0 = 25 °С = 298 К;
Р0 = 1 атм.
n(H2) = ?
m(H2) = ?
V0(Н2) = ?
Для решения задачи прменим уравнение Менделеева — Клапейрона:
n – число молей газа;
P – давление газа (например, в атм или Па;
V – объем газа (в литрах);
T – температура газа (в кельвинах);
R – газовая постоянная [0,0821 л·атм/моль·K)] или [8,314 Дж/(моль / К)].
1. Расчитаем сколько молей водорода в баллоне, получим:
PV = nRT, n = PV/RT;
n(H2) = P1V1/RT1 = (60 . 40)/(0,0821 . 298) = 2400/24,4658 = 98,1 моль.
2. Находим массу водорода в баллоне:
m(H2) = n(H2) . М(Н2) = 98,1 . 2 = 196,2 г.
3. Рассчитаем объем водорода из баллона (н.у.), получим:
PV = nRT, V = nRT/P;
V0(Н2) = n(H2)RT0/P0 = (98,1 . 0,0821 . 298)/1 = 2400 л.
источники:
http://wika.tutoronline.ru/fizika/class/10/uravnenie-klapejronamendeleeva
http://buzani.ru/zadachi/obshchaya-khimiya/1622-raschet-kolichestva-i-ob-ema-gazov-zadachi-36-38