Корень из числа
- Квадратный корень
- Арифметический квадратный корень
Корень n-ой степени из числа a — это число, n-ая степень которого равна a. Например, корнем второй степени из 36 будет число 6, так как:
62 = 36.
Для записи корня используется знак √
(знак корня или радикал). Под чертой знака записывается подкоренное число, а над знаком, в левом верхнем углу, показатель корня:
2√36.
Подкоренное число — это степень, показатель корня — это показатель степени, корень — основание степени. Если
 ,
,
то
 .
.
Эта запись читается так: корень n-ой степени из числа a равен x
.
Извлечение корня — это действие, обратное возведению в степень, с помощью которого по данной степени и по данному показателю степени находят основание степени.
Примеры:
3√125 = 5, так как 53 = 125;
2√81 = 9, так как 92 = 81;
5√32 = 2, так как 25 = 32.
Квадратный корень
Квадратным корнем из числа a называется число, квадрат которого равен a.
Например, квадратными корнями из числа 16 являются числа 4 и -4:
2√16 = 4 или 2√16 = -4.
Рассмотрим уравнение
x2 = a
при различных значениях a:
- a < 0:
В данном случае уравнение не будет иметь решений, так как квадрат любого числа всегда является положительным числом или нулём. Следовательно, x2 не может быть равен отрицательному числу.
- a = 0:
В этом случае уравнение имеет единственное решение:
x = 0.
- a > 0:
В этом случае уравнение имеет два корня: положительный и отрицательный, модули которых равны. Так как вторая степень отрицательного числа является числом положительным:
x = ±√a .
Из рассмотренного примера можно сделать вывод, что для того чтобы из числа можно было извлечь квадратный корень, необходимо, чтобы оно было числом положительным или нулём.
Арифметический квадратный корень
Арифметический квадратный корень из положительного числа a — это положительное число x, квадрат которого равен a:
2√a = x, следовательно x2 = a.
При обозначении квадратного корня показатель корня опускается, то есть квадратный корень обозначается знаком корня без показателя. Например:
√a — квадратный корень из a.
Обратите внимание, что при чтении выражения слово арифметический
опускается.
Действие, с помощью которого вычисляется квадратный корень, называется извлечением квадратного корня.
Извлечение квадратного корня — действие обратное возведению в квадрат (или возведению числа во вторую степень). При возведении в квадрат известно число, требуется найти его квадрат. При извлечении квадратного корня известен квадрат числа, требуется по нему найти само число.
Поэтому для проверки полученного результата можно найденный корень возвести во вторую степень, если степень будет равна подкоренному числу, значит корень был найден правильно.
Рассмотрим извлечение арифметического квадратного корня и его проверку на примере. Найдём √36, для этого надо найти число, при возведении которого во вторую степень получится 36. Таким числом является 6, так как
62 = 36.
Значит, √36 = 6. Корень -6 мы не рассматриваем, потому что арифметический корень является положительным числом.
Факт 1.
(bullet) Возьмем некоторое неотрицательное число (a) (то есть (ageqslant 0)). Тогда (арифметическим) квадратным корнем из числа (a) называется такое неотрицательное число (b), при возведении которого в квадрат мы получим число (a): [sqrt a=bquad text{то же самое, что }quad a=b^2] Из определения следует, что (ageqslant 0, bgeqslant 0). Эти ограничения являются важным условием существования квадратного корня и их следует запомнить!
Вспомним, что любое число при возведении в квадрат дает неотрицательный результат. То есть (100^2=10000geqslant 0) и ((-100)^2=10000geqslant 0).
(bullet) Чему равен (sqrt{25})? Мы знаем, что (5^2=25) и ((-5)^2=25). Так как по определению мы должны найти неотрицательное число, то (-5) не подходит, следовательно, (sqrt{25}=5) (так как (25=5^2)).
Нахождение значения (sqrt a) называется извлечением квадратного корня из числа (a), а число (a) называется подкоренным выражением.
(bullet) Исходя из определения, выражения (sqrt{-25}), (sqrt{-4}) и т.п. не имеют смысла.
Факт 2.
Для быстрых вычислений полезно будет выучить таблицу квадратов натуральных чисел от (1) до (20): [begin{array}{|ll|}
hline
1^2=1 & quad11^2=121 \
2^2=4 & quad12^2=144\
3^2=9 & quad13^2=169\
4^2=16 & quad14^2=196\
5^2=25 & quad15^2=225\
6^2=36 & quad16^2=256\
7^2=49 & quad17^2=289\
8^2=64 & quad18^2=324\
9^2=81 & quad19^2=361\
10^2=100& quad20^2=400\
hline end{array}]
Факт 3.
Какие действия можно выполнять с квадратными корнями?
(bullet) Сумма или разность квадратных корней НЕ РАВНА квадратному корню из суммы или разности, то есть [sqrt apmsqrt bne sqrt{apm b}] Таким образом, если вам нужно вычислить, например, (sqrt{25}+sqrt{49}), то первоначально вы должны найти значения (sqrt{25}) и (sqrt{49}), а затем их сложить. Следовательно, [sqrt{25}+sqrt{49}=5+7=12] Если значения (sqrt a) или (sqrt b) при сложении (sqrt
a+sqrt b) найти не удается, то такое выражение дальше не преобразуется и остается таким, как есть. Например, в сумме (sqrt
2+ sqrt {49}) мы можем найти (sqrt{49}) – это (7), а вот (sqrt
2) никак преобразовать нельзя, поэтому (sqrt 2+sqrt{49}=sqrt
2+7). Дальше это выражение, к сожалению, упростить никак нельзя
(bullet) Произведение/частное квадратных корней равно квадратному корню из произведения/частного, то есть [sqrt acdot sqrt b=sqrt{ab}quad text{и}quad
sqrt a:sqrt b=sqrt{a:b}] (при условии, что обе части равенств имеют смысл)
Пример: (sqrt{32}cdot sqrt 2=sqrt{32cdot
2}=sqrt{64}=8);
(sqrt{768}:sqrt3=sqrt{768:3}=sqrt{256}=16);
(sqrt{(-25)cdot (-64)}=sqrt{25cdot 64}=sqrt{25}cdot sqrt{64}=
5cdot 8=40).
(bullet) Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
Рассмотрим пример. Найдем (sqrt{44100}). Так как (44100:100=441), то (44100=100cdot 441). По признаку делимости число (441) делится на (9) (так как сумма его цифр равна 9 и делится на 9), следовательно, (441:9=49), то есть (441=9cdot 49).
Таким образом, мы получили: [sqrt{44100}=sqrt{9cdot 49cdot 100}=
sqrt9cdot sqrt{49}cdot sqrt{100}=3cdot 7cdot 10=210] Рассмотрим еще один пример: [sqrt{dfrac{32cdot 294}{27}}=
sqrt{dfrac{16cdot 2cdot 3cdot 49cdot 2}{9cdot 3}}= sqrt{
dfrac{16cdot4cdot49}{9}}=dfrac{sqrt{16}cdot sqrt4 cdot
sqrt{49}}{sqrt9}=dfrac{4cdot 2cdot 7}3=dfrac{56}3]
(bullet) Покажем, как вносить числа под знак квадратного корня на примере выражения (5sqrt2) (сокращенная запись от выражения (5cdot
sqrt2)). Так как (5=sqrt{25}), то [5sqrt2=sqrt{25}cdot sqrt2=sqrt{25cdot 2}=sqrt{50}] Заметим также, что, например,
1) (sqrt2+3sqrt2=4sqrt2),
2) (5sqrt3-sqrt3=4sqrt3)
3) (sqrt a+sqrt a=2sqrt a).
Почему так? Объясним на примере 1). Как вы уже поняли, как-то преобразовать число (sqrt2) мы не можем. Представим, что (sqrt2) – это некоторое число (a). Соответственно, выражение (sqrt2+3sqrt2) есть не что иное, как (a+3a) (одно число (a) плюс еще три таких же числа (a)). А мы знаем, что это равно четырем таким числам (a), то есть (4sqrt2).
Факт 4.
(bullet) Часто говорят “нельзя извлечь корень”, когда не удается избавиться от знака (sqrt {} ) корня (радикала) при нахождении значения какого-то числа. Например, извлечь корень из числа (16) можно, потому что (16=4^2), поэтому (sqrt{16}=4). А вот извлечь корень из числа (3), то есть найти (sqrt3), нельзя, потому что нет такого числа, которое в квадрате даст (3).
Такие числа (или выражения с такими числами) являются иррациональными. Например, числа (sqrt3, 1+sqrt2, sqrt{15}) и т.п. являются иррациональными.
Также иррациональными являются числа (pi) (число “пи”, приблизительно равное (3,14)), (e) (это число называют числом Эйлера, приблизительно оно равно (2,7)) и т.д.
(bullet) Обращаем ваше внимание на то, что любое число будет либо рациональным, либо иррациональным. А вместе все рациональные и все иррациональные числа образуют множество, называющееся множеством действительных (вещественных) чисел. Обозначается это множество буквой (mathbb{R}).
Значит, все числа, которые на данный момент мы знаем, называются вещественными числами.
Факт 5.
(bullet) Модуль вещественного числа (a) – это неотрицательное число (|a|), равное расстоянию от точки (a) до (0) на вещественной прямой. Например, (|3|) и (|-3|) равны 3, так как расстояния от точек (3) и (-3) до (0) одинаковы и равны (3). 
(bullet) Если (a) – неотрицательное число, то (|a|=a).
Пример: (|5|=5); (qquad |sqrt2|=sqrt2).
(bullet) Если (a) – отрицательное число, то (|a|=-a).
Пример: (|-5|=-(-5)=5); (qquad |-sqrt3|=-(-sqrt3)=sqrt3).
Говорят, что у отрицательных чисел модуль “съедает” минус, а положительные числа, а также число (0), модуль оставляет без изменений.
НО такое правило годится только для чисел. Если у вас под знаком модуля находится неизвестная (x) (или какая-то другая неизвестная), например, (|x|), про которую мы не знаем, положительная она, равна нулю или отрицательная, то избавиться от модуля мы не можем. В этом случае это выражение таким и остается: (|x|).
(bullet) Имеют место следующие формулы: [{large{sqrt{a^2}=|a|}}] [{large{(sqrt{a})^2=a}},
text{ при условии } ageqslant 0] Очень часто допускается такая ошибка: говорят, что (sqrt{a^2}) и ((sqrt a)^2) – одно и то же. Это верно только в том случае, когда (a) – положительное число или ноль. А вот если (a) – отрицательное число, то это неверно. Достаточно рассмотреть такой пример. Возьмем вместо (a) число (-1). Тогда (sqrt{(-1)^2}=sqrt{1}=1), а вот выражение ((sqrt {-1})^2) вообще не существует (ведь нельзя под знак корня помещать отрицательные числа!).
Поэтому обращаем ваше внимание на то, что (sqrt{a^2}) не равен ((sqrt a)^2)!
Пример: 1) (sqrt{left(-sqrt2right)^2}=|-sqrt2|=sqrt2), т.к. (-sqrt2<0);
(phantom{00000}) 2) ((sqrt{2})^2=2).
(bullet) Так как (sqrt{a^2}=|a|), то [sqrt{a^{2n}}=|a^n|] (выражение (2n) обозначает четное число)
То есть при извлечении корня из числа, находящегося в какой-то степени, эта степень уменьшается в два раза.
Пример:
1) (sqrt{4^6}=|4^3|=4^3=64)
2) (sqrt{(-25)^2}=|-25|=25) (заметим, что если модуль не поставить, то получится, что корень из числа равен (-25); но мы помним, что по определению корня такого быть не может: у нас всегда при извлечении корня должно получаться положительное число или ноль)
3) (sqrt{x^{16}}=|x^8|=x^8) (так как любое число в четной степени неотрицательно)
Факт 6.
Как сравнить два квадратных корня?
(bullet) Для квадратных корней верно: если (sqrt a<sqrt b), то (a<b); если (sqrt a=sqrt b), то (a=b).
Пример:
1) сравним (sqrt{50}) и (6sqrt2). Для начала преобразуем второе выражение в (sqrt{36}cdot sqrt2=sqrt{36cdot 2}=sqrt{72}). Таким образом, так как (50<72), то и (sqrt{50}<sqrt{72}). Следовательно, (sqrt{50}<6sqrt2).
2) Между какими целыми числами находится (sqrt{50})?
Так как (sqrt{49}=7), (sqrt{64}=8), а (49<50<64), то (7<sqrt{50}<8), то есть число (sqrt{50}) находится между числами (7) и (8).
3) Сравним (sqrt 2-1) и (0,5). Предположим, что (sqrt2-1>0,5): [begin{aligned}
&sqrt 2-1>0,5 big| +1quad text{(прибавим единицу к обеим
частям)}\[1ex]
&sqrt2>0,5+1 big| ^2 quadtext{(возведем обе части в
квадрат)}\[1ex]
&2>1,5^2\
&2>2,25 end{aligned}] Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и (sqrt 2-1<0,5).
Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
Возводить обе части уравнения/неравенства в квадрат можно ТОЛЬКО ТОГДА, когда обе части неотрицательные. Например, в неравенстве из предыдущего примера возводить обе части в квадрат можно, в неравенстве (-3<sqrt2) нельзя (убедитесь в этом сами)!
(bullet) Следует запомнить, что [begin{aligned}
&sqrt 2approx 1,4\[1ex]
&sqrt 3approx 1,7 end{aligned}] Знание приблизительного значения данных чисел поможет вам при сравнении чисел!
(bullet) Для того, чтобы извлечь корень (если он извлекается) из какого-то большого числа, которого нет в таблице квадратов, нужно сначала определить, между какими “сотнями” оно находится, затем – между какими “десятками”, а потом уже определить последнюю цифру этого числа. Покажем, как это работает, на примере.
Возьмем (sqrt{28224}). Мы знаем, что (100^2=10,000), (200^2=40,000) и т.д. Заметим, что (28224) находится между (10,000) и (40,000). Следовательно, (sqrt{28224}) находится между (100) и (200).
Теперь определим, между какими “десятками” находится наше число (то есть, например, между (120) и (130)). Также из таблицы квадратов знаем, что (11^2=121), (12^2=144) и т.д., тогда (110^2=12100), (120^2=14400), (130^2=16900), (140^2=19600), (150^2=22500), (160^2=25600), (170^2=28900). Таким образом, мы видим, что (28224) находится между (160^2) и (170^2). Следовательно, число (sqrt{28224}) находится между (160) и (170).
Попробуем определить последнюю цифру. Давайте вспомним, какие однозначные числа при возведении в квадрат дают на конце (4)? Это (2^2) и (8^2). Следовательно, (sqrt{28224}) будет заканчиваться либо на 2, либо на 8. Проверим это. Найдем (162^2) и (168^2):
(162^2=162cdot 162=26224)
(168^2=168cdot 168=28224).
Следовательно, (sqrt{28224}=168). Вуаля!
Основные сведения
Чтобы найти площадь квадрата, нужно длину его стороны возвести во вторую степень.
Найдём площадь квадрата, длина стороны которого 3 см
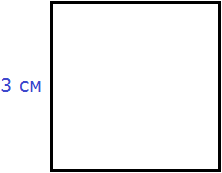
S = 32 = 9 см2
Теперь решим обратную задачу. А именно, зная площадь квадрата определим длину его стороны. Для этого воспользуемся таким инструментом как кóрень. Корень бывает квадратный, кубический, а также n-й степени.
Сейчас наш интерес вызывает квадратный корень. По другому его называют кóрнем второй степени.
Для нахождения длины стороны нашего квадрата, нужно найти число, вторая степень которого равна 9. Таковым является число 3. Это число и является кóрнем.
Введём для работы с корнями новые обозначения.
Символ кóрня выглядит как ![]() . Это по причине того, что слово корень в математике употребляется как радикал. А слово радикал происходит от латинского radix (что в переводе означает корень). Первая буква слова radix это r впоследствии преобразилась в символ корня
. Это по причине того, что слово корень в математике употребляется как радикал. А слово радикал происходит от латинского radix (что в переводе означает корень). Первая буква слова radix это r впоследствии преобразилась в символ корня ![]() .
.
Под корнем располагáют подкореннóе выражение. В нашем случае подкоренным выражением будет число 9 (площадь квадрата)
![]()
Нас интересовал квадратный корень (он же корень второй степени), поэтому слева над корнем указываем число 2. Это число называют показателем корня (или степенью корня)
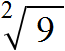
Получили выражение, которое читается так: «квадратный корень из числа 9». С этого момента возникает новая задача по поиску самогó корня.
Если число 3 возвести во вторую степень, то получится число 9. Поэтому число 3 и будет ответом:
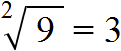
Значит квадрат площадью 9 см2 имеет сторону, длина которой 3 см. Приведённое действие называют извлечéнием квадрáтного кóрня.
Нетрудно догадаться, что квадратным корнем из числа 9 также является отрицательное число −3. При его возведении во вторую степень тоже получается число 9
![]()
Получается, что выражение ![]() имеет два значения: 3 и −3. Но длина стороны квадрата не может быть отрицательным числом, поэтому для нашей задачи ответ будет только один, а именно 3.
имеет два значения: 3 и −3. Но длина стороны квадрата не может быть отрицательным числом, поэтому для нашей задачи ответ будет только один, а именно 3.
Вообще, квадратный корень имеет два противоположных значения: положительное и отрицательное.
Например, извлечём квадратный корень из числа 4
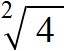
Это выражение имеет два значения: 2 и −2, поскольку при возведении этих чисел во вторую степень, получится один и тот же результат 4
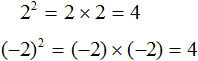
Поэтому ответ к выражению вида ![]() записывают с плюсом и минусом. Плюс с минусом означает, что квадратный корень имеет два противоположных значения.
записывают с плюсом и минусом. Плюс с минусом означает, что квадратный корень имеет два противоположных значения.
Запишем ответ к выражению ![]() с плюсом и минусом:
с плюсом и минусом:
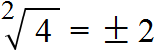
Определения
Дадим определение квадратному корню.
Квадратным корнем из числа a называют такое число b, вторая степень которого равна a.
То есть число b должно быть таким, чтобы выполнялось равенство b2 = a. Число b (оно же корень) обозначается через радикал ![]() так, что
так, что ![]() . На практике левая и правая часть поменяны местами и мы видим привычное выражение
. На практике левая и правая часть поменяны местами и мы видим привычное выражение ![]()
Например, квадратным корнем из числá 16 есть число 4, поскольку число 4 во второй степени равно 16
42 = 16
Корень 4 можно обозначить через радикал ![]() так, что
так, что ![]() .
.
Также квадратным корнем из числá 16 есть число −4, поскольку число −4 во второй степени равно 16
(−4)2 = 16
Если при решении задачи интересует только положительное значение, то корень называют не просто квадратным, а арифметическим квадратным.
Арифметический квадратный корень из числá a — это неотрицательное число b (b ≥ 0), при котором выполняется равенство b2 = a.
В нашем примере квадратными корнями из числá 16 являются корни 4 и −4, но арифметическим из них является только корень 4.
В разговорном языке можно использовать сокращение. К примеру, выражение ![]() полностью читается так: «квадратный корень из числá шестнадцать», а в сокращённом варианте можно прочитать так: «корень из шестнадцати».
полностью читается так: «квадратный корень из числá шестнадцать», а в сокращённом варианте можно прочитать так: «корень из шестнадцати».
Не следует путать понятия корень и квадрат. Квадрат это число, которое получилось в результате возведения какого-нибудь числá во вторую степень. Например, числа 25, 36, 49 являются квадратами, потому что они получились в результате возведения во вторую степень чисел 5, 6 и 7 соответственно.
Корнями же являются числа 5, 6 и 7. Они являются теми числами, которые во второй степени равны 25, 36 и 49 соответственно.
Чаще всего в квадратных корнях показатель кóрня вообще не указывается. Так, вместо записи ![]() можно использовать запись
можно использовать запись![]() . Если в учебнике по математике встретится корень без показателя, то нужно понимать, что это квадратный корень.
. Если в учебнике по математике встретится корень без показателя, то нужно понимать, что это квадратный корень.
Квадратный корень из единицы равен единице. То есть справедливо следующее равенство:
![]()
Это по причине того, что единица во второй степени равна единице:
12 = 1
и квадрат, состоящий из одной квадратной единицы, имеет сторону, равную единице:
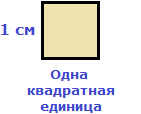
Квадратный корень из нуля равен нулю. То есть справедливо равенство ![]() , поскольку 02 = 0.
, поскольку 02 = 0.
Выражение вида ![]() смысла не имеет. Например, не имеет смысла выражение
смысла не имеет. Например, не имеет смысла выражение ![]() , поскольку вторая степень любого числа есть число положительное. Невозможно найти число, вторая степень которого будет равна −4.
, поскольку вторая степень любого числа есть число положительное. Невозможно найти число, вторая степень которого будет равна −4.
Если выражение вида ![]() возвести во вторую степень, то есть если записать
возвести во вторую степень, то есть если записать ![]() , то это выражение будет равно подкореннóму выражению a
, то это выражение будет равно подкореннóму выражению a
![]()
Например, выражение ![]() равно 4
равно 4
![]()
Это потому что выражение ![]() равно значению 2. Но это значение сразу возвóдится во вторую степень и получается результат 4.
равно значению 2. Но это значение сразу возвóдится во вторую степень и получается результат 4.
Еще примеры:
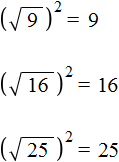
Корень из квадрата числá равен модулю этого числá:
![]()
Например, корень из числá 5, возведённого во вторую степень, равен модулю числá 5
![]()
Это же правило будет срабатывать, если во вторую степень возвóдится отрицательное число. То есть, ответ опять же станет положительным. Например, корень из числá −5, возведённого во вторую степень, равен модулю числá −5. А модуль числа −5 равен 5
![]()
Действительно, если не пользуясь правилом ![]() , вычислять выражение
, вычислять выражение ![]() обычным методом — сначала возвести число −5 во вторую степень, затем извлечь полученный результат, то полýчим ответ 5
обычным методом — сначала возвести число −5 во вторую степень, затем извлечь полученный результат, то полýчим ответ 5
![]()
Не следует путать правило ![]() с правилом
с правилом ![]() . Правило
. Правило ![]() верно при любом a, тогда как правило
верно при любом a, тогда как правило ![]() верно в том случае, если выражение
верно в том случае, если выражение ![]() имеет смысл.
имеет смысл.
В некоторых учебниках знак корня может выглядеть без верхней линии. Выглядит это так:
![]()
Примеры: √4, √9, √16.
Мéньшему числу соответствует мéньший корень, а бóльшему числу соответствует бóльший корень.
Например, рассмотрим числа 49 и 64. Число 49 меньше, чем число 64.
49 < 64
Если извлечь квадратные корни из этих чисел, то числу 49 будет соответствовать меньший корень, а числу 64 — бóльший. Действительно, √49 = 7, а √64 = 8,
√49 < √64
Отсюда:
7 < 8
Примеры извлечения квадратных корней
Рассмотрим несколько простых примеров на извлечение квадратных корней.
Пример 1. Извлечь квадратный корень √36
Данный квадратный корень равен числу, квадрат которого равен 36. Таковым является число 6, поскольку 62 = 36
√36 = 6
Пример 2. Извлечь квадратный корень √49
Данный квадратный корень равен числу, квадрат которого равен 49. Таковым является число 7, поскольку 72 = 49
√49 = 7
В таких простых примерах достаточно знать таблицу умножения. Так, мы помним, что число 49 входит в таблицу умножения на семь. То есть:
7 × 7 = 49
Но 7 × 7 это 72
72 = 49
Отсюда, √49 = 7.
Пример 3. Извлечь квадратный корень √100
Данный квадратный корень равен числу, квадрат которого равен 100. Таковым является число 10, поскольку 102 = 100
√100 = 10
Число 100 это последнее число, корень которого можно извлечь с помощью таблицы умножения. Для чисел, бóльших 100, квадратные корни можно находить с помощью таблицы квадратов.
Пример 3. Извлечь квадратный корень √256
Данный квадратный корень равен числу, квадрат которого равен 256. Чтобы найти это число, воспользуемся таблицей квадратов.
Нахóдим в таблице квадратов число 256 и двигаясь от него влево и вверх определяем цифры, которые образуют число, квадрат которого равен 256.
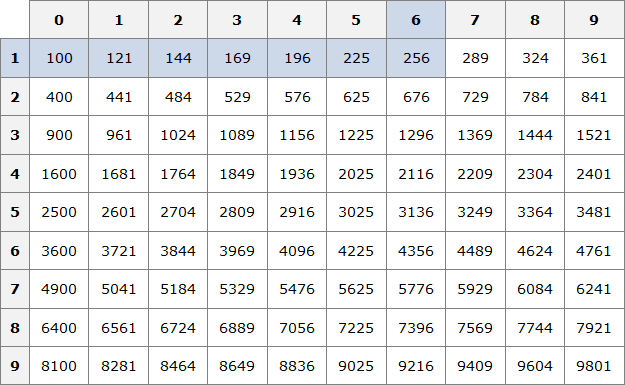
Видим, что это число 16. Значит √256 = 16.
Пример 4. Найти значение выражения 2√16
В данном примере число 2 умножается на выражение с корнем. Сначала вычислим корень √16, затем перемнóжим его с числом 2
![]()
Пример 7. Решить уравнение ![]()
В данном примере нужно найти значение переменной x, при котором левая часть будет равна 4.
Значение переменной x равно 16, поскольку ![]() . Значит корень уравнения равен 16.
. Значит корень уравнения равен 16.
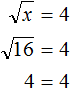
Примечание. Не следует путать корень уравнения и квадратный корень. Корень уравнения это значение переменной, при котором уравнение обращается в верное числовое равенство. А квадратный корень это число, вторая степень которого равна выражению, находящемуся под радикалом ![]() .
.
Подобные примеры решают, пользуясь определением квадратного корня. Давайте и мы поступим так же.
Из определения мы знаем, что квадратный корень ![]() равен числу b, при котором выполняется равенство b2 = a.
равен числу b, при котором выполняется равенство b2 = a.
![]()
Применим равенство b2 = a к нашему примеру ![]() . Роль переменной b у нас играет число 4, а роль переменной a — выражение, находящееся под корнем
. Роль переменной b у нас играет число 4, а роль переменной a — выражение, находящееся под корнем ![]() , а именно переменная x
, а именно переменная x
![]()
В выражении 42 = x вычислим левую часть, полýчим 16 = x. Поменяем левую и правую часть местами, полýчим x = 16. В результате приходим к тому, что нашлось значение переменной x.
Пример 8. Решить уравнение ![]()
Перенесем −8 в правую часть, изменив знак:
![]()
Возведем правую часть во вторую степень и приравняем её к переменной x
![]()
Вычислим правую часть, полýчим 64 = x. Поменяем левую и правую часть местами, полýчим x = 64. Значит корень уравнения ![]() равен 64
равен 64
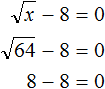
Пример 9. Решить уравнение ![]()
Воспользуемся определением квадратного корня:
![]()
Роль переменной b играет число 7, а роль переменной a — подкореннóе выражение 3 + 5x. Возведем число 7 во вторую степень и приравняем его к 3 + 5x
![]()
В выражении 72 = 3 + 5x вычислим левую часть полýчим 49 = 3 + 5x. Получилось обычное линейное уравнение. Решим его:
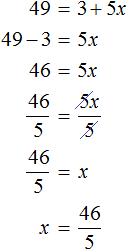
Корень уравнения ![]() равен
равен ![]() . Выполним проверку, подставив его в исходное уравнение:
. Выполним проверку, подставив его в исходное уравнение:
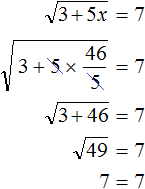
Пример 10. Найти значение выражения ![]()
В этом выражении число 2 умножается на квадратный корень из числа 49.
Сначала нужно извлечь квадратный корень и перемножить его с числом 2
![]()
Приближённое значение квадратного корня
Не каждый квадратный корень можно извлечь. Извлечь квадратный корень можно только в том случае, если удаётся найти число, вторая степень которого равна подкореннóму выражению.
Например, извлечь квадратный корень ![]() можно, потому что удаётся найти число, вторая степень которого равна подкореннóму выражению. Таковым является число 8, поскольку 82 = 64. То есть
можно, потому что удаётся найти число, вторая степень которого равна подкореннóму выражению. Таковым является число 8, поскольку 82 = 64. То есть ![]()
А извлечь квадратный корень ![]() нельзя, потому что невозможно найти число, вторая степень которого равна 3. В таком случае говорят, что квадратный корень из числа 3 не извлекается.
нельзя, потому что невозможно найти число, вторая степень которого равна 3. В таком случае говорят, что квадратный корень из числа 3 не извлекается.
Зато можно извлечь квадратный корень из числа 3 приближённо. Извлечь квадратный корень приближённо означает найти значение, которое при возведении во вторую степень будет максимально близко к подкореннóму выражению.
Приближённое значение ищут с определенной точностью: с точностью до целых, с точностью до десятых, с точностью до сотых и так далее.
Найдём значение корня ![]() приближённо с точностью до десятых. Словосочетание «с точностью до десятых» говорит о том, что приближённое значение корня
приближённо с точностью до десятых. Словосочетание «с точностью до десятых» говорит о том, что приближённое значение корня ![]() будет представлять собой десятичную дробь, у которой после запятой одна цифра.
будет представлять собой десятичную дробь, у которой после запятой одна цифра.
Для начала найдём ближайшее меньшее число, корень которого можно извлечь. Таковым является число 1. Корень из этого числа равен самому этому числу:
√1 = 1
Аналогично находим ближайшее бóльшее число, корень которого можно извлечь. Таковым является число 4. Корень из этого числа равен 2
√4 = 2
√1 меньше, чем √4
√1 < √4
А √3 больше, чем √1 но меньше, чем √4. Запишем это в виде двойного неравенства:
√1 < √3 < √4
Точные значения корней √1 и √4 известны. Это числа 1 и 2
1 < √3 < 2
Тогда очевидно, что значение корня √3 будет представлять собой десятичную дробь, потому что между числами 1 и 2 нет целых чисел.
Для нахождения приближённого значения квадратного корня √3 будем проверять десятичные дроби, располагающиеся в интервале от 1 до 2, возводя их в квадрат. Делать это будем до тех пор пока не полýчим значение, максимально близкое к 3. Проверим к примеру дробь 1,1
1,12 = 1,21
Получился результат 1,21, который не очень близок к подкореннóму выражению 3. Значит 1,1 не годится в качестве приближённого значения квадратного корня √3, потому что оно малó.
Проверим тогда дробь 1,8
1,82 = 3,24
Получился результат 3,24, который близок к подкореннóму выражению, но превосходит его на 0,24. Значит 1,8 не годится в качестве приближенного значения корня √3, потому что оно великó.
Проверим тогда дробь 1,7
1,72 = 2,89
Получился результат 2,89, который уже близок к подкореннóму выражению. Значит 1,7 и будет приближённым значением квадратного корня √3. Напомним, что знак приближенного значения выглядит как ≈
√3 ≈ 1,7
Значение 1,6 проверять не нужно, потому что в результате получится число 2,56, которое дальше от трёх, чем значение 2,89. А значение 1,8, как было показано ранее, является уже большим.
В данном случае мы нашли приближенное значение корня √3 с точностью до десятых. Значение можно получить ещё более точно. Для этого его следует находить с точностью до сотых.
Чтобы найти значение с точностью до сотых проверим десятичные дроби в интервале от 1,7 до 1,8
1,7 < √3 < 1,8
Проверим дробь 1,74
1,742 = 3,0276
Получился результат 3,0276, который близок к подкореннóму выражению, но превосходит его на 0,0276. Значит значение 1,74 великó для корня √3.
Проверим тогда дробь 1,73
1,732 = 2,9929
Получился результат 2,9929, который близок к подкореннóму выражению √3. Значит 1,73 будет приближённым значением квадратного корня √3 с точностью до сотых.
Процесс нахождения приближённого значения квадратного корня продолжается бесконечно. Так, корень √3 можно находить с точностью до тысячных, десятитысячных и так далее:
√3 = 1,732 (вычислено с точностью до тысячных)
√3 = 1,7320 (вычислено с точностью до десятитысячных)
√3 = 1,73205 (вычислено с точностью до ста тысячных).
Ещё квадратный корень можно извлечь с точностью до целых. Приближённое значение квадратного корня √3 с точностью до целых равно единице:
√3 ≈ 1
Значение 2 будет слишком большим, поскольку при возведении этого числа во вторую степень получается число 4, которое больше подкоренного выражения. Нас же интересуют значения, которые при возведении во вторую степень равны подкореннóму выражению или максимально близки к нему, но не превосходят его.
В зависимости от решаемой задачи допускается находить значение, вторая степень которого больше подкоренного выражения. Это значение называют приближённым значением квадратного корня с избытком. Поговорим об этом подробнее.
Приближенное значение квадратного корня с недостатком или избытком
Иногда можно встретить задание, в котором требуется найти приближённое значение корня с недостатком или избытком.
В предыдущей теме мы нашли приближённое значение корня √3 с точностью до десятых с недостатком. Недостаток понимается в том смысле, что до значения 3 нам недоставало ещё некоторых частей. Так, найдя приближённое значение √3 с точностью до десятых, мы получили 1,7. Это значение является значением с недостатком, поскольку при возведении этого числа во вторую степень полýчим результат 2,89. Этому результату недостаёт ещё 0,11 чтобы получить число 3. То есть, 2,89 + 0,11 = 3.
С избытком же называют приближённые значения, которые при возведении во вторую степень дают результат, который превосходит подкореннóе выражение. Так, вычисляя корень √3 приближённо, мы проверили значение 1,8. Это значение является приближённым значением корня √3 с точностью до десятых с избытком, поскольку при возведении 1,8 во вторую степень, получаем число 3,24. Этот результат превосходит подкореннóе выражение на 0,24. То есть 3,24 − 3 = 0,24.
Приближённое значение квадратного корня √3 с точностью до целых тоже был найден с недостатком:
√3 ≈ 1
Это потому что при возведении единицы в квадрат получаем единицу. То есть до числа 3 недостаёт ещё 2.
Приближённое значение квадратного корня √3 с точностью до целых можно найти и с избытком. Тогда этот корень приближённо будет равен 2
√3 ≈ 2
Это потому что при возведении числа 2 в квадрат получаем 4. Число 4 превосходит подкореннóе выражение 3 на единицу. Извлекая приближённо квадратный корень с избытком желательно уточнять, что корень извлечен именно с избытком:
√3 ≈ 2 (с избытком)
Потому что приближённое значение чаще всего ищется с недостатком, чем с избытком.
Дополнительно следует упомянуть, что в некоторых учебниках словосочетания «с точностью до целых», «с точностью до десятых», с «точностью до сотых», заменяют на словосочетания «с точностью до 1», «с точностью до 0,1», «с точностью до 0,01» соответственно.
Так, если в задании сказано извлечь квадратный корень из числа 5 с точностью до 0,01, то это значит что корень следует извлекать приближённо с точностью до сотых:
√5 ≈ 2,23
Пример 2. Извлечь квадратный корень из числа 51 с точностью до 1
√51 ≈ 7
Пример 3. Извлечь квадратный корень из числа 51 с точностью до 0,1
√51 ≈ 7,1
Пример 4. Извлечь квадратный корень из числа 51 с точностью до 0,01
√51 ≈ 7,14
Границы, в пределах которых располагаются корни
Если исходное число принадлежит промежутку [1; 100], то квадратный корень из этого исходного числа будет принадлежать промежутку [1; 10].
Например, пусть исходным числом будет 64. Данное число принадлежит промежутку [1; 100]. Сразу делаем вывод, что квадратный корень из числа 64 будет принадлежать промежутку [1; 10]. Теперь вспоминаем таблицу умножения. Какое перемножение двух одинаковых сомножителей даёт в результате 64? Ясно, что перемножение 8 × 8, а это есть 82 = 64. Значит квадратный корень из числа 64 есть 8
![]()
Пример 2. Извлечь квадратный корень из числа 49
Число 49 принадлежит промежутку [1; 100]. Значит квадратный корень будет принадлежать промежутку [1; 10]. Этим корнем будет число 7, поскольку 72 = 49
√49 = 7
Пример 2. Извлечь квадратный корень из числа 1
Число 1 принадлежит промежутку [1; 100]. Значит квадратный корень будет принадлежать промежутку [1; 10]. Этим корнем будет число 1, поскольку 12 = 1
√1 = 1
Пример 3. Извлечь квадратный корень из числа 100
Число 100 принадлежит промежутку [1; 100]. Значит квадратный корень будет принадлежать промежутку [1; 10]. Этим корнем будет число 10, поскольку 102 = 100
√100 = 10
Понятно, что промежуток [1; 100] содержит ещё и числа, квадратные корни из которых не извлекаются. Для таких чисел корень нужно извлекать приближённо. Тем не менее, приближённый корень тоже будет располагаться в пределах промежутка [1; 10].
Например, извлечём квадратный корень из числа 37. Нет целого числа, вторая степень которого была бы равна 37. Поэтому извлекать квадратный корень следует приближённо. Извлечём его к примеру с точностью до сотых:
√37 ≈ 6,08
Для облегчения можно находить ближайшее меньшее число, корень из которого извлекается. Таковым в данном примере было число 36. Квадратный корень из него равен 6. И далее отталкиваясь от числа 6, можно находить приближённое значение корня √37, проверяя различные десятичные дроби, целая часть которых равна 6.
Квадраты чисел от 1 до 10 обязательно нужно знать наизусть. Ниже представлены эти квадраты:
12 = 1
22 = 4
32 = 9
42 = 16
52 = 25
62 = 36
72 = 49
82 = 64
92 = 81
102 = 100
И обратно, следует знать значения квадратных корней этих квадратов:

Если к любому числу от 1 до 10 в конце дописать ноль (или несколько нулей), и затем возвести это число во вторую степень, то в полученном числе будет в два раза больше нулей.
Например, 62 = 36. Допишем к числу 6 один ноль, полýчим 60. Возведём число 60 во вторую степень, полýчим 3600
602 = 3600
А если к числу 6 дописать два нуля, и возвести это число во вторую степень, то полýчим число, в котором четыре нуля. То есть в два раза больше нулей:
6002 = 360000
Тогда можно сделать следующий вывод:
Если исходное число содержит знакомый нам квадрат и чётное количество нулей, то можно извлечь квадратный корень из этого числа. Для этого следует извлечь корень из знакомого нам квадрата и затем записать половину количества нулей из исходного числа.
Например, извлечём квадратный корень из числа 900. Видим, что в данном числе есть знакомый нам квадрат 9. Извлекаем из него корень, получаем 3
![]()
Теперь из исходного числа записываем половину от количества нулей. В исходном числе 900 содержится два нуля. Половина этого количества нулей есть один ноль. Записываем его в ответе после цифры 3
![]()
Пример 2. Извлечём квадратный корень из числа 90000
Здесь опять же имеется знакомый нам квадрат 9 и чётное количество нулей. Извлекаем корень из числа 9 и записываем половину от количества нулей. В исходном числе содержится четыре нуля. Половиной же этого количества нулей будет два нуля:
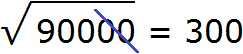
Пример 3. Извлечем квадратный корень из числа 36000000
Здесь имеется знакомый нам квадрат 36 и чётное количество нулей. Извлекаем корень из числа 36 и записываем половину от количества нулей. В исходном числе шесть нулей. Половиной же будет три нуля:
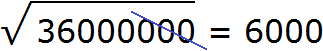
Пример 4. Извлечем квадратный корень из числа 2500
Здесь имеется знакомый нам квадрат 25 и чётное количество нулей. Извлекаем корень из числа 25 и записываем половину от количества нулей. В исходном числе два нуля. Половиной же будет один ноль:
![]()
Если подкореннóе число увеличить (или уменьшить) в 100, 10000 то корень увеличится (или уменьшится) в 10, 100 раз соответственно.
Например, ![]() . Если увеличим подкореннóе число в 100 раз, то квадратный корень увеличится в 10 раз:
. Если увеличим подкореннóе число в 100 раз, то квадратный корень увеличится в 10 раз:
![]()
И наоборот, если в равенстве ![]() уменьшим подкореннóе число в 100 раз, то квадратный корень уменьшится в 10 раз:
уменьшим подкореннóе число в 100 раз, то квадратный корень уменьшится в 10 раз:
![]()
Пример 2. Увеличим в равенстве ![]() подкореннóе число в 10000, тогда квадратный корень 70 увеличиться в 100 раз
подкореннóе число в 10000, тогда квадратный корень 70 увеличиться в 100 раз
![]()
Пример 3. Уменьшим в равенстве ![]() подкореннóе число в 100 раз, тогда квадратный корень 70 уменьшится в 10 раз
подкореннóе число в 100 раз, тогда квадратный корень 70 уменьшится в 10 раз
![]()
Эта закономерность позволяет извлечь квадратный корень из десятичной дроби, если в данной дроби после запятой содéржатся две цифры, и эти две цифры образуют знакомый нам квадрат. В таких случаях данную десятичную дробь следует умножить на 100. Затем извлечь квадратный корень из получившегося числа и уменьшить подкореннóе число в сто раз.
Например, извлечём квадратный корень из числа 0,25. В данной десятичной дроби после запятой содержатся две цифры и эти две цифры образуют знакомый нам квадрат 25.
Умнóжим десятичную дробь 0,25 на 100, полýчим 25. А из числа 25 квадратный корень извлекается легко:
![]()
Но нам изначально нужно было извлечь корень из 0,25, а не из 25. Чтобы исправить ситуацию, вернём нашу десятичную дробь. Если в равенстве ![]() подкореннóе число уменьшить в 100 раз, то полýчим под корнем 0,25 и соответственно ответ уменьшится в 10 раз:
подкореннóе число уменьшить в 100 раз, то полýчим под корнем 0,25 и соответственно ответ уменьшится в 10 раз:
![]()
Обычно в таких случаях достаточно уметь передвигáть запятую. Потому что сдвинуть в числе запятую вправо на две цифры это всё равно что умножить это число на 100.
В предыдущем примере в подкоренном числе 0,25 можно было сдвинуть запятую вправо на две цифры, а в полученном ответе сдвинуть её влево на одну цифру.
Например, извлечем корень из числа 0,81. Мысленно передвинем запятую вправо на две цифры, полýчим 81. Теперь извлечём квадратный корень из числа 81, полýчим ответ 9. В ответе 9 передвинем запятую влево на одну цифру, полýчим 0,9. Значит, ![]() .
.
Это правило работает и в ситуации, когда после запятой содержатся четыре цифры и эти цифры образуют знакомый нам квадрат.
Например, десятичная дробь 0,1225 содержит после запятой четыре цифры. Эти четыре цифры образуют число 1225, квадратный корень из которого равен 35.
Тогда можно извлечь квадратный корень и из 0,1225. Умнóжим данную десятичную дробь на 10000, полýчим 1225. Из числа 1225 квадратный корень можно извлечь с помощью таблицы квадратов:
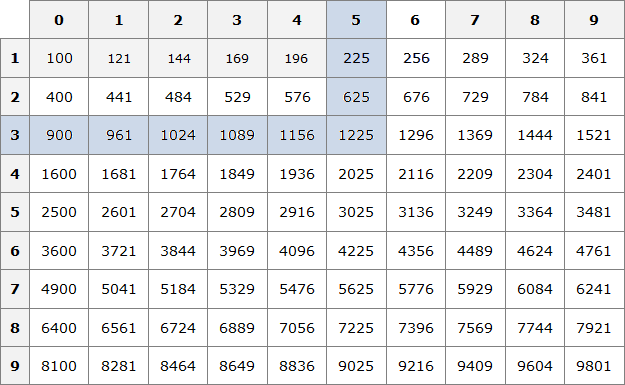
![]()
Но нам изначально нужно было извлечь корень из 0,1225, а не из 1225. Чтобы исправить ситуацию, в равенстве ![]() подкореннóе число уменьшим в 10000 раз. В результате под корнем образуется десятичная дробь 0,1225, а правая часть уменьшится в 100 раз
подкореннóе число уменьшим в 10000 раз. В результате под корнем образуется десятичная дробь 0,1225, а правая часть уменьшится в 100 раз
![]()
Эта же закономерность будет работать и при извлечении корней из дробей вида 12,25. Если цифры из которых состоит десятичная дробь образуют знакомый нам квадрат, при этом после запятой содержится чётное количество цифр, то можно извлечь корень из этой десятичной дроби.
Умнóжим десятичную дробь 12,25 на 100, полýчим 1225. Извлечём корень из числа 1225
![]()
Теперь в равенстве ![]() уменьшим подкореннóе число в 100 раз. В результате под корнем образуется число 12,25, и соответственно ответ уменьшится в 10 раз
уменьшим подкореннóе число в 100 раз. В результате под корнем образуется число 12,25, и соответственно ответ уменьшится в 10 раз
![]()
Если исходное число принадлежит промежутку [100; 10000], то квадратный корень из этого исходного числа будет принадлежать промежутку [10; 100].
В этом случае применяется таблица квадратов:
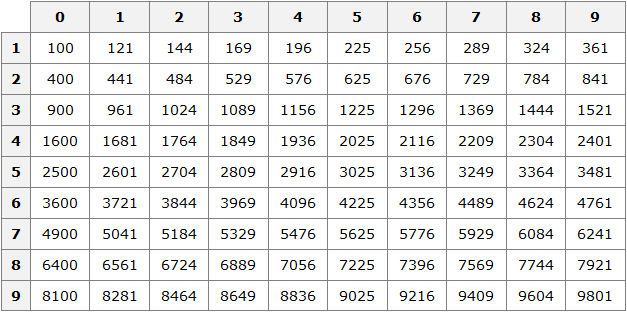
Например, пусть исходным числом будет 576. Данное число принадлежит промежутку [100; 10000]. Сразу делаем вывод, что квадратный корень из числа 576 будет принадлежать промежутку [10; 100]. Теперь открываем таблицу квадратов и смотрим какое число во второй степени равно 576
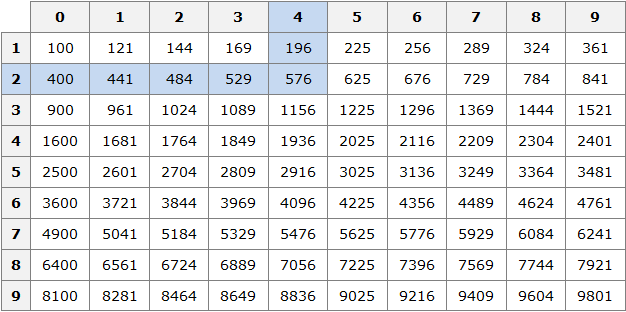
Видим, что это число 24. Значит ![]() .
.
Пример 2. Извлечь квадратный корень из числа 432.
Число 432 принадлежит промежутку [100; 10000]. Значит квадратный корень следует искать в промежутке [10; 100]. Открываем таблицу квадратов и смотрим какое число во второй степени равно 432. Обнаруживаем, что число 432 в таблице квадратов отсутствует. В этом случае квадратный корень следует искать приближённо.
Извлечем квадратный корень из числа 432 с точностью до десятых.
В таблице квадратов ближайшее меньшее число к 432 это число 400. Квадратный корень из него равен 20. Отталкиваясь от числа 20, будем проверять различные десятичные дроби, целая часть которых равна 20.
Проверим, например, число 20,8. Для этого возведём его в квадрат:
20,82 = 432,64
Получилось число 432,64 которое превосходит исходное число 432 на 0,64. Видим, что значение 20,8 великó для корня √432. Проверим тогда значение 20,7
20,72 = 428,49
Значение 20,7 годится в качестве корня, поскольку в результате возведения этого числа в квадрат получается число 428,49, которое меньше исходного числа 432, но близко к нему. Значит √432 ≈ 20,7.
Необязательно запоминать промежутки чтобы узнать в каких границах располагается корень. Можно воспользоваться методом нахождения ближайших квадратов с чётным количеством нулей на конце.
Например, извлечём корень из числа 4225. Нам известен ближайший меньший квадрат 3600, и ближайший больший квадрат 4900
3600 < 4225 < 4900
Извлечём квадратные корни из чисел 3600 и 4900. Это числа 60 и 70 соответственно:
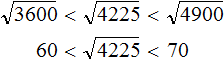
Тогда можно понять, что квадратный корень из числа 4225 располагается между числами 60 и 70. Можно даже найти его методом подбора. Корни 60 и 70 исключаем сразу, поскольку это корни чисел 3600 и 4900. Затем можно проверить, например, корень 64. Возведём его в квадрат (или умнóжим данное число само на себя)
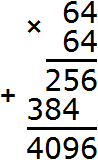
Корень 64 не годится. Проверим корень 65
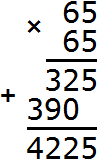
Получается 4225. Значит 65 является корнем числа 4225
![]()
Тождественные преобразования с квадратными корнями
Над квадратными корнями можно выполнять различные тождественные преобразования, тем самым облегчая их вычисление. Рассмотрим некоторые из этих преобразований.
Квадратный корень из произведения
Квадратный корень из произведения это выражение вида ![]() , где a и b некоторые числа.
, где a и b некоторые числа.
Например, выражение ![]() является квадратным корнем из произведения чисел 4 и 9.
является квадратным корнем из произведения чисел 4 и 9.
Чтобы извлечь такой квадратный корень, нужно по отдельности извлечь квадратные корни из множителей 4 и 9, представив выражение ![]() в виде произведения корней
в виде произведения корней ![]() . Вычислив по отдельности эти корни полýчим произведение 2 × 3, которое равно 6
. Вычислив по отдельности эти корни полýчим произведение 2 × 3, которое равно 6
![]()
Конечно, можно не прибегать к таким манипуляциям, а вычислить сначала подкореннóе выражение 4 × 9, которое равно 36. Затем извлечь квадратный корень из числа 36
![]()
Но при извлечении квадратных корней из больших чисел это правило может оказаться весьма полезным.
Допустим, потребовалось извлечь квадратный корень из числа 144. Этот корень легко определяется с помощью таблицы квадратов — он равен 12
![]()
Но предстáвим, что таблицы квадратов под рукой не оказалось. В этом случае число 144 можно разложить на простые множители. Затем из этих простых множителей составить числа, квадратные корни из которых извлекаются.
Итак, разлóжим число 144 на простые множители:

Получили следующее разложение:
![]()
В разложéнии содержатся четыре двойки и две тройки. При этом все числа, входящие в разложение, перемнóжены. Это позволяет предстáвить произведения одинаковых сомножителей в виде степени с показателем 2.
Тогда четыре двойки можно заменить на запись 22 × 22, а две тройки заменить на 32
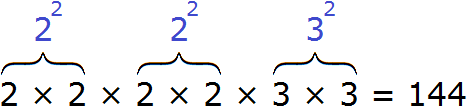
В результате будем иметь следующее разложение:
![]()
Теперь можно извлекáть квадратный корень из разложения числа 144
![]()
Применим правило извлечения квадратного корня из произведения:
![]()
Ранее было сказано, что если подкореннóе выражение возведенó во вторую степень, то такой квадратный корень равен модулю из подкореннóго выражения.
Тогда получится произведение 2 × 2 × 3, которое равно 12
![]()
Простые множители представляют в виде степени для удобства и короткой записи. Допускается также записывать их под кóрнем как есть, чтобы впоследствии перемнóжив их, получить новые сомножители.
Так, разложив число 144 на простые множители, мы получили разложение 2 × 2 × 2 × 2 × 3 × 3. Это разложение можно записать под кóрнем как есть:
![]()
затем перемнóжить некоторые сомножители так, чтобы получились числа, квадратные корни из которых извлекаются. В данном случае можно дважды перемнóжить две двойки и один раз перемнóжить две тройки:
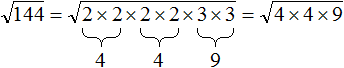
Затем применить правило извлечения квадратного корня из произведения и получить окончательный ответ:
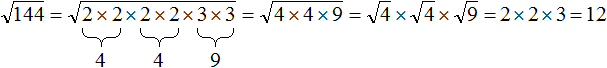
С помощью правила извлечения квадратного корня из произведения можно извлекать корень и из других больших чисел. В том числе, из тех чисел, которых нет в таблице квадратов.
Например, извлечём квадратный корень из числа 13456. Этого числа нет в таблице квадратов, поэтому воспользуемся правилом извлечения квадратного корня из произведения, предварительно разложив число 13456 на простые множители.
Итак, разложим число 13456 на простые множители:

В разложении имеются четыре двойки и два числа 29. Двойки дважды предстáвим как 22. А два числа 29 предстáвим как 292. В результате полýчим следующее разложение числа 13456
![]()
Теперь будем извлекать квадратный корень из разложения числа 13456
![]()
Итак, если a ≥ 0 и b ≥ 0, то ![]() . То есть корень из произведения неотрицательных множителей равен произведению корней из этих множителей.
. То есть корень из произведения неотрицательных множителей равен произведению корней из этих множителей.
Докажем равенство ![]() . Для этого воспользуемся определением квадратного корня.
. Для этого воспользуемся определением квадратного корня.
Согласно определению, квадратным корня из числа a есть число b, при котором выполняется равенство b2 = a.
В нашем случае нужно удостовериться, что правая часть равенства ![]() при возведении во вторую степень даст в результате подкореннóе выражение левой части, то есть выражение ab.
при возведении во вторую степень даст в результате подкореннóе выражение левой части, то есть выражение ab.
Итак, выпишем правую часть равенства ![]() и возведём ее во вторую степень:
и возведём ее во вторую степень:
![]()
Теперь воспользуемся правилом возведения в степень произведения. Согласно этому правилу, каждый множитель данного произведения нужно возвести в указанную степень:
![]()
Ранее было сказано, что если выражение вида ![]() возвести во вторую степень, то получится подкореннóе выражение. Применим это правило. Тогда полýчим ab. А это есть подкореннóе выражение квадратного корня
возвести во вторую степень, то получится подкореннóе выражение. Применим это правило. Тогда полýчим ab. А это есть подкореннóе выражение квадратного корня ![]()
![]()
Значит равенство ![]() справедливо, поскольку при возведéнии правой части во вторую степень, получается подкореннóе выражение левой части.
справедливо, поскольку при возведéнии правой части во вторую степень, получается подкореннóе выражение левой части.
Правило извлечения квадратного корня из произведения работает и в случае, если под кóрнем располагается более двух множителей. То есть справедливым будет следующее равенство:
![]() , при a ≥ 0 и b ≥ 0, c ≥ 0.
, при a ≥ 0 и b ≥ 0, c ≥ 0.
Пример 1. Найти значение квадратного корня ![]()
Запишем корень ![]() в виде произведения корней, извлечём их, затем найдём значение полученного произведения:
в виде произведения корней, извлечём их, затем найдём значение полученного произведения:
![]()
Пример 2. Найти значение квадратного корня ![]()
Предстáвим число 250 в виде произведения чисел 25 и 10. Делать это будем под знáком корня:
![]()
Теперь под кóрнем образовалось два одинаковых множителя 10 и 10. Перемнóжим их, полýчим 100
![]()
Далее применяем правило извлечения квадратного кóрня из произведения и получáем окончательный ответ:
![]()
Пример 3. Найти значение квадратного корня ![]()
Воспользуемся правилом возведения степени в степень. Степень 114 предстáвим как (112)2.
![]()
Теперь воспользуемся правилом извлечения квадратного кóрня из квадрата числа:
![]()
В нашем случае квадратный корень из числа (112)2 будет равен 112. Говоря простым языком, внешний показатель степени 2 исчезнет, а внутренний останется:
![]()
Далее возводим число 11 во вторую степень и получаем окончательный ответ:
![]()
Этот пример также можно решить, воспользовавшись правилом извлечения квадратного корня из произведения. Для этого подкореннóе выражение 114 нужно записать в виде произведения 112 × 112. Затем извлечь квадратный корень из этого произведения:
![]()
Пример 4. Найти значение квадратного корня ![]()
Перепишем степень 34 в виде (32)2, а степень 56 в виде (53)2
![]()
Далее используем правило извлечения квадратного кóрня из произведения:
![]()
Далее используем правило извлечения квадратного кóрня из квадрата числа:
![]()
Вычислим произведение получившихся степеней и полýчим окончательный ответ:
![]()
Сомножители, находящиеся под корнем, могут быть десятичными дробями. Например, извлечём квадратный корень из произведения ![]()
Запишем корень ![]() в виде произведения корней, извлечём их, затем найдём значение полученного произведения:
в виде произведения корней, извлечём их, затем найдём значение полученного произведения:
![]()
Пример 6. Найти значение квадратного корня ![]()
![]()
Пример 7. Найти значение квадратного корня ![]()
![]()
Если первый сомножитель умножить на число n, а второй сомножитель разделить на это число n, то произведение не изменится.
Например, произведение 8 × 4 равно 32
8 × 4 = 32
Умнóжим сомножитель 8 скажем на число 2, а сомножитель 4 раздéлим на это же число 2. Тогда получится произведение 16 × 2, которое тоже равно 32.
(8 × 2) × (4 : 2) = 32
Это свойство полезно при решении некоторых задач на извлечение квадратных корней. Сомножители подкореннóго выражения можно умнóжить и разделить так, чтобы корни из них извлекались.
Например, извлечём квадратный корень из произведения ![]() . Если сразу воспользоваться правилом извлечения квадратного корня из произведения, то не полýчится извлечь корни √1,6 и √90, потому что они не извлекаются.
. Если сразу воспользоваться правилом извлечения квадратного корня из произведения, то не полýчится извлечь корни √1,6 и √90, потому что они не извлекаются.
Проанализировав подкореннóе выражение 1,6 × 90, можно заметить, что если первый сомножитель 1,6 умножить на 10, а второй сомножитель 90 разделить на 10, то полýчится произведение 16 × 9. Из такого произведения квадратный корень можно извлечь, пользуясь правилом извлечения квадратного корня из произведения.
Запишем полное решение данного примера:
![]()
Процесс умножения и деления можно выполнять в уме. Также можно пропустить подробную запись извлечения квадратного корня из каждого сомножителя. Тогда решение станóвится короче:
![]()
Пример 9. Найти значение квадратного корня ![]()
Умнóжим первый сомножитель на 10, а второй раздéлим на 10. Тогда под кóрнем образуется произведение 36 × 0,04, квадратный корень из которого извлекается:
![]()
Если в равенстве ![]() поменять местами левую и правую часть, то полýчим равенство
поменять местами левую и правую часть, то полýчим равенство ![]() . Это преобразовáние позволяет упрощáть вычисление некоторых корней.
. Это преобразовáние позволяет упрощáть вычисление некоторых корней.
Например, узнáем чему равно значение выражения ![]() .
.
Квадратные корни из чисел 10 и 40 не извлекаются. Воспользуемся правилом ![]() , то есть заменим выражение из двух корней
, то есть заменим выражение из двух корней ![]() на выражение с одним корнем, под которым будет произведение из чисел 10 и 40
на выражение с одним корнем, под которым будет произведение из чисел 10 и 40
![]()
Теперь найдём значение произведения, находящегося под корнем:
![]()
А квадратный корень из числа 400 извлекается. Он равен 20
![]()
Сомножители, располагáющиеся под корнем, можно расклáдывать на множители, группировáть, представлять в виде степени, а также перемножáть для получения новых сомножителей, корни из которых извлекаются.
Например, найдём значение выражения ![]() .
.
Воспользуемся правилом ![]()
![]()
Сомножитель 32 это 25. Предстáвим этот сомножитель как 2 × 24
![]()
Перемнóжим сомножители 2 и 2, полýчим 4. А сомножитель 24 предстáвим в виде степени с показателем 2
![]()
Теперь воспóльзуемся правилом ![]() и вычислим окончательный ответ:
и вычислим окончательный ответ:
![]()
Пример 12. Найти значение выражения ![]()
Воспользуемся правилом ![]()
![]()
Сомножитель 8 это 2 × 2 × 2, а сомножитель 98 это 2 × 7 × 7
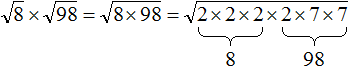
Теперь под кóрнем имеются четыре двойки и две семёрки. Четыре двойки можно записать как 22 × 22, а две семёрки как 72
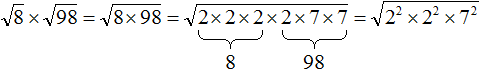
Теперь воспользуемся правилом ![]() и вычислим окончательный ответ:
и вычислим окончательный ответ:
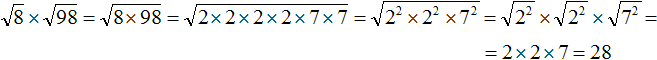
Квадратный корень из дроби
Квадратный корень вида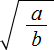 равен дроби, в числителе которой квадратный корень из числа a, а в знаменателе — квадратный корень из числа b
равен дроби, в числителе которой квадратный корень из числа a, а в знаменателе — квадратный корень из числа b

Например, квадратный корень из дроби ![]() равен дроби, в числителе которой квадратный корень из числа 4, а в знаменателе — квадратный корень из числа 9
равен дроби, в числителе которой квадратный корень из числа 4, а в знаменателе — квадратный корень из числа 9
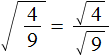
Вычислим квадратные корни в числителе и знаменателе:
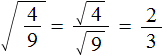
Значит, квадратный корень из дроби ![]() равен
равен .
Докáжем, что равенство  является верным.
является верным.
Возведём правую часть во вторую степень. Если в результате полýчим дробь ![]() , то это будет означать, что равенство
, то это будет означать, что равенство  верно:
верно:
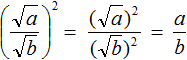
Пример 1. Извлечь квадратный корень 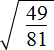
Воспользуемся правилом извлечения квадратного корня из дроби:
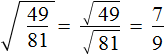
Пример 2. Извлечь квадратный корень 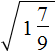
Переведём подкореннóе выражение в неправильную дробь, затем воспользуемся правилом извлечения квадратного корня из дроби:
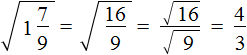
Пример 3. Извлечь квадратный корень ![]()
Квадратным корнем из числа 0,09 является 0,3. Но можно извлечь этот корень, воспользовавшись правилом извлечения квадратного корня из дроби.
Предстáвим подкоренное выражение в виде обыкновенной дроби. 0,09 это девять сотых:
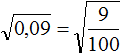
Теперь можно воспользоваться правилом извлечения квадратного корня из дроби:
Пример 4. Найти значение выражения ![]()
Извлечём корни из 0,09 и 0,25, затем сложим полученные результаты:
![]()
Также можно воспользоваться правилом извлечения квадратного корня из дроби:
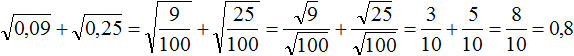
В данном примере первый способ оказался проще и удобнее.
Пример 5. Найти значение выражения ![]()
Сначала вычислим квадратный корень, затем перемнóжим его с 10. Получившийся результат вычтем из 4
![]()
Пример 6. Найти значение выражения ![]()
Сначала найдём значение квадратного корня ![]() . Он равен 0,6 поскольку 0,62 = 0,36
. Он равен 0,6 поскольку 0,62 = 0,36
![]()
Теперь вычислим получившееся выражение. Согласно порядку действий, сначала надо выполнить умножение, затем сложение:
![]()
Вынесение множителя из-под знака корня
В некоторых задачах может быть полезным вынесение множителя из-под знака корня.
Рассмотрим квадратный корень из произведения ![]() . Согласно правилу извлечения квадратного корня из произведения, нужно извлечь квадратный корень из каждого множителя данного произведения:
. Согласно правилу извлечения квадратного корня из произведения, нужно извлечь квадратный корень из каждого множителя данного произведения:
![]()
В нашем примере квадратный корень извлекается только из множителя 4. Его мы извлечём, а выражение ![]() оставим без изменений:
оставим без изменений:
![]()
Это и есть вынесение множителя из-под знака корня.
На практике подкореннóе выражение чаще всего требуется разложить на множители.
Пример 2. Вынести множитель из-под знака корня в выражении ![]()
Разлóжим подкореннóе выражение на множители 9 и 2. Тогда полýчим:
![]()
Теперь воспользуемся правило извлечения квадратного корня из произведения. Извлечь можно только корень из множителя 9. Множитель 2 остáвим под кóрнем:
![]()
Пример 3. Вынести множитель из-под знака корня в выражении ![]()
Разлóжим подкореннóе выражение на множители 121 и 3. Тогда полýчим:
![]()
Теперь воспользуемся правилом извлечения квадратного корня из произведения. Извлечь можно только корень из множителя 121. Выражение √3 остáвим под корнем:
![]()
Пример 4. Вынести множитель из-под знака корня в выражении ![]()
Воспользуемся правилом извлечения квадратного корня из произведения:
![]()
Квадратный корень извлекается только из числа 121. Извлечём его, а выражение √15 оставим без изменений:
![]()
Получается, что множитель 11 вынесен из-под знака корня. Вынесенный множитель принято записывать до выражения с корнем. Поменяем выражения √15 и 11 местами:
![]()
Пример 5. Вынести множитель из-под знака корня в выражении ![]()
Разлóжим подкореннóе выражение на множители 4 и 3
![]()
Воспользуемся правилом извлечения квадратного корня из произведения:
![]()
Извлечём корень из числа 4, а выражение √3 остáвим без изменений:
![]()
Пример 6. Упростить выражение ![]()
Предстáвим второе слагаемое ![]() в виде
в виде ![]() . А третье слагаемое
. А третье слагаемое ![]() предстáвим в виде
предстáвим в виде ![]()
![]()
Теперь в выражениях ![]() и
и ![]() вынесем множитель из-под знака корня:
вынесем множитель из-под знака корня:
![]()
Во втором слагаемом ![]() перемнóжим числа −4 и 4. Остальное перепишем без изменений:
перемнóжим числа −4 и 4. Остальное перепишем без изменений:
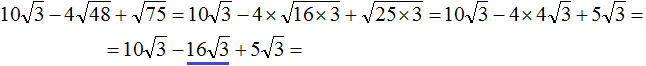
Замечáем, что получившемся выражении квадратный корень √3 является общим множителем. Вынесем его за скобки:
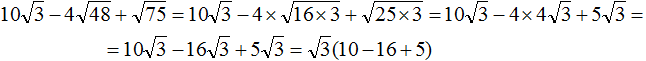
Вычислим содержимое скобок, полýчим −1
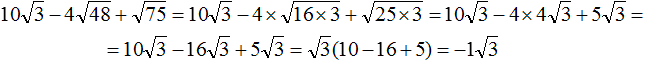
Если множителем является −1, то записывают только минус. Единица опускается. Тогда полýчим окончательный ответ −√3
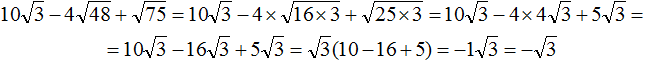
Внесение множителя под знак корня
Рассмотрим следующее выражение:
![]()
В этом выражении число 5 умнóжено на квадратный корень из числа 9. Найдём значение этого выражения.
Сначала извлечём квадратный корень, затем перемнóжим его с числом 5.
Квадратный корень из 9 равен 3. Перемнóжим его с числом 5. Тогда полýчим 15
![]()
Число 5 в данном случае было множителем. Внесём этот множитель под знак корня. Но сделать это нужно таким образом, чтобы в результате наших действий значение исходного выражения не изменилось. Проще говоря, после внесения множителя 5 под знак корня, получившееся выражение по-прежнему должно быть равно 15.
Значение выражения не изменится, если число 5 возвести во вторую степень и только тогда внести его под корень:
![]()
Итак, если данó выражение ![]() , и нужно внести множитель a под знак корня, то надо возвести во вторую степень множитель a и внести его под корень:
, и нужно внести множитель a под знак корня, то надо возвести во вторую степень множитель a и внести его под корень:
![]()
Пример 1. Внести множитель под знак корня в выражении ![]()
Возведём число 7 во вторую степень и внесём его под знак корня:
![]()
Пример 2. Внести множитель под знак корня в выражении ![]()
Возведём число 10 во вторую степень и внесем его под знак корня:
![]()
Пример 3. Внести множитель под знак корня в выражении ![]()
![]()
Вносить под знак корня можно только положительный множитель. Ранее было сказано, что выражение вида ![]() не имеет смысла.
не имеет смысла.
Однако, если перед знаком кóрня располагается отрицательный множитель, то минус можно оставить за знáком корня, а самó число внести под знак корня.
Пример 4. Внести множитель по знак корня в выражении ![]()
В этом примере под знак корня внóсится только 3. Минус остаётся за знáком корня:
![]()
Пример 5. Выполнить возведéние в степень в следующем выражении:
![]()
Воспользуемся формулой квадрата суммы двух выражений:
(a + b)2 = a2 + 2ab + b2
Роль переменной a в данном случае играет выражение √3, роль переменной b — выражение √2. Тогда полýчим:
![]()
Теперь необходимо упростить получившееся выражение.
Для выражений ![]() и
и ![]() применим правило
применим правило ![]() . Ранее мы говорили, что если выражение вида
. Ранее мы говорили, что если выражение вида ![]() возвести во вторую степень, то это выражение будет равно подкореннóму выражению a.
возвести во вторую степень, то это выражение будет равно подкореннóму выражению a.
А в выражении ![]() для множителей
для множителей ![]() и
и ![]() применим правило
применим правило ![]() . То есть заменим произведение корней на один общий корень:
. То есть заменим произведение корней на один общий корень:
![]()
Приведём подобные слагаемые. В данном случае можно сложить слагаемые 3 и 2. А в слагаемом ![]() вычислить произведение, которое под кóрнем:
вычислить произведение, которое под кóрнем:
![]()
Задания для самостоятельного решения
Задание 1. Найдите значение квадратного корня:
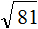
Решение:

Задание 2. Найдите значение квадратного корня:

Решение:
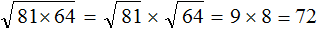
Задание 3. Найдите значение квадратного корня:
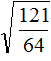
Решение:
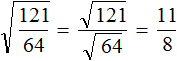
Задание 4. Найдите значение выражения:
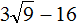
Решение:

Задание 5. Найдите значение квадратного корня:
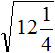
Решение:
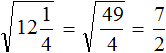
Задание 6. Найдите значение квадратного корня:
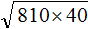
Решение:
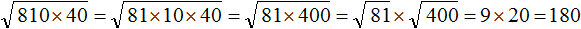
Задание 7. Найдите значение квадратного корня:
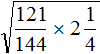
Решение:
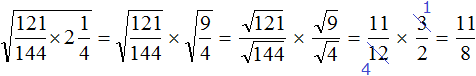
Задание 8. Найдите значения следующих выражений:
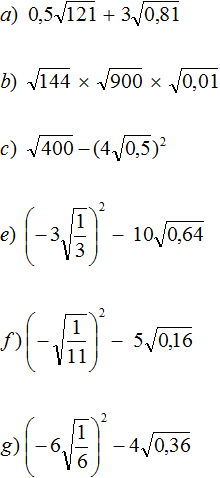
Решение:
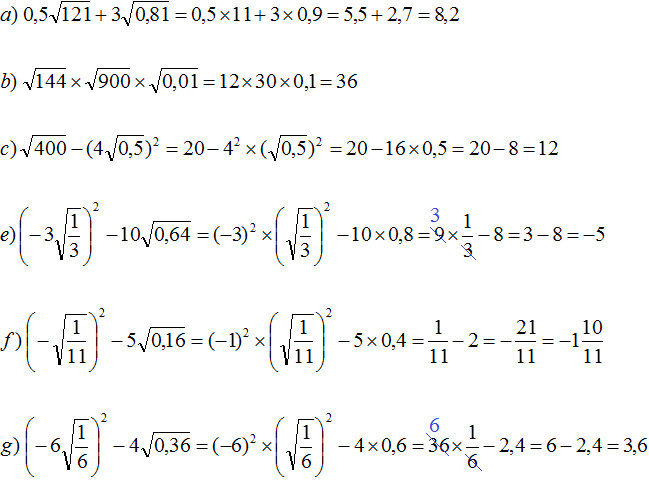
Задание 9. Извлеките квадратный корень из числа 4624
Решение:
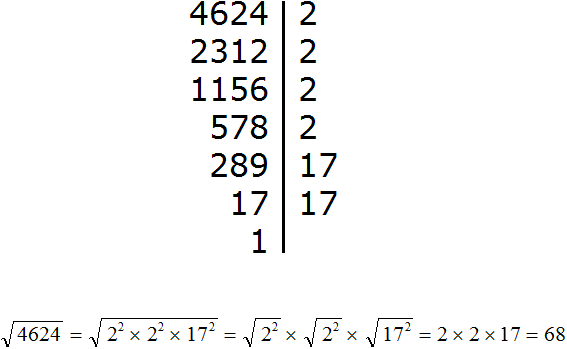
Задание 10. Извлеките квадратный корень из числа 11025
Решение:

Задание 11. Найдите значение квадратного корня:
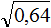
Решение:

Задание 12. Найдите значение квадратного корня:
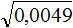
Решение:

Задание 13. Найдите значение квадратного корня:
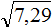
Решение:

Задание 14. Найдите значение квадратного корня:
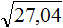
Решение:
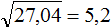
Задание 15. Найдите значение квадратного корня:
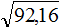
Решение:
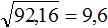
Задание 16. Найдите значение выражения:
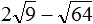
Решение:
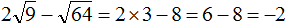
Задание 17. Найдите значение выражения:
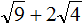
Решение:
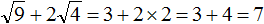
Задание 18. Найдите значение выражения:

Решение:

Задание 19. Найдите значение выражения:
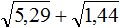
Решение:

Задание 20. Найдите значение выражения:

Решение:

Задание 21. Найдите значение выражения:

Решение:

Задание 22. Найдите значение выражения:
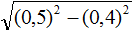
Решение:
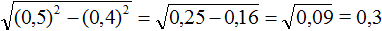
Задание 23. Найдите значение выражения:
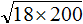
Решение:
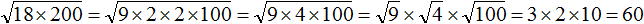
Задание 24. Найдите значение выражения:
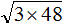
Решение:

Задание 25. Найдите значение выражения:
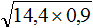
Решение:
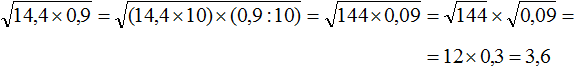
Задание 26. Найдите значение выражения:
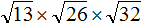
Решение:

Задание 27. Найдите значение выражения:
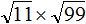
Решение:

Задание 28. Найдите значение выражения:

Решение:

Задание 29. Найдите значение выражения:
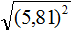
Решение:

Задание 30. Найдите значение выражения:
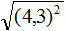
Решение:

Задание 31. Найдите значение выражения:
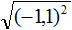
Решение:
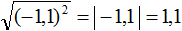
Задание 32. Найдите значение выражения:

Решение:
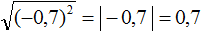
Задание 33. Найдите значение выражения:

Решение:
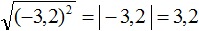
Задание 34. Вынести множитель из-под знака корня:

Решение:
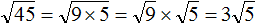
Задание 35. Вынести множитель из-под знака корня:
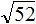
Решение:

Задание 36. Вынести множитель из-под знака корня:
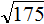
Решение:
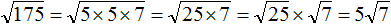
Задание 37. Вынести множитель из-под знака корня:
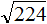
Решение:
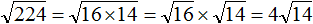
Задание 38. Вынести множитель из-под знака корня:
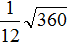
Решение:

Задание 39. Вынести множитель из-под знака корня:
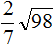
Решение:
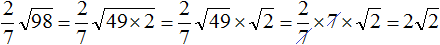
Задание 40. Вынести множитель из-под знака корня:
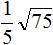
Решение:

Задание 41. Вынести множитель из-под знака корня:

Решение:

Задание 42. Вынести множитель из-под знака корня:
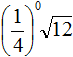
Решение:

Задание 43. Вынести множитель из-под знака корня:
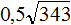
Решение:

Задание 44. Вынести множитель из-под знака корня в следующих выражениях:

Решение:
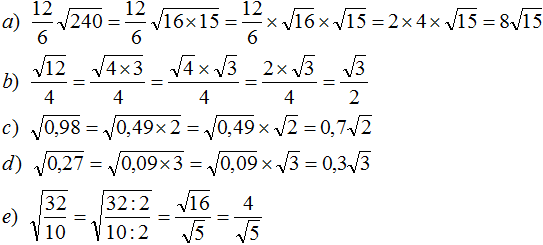
Задание 45. Внести множитель под знак корня:
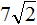
Решение:

Задание 46. Внести множитель под знак корня:
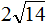
Решение:
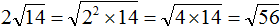
Задание 47. Внести множитель под знак корня:

Решение:
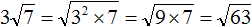
Задание 48. Внести множитель под знак корня:
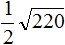
Решение:
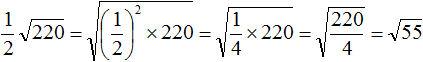
Задание 49. Внести множитель под знак корня:
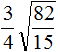
Решение:
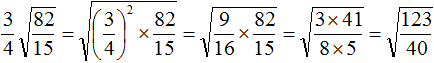
Задание 50. Внести множитель под знак корня в следующих выражениях:
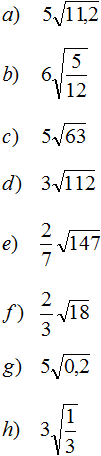
Решение:

Задание 51. Упростить выражение:

Решение:
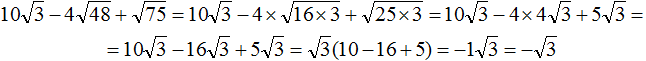
Задание 52. Упростить выражение:

Решение:

Задание 53. Упростить выражение:

Решение:

Задание 54. Упростить выражение:
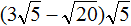
Решение:

Задание 55. Упростить выражение:
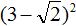
Решение:

Задание 56. Упростить выражение:

Решение:
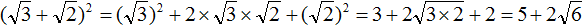
Задание 57. Упростить выражение:

Решение:
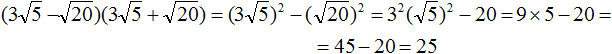
Задание 58. Упростить выражение:
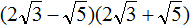
Решение:
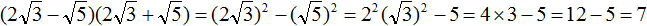
Задание 59. Упростить выражение:
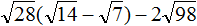
Решение:

Задание 60. Упростить выражение:
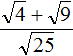
Решение:
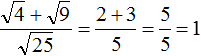
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже


Как решать уравнения с корнем (с иллюстрациями)
‘).insertAfter(«#intro»),$(‘
‘).insertBefore(«.youmightalsolike»),$(‘
‘).insertBefore(«#quiz_container»),$(‘
‘).insertBefore(«#newsletter_block_main»),fa(!
0),b=document.getElementsByClassName(«scrolltomarker»),a=0;a
В этой статье:
Понимание квадратов чисел и квадратных корней
Использование алгоритма деления столбиком
Быстрый подсчет неполных квадратов
Дополнительные статьи
Источники
Хотя пугающий вид символа квадратного корня и может заставить съежиться человека, не сильного в математике, задачи с квадратным корнем не такие уж и трудные, как это может вначале показаться. Простые задачи с квадратным корнем довольно часто можно решить так же легко, как обычные задачи с умножением или делением. С другой стороны, более сложные задачи могут потребовать некоторых усилий, но с правильным подходом даже они не составят вам труда.
Начните решать задачи с корнем уже сегодня, чтобы научиться этому радикально новому математическому умению!
Шаги
-
1
Возведите число в квадрат, умножив его само на себя. Для того чтобы понять квадратные корни, лучше начать с квадратов чисел. Квадраты чисел довольно просты: возведение числа в квадрат означает умножение его само на себя. Например, 3 в квадрате это то же самое, что и 3 × 3 = 9, а 9 в квадрате это то же самое, что и 9 × 9 = 81. Квадраты помечаются написанием небольшой цифры «2» справа над возводящим в квадрат числом. Пример: 32, 92, 1002 и так далее.
- Попробуйте сами возвести в квадрат еще несколько чисел, чтобы опробовать эту концепцию. Помните, возведение числа в квадрат означает, что это число следует умножить само на себя. Это можно сделать даже для отрицательных чисел. В таком случае результат всегда будет положительным. Например: -8
2 = -8 × -8 = 64.
- Попробуйте сами возвести в квадрат еще несколько чисел, чтобы опробовать эту концепцию. Помните, возведение числа в квадрат означает, что это число следует умножить само на себя. Это можно сделать даже для отрицательных чисел. В таком случае результат всегда будет положительным. Например: -8
-
2
Когда речь идет о квадратных корнях, то здесь идет обратный процесс возведению в квадрат. Символ корня (√, его также называют радикалом) по существу означает противоположность символа 2. Когда вы видите радикал, вы должны спросить себя: «Какое число может умножиться само на себя, чтобы получилось число под корнем?». Например, если вы видите √(9), тогда вы должны найти число, которое при возведении в квадрат давало бы число девять. В нашем случае этим числом будет три, потому что 32 = 9.
- Рассмотрим еще один пример и найдем корень из 25 (√(25)). Это означает, что нам необходимо найти число, которое бы в квадрате давало нам 25. Так как 52 = 5 × 5 = 25, можно сказать, что √(25) = 5.
- Вы также может думать об этом, как об «аннулировании» возведения в квадрат. Например, если нам необходимо найти √(64), квадратный корень 64, то давайте думать об этом числе, как о 82.
 Так как символ корня «отменяет» возведение в квадрат, то мы можем сказать, что √(64) = √(82) = 8.
Так как символ корня «отменяет» возведение в квадрат, то мы можем сказать, что √(64) = √(82) = 8.
-
3
Знайте разницу между идеальным и не идеальным возведением в квадрат. До этих пор ответами на наши задачи с корнем были хорошие и круглые числа, но это не всегда так. Ответами задач с квадратным корнем могут быть очень длинные и неудобные числа с десятичной дробью. Числа, корень которых представляет собой целые числа (другими словами, числа которые не являются дробью) называются полными квадратами. Все вышеупомянутые примеры (9, 25 и 64) являются полными квадратами, потому что их корнем будет целое число (3,5 и 8).
- С другой стороны, числа, которые при возведении под корень не дают целого числа, называются неполными квадратами. Если поставить одно из этих чисел под корень, то вы получите число с десятичной дробью. Иногда такое число может оказаться весьма длинным. Например, √(13) = 3,605551275464.
 ..
..
- С другой стороны, числа, которые при возведении под корень не дают целого числа, называются неполными квадратами. Если поставить одно из этих чисел под корень, то вы получите число с десятичной дробью. Иногда такое число может оказаться весьма длинным. Например, √(13) = 3,605551275464.
-
4
Запомните первые 1-12 полных квадратов. Как вы, вероятно, уже заметили, найти корень полного квадрата довольно легко! Из-за того, что эти задачи такие простые, стоит запомнить корни первой дюжины полных квадратов. Вы не раз столкнетесь с этими числами, так что потратьте немного времени, чтобы запомнить их пораньше и сэкономить время в будущем.
- 12 = 1 × 1 = 1
- 22 = 2 × 2 = 4
- 32 = 3 × 3 = 9
- 42 = 4 × 4 = 16
- 52 = 5 × 5 = 25
- 62 = 6 × 6 = 36
- 72 = 7 × 7 = 49
- 82 = 8 × 8 = 64
- 92 = 9 × 9 = 81
- 102 = 10 × 10 = 100
- 112 = 11 × 11 = 121
- 122 = 12 × 12 = 144
-
5
Упростите корни, убрав из него полные квадраты, если это возможно.
 Найти корень неполного квадрата иногда может оказаться нелегко, особенно если вы не используете калькулятор (в разделе ниже вы найдете несколько трюков, как сделать этот процесс легче). Однако зачастую можно упростить число под корнем, чтобы с ним было легче работать. Чтобы сделать это, вам просто необходимо разделить число под корнем на множители, а затем найти корень множителя, который является полным квадратом, и записать его снаружи корня. Это проще, чем кажется. Читайте далее, чтобы получить больше информации.
Найти корень неполного квадрата иногда может оказаться нелегко, особенно если вы не используете калькулятор (в разделе ниже вы найдете несколько трюков, как сделать этот процесс легче). Однако зачастую можно упростить число под корнем, чтобы с ним было легче работать. Чтобы сделать это, вам просто необходимо разделить число под корнем на множители, а затем найти корень множителя, который является полным квадратом, и записать его снаружи корня. Это проще, чем кажется. Читайте далее, чтобы получить больше информации.[1]
X
Источник информации- Давайте предположим, что нам необходимо найти квадратный корень 900. На первый взгляд это кажется довольно тяжелой задачей! Однако это не будет так тяжело, если мы разделим число 900 на множители. Множители – это числа, которые умножаются друг на друга для того, чтобы дать новое число. Например, число 6 можно получить, умножив 1 × 6 и 2 × 3, его множителями будут числа 1, 2, 3 и 6.
- Вместо того чтобы искать корень числа 900, что немного затруднительно, давайте запишем 900, как умножение 9 × 100.
 Теперь, когда число 9, которое является полным квадратом, отделено от 100, мы можем найти его корень. √(9 × 100) = √(9) × √(100) = 3 × √(100). Другими словами, √(900) = 3√(100).
Теперь, когда число 9, которое является полным квадратом, отделено от 100, мы можем найти его корень. √(9 × 100) = √(9) × √(100) = 3 × √(100). Другими словами, √(900) = 3√(100). - Мы даже можем пойти еще дальше, разделив 100 на два множителя, 25 и 4. √(100) = √(25 × 4) = √(25) × √(4) = 5 × 2 = 10. Поэтому мы можем сказать, что √(900) = 3(10) = 30
-
6
Используйте мнимые числа, чтобы найти корень отрицательного числа. Спросите себя, какое число при умножении само на себя даст -16? Это не 4 и не -4, так как возведение этих чисел в квадрат даст нам положительное число 16. Сдались? На самом деле не существует способа записать корень -16 или любого другого отрицательного числа обычными числами. В таком случае мы должны подставить мнимые числа (обычно в форме букв или символов), чтобы они оказались вместо корня отрицательного числа. Например, переменная «i» обычно используется для возведения под корень числа -1. Как правило, корнем отрицательного числа всегда будет мнимое число (или включенное в него).

- Знайте, что хотя мнимые числа и не могут быть представлены обычными цифрами, к ним все равно можно относиться, как к таковым. Например, квадратный корень отрицательного числа можно возвести в квадрат, чтобы придать этим отрицательным числам, как и любым другим, квадратный корень. Например, i2 = -1
Реклама
-
1
Запишите задачу с корнем, как задачу деления столбиком. Хотя это может отнять довольно много времени, таким образом, вы сможете решить задачу с корнем неполных квадратов, не прибегая к помощи калькулятора. Для этого мы воспользуемся методом решения (или алгоритмом), который похож (но не точно такой же) на обычное деление столбиком. [2]
X
Источник информации
- Для начала запишите задачу с корнем в такую же форму, что и при делении столбиком. Предположим, что мы хотим найти квадратный корень числа 6,45, которое точно не является полным квадратом.

Сперва мы напишем обычный символ квадрата, а затем под ним мы напишем число. Далее над числом мы нарисуем линию, чтобы оно оказалось в небольшой «коробочке», так же как и при делении столбиком. После этого у нас получится корень с длинным хвостом и числом 6,45 под ним. - Над корнем мы будем писать числа, так что обязательно оставьте там место.
- Для начала запишите задачу с корнем в такую же форму, что и при делении столбиком. Предположим, что мы хотим найти квадратный корень числа 6,45, которое точно не является полным квадратом.
-
2
Сгруппируйте цифры по парам. Для того чтобы начать решать задачу, необходимо сгруппировать цифры числа под радикалом по парам, начав с точки в десятичной дроби. Если хотите, можете делать небольшие отметки (вроде точек, косой линии, запятых и прочего) между парами, чтобы не запутаться.
- В нашем примере, мы должны разделить на пары число 6,45 следующим образом: 6-,45-00. Обратите внимание, что слева присутствует «оставшаяся» цифра – это нормально.
-
3
Найдите наибольшее число, квадрат которого меньше или равен первой «группе».
 Начните с первого числа или пары слева. Выберите наибольшее число, квадрат которого меньше или равен оставшейся «группе». Например, если бы группа была равна 37, вы бы выбрали число 6, потому что 62 = 36 < 37, а 72 = 49 > 37. Запишите это число над первой группой. Это будет первой цифрой вашего ответа.
Начните с первого числа или пары слева. Выберите наибольшее число, квадрат которого меньше или равен оставшейся «группе». Например, если бы группа была равна 37, вы бы выбрали число 6, потому что 62 = 36 < 37, а 72 = 49 > 37. Запишите это число над первой группой. Это будет первой цифрой вашего ответа.
- В нашем примере, первой группой в 6-,45-00 будет цифра 6. Наибольшее число, которое в квадрате будет меньше или равно 6 это 22 = 4. Напишите цифру 2 над цифрой 6, которая стоит под корнем.
-
4
Удвойте только что написанное число, затем опустите его под корень и отнимите.
Возьмите первую цифру вашего ответа (число, которое вы только что нашли) и удвойте ее. Запишите результат под первой своей группой и отнимите, чтобы найти разницу. Опустите следующую пару чисел рядом с ответом. И наконец, напишите слева последнюю цифру удвоения первой цифры своего ответа, а рядом оставьте пробел.

- В нашем примере, мы начнем с удвоения цифры 2, которая является первой цифрой нашего ответа. 2 × 2 = 4. Затем мы отнимем 4 от 6 (нашей первой «группы»), получив при этом 2. Далее мы опустим следующую группу (45), чтобы получить 245. И наконец, слева мы еще раз напишем цифру 4, оставив в конце небольшой пробел, вот так: 4_
-
5
Заполните пробел. Затем вы должны прибавить цифру к правой части записанного числа, которое находится слева. Выберите цифру, перемножив которую с вашим новым числом, вы получили бы максимально большой результат, но который бы был меньше или равен «опущенному «числу». Например, если ваше «опущенное» число равно 1700, а ваше число слева это 40_, в пробел необходимо написать цифру 4, так как 404 × 4 = 1616 < 1700, в то время как 405 × 5 = 2025. Найденная в этом шаге цифра и будет второй цифрой вашего ответа, так вы можете записать ее над знаком корня.
- В нашем примере, мы должны найти число и записать его в пробелы 4_ × _, что сделает ответ как можно большим, но все же меньшим или равным 245.
 В нашем случае это цифра 5. 45 × 5 = 225, в то время как 46 × 6 = 276
В нашем случае это цифра 5. 45 × 5 = 225, в то время как 46 × 6 = 276
- В нашем примере, мы должны найти число и записать его в пробелы 4_ × _, что сделает ответ как можно большим, но все же меньшим или равным 245.
-
6
Продолжайте использовать «пустые» числа, чтобы найти ответ. Продолжайте решать это измененное деление столбиком, пока не начнете получать нули при вычитании «опущенного» числа или пока не получите желаемый уровень точности ответа. Когда вы закончите, числа, которые вы использовали, чтобы заполнить пробелы в каждом шаге (плюс самое первое число) будут составлять число вашего ответа.
- Продолжая наш пример, мы отнимем 225 от 245, чтобы получить 20. Затем, мы опустим следующую пару чисел, 00, чтобы получить 2000. Удвоим число над знаком корня. Мы получим 25 × 2 = 50. Решив пример с пробелами, 50_ × _ =/< 2,000, мы получим 3. На этом этапе над радикалом у нас будет написано 253, а повторив этот процесс снова, следующим нашим числом будет цифра 9.
-
7
Передвиньте точку десятичной дроби вперед от изначального «делимого» числа.
 Чтобы завершить свой ответ, вы должны поставить точку десятичной дроби в правильное место. К счастью, сделать это довольно легко. Все, что вам необходимо сделать, это выровнять ее относительно точки изначального числа. Например, если под корнем будет стоять число 49,8, вы должны будете поставить точку между двумя цифрами над девяткой и восьмеркой.
Чтобы завершить свой ответ, вы должны поставить точку десятичной дроби в правильное место. К счастью, сделать это довольно легко. Все, что вам необходимо сделать, это выровнять ее относительно точки изначального числа. Например, если под корнем будет стоять число 49,8, вы должны будете поставить точку между двумя цифрами над девяткой и восьмеркой.
- В нашем примере под радикалом стоит число 6,45, так что мы просто переместим точку и поставим ее между цифрами 2 и 5 в нашем ответе, получив при этом ответ равный 2,539.
Реклама
-
1
Найдите неполные квадраты, подсчитав их. Когда вы запомните полные квадраты, поиск корня неполных квадратов станет намного проще. Так как вы уже знаете дюжину полных квадратов, любое число, которое попадает в область между этими двумя полными квадратами можно найти, сведя все к приблизительному подсчету между этих значений. Начните с поиска двух полных квадратов, между которыми находится ваше число.
 Затем определите, к которому из этих чисел ваше число находится ближе.
Затем определите, к которому из этих чисел ваше число находится ближе.
- Например, предположим, что нам необходимо найти квадратный корень числа 40. Так как мы запомнили полные квадраты, мы можем сказать, что число 40 находится между 62 и 72или числам 36 и 49. Так как 40 больше 62, его корень будет больше 6, а так как оно меньше 72, его корень также будет и меньше 7. 40 немного ближе к 36, чем к 49, так что ответ, скорее всего, будет немного ближе к 6. В следующих нескольких шагах мы сузим наш ответ.
-
2
Подсчитайте квадратный корень до первого знака после десятичной точки. После того как вы выберите два полных квадрата, между которых находится ваше число, все сводится к вашему подсчету, пока вы не получите желаемый ответ. Чем больше вы подсчитаете, тем более точным будет ваш ответ. Начните с того, что выберите, куда поставить точку десятичной дроби в свой ответ. Она не должна обязательно быть верной, но зато вы сэкономите время, если воспользуетесь логикой и поставите точку как можно ближе к правильному ответу.

- В нашем примере, разумной оценкой квадратного корня числа 40 может быть 6,4, так как, исходя из вышеупомянутой информации, мы знаем, что ответ ближе к 6, чем к 7.
-
3
Умножьте приблизительное число само на себя. Следующее, что вы должны сделать, это возвести приблизительное число в квадрат. Вам, скорее всего, не повезет и вы не получите изначальное число. Оно будет или немного большим, или немного меньшим. Если ваш результат слишком большой, тогда попробуйте снова, но с немного меньшим приблизительным числом (и наоборот, если результат слишком низкий).
- Умножьте 6,4 само на себя, и вы получите 6,4 × 6,4 = 40,96, что немного больше за изначальное число.
- Так как наш ответ оказался больше, мы должны умножит число на одну десятую меньше за приблизительное и получить следующее: 6,3 × 6,3 = 39,69. Это немного меньше за изначальное число. Это значит, что квадратный корень 40 находится между 6,3 и 6,4.
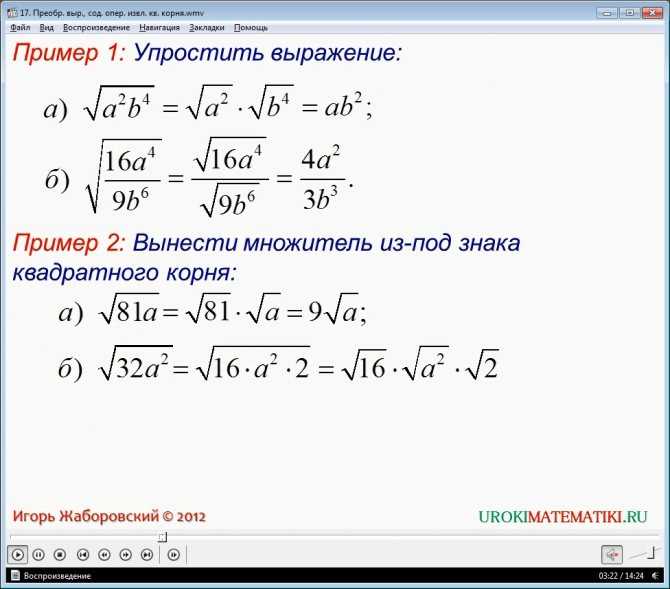 И снова, так как 39,69 ближе к 40, чем 40,96, мы знаем, что квадратный корень будет ближе к 6,3, чем к 6,4.
И снова, так как 39,69 ближе к 40, чем 40,96, мы знаем, что квадратный корень будет ближе к 6,3, чем к 6,4.
-
4
Продолжайте расчет. На этом этапе, если вы довольны своим ответом, вы можете просто взять первое угаданное приблизительное значение. Однако если вы хотите получить более точный ответ, все что вам необходимо сделать, это выбрать приблизительное значение с двумя знаками десятичной дроби, которое ставит это приблизительное значение между первыми двумя числами. Продолжив этот подсчет, вы сможете получить для своего ответа три, четыре и больше знаков после запятой. Все зависит от того, насколько далеко вы захотите зайти.
- В нашем примере давайте выберем 6,33 в качестве приблизительного значения с двумя знаками после запятой. Умножьте 6,33 само на себя, чтобы получить 6,33 × 6,33 = 40,0689. так как это немного больше нашего числа, мы возьмем число поменьше, например, 6,32. 6,32 × 6,32 = 39.9424. Этот ответ немного меньше нашего числа, так что мы знаем, что точный квадратный корень находится между 6,32 и 6,33.
 Если бы мы захотели продолжить, мы бы продолжали использовать тот же подход, чтобы получить ответ, который становился бы все точнее и точнее.
Если бы мы захотели продолжить, мы бы продолжали использовать тот же подход, чтобы получить ответ, который становился бы все точнее и точнее.
Реклама
- В нашем примере давайте выберем 6,33 в качестве приблизительного значения с двумя знаками после запятой. Умножьте 6,33 само на себя, чтобы получить 6,33 × 6,33 = 40,0689. так как это немного больше нашего числа, мы возьмем число поменьше, например, 6,32. 6,32 × 6,32 = 39.9424. Этот ответ немного меньше нашего числа, так что мы знаем, что точный квадратный корень находится между 6,32 и 6,33.
Советы
- Для быстрого поиска решения, воспользуйтесь калькулятором. Большинство современных калькуляторов могут мгновенно найти квадратный корень числа. Все что вам необходимо сделать, это ввести свое число, а затем нажать на кнопку со знаком корня. Например, для того чтобы найти корень 841, вы должны будет нажать 8, 4, 1 и (√). В результате чего вы получите ответ 39.
Реклама
Источники
Об этой статье
На других языках
Как решать уравнения с корнем — Wiki How Русский
Хотя пугающий вид символа квадратного корня и может заставить съежиться человека, не сильного в математике, задачи с квадратным корнем не такие уж и трудные, как это может вначале показаться. Простые задачи с квадратным корнем довольно часто можно решить так же легко, как обычные задачи с умножением или делением. С другой стороны, более сложные задачи могут потребовать некоторых усилий, но с правильным подходом даже они не составят вам труда. Начните решать задачи с корнем уже сегодня, чтобы научиться этому радикально новому математическому умению!
С другой стороны, более сложные задачи могут потребовать некоторых усилий, но с правильным подходом даже они не составят вам труда. Начните решать задачи с корнем уже сегодня, чтобы научиться этому радикально новому математическому умению!
Эту страницу просматривали 62 680 раз.
Реклама
Методы извлечения квадратного корня | Статья в журнале «Юный ученый»
Автор:
Прямостанов Савелий Михайлович
Научный руководитель:
Лысогорова Людмила Васильевна
Рубрика: Спецвыпуск
Опубликовано
в
Юный учёный
№2 (11) апрель 2017 г.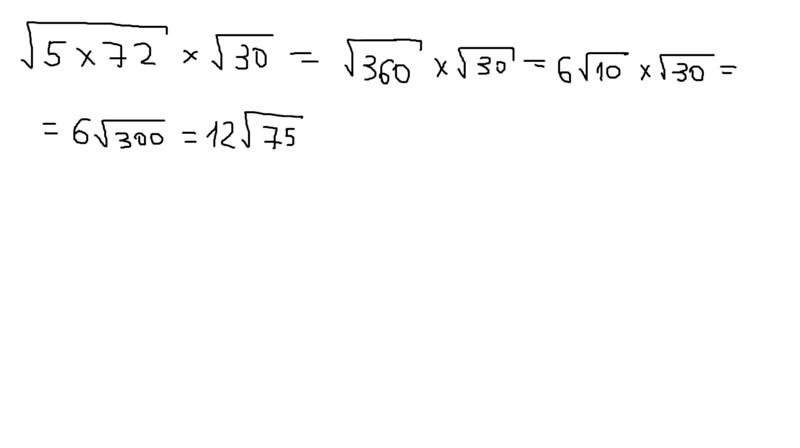
Дата публикации: 26.03.2017
2017-03-26
Статья просмотрена:
5151 раз
Скачать электронную версию
Библиографическое описание:
Прямостанов, С. М. Методы извлечения квадратного корня / С. М. Прямостанов, Л. В. Лысогорова. — Текст : непосредственный // Юный ученый. — 2017. — № 2.2 (11.2). — С. 76-77. — URL: https://moluch.ru/young/archive/11/823/ (дата обращения: 06.10.2022).
В статье описываются способы извлечения квадратного корня, и приведены примеры извлечения корней.
Ключевые слова: квадратный корень, извлечение квадратного корня.
На уроках математики я познакомился с понятием квадратного корня, и операцией извлечения квадратного корн. Мне стало интересно извлечение квадратного корня возможно только по таблице квадратов, с помощью калькулятора или есть способ извлечения вручную. Я нашел несколько способов: формула Древнего Вавилона, через решение уравнений, способ отбрасывания полного квадрата, метод Ньютона, геометрический метод, графический метод (, ), метод подбора угадыванием, метод вычетов нечётного числа.
Мне стало интересно извлечение квадратного корня возможно только по таблице квадратов, с помощью калькулятора или есть способ извлечения вручную. Я нашел несколько способов: формула Древнего Вавилона, через решение уравнений, способ отбрасывания полного квадрата, метод Ньютона, геометрический метод, графический метод (, ), метод подбора угадыванием, метод вычетов нечётного числа.
Рассмотрим следующие способы:
- Извлечение корня путем разложения подкоренного числа на простые множители. Например.
Разложим на простые множители, используя признаки делимости 27225=5*5*3*3*11*11. Таким образом
- Канадский метод. Этот быстрый метод был открыт молодыми учёными одного из ведущих университетов Канады в 20 веке. Его точность — не более двух — трёх знаков после запятой.
где х-число, из которого надо извлечь корень, с-число ближайшего квадрата), например:
=5,92
-
Столбиком.
 Этот способ позволяет найти приближённое значение корня из любого действительного числа с любой наперёд заданной точностью. К недостаткам способа можно отнести увеличивающуюся сложность вычисления с увеличением количества найденных цифр. Для ручного извлечения корня применяется запись, похожая на деление столбиком
Этот способ позволяет найти приближённое значение корня из любого действительного числа с любой наперёд заданной точностью. К недостаткам способа можно отнести увеличивающуюся сложность вычисления с увеличением количества найденных цифр. Для ручного извлечения корня применяется запись, похожая на деление столбиком
Алгоритм извлечения квадратного корня
1.От запятой отдельно дробную и отдельно целую части делим на грани по две цифры в каждой грани (целую часть — справа налево; дробную — слева направо). Возможно, что в целой части может оказаться одна цифра, а в дробной — нули.
2.Извлечение начинается слева направо, и подбираем число, квадрат которого не превосходит числа, стоящего в первой грани. Это число возводим в квадрат и записывает под числом, стоящим в первой грани.
3.Находим разность между числом, стоящим в первой грани, и квадратом подобранного первого числа.
4.К получившейся разности сносим следующую грань, полученное число будет делимым. Образовываем делитель. Первую подобранную цифру ответа удваиваем (умножаем на 2), получаем число десятков делителя, а число единиц должно быть таким, чтобы его произведение на весь делитель не превосходило делимого. Подобранную цифру записываем в ответ.
Образовываем делитель. Первую подобранную цифру ответа удваиваем (умножаем на 2), получаем число десятков делителя, а число единиц должно быть таким, чтобы его произведение на весь делитель не превосходило делимого. Подобранную цифру записываем в ответ.
5.К получившейся разности сносим следующую грань и выполняем действия по алгоритму. Если данная грань окажется гранью дробной части, то в ответе ставим запятую. (Рис. 1.)
Данным способом можно извлекать числа с разной точностью, например с точностью до тысячных. (Рис.2)
Рассматривая различные способы извлечения квадратного корня, можно сделать вывод: в каждом конкретном случае нужно определиться с выбором наиболее эффективного для того, чтобы меньше затратить времени для решения
Литература:
-
Киселев А.
 Элементы алгебры и анализа. Часть первая.-М.-1928 г
Элементы алгебры и анализа. Часть первая.-М.-1928 г
Основные термины (генерируются автоматически): квадратный корень, целая часть, грань, способ извлечения, получившаяся разность, число.
Ключевые слова
квадратный корень,
извлечение квадратного корня
квадратный корень, извлечение квадратного корня
Похожие статьи
Метод бисекции в двоичной системе счисления на примере…
Методы извлечения квадратного корня. К недостаткам способа можно отнести увеличивающуюся сложность вычисления с
Алгоритм извлечения квадратного корня. 1.От запятой отдельно дробную и отдельно целую части делим на грани по две цифры в каждой…
1.От запятой отдельно дробную и отдельно целую части делим на грани по две цифры в каждой…
Формирование устойчивого познавательного интереса…
Методы извлечения квадратного корня. Для ручного извлечения корня применяется запись, похожая на деление столбиком.
3.Находим разность между числом, стоящим в первой грани, и квадратом подобранного.
В следующей книге излагается выполнение действий над целыми и дробными числами в шестидесятичной.
Разработка
способа представления длинных чисел в памяти…
Методы извлечения квадратного корня. Его точность — не более двух — трёх знаков после запятой. где х-число, из которого надо извлечь
Его точность — не более двух — трёх знаков после запятой. где х-число, из которого надо извлечь
Для ручного извлечения корня применяется запись, похожая на деление столбиком. Возможно, что в целой части может оказаться одна…
О необходимости обучения детей делению в столбик на уроках…
Сначала расскажем про метод извлечения квадратного корня из чисел. Об этом методе пишет еще сэр Исаак Ньютон (1643–1727 гг) в
Здесь приводится метод, по которому можно извлечь корень из данного числа с точностью до 1. Покажем метод так, как он описывается в…
Исследование алгоритмов генерации простых
чисел
Методы извлечения квадратного корня. Извлечение корня путем разложения подкоренного числа на простые множители. Например . Разложим на простые множители, используя признаки делимости 27225=5*5*3*3*11*11. 5.К получившейся разности сносим следующую грань и…
Извлечение корня путем разложения подкоренного числа на простые множители. Например . Разложим на простые множители, используя признаки делимости 27225=5*5*3*3*11*11. 5.К получившейся разности сносим следующую грань и…
Основные
методы построения магических квадратов с нечетным…
Методы извлечения квадратного корня. Я нашел несколько способов: формула Древнего Вавилона, через решение уравнений, способ отбрасывания полного квадрата, метод Ньютона, геометрический метод, графический метод ( , ), метод подбора угадыванием, метод вычетов…
Интегрированный урок на тему «Положительные и отрицательные.
 ..
..
Методы извлечения квадратного корня. Это число возводим в квадрат и записывает под числом, стоящим в первой грани. 3.Находим разность между числом, стоящим в первой грани, и квадратом подобранного первого числа. Деление суммы (разности) чисел, составленных из…
Расширение набора арифметических операций до множества…
Рассмотрены обратные арифметические операции как отрицательные значения операционного параметра в общем действии a[n]kh. С использованием двух аксиом знака расширено множество натуральных операций до множества целых операций. Показано, что все 7 арифметических…
Метод «переброски» при решении квадратных уравнений
На сегодняшний день перед выпускниками школ стоит главная задача – это успешная сдача итоговой аттестации, ЕНТ и поступление в ВУЗ. В числе обязательных предметов при сдаче государственного экзамена стоит математика.
В числе обязательных предметов при сдаче государственного экзамена стоит математика.
- Как издать спецвыпуск?
- Правила оформления статей
- Оплата и скидки
Похожие статьи
Метод бисекции в двоичной системе счисления на примере…
Методы извлечения квадратного корня. К недостаткам способа можно отнести увеличивающуюся сложность вычисления с
Алгоритм извлечения квадратного корня. 1.От запятой отдельно дробную и отдельно целую части делим на грани по две цифры в каждой…
Формирование устойчивого познавательного интереса…
Методы извлечения квадратного корня. Для ручного извлечения корня применяется запись, похожая на деление столбиком.
Для ручного извлечения корня применяется запись, похожая на деление столбиком.
3.Находим разность между числом, стоящим в первой грани, и квадратом подобранного.
В следующей книге излагается выполнение действий над целыми и дробными числами в шестидесятичной.
Разработка
способа представления длинных чисел в памяти…
Методы извлечения квадратного корня. Его точность — не более двух — трёх знаков после запятой. где х-число, из которого надо извлечь
Для ручного извлечения корня применяется запись, похожая на деление столбиком. Возможно, что в целой части может оказаться одна…
О необходимости обучения детей делению в столбик на уроках.
 ..
..
Сначала расскажем про метод извлечения квадратного корня из чисел. Об этом методе пишет еще сэр Исаак Ньютон (1643–1727 гг) в
Здесь приводится метод, по которому можно извлечь корень из данного числа с точностью до 1. Покажем метод так, как он описывается в…
Исследование алгоритмов генерации простых
чисел
Методы извлечения квадратного корня. Извлечение корня путем разложения подкоренного числа на простые множители. Например . Разложим на простые множители, используя признаки делимости 27225=5*5*3*3*11*11. 5.К получившейся разности сносим следующую грань и. ..
..
Основные
методы построения магических квадратов с нечетным…
Методы извлечения квадратного корня. Я нашел несколько способов: формула Древнего Вавилона, через решение уравнений, способ отбрасывания полного квадрата, метод Ньютона, геометрический метод, графический метод ( , ), метод подбора угадыванием, метод вычетов…
Интегрированный урок на тему «Положительные и отрицательные…
Методы извлечения квадратного корня. Это число возводим в квадрат и записывает под числом, стоящим в первой грани. 3.Находим разность между числом, стоящим в первой грани, и квадратом подобранного первого числа. Деление суммы (разности) чисел, составленных из…
Деление суммы (разности) чисел, составленных из…
Расширение набора арифметических операций до множества…
Рассмотрены обратные арифметические операции как отрицательные значения операционного параметра в общем действии a[n]kh. С использованием двух аксиом знака расширено множество натуральных операций до множества целых операций. Показано, что все 7 арифметических…
Метод «переброски» при решении квадратных уравнений
На сегодняшний день перед выпускниками школ стоит главная задача – это успешная сдача итоговой аттестации, ЕНТ и поступление в ВУЗ. В числе обязательных предметов при сдаче государственного экзамена стоит математика.
Сколько будет если вычесть одинаковые корни. Как складывать и вычитать квадратные корни
В наше время современных электронных вычислительных машин вычисление корня из числа не представляется сложной задачей. Например, √2704=52, это вам подсчитает любой калькулятор. К счастью, калькулятор есть не только в Windows, но и в обычном, даже самом простеньком, телефоне. Правда если вдруг (с малой долей вероятности, вычисление которой, между прочим, включает в себя сложение корней) вы окажитесь без доступных средств, то, увы, придется рассчитывать только на свои мозги.
Например, √2704=52, это вам подсчитает любой калькулятор. К счастью, калькулятор есть не только в Windows, но и в обычном, даже самом простеньком, телефоне. Правда если вдруг (с малой долей вероятности, вычисление которой, между прочим, включает в себя сложение корней) вы окажитесь без доступных средств, то, увы, придется рассчитывать только на свои мозги.
Тренировка ума никогда не помещает. Особенно для тех, кто не так часто работает с цифрами, а уж тем более с корнями. Сложение и вычитание корней — хорошая разминка для скучающего ума. А еще я покажу поэтапно сложение корней. Примеры выражений могут быть следующие.
Уравнение, которое нужно упростить:
√2+3√48-4×√27+√128
Это иррациональное выражение. Для того чтобы его упростить нужно привести все подкоренные выражения к общему виду. Делаем поэтапно:
Первое число упростить уже нельзя. Переходим ко второму слагаемому.
3√48 раскладываем 48 на множители: 48=2×24 или 48=3×16. из 24 не является целочисленным, т. 2×2)
2×2)
Переписываем выражение с упрощенными слагаемыми:
√2+12×√3-12×√3+8×√2
Теперь складываем числа одним и тем же подкоренным выражением. Нельзя складывать или вычитать выражения с разными подкоренными выражениями. Сложение корней требует соблюдение этого правила.
Ответ получаем следующий:
√2+12√3-12√3+8√2=9√2
√2=1×√2 — надеюсь, то, что в алгебре принято опускать подобные элементы, не станет для вас новостью.
Выражения могут быть представлены не только квадратным корнем, но так же и с кубическим или корнем n-ной степени.
Сложение и вычитание корней с разными показателями степени, но с равнозначным подкоренным выражением, происходит следующим образом:
Если мы имеем выражение вида √a+∛b+∜b, то мы можем упростить это выражение так:
∛b+∜b=12×√b4 +12×√b3
12√b4 +12×√b3=12×√b4 + b3
Мы привели два подобных члена к общему показателю корня. Здесь использовалось свойство корней, которое гласит: если число степени подкоренного выражения и число показателя корня умножить на одно и то же число, то его вычисление останется неизменным.
На заметку: показатели степени складываются только при умножении.
Рассмотрим пример, когда в выражении присутствуют дроби.
5√8-4×√(1/4)+√72-4×√2
Будем решать по этапам:
5√8=5*2√2 — мы выносим из-под корня извлекаемую часть.
4√(1/4)=-4 √1/(√4)= — 4 *1/2= — 2
Если в тело корня представлено дробью, то часто этой дроби не измениться, если извлечь квадратный корень из делимого и делителя. В итоге мы получили описанное выше равенство.
√72-4√2=√(36×2)- 4√2=2√2
10√2+2√2-2=12√2-2
Вот и получился ответ.
Главное помнить, что из отрицательных чисел не извлекается корень с четным показателем степени. Если четной степени подкоренное выражение является отрицательным, то выражение является нерешаемым.
Сложение корней возможно только при совпадении подкоренных выражений, так как они являются подобными слагаемыми. То же самое относиться и к разности.
Сложение корней с разными числовыми показателями степени производиться посредством приведения к общей корневой степени обоих слагаемых. Это закон действует так же как приведение к общему знаменателю при сложении или вычитании дробей.
Это закон действует так же как приведение к общему знаменателю при сложении или вычитании дробей.
Если в подкоренном выражении имеется число, возведенное в степень, то это выражение можно упростить при условии, что между показателем корня и степени существует общий знаменатель.
Содержимое:
В математике корни могут быть квадратными, кубическими или иметь любой другой показатель (степень), который пишется слева над знаком корня. Выражение, стоящее под знаком корня, называется подкоренным выражением. Сложение корней похоже на сложение членов алгебраического выражения, то есть требует определения подобных корней.
Шаги
Часть 1
Определение корней
- 1
Обозначение корней.
Выражение под знаком корня (√) означает, что из этого выражения необходимо извлечь корень определенной степени.- Корень обозначают знаком √.
- Показатель (степень) корня пишется слева над знаком корня. Например, кубический корень из 27 записывается так: 3 √(27)
- Если показатель (степень) корня отсутствует, то показатель считается равным 2, то есть это квадратный корень (или корень второй степени).

- Число, записанное перед знаком корня, называется множителем (то есть это число умножается на корень), например 5√(2)
- Если множителя перед корнем нет, то он равен 1 (напомним, что любое число, умноженное на 1, равняется самому себе).
- Если вы впервые работаете с корнями, сделайте соответствующие пометки над множителем и показателем корня, чтобы не запутаться и лучше понять их назначение.
- 2
Запомните, какие корни можно складывать, а какие нельзя.
Также, как нельзя складывать разные члены выражения, например, 2а + 2b ≠ 4ab, вы не можете складывать разные корни.- Нельзя складывать корни с разными подкоренными выражениями, например, √(2) + √(3) ≠ √(5). Но вы можете сложить числа, стоящие под одним корнем, например, √(2 + 3) = √(5) (квадратный корень из 2 примерно равен 1,414, квадратный корень из 3 примерно равен 1,732, а квадратный корень из 5 примерно равен 2,236).
- Нельзя складывать корни с одинаковыми подкоренными выражениями, но разными показателями, например, √(64) + 3 √(64) (эта сумма не равна 5 √(64), так как квадратный корень из 64 равен 8, кубический корень из 64 равен 4, 8 + 4 = 12, что гораздо больше, чем корень пятой степени из 64, который примерно равен 2,297).

Часть 2
Упрощение и сложение корней
- 1
Определите и сгруппируйте подобные корни.
Подобные корни – корни, у которых одинаковые показатели и одинаковые подкоренные выражения. Например, рассмотрим выражение:
2√(3) + 3 √(81) + 2√(50) + √(32) + 6√(3)- Во-первых, перепишите выражение так, чтобы корни с одинаковым показателем располагались последовательно.
2√(3) + 2√(50) + √(32) + 6√(3) + 3 √(81) - Затем перепишите выражение так, чтобы корни с одинаковым показателем и с одинаковым подкоренным выражением располагались последовательно.
2√(50) + √(32) + 2√(3) + 6√(3) + 3 √(81)
- Во-первых, перепишите выражение так, чтобы корни с одинаковым показателем располагались последовательно.
- 2
Упростите корни.
Для этого разложите (где возможно) подкоренные выражения на два множителя, один из которых вынесите из-под корня. В этом случае вынесенное число и множитель корня перемножаются.- В приведенном выше примере разложите число 50 на 2*25, а число 32 – на 2*16. Из 25 и 16 можно извлечь квадратные корни (соответственно 5 и 4) и вынести 5 и 4 из-под корня, соответственно умножив их на множители 2 и 1.
 Таким образом, вы получите упрощенное выражение: 10√(2) + 4√(2) + 2√(3) + 6√(3) + 3 √(81)
Таким образом, вы получите упрощенное выражение: 10√(2) + 4√(2) + 2√(3) + 6√(3) + 3 √(81) - Число 81 можно разложить на множители 3*27, а из числа 27 можно извлечь кубический корень, равный 3. Это число 3 можно вынести из-под корня. Таким образом, вы получите еще более упрощенное выражение: 10√(2) + 4√(2) + 2√(3)+ 6√(3) + 3 3 √(3)
- В приведенном выше примере разложите число 50 на 2*25, а число 32 – на 2*16. Из 25 и 16 можно извлечь квадратные корни (соответственно 5 и 4) и вынести 5 и 4 из-под корня, соответственно умножив их на множители 2 и 1.
- 3
Сложите множители подобных корней.
В нашем примере есть подобные квадратные корни из 2 (их можно сложить) и подобные квадратные корни из 3 (их тоже можно сложить). У кубического корня из 3 подобных корней нет.- 10√(2) + 4√(2) = 14√(2).
- 2√(3)+ 6√(3) = 8√(3).
- Окончательное упрощенное выражение: 14√(2) + 8√(3) + 3 3 √(3)
- Не существует общепринятых правил порядка записи корней в выражении. Потому вы можете записывать корни в порядке возрастания их показателей и в порядке возрастания подкоренных выражений.
Содержимое:
Складывать и вычитать квадратные корни можно только при условии, что у них одинаковое подкоренное выражение, то есть вы можете сложить или вычесть 2√3 и 4√3, но не 2√3 и 2√5. Вы можете упростить подкоренное выражение, чтобы привести их к корням с одинаковыми подкоренными выражениями (а затем сложить или вычесть их).
Вы можете упростить подкоренное выражение, чтобы привести их к корням с одинаковыми подкоренными выражениями (а затем сложить или вычесть их).
Шаги
Часть 1
Постигаем основы
- 1
(выражение под знаком корня).
Для этого разложите подкоренное число на два множителя, один из которых является квадратным числом (число, из которого можно извлечь целый корень, например, 25 или 9). После этого извлеките корень из квадратного числа и запишите найденное значение перед знаком корня (под знаком корня останется второй множитель). Например, 6√50 — 2√8 + 5√12. Числа, стоящее перед знаком корня, являются множителями соответствующих корней, а числа под знаком корня – это подкоренные числа (выражения). Вот как решать данную задачу:- 6√50 = 6√(25 x 2) = (6 x 5)√2 = 30√2. Здесь вы раскладываете 50 на множители 25 и 2; затем из 25 извлекаете корень, равный 5, и 5 выносите из-под корня. Затем 5 умножаете на 6 (множитель у корня) и получаете 30√2.
- 2√8 = 2√(4 x 2) = (2 x 2)√2 = 4√2.
 Здесь вы раскладываете 8 на множители 4 и 2; затем из 4 извлекаете корень, равный 2, и 2 выносите из-под корня. Затем 2 умножаете на 2 (множитель у корня) и получаете 4√2.
Здесь вы раскладываете 8 на множители 4 и 2; затем из 4 извлекаете корень, равный 2, и 2 выносите из-под корня. Затем 2 умножаете на 2 (множитель у корня) и получаете 4√2. - 5√12 = 5√(4 x 3) = (5 x 2)√3 = 10√3. Здесь вы раскладываете 12 на множители 4 и 3; затем из 4 извлекаете корень, равный 2, и 2 выносите из-под корня. Затем 2 умножаете на 5 (множитель у корня) и получаете 10√3.
- 2
Подчеркните корни, подкоренные выражения которых одинаковы.
В нашем примере упрощенное выражение имеет вид: 30√2 — 4√2 + 10√3. В нем вы должны подчеркнуть первый и второй члены (30√2
и 4√2
), так как у них одинаковое подкоренное число 2. Только такие корни вы можете складывать и вычитать. - 3
Если вам дано выражение с большим количеством членов, многие из которых имеют одинаковые подкоренные выражения, используйте одинарное, двойное, тройное подчеркивание для обозначения таких членов, чтобы облегчить решение этого выражения. - 4
У корней, подкоренные выражения которых одинаковы, сложите или вычтите множители, стоящие перед знаком корня, а подкоренное выражение оставьте прежним (не складывайте и не вычитайте подкоренные числа!
). Идея в том, чтобы показать, сколько всего корней с определенным подкоренным выражением содержится в данном выражении.
Идея в том, чтобы показать, сколько всего корней с определенным подкоренным выражением содержится в данном выражении.
- 30√2 — 4√2 + 10√3
= - (30 — 4)√2 + 10√3
= - 26√2 + 10√3
- 30√2 — 4√2 + 10√3
Часть 2
Практикуемся на примерах
- 1
Пример 1:
√(45) + 4√5.- Упростите √(45). Разложите 45 на множители: √(45) = √(9 x 5).
- Вынесите 3 из-под корня (√9 = 3): √(45) = 3√5.
- Теперь сложите множители у корней: 3√5 + 4√5 = 7√5
- 2
Пример 2:
6√(40) — 3√(10) + √5.- Упростите 6√(40). Разложите 40 на множители: 6√(40) = 6√(4 x 10).
- Вынесите 2 из-под корня (√4 = 2): 6√(40) = 6√(4 x 10) = (6 x 2)√10.
- Перемножьте множители перед корнем и получите 12√10.
- Теперь выражение можно записать в виде 12√10 — 3√(10) + √5. Так как у первых двух членов одинаковые подкоренные числа, вы можете вычесть второй член из первого, а первый оставить без изменений.
- Вы получите: (12-3)√10 + √5 = 9√10 + √5.

- 3
Пример 3.
9√5 -2√3 — 4√5. Здесь ни одно из подкоренных выражений нельзя разложить на множители, поэтому упростить это выражение не получится. Вы можете вычесть третий член из первого (так как у них одинаковые подкоренные числа), а второй член оставить без изменений. Вы получите: (9-4)√5 -2√3 = 5√5 — 2√3. - 4
Пример 4.
√9 + √4 — 3√2.- √9 = √(3 х 3) = 3.
- √4 = √(2 х 2) = 2.
- Теперь вы можете просто сложить 3 + 2, чтобы получить 5.
- Окончательный ответ: 5 — 3√2.
- 5
Пример 5.
Решите выражение, содержащее корни и дроби. Вы можете складывать и вычислять только те дроби, у которых общий (одинаковый) знаменатель. Дано выражение (√2)/4 + (√2)/2.- Найдите наименьший общий знаменатель этих дробей. Это число, которое делится нацело на каждый знаменатель. В нашем примере на 4 и на 2 делится число 4.
- Теперь вторую дробь умножьте на 2/2 (чтобы привести ее к общему знаменателю; первая дробь уже приведена к нему): (√2)/2 х 2/2 = (2√2)/4.

- Сложите числители дробей, а знаменатель оставьте прежним: (√2)/4 + (2√2)/4 = (3√2)/4 .
- Перед суммированием или вычитанием корней обязательно упростите (если возможно) подкоренные выражения.
Предупреждения
- Никогда не суммируйте и не вычитайте корни с разными подкоренными выражениями.
- Никогда не суммируйте и не вычитайте целое число и корень, например, 3 + (2x) 1/2
.- Примечание: «х» в одной второй степени и квадратный корень из «х» – это одно и то же (то есть x 1/2 = √х).
Корень из числа проще всего вычесть с помощью калькулятора. Но, если у вас нет калькулятора, тогда надо знать алгоритм вычисления квадратного корня. Дело в том, что под корнем сидит число в квадрате. Например, 4 в квадрате — это 16. То есть корень квадратный из 16 будет равен четырем. Так же 5 в квадрате — это 25. Поэтому корень из 25 будет 5. И так далее.
Если число небольшое, то его можно легко вычесть устно, к примеру, корень из 25 будет равен 5, а корень из 144-12. Также на калькуляторе можно посчитать, есть специальный значок корня, нужно вбить число и нажать на значок.
Также на калькуляторе можно посчитать, есть специальный значок корня, нужно вбить число и нажать на значок.
Поможет также таблица квадратных корней:
Есть еще способы, которые более сложные, однако очень эффективные:
Корень из какого либо числа можно вычесть с помощью калькулятора, тем более они есть в каждом телефоне на сегодняшний день.
Можно попробовать примерно прикинуть как может получится данное число, умножив одно число само на себя.
Вычислить корень квадратный из числа не сложно, особенно, если есть специальная таблица. Всем хорошо известная таблица еще с уроков алгебры. Такая операция называется извлечение квадратного корня из числа quot;aquot;, другими словами решение уравнения. Почти все калькуляторы, в смартфонах имеют функцию определения квадратного корня.
Результатом извлечения квадратного корня из известного числа будет другое число, которое, при возведении во вторую степень (квадрат), даст то самое число, которое нам известно. Рассмотрим одно из описаний расчтов, которое представляется кратким и понятным:
Рассмотрим одно из описаний расчтов, которое представляется кратким и понятным:
Вот видео по теме:
Вычеслить корень квадратный из числа можно несколькими способами.
Самым популярным способом — является использование специальной таблицы кореня (смотрите ниже).
Также на каждом калькуляторе есть функция при помощи которой можно узнать корень.
Или при помощи специальной формулы.
Извлечь квадратный корень из числа можно несколькими способами. Один из них — самый быстрый, с помощью калькулятора.
Но если нет калькулятора, то можно это сделать вручную.
Результат получится точным.
Принцип практически такой же как деление столбиком:
Попробуем без калькулятора найти значение квадратного корняот числа, к примеру, 190969.
Таким образом, вс предельно просто. В вычислениях главное придерживаться определнных простых правил и логически размышлять.
Для этого нужна таблица квадратов
Вот например, корень из 100 = 10, из 20 = 400 из 43 = 1849
Сейчас практически все калькуляторы, в том числе и на смартфонах умеют высчитывать квадратный корень из числа. НО если калькулятора у вас нет, то можно найти корень из числа несколькими простыми способами:
Разложение на простые множители
Разложите подкоренное число на множители, являющиеся квадратными числами. В зависимости от подкоренного числа, вы получите приблизительный или точный ответ. Квадратные числа числа, из которых можно извлечь целый квадратный корень. Множители числа, которые при перемножении дают исходное число. Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как 25 = 5, 36 = 6, 49 = 7. Квадратные множители это множители, являющиеся квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.

Например, вычислите квадратный корень из 400 (вручную). Сначала попытайтесь разложить 400 на квадратные множители. 400 кратно 100, то есть делится на 25 это квадратное число. Разделив 400 на 25, вы получите 16, которое также является квадратным числом. Таким образом, 400 можно разложить на квадратные множители 25 и 16, то есть 25 х 16 = 400.
Запишите это как: 400 = (25 х 16).
Квадратные корень из произведения некоторых членов равен произведению квадратных корней из каждого члена, то есть (а х b) = a x b . Воспользовавшись этим правилом, извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ.
В нашем примере извлеките корень из 25 и из 16.
Если подкоренное число не раскладывается на два квадратных множителя (а это происходит в большинстве случаев), вы не сможете найти точный ответ в виде целого числа. Но вы можете упростить задачу, разложив подкоренное число на квадратный множитель и обыкновенный множитель (число, из которого целый квадратный корень извлечь нельзя).
Затем вы извлечете квадратный корень из квадратного множителя и будете извлекать корень из обыкновенного множителя.
Например, вычислите квадратный корень из числа 147. Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:
Теперь вы можете оценить значение корня (найти приблизительное значение), сравнив его со значениями корней квадратных чисел, находящихся ближе всего (с обеих сторон на числовой прямой) к подкоренному числу. Вы получите значение корня в виде десятичной дроби, которую необходимо умножить на число, стоящее за знаком корня.
Вернемся к нашему примеру. Подкоренное число 3. Ближайшими к нему квадратными числами будут числа 1 (1 = 1) и 4 (4 = 2). Таким образом, значение 3 расположено между 1 и 2. Та как значение 3, вероятно, ближе к 2, чем к 1, то наша оценка: 3 = 1,7. Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.

Этот метод также работает с большими числами. Например, рассмотрим 35. Подкоренное число 35. Ближайшими к нему квадратными числами будут числа 25 (25 = 5) и 36 (36 = 6). Таким образом, значение 35 расположено между 5 и 6. Та как значение 35 намного ближе к 6, чем к 5 (потому что 35 всего на 1 меньше 36), то можно заявить, что 35 немного меньше 6. Проверка на калькуляторе дает нам ответ 5,92 — мы были правы.
Еще один способ разложите подкоренное число на простые множители. Простые множители числа, которые делятся только на 1 и самих себя. Запишите простые множители в ряд и найдите пары одинаковых множителей. Такие множители можно вынести за знак корня.
Например, вычислите квадратный корень из 45. Раскладываем подкоренное число на простые множители: 45 = 9 х 5, а 9 = 3 х 3. Таким образом, 45 = (3 х 3 х 5). 3 можно вынести за знак корня: 45 = 35. Теперь можно оценить 5.
Рассмотрим другой пример: 88.
= (2 х 4 х 11)
= (2 х 2 х 2 х 11).
Вы получили три множителя 2; возьмите пару из них и вынесите за знак корня.
2(2 х 11) = 22 х 11. Теперь можно оценить 2 и 11 и найти приблизительный ответ.
Может быть полезным будет еще это обучающее видео:
Чтобы извлечь корень из числа следует воспользоваться калькулятором, либо если нет подходящего, советую зайти вот на этот сайт и решить задачу с помощью онлайн калькулятора, который за секунды выдаст правильное значение.
В математике любое действие имеет свою пару-противоположность – в сущности, это представляет собою одно из проявлений гегелевского закона диалектики: «единство и борьба противоположностей». Одно из действий в такой «паре» направлено на увеличение числа, а другое, обратное ему – на уменьшение. Например, действие, противоположное сложению – это вычитание, умножению соответствует деление. Имеется и своя диалектическая пара-противоположность и у возведения в степень. Речь идет об извлечении корня.
Извлечь из числа корень такой-то степени – это значит вычислить, какое число необходимо возвести в соответствующую степень, чтобы в итоге получилось данное число. Две степени имеют свои отдельные названия: вторая степень называется «квадратом», а третья – «кубом». Соответствено, корни данных степеней приятно именовать квадратным корнем и кубическим. Действия с кубическими корнями – тема для отдельного разговора, а сейчас поговорим о сложении квадратных корней.
Две степени имеют свои отдельные названия: вторая степень называется «квадратом», а третья – «кубом». Соответствено, корни данных степеней приятно именовать квадратным корнем и кубическим. Действия с кубическими корнями – тема для отдельного разговора, а сейчас поговорим о сложении квадратных корней.
Начнем с того, что в ряде случаев квадратные корни проще сначала извлечь, а потом уже складывать результаты. Предположим, нам необходимо найти значение такого выражения:
Ведь совсем не сложно вычислить, что корень квадратный из 16 равен 4, а из 121 – 11. Следовательно,
√16+√121=4+11=15
Впрочем, это самый простой случай – здесь речь идет о полных квадратах, т.е. о таких числах, которые получаются при возведении в квадрат целых чисел. Но так бывает не всегда. Например, число 24 – это не полный квадрат (не найти такого целого числа, которое при возведении его во вторую степень дало бы в результате 24). То же самое относится к такому числу, как 54… Что делать, если нам необходимо сложить корни квадратные из этих чисел?
В таком случае мы получим в ответе не число, а другое выражение.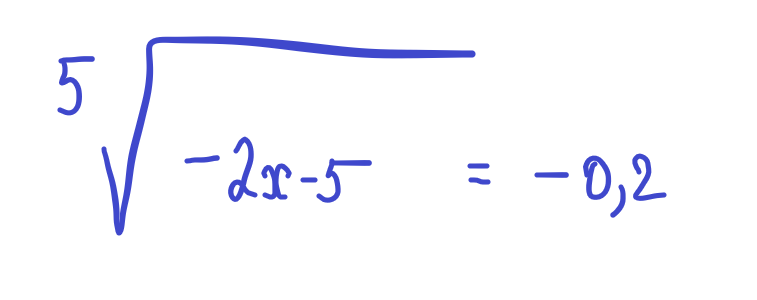 Максимум, что мы можем тут сделать – это максимально упростить исходное выражение. Для этого придется вынести множители из-под корня квадратного. Посмотрим, как это делается, на примере упомянутым чисел:
Максимум, что мы можем тут сделать – это максимально упростить исходное выражение. Для этого придется вынести множители из-под корня квадратного. Посмотрим, как это делается, на примере упомянутым чисел:
Для начала разложим на множители 24 – таким образом, чтобы из одного из них легко можно было извлечь корень квадратный (т.е., чтобы он был полным квадратом). Такое числи есть – это 4:
Теперь проделаем то же самое с 54. В его составе таким числом будет 9:
Т.о., у нас получается следующее:
√24+√54=√(4*6)+ √(9*6)
Теперь извлечем корни из того, из чего можем их извлечь: 2*√6+3*√6
Здесь есть общий множитель, который мы можем вынести за скобки:
(2+3)* √6=5*√6
Это и будет результатом сложения – больше ничего тут извлечь нельзя.
Правда, можно прибегнуть к помощи калькулятора – правда, результат будет приблизительным и с огромным количеством знаков после запятой:
√6=2,449489742783178
Постепенно округляя его, мы получим приблизительно 2,5. Если нам все-таки хотелось бы довести до логического завершения решение предыдущего примера, мы можем умножить этот результат на 5 – и получится у нас 12,5. Более точного результата при таких исходных данных получить нельзя.
Если нам все-таки хотелось бы довести до логического завершения решение предыдущего примера, мы можем умножить этот результат на 5 – и получится у нас 12,5. Более точного результата при таких исходных данных получить нельзя.
Левый и правый пределы
Левый и правый пределы
В некоторых случаях вы позволяете x приближаться к числу a слева или справа.
правильно, а не «обе стороны сразу», как обычно.
1. означает: вычислить
предел по мере того, как x приближается к c от вправо
— то есть через числа больше c.
2. означает: вычислить
предел по мере того, как x приближается к c от до
— то есть через числа меньше с.
Эти ситуации могут возникнуть, если определено только
слева или справа от c. Например, функция определена только для (поскольку квадратный корень из отрицательного числа не
действительное число).
Также можно рассмотреть левый и правый пределы, когда определено по обе стороны от c. В этом случае
В этом случае
важный вопрос: равны ли левый и правый пределы?
Пример. На рисунках показаны графики некоторых
функции. В каждом случае укажите, соответствуют ли левый и правый пределы
в c определены. Если оба определены, скажите, равны ли они.
В (а) правый предел определен, потому что график приближается
определенной высоте справа (высота точки).
левый предел не определен, потому что график не приближается к
определенная высота: имеется вертикальная асимптота. (Можно также сказать
левый предел равен , как мы обсудим
ниже.)
Аналогично, в (b) правый предел не определен, а
определен левый предел. (Можно также сказать, что правый предел
есть , как мы обсудим ниже.)
Наконец, в (c) определены как правый, так и левый пределы, но
они не равны. (Это означает, что обычный
(«двусторонний») предел не определен.
Я не буду излагать много теорем о левых и правых пределах,
потому что в целом результаты, справедливые для обычных
(«двусторонние») пределы сохраняются для односторонних пределов. Например
Например
(опуская обычные технические предположения), вот правило для сумм
для правых пределов:
Вы можете видеть, что это то же самое, что правило для сумм для обычных
пределы, с той лишь разницей, что теперь я пишу » » вместо » «.
Один важный момент, который мы уже отметили, — это отношение
между левым и правым пределами и обычным
(«двусторонние») ограничения. Чтобы дать немного больше деталей, я
сначала дайте формальные определения для левого и правого пределов.
Определение. (а) ( Правый
пределы ) Предположим, определен на
интервал для . Сказать это означает: для каждого числа существует число такое, что
(b) ( Левые пределы ) Предположим, определено на интервале для . Сказать это означает: для каждого
число, существует число такое, что
Обратите внимание, что в каждом случае на самом деле может быть
определяется по обеим сторонам c. Мы говорим, что для правой руки
Мы говорим, что для правой руки
предел существования, его нужно только определить справа от
в; чтобы существовал левый предел, достаточно, чтобы он был равен .
определено слева от c. (Как обычно, может быть определено или не определено в c.)
Вот результат, который мы неофициально использовали до того, как это относится
левый и правый пределы до обычных («двухсторонних»)
пределы. Доказательство — это доказательство, подобное
те, которые я привел в разделах об определении лимитов и предельных
теоремы; если вы учитесь на обычном курсе математического анализа для первого семестра, вы
можете пропустить доказательство, если хотите.
Теорема. Предположим, определено на открытом интервале, содержащем c.
Затем определяется
тогда и только тогда, когда и определены и равны.
В этом случае равно общему значению и .
Доказательство. Доказательство этой теоремы сводится к
следующий факт об абсолютных значениях:
Причина в том, что
означает, что x находится внутри c, но не
равно с.
С другой стороны, означает, что x
меньше с и находится в пределах с, и означает, что х больше с и
в пределах с. Таким образом, если одно из этих двух утверждений
верно, то верно и предыдущее утверждение, а если предыдущее
утверждение истинно, то одно из них должно быть истинным.
Таким образом, предположим. я покажу это
Позволять . Так как существует число
такой, что если , то .
Во-первых, если , то . Следовательно, .
Во-вторых, если , то . Следовательно, .
Далее я докажу обратное. Предположим, что
я покажу это
Позволять . Так как , есть
число такое, что если , то .
Аналогично, поскольку существует такое число, что если
тогда .
Теперь пусть
. Помните, что это означает, что это меньшее из и , так что это в
как минимум такой же маленький, как любой.
Предполагать . Это означает, что либо
В первом случае у меня
Следовательно, .
Во втором случае у меня
Следовательно, .
Это доказывает, что .
На словах этот результат говорит о том, что обычный («двусторонний»)
предел определен тогда и только тогда, когда левый и правый пределы
определены и равны, и в этом случае их общим значением является значение
обычного лимита.
Пример. Вычислить
Является
определенный?
Посмотрите на первый предел более внимательно. x приближается к 0 из
правильно . Числа рядом с 0, но справа от него маленькие
положительные числа: 0,01, например. Маленькие положительные числа дают положительные:
, Например. Если положительно, то , значит
(Обратите внимание, что вы не позволяете x равняться 0, поэтому , и отмена допустима.)
Следовательно,
Вот картинка:
Так как левый и правый пределы не совпадают,
неопределенный.
Пример. Предположим
Вычислить , и .
Для вычисления я использую
часть определения для f, которая применяется к:
Точно так же для вычисления я использую ту часть определения f, которая
относится к :
Поскольку левый и правый пределы равны, двусторонний предел
определяется, и .
Тот факт, что не входит в
проблема.
Пример. Функция определяется
Для какого значения k определено?
Чтобы быть определенными, левый и правый пределы в 2
должны быть определены и равны. Вычислите их:
Установите левый и правый пределы равными и найдите k:
Пример. Рассмотрим функцию, график которой изображен ниже:
Вычислить .
затем
Поскольку левые и правые пределы не совпадают,
Пример. Рассмотрим функцию, график которой изображен ниже:
Рассмотрим функцию, график которой изображен ниже:
Вычислить
Зависят ли эти пределы от значения ?
затем
Следовательно,
Значение не влияет на существование
Лимит. На самом деле, предположим, я изменил функцию следующим образом:
Сейчас не определено, но
Левый и правый пределы могут привести к
бесконечные пределы , поэтому я кратко обсужу идеи, прежде чем дать
Некоторые примеры. Как обычно с теорией в этом курсе, точные
определения приведены здесь для полноты и для тех, кто
заинтересованы. Для большинства людей достаточно иметь хороший
хватка как это выглядит графически когда предел бесконечен,
и как бесконечные пределы могут возникнуть в предельных вычислениях.
Определение. (a) означает: Для каждого
число , есть такое число , что если , то .
Иногда я буду писать » » вместо
» » для акцента, чтобы помочь отличить его
от » » в следующей части
определение.
Определения правого и левого пределов:
(i) (Правые пределы) означает: Для каждого числа существует число такое, что если , то .
(ii) (Левые пределы) означает: Для каждого числа существует число такое, что если , то .
(б)
означает: для каждого числа существует число
, такое что если , то .
Определения правого и левого пределов:
(i) (Правые пределы) означает: Для каждого числа существует число такое, что если , то .
(ii) (Левые пределы) означает: Для каждого числа существует число такое, что если , то .
Таким образом, чтобы сказать приближается, когда x приближается к c (слева, справа или от
обе стороны) означает, что по мере увеличения и
положительный, без какой-либо верхней границы, когда x приближается к c.
Точно так же, чтобы сказать приближается, когда x приближается к c (слева, справа или от
обе стороны) означает, что по мере увеличения и
отрицательно, без какой-либо верхней границы, когда x приближается к c.
Во всех этих случаях не будет ошибкой сказать, что предел
undefined, в том смысле, что это не номер . Но если ты
можно сказать это или , это лучше, так как вы даете больше информации
о происходящем.
Пример. Каждое изображение ниже показывает график
функция . В каждом случае найти:
В),
Поскольку левый и правый пределы не совпадают, не определено.
В (б),
Пример. Вычислить .
Подключение дает. Лимит
не определено . Но я могу сказать больше.
Попробуйте подставить число близкое к 1: Когда ,
Похоже, что получается больших и отрицательных . Фактически,
Чтобы понять, почему это так, вспомним, что x приближается к 1 от
правильно . Это означает, что он будет небольшим и
положительный. С другой стороны, .
Так как верх отрицателен, а низ положителен, результат должен
быть отрицательный .
Что касается размера, то у меня
Так как результат должен быть большой и отрицательный , это
разумно, что это .
Другой способ увидеть это — нарисовать график рядом с . По мере продвижения к 1 справа график становится
вниз к .
Ранее я отметил следующий факт: предположим,
Тогда двусторонний предел равен не определено . Как пример выше
показывает, что с односторонними пределами ситуация иная.
Если в этой ситуации имеет то же самое
знак для всех значений x, достаточно близких к c и превышающих c,
тогда правый предел будет или или . Конкретный
знак зависит от знаков верха и низа дроби.
Точно так же, если имеет один и тот же знак для всех
x достаточно близко к c и меньше c, то левый предел
будет или или .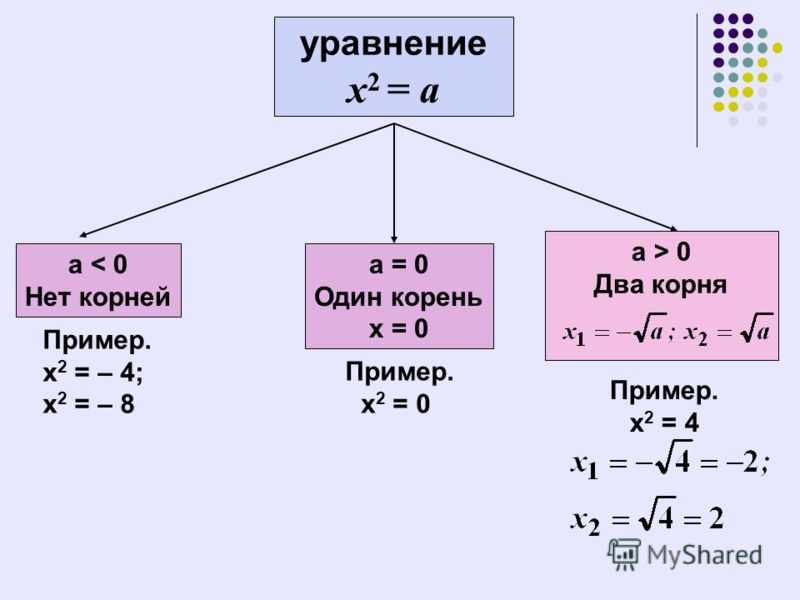 Опять же,
Опять же,
конкретный знак зависит от знаков верха и низа
дробная часть.
Условие «одинакового знака» будет выполнено, например,
если f и g полиномы — то есть, если является рациональной функцией. Так и будет
также удовлетворяться такими функциями, как
Пример. Вычислить .
Подключение дает. Так как это рациональная функция, то
правый предел либо или ; я должен
определите, какой из двух. посмотрю верх и низ
отдельно.
В качестве , .
Что касается дна, так как x приближается к -3 от справа ,
Я считаю, что x больше, чем -3. Таким образом, , поэтому — положительно.
Поскольку приближается к отрицательному числу и приближается к положительному числу, частное равно
отрицательный. Следовательно,
Я также могу увидеть это, если возьму число близкое к -3, но вправо
of -3 — , например — и подключите его:
у меня большой отрицательное число , что говорит о том, что предел
должно быть .
Я мог также увидеть это, построив график функции, как в предыдущем
пример.
В случае одностороннего ограничения и формы вы можете спросить:
«Какой из этих методов лучший для определения
значение?» Я чувствую, что для первого курса математического анализа все три
являются приемлемыми .
Однако при подстановке чисел и построении графиков
поддерживают для заключения, они на самом деле не дают
доказательство . Графики могут быть обманчивы. И когда вы подключаете
номер, откуда вы знаете, что номер, который вы выбрали,
«типичный»? Первый способ — рассуждения о знаках с использованием
неравенства — намного ближе к строгому доказательству результата.
Контактная информация
Домашняя страница Брюса Икенаги
Copyright 2018 Брюс Икенага
Алгоритм извлечения квадратного корня. Посмотрите на красивую алгебру… | Уджвал Сингх
Символ квадратного корня ( Credits : By historicair 17:50, 4 июня 2007 (UTC) — Изображение: Nuvola apps edu Mathmatic-p. svg, LGPL, https://commons.wikimedia.org/w/ index.php?curid=2201984)
svg, LGPL, https://commons.wikimedia.org/w/ index.php?curid=2201984)
Люди были очарованы квадратными корнями с незапамятных времен, ранняя мотивация подпитывалась утилитарными вопросами, такими как — «данная площадь, построить квадрат, равный площади». Для этого нам нужно знать длину стороны квадрата, которая, конечно, равна квадратному корню из площади.
Вскоре мы поняли, что не каждое натуральное число является полным квадратом. Со временем мы обнаружили, что квадратные корни таких чисел не только нецелые, но и нерациональные. На самом деле первоначальные открытия, касающиеся природы корня 2, были нашей первой встречей с иррациональной сферой. Конечно, погоня за квадратными корнями многому нас научила!
Содержание
Эта статья, однако, посвящена идеальным квадратам. Вот краткий обзор контента, описанного ниже —
- Резюме: Процедуры вычисления квадратных корней.
- Алгоритм извлечения квадратного корня.
- Почему алгоритм работает? — Обоснование алгоритма.

- Алгоритм извлечения квадратного корня в двоичной системе счисления.
- Заключительные замечания.
Итак, имея полный квадрат, как мы можем определить его квадратный корень? Как вы, возможно, помните, для этой цели в средней школе повсеместно преподаются две элементарные процедуры —
- Факторизация простых чисел: это наивный способ извлечения квадратных корней. Здесь мы выполняем простую факторизацию данного числа, а затем группируем факторы в пары по два. Затем мы умножаем числа из каждой группы, чтобы получить квадратный корень. Суть процедуры понятна. Например,
Вычисление квадратного корня из 900 с использованием простой факторизации.
- Посимвольный расчет: обратите внимание, что описанный выше метод оказывается чрезвычайно утомительным при работе с большими числами. Кроме того, в случаях, когда наименьший простой множитель данного числа достаточно велик, мы можем даже не начать процедуру (например, 12643277 = 3089 * 4093).
 Вот где метод вычисления цифра за цифрой (далее именуемый алгоритмом квадратного корня или просто алгоритмом) оказывается очень кстати. И именно об этом эта статья — как работает алгоритм, его особенности и, самое главное, почему он работает (вероятно, самая упускаемая из виду часть)! Итак, давайте погрузимся прямо в это.
Вот где метод вычисления цифра за цифрой (далее именуемый алгоритмом квадратного корня или просто алгоритмом) оказывается очень кстати. И именно об этом эта статья — как работает алгоритм, его особенности и, самое главное, почему он работает (вероятно, самая упускаемая из виду часть)! Итак, давайте погрузимся прямо в это.
Краткое примечание по используемым символам
Прежде всего, ниже приводится краткое описание некоторых символов. Пусть a и b — два натуральных числа. Тогда —
- . Через ab мы представляем обычное умножение, т. е. ab = a * b .
- Через a|b мы представляем число, образованное размещением b справа от .
Например, если a = 789 и b = 23, то a|b = 78923.
Как обычно, алгоритм лучше всего понять на примере пошагового руководства. Итак, ниже вычисление корня 50 965 321 с последующими подробными шагами:
Квадратный корень из 50 965 321 с использованием алгоритма квадратного корня.
Шаги
- Сопряжение : Начиная справа, сгруппируйте цифры заданного числа парами по два. В приведенном выше примере группы выделены подчеркиванием — (21), (53), (96) и (50). Примечание. Если номер содержит нечетное количество цифр, то в самой левой группе будет только одна цифра.
- Начальная догадка : Начните с самой левой группы. Найдите максимальную цифру, квадрат которой меньше или равен крайней левой группе.
В нашем примере число, представленное группой, = 50.
Таким образом, максимальная цифра, квадрат которой ≤ 50, равна 7. - Запишите вверху число, полученное на предыдущем шаге. Это сформирует первую цифру квадратного корня. Давайте назовем текущее число, представленное вверху, как « текущий частичный квадратный корень », обозначаемый p .
В нашем случае текущий частичный квадратный корень, p = 7.
Вычтите квадрат этого числа из самой левой группы и запишите остаток.
В нашем случае остаток = 50–49 = 1. - Теперь опустим цифры следующей группы рядом с остатком.
Позвоните на новый номер r .
В нашем примере мы уменьшаем 96, чтобы получить 196. Это r = 196. - Удар и испытание :
Теперь найдите наибольшую цифру 9.0005 d такое, что ((2p) |d) * d ≤ r .
В нашем примере 2п = 2* 7= 14 (на рисунке показано красным цветом).
Начнем с d = 1, 141 * 1 = 141. Далее
С d = 2, 142 * 2 = 284 > 196.
Следовательно, для нашего случая d = 1. - d , полученное на предыдущем шаге, является следующей цифрой квадратного корня. Итак, поместите его вверху, справа от текущего частичного квадратного корня.
То есть p_new = p_old | д .
Далее узнать новый остаток как —
остаток = r— (((2p)|d) * d)
В нашем случае новое значение остаток = 196–141 = 55.
- Повторить шаги от 4 до 6, пока не исчерпаем заданное число. Если бы число было полным квадратом, то у нас был бы 0 в качестве последнего остатка, а квадратный корень был бы равен числу, стоящему вверху!
Вот еще один пример, который поможет вам понять. Обратите внимание, что в приведенном ниже случае самая левая группа состоит только из одной цифры (поскольку общее количество цифр нечетное) —
Квадратный корень из 2 989 441 с использованием алгоритма извлечения квадратного корня.
Вот мы и подошли к сути этой статьи! Почему работает алгоритм квадратного корня, в чем причина этого?
В двух словах ответ заключается в том, что алгоритм использует базовую алгебру десятичной разрядной системы .
Представьте, что у вас есть натуральное число, и . Кроме того, у вас есть цифра b . То есть b является одним из 0–9.
Тогда имеем —
Алгоритм использует именно это. Основной принцип —
Если мы знаем все, кроме одной последней цифры квадратного корня числа, то мы можем получить оставшуюся цифру, вычитая в 100 раз квадрат числа, образованного другими цифрами, из квадрата заданного числа, а затем поиск цифры d такой, что ((2a)|d)d равно этой разнице.

Алгоритм начинается с начального предположения (этап 2 выше), а затем итеративно применяет описанный выше принцип для получения квадратного корня.
Дополнительное примечание : Этот принцип также объясняет, почему мы группируем цифры по две —
- Во-первых, интуитивно понятно, что квадрат числа содержит примерно в два раза больше цифр, чем само число. Это потому, что если a является n-значным числом, то —
- Таким образом, справедливо ожидать, что две цифры из квадрата будут соответствовать одной цифре квадратного корня.
- Теперь обратите внимание, что мы вычитаем 100-кратное значение квадрата частичного квадратного корня из (текущий остаток | следующая группа). Вот почему следующая группа должна состоять из двух цифр (с одной цифрой мы можем столкнуться с отрицательными числами).
- Почему мы начинаем группировку справа, а не слева?
Это потому, что если мы начнем группировать слева число, содержащее нечетное количество цифр, то справа у нас будет одна цифра. Таким образом, в последней итерации у нас будет только одна цифра, которую нужно записать рядом с остатком, чего не должно происходить. В таких случаях, хотя на первом шаге у нас будет одна цифра, это нормально, так как это начальный шаг предположения. Важно то, что каждая группа, поступающая в последующих итерациях, должна иметь две цифры .
Таким образом, в последней итерации у нас будет только одна цифра, которую нужно записать рядом с остатком, чего не должно происходить. В таких случаях, хотя на первом шаге у нас будет одна цифра, это нормально, так как это начальный шаг предположения. Важно то, что каждая группа, поступающая в последующих итерациях, должна иметь две цифры .
Давайте рассмотрим другой пример —
Квадратный корень из 383 161 с использованием алгоритма квадратного корня.
шагов —
- Первоначальное предположение: поскольку 6 — это самая большая цифра, квадрат которой ≤ 38 (крайняя левая группа), первая цифра нашего квадратного корня равна 6.
- Затем мы используем описанный выше принцип, чтобы получить следующую цифру. квадратного корня. Наше число (чей квадратный корень нужно найти) на этой итерации равно 3831. Итак, из 3831 мы вычитаем 100-кратный квадрат текущего частичного квадратного корня. То есть 3831 — 100,6² = 231,9.0424
- Теперь мы ищем самую большую цифру, d , такую, что (12|d)d ≤ 231 (поскольку 2 * текущий частичный квадратный корень = 2 * 6 = 12).
 Получаем d = 1.
Получаем d = 1. - Далее опускаем следующую группу справа от остатка, чтобы получить 11061. Обратите внимание, что 11061 = 383161 — 100,61² (61 — текущий частичный квадратный корень).
- Теперь мы ищем самую большую цифру, d , такую, что (122|d)d ≤ 11061 (поскольку 2 * текущий частичный квадратный корень = 2 * 61 = 122). мы получаем d = 9.
- Поскольку последний остаток равен 0, мы нашли точный квадратный корень для данного числа!
Примечание : На каждом шаге алгоритма мы получаем наибольшее число, квадрат которого меньше или равен числу, образованному цифрами, покрытыми до этого момента. Используя приведенный выше пример,
- 6 — наибольшее число, квадрат которого ≤ 38.
- 61 — наибольшее число, квадрат которого ≤ 3831.
- 619 — наибольшее число, квадрат которого ≤ 383161.
Теперь давайте проверим наше понимание алгоритма, попробовав его в двоичной системе счисления!
Суть алгоритма остается прежней. То есть мы находим квадратный корень цифра за цифрой, опираясь на полученное до сих пор значение. Обратите внимание, что двоичная система счисления имеет только две цифры (также известные как биты) — 0 и 1. Давайте посмотрим, какие настройки нужны нашему алгоритму в двоичном мире.
То есть мы находим квадратный корень цифра за цифрой, опираясь на полученное до сих пор значение. Обратите внимание, что двоичная система счисления имеет только две цифры (также известные как биты) — 0 и 1. Давайте посмотрим, какие настройки нужны нашему алгоритму в двоичном мире.
Допустим, у вас есть двоичное число, a . Кроме того, у вас есть немного, б . То есть b равно 0 или 1.
Тогда —
Итак, основной принцип здесь —
Если мы знаем все, кроме последнего бита квадратного корня числа, то мы можем получить к оставшемуся биту путем вычитания 4-кратного квадрата числа, образованного другими битами, из квадрата заданного числа, а затем поиска бита d, такого, что (a|0d)d равно этой разнице.
Давайте разберемся с этим на примере квадратного корня из 10101001 (169)—
Квадратный корень из 169 по основанию 2 с использованием алгоритма извлечения квадратного корня.
Шаги (поскольку большинство приведенных ниже шагов аналогичны шагам, описанным выше для вычислений с основанием 10, поэтому здесь мы использовали краткие формулировки, пожалуйста, обратитесь к примерам с основанием 10, если вы столкнулись с какими-либо пробелами в понимании) —
- Сопряжение: как прежде мы соединяем числа в группы по два справа налево.

- Первоначальное предположение: Крайняя левая группа равна 10 (т. е. 2). Итак, находим самый большой бит, d , так что d² ≤ 10. Получаем d = 1. Это первый бит нашего квадратного корня.
- Вычитаем 1 из 10 и опускаем следующую группу справа от остатка. По сути, здесь мы делаем ((a|b)² — a²|00) .
- Теперь попробуем найти наибольший бит d такой, что (1|0d)d ≤ 110 . Получаем d = 1. Это следующий бит квадратного корня.
- Повторяем шаги 3 и 4, пока не будет исчерпано заданное число. Если бы число было полным квадратом, в конце мы получили бы нулевой остаток, а число наверху представляло бы квадратный корень. В нашем случае, поскольку мы начали с идеального квадрата (169= 13²), мы получили 1101 как окончательный ответ. 1101 — это двоичный эквивалент 13!
Pros
Обратите внимание, как упрощает выполнение алгоритма в двоичном мире!
Минусы
Однако за простоту приходится платить. Количество шагов для выполнения увеличивается, так как заданное число занимает больше цифр в двоичной системе по сравнению с десятичной системой. В приведенном выше примере нам потребовалось бы две итерации, чтобы получить квадратный корень из 169 по основанию 10. Однако в двоичной системе нам потребовалось бы четыре итерации, чтобы получить это.
Количество шагов для выполнения увеличивается, так как заданное число занимает больше цифр в двоичной системе по сравнению с десятичной системой. В приведенном выше примере нам потребовалось бы две итерации, чтобы получить квадратный корень из 169 по основанию 10. Однако в двоичной системе нам потребовалось бы четыре итерации, чтобы получить это.
Обратите также внимание на то, что алгоритм сохраняет свою существенную особенность итеративного получения наибольшего числа, квадрат которого меньше или равен пройденному числу. Из приведенного выше —
- 1 (1) — наибольшее число, квадрат которого меньше или равен 10 (2).
- 11 (3) — наибольшее число, квадрат которого меньше или равен 1010 (10).
- 110 (6) — наибольшее число, квадрат которого меньше или равен 101010 (42).
- 1101 (13) — наибольшее число, квадрат которого меньше или равен 10101001 (169).
Как отмечалось в начале, хотя алгоритм квадратного корня широко применяется, его обоснование редко подвергается должной осмотрительности. Эта статья была попыткой исправить ситуацию. Как и большинство людей, я лично изучил этот алгоритм в средней школе. И, как и большинство людей, я понятия не имел, почему этот алгоритм работает. Это осталось, пожалуй, единственным в школьной математике, что я не мог оправдать перед собой.
Эта статья была попыткой исправить ситуацию. Как и большинство людей, я лично изучил этот алгоритм в средней школе. И, как и большинство людей, я понятия не имел, почему этот алгоритм работает. Это осталось, пожалуй, единственным в школьной математике, что я не мог оправдать перед собой.
К счастью, недавно я пришел к доказательству алгоритма, просматривая что-то похожее в великом произведении Арьябхаты, Арьябхатия. Да, в итоге мне потребовалось 15 лет, чтобы окончательно убедить себя, почему алгоритм работает, но ожидание того стоило!
Однако более важным является понимание того, как алгоритм квадратного корня олицетворяет простоту и эффективность десятичной разрядной системы. В сегодняшнем мире, где мы воспринимаем эту замечательную систему как должное, крайне важно сделать шаг назад и осознать, насколько важным было это открытие.
Цитируя Лапласа (1749–1827),
Гениальный метод выражения всех возможных чисел с помощью набора из десяти символов (каждый символ имеет разрядное значение и абсолютное значение) появился в Индии.
Идея кажется настолько простой в наши дни, что ее значение и глубокая важность уже не оценивается. Его простота заключается в том, что он облегчил вычисления и поставил арифметику на первое место среди полезных изобретений. Важность этого изобретения легче оценить, если учесть, что оно было выше двух величайших мужей древности, Архимеда и Аполлония.
— Лаплас
Чтобы почувствовать, насколько десятичная система разрядов облегчает наши вычисления — забудьте о квадратных корнях, попробуйте умножить 14 (XIV) на 42 (XLII) римскими цифрами и убедитесь сами!
- Методы вычисления квадратных корней
- Индийские цифры
- Пьер-Симон Лаплас
Анатомия, грудная клетка, легкие — StatPearls
Raheel Chaudhry; Бруно Бордони.
Информация об авторе
Последнее обновление: 31 июля 2021 г.
Введение
Целью легких является снабжение крови кислородом. Дыхательная система делится на дыхательные пути и легочную паренхиму. Дыхательные пути состоят из бронха, который отходит от трахеи и делится на бронхиолы, а затем на альвеолы. Паренхима отвечает за газообмен и включает альвеолы, альвеолярные протоки и бронхиолы. Легкие имеют губчатую консистенцию и розовато-серый оттенок. Кроме того, они анатомически описываются как имеющие вершину, три границы и три поверхности. Далее они подразделяются на доли и сегменты. Паренхима легких также покрыта плеврой.[1][2][3]
Дыхательные пути состоят из бронха, который отходит от трахеи и делится на бронхиолы, а затем на альвеолы. Паренхима отвечает за газообмен и включает альвеолы, альвеолярные протоки и бронхиолы. Легкие имеют губчатую консистенцию и розовато-серый оттенок. Кроме того, они анатомически описываются как имеющие вершину, три границы и три поверхности. Далее они подразделяются на доли и сегменты. Паренхима легких также покрыта плеврой.[1][2][3]
Анатомия
Анатомически легкое имеет верхушку, три края и три поверхности. Вершина лежит над первым ребром.
Три границы включают переднюю, заднюю и нижнюю границы. Передняя граница легкого соответствует плевральному отражению и образует сердечную вырезку в левом легком. Сердечная вырезка представляет собой вогнутость в легком, которая формируется для размещения сердца. Нижняя граница тонкая и отделяет основание легкого от реберной поверхности. Задняя граница толстая и простирается от С7 до Т10 позвонка, а также от верхушки легкого до нижней границы.
Три поверхности легкого включают реберную, медиальную и диафрагмальную поверхности. Реберная поверхность покрыта реберной плеврой и проходит вдоль грудины и ребер. Он также соединяется с медиальной поверхностью у переднего и заднего краев и с диафрагмальной поверхностью у нижнего края. Медиальная поверхность делится спереди и сзади. Спереди она связана с грудиной, а сзади с позвонком. Диафрагмальная поверхность (основание) вогнута и опирается на купол диафрагмы; правый купол также выше левого купола из-за печени.
Анатомия правого и левого легкого сходна, но асимметрична. Правое легкое состоит из трех долей: правой верхней доли (ПЛУ), правой средней доли (РМЛ) и правой нижней доли (ПНЛ). Левое легкое состоит из двух долей: левой верхней доли (LUL) и левой нижней доли (LLL). Правая доля разделена косой и горизонтальной бороздами, где горизонтальная щель разделяет верхнюю и среднюю доли, а косая щель разделяет среднюю и нижнюю доли. В левой доле имеется только косая щель, разделяющая верхнюю и нижнюю доли.
Доли далее делятся на сегменты, которые связаны с определенными сегментарными бронхами. Сегментарные бронхи являются ответвлениями третьего порядка от ветвей второго порядка (долевых бронхов), отходящих от главного бронха.
Правое легкое состоит из десяти сегментов. В RUL есть три сегмента (апикальный, передний и задний), два в RML (медиальный и латеральный) и пять в RLL (верхний, медиальный, передний, латеральный и задний). Косая щель отделяет РПН от РМЛ, а горизонтальная щель отделяет ПЗЛ от РМЛ и РПН.
Слева от восьми до девяти сегментов, в зависимости от деления доли. В целом в левой верхней доле имеется четыре сегмента (передний, апикозадний, нижний и верхний язычки) и четыре или пять сегментов в левой нижней доле (латеральный, переднемедиальный, верхний и задний).
Ворота (корни) представляют собой вдавленную поверхность в центре медиальной поверхности легкого и лежат кпереди от пятого до седьмого грудных позвонков. Это точка, в которой различные структуры входят и выходят из легкого. Ворота окружены плеврой, которая простирается вниз и образует легочную связку. Ворота содержат в основном бронхи и легочную сосудистую сеть, а также диафрагмальный нерв, лимфатические сосуды, узлы и бронхиальные сосуды. И левые, и правые ворота содержат легочную артерию, легочные вены (верхнюю и нижнюю) и бронхиальные артерии. Кроме того, в левых воротах есть один бронх, главный бронх, а в правых воротах есть два бронха, эпартериальный и гипокинетический бронхи. Спереди назад порядок в воротах — вена, артерия и бронх.
Ворота окружены плеврой, которая простирается вниз и образует легочную связку. Ворота содержат в основном бронхи и легочную сосудистую сеть, а также диафрагмальный нерв, лимфатические сосуды, узлы и бронхиальные сосуды. И левые, и правые ворота содержат легочную артерию, легочные вены (верхнюю и нижнюю) и бронхиальные артерии. Кроме того, в левых воротах есть один бронх, главный бронх, а в правых воротах есть два бронха, эпартериальный и гипокинетический бронхи. Спереди назад порядок в воротах — вена, артерия и бронх.
Структура и функция
Функция легких заключается в доставке кислорода из воздуха в кровь, выполняемая альвеолами. Альвеолы представляют собой одноклеточную мембрану, обеспечивающую газообмен с легочными сосудами. Есть несколько мышц, которые помогают при вдохе и выдохе, например, диафрагма и межреберные мышцы. Грудино-ключично-сосцевидная и лестничная мышцы используются для вспомогательного дыхания, когда пациент находится в состоянии дыхательной недостаточности или недостаточности. Мышцы помогают создать отрицательное давление в грудной клетке, где давление в легких меньше атмосферного, что способствует вдоху и наполнению легких. Кроме того, мышцы помогают создавать положительное давление в грудной клетке, где давление в легких превышает атмосферное, что способствует выдоху и опорожнению легких.
Мышцы помогают создать отрицательное давление в грудной клетке, где давление в легких меньше атмосферного, что способствует вдоху и наполнению легких. Кроме того, мышцы помогают создавать положительное давление в грудной клетке, где давление в легких превышает атмосферное, что способствует выдоху и опорожнению легких.
Кровоснабжение и лимфатическая система
Основное различие между легочной артерией и бронхиальной артерией. Легочная артерия берет деоксигенированную кровь от сердца для насыщения кислородом паренхимой легких. Однако бронхиальные артерии обеспечивают паренхиму легких кислородом для выживания.
Основная легочная артерия выходит из правого желудочка и разветвляется на левую главную и правую главные легочные артерии. Ветви легочной артерии обычно тянутся и расширяются вдоль ветвей бронхиального дерева и в конечном итоге становятся капиллярами вокруг альвеол. Легочные вены получают насыщенную кислородом кровь из альвеолярных капилляров и деоксигенированную кровь из бронхиальных артерий и висцеральной плевры. Четыре легочные вены сходятся в правом предсердии.
Четыре легочные вены сходятся в правом предсердии.
Бронхиальное кровообращение является частью большого круга кровообращения. Левая бронхиальная артерия отходит в виде двух (верхней и нижней) от грудной аорты. Правая плечевая артерия обычно отходит от одного из следующих трех: правой задней межреберной артерии с левой верхней бронхиальной артерией вне аорты или непосредственно от аорты. Бронхиальные вены собирают дезоксигенированную кровь и опорожняют ее в непарную вену.
Поверхностное и глубокое лимфатические сплетения дренируют легкое. Отток лимфы из легочной паренхимы сначала оттекает во внутрипаренхиматозные узлы, а затем в перибронхиальные. Впоследствии лимфатические сосуды будут оттекать в трахеобронхиальные, паратрахеальные лимфатические узлы, бронхомедиастинальный ствол, а затем в грудной проток.
Нервы
Диафрагмальный нерв отходит от корешков C3,4,5 шейных нервов. Он иннервирует фиброзный перикард, участки висцеральной плевры и диафрагму.
Легкие получают иннервацию из двух основных источников: легочного сплетения (сочетание парасимпатической и симпатической иннервации) и диафрагмального нерва. Легочное сплетение находится в корне легкого и состоит из эфферентных и афферентных вегетативных нервных волокон. Состоит из ветвей блуждающего нерва (парасимпатических) и симпатических волокон — ветвей сплетения вокруг легочной сосудистой сети и бронхов. Парасимпатическая иннервация вызывает сужение бронхов, расширение легочных сосудов и усиление секреции желез. Симпатическая иннервация вызывает расширение бронхов и сужение легочных сосудов.
Легочное сплетение находится в корне легкого и состоит из эфферентных и афферентных вегетативных нервных волокон. Состоит из ветвей блуждающего нерва (парасимпатических) и симпатических волокон — ветвей сплетения вокруг легочной сосудистой сети и бронхов. Парасимпатическая иннервация вызывает сужение бронхов, расширение легочных сосудов и усиление секреции желез. Симпатическая иннервация вызывает расширение бронхов и сужение легочных сосудов.
Физиологические варианты
Могут возникать дополнительные трещины; они могут быть поверхностными или глубокими в воротах. При определенных патологиях они могут вызывать странные рентгенограммы.
Другие возможные вариации включают агенезию (отсутствие легкого), аплазию или добавочные доли (могут вызвать вариации визуализации).
Хирургические соображения
Когда иссекается вся доля легкого, это называется лобэктомией, а удаление только сегмента — сегментэктомией. Лобэктомия может потребоваться, когда патология затрагивает только одну долю, и для предотвращения распространения заболевания, например, при туберкулезе, абсцессе легкого, эмфиземе, доброкачественной опухоли или раке легкого. Сегментэктомия выполняется при доброкачественных поражениях, чтобы сохранить легкое, или при бронхоэктазах, ранней стадии рака I, узлах в легких или туберкулезе.[4][5][6]
Сегментэктомия выполняется при доброкачественных поражениях, чтобы сохранить легкое, или при бронхоэктазах, ранней стадии рака I, узлах в легких или туберкулезе.[4][5][6]
Седловидная эмболия легочной артерии представляет собой закупорку бифуркации легочного ствола. Это неотложная хирургическая операция, требующая эмболэктомии.
Клиническое значение
Перкуссия грудной клетки в норме резонансная. Если есть скопление жидкости, он может стать тусклым.[7]
Если при аускультации есть хрипы, то это связано с бронхоконстрикцией (астмой). Если появляются хрипы (хрипы), возможно, это связано с отеком легких (застойная сердечная недостаточность, интерстициальное заболевание легких, пневмония). Если есть хрипы, то это связано с выделениями в более крупные дыхательные пути, вызывающими обструкцию (хронический бронхит, муковисцидоз).
При чтении рентгеновских снимков легкие черные, потому что воздух прозрачен. Снимки лучше всего получаются, когда пациент вдыхает.
Торакоцентез — это процедура, при которой используется игла для забора жидкости из легкого. Это помогает определить причину плеврального выпота или абсцесса. Это может быть диагностическое или терапевтическое (для облегчения таких симптомов, как боль или одышка) [8].
Пневмония – это воспаление легких, которое может вызвать плевральный выпот. Пациенты могут жаловаться на лихорадку, кашель, боль в груди, тошноту и рвоту.
Контрольные вопросы
-
Получите бесплатный доступ к вопросам с несколькими вариантами ответов по этой теме.
-
Комментарий к этой статье.
Рисунок
Плевра, висцеральная плевра, левое легкое, париетальная плевра, левая плевральная полость, средостение, правая плевральная полость, правое легкое. Предоставлена иллюстрация Бекки Палмер
Рисунок
Структуры сердца и легких; Левое и правое легкое, трахея. Предоставлено Grey’s Anatomy Plates
Рисунок
Поперечный разрез грудины; Включая легкие и сердце, легочную плевру, реберную плевру, непарную вену, блуждающие нервы, грудной проток, симпатический ствол, левый диафрагмальный нерв, внутренний грудной сосуд, поперечную мышцу грудной клетки, сердце, левое и правое легкое, (подробнее. ..)
..)
Рисунок
Задний вид сердца и легких, входа в непарную вену, ветви легочной артерии, левого желудочка, левого предсердия, большой коронарной вены. Поддержите Анатомические Пластины Грея
Рисунок
Плевра, боковой вид грудной клетки; показаны отношения плевры и легких к стенке грудной клетки, плевра выделена синим цветом; легкие фиолетового цвета. Предоставлено Gray’s Anatomy Plates
Ссылки
- 1.
-
Tucker WD, Weber C, Burns B. StatPearls [Интернет]. Издательство StatPearls; Остров сокровищ (Флорида): 26 июля 2021 г. Анатомия, грудная клетка, легочные артерии сердца. [PubMed: 30521233]
- 2.
-
Burlew JT, Weber C, Banks KP. StatPearls [Интернет]. Издательство StatPearls; Остров сокровищ (Флорида): 27 июля 2021 г. Анатомия, грудная клетка, лимфатические узлы средостения. [В паблике: 30422458]
- 3.
-
Донли Э.Р., Холм М.Р., Лойд Дж.В. StatPearls [Интернет]. Издательство StatPearls; Остров сокровищ (Флорида): 8 мая 2021 г.
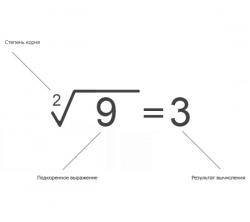 Анатомия, грудная клетка, движения стен. [PubMed: 30252279]
Анатомия, грудная клетка, движения стен. [PubMed: 30252279] - 4.
-
Бейнс КНС, Кашьяп С., Лаппин С.Л. StatPearls [Интернет]. Издательство StatPearls; Остров сокровищ (Флорида): 26 июля 2021 г. Анатомия, грудная клетка, диафрагма. [PubMed: 30137842]
- 5.
-
Michael CW, Faquin W, Jing X, Kaszuba F, Kazakov J, Moon E, Toloza E, Wu RI, Moreira AL. Комитет II: Руководство по методам цитологического исследования легких и медиастинальных лимфатических узлов. Диагностика Цитопатол. 2018 Октябрь; 46 (10): 815-825. [ПубМед: 30195266]
- 6.
-
Махабади Н., Гойзуэта А.А., Бордони Б. StatPearls [Интернет]. Издательство StatPearls; Остров сокровищ (Флорида): 26 июля 2021 г. Анатомия, грудная клетка, легочная плевра и средостение. [PubMed: 30085590]
- 7.
-
Гарвин У.Х. Клиническое исследование легких. Компр Тер. 1979 окт; 5(10):7-11. [PubMed: 498746]
- 8.
-
Koegelenberg CF, Irusen EM, von Groote-Bidlingmaier F, Bruwer JW, Batubara EM, Diacon AH.

Что такое арифметический квадратный корень
Квадратным корнем (арифметическим квадратным корнем) из неотрицательного числа (a) называется такое неотрицательное число, квадрат которого равен (a). ( (sqrt{a}=x, {{x}^{2}}=a; x, age 0)).
А почему же число ( a) (число под корнем) должно быть обязательно неотрицательным?
Например, чему равен ( sqrt{-9})?
Так-так, попробуем подобрать. Может, три?
Проверим: ( {{3}^{2}}=9), а не ( -9).
Может, ( left( -3 right))?
Опять же, проверяем: ( {{left( -3 right)}^{2}}=9).
Ну что же, не подбирается?
Это и следовало ожидать – потому что нет таких чисел, которые при возведении в квадрат дают отрицательное число! Это надо запомнить!
Число или выражение под знаком корня должно быть неотрицательным!
Однако ты наверняка уже заметил, что не только число под корнем должно быть неотрицательным, но и само значение тоже должно быть неотрицательным!
Ведь в определении сказано, что «квадратным корнем из числа( a)называется такое неотрицательное число, квадрат которого равен( a)».
Но подождите! В самом начале мы разбирали пример ( {{x}^{2}}=4) и один из ответов был отрицательным числом!
Мы подбирали числа, которые можно возвести в квадрат и получить при этом ( displaystyle 4). Ответом были ( displaystyle 2) и ( displaystyle -2)
А тут говорится, что квадратным корнем должно быть «неотрицательное число»! Почему?
Такой вопрос вполне уместен. Здесь необходимо просто разграничить понятия квадратного уравнения и арифметического квадратного корня.
К примеру, ( displaystyle {{x}^{2}}=4) (квадратное уравнение) не равносильно выражению ( x=sqrt{4}) (арифмитический квадратный корень).
Из ( {{x}^{2}}=4) следует, что
( left| x right|=sqrt{4}), то есть ( x=pm sqrt{4}=pm 2) или ( {{x}_{1}}=2); ( {{x}_{2}}=-2)
(не помнишь почему так? Почитай тему «Модуль числа»!)
А из ( x=sqrt{4}) следует, что ( x=2).
Конечно, это очень путает, но это необходимо запомнить, что знаки «плюс-минус» являются результатом решения квадратного уравнения, так как при решении уравнения мы должны записать все иксы, которые при подстановке в исходное уравнение дадут верный результат.
В наше квадратное уравнение подходит как ( 2), так и ( x=-2).
Однако, если просто извлекать квадратный корень из чего-либо, то всегда получаем один неотрицательный результат.
Запись иррациональных чисел с помощью квадратного корня
А теперь попробуй решить такое уравнение ( {{x}^{2}}=3).
Уже все не так просто и гладко, правда? Попробуй перебрать числа, может, что-то и выгорит?
Начнем с самого начала – с нуля: ( {{0}^{2}}=0) – не подходит.
Двигаемся дальше ( displaystyle x=1); ( displaystyle {{1}^{2}}=1) – меньше трех, тоже отметаем.
А что если ( displaystyle x=2)?
Проверим: ( displaystyle {{2}^{2}}=4) – тоже не подходит, т.к. это больше трех.
С отрицательными числами получится такая же история.
И что же теперь делать? Неужели перебор нам ничего не дал?
Совсем нет, теперь мы точно знаем, что ответом будет некоторое число между ( displaystyle 1) и ( displaystyle 2), а также между ( displaystyle -2) и ( displaystyle -1).
Кроме того, очевидно, что решения не будут целыми числами. Более того, они не являются рациональными.
И что дальше?
Давай построим график функции ( displaystyle y={{x}^{2}}) и отметим на нем решения.
Попробуем обмануть систему и получить ответ с помощью калькулятора (как мы это делали в начале)!
Извлечем корень из ( displaystyle 3), делов-то!
Ой-ой-ой, выходит, что ( sqrt{3}=1,732050807568ldots ) Такое число никогда не кончается.
Как же такое запомнить, ведь на экзамене калькулятора не будет!?
Все очень просто, это и не надо запоминать, необходимо помнить (или уметь быстро прикинуть) приблизительное значение. ( sqrt{3}) и ( -sqrt{3}) уже сами по себе ответы.
Такие числа называются иррациональными, именно для упрощения записи таких чисел и было введено понятие квадратного корня.
Деление корней
С умножением корней разобрались, теперь приступим к свойству деления.
Напомню, что формула в общем виде выглядит так:
( displaystyle sqrt[{}]{frac{a}{b}}=frac{sqrt[{}]{a}}{sqrt[{}]{b}}), если ( displaystyle age 0 , b>0).
А значит это, что корень из частного равен частному корней.
Ну что, давай разбираться на примерах:
( displaystyle frac{sqrt{12}}{sqrt{3}}=sqrt{frac{12}{3}}=sqrt{4}=2)
Вот и вся наука. А вот такой пример:
( displaystyle frac{sqrt{12}}{3}=frac{sqrt{12}}{sqrt{9}}=sqrt{frac{12}{9}}=sqrt{frac{4}{3}}=frac{2}{sqrt{3}})
Все не так гладко, как в первом примере, но, как видишь, ничего сложного нет.
А что, если попадется такое выражение:
( displaystyle sqrt{frac{144}{225}}=?)
Надо просто применить формулу в обратном направлении:
( displaystyle sqrt{frac{144}{225}}=frac{sqrt{144}}{sqrt{225}}=frac{12}{15}=frac{4}{5}=0,8)
А вот такой примерчик:
( displaystyle sqrt{0,16}=sqrt{frac{16}{100}}=frac{4}{10}=0,4)
Еще ты можешь встретить такое выражение:
( displaystyle sqrt{5frac{19}{25}}=?)
Все то же самое, только здесь надо вспомнить, как переводить дроби (если не помнишь, загляни в тему дроби и возвращайся!). Вспомнил? Теперь решаем!
( displaystyle sqrt{5frac{19}{25}}=sqrt{frac{144}{25}}=frac{12}{5}=2,4)
Уверена, что ты со всем, всем справился, теперь попробуем возводить корни в степени.
Возведение в степень
А что же будет, если квадратный корень возвести в квадрат? Все просто, вспомним смысл квадратного корня из числа ( displaystyle a) – это число, квадратный корень которого равен ( displaystyle a).
Так вот, если мы возводим число, квадратный корень которого равен ( displaystyle a), в квадрат, то что получаем?
Ну, конечно, ( displaystyle a)!
Рассмотрим на примерах:
( displaystyle {{left( sqrt{12} right)}^{2}}=12)
( displaystyle {{left( sqrt{17} right)}^{2}}=17)
Все просто, правда? А если корень будет в другой степени? Ничего страшного!
Придерживайся той же логики и помни свойства и возможные действия со степенями.
Забыл?
Почитай теорию по теме «Степень и ее свойства» и тебе все станет предельно ясно.
Вот, к примеру, такое выражение:
( displaystyle {{left( sqrt{5} right)}^{6}}={{left( {{left( sqrt{5} right)}^{2}} right)}^{3}}={{5}^{3}}=125)
В этом примере степень четная, а если она будет нечетная? Опять же, примени свойства степени и разложи все на множители:
( displaystyle {{left( sqrt{5} right)}^{7}}={{left( sqrt{5} right)}^{6}}cdot sqrt{5}=125sqrt{5})
С этим вроде все ясно, а как извлечь корень из числа в степени? Вот, к примеру, такое:
( displaystyle sqrt{{{3}^{2}}}=sqrt{9}=3)
Довольно просто, правда? А если степень больше двух? Следуем той же логике, используя свойства степеней:
( displaystyle sqrt{{{3}^{6}}}=sqrt{{{left( {{3}^{3}} right)}^{2}}}={{3}^{3}}=27)
( displaystyle sqrt{{{3}^{5}}}=sqrt{{{3}^{4}}cdot 3}=sqrt{{{left( {{3}^{2}} right)}^{2}}cdot 3}={{3}^{2}}cdot sqrt{3}=9sqrt{3})
Ну как, все понятно? Тогда реши самостоятельно примеры:
- ( displaystyle sqrt{{{left( -3 right)}^{2}}})
- ( displaystyle sqrt{{{6}^{6}}})
- ( displaystyle {{left( sqrt{8} right)}^{7}})
А вот и ответы:
Извлечение корней из больших чисел
До этого мы вносили множитель под знак корня, а как его вынести? Надо просто разложить его на множители и извлечь то, что извлекается!
( displaystyle sqrt{98}=sqrt{49cdot 2}=sqrt{49}cdot sqrt{2}=7sqrt{2})
Можно было пойти по иному пути и разложить на другие множители:
( displaystyle sqrt{98}=sqrt{7cdot 14})
Что дальше? А дальше раскладываем на множители до самого конца:
( displaystyle sqrt{98}=sqrt{7cdot 14}=sqrt{7cdot 7cdot 2}=sqrt{{{7}^{2}}cdot 2}=7sqrt{2})
Неплохо, да? Любой из этих подходов верен, решай как тебе удобно.
Разложение на множители очень пригодится при решении таких нестандартных заданий, как вот это:
( displaystyle sqrt{15}cdot sqrt{180}cdot sqrt{12})
Не пугаемся, а действуем! Разложим каждый множитель под корнем на отдельные множители:
А теперь попробуй самостоятельно (без калькулятора! его на экзамене не будет):
( displaystyle sqrt{15}cdot sqrt{180}cdot sqrt{12}=sqrt{5cdot 3}cdot sqrt{36cdot 5}cdot sqrt{2cdot 6})
Разве это конец? Не останавливаемся на полпути!
( displaystyle begin{array}{l}sqrt{5cdot 3}cdot sqrt{36cdot 5}cdot sqrt{2cdot 6}=sqrt{5cdot 3}cdot sqrt{3cdot 12cdot 5}cdot sqrt{2cdot 3cdot 2}=\=sqrt{5cdot 3}cdot sqrt{3cdot 2cdot 2cdot 3cdot 5}cdot sqrt{2cdot 3cdot 2}end{array})
На простые множители разложили. Что дальше? А дальше пользуемся свойством умножение корней и записываем все под одним знаком корня:
( displaystyle begin{array}{l}sqrt{5cdot 3cdot 3cdot 2cdot 2cdot 3cdot 5cdot 2cdot 3cdot 2}=sqrt{5cdot 5cdot 3cdot 3cdot 3cdot 3cdot 2cdot 2cdot 2cdot 2}=\=sqrt{25}cdot sqrt{81}cdot sqrt{16}=5cdot 9cdot 4=180end{array})
Вот и все, не так все и страшно, правда?
( displaystyle sqrt{15}cdot sqrt{54}cdot sqrt{10}=?)
Получилось ( displaystyle 90)? Молодец, все верно!
А теперь попробуй вот такой пример решить:
( displaystyle sqrt{4225}=?)
А пример-то – крепкий орешек, так сходу и не разберешься, как к нему подступиться. Но нам он, конечно, по зубам.
