Enter the total number of crimes that have occurred in a given area and the number of people in the area into the calculator to determine the crime rate per 100,000 people.
- Population Proportion Calculator
- Population Growth Calculator
- Rate Per 1000 Calculator
Crime Rate Formula
The following formula is used to calculate a crime rate.
- Where CR is the rate of crimes per 100,000 people
- TC is the total number of crimes committed in an area
- P is the total population of the area
To calculate a crime rate, divide the number of crimes committed in an area by the population, then multiply by 100,000.
Crime Rate Definition
What is a crime rate? A crime rate is defined as the total number of crimes performed per a certain number of people in a specified area. This is typically expressed per 100,000 people.
Example Problem
How to calculate crime rate?
- First, determine the number of crimes committed in an area.
For this example, the area of a city was found to have 1,000 crimes over an entire year.
- Next, determine the total population.
The city has a population of 95,000.
- Finally, calculate the crime rate.
Using the formula above, the crime rate is found to be 1,000/95,000*100,000 = 1,052 crimes per 100,000 people.
About Crime Rate
What is the crime rate in the US? In 2019, the violent crime rate was 366.7 per 100,000 people.
Are crime rates decreasing or increasing? Crimes in the United States have been decreasing since the mid 1900’s.
Коэффициент преступности – это конкретный обобщающий показатель общего количества учтенных преступлений, соотнесенного с численностью населения. Он расшифровывается как число преступлений на 100 тыс. , 10 тыс. или 1 тыс. населения и является объективным измерителем преступности, позволяющим сопоставлять ее уровни в разных регионах и в разные годы.
Для комплексных качественных сравнений уровня криминализации деяний, полноты их регистрации, эффективности работы правоприменительных органов и т. д. необходимы объективные количественные сравнения, т. е. без коэффициента преступности это сделать трудно.
Коэффициент преступности помогает более адекватно оценить и динамику уровня преступности, рассчитанного на душу населения.
Коэффициент преступности рассчитывается по формуле:
КП = (П х 100000) : Н,
где П – абсолютное число учтенных преступлений; а Н – абсолютная численность всего населения.
Оба показателя берутся в одном и том же территориальном и временном объеме. Число преступлений обычно рассчитывается на 100 тыс. населения. Но при малых числах преступлений и населения (в городе, районе, на предприятии) коэффициент преступности может рассчитываться на 10 тыс. или на 1 тыс. жителей. в любом случае эти числа означают размерность рассматриваемого коэффициента, которая обязательно указывается: число преступлений на 100 тыс. или 10 тыс. населения.
Доказать, что: 1) параллельные переносы образуют нормальную подгруппу группы ортогональных преобразований плоскости; 2) преобразования, имеющие общую неподвижнук> точку, образуют подгруппу группы ортогональных преобразований плоскости, но она не является нормальной. 13.21. Доказать, что: 1) если конечное множество аффинных преобразований плоскости образует группу, то все преобразования из этого множества имеют общую неподвижную точку; 2) всякая конечная группа ортогональных преобразований плоскости является группой симыетрии или группой врап|ений некоторого правильного многоугольника. 13.22.
Найти (с точностью до изоморфизма) факторгруппу С(Н, если: 1) С . группа всех комплексных чисел с операцией сложения, Н подгруппа всех вещественных чисел. 2) С – группа ненулевых комплексных чисел с операцией умножения, Н . подгруппа положительных вещественных чисел. 3) С группа ненулевых комплексных чисел с операцией умножения, Н подгруппа чисел, по модулю равных 1.
4) С группа всех вещественных чисел с операцией сложения, Н вЂ” подгруппа целых чисел. 5) С = К вЂ” группа целых чисел с операцией сложения, Н = пК подгруппа чисел, кратных данному натуральному числу и,. 126 Гл. 5. Преобразования плоскости. Группы 6) С группа всех ортогональных преобразований плоскости первого рода с операцией умножения преобразований, Н подгруппа параллельных переносов. 13.23. 1) Доказать, что множество Я„всех подстановок степени и является группой относительно операции умножсния преобразований (симметрической группой степени п).
Найти порядок этой группы. 2) Доказать, что группы Я„некоммутативны при п > 3. 13.24. Вычислить 21 ‘ ) 213 231 2341 4321 4321 2341 13.25. Доказать, что все четные перестановки (см. введение к ~ 14) образуют нормальную подгруппу А„в Я„, и найти ее порядок.
13.26. Пусть 1г нецикличсская подгруппа четвертого порядка в Я4. Доказать, что: 1) 1′ С Асб 2) $’ нормальна в Я4′, 3) иззу = оз. 13.27. Найти; 1) все подгруппы в Яз, 2) все нормальные подгруппы в Я4. Глава 6 МАТРИЦЫ 3 14. Определители В этом параграфе используются следующие основные понятия: матрица, подматрица, строка матрицы, столбец матрицы, перестановка, четнаа или нечетная перестановка, число нарушений порядка в перестановке, определитель (детерминант) квадратной магарицы, минор матрицы„элементарные преобразования матрицы, транспонирование матрицы.
В задачах 14.33 — 14.44 используются и другие операции с матрицами и некоторые специальные виды матриц; соответствующие обозначения и определения даны во введении к 3 15. Квадратная матрица порядка и аы а12 … а1„ а21 а22 ° ° а2 А= а„1 аьг ., а„„ обозначается также через ~)а,.~~ или (а,, ). Элементы агз,…,а„, образуют 1-ю строку, элементы а1,…,а„э — утй столбец матрицы А. Говорят, что элемент аз лежит на пересечении ее 1-й строки и у-го столбца. Всюду в этой главе, кроме нескольких специально оговоренных случаев, предполагается, что элементы матриц — вещественные или комплексные числа.
Определитель матрицы А обозначается через с1еФА, ~А~ или а11 а12 ° а1п а„,а,г ..а„„ Приведем основные формулы для вычисления определителей: = аН вЂ” Ьс; 1 ай ~ сд ~ а1 Ь1 с1 ,’ Ь2 с2 а2 с2 аг Ьг ~ агЬгсг ~ =а1, — Ь1 +с1 йз сз аз сз аз йз азйзсз ~ = а1Ьгсз — азйзсг+ азЬ1сг — агЬ1сз+ агЬзс1 — азЬгс1. (2) Рекуррентные формулы: 128 Гл.
б. Матрицы и с1е1 А = ~~г ( — 1)’э ьа,гМгь г=-1 (3) (1бормула разлозгсения определителя по г-й строке), и бес А = ~ ~( — 1) ~тг агу Мь, (4) я=1 (формула разложения определителя по у’-му столбцу). В формулах (3), (4) через М,ь обозначен дополнительный минор элемента аем т.е. определитель матрицы порядка и — 1, полученной из А вычеркиванием строки и столбца, в которых расположен элемент а,ы аы ..а1„ (-1) 1’1″”лпга1г …а,„,п (5) ап1 ..
апп 1г1,…,гпд — формула полного разложения (или полного развертывания) определителя, выражающая определитель матрицы и-го порядка через ее элементы. В слагаемых формулы (5) значения индексов гы …, гп образуют всевозможные перестановки чисел 1, 2, …, и, а через Аг(1м …, г ) обозначено число нарушений порядка в перестановке (гы …,г„). Напомним, что перестановка (гы …, 1„) называется четной, если число Х (1ы …, 1„) четно, и нечетной в противном случае.
Приведем формулировку теоремы Лапласа. Минором, порядка з (з < п) матрицы А называется определитель матрицы, образующейся в пересечении каких-либо .з строк и з столбцов матрицы А. Если эти строки имеют номера (гы…,г,), а столбцы — номера Оы…,у,), то соответствующий минор обозначается через Г аг1г1 .. аг1гг г1,…,гг 31,— дг а; .,,аг.. г1…гг 11 Через М “‘. обозначаем минор, дополнительный к минору Ьу ‘” 11» уг 11″ уг’ т.
е. определитель матрицы порядка и — з, полученной из А вычеркиванием выделенных строк и столбцов. Для любого натурального числа з (з < и) и любого фиксированного набора строк с номерами 1г,…,1, таких, что 11 < гг « … 1„справедлива формула — “‘+ (6) 11” зг г1 “зг’ 01,”,Ы где сумма берется по всевозможным наборам значений индексов уы…,у„таким, что 1 < у1 < уг « … у, < и.
Формулу (6) можно назвать формулой разложения определителя по данным з строкам. Аналогична формула разложения определителя по данныъг з столбцам: ~ Ц. Определители 129 ЫА= ~ (-Ц’+ – +*”*7,”.””ЛХ”.””.. и о8 1г и йп —,и) Здесь индексы 1ы…, 1„фиксированы, а сумма берется по всевозможным наборам значений индексов 1ы.,,,1, таким, что 1 < 11 < … … < 1, < и.
Перестановки (14.1 — 14.3) 14.1. 1) Доказать, что последовательно переставляя соседние числа, можно поменять местами любые два элемента перестановки, сохранив при этом расположение остальньгх элементов. 2) Доказать, что четность перестановки изменится, если в ней поменять местами два элемента. 14.2. 1) Доказать, что конечное число (Й) раз переставляя соседние числа, можно расположить элементы перестановки в порядке возрастания. Однозначно ли определено к? 2) Пусть а число нарушений порядка в перестановке.
Доказать, что числа Й и э имеют одинаковую четность. 3) Указать последовательность из з перемен мест в парах соседних чисел, в результате которой все элементы перестановки будут расположены в порядке возрастания. 14.3. Последовательно переставляя соседние числа, расположить элементы следующих перестановок в порядке возрастания. Найти число нарушений порядка и определить четность перестановки: 1) (5 4 3 2 1); 2) (6 4 5 2 3 1); 3) ( 1 2 4 5 6 3 ); 4) ( 1 2 4 3 5 9 8 7 6 ); 5) ( 9 8 7 6 5 4 3 2 1 ); 6) ( 4 3 2 1 5 9 8 7 6 ); 7) ( п, п — 1, …, 1 ); 8) ( 1, 3, 5, …, 2п — 1, 2, 4, 6, …, 2п ); 9) ( 2, 4, 6, …, 2п, 1, 3, 5, …, 2п + 1 ).
Вычисление определителей (14.4 — 14.32) 14.4. Вычислить определитель второго порядка: 1) )Аь); 2) (Ае(; 3) (Ат(; 4) )Аэ1); 5) )Атт); 6) (Аэ!. 14.5. Вычислить /Ага/ при е = е”?з. 14.6. Пусть х = тсоьд, у = тяпу. Вычислить якобиан дх/дт дх/ду ду/дт ду/дх Гл. б. Магприцы 14.7.
Вычислить определитель третьего порядка: 1) )Агоо1′ 2) )Аго1~’ 3) (Агог~; 4) ~Агоз!; б) ~Аго4~; б) 1Агоз|; 7) ~Агоо~; 8) ~Аг1а!:, 9) )Азоз|; 10) (А354~; 11) /Азов~; 12) )Азов~. 14.8. Вычислить /Азоз! при ы = ег”‘?3. 14.9. Пусть х = гсое рсоз4О, у = гв1п«рсов4р, 3 = гв1п4р. дх/дг дх/д~р дх(д~~ ду(дг ду/дд ду/дф д /дг дз/дд дз/д4)~ Вычислить якобиан 14.10. Решить относительно неизвестного Л уравнение: 1) )Аг11 — ЛЕ! =О; 2) /Аг1г — ЛЕ~ =0; з) ~А„,— ле!=о. 14.11.
Сколько слагаемых входит: 1) в формулу полного разложения определителя четвертого порядка; 2) в формулу полного разложения определителя пятого порядка? 14. 12. 1) Имеются ли в формуле полного разложения определителя матрицы Оап~( пятого порядкаслагаемые а15а1га34аг1а43, а55п1го34пг1п43 2) С какими знаками входят в формулу полного разложения определителя матрицы пятого порядка слагаемые аггог1аз4а45азз, агзагзоз4а41азг? 14.13. Пусть в матрице А порядка и точно и элементов равны 1, а остальные -. нули.
Чему может быть равен определитель матрицы А? 14.14. Доказать, что определитель диагональной матрицы равен произведению ее диагональных элементов. 14.15. Доказать, что определитель треугольной матрицы равен произведению ее диагональных элементов. 14.10. 1) Как иззленится определитель, если в златрице переставить две строки? 2) Как изменится определитель, если к одной строке матрицы прибавить другую? 3) Как изменится определитсль, если одну строку в матрице умножить на число Л? 4) Как будет изменяться определитель, сели со столбцами матрицы совершать такие же элементарные преобразования? 14.17. Изменится ли опрсделитслгч если матрицу транспонировать? З Ц. Определители 1 — а” Ь” 1 1 1 — а” Ь” и 1 — а1Ь„ 1 — а1Ь1 8) 1 — а„”Ь„” 1 — а” Ь” е 1 1 — а„Ь1 1 х 1 — а„Ь„ + хл + хпг + Ф …
1 1+хг … 1 и 2о 1 0 …0 0 1 2ее 1 … 0 0 О 1 2ее…О 0 10) (р) 0 0 О … 1 2ее 14.18. Как изменится определитель, если все элементы матрицы заменить комплексно сопряженными числами? 14.19. Сформулировать несколько достаточных условий, прн которых определитель матрицы А равен О. Сформулировать необходимое и достаточное условие. 14.20. Пусть деФА ф О. Доказать, что, применяя к строкам матрицы элементарные преобразования, сохраняющие определитель, можно получить: 1) треугольную матрицу: 2) диагональную матрицу.
14.21. Вычислить определитель четвертого порядка: 1) )Алзо~; 2) )А4зг(; 3) (Алзг); 4) )Аезз); 5) )А466); 6) )Аззт~; 7) )Алзз~; 8) )Алзо~; 9) )Адо); 10) (А461(; 11) (А464); 12) )А44г); 13) )А44з); 14) (А444); 15) )А446(. 14.22. Вычислить определитель пятого порядка: 1) )Аззо~:, 2) )Аззг~’ 3) )Аззз~’ 4) )А64Ф(:, 5) )Аззо~ 14.23. Вычислить определитель порядка ги 1) )А600~, 2) (А601~, 3) (А610~, 4) )Аод~(; 5) (Аозз(; 6) )А606); 7) (А6~4/; 8) /А6~); 9) (Аогг(; 10) (Аозз(; и) ~Аогз~; 12) ~Аого~; 13) !А гз(; 14) ~Аог ~; 15) !А64Ф!; 16) !Аозо!; 17) /Аозо/; 18) !Аогд/ (и = 2й).
| Меню сайта |
|---|
| Категории раздела |
|---|
|
Документы |
| Наши новости | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| Последние статьи | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| Статистика |
|---|
|
Онлайн всего: 2 Гостей: 1 Пользователей: 1 Rolandopaf |
Каталог статей
Расчет посещаемости и заболеваемости в дошкольной образовательной организации.
| Расчет (формула) посещаемости и заболеваемости в дошкольной образовательной организации. Формула по посещаемости и заболеваемости для детского сада: ПП=КДПхРД 1. План по посещаемости – ПП Количество детей в ДОО по плану– КДП Количество рабочих дней в месяц – РД Х – умножить Пример: КДП в ДОО – 328 детей, в январе 17 рабочих дней (2017г.). План по посещаемости равен – 5576. 328х17=5576 2. Фактическая посещаемость – ФП ФП= КДПхРД 280 – Количество детей, посещавших ДОО в январе умножаем на рабочие 17. Фактическая посещаемость равна – 4760. Пример: 280х17=4760 3. Количество пропусков – Кп Кп=ПП-ФП 4. Число дней по заболеваемости – ЧДз Количество дней пропущенных по заболеванию – (Дз) всеми детьми в течение месяца по справкам. 5. Заболеваемость на одного ребёнка – ЗР ЗР= ЧДС:КДП Заболеваемость на одного ребёнка высчитывается по формуле: ЧДз число дней по заболеваемости делим на КДП- количество детей по плану и получаем заболеваемость на 1 ребенка. Пример: в течение месяца пропусков по заболеванию (ЧДз)-200 делим на количество детей по плану (КДП) – 328 равно 0,6 0,6=200:328 6.Посещаемость 1 ребенком – Пр Пр=ФП:КДП высчитывается по формуле: Фактическая посещаемость детьми в месяц делится на количество детей в ДОО по плану. Пример: 10=4760:328 7. Средняя посещаемость – СПд Средняя посещаемость детьми СПд высчитывается по формуле: фактическая посещаемость ФП делится на количество рабочих дней РД. СПд=ФП : РД Источник: http://ds97sar.schoolrm.ru/sveden/document |
| Категория: Документы | Добавил: mdou97 (05.04.2017) |
| Просмотров: 87218 | Теги: формула заболеваемости для детского, Формула посещаемости | Рейтинг: 4.7/13 | |
| Форма входа | |||||||
|---|---|---|---|---|---|---|---|
|
| Поиск |
|---|
| Наши фотографии |
|---|
|
[Праздники, вечера, конкурсы] [Праздники, вечера, конкурсы] [Праздники, вечера, конкурсы] [Праздники, вечера, конкурсы] |
| Реклама |
|---|
Актуально на 2023 год
Как посмотреть старые штрафы, включая ранее оплаченные
Бывает, что водителю нужно найти уже оплаченный штраф. Так можно проверить, прошел ли платеж и не было ли двойной оплаты. Посмотреть архив и историю оплаченных нарушений получается не всегда. Рассказываем, как получить список всех своих штрафов и стоит ли опасаться, что их увидят мошенники.
Свидетельство о регистрации ТС
Водительское удостоверение
Проверяем информацию о штрафах,
пожалуйста, подождите несколько секунд
Когда нужна история оплаченных штрафов
Оплатил два раза. Водитель оплачивает штраф, но позднее получает письмо от приставов с долгом. В такой ситуации надо проверить, когда была оплата, чтобы запросить у банка квитанцию и доказать ошибку.
Платеж не прошел. Другой вариант — штраф остается в базе как неоплаченный, водитель видит это сразу или получает уведомление. Такое бывает из-за ошибки в реквизитах или сбоя. Начать стоит с того, чтобы проверить последние оплаты.
Где можно посмотреть историю штрафов ГИБДД
Недавно оплаченные штрафы. Если вы регулярно оплачиваете штрафы онлайн, то можете посмотреть историю всех оплат. Она доступна:
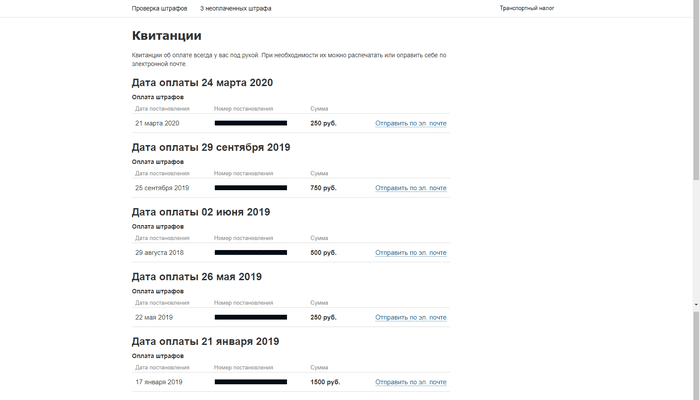
- На сервисах вроде «Штрафов ГИБДД». Сервис хранит полные данные об оплате со сведениями о машине, фотографиями нарушений и квитанциями. При необходимости их можно отправить себе на почту. Войдите в сервис по электронной почте и перейдите в раздел «Квитанции об оплате».
- На Госуслугах. Войдите в сервис по логину и паролю, выберите услугу «Проверка штрафов», нажмите «Получить услугу» и откройте вкладку «История платежей». Сайт Госуслуг не всегда работает стабильно, если возникла ошибка — попробуйте снова через час.
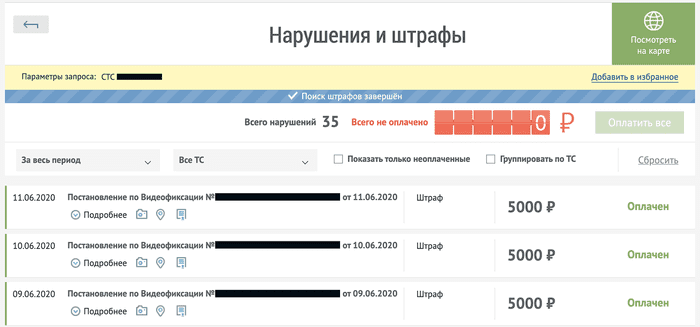
История всех штрафов. Указанные сервисы показывают архив только тех оплат, которые провели через них. Если вы оплачивали штрафы через банк, попробуйте посмотреть историю в сервисе «Автокод» мэрии Москвы.
Он показывает пользователю данные о старых оплатах. Сервис можно использовать, даже если вы не из Москвы. Войдите через Госуслуги, введите данные о правах и номер свидетельства о регистрации ТС и нажмите кнопку «Проверить».
«Штрафы ГИБДД» сохраняют квитанции, если вы платите через сервис
Сервис «Автокод» мэрии Москвы показывает все штрафы, в том числе оплаченные через банк
Как получить выписку по оплаченным и просроченным штрафам
Оплаченные штрафы — в ГИБДД. Информация об оплаченных штрафах хранится в базе ГИС ГМП. Оттуда данные получают некоторые сервисы и сотрудники ГИБДД.
За выпиской можно обратиться в отделение ГИБДД, с собой нужно иметь паспорт, водительские права и СТС.
Просроченные штрафы — в ФССП. У водителя есть 10 дней на то, чтобы оспорить постановление, еще 60 — чтобы оплатить штраф. Если этого не сделать, постановление передадут судебным приставам, те начнут исполнительное производство, а еще через 5 дней выпишут исполнительский сбор.
Просроченный штраф можно также увидеть на сервисе «Штрафы ГИБДД», либо проверить на сайте ФССП. Дальше можно будет позвонить приставам, которые выписали штраф, записаться на прием и запросить выписку.
Могут ли мошенники получить доступ к истории платежей
Незнакомые люди могут получить доступ к информации о ваших штрафах. Но для этого им нужно знать номер вашего СТС и водительских прав.
Скорее всего, они смогут увидеть информацию о нескольких неоплаченных штрафах или только сообщение о том, что штрафов у водителя нет. Эти данные вряд ли можно использовать против вас, особенно если вы вовремя проверяете и платите штрафы.
Запомнить
- Найти уже оплаченный штраф иногда нужно, чтобы проверить, прошел ли платеж и не было ли двойной оплаты.
- Данные об оплатах хранят сервисы, через которые вы проверяете и гасите штрафы, например «Штрафы ГИБДД».
- Историю оплаченных штрафов, которые вы гасили через банк, можно посмотреть на сервисе «Автокод» правительства Москвы.
- Получить выписку по оплаченным штрафам можно в ГИБДД, по просроченным — в ФССП.
- Злоумышленники могут получить доступ к данным о ваших штрафах, если знают номер СТС и прав. Скорее всего, они увидят только неоплаченные штрафы.