Независимые множества
Независимое
множество вершин
– множество вершин графа G:
SV
такое, что любые две вершины в нем
несмежны, то есть никакая пара вершин
не соединена ребром.
подграф,
порожденный независимым множеством
– пустой
граф.
Максимальное
независимое множество –
не является собственным подмножеством
другого независимого множества.
Наибольшее
независимое множество – наибольшее
по мощности среди всех независимых
множеств.
Число
независимости (G)
графа G
– мощность
наибольшего независимого множества.
Например:
М
Граф
G:
аксимальные независимые множества:

X3};
S2={X2,
X7,
X8};
S3={X2,
X5,
X7,
X8};
S4={X4,
X6};
S5={X1,
X3,
X7};
S6={X2,
X4,
X8};
S7={X3,
X6};
S8={X1,
X4}.
Наибольшее
независимое множество: S3={X2,
X5,
X7,
X8}.
Число
независимости графа G
: (G)=4.
Клика
Клика
– антипод
независимого множества. Подмножество
вершин графа G
такое, что любая пара из этого множества
является смежной.
подграф,
порожденный кликой – полный граф.
Максимальная
клика – не
является собственным подмножеством
никакой другой клики графа G.
Наибольшая
клика – наибольшая
по мощности среди всех остальных клик
графа G.
Кликовое
число или плотность (G)
графа G
–
мощность
наибольшей клики.
Н
Граф
G
апример:
клики
графа G:
S1={a,b,с};
S2={b,d,e};
S3={b,c,e};
S4={b,d,c};
S5={c,d,e};
S6={b,c,d,e}.
Максимальные
клики: S1={a,b,с},
S6={b,c,d,e}.
Наибольшая
клика: S6={b,c,d,e}.
Кликовое
число: (G)=4
Доминирующие множества
Доминирующее (внешне устойчивое)
множество –
подмножество V’V
вершин графа такое, что каждая вершина
из VV’
смежна с некоторой вершиной из V’.
Иначе, каждая вершина графа находится
на расстоянии не более одного ребра от
данного множества.
Минимальное
доминирующее множество – нет
другого доминирующего множества,
содержащегося в данном.
Наименьшее
доминирующее множество – доминирующее
множество с наименьшей мощностью.
Число
доминирования (G)
– мощность
наименьшего доминирующего множества.
Например:
Минимальные
доминирующие множества:
S1={X1,
X4}
S2={X3,
X5,
X6}
наименьшее
доминирующее множество: S1={X1,
X4}.
Число
доминирования: (G)=2.
Задание к лабораторной работе
-
Используя
алгоритм генерации варианта GV
(приложение А), построить неориентированный
граф G:
GV(7,{2,3}). -
Описать
граф матрицей смежности и матрицей
инцидентности. -
И
зобразить
графически графG
и его дополнение
G. -
Построить
произвольный остовный подграф и подграф,
порожденный вершинами {1,2,5,6,7}; -
Построить
все помеченные 5-графы, изоморфно
вложимые в граф G.
5.1. Определить
классы изоморфных графов.
5.2. Построив биекцию
их вершин.
5.3 Для каждого
класса изоморфных графов привести
рисунок абстрактного графа.
-
Построить
все помеченные (5-7)-графы (до 20 штук),
изоморфные некоторому подграфу G.
6.1. Определить
классы изоморфных графов.
6.2. Построив биекцию
их вершин.
6.3. Для каждого
класса таких графов привести рисунок
абстрактного графа.
-
Найти
все максимальные и наибольшие независимые
множества исходного графа, определить
число независимости. -
Найти
все максимальные и наибольшие клики
данного графа. Определить плотность
графа G. -
Найти
все минимальные и наименьшие доминирующие
множества, определить число доминирования. -
Найти
полный двудольный подграф
Kp,q,
изоморфно вложимый в G
с максимальным
количеством вершин p+q
(p≠1).
Найти звезду K1,n
, изоморфно вложимую в G
с максимальным
n.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
16.11.2019316.42 Кб0om.doc
- #
Зада́ча о незави́симом мно́жестве относится к классу NP-полных задач в области теории графов. Эквивалентна задаче о клике.
Определения[править | править код]
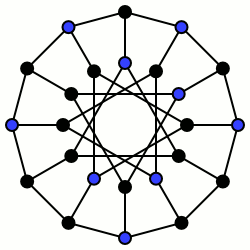
Независимый набор из 9 голубых вершин
Множество вершин графа называется независимым, если никакие две вершины этого множества не соединены ребром. Другими словами, индуцированный этим множеством подграф состоит из изолированных вершин. Иногда также говорят, что каждое ребро графа инцидентно не более чем одной вершине из независимого множества. Задача распознавания (проблема разрешимости) выглядит так: существует ли в заданном графе G независимое множество размера k? Соответствующая ей оптимизационная задача, она же задача о независимом множестве, формулируется следующим образом: в заданном графе G требуется найти независимое множество максимального размера. Этот размер называют числом независимости, числом внутренней плотности или неплотностью и обозначают как 
Иногда эту задачу называют поиском наибольшего независимого множества. Не стоит путать это понятие с максимальным независимым множеством, или максимальным по включению независимым множеством, которое определяется как такое независимое множество вершин, что при добавлении к нему ещё одной (любой) вершины исходного графа оно перестаёт быть независимым (вообще говоря, таких множеств может быть несколько и разных размеров). Максимальное по включению независимое множество отнюдь не всегда является наибольшим. В то же время каждое наибольшее независимое множество по определению является также и максимальным по включению. Для нахождения (какого-то) максимального по включению независимого множества можно воспользоваться жадным алгоритмом, работающим за полиномиальное время, тогда как задача о наибольшем независимом множестве принадлежит к классу NP-полных задач.
Максимальное по включению независимое множество является доминирующим множеством. Любой граф содержит максимум 3n/3 максимальных по включению независимых множеств[3], однако бо́льшая часть графов имеет их куда меньше.
Число максимальных по включению независимых множеств в циклах из n вершин — это числа Перрина, а число максимальных по включению независимых множеств в путях с n вершинами задаётся последовательностью Падована[4]. Таким образом, оба числа пропорциональны степени 1,324718, пластическому числу.
Наименьшим независимым подмножеством в графе является любая вершина этого графа.
Связь с другими параметрами графов[править | править код]
Множество независимо тогда и только тогда, когда оно является кликой в дополнении графа, так что два понятия дополняют друг друга. Достаточно большие графы без больших клик имеют большие независимые множества, что является предметом исследования в теории Рамсея.
Множество независимо тогда и только тогда, когда его дополнение является вершинным покрытием. Сумма числа независимости 

Раскраска вершин графа 



В двудольных графах, не имеющих изолированных вершин, число вершин в наибольшем независимом множестве равно числу рёбер в наименьшем рёберном покрытии (следствие из теоремы Кёнига).
Поиск независимых множеств[править | править код]
В информатике изучается несколько вычислительных задач[en], связанных с независимыми множествами:
- В задаче о наибольшем независимом множестве входом служит неориентированный граф, а выходом — наибольшее независимое множество в этом графе. Если существует несколько таких множеств, достаточно найти одно.
- В задаче о независимом множестве максимального веса входом служит неориентированный граф с весами, заданными для вершин, а выходом — независимое множество с максимальным общим весом. Задача о максимальном по включению независимом множестве является частным случаем этой задачи с весами, равными единице.
- В задаче перечисления максимальных по включению независимых множеств входом служит неориентированный граф, а выходом — список всех максимальных по включению независимых множеств. Задачу о наибольшем независимом множестве можно решать как подзадачу данной задачи, поскольку наибольшее независимое множество является максимальным по включению и должно попасть в этот список.
- В задаче о наличии независимого множества заданного размера входом служит неориентированный граф и число k, а выходом — Да/Нет: Да, если граф содержит независимое множество размера k, и Нет в противном случае.
Первые три задачи важны в практических приложениях, последняя же важна для теории NP-полноты для задач, связанных с независимыми множествами.
Задача о независимом множестве и задача о клике являются двойственными: клика в G — это независимое множество в дополнении графа G и наоборот. Таким образом, многие вычислительные результаты могут быть приложены одинаково хорошо к обоим задачам. Например, результаты, связанные с задачей о клике, имеют следующие следствия:
- Задача о наличии является NP-полной, а это означает, что существование (ровно как и не существование) эффективного алгоритма её решения не доказано. Существует эффективные (аппроксимирующие[5]) эвристические алгоритмы поиска максимального по весу независимого множества вершин в графе, примером которых может служить алгоритм Русова В.С. и Захаровой Д.А. имеющий сложность O(n3).
- Задача о наибольшем независимом множестве NP-трудна и её, кроме того, трудно аппроксимировать.
Поиск наибольшего независимого множества[править | править код]
Эту задачу иногда называют «упаковкой вершин».
Задача нахождения наибольшего независимого множества и задача о наибольшей клике полиномиально эквивалентны — можно найти наибольшее независимое множество путём поиска максимальной клики в дополнении графа, так что многие авторы особенно не заботятся о разделении этих двух задач. Обе задачи NP-полны, так что вряд ли их можно решить за полиномиальное время. Тем не менее, задача о наибольшем независимом множестве может быть решена эффективнее, чем за время O(n2 2n), которое даёт полный перебор, проверяющий все подмножества вершин, являются ли они независимыми множествами. Алгоритм Робсона[6] решает задачу за время O(20.276n), используя экспоненциальное пространство. Если есть ограничение на размер (полиномиальность пространства), существует алгоритм решения за время O*(1.2127n)[7].
Вопреки близкой связи между наибольшей кликой и наибольшим независимым множеством в произвольном графе, задачи нахождения независимого множества и клики могут существенно отличаться, когда решаются на специальном классе графов. Например, для разреженных графов (графы, в которых в любом подграфе число рёбер не больше числа вершин, умноженного на некоторую константу) наибольшая клика имеет ограниченный размер и может быть найдена точно за линейное время[8]. Тем не менее, для тех же классов графов, или даже для случая более жёстких ограничений у класса графов с ограниченной степенью, поиск наибольшего независимого множества является MAXSNP-полной[en], что означает, что для некоторой константы c (зависящей от степени) NP-трудно найти приближённое решение, отличающееся на множитель c от оптимального[9]. Однако эффективные приближённые алгоритмы известны, но для них гарантированная эффективность хуже, чем этот порог. Например, жадный алгоритм создаёт максимальное по включению независимое множество, на каждом шаге выбирая вершину с минимальной степенью и удаляя её соседей. Этот алгоритм достигает гарантированной эффективности (Δ+2)/3 на графах с максимальной степенью Δ[10].
В некоторых классах графов (включая графы без клешней[11] и совершенные графы[12]; к последнему классу принадлежат и деревья) наибольшее независимое множество может быть найдено за полиномиальное время. Для планарных графов задача о наибольшем независимом множестве остаётся NP-полной для точного решения, но может быть аппроксимирована с любой гарантированной эффективностью c < 1 за полиномиальное время. Похожие приближённые схемы полиномиального времени существуют в любом семействе минорно замкнутых графов[13][14].
В двудольных графах все вершины, не входящие в наименьшее вершинное покрытие, могут быть включены в наибольшее независимое множество (смотри теорему Кёнига). Поэтому наибольшее независимое множество может быть найдено с помощью алгоритма нахождения наибольшего паросочетаний в двудольных графах.
Поиск максимальных по включению независимых множеств[править | править код]
Все максимальные по включению независимые множества можно найти за время O(3n/3).
Программное обеспечение для поиска независимых множеств[править | править код]
| Название | Лицензия | Язык API | Описание |
|---|---|---|---|
| igraph | GPL | C, Python, R, Ruby | точное решение |
| NetworkX | BSD | Python | приближённое решение, см. процедуру maximum_independent_set |
| OpenOpt | BSD | Python | точные и приближённые решения, возможность указать вершины, которые следует включить / исключить. См. класс STAB для деталей и примеров |
Наибольшее независимое множество в дереве[править | править код]
Если данный граф является деревом, то задача о независимом множестве эффективно решается методом динамического программирования.
Оптимальная подструктура задачи[править | править код]
Структура дерева сама подсказывает решение задачи. Именно, обозначим корнем дерева любую вершину и назовем её 



Нетрудно видеть, что если мы включаем вершину u в наибольшее независимое множество, то его мощность увеличивается на 1, но его детей мы брать не можем (так как они соединены ребром с вершиной u); если же мы не включаем эту вершину, то мощность наибольшего независимого множества будет равна сумме размеров независимых множеств детей этой вершины. Остается только выбрать максимум из этих двух вариантов, чтобы получить решение задачи:
где grandchild обозначает всякого «внука» вершины, а child обозначает всякого потомка вершины.
Псевдокод[править | править код]
Считаем, что в вершине u хранится 
function get_independent_set(Node u)
{
если I(u) уже посчитано, то возвратить I(u)
// мощность множества, которое можно получить, если не брать вершину u
children_sum = 0
// мощность множества, которое можно получить, если взять вершину u
grandchildren_sum = 0
// цикл по всем детям
for i := 1 to child_num do
children_sum = children_sum + get_independent_set(children[i])
// цикл по всем внукам
for i:= 1 to grandchildren_num
grandchildren_sum = grandchildren_sum + get_independent_set(grandchildren[i])
// запоминаем, чтобы не пересчитывать ещё раз
I(u) = max(1 + grandchildren_sum, children_sum)
возвратить I(u)
}
Вызов get_independent_set(r) даст ответ на задачу. Время выполнения алгоритма, очевидно, O(|V| + |E|).
См. также[править | править код]
- Алгоритм Брона — Кербоша для нахождения максимальных по включению независимых множеств вершин.
Примечания[править | править код]
- ↑ Chris Godsil, Gordon Royle. . Algebraic Graph Theory. — New York: Springer, 2001. — ISBN 0-387-95220-9. — P. 3.
- ↑ Евстигнеев В. А., Касьянов В. Н. . Словарь по графам в информатике. — Новосибирск, 200. — (Конструирование и оптимизация программ, вып. 17). — ISBN 978-591124-036-3.
- ↑ Moon J. W., Moser L. On cliques in graphs // Israel Journal of Mathematics. — 1965. — Vol. 3, no. 1. — P. 23–28. — doi:10.1007/BF02760024.
- ↑ Füredi, Zoltán. The number of maximal independent sets in connected graphs // Journal of Graph Theory. — 1987. — Vol. 11, no. 4. — P. 463–470. — doi:10.1002/jgt.3190110403.
- ↑ Из приведённой ниже статьи Русова и Захаровой: В последнее время наибольший интерес для решения подобного рода задач представляют эвристические алгоритмы, то есть алгоритмы, которые всё же позволяют решить NP-полную задачу, но с некоторой погрешностью. Основными критериями оценки эвристического алгоритма являются «эффективность по времени» и погрешность по отношению к точному алгоритму.
- ↑ Robson J. M. Algorithms for maximum independent sets // Journal of Algorithms. — 1986. — Vol. 7, no. 3. — P. 425–440. — doi:10.1016/0196-6774(86)90032-5.
- ↑ Nicolas Bourgeois, Bruno Escoffier, Vangelis Th. Paschos, Johan M. M. van Rooij. . A bottom-up method and fast algorithms for MAX INDEPENDENT SET // Algorithm theory—SWAT 2010. — Berlin: Springer, 2010. — (Lecture Notes in Computer Science, vol. 6139). — doi:10.1007/978-3-642-13731-0_7. — P. 62–73.
- ↑ Chiba N., Nishizeki T. Arboricity and subgraph listing algorithms // SIAM Journal on Computing. — 1985. — Vol. 14, no. 1. — P. 210–223. — doi:10.1137/0214017.
- ↑ Piotr Berman, Toshihiro Fujito. . On approximation properties of the Independent set problem for degree 3 graphs // Fourth International Workshop on Algorithms and Data Structures. — Springer, 1995. — (Lecture Notes in Computer Science, vol. 995). — doi:10.1007/3-540-60220-8_84. — P. 449–460.
- ↑ Halldórsson M. M., Radhakrishnan J. Greed is good: Approximating independent sets in sparse and bounded-degree graphs // Algorithmica. — 1997. — Vol. 18, no. 1. — P. 145–163. — doi:10.1007/BF02523693..
- ↑ Sbihi, 1980.
- ↑ Grötschel, Lovász, Schrijver, 1988.
- ↑ Brenda S. Baker. Approximation algorithms for NP-complete problems on planar graphs // Journal of the ACM. — 1994. — Vol. 41, no. 1. — P. 153–180. — doi:10.1145/174644.174650.
- ↑ Martin Grohe. Local tree-width, excluded minors, and approximation algorithms // Combinatorica. — 2003. — Vol. 23, no. 4. — P. 613–632. — doi:10.1007/s00493-003-0037-9.
Литература[править | править код]
- Chris Godsil, Gordon Royle. . Algebraic Graph Theory. — New York: Springer, 2004. — ISBN 0-387-95220-9.
- Grötschel M., Lovász L., Schrijver A. . 9.4. Coloring Perfect Graphs // Geometric Algorithms and Combinatorial Optimization. — Springer, 1988. — (Algorithms and Combinatorics, vol. 2). — ISBN 0-387-13624-X. — P. 296–298.
- Karp, Richard. Reducibility Among Combinatorial Problems // Proceedings of a Symposium on the Complexity of Computer Computations. — 1972.
- Michael R. Garey, David S. Johnson. . Computers and Intractability: A Guide to the Theory of NP-Completeness. — W. H. Freeman, 1979. — ISBN 0-7167-1045-5.
- Sanjoy Dasgupta, Christos H. Papadimitriou, Umesh Vazirani. . Chapter 6. Dynamic Programming // Algorithms. — McGraw-Hill Science/Engineering/Math, 2006. — ISBN 0073523402. — P. 336.
- Sbihi, Najiba Sbihi. Algorithme de recherche d’un stable de cardinalité maximum dans un graphe sans étoile // Discrete Mathematics. — 1980. — Vol. 29, no. 1. — P. 53–76. — doi:10.1016/0012-365X(90)90287-R.
Ссылки[править | править код]
- Weisstein, Eric W. Maximal Independent Vertex Set (англ.) на сайте Wolfram MathWorld.
- Challenging Benchmarks for Maximum Clique, Maximum Independent Set, Minimum Vertex Cover and Vertex Coloring
- Поликарпова Н., Герасименко А. Методы решения труднорешаемых задач
- Слайды лекции о динамическом программировании
- Видео лекции о динамическом программировании
- Русов В.С., Захарова Д.А. Эвристический алгоритм поиска максимального по весу независимого множества вершин в графе
Аннотация: Независимые множества, клики, вершинные покрытия . Три задачи.
Стратегия перебора для задачи о независимом множестве.
Эвристики для задачи о независимом множестве. Приближенный
алгоритм для задачи о вершинном покрытии. Перебор максимальных
независимых множеств.
Независимые множества, клики, вершинные покрытия
Во многих задачах на графах требуется найти какой-нибудь максимум или
минимум, например, наибольший подграф с заданным свойством, или разбиение
графа на наименьшее число частей, удовлетворяющих каким-то условиям,
и т.д. В оставшихся лекциях рассматриваются несколько задач такого рода,
считающихся классическими в теории графов. Некоторые из них известны как
NP-трудные, для них рассматриваются переборные алгоритмы, приемы
рационализации, эвристики и приближенные алгоритмы. Для других задач
излагаются известные эффективные алгоритмы.
Три задачи
Независимым
множеством вершин графа называется любое множество
попарно не смежных вершин, т.е. множество вершин, порождающее пустой
подграф. Независимое множество называется максимальным, если оно не
является собственным подмножеством другого независимого множества,
и наибольшим, если оно
содержит наибольшее количество вершин. Число
вершин в наибольшем независимом множестве графа 
через 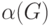
Задача о независимом множестве состоит в нахождении наибольшего
независимого множества.
Кликой графа называется множество
вершин, порождающее полный
подграф, т.е. множество вершин, каждые две из которых смежны. Число вершин
в клике наибольшего размера называется кликовым числом графа и
обозначается через 
множестве преобразуется в задачу о клике и наоборот простым переходом от
данного графа 


Вершинное покрытие
графа – это такое множество вершин, что каждое
ребро графа инцидентно хотя бы одной из этих вершин. Наименьшее число
вершин в вершинном покрытии графа 
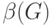
рис. 9.1 наибольшим независимым множеством является
множество 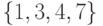
множество 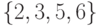
покрытием – множество 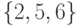
Рис.
9.1.
Между задачами о независимом множестве и о вершинном покрытии тоже имеется
простая связь благодаря следующему факту.
Теорема 1. Подмножество 

покрытием тогда и только тогда, когда 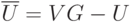
множество.
Доказательство. Если 
ребро содержит хотя бы одну вершину из множества 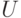
нет
ни одного ребра, соединяющего две вершины из множества 
Следовательно, 
если 
вершины из 
принадлежат
множеству 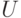
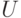
покрытие.
Из этой теоремы следует, что 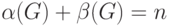
любого
графа 

Таким образом, все три задачи тесно связаны друг с другом, так что
достаточно научиться решать одну из них, и мы будем уметь решать остальные
две. Вместе с тем известно, что эти задачи NP-полны. Для таких задач не
известно эффективных алгоритмов, а накопленный к настоящему времени опыт
делает правдоподобным предположение о том, что таких алгоритмов и не
существует. Тем не менее, алгоритмы для подобных задач разрабатывались и
продолжают разрабатываться, и в некоторых случаях они могут быть полезны.
Все эти алгоритмы в той или иной форме осуществляют перебор вариантов
(число которых может быть очень большим). Далее рассмотрим один из
способов такого перебора для задачи о независимом множестве.
Привет, Вы узнаете про задача о наименьшем покрытии графа, Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое
задача о наименьшем покрытии графа, покрытие графа , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.
Основные определения
Рассмотрим неориентированный граф G = (V, E).
Независимое множество вершин (внутренне устойчивое множество) — это множество вершин графа G такое, что любые две вершины в нем не смежны, то есть никакая пара вершин не соединена ребром. Множество S ⊂ V, удовлетворяющее условию
S ∩ E(S) = Ø (1)
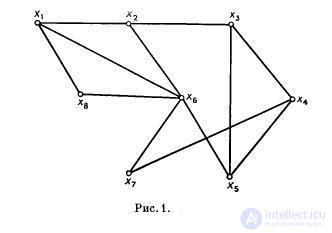
называется независимым множеством вершин. Для графа, изображенного на рисунке 1, независимыми являются {x7, x8, x2}, {x3, x1} множества вершин.
Независимое множество называется максимальным, когда нет другого независимого множества, в которое оно бы входило. Если множество удовлетворяет условию (1) и условию
H ∩ E(H) ≠ Ø ∀ H ⊃ S (2)
является максимальным независимым множеством. Например, множества {x1, x3, x7} и {x4, x6} максимальные независимые, а {x7, x8, x2} — нет. В графе может быть более одного независимого множества.
Если Q является семейством всех независимых множеств графа G, то
α[G] = maxS ∈ Q |S| (3)
называется числом независимости графа G, а множество S*, на котором достигается этот максимум, называется наибольшим независимым множеством.
Пример: выбор проекта
Имеется n проектов, которые должны быть выполнены. Для выполнения проекта xi требуется некоторое подмножетсво Ri наличных ресурсов из множества {1, …, p}. Пусть каждый проект, задаваемый совокупностью средств, необходимых для его реализации, может быть выполнен за один и тот же промежуток времени. Построим граф G, каждая вершина которого соответствует некоторому проекту, а ребро (xi, xj) наличию общих средств обеспечения у проектов xi и xj. Максимальное независимое множество графа G представляет максимальное множество проектов, которое можно выполнить одновременно за один и тот же промежуток времени.
В динамической системе происходит постоянное обновление проектов через определенный промежуток времени, так что каждый раз нужно заново повторять процедуру построения максимального независимого множества в соответствующем графе G. На практике не всегда можно выполнить работы, соответствующие максимальному независимому множеству. Тогда можно каждой работе (вершине xi) сопоставить некоторый штраф pi, который будет увеличиваться с увеличением срока исполнения работы. В каждый момент времени нужно выбирать из семейства максимальных независимых множеств такое множество, которое максимизирует некоторую функцию штрафов на вершинах, содержащихся в выбранном множестве.
Максимальный полный подграф (клика) графа G это порожденный подграф, построенный на подмножестве S вершин графа и являющийся полным и максимальным в том смысле, что любой другой подграф графа G, построенный на множестве вершин H, содержащем S, не является полным. То есть, в отличие от максимального независимого множества, в клике все вершины попарно смежны.
Аналогично тому, как было определено число независимости графа, с помощью соотношения (3) мы можем определить кликовое число графа (известное также как густота илиплотность). Это — максимальное число вершин в кликах данного графа. Тогда, образно говоря, у “плотного” графа кликовое число будет, вероятно, больше, а число независимости меньше, в то время как у “разреженного” графа, по всей вероятности, будет иметь место противоположное соотношение между этими числами.
Построение всех максимальных независимых множеств
Если граф небольшой (например, с числом вершин, не превосходящим 20), то построить максимальное независимое множество можно последовательным перебором независимых множеств с одновременной проверкой каждого множества на максимальность. Если же вершин много, то этот процесс становится сложным технически. Число максимальных независимых множеств возрастает, но во время поиска большое число независимых множеств формируется, а затем вычеркивается, так как обнаруживается, что они содержатся в других, ранее полученных множествах и поэтому не являются максимальными.
Обоснование алгоритма
Этот алгоритм является существенно упрощенным перебором, использующим дерево поиска. В процессе поиска — на некотором этапе k — независимое множество вершин Sk расширяется путем добавления к нему подходящим образом выбранной вершины (чтобы получилось новое независимое множество Sk+1) на этапе k+1, и так поступают до тех пор, пока добавление вершин станет невозможным, а порождаемое множество не станет максимальным независимым множеством. Пусть Qk будет на этапе k наибольшим множеством вершин, для которогоSk ∩ Qk = Ø, то есть после добавления любой вершины из Qk к Sk получается независимое множество Sk+1. В некоторый произвольный момент работы алгоритма множество Qk состоит из вершин двух типов: подмножества Qk– тех вершин, которые уже использовались в процессе поиска для расширения множеств Sk, и подмножества Qk+ таких вершин, которые еще не использовались. Тогда дальнейшее ветвление в дереве поиска включает процедуру выбора вершины xik ∈ Qk+, добавление ее к Sk для построения множества
Sk+1 = Sk ∪ {xik} (4)
и порождение новых множеств:
Qk+1– = Qk– − E(xik) (5)
и
Qk+1+ = Qk+ − (E(xik) ∪ {xik}). (6)
Шаг возвращения алгоритма состоит в удалении вершины xik из Sk+1, чтобы вернуться к Sk, изъятии xik из старого множества Qk+ и добавлении xik к старому множеству Qk– для формирования новых множеств Qk+ и Qk–.
Множество Sk является максимальный независимым множеством только тогда, когда невозможно его дальнейшее расширение, т. е. когда Qk+ = Ø. Если Qk+ ≠ Ø, то текущее множество Skбыло расширено на некотором предшествующем этапе работы алгоритма путем добавления вершины из Qk–, и поэтому оно не является максимальным независимым множеством. Таким образом, необходимым и достаточным условием того, что Sk — максимальное независимое множество, является выполнение равенств
Qk+ = Qk– = Ø. (7)
Если очередной этап работы алгоритма наступает тогда, когда существует некоторая вершина х ∈ Qk–, для которой E(x) ∩ Qk+ = Ø, то безразлично, какая из вершин, принадлежащих Qk+, используется для расширения Sk, и это справедливо при любом числе дальнейших ветвлений; вершина х не может быть удалена из Qp– на любом следующем шаге р > k . Об этом говорит сайт https://intellect.icu . Таким образом, условие
∃ x ∈ Qk–, такая, что E(x) ∩ Qk+ = Ø, (8)
является достаточным для осуществления шага возвращения, поскольку из Sk при всяком дальнейшем ветвлении уже не получится максимальное независимое множество.
Как и во всяком методе, использующем дерево поиска, здесь выгодно стремиться начать шаги возвращения как можно раньше, поскольку это ограничит “размеры” “ненужной” части дерева поиска. Следовательно, целесообразно сосредоточить усилия на том, чтобы возможно раньше добиться выполнения условия (8) с помощью подходящего выбора вершин, используемых при расширении множеств Sk. На каждом следующем шаге процедуры можно выбирать для добавления к Sk любую вершину xik ∈ Qk+ на шаге возвращения xik будет удалена из Qk+ и включена в Qk–. Если вершину xk выбрать так, чтобы она принадлежала множеству E(х) при некоторой вершине х из Qk–, то на соответствующем шаге возвращения величина
Δ(x) = |E(x) ∪ Qk+| (9)
уменьшится на единицу (по сравнению с тем значением, которое было до выполнения прямого шага в шага возвращения), так что условие (8) теперь станет выполняться раньше.
Таким образом, один из возможных способов выбора вершины xik для расширения множества Sk состоит, во-первых, в нахождении вершины x* ∈ Qk– с возможно меньшим значением величины Δ(х*) и, кроме того, в выборе вершины xi из множества E(x*) ∩ Qk+. Такой выбор вершины xik будет приводить на шаге возвращения к уменьшению величины Δ(x*) — каждый раз на единицу — до тех пор, пока вершина x* не станет удовлетворять условию (8) при выполнении шага возвращения.
Следует отметить, что поскольку на шаге возвращения вершина xik попадает в Qk–, то может оказаться, что при этом новом входе значение величины Δ меньше, чем для ранее фиксированной вершины x*. Значит, надо проверить, не ускорит ли эта новая вершина выполнение условия (8). Это особенно важно в начале ветвления, когда Qk– = Ø.
Описание алгоритма
- Пусть S0 = Qk– = Ø, Q0+, Qk– = V, k = 0.
- Выбрать вершину xik ∈ Qk+, как упоминалось ранее, и сформировать Sk, Qk+1– и Qk+1+, оставляя Qk– и Qk+ нетронутыми. Положить k = k + 1.
- Если удовлетворяется условие (8), то перейти к шагу 5, иначе к шагу 4.
- Если Qk+ = Qk– = Ø, то напечатать максимальное независимое множество Sk и перейти к шагу 5. Если Qk+ = Ø, a Qk– ≠ Ø, то перейти к шагу 5. Иначе перейти к шагу 2.
- Положить k = k − 1. Удалить xik из Sk + 1, чтобы получить Sk. Исправить Qk– и Qk+, удалив вершину xik из Qk+ и добавив ее к Qk–. Если k = 0 и Qk+ = Ø, то остановиться. (К этому моменту будут уже напечатаны все максимальные независимые множества.) Иначе перейти к шагу 3.
Доминирующие множества
Для графа G = (V, E) доминирующее множество вершин (называемое также внешне устойчивым множеством) есть множество вершин S ⊆ E, выбранное так, что для каждой вершины xj, не входящей в S, существует дуга, идущая из некоторой вершины множества S в вершину xj.
Таким образом, S есть доминирующее множество вершин, если
S ∪ E (S) = V (10)
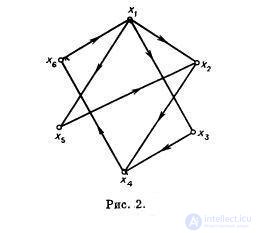
Для графа, приведенного на рис. 2, множества вершин {x1, x4, x6}, {x1, x4}, {x3, x5, x6} являются доминирующими множествами.
Доминирующее множество называется минимальным, если нет другого доминирующего множества, содержащегося в нем.
Множество S является минимальным доминирующим множеством, если оно удовлетворяет соотношению (10) и нет собственного подмножества в S, которое удовлетворяет условию, аналогичному (10). Так, например, для графа, приведенного на рис. 2, множество {x1, x4} — минимальное, а {x1, x4, x6} нет. Минимальным доминирующим множеством является также множество {x3, x5, x6}, и еще существует несколько таких множеств в этом графе. Следовательно, как и в случае максимальных независимых множеств, в графе может быть несколько минимальных доминирующих множеств, и они не обязательно содержат одинаковое число вершин.
Если Р — семейство всех минимальных доминирующих множеств графа, то число
β[G] = minS ∈ P |S| (11)
называется числом доминирования графа G, а множество S*, на котором достигается минимум, называется наименьшим доминирующим множеством.
Для графа, приведенного на рис. 2, наименьшим доминирующим множеством является множество {x1, x4} и, следовательно, β[G] = 2.
Задача о наименьшем покрытии
Пусть At — транспонированная матрица смежности графа G с единичными диагональными элементами. Задача определения наименьшего доминирующего множества графа Gэквивалентна задаче нахождения такого наименьшего множества столбцов в матрице At, что каждая строка матрицы содержит единицу хотя бы в одном из выбранных столбцов. Эта последняя задача о поиске наименьшего множества столбцов, «покрывающих» все строки, изучалась довольно интенсивно под названием задачи о наименьшем покрытии (ЗНП).
В общей ЗНП матрица, состоящая из 0 и 1, не обязательно является квадратной. Кроме того, каждому столбцу j (в нашем случае каждой вершине xj) сопоставляется некоторая стоимость cj и требуется выбрать покрытие (или, в другой терминологии — для случая графов — доминирующее множество вершин) с наименьшей общей стоимостью). Поскольку задача построения наименьшего доминирующего множества вершин является весьма частной задачей о покрытии с cj = 1 для всех j = 1, …, n, то на первый взгляд кажется, что нахождение такого множества осуществляется на деле значительно проще, чем решение общей ЗНП.
Постановка задачи
ЗНП своим названием обязана следующей теоретико-множественной интерпретации. Даны множество R = {r1, …, rM} и семейство I = {S1, …, SN} множеств Sj ⊂ R. Любое подсемейство I′ = {Sj1, Sj2, …, Sjk} семейства I, такое, что
∪i = 1…k Si = R (12)
называется покрытием множества R, а множества Sji называются покрывающими множествами. Если вместе с соотношением (12) I′ удовлетворяет условию
Sjh ∩ Sjl = Ø, ∀h, l ∈ {1, …, k} (13)
т. е. множества Sji {i = 1, …, k} попарно не пересекаются, то называется разбиением множества R.
Если каждому Sj ∈ I поставлена в соответствие положительная стоимость cj, то ЗНП формулируется так: найти покрытие множества R, имеющее наименьшую стоимость, причем стоимость семейства I′ = {Sj1, …, Sjk} определяется как ∑i = 1k cji. Аналогично формулируется и задача о наименьшем разбиении (ЗНР).
Упрощение задачи
Вследствие особой природы ЗНП часто удается сделать при ее исследовании определенные, хорошо известные заранее выводы и упрощения. Например:
- если для некоторого элемента ri из R справедливы соотно шения ri ∉ Sj ∀ j = 1, …, N, то ri покрыть нельзя и, следова тельно, задача не имеет решения;
- если ∃ri ∈ R такое, что ri ∈ Sk и ri ∉ Sj, то Sk должно присутствовать во всех решениях и задачу можно свести к меньшей, положив R = R − {ri} и I = I − {Sk}
- пусть Vi = {j | ri, ∈ Sj}; тогда если ∃p, q ∈ {1, …, M} такие, что Vp ⊆ Vq, то rq можно удалить из R, поскольку любое множество, которое покрывает rp, должно также покрывать rq, т. е.rp доминирует над rq;
- если для некоторого семейства множеств I′ ⊂ I справедливы соотношения ∪Sj∈I′Sj ⊇ Sk и ∑Sj∈I′ cj ≤ Sk для любых Sk ∈ I − I′, то Sk может быть вычеркнуто из I поскольку ∪Sj∈I′Sjдоминирует над Sk.
Предположим, что все эти упрощения выполнены (если они возможны) и что исходная ЗНП уже переформулирована в соответствующей неприводимой форме.
Алгоритм решения ЗНР, использующий дерево поиска
ЗНР тесно связана с ЗНП, являясь по существу ЗНП с дополнительным ограничением (неперекрываемость). Это ограничение выгодно, если решать задачу с помощью некоторого метода, использующего дерево поиска: при таком ограничений может рано выясниться, что некоторые возможные ветвления дерева рассматривать не надо,
Простые методы решения ЗНР, использующие дерево поиска, были предложены Пирсом, Гарфинкелем и Немхаузеро.
Сущность этих методов такова. Вначале строятся “блоки” столбцов, по одному на каждый элемент rk из R, т. е. всего М блоков, k-й блок состоит из таких множеств семейства I(представленных столбцами), в которых содержится элемент ri, но отсутствуют элементы с меньшими индексами — r1, …, rk−1. Следовательно, каждое множество (столбец) появляется точно в одном определенном блоке и совокупность блоков может быть представлена в виде таблицы. В конкретных задачах некоторые из блоков могут отсутствовать.
В процессе работы алгоритма блоки отыскиваются последовательно и формирование k-гo блока начинается после того, как каждый элемент ri 1 ≤ i ≤ k − 1, будет покрыт частным решением. Таким образом, если какое-то множество в блоке k содержит элементы с индексами, меньшими k, то оно должно быть отброшено (на этом этапе) в соответствии с требованием неперекрываемости. Множества в пределах каждого блока размещаются в порядке возрастания их стоимостей и перенумеровываются так, что Sk теперь уже обозначает множество, соответствующее j-му столбцу таблицы.
Текущее “наилучшее” решение B′ сo стоимостью z′ известно на любом этапе поиска (B′ обозначает семейство соответствующих покрывающих множеств). Если В и z — соответствующие семейство и стоимость на данной стадий поиска, а Е — множество, представляющее те элементы (т. е. строки) ri, которые покрываются множествами из В, то одна из простых алгоритмов, использующих дерево поиска, можно вписать следующим образом.
- Построить исходную таблицу и начать с частного решения: B = Ø, E = Ø, z = 0, z′ = ∞.
- Найти р = min[i |ri ∉ E]. Над блоком р поставить метку (над его первым множеством, которое, как следует из построения таблицы, имеет наименьшую стоимость).
- Начиная с отмеченной позиции в блоке р, перебирать его множества Sjp скажем, в порядке возрастания индекса j.
(i) Если найдено множество Sjp, такое, что Sjp ∩ E = Ø и z + cjp < z′ (где cjp — стоимость множества Sjp), то перейти к шагу 5. - В не может привести к лучшему решению. Если B = Ø (т. е. блок 1 исчерпан), то алгоритм заканчивает работу и оптимальным решением является B′. В противном случае удалить последнее множество, скажем, Snl добавить его в В, положить р = I, поставить метку над множеством Sk+1l, удалить предшествующую метку в блоке I и перейти к шагу 3.
- Обновить данные: B = B ∪ {Sjp}, E = E ∪ Sjp, z = z + cjp. Если найдено лучшее решение Е = R, то положить B′ = B, z′ = z и перейти к шагу 4. Иначе перейти к шагу 2.
Если поиск оканчивается с исчерпыванием блока 1 (см. шаг 4), то целесообразно переставить блоки в порядке возрастания числа столбцов (множеств) в каждом блоке. Это может быть осуществлено (перед построением исходной таблицы) перенумерацией элементов (строк) r1 … rM в порядке увеличения числа множеств из S, содержащих соответствующие элементы.
Применение задачи о покрытии
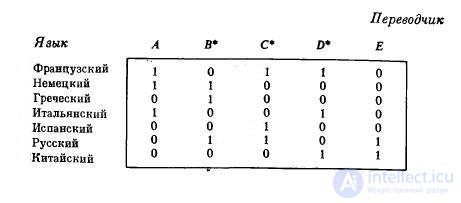
Выбор переводчиков
Предположим, что организации нужно нанять переводчиков французского, немецкого, греческого, итальянского, испанского, русского и китайского языков на английский и что имеется пять кандидатур А, В, С, D и Е. Каждая кандидатура владеет только некоторым собственным подмножеством из указанного выше множества языков и требует вполне определенную зарплату. Необходимо решить, каких переводчиков (с указанных выше языков на английский) надо нанять, чтобы затраты на зарплату были наименьшими. Это задача о наименьшем покрытии.
Если, например, требования на оплату труда у всех претендентов одинаковые и группы языков, на которых они говорят, указаны ниже в матрице Т, то решение задачи будет таким: нужно нанять переводчиков В, С, D.
Информационный поиск
Предположим, что некоторое количество единиц информации хранится в N массивах длины cj, j = 1, 2, …, N, причем на каждую единицу информации отводится по меньшей мере один массив. В некоторый момент делается запрос о М единицах информации. Они могут быть получены различными способами при помощи поиска в массиве. Для того чтобы получить все Mединиц информации и при этом произвести просмотр массивов наименьшей длины, надо решить ЗНП, вкоторой элемент ti j матрицы T равен 1, если информация i находится в массиве, и 0 в противном случае.
Маршруты полетов самолетов
Пусть вершины неориентированного графе G представляют аэропорты, а дуги графа G — этапы полетов (беспосадочные перелеты), которые осуществляются в заданное время. Любой маршрут в этом графе (удовлетворяющий ряду условий, которые могут встретиться на практике) соответствует некоторому реально выполнимому маршруту полета. Пусть имеется N таких возможных маршрутов и для каждого из них каким-то способом подсчитана его стоимость (например, стоимость j-го маршрута равна cj). Задача нахождения множества маршрутов, имеющего наименьшую суммарную стоимость и такого, что каждый этап полета содержится хотя бы в одном выбранном маршруте, является задачей о наименьшем покрытии с матрицейТ = [ti j] в которой элемент ti j равен 1, если i-й этап содержится в j-м маршруте, и равен 0 в противном случае.
К сожалению, в одной статье не просто дать все знания про задача о наименьшем покрытии графа. Но я – старался.
Если ты проявишь интерес к раскрытию подробностей,я обязательно напишу продолжение! Надеюсь, что теперь ты понял что такое задача о наименьшем покрытии графа, покрытие графа
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Алгоритмы и теория алгоритмов


 зобразить
зобразить