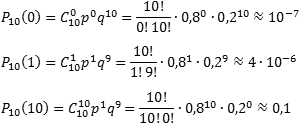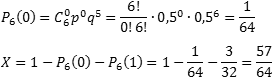Как найти число независимых испытаний

Как найти число независимых испытаний

Схема повторных независимых испытаний.
Формула Бернулли

  • Краткая теория
  • Примеры решения задач
  • Задачи контрольных и самостоятельных работ

Краткая теория

Схема Бернулли

Теория вероятностей имеет дело с такими экспериментами, которые
можно повторять (по крайней мере теоретически)
неограниченное число раз. Пусть некоторый эксперимент повторяется

 раз, причем результаты каждого повторения не
зависят от исходов предыдущих повторений. Такие серии повторений называют
независимыми испытаниями. Частным случаем таких испытаний являются независимые
испытания Бернулли, которые характеризуются двумя условиями:

1) результатом каждого испытания является один из двух возможных
исходов, называемых соответственно 
«успехом» или «неудачей».

2) вероятность «успеха»,  в
каждом последующем испытании не зависит от результатов предыдущих испытаний и
остается постоянной.

Схему испытаний Бернулли
называют также
биномиальной схемой,
а соответствующие вероятности –
биномиальными, что связано с использованием биномиальных коэффициентов

.

Теорема Бернулли

Если производится серия из

 независимых
испытаний Бернулли, в каждом из которых «успех» появляется с вероятностью

, то вероятность того, что «успех» в

 испытаниях
появится ровно

 раз,
выражается формулой:

где

 – вероятность
«неудачи».

 – число сочетаний

 элементов по

 
(см.
основные формулы комбинаторики)

Эта формула называется
формулой Бернулли.

Формула Бернулли позволяет
избавиться от большого числа вычислений — сложения и умножения вероятностей –
при достаточно большом количестве испытаний.

Если число испытаний n велико, то пользуются:

  • локальной формулой Муавра – Лапласа
  • интегральной формулой Муавра – Лапласа
  • формулой Пуассона

Примеры решения задач

Пример 1

Всхожесть
семян некоторого растения составляет 70%. Какова вероятность того, что из 10
посеянных семян взойдут: 8, по крайней мере 8; не менее 8?

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Решение

Воспользуемся
формулой Бернулли:

В нашем
случае

Пусть
событие

 – из 10 семян взойдут 8:

Пусть
событие

 – взойдет по крайней мере 8 (это значит 8, 9
или 10)

Пусть
событие

 – взойдет не менее 8 (это значит 8,9 или 10)

Ответ: P(A)=0.2335;P(B)=0.3828;  P(C)=0.3828

Пример 2

В
результате обследования были выделены семьи, имеющие по четыре ребенка. Считая
вероятности появления мальчика и девочки в семье равными, определить
вероятности появления в ней:

а) одного
мальчика;

б) двух мальчиков.

Решение

Вероятность
появления мальчика или девочки равна

. Вероятность появления
мальчика в семье, имеющей четырех детей, находится по формуле Бернулли:

В нашем
случае:

б)
Вероятность появления в семье двух мальчиков:

Ответ: а)

; б)

.

Пример 3

Два
равносильных противника играют в шахматы. Что вероятнее а) выиграть одну партию
из двух или две партии из четырех? б) выиграть не менее двух партий из четырех
или не менее трех партий из пяти? Ничьи во внимание не принимаются.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Играют
равносильные шахматисты, поэтому вероятность выигрыша

, следовательно вероятность проигрыша
тоже равна 1/2. Так как во всех партиях вероятность выигрыша постоянна и
безразлично, в какой последовательности будут выиграны партии, то применима
формула Бернулли:

а) Вероятность
выиграть 1 партию из двух:

Вероятность
выиграть 2 партии из четырех:

Вероятнее
выиграть одну партию из 2-х.

б) Вероятность
выиграть не менее 2-х партий из 4:

Вероятность
выиграть не менее 3-х партий из 5:

Вероятнее
выиграть не менее 2-х партий из 4.

Ответ: а) Вероятнее выиграть одну партию из
2-х; б) Вероятнее выиграть не менее 2-х партий из 4.

Задачи контрольных и самостоятельных работ

Задача 1

Всхожесть
семян данного сорта имеет вероятность 0.7. Оценить вероятность того, что из 9 семян
взойдет не менее 4 семян.

Задача 2

Найти
вероятность того, что в n независимых испытаниях
событие A появится ровно k раз, зная, что в каждом
испытании вероятность появления события равна p.

.

Задача 3

а) Найти
вероятность того, что событие А появится не менее трех раз в четырех
независимых испытаниях, если вероятность появления события А в одном испытании
равна 0,4.  б) событие В появится в
случае, если событие А наступит не менее четырех раз. Найти вероятность
наступления события В, если будет произведено пять независимых испытаний, в
каждом из которых вероятность появления события А равна 0,8.

Задача 4

В ралли участвует
10 однотипных машин. Вероятность выхода из строя за период соревнований каждой
из них 1/20.

Найти
вероятность того, что к финишу придут не менее 8 машин.

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 5

Баскетболист
бросает мяч 4 раза. Вероятность попадания при каждом броске равна 0,7. Найти
вероятность того, что он попадет в корзину: а) три раза; б) менее 3 раз; б)
более трех раз.

Задача 6

В семье
пятеро детей. Считая, что вероятность рождения мальчика равна 0.4, найти
вероятность того, что среди этих детей есть не менее двух девочек.

Задача 7

В
микрорайоне пять машин технической службы. Для бесперебойной работы необходимо,
чтобы не меньше трех машин были в исправном состоянии. Считая верояность
исправного состояния для всех машин одинаковой и равной 0,75, найти вероятность
бесперебойной работы технической службы в микрорайоне.

Задача 8

В среднем
каждый десятый договор страховой компании завершается выплатой по страховому
случаю. Компания заключила пять договоров. Найти вероятность того, что
страховой случай наступит: а) один раз; б) хотя бы один раз.

Задача 9

В
мастерской работают 6 моторов. Для каждого мотора вероятность перегрева к
обеленному перерыву равна 0,8. Найти вероятность того, что к обеденному
перерыву перегреются 4 мотора.

Задача 10

Пусть
вероятность того, что телевизор потребует ремонта в течение гарантийного срока,
равна 0,2. Найти вероятность того, что в течение гарантийного срока из 6
телевизоров: а) не более одного потребует ремонта; б) хотя бы один не потребует
ремонта.

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 11

Контрольное
задание состоит из 5 вопросов, на каждый из которых дается 4 варианта ответа,
причем один из них правильный, а остальные неправильные. Найдите вероятность
того, что учащийся, не знающий ни одного вопроса, дает: а) 3 правильных ответа;
б) не менее 3-х правильных ответов (предполагается, что учащийся выбирает
ответы наудачу).

Задача 12

Стрелок
попадает в мишень с вероятностью 0,6. Производится серия из 4 выстрелов.

а) Какова
вероятность того, что число промахов будет равно числу попаданий?

б) Найти
вероятность хотя бы одного промаха.

Задание 13

Дана
вероятность p=0.5 появления события A в серии из

 независимых испытаний. Найти вероятность того,
что в этих испытаниях событие

 появится:

а) ровно

 раза

б) не
менее

 раз

в) не
менее

 раза и не более

 раза.

Задача 14

Применяемый
метод лечения в 80% случаев приводит к выздоровлению. Найти вероятность того,
что из четырех больных поправятся:

а) трое;

б) хотя
бы один;

в) найти
наивероятнейшее количество поправившихся больных и соответствующую этому
событию вероятность.

  • Краткая теория
  • Примеры решения задач
  • Задачи контрольных и самостоятельных работ
Источник

Повторные независимые испытания.
Схема и формула Бернулли

Определение повторных независимых испытаний. Формулы Бернулли для вычисления вероятности и наивероятнейшего числа. Асимптотические формулы для формулы Бернулли (локальная и интегральная, теоремы Лапласа). Использование интегральной теоремы. Формула Пуассона, для маловероятных случайных событий.

Повторные независимые испытания

На практике приходится сталкиваться с такими задачами, которые можно представить в виде многократно повторяющихся испытаний, в результате каждого из которых может появиться или не появиться событие A. При этом интерес представляет исход не каждого “отдельного испытания, а общее количество появлений события A в результате определенного количества испытаний. В подобных задачах нужно уметь определять вероятность любого числа m появлений события A в результате n испытаний. Рассмотрим случай, когда испытания являются независимыми и вероятность появления события A в каждом испытании постоянна. Такие испытания называются повторными независимыми.

Примером независимых испытаний может служить проверка на годность изделий, взятых по одному из ряда партий. Если в этих партиях процент брака одинаков, то вероятность того, что отобранное изделие будет бракованным, в каждом случае является постоянным числом.

Формула Бернулли

Воспользуемся понятием сложного события, под которым подразумевается совмещение нескольких элементарных событий, состоящих в появлении или непоявлении события A в i–м испытании. Пусть проводится n независимых испытаний, в каждом из которых событие A может либо появиться с вероятностью p, либо не появиться с вероятностью q=1-p. Рассмотрим событие B_m, состоящее в том, что событие A в этих n испытаниях наступит ровно m раз и, следовательно, не наступит ровно (n-m) раз. Обозначим A_i~(i=1,2,ldots,{n}) появление события A, a overline{A}_i — непоявление события A в i–м испытании. В силу постоянства условий испытания имеем

begin{gathered}P{A_1}=P{A_2}=cdots=P{A_n}=p,\P{overline{A}_1}=P{overline{A}_2}=cdots=P{overline{A}_n}=1-p=qend{gathered}

Событие A может появиться m раз в разных последовательностях или комбинациях, чередуясь с противоположным событием overline{A}. Число возможных комбинаций такого рода равно числу сочетаний из n элементов по m, т. е. C_n^m. Следовательно, событие B_m можно представить в виде суммы сложных несовместных между собой событий, причем число слагаемых равно C_n^m:

B_m=A_1A_2cdots{A_m}overline{A}_{m+1}cdotsoverline{A}_n+cdots+overline{A}_1overline{A}_2cdotsoverline{A}_{n-m}A_{n-m+1}cdots{A_n},

(3.1)

где в каждое произведение событие A входит m раз, а overline{A} — (n-m) раз.

Вероятность каждого сложного события, входящего в формулу (3.1), по теореме умножения вероятностей для независимых событий равна p^{m}q^{n-m}. Так как общее количество таких событий равно C_n^m, то, используя теорему сложения вероятностей для несовместных событий, получаем вероятность события B_m (обозначим ее P_{m,n})

P_{m,n}=C_n^mp^{m}q^{n-m}quad text{or}quad P_{m,n}=frac{n!}{m!(n-m)!}p^{m}q^{n-m}.

(3.2)

Формулу (3.2) называют формулой Бернулли, а повторяющиеся испытания, удовлетворяющие условию независимости и постоянства вероятностей появления в каждом из них события A, называют испытаниями Бернулли, или схемой Бернулли.

Пример 1. Вероятность выхода за границы поля допуска при обработке деталей на токарном станке равна 0,07. Определить вероятность того, что из пяти наудачу отобранных в течение смены деталей у одной размеры диаметра не соответствуют заданному допуску.

Решение. Условие задачи удовлетворяет требования схемы Бернулли. Поэтому, полагая n=5,,m=1,,p=0,!07, по формуле (3.2) получаем

P_{1,5}=C_5^1(0,!07)^{1}(0,!93)^{5-1}approx0,!262.

Пример 2. Наблюдениями установлено, что в некоторой местности в сентябре бывает 12 дождливых дней. Какова вероятность того, что из случайно взятых в этом месяце 8 дней 3 дня окажутся дождливыми?

Решение.

P_{3;8}=C_8^3{left(frac{12}{30}right)!}^3{left(1-frac{12}{30}right)!}^{8-3}=frac{8!}{3!(8-3)!}{left(frac{2}{5}right)!}^3{left(frac{3}{5}right)!}^5=56cdotfrac{8}{125}cdotfrac{243}{3125}=frac{108,864}{390,625}approx0,!2787.

Наивероятнейшее число появлений события

Наивероятнейшим числом появления события A в n независимых испытаниях называется такое число m_0, для которого вероятность, соответствующая этому числу, превышает или, по крайней мере, не меньше вероятности каждого из остальных возможных чисел появления события A. Для определения наивероятнейшего числа не обязательно вычислять вероятности возможных чисел появлений события, достаточно знать число испытаний n и вероятность появления события A в отдельном испытании. Обозначим P_{m_0,n} вероятность, соответствующую наивероятнейшему числу m_0. Используя формулу (3.2), записываем

P_{m_0,n}=C_n^{m_0}p^{m_0}q^{n-m_0}=frac{n!}{m_0!(n-m_0)!}p^{m_0}q^{n-m_0}.

(3.3)

Согласно определению наивероятнейшего числа, вероятности наступления события A соответственно m_0+1 и m_0-1 раз должны, по крайней мере, не превышать вероятность P_{m_0,n}, т. е.

P_{m_0,n}geqslant{P_{m_0+1,n}};quad P_{m_0,n}geqslant{P_{m_0-1,n}}

Подставляя в неравенства значение P_{m_0,n} и выражения вероятностей P_{m_0+1,n} и P_{m_0-1,n}, получаем

begin{gathered}frac{n!}{m_0!(n-m_0)!}p^{m_0}q^{n-m_0}geqslantfrac{n!}{(m_0+1)!(n-m_0-1)!}p^{m_0+1}q^{n-m_0-1}\\frac{n!}{m_0!(n-m_0)!}p^{m_0}q^{n-m_0}geqslantfrac{n!}{(m_0-1)!(n-m_0+1)!}p^{m_0-1}q^{n-m_0+1}end{gathered}

Решая эти неравенства относительно m_0, получаем

m_0geqslant{np-q},quad m_0leqslant{np+p}

Объединяя последние неравенства, получаем двойное неравенство, которое используют для определения наивероятнейшего числа:

np-qleqslant{m_0}leqslant{np+p}.

(3.4)

Так как длина интервала, определяемого неравенством (3.4), равна единице, т. е.

(np+p)-(np-q)=p+q=1,

и событие может произойти в n испытаниях только целое число раз, то следует иметь в виду, что:

1) если np-q — целое число, то существуют два значения наивероятнейшего числа, а именно: m_0=np-q и m'_0=np-q+1=np+p;

2) если np-q — дробное число, то существует одно наивероятнейшее число, а именно: единственное целое, заключенное между дробными числами, полученными из неравенства (3.4);

3) если np — целое число, то существует одно наивероятнейшее число, а именно: m_0=np.

При больших значениях n пользоваться формулой (3.3) для расчета вероятности, соответствующей наивероятнейшему числу, неудобно. Если в равенство (3.3) подставить формулу Стирлинга

n!approx{n^ne^{-n}sqrt{2pi{n}}},

справедливую для достаточно больших n, и принять наивероятнейшее число m_0=np, то получим формулу для приближенного вычисления вероятности, соответствующей наивероятнейшему числу:

P_{m_0,n}approxfrac{n^ne^{-n}sqrt{2pi{n}},p^{np}q^{nq}}{(np)^{np}e^{-np}sqrt{2pi{np}},(nq)^{nq}e^{-nq}sqrt{2pi{nq}}}=frac{1}{sqrt{2pi{npq}}}=frac{1}{sqrt{2pi}sqrt{npq}}.

(3.5)

Пример 2. Известно, что frac{1}{15} часть продукции, поставляемой заводом на торговую базу, не удовлетворяет всем требованиям стандарта. На базу была завезена партия изделий в количестве 250 шт. Найти наивероятнейшее число изделий, удовлетворяющих требованиям стандарта, и вычислить вероятность того, что в этой партии окажется наивероятнейшее число изделий.

Решение. По условию n=250,,q=frac{1}{15},,p=1-frac{1}{15}=frac{14}{15}. Согласно неравенству (3.4) имеем

250cdotfrac{14}{15}-frac{1}{15}leqslant{m_0}leqslant250cdotfrac{14}{15}+frac{14}{15}

откуда 233,!26leqslant{m_0}leqslant234,!26. Следовательно, наивероятнейшее число изделий, удовлетворяющих требованиям стандарта, в партии из 250 шт. равно 234. Подставляя данные в формулу (3.5), вычисляем вероятность наличия в партии наивероятнейшего числа изделий:

P_{234,250}approxfrac{1}{sqrt{2picdot250cdotfrac{14}{15}cdotfrac{1}{15}}}approx0,!101

Локальная теорема Лапласа

Пользоваться формулой Бернулли при больших значениях n очень трудно. Например, если n=50,,m=30,,p=0,!1, то для отыскания вероятности P_{30,50} надо вычислить значение выражения

P_{30,50}=frac{50!}{30!cdot20!}cdot(0,!1)^{30}cdot(0,!9)^{20}

Естественно, возникает вопрос: нельзя ли вычислить интересующую вероятность, не используя формулу Бернулли? Оказывается, можно. Локальная теорема Лапласа дает асимптотическую формулу, которая позволяет приближенно найти вероятность появления событий ровно m раз в n испытаниях, если число испытаний достаточно велико.

Теорема 3.1. Если вероятность p появления события A в каждом испытании постоянна и отлична от нуля и единицы, то вероятность P_{m,n} того, что событие A появится в n испытаниях ровно m раз, приближенно равна (тем точнее, чем больше n) значению функции

y=frac{1}{sqrt{npq}}frac{e^{-x^2/2}}{sqrt{2pi}}=frac{varphi(x)}{sqrt{npq}} при x=frac{m-np}{sqrt{npq}}.

Существуют таблицы, которые содержат значения функции varphi(x)=frac{1}{sqrt{2pi}},e^{-x^{2}/2}, соответствующие положительным значениям аргумента x. Для отрицательных значений аргумента используют те же таблицы, так как функция varphi(x) четна, т. е. varphi(-x)=varphi(x).

Итак, приближенно вероятность того, что событие A появится в n испытаниях ровно m раз,

P_{m,n}approxfrac{1}{sqrt{npq}},varphi(x), где x=frac{m-np}{sqrt{npq}}.

Пример 3. Найти вероятность того, что событие A наступит ровно 80 раз в 400 испытаниях, если вероятность появления события A в каждом испытании равна 0,2.

Решение. По условию n=400,,m=80,,p=0,!2,,q=0,!8. Воспользуемся асимптотической, формулой Лапласа:

P_{80,400}approxfrac{1}{sqrt{400cdot0,!2cdot0,!8}},varphi(x)=frac{1}{8},varphi(x).

Вычислим определяемое данными задачи значение x:

x=frac{m-np}{sqrt{npq}}=frac{80-400cdot0,!2}{8}=0.

По таблице прил, 1 находим varphi(0)=0,!3989. Искомая вероятность

P_{80,100}=frac{1}{8}cdot0,!3989=0,!04986.

Формула Бернулли приводит примерно к такому же результату (выкладки ввиду их громоздкости опущены):

P_{80,100}=0,!0498.

Интегральная теорема Лапласа

Предположим, что проводится n независимых испытаний, в каждом из которых вероятность появления события A постоянна и равна p. Необходимо вычислить вероятность P_{(m_1,m_2),n} того, что событие A появится в n испытаниях не менее m_1 и не более m_2 раз (для краткости будем говорить “от m_1 до m_2 раз”). Это можно сделать с помощью интегральной теоремы Лапласа.

Теорема 3.2. Если вероятность p наступления события A в каждом испытании постоянна и отлична от нуля и единицы, то приближенно вероятность P_{(m_1,m_2),n} того, что событие A появится в испытаниях от m_1 до m_2 раз,

P_{(m_1,m_2),n}approxfrac{1}{sqrt{2pi}}intlimits_{x'}^{x''}e^{-x^2/2},dx, где x'=frac{m_1-np}{sqrt{npq}};~x''=frac{m_2-np}{sqrt{npq}}.

При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами, так как неопределенный интеграл int{e^{-x^2/2},dx} не выражается через элементарные функции. Таблица для интеграла Phi(x)=frac{1}{sqrt{2pi}}intlimits_{0}^{x}e^{-z^2/2},dz приведена в прил. 2, где даны значения функции Phi(x) для положительных значений x, для x<0 используют ту же таблицу (функция Phi(x) нечетна, т. е. Phi(-x)=-Phi(x)). Таблица содержит значения функции Phi(x) лишь для xin[0;5]; для x>5 можно принять Phi(x)=0,!5.

Итак, приближенно вероятность того, что событие A появится в n независимых испытаниях от m_1 до m_2 раз,

P_{(m_1,m_2),n}approxPhi(x'')-Phi(x'), где x'=frac{m_1-np}{sqrt{npq}};~x''=frac{m_2-np}{sqrt{npq}}.

Пример 4. Вероятность того, что деталь изготовлена с нарушениями стандартов, p=0,!2. Найти вероятность того, что среди 400 случайно отобранных деталей нестандартных окажется от 70 до 100 деталей.

Решение. По условию p=0,!2,,q=0,!8,,n=400,,m_1=70,,m_2=100. Воспользуемся интегральной теоремой Лапласа:

P_{(70,100),400}approxPhi(x'')-Phi(x').

Вычислим пределы интегрирования:

нижний

x'=frac{m_1-np}{sqrt{npq}}=frac{70-400cdot0,!2}{sqrt{400cdot0,!2cdot0,!8}}=-1,!25,

верхний

x''=frac{m_2-np}{sqrt{npq}}=frac{100-400cdot0,!2}{sqrt{400cdot0,!2cdot0,!8}}=2,!5,

Таким образом

P_{(70,100),400}approxPhi(2,!5)-Phi(-1,!25)=Phi(2,!5)+Phi(1,!25).

По таблице прил. 2 находим

Phi(2,!5)=0,!4938;~~~~~Phi(1,!25)=0,!3944.

Искомая вероятность

P_{(70,100),400}=0,!4938+0,!3944=0,!8882.

Применение интегральной теоремы Лапласа

Если число m (число появлений события A при n независимых испытаниях) будет изменяться от m_1 до m_2, то дробь frac{m-np}{sqrt{npq}} будет изменяться от frac{m_1-np}{sqrt{npq}}=x' до frac{m_2-np}{sqrt{npq}}=x''. Следовательно, интегральную теорему Лапласа можно записать и так:

Pleft{x'leqslantfrac{m-np}{sqrt{npq}}leqslant{x''}right}=frac{1}{sqrt{2pi}}intlimits_{x'}^{x''}e^{-x^2/2},dx.

(3.6)

Поставим задачу найти вероятность того, что отклонение относительной частоты frac{m}{n} от постоянной вероятности p по абсолютной величине не превышает заданного числа varepsilon>0. Другими словами, найдем вероятность осуществления неравенства left|frac{m}{n}-pright|leqslantvarepsilon, что то же самое, -varepsilonleqslantfrac{m}{n}-pleqslantvarepsilon. Эту вероятность будем обозначать так: Pleft{left|frac{m}{n}-pright|leqslantvarepsilonright}. С учетом формулы (3.6) для данной вероятности получаем

Pleft{left|frac{m}{n}-pright|leqslantvarepsilonright}approx2Phileft(varepsilon,sqrt{frac{n}{pq}}right).

(3.7)

Пример 5. Вероятность того, что деталь нестандартна, p=0,!1. Найти вероятность того, что среди случайно отобранных 400 деталей относительная частота появления нестандартных деталей отклонится от вероятности p=0,!1 по абсолютной величине не более чем на 0,03.

Решение. По условию n=400,,p=0,!1,,q=0,!9,,varepsilon=0,!03. Требуется найти вероятность Pleft{left|frac{m}{400}-0,!1right|leqslant0,!03right}. Используя формулу (3.7), получаем

Pleft{left|frac{m}{400}-0,!1right|leqslant0,!03right}approx2Phileft(0,!03sqrt{frac{400}{0,!1cdot0,!9}}right)=2Phi(2)

По таблице прил. 2 находим Phi(2)=0,!4772, следовательно, 2Phi(2)=0,!9544. Итак, искомая вероятность приближенно равна 0,9544. Смысл полученного результата таков: если взять достаточно большое число проб по 400 деталей в каждой, то примерно в 95,44% этих проб отклонение относительной частоты от постоянной вероятности p=0,!1 по абсолютной величине не превысит 0,03.

Формула Пуассона для маловероятных событий

Если вероятность p наступления события в отдельном испытании близка к нулю, то даже при большом числе испытаний n, но при небольшом значении произведения np получаемые по формуле Лапласа значения вероятностей P_{m,n} оказываются недостаточно точными и возникает потребность в другой приближенной формуле.

Теорема 3.3. Если вероятность p наступления события A в каждом испытании постоянна, но мала, число независимых испытаний n достаточно велико, но значение произведения np=lambda остается небольшим (не больше десяти), то вероятность того, что в этих испытаниях событие A наступит m раз,

P_{m,n}approxfrac{lambda^m}{m!},e^{-lambda}.

Для упрощения расчетов с применением формулы Пуассона составлена таблица значений функции Пуассона frac{lambda^m}{m!},e^{-lambda} (см. прил. 3).

Пример 6. Пусть вероятность изготовления нестандартной детали равна 0,004. Найти вероятность того, что среди 1000 деталей окажется 5 нестандартных.

Решение. Здесь n=1000,p=0,004,~lambda=np=1000cdot0,!004=4. Все три числа удовлетворяют требованиям теоремы 3.3, поэтому для нахождения вероятности искомого события P_{5,1000} применяем формулу Пуассона. По таблице значений функции Пуассона (прил. 3) при lambda=4;m=5 получаем P_{5,1000}approx0,!1563.

Найдем вероятность того же события по формуле Лапласа. Для этого сначала вычисляем значение x, соответствующее m=5:

x=frac{5-1000cdot0,!004}{sqrt{1000cdot0,!004cdot0,!996}}approxfrac{1}{1,!996}approx0,!501.

Поэтому согласно формуле Лапласа искомая вероятность

P_{5,1000}approxfrac{varphi(0,!501)}{1,!996}approxfrac{0,!3519}{1,!996}approx0,!1763

а согласно формуле Бернулли точное ее значение

P_{5,1000}=C_{1000}^{5}cdot0,!004^5cdot0,!996^{995}approx0,!1552.

Таким образом, относительная ошибка вычисления вероятностей P_{5,1000} по приближенной формуле Лапласа составляет

frac{0,!1763-0,!1552}{0,!1552}approx0,!196, или 13,!6%

а по формуле Пуассона —

frac{0,!1563-0,!1552}{0,!1552}approx0,!007, или 0,!7%

т.е. во много раз меньше.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Лучшее спасибо – порекомендовать эту страницу

При решении вероятностных задач часто приходится сталкиваться с ситуациями, в которых одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других. Такой эксперимент еще называется схемой повторных независимых испытаний или схемой Бернулли.

Примеры повторных испытаний:

  • бросание монеты или игрального кубика (вероятности выпадения герба/решки или определенной цифры одинаковы в каждом броске);
  • извлечение из урны шара при условии, что вынутый шар после записи его цвета кладется обратно в урну (то есть состав
    шаров в урне не меняется и не меняется вероятность вынуть шар нужного цвета);
  • включение приборов (ламп, станков и т.п.) с заранее заданной одинаковой вероятностью выхода из строя каждого;
  • повторение стрелком выстрелов по одной и той же мишени при условии, что вероятность удачного попадания при каждом выстреле принимается одинаковой и т.д.

Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем $n$ испытаний Бернулли. Это означает, что все $n$ испытаний независимы; вероятность появления события $А$ в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях). Обозначим вероятность появления события $А$ в единичном испытании буквой $р$, т.е. $p=P(A)$, а вероятность противоположного события (событие $А$ не наступило) – буквой $q=P(overline{A})=1-p$.

Тогда вероятность того, что событие $А$ появится в этих $n$ испытаниях ровно $k$ раз, выражается формулой Бернулли

$$P_n(k)=C_n^k cdot p^k cdot q^{n-k}, quad q=1-p.$$

Распределение числа успехов (появлений события) носит название биномиального распределения.

Онлайн-калькуляторы для формулы Бернулли

Некоторые наиболее популярные типы задач, в которых используется формула Бернулли, разобраны в статьях и снабжены онлайн-калькулятором, вы можете перейти к ним по ссылкам:

  • Задача про партии в шахматы
  • Задача про выстрелы
  • Задача про мальчиков и девочек
  • Задача про лотерейные билеты
  • Задача о наивероятнейшем значении
  • Формула Пуассона

Примеры задач с решениями

Пример. В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется 2 белых.

Решение. Событие А – достали белый шар. Тогда вероятности
, .
По формуле Бернулли требуемая вероятность равна
.

Пример. Определить вероятность того, что в семье, имеющей 5 детей, будет не больше трех девочек. Вероятности рождения мальчика и девочки предполагаются одинаковыми.

Решение. Вероятность рождения девочки
, тогда .

Найдем вероятности того, что в семье нет девочек, родилась одна, две или три девочки:

, ,

, .

Следовательно, искомая вероятность

.

Пример. Среди деталей, обрабатываемых рабочим, бывает в среднем 4% нестандартных. Найти вероятность того, что среди взятых на испытание 30 деталей две будут нестандартными.

Решение. Здесь опыт заключается в проверке каждой из 30 деталей на качество. Событие А – «появление нестандартной детали», его вероятность , тогда . Отсюда по формуле Бернулли находим
.

Пример. При каждом отдельном выстреле из орудия вероятность поражения цели равна 0,9. Найти вероятность того, что из 20 выстрелов число удачных будет не менее 16 и не более 19.

Решение. Вычисляем по формуле Бернулли:

Пример. Независимые испытания продолжаются до тех пор, пока событие А не произойдет k раз. Найти вероятность того, что потребуется n испытаний (n ³ k), если в каждом из них .

Решение. Событие В – ровно n испытаний до k-го появления события А – есть произведение двух следующий событий:

D – в n-ом испытании А произошло;

С – в первых (n–1)-ом испытаниях А появилось (к-1) раз.

Теорема умножения и формула Бернулли дают требуемую вероятность:

Еще больше примеров решений

Надо заметить, что использование биномиального закона при большом числе испытаний вычислительно трудно. Поэтому с возрастанием значений $n$ становится целесообразным применение приближенных формул (Пуассона, Муавра-Лапласа), которые будут рассмотрены в следующих разделах.

Видеоурок про формулу Бернулли

Для тех, кому нагляднее последовательное видеообъяснение, 15-минутный ролик:

Источник

Схема Бернулли. Примеры решения задач

5 июля 2011

Не будем долго размышлять о высоком — начнем сразу с определения.

Схема Бернулли — это когда производится n однотипных независимых опытов, в каждом из которых может появиться интересующее нас событие A, причем известна вероятность этого события P(A) = p. Требуется определить вероятность того, что при проведении n испытаний событие A появится ровно k раз.

Задачи, которые решаются по схеме Бернулли, чрезвычайно разнообразны: от простеньких (типа «найдите вероятность, что стрелок попадет 1 раз из 10») до весьма суровых (например, задачи на проценты или игральные карты). В реальности эта схема часто применяется для решения задач, связанных с контролем качества продукции и надежности различных механизмов, все характеристики которых должны быть известны до начала работы.

Вернемся к определению. Поскольку речь идет о независимых испытаниях, и в каждом опыте вероятность события A одинакова, возможны лишь два исхода:

  1. A — появление события A с вероятностью p;
  2. «не А» — событие А не появилось, что происходит с вероятностью q = 1 − p.

Важнейшее условие, без которого схема Бернулли теряет смысл — это постоянство. Сколько бы опытов мы ни проводили, нас интересует одно и то же событие A, которое возникает с одной и той же вероятностью p.

Между прочим, далеко не все задачи в теории вероятностей сводятся к постоянным условиям. Об этом вам расскажет любой грамотный репетитор по высшей математике. Даже такое нехитрое дело, как вынимание разноцветных шаров из ящика, не является опытом с постоянными условиями. Вынули очередной шар — соотношение цветов в ящике изменилось. Следовательно, изменились и вероятности.

Если же условия постоянны, можно точно определить вероятность того, что событие A произойдет ровно k раз из n возможных. Сформулируем этот факт в виде теоремы:

Теорема Бернулли. Пусть вероятность появления события A в каждом опыте постоянна и равна р. Тогда вероятность того, что в n независимых испытаниях событие A появится ровно k раз, рассчитывается по формуле:

Формула Бернулли

где Cnk — число сочетаний, q = 1 − p.

Эта формула так и называется: формула Бернулли. Интересно заметить, что задачи, приведенные ниже, вполне решаются без использования этой формулы. Например, можно применить формулы сложения вероятностей. Однако объем вычислений будет просто нереальным.

Задача. Вероятность выпуска бракованного изделия на станке равна 0,2. Определить вероятность того, что в партии из десяти выпущенных на данном станке деталей ровно k будут без брака. Решить задачу для k = 0, 1, 10.

По условию, нас интересует событие A выпуска изделий без брака, которое случается каждый раз с вероятностью p = 1 − 0,2 = 0,8. Нужно определить вероятность того, что это событие произойдет k раз. Событию A противопоставляется событие «не A», т.е. выпуск бракованного изделия.

Таким образом, имеем: n = 10; p = 0,8; q = 0,2.

Итак, находим вероятность того, что в партии все детали бракованные (k = 0), что только одна деталь без брака (k = 1), и что бракованных деталей нет вообще (k = 10):

Пример вычислений по формуле Бернулли

Задача. Монету бросают 6 раз. Выпадение герба и решки равновероятно. Найти вероятность того, что:

  1. герб выпадет три раза;
  2. герб выпадет один раз;
  3. герб выпадет не менее двух раз.

Итак, нас интересует событие A, когда выпадает герб. Вероятность этого события равна p = 0,5. Событию A противопоставляется событие «не A», когда выпадает решка, что случается с вероятностью q = 1 − 0,5 = 0,5. Нужно определить вероятность того, что герб выпадет k раз.

Таким образом, имеем: n = 6; p = 0,5; q = 0,5.

Определим вероятность того, что герб выпал три раза, т.е. k = 3:

Герб выпадет три раза

Теперь определим вероятность того, что герб выпал только один раз, т.е. k = 1:

Герб выпадет один раз

Осталось определить, с какой вероятностью герб выпадет не менее двух раз. Основная загвоздка — во фразе «не менее». Получается, что нас устроит любое k, кроме 0 и 1, т.е. надо найти значение суммы X = P6(2) + P6(3) + … + P6(6).

Заметим, что эта сумма также равна (1 − P6(0) − P6(1)), т.е. достаточно из всех возможных вариантов «вырезать» те, когда герб выпал 1 раз (k = 1) или не выпал вообще (k = 0). Поскольку P6(1) нам уже известно, осталось найти P6(0):

Герб выпадет не менее двух раз

Задача. Вероятность того, что телевизор имеет скрытые дефекты, равна 0,2. На склад поступило 20 телевизоров. Какое событие вероятнее: что в этой партии имеется два телевизора со скрытыми дефектами или три?

Интересующее событие A — наличие скрытого дефекта. Всего телевизоров n = 20, вероятность скрытого дефекта p = 0,2. Соответственно, вероятность получить телевизор без скрытого дефекта равна q = 1 − 0,2 = 0,8.

Получаем стартовые условия для схемы Бернулли: n = 20; p = 0,2; q = 0,8.

Найдем вероятность получить два «дефектных» телевизора (k = 2) и три (k = 3):

[begin{array}{l}{P_{20}}left( 2 right) = C_{20}^2{p^2}{q^{18}} = frac{{20!}}{{2!18!}} cdot {0,2^2} cdot {0,8^{18}} approx 0,137\{P_{20}}left( 3 right) = C_{20}^3{p^3}{q^{17}} = frac{{20!}}{{3!17!}} cdot {0,2^3} cdot {0,8^{17}} approx 0,41end{array}]

Очевидно, P20(3) > P20(2), т.е. вероятность получить три телевизора со скрытыми дефектами больше вероятности получить только два таких телевизора. Причем, разница неслабая.

Небольшое замечание по поводу факториалов. Многие испытывают смутное ощущение дискомфорта, когда видят запись «0!» (читается «ноль факториал»). Так вот, 0! = 1 по определению.

P. S. А самая большая вероятность в последней задаче — это получить четыре телевизора со скрытыми дефектами. Подсчитайте сами — и убедитесь.

Смотрите также:

  1. Локальная теорема Муавра — Лапласа
  2. Формула полной вероятности
  3. Тест к уроку «Сложение и вычитание дробей» (легкий)
  4. Сводный тест по задачам B12 (2 вариант)
  5. Как решать задачи про летающие камни?
  6. Задача C1: тригонометрические уравнения и формула двойного угла
Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 ноября 2021 года; проверки требует 1 правка.

Формула Бернулли — формула в теории вероятностей, позволяющая находить вероятность появления события A определённое количество раз при любом числе независимых испытаний. Формула Бернулли позволяет избавиться от большого числа вычислений — сложения и умножения вероятностей — при достаточно большом количестве испытаний. Названа в честь выдающегося швейцарского математика Якоба Бернулли, который вывел эту формулу.

Формулировка[править | править код]

Теорема. Если вероятность p наступления некоторого события в каждом испытании постоянна, то вероятность {displaystyle P_{n}^{k}} того, что данное событие наступит ровно k раз в n независимых испытаниях, равна {displaystyle P_{n}^{k}=C_{n}^{k}p^{k}q^{n-k}}, где q=1-p.[1]

Доказательство[править | править код]

Пусть проводится n независимых испытаний, причём известно, что в результате каждого испытания событие A наступает с вероятностью {displaystyle P(A)=p} и, следовательно, не наступает с вероятностью {displaystyle P({bar {A}})=1-p=q}. Пусть также в ходе испытаний вероятности p и q остаются неизменными. Какова вероятность того, что в результате n независимых испытаний событие A наступит ровно k раз?

Оказывается можно точно подсчитать число «удачных» комбинаций исходов испытаний, для которых событие A наступает k раз в n независимых испытаниях, — в точности это количество сочетаний из n по k:

{displaystyle C_{n}^{k}={frac {n!}{k!(n-k)!}}.}

В то же время, так как все испытания независимы и их исходы несовместимы (событие A либо наступает, либо нет), то вероятность получения «удачной» комбинации в точности равна {displaystyle p^{k}q^{n-k}}.

Окончательно, для того чтобы найти вероятность того, что в n независимых испытаниях событие A наступит ровно k раз, нужно сложить вероятности получения всех «удачных» комбинаций. Вероятности получения всех «удачных» комбинаций одинаковы и равны {displaystyle p^{k}q^{n-k}}, количество «удачных» комбинаций равно C_{n}^{k}, поэтому окончательно получаем:

{displaystyle P_{n}^{k}=C_{n}^{k}p^{k}q^{n-k}=C_{n}^{k}p^{k}(1-p)^{n-k}.}

Последнее выражение есть не что иное, как Формула Бернулли. Полезно также заметить, что в силу полноты группы событий будет справедливо

{displaystyle sum _{k=0}^{n}(P_{n}^{k})=1.}

См. также[править | править код]

  • Факториал
  • Биномиальный коэффициент
  • Локальная теорема Муавра — Лапласа

Примечания[править | править код]

  1. ↑ Гмурман В. Е. Теория вероятностей и математическая статистика: учебное пособие для бакалавров. — 12-е изд. — М.: Юtypz, 2013. — 478 с. — ISBN 9785991626477, 5991626472.

Ссылки[править | править код]

  • Повторение испытаний. Формула Бернулли
Источник

Добавить комментарий