Как найти число перестановок с повторениями

Формула числа перестановок с повторениями

Чтобы прийти к нужной формуле, используют одну из общеизвестных постановок задач:

1. Пусть имеется $n$ различных шаров и $k$ ящиков. Сколькими способами можно разложить шары по ящикам так, чтобы $n_1$ шаров оказались в первом ящике, $n_2$ шаров – во втором, …, $n_k$ шаров – в $k$-ом ящике. $n=n_1+n_2+…+n_k$.

2. Пусть имеется $n$ объектов различных типов: $n_1$ объектов первого типа, $n_2$ объектов второго типа,… $n_k$ объектов $k$-го типа. Сколькими способами можно переставить все объекты между собой?

Будем переставлять $n$ объектов всеми возможными способами (их будет $n!$). Но так как некоторые объекты совпадают, итоговое число будет меньше. В частности, $n_1$ объектов первого типа можно переставлять между собой $n_1!$ способами, но они не меняют итоговую перестановку. Аналогично для всех остальных объектов, поэтому число перестановок с повторениями есть

$$ P_n (n_1,n_2,…,n_k)=frac{n!}{n_1! cdot n_2!cdot … cdot n_k!}. $$

Напомним, что символ $n!$ называется факториалом, калькулятор и описание смотрите тут

Заметим, что для случая двух типов объектов $(n=n_1+n_2)$ формула перестановок с повторениями дает как частный случай формулу сочетаний без повторений.

Примеры решений

Рассмотрим решение типовых задач.

Пример 1. Сколькими способами можно собрать гирлянду из 4 красных, 4 синих и 8 желтых флажков?

Решение. У нас имеется $n_1=4$ объекта первого типа (красные флажки), $n_2=4$ объекта второго типа (синие флажки) и $n_3=8$ объектов третьего типа (желтые флажки). Все эти $n=4+4+8=16$ флажков нужно развесить на веревке всеми возможными способами. Применяем формулу числа перестановок с повторенями:

$$ P_{16} (4,4,8)=frac{16!}{4! cdot 4!cdot 8!}=900900.$$

Пример 2. Сколькими способами можно разбить группу 10 друзей на команды из 2 бандитов, 2 полицейских, 1 сыщика и 5 прохожих для игры?

Решение. В самой задаче объекты (люди) уже разбиты по типам: $n_1=2$, $n_2=2$, $n_3=1$, $n_4=5$. Осталось лишь применить формулу. Тогда искомое число способов разбиться на персонажи равно:

$$ P_{10} (2,2,1,5)=frac{10!}{2! cdot 2!cdot 1!cdot 5!}=7560.$$

Калькулятор перестановок с повторениями онлайн

Введите число типов объектов $K$ и затем количество объектов каждого типа $n_1$, …, $n_K$.

Видеоролик о перестановках с повторениями в Excel

Посмотрите наш видеообзор для формулы перестановок с повторениями: как использовать Excel, как решать типовые задачи.

Расчетный файл из видео можно бесплатно скачать

Полезные ссылки

• Как решать задачи по теории вероятностей
• Основные формулы комбинаторики
• Решенные примеры по теории вероятностей
• Заказать контрольную по ТВ

Решебник по комбинаторике и теории вероятностей:

План урока:

Комбинаторика и ее основные принципы

Перестановки

Перестановки с повторениями

Размещения

Сочетания

Комбинаторика и ее основные принципы

Очень часто приходится решать задачи, в которых надо посчитать количество возможных вариантов для той или иной ситуации. Например, сколько позиций может возникнуть на шахматной доске после первого хода обоих игроков? Сколько разных паролей длиною в десять символов можно записать, если ни один символ не использовать дважды? Сколько разнообразных комбинаций чисел может выпасть при игре в лотерею «6 из 49»? На все эти вопросы помогает ответить специальный раздел математики, называемый комбинаторикой. Почти всегда комбинаторную задачу можно сформулировать так, чтобы ее вопрос начинался словами «сколькими способами…».

Очевидно, что если в конечном множестве содержится n элементов, то есть ровно n способов выбрать один из них.

Пример. В классе 15 человек. Сколькими способами учитель может назначить одного из них ответственным за чистоту доски?

Ответ. Таких способов ровно 15.

В комбинаторике существует два основных правила. Первое из них называется правилом сложения.

Несмотря на формулировку, по сути это очень простое правило.

Пример. В магазине продается 14 телевизоров Panasonic и 17 телевизоров Sony. Петя хочет купить один телевизор. Сколько у него вариантов покупки?

Решение. По правилу сложения Петя может выбрать один из 14 + 17 = 31 телевизоров.

Ответ: 31 телевизор.

Особое значение имеет второе правило, которое называют правилом умножения.

Проиллюстрируем это правило.

Пример. В секции бадминтона 15 мальчиков и 20 девочек. Тренер должен отправить на соревнования смешанную пару. Сколько вариантов действий у него?

Решение. Тренер может составить 15•20= 300 разнополых пар из своих воспитанников.

Ответ: 300

Пример. Пете нужно купить технику для компьютера. В магазине продается 20 различных клавиатур, 25 моделей геймпадов и 30 компьютерных мышей. Купить надо по одному экземпляру каждого из этих устройств. Сколько вариантов покупки есть у него?

Решение. Сначала подсчитаем число возможных пар «клавиатура-геймпад». Их количество равно 20•25 = 500. Теперь составим «тройку» из одной из 500 пар и одной из 30 мышей. Число троек равно 500•30 = 15000.

Ответ: 15000

Правила сложения и умножения можно комбинировать.

Пример. Сколько слов не более чем из трех букв можно составить, используя алфавит, содержащий ровно 30 букв?

Решение. Очевидно, что слов из одной буквы можно составить ровно 30. Количество двухбуквенных слов равно количеству пар, которые можно составить из этих букв, то есть 30•30 = 900. Трехбуквенных слов можно составить 30•30•30 = 27000. Всего же слов длиною не более 3 букв будет

30 + 900 + 27000 = 27930

Ответ: 27930

Далее мы изучим основные понятия комбинаторики – перестановки, размещения, сочетания.

Перестановки

Рассмотрим простейшую комбинаторную задачу. На полке расставляют по порядку книги. Их ставят вертикально друг за другом. Сколькими способами можно расставить на полке 2 книги? Очевидно, что двумя:

Либо синяя книжка будет первой слева, либо она будет находиться в конце полки, третьего варианта здесь нет. Здесь условно считается, что варианты, когда между книгами есть зазоры, идентичны вариантам без зазоров:

То есть нас интересует исключительно порядок, в котором стоят книги. Каждый из найденных вариантов называется перестановкой книг. Перестановкой называют любое конечное множество, для элементов которого указан порядок элементов.В комбинаторике перестановки являются одними из основных объектов изучения.

Например, если в забеге на 100 метров стартует 8 спортсменов, то они образуют множество участников забега. После финиша становится известно, кто занял 1-ое место, кто оказался вторым или третьим, а кто стал последним. Результат забега будет перестановкой, ведь он представляет собой список спортсменов с указанием их мест, то есть он определяет порядок между ними.

Вернемся к примеру с книгами. Обозначим количество возможных перестановок n элементов как Р_n. Две книжки можно расставить двумя разными способами, поэтому Р₂ = 2. Обозначим эти перестановки как АБ и БА. Сколько способов расстановки есть в случае трех книжек? Их все можно получить из вариантов с 2 книжками, добавляя между ними книгами ещё один том:

Видно, что между 2 книгами есть три позиции, на которые можно поставить 3-ий том. Общее количество вариантов равно произведению числа этих позиций и количества вариантов для 2 книг, то есть Р₃ = 3•Р₂ = 3•2 = 6:

Итак, мы имеем 6 перестановок для 3 книг:

ВАБ

АВБ

АБВ

ВБА

ВБА

БАВ

А сколько перестановок существует для 4 книг? Снова-таки, между тремя книгами 4-ый том можно поставить четырьмя способами:

То есть из перестановки трех книг АБВ можно получить 4 перестановки:

ГАБВ

АГБВ

АБГВ

АБВГ

Всего существует 6 перестановок для 3 книг (Р₃ = 6), и для каждой из них можно построить 4 перестановки из 4 книг. Получается, что общее количество перестановок 4 книг равно

Р₄ = 4Р₃ = 4•6 = 24.

Продолжая подобные рассуждения, можно убедиться, что количество перестановок 5 предметов в 5 раз больше, чем перестановок для 4 объектов:

Р₅ = 5Р₄

И вообще, если число перестановок n объектов равно Р_n, то количество перестановок (n + 1)объекта равно в (n + 1)раз больше:

Р_n+1 = (n + 1)Р_n

При этом отметим, что 1 книгу можно расставить на полке только одним способом:

То есть Р₁ = 1. Теперь выпишем значения чисел Р при разном количестве переставляемых предметов, используя формулуР_n+1 = (n + 1)Р_n

Р₁ = 1

Р₂ = 2•Р₁= 2•1 = 2

Р₃ = 3Р₂ = 3•2•1 = 6

Р₄ = 4Р₃ = 4•3•2•1 = 24

Р₅ = 5Р₄ = 5•4•3•2•1 = 120

Видно, что количество перестановок n объектов равно произведению всех натуральных чисел от 1 до n. В математике есть специальная функция для вычисления значения этого произведения. Она называется факториалом и обозначается восклицательным знаком.

Например, факториал 6 вычисляется так:

6! = 1•2•3•4•5•6 = 720

Мы убедились на примере с книгами, что количество перестановок из n различных объектов, которое обозначается как Р_n, равно n!.

Относительно факториала надо заметить несколько важных моментов. Во-первых, очевидно, что факториал единицы равен 1:

1! = 1

Во-вторых, иногда в комбинаторных задачах приходится вычислять факториал нуля. По ряду соображений эта величина также принимается равной единице

0! = 1

Объяснить это можно так. Факториал числа можно представить как произведение этого числа и факториала предыдущего числа, например:

5! = 1•2•3•4•5 = (1•2•3•4)•5 = 4!•5

7! = 1•2•3•4•5•6•7 = (1•2•3•4•5•6)•7 = 6!•7

В общем случае формула выглядит так:

n! = (n– 1)!•n

Из неё несложно получить, что

(n– 1)! = n!/n

Например: 5! = 4!•5

Подставив в эту формулу единицу, получим

(1 – 1)! = 1!/1

0! = 1/1

0! = 1

Пример. Сколькими способами тренер может расставить 4 участников эстафеты 4х400 м по этапам эстафеты?

Решение. Количество таких способов равно числу перестановок 4 различных объектов Р₄:

Р₄ = 4! = 1•2•3•4 = 24

Ответ: 24

Пример. Вася решил изучать сразу 7 иностранных языков, причем на занятия по каждому из них он собирается выделить ровно один день в неделе. Сколько вариантов расписаний занятий может составить себе Вася?

Решение. В данном случае расписание занятий – это порядок, в котором Вася в течение недели будет изучать иностранные языки, например:

Такое расписание можно описать последовательностью символов:

Ф, Ан, И, К, Я, Ар, П

Создавая расписание, Вася переставляет 7 языков, поэтому общее количество расписаний равно 7!:

Р₇ = 1•2•3•4•5•6•7 = 5040

Ответ: 5040

Пример. Сколько пятизначных цифр можно записать, используя цифры 0, 1, 2, 3, 4, причем каждую не более одного раза?

Решение. Общее количество перестановок 5 цифр составляет Р₅. Однако нельзя начинать запись числа с нуля. Так как, перестановка 12340 – это пятизначное число (двенадцать тысяч триста сорок), а перестановка 03241 – не является пятизначным числом.

Расстановок, начинающихся с нуля, ровно Р₄, поэтому общее количество допустимых цифр равно Р₅ – Р₄:

Р₅ – Р₄ = 5! – 4! = 120 – 24 = 96

Ответ: 96

Пример. На полке расставляют 7 книг, однако 3 из них образуют трехтомник. Тома трехтомника должны стоять друг за другом и в определенном порядке. Сколько существует способов расстановки книг?

Решение. Будем считать трехтомник одной книгой. Тогда нам надо расставить 5 книг

Р₅ = 5! = 120

Ответ: 120

Пример. Необходимо расставить 7 книг на полке, но три из них принадлежат одному автору. Их надо поставить друг с другом, но они могут стоять в любом порядке. Сколько возможно перестановок книг.

Решение. Снова будем считать три книги как один трехтомник. Получается, что существует 5! = 120 вариантов. Однако каждому из них соответствует 3! = 6 расстановок книг внутри трехтомника, например:

В итоге на каждую из 120 расстановок приходится 6 вариантов расстановки трехтомника, а общее число расстановок равно, согласно правилу умножения, произведению этих чисел:

120•6 = 720

Ответ: 720

Перестановки с повторениями

До этого мы рассматривали случаи, когда все переставляемые объекты были различными. Однако порою некоторые из них не отличаются друг от друга. Пусть на полке надо расставить 3 книги, но две из них одинаковые. Сколько тогда существует перестановок? Общее число перестановок 3 книг составляет 3! = 6:

Здесь одинаковые книги отмечены как А и А1. Очевидно, что 1-ый и 2-ой варианты (А1АБ) и (АА1Б) на самом деле не отличаются друг от друга. В них отличается лишь порядок одинаковых книг А и А1. В первом случае за А1 следует А, а во втором, наоборот, за А следует А1. Тоже самое можно сказать про варианты 3 и 4, 5 и 6. Получается, что все возможные перестановки можно разбить на группы, в которых находятся «перестановки-дубликаты»:

А1АБ и АА1Б

А1БА и АБА1

БА1А и БАА1

В каждой группе находится ровно по два «дубликата». Почему именно по два? Это число равно количеству перестановок одинаковых книг. Так как одинаковых томов 2, а Р₂ = 2, то в каждой группе по 2 «дубликата». Действительно, если бы мы «убрали» с полки все книги, кроме повторяющихся, то там осталось бы только 2 одинаковых тома, которые можно переставить двумя способами.

Для того чтобы найти количество «оригинальных» перестановок, надо их общее количество поделить на число дубликатов в каждой группе.

6:2 = 3

Пусть теперь надо расставить 4 книги, из которых 3 одинаковы. Обозначим тома как А, А1, А2 и Б. Всего можно записать 4! = 24 перестановки. Однако каждые 6 из них будут дублировать друг друга. То есть их можно разбить на группы, в каждой из которых будет 6 идентичных «дубликатов»:

1-ая группа: БАА1А2, БАА2А1, БА1АА2, БА1А2А, БА2АА1, БА2А1А

2-ая группа: АБА1А2, АБА2А1, А1БАА2, А1БА2А, А2БАА1, А2БА1А

3-ая группа: АА1БА2, АА2БА1, А1АБА2, А1А2БА, А2АБА1, А2А1БА

4-ая группа: АА1А2Б, АА2А1Б, А1АА2Б, А1А2АБ, А2АА1Б, А2А1АБ

И снова для подсчета числа оригинальных перестановок надо из общее число расстановок поделить на количество дубликатов в каждой группе:

Р₄/Р₃ = 4!/3! = 24/6 = 4

Для обозначения перестановок с повторениями используется запись

Р_n(n₁, n₂, n₃,… n_k)

где n – общее количество объектов, а n₁, n₂, n₃,… n_k – количество одинаковых элементов. Например, в задаче с 4 книгами мы искали величину Р₄(3, 1), потому что всего книг было 4, но они были разбиты на две группы, в одной из которых находилось 3 одинаковых тома (буквы А, А1, А2), а ещё одна книга (Б) составляла вторую группу. Мы заметили, что для вычисления числа перестановок с повторениями надо общее число перестановок делить на количество дублирующих перестановок. Формула в общем случае выглядит так:

Пример. Вася решил, что ему стоит изучать только два иностранных языка. Он решил 4 дня в неделю тратить на английский, а оставшиеся три дня – на испанский. Сколько расписаний занятий он может себе составить.

Решение. Вася должен расставить 3 урока испанского и 4 урока английского, тогда n₁ = 3, а n₂ = 4. Общее количество уроков равно 3 + 4 = 7. Тогда

Ответ: 35

Обратите внимание, что для удобства при делении факториалов мы не вычисляли их сразу, а пытались сократить множители. Так как в ответе любой комбинаторной задачи получается целое число, то весь знаменатель дроби обязательно сократится с какими-нибудь множителями в числителе.

Пример. У мамы есть 3 яблока, 2 банана и 1 апельсин. Эти фрукты она распределяет между 6 детьми. Сколькими способами она может это сделать, если каждый должен получить по фрукту?

Решение. Всего есть три группы фруктов. В первой находится 3 яблока, поэтому n₁ = 3. Во второй группе 2 банана, поэтому n₂ = 2. В третьей группе только 1 апельсин, поэтому n_k = 1. Общее число фруктов равно 6. Используем формулу:

Ответ: 60

В знаменателе формулы для перестановок с повторениями мы записываем число объектов в каждой группе одинаковых предметов. Так, если переставляются 3 яблока, 2 банана и 1 апельсин, то в знаменателе мы пишем 3!•2!•1!. Но что будет, если в каждой группе будет находиться ровно один уникальный объект? Тогда мы запишем в знаменателе произведение единиц:

В итоге мы получили ту же формулу, что и для перестановок без повторов. Другими словами, перестановки без повтора могут рассматриваться просто как частный случай перестановок с повторами.

Размещения

Пусть в футбольном турнире участвуют 6 команд. Нам предлагают угадать те команды, которые займут призовые места (то есть первые три места). Сколько вариантов таких троек существует?

Сначала запишем ту команду, которая выиграет турнир. Здесь есть шесть вариантов, по количеству участвующих команд. Запишем эти варианты:

Далее выберем один из вариантов и для него укажем серебряного призера соревнований. Здесь есть только 5 вариантов, ведь 1 из 6 команд уже записана на 1-ом месте:

Такую пятерку можно записать для каждого из шести вариантов того, кто станет чемпионом. Получается, что всего есть 6•5 = 30 пар «чемпион – серебряный призер». Наконец, для одной такой пары можно записать 4 варианта того, кто окажется третьим (две команды писать нельзя, так как они уже записаны на первых двух строчках):

Для каждой пары можно записать 4 тройки призеров. Так как число пар «чемпион – вице-чемпион» равно 6•5 = 30, то число троек составит 6•5•4 = 120.

В данном случае из некоторого множества команд мы выбрали несколько и расположили их в каком-то порядке. То есть мы выбрали упорядоченное множество. В комбинаторике оно называется размещением.

Если общее число команд обозначить как n (в этом примере n = 6), а количество упорядочиваемых команд равно k, то количество таких размещений в комбинаторике обозначается как

В примере с командами количество размещений равнялось 120:

Читается эта запись как «число размещений из 6 по 3 равно 120».

Для нахождения этого числа мы перемножили k (3)множителей. Первый из них был равен n(6), так как каждая из n команд могла занять первая место. Второй множитель был равен (n– 1), так как после определения чемпиона мы могли поставить на вторую позицию одну из (n– 1) команд. Третий множитель был равен (n– 2). По этой логике каждый следующий множитель будет меньше предыдущего на единицу. Например, чтобы вычислить число размещений из 7 по 4, надо перемножить 4 множителя, первый из которых равен 7, а каждый следующий меньше на 1:

Однако математически удобнее представлять это произведение как отношение двух факториалов. Для этого умножим количество размещений на дробь 3!/3!, равную единице. Естественно, число размещений из-за умножения на единицу не меняется:

Число 3 в данном случае можно получить, если из 7 вычесть 4. В общем случае из числа n надо вычесть число k. Тогда формула для вычисления количества размещений примет вид:

Пример. В программе 8 «А» класса 12 различных предметов. В понедельник проводится 5 занятий подряд. Сколько существует вариантов расписаний для класса, если в течение понедельника нельзя проводить два одинаковых урока?

Решение. Для составления расписания нужно выбрать 5 предметов и расставить их по порядку. Поэтому нам необходимо найти размещение из 12 по 5:

Ответ: 95040

Пример. В вагоне 10 свободных мест. В него зашло 6 пассажиров. Сколькими способами они могут расположиться в вагоне?

Решение. Из десяти мест надо выбрать шесть и указать для каждого, какому пассажиру оно соответствует. То есть каждый вариант рассадки пассажиров – это размещение из 10 по 6. Найдем их количество:

Ответ: 151200

Заметим, что перестановка – это частный случай размещения, когда k = n. Действительно, если нам надо указать тройку призеров турнира, в котором участвуют 6 команд, то мы указываем размещение из 6 по 3. Но если мы указываем для каждой из 6 команд, какое место она займет в чемпионате, то это размещение из 6 по 6. С другой стороны, это расстановка одновременно является и перестановкой 6 команд. Убедимся, что в этом частном случае формула для подсчета количества размещений покажет тот же результат, что и формула для перестановок

Для примера с 6 командами это будет выглядеть так:

Здесь мы использовали тот факт, что факториал нуля принимается равным единице. Данное рассуждение можно, наоборот, использовать для того, чтобы доказать, что факториал нуля – это единица.

Сочетания

Выбирая размещение, мы должны были выбрать из множества несколько объектов и упорядочить их. В частности, мы выбирали три команды из шести и указывали, какая из них будет первой, какая второй, а какая третьей. Поэтому размещения «Локомотив, Зенит, Краснодар» и «Локомотив, Краснодар, Зенит» отличались друг от друга.

Однако порою этот порядок не имеет значения. Так, существует известная лотерея, где предлагается угадать 7 чисел из 49, которые выпадут во время розыгрыша из барабана. При этом порядок их выпадения не играет никакой роли. Игрок, выбирая эти 7 чисел, с точки зрения математики формирует сочетание из 49 по 7.

Количество возможных сочетаний из n по k обозначается буквой С:

Для вычисления количеств сочетаний из n по k сначала найдем количество аналогичных размещений. Оно вычисляется по формуле:

Однако ясно, что, как и в случае с перестановками с повторениями, некоторые сочетания мы посчитали несколько раз. Вернемся к примеру с командами. Если мы выбрали команды Л (Локомотив) , З (Зенит) и К (Краснодар), то мы можем составить ровно 3! = 6 размещений из них:

ЛЗК

ЛКЗ

ЗЛК

ЗКЛ

КЛЗ

КЗЛ

Однако все они соответствуют только одному сочетании – ЛКЗ. Таким образом, считая количество размещений, мы посчитали каждое сочетание не один, а 3! раз. Поэтому для нахождения количества сочетаний в комбинаторике надо поделить число размещений на число перестановок k элементов:

Эта формула связывает важнейшие понятия комбинаторики – перестановки, сочетания и размещения. Подставим в неё формулы для размещений и перестановок и получим:

Пример. Сколько троек призеров турнира можно составить, выбирая три футбольные команды из шести?

Решение. Посчитаем число сочетаний из 6 по 3:

Ответ: 20

Пример. Сколько комбинаций чисел может составить игрок, играющий в лотереи «5 из 36», «6 из 45», «7 из 49»?

Решение. В каждом из этих случаев игрок выбирает сочетание нескольких чисел. Посчитаем их число:

Ответ: 376992; 8145060; 85900584

Пример. На плоскости отмечены 8 точек, причем никакие три из них не лежат на одной прямой. Сколько различных прямых можно провести через них? Сколько треугольников и четырехугольников можно построить с вершинами в этих точках?

Решение. Для того чтобы провести прямую, достаточно выбрать любые 2 точки из 8. Общее количество прямых будет равно числу сочетаний из 8 по 2:

Заметим принципиальную важность того условия, что никакие три точки не лежат на одной прямой. Оно гарантирует, что при выборе двух различных точек мы будем получать различные прямые. Если бы, например, точки АВС лежали бы на одной прямой, то при выборе сочетаний АВ, ВС и АС мы получали бы одну и ту же прямую:

Это же условие гарантирует, что, выбрав любые 3 и 8 точек, мы сможем построить треугольник с вершинами в этих точках, а выбрав 4 точки, получим четырехугольник. Поэтому для подсчета количества треугольников и четырехугольников следует искать число сочетаний по 3 и 4:

Ответ: 28 прямых, 56 треугольников и 70 четырехугольников.

Пример. В одной урне находится 10 различных шаров с номерами от 0 до 9, а в другой – 8 различных шаров с первыми восемью буквами алфавита. По условиям лотереи ведущий вытаскивает из первой урны два шара с числами, а из второй – три шара с буквами. Для победы в лотерее надо угадать выпавшие шары. Сколько комбинаций шаров может выпасть в игре?

Решение. Посчитаем отдельно, сколькими способами можно выбрать 2 шара с цифрами из 10 и 3 шара с буквами из 8:

По правилу умножения мы должны перемножить эти числа, чтобы найти общее количество возможных вариантов:

56•45 = 2520

Ответ: 2520

Заметим, что выбирая, например, сочетание из 49 по 7, мы одновременно выбираем и сочетание из 49 по 49 – 7 = 42. Действительно, игрок, обводящий в кружок в лотерейном билете свои 7 счастливых чисел, одновременно и определяет остальные 42 числа, какие числа он НЕ считает счастливыми. Для наглядности запишем число сочетаний в обоих случаях:

Получили одну и ту же дробь, в которой отличается лишь последовательность множителей в знаменателе. Можно показать, что и в общем случае число сочетаний из n по k совпадает с количеством сочетаний из n по (n– k):

Перестановки

Перестановки с повторениями

Определение.
Перестановкой
с повторениями из m
элементов состава k₁,
k₂,…,k_m
называют кортеж длины суммы k₁+k₂+…+k_m,
где k₁
– число повторений одного элемента
множества, k₂
– число повторений другого элемента
множества и т.д., k_m
– количество повторений оставшегося
элемента множества.

Обозначают:
.

Теорема
10. Число
различных перестановок с повторениями
данного состава (n₁,
n,
…,n)
вычисляют по формуле

,
где
n
=n₁
+n+…+
n_т.

 Рассмотрим
одну перестановку и заменим в ней все
одинаковые элементы разными. Тогда
число различных перестановок, которые
можно составить из рассматриваемой
нами перестановки, по правилу произведения
равно n₁,
n,…,
n.
Проделав это для каждой перестановки,
получим n!
перестановок.

Следовательно,

∙n₁!∙n₂∙…∙n_m!
= n!.

Теорема
доказана.

Задача. Сколькими
способами можно расставить белые фигуры:
2 коня, 2 слона, 2 ладьи, ферзя и короля на
первой линии шахматной доски?

Решение.
В
этой задаче надо найти число кортежей
длины 8, имеющих заданный состав (2, 2, 2,
1, 1). Число таких кортежей, то есть
перестановок с повторениями, равно
5040.

.

Ответ:
5 040
способами.

Общую
задачу о перестановках с повторениями
можно сформулировать следующим образом:
имеются предметы m
различных
типов. Сколько перестановок можно
сделать, взяв n₁
элементов первого типа, n₂
типа, …, n_m
элементов m-го
типа?

Задача. Сколько
различных буквенных комбинаций (не
обязательно имеющих смысл) можно
получить, переставляя буквы слова
«кишмиш»?

Решение.
В данном
слове одна буква «к», две буквы «и», две
буквы «ш», одна буква «м», всего 1+2+2+1=6
(букв).

Значит,
Р(1,2,2,1)=(слов).

Ответ:
180 слов.

Задачи для самостоятельного решения

1. Сколько слов,
   состоящих из восьми букв, можно образовать
   из 6 букв алфавита?

2. В магазине имеется
   7 видов тетрадей в клеточку. Сколькими
   способами можно купить 12 тетрадей?

3. Сколькими
   способами можно расставить белые
   фигуры: два коня, две ладьи, ферзя и
   четыре пешки – на одной линии шахматной
   доски?

4. Сколько будет
   костей геометрического домино, если
   использовать в их образовании следующие
   геометрические фигуры: квадрат,
   треугольник, круг, ромб?

5. Сколько
   различных буквенных комбинаций (не
   обязательно имеющих смысл) можно
   получить, переставляя буквы слова
   «комбинаторика»? Переставляя буквы
   слова «математика»?

6. Сколькими
   способами можно обить 12 стульев, если
   имеется 5 сортов обивочного материала?

Бином Ньютона

В
алгебре довольно часто приходится
возводить в степень двучлен (a+b).
Недаром каждый школьник заучивает
наизусть формулы квадрата и куба суммы
двух чисел. Аналогичная формула, но уже
для произвольного натурального числа
п≥1
называютбиномом
Ньютона, хотя и была известна задолго
до того времени, когда жил Ньютон.
Слово «бином» в переводе с латыни
означает «двучлен».

Теорема
11. Для
любого целого неотрицательного n
справедливо тождество:

.

Левая
часть равенства является произведением
n
одинаковых сомножителей:
.
Если раскрыть скобки, не приводя подобных
и не группируя одинаковые сомножители
в степени, получится сумма, в которой
каждое слагаемое является произведениемn переменных,
по одной из каждого сомножителя. Например,

.

Каждое
слагаемое в этой сумме имеет вид слова
в алфавите {x,y},
в котором i–тую
позицию занимает переменная, выбираемая
из i–того
сомножителя. Нетрудно видеть, что каждое
слово длины n
появится в этом выражении в точности
один раз. После группировки сомножителей
каждое слово, в котором буква x
встречается k
раз, превращается в слагаемое вида
.
Таких слов имеется ровноC,
поэтому после приведения подобных
получается правая часть равенства.

Ранее
были приведены следующие свойства
биномиальных коэффициентов:

1)
;
4);

2)
;
5);

3)
;
6).

Особенно
важным свойством является последнее.
Оно позволяет с помощью одних только
операций сложения найти все числа
сочетаний из n
элементов,
если известны числа сочетаний из ()
элемента. Это же свойство лежит в основе
построения таблицы биномиальных
коэффициентов, называемой треугольником
Паскаля.

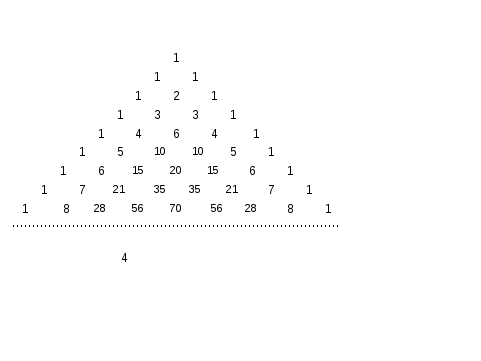
Треугольник
Паскаля является, пожалуй, одной из
наиболее известных и изящных числовых
схем во всей математике. Блез Паскаль,
французский математик и философ, посвятил
ей специальный «Трактат об арифметическом
треугольнике». Впрочем, эта треугольная
таблица была известна задолго до 1665
года – даты выхода в свет трактата.

Так,
в 1529 году треугольник Паскаля был
воспроизведен на титульном листе
учебника арифметики, написанного
астрономом Петром Апианом.

Изображен
треугольник и на иллюстрации книги
«Яшмовое зеркало четырех элементов»
китайского математика Чжу Шицзе,
выпущенной в 1303 году. Омар Хайям, бывший
не только философом и поэтом, но и
математиком, знал о существовании
треугольника в 1110 году, в свою очередь,
заимствовав его из более ранних китайских
или индийских источников.

В
треугольнике Паскаля биномиальные
коэффициенты располагаются следующим
образом:

C

.
. . . . . . . .

В
этой бесконечной таблице строка с
номером n
(n=0,1,2,…)
образована числами C,
k
пробегает все значения от 0 до n.
При этом каждая следующая строчка
сдвинута относительно предыдущей таким
образом, что непосредственно над числом
C
левее и правее его оказываются расположены
числа
и,
сумма которых, по свойству 6), как раз и
равнаC.
Таким образом, если строка с номером
()
заполнена, то легко заполняется строка
с номером n:
первый и последний элементы всегда
равны 1, а каждый из остальных получается
сложением двух расположенных над ним
элементов предыдущей строки.

В
треугольнике Паскаля прослеживаются
следующие закономерности.

1.
Члены
всякой строки треугольника Паскаля
сначала возрастают (до середины строки),
а затем − убывают.

Например, 1<4<6,
6>4>1 (четвертая строка); 1<5<10, 10>5>1
(пятая строка).

2.
Всякая строка треугольника Паскаля
симметрична относительно своей середины
(то есть члены всякой строки треугольника
Паскаля, равноудаленные от ее краев,
равны между собой).

Формально
это свойство записывается в виде
упоминавшегося нами равенства
.

3.
Сумма
членов n-й
строки треугольника Паскаля равна 2.

То
есть
.Это
можно рассматривать как следствие
формулы бинома Ньютона,
если положить
.Важно,
однако, разобраться в теоретико-множественной
интерпретации данного свойства. Число

равно
количеству m-элементных
подмножеств n–элементного
множества. Поэтому левую часть формулы
бинома Ньютона можно рассматривать как
число всех подмножеств n–элементного
множества (включая пустое подмножество
и само n-элементное
множество).

4.
Всякое
непустое множество имеет столько
подмножеств с четным числом элементов,
сколько и подмножеств с нечетным числом
элементов; иными словами, при
n≤1

C
+ C
+ C
+ …=C
+ C
+ C
+ …

Данное
соотношение получается применением
формулы бинома Ньютона к левой части
тождества (1
–
1)^п=0.

С
помощью утверждения 3 можно конкретизировать:

C
+ C
+ C
+ … = C
+ C
+ C
+ …=2.

Приведем
комбинаторное доказательство этого
утверждения.

С
каждым подмножеством X
данного
непустого множества

А={а_1,
а₂,
… , а_п}
свяжем
подмножество Y,
определяемое
следующим образом: Y
получается
из X
путем
исключения или, наоборот, путем добавления
к нему элемента а_i
в зависимости от того, содержит X
элемент
а_i
или не содержит.

Все
подмножества множества А
можно
таким образом разбить на пары подмножеств
(X,
У),
причем в каждой такой паре одно из
подмножеств содержит четное, а другое
–
нечетное число элементов. Следовательно,
подмножеств с четным числом элементов
столько же, сколько и подмножеств с
нечетным числом элементов.

5.
Крайние
члены треугольника Паскаля равны 1.
Каждый же из остальных членов равен
сумме двух смежных с ним членов, стоящих
в предыдущей строке.

Например
(см. строку с номером п=4),

4=1
+ 3; 6=3 + 3; 4=3 + 1.

В
общем случае (при 1≤m≤п)
C=C
+ C.

Последняя
формула интересна и тем, что несет в
себе правило построения каждой последующей
строки треугольника Паскаля по предыдущей
строке.

Доказать
это равенство можно непосредственными
вычислениями с помощью формулы
.

Однако гораздо
интересней обратиться к ее комбинаторной
трактовке: тех сочетаний из элементов
{ а_1,
а₂,
… , а_п,
a_n+1}
по т,
которые не
содержат а_п+1,
будет, очевидно, С;
тех же сочетаний, которые содержатa_n+1,
будет C.

6.
.

Это
получается при
.

7.
.

Получается
применением формул
и.

Рассмотрим
примеры использования формулы бинома.

Пример.
Разложить
по формуле бинома Ньютона двучлен

Решение.

Пример.
Разложить
по формуле бинома Ньютона двучлен

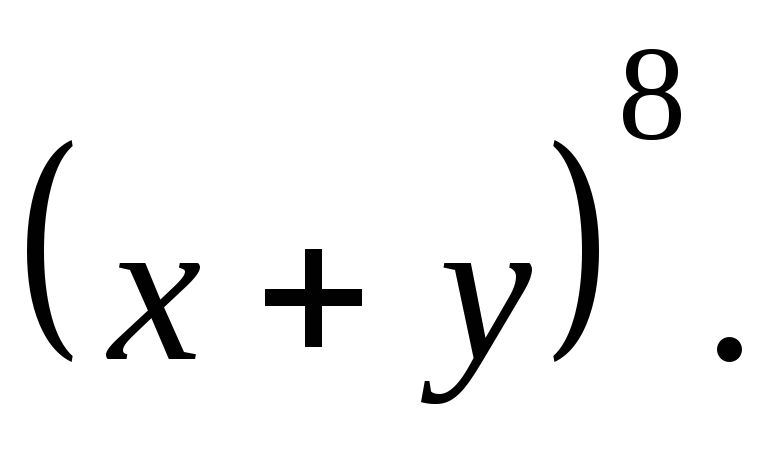
Решение.

Пример.
Запишите
формулу Бинома Ньютона для (х–2у).

=
.

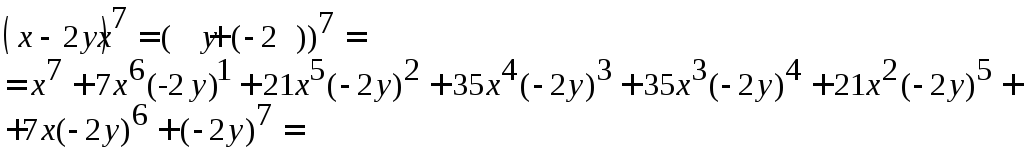Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Перестановки, размещения и сочетания. Формулы.

Чтобы в материале было легче ориентироваться, добавлю содержание данной темы:

1. Введение. Множества и выборки.
2. Размещения без повторений из $n$ элементов по $k$.
3. Размещения с повторениями из $n$ элементов по $k$.
4. Перестановки без повторений из $n$ элементов
5. Перестановки с повторениями.
6. Сочетания без повторений из $n$ элементов по $k$.
7. Сочетания с повторениями из $n$ элементов по $k$.

Введение. Множества и выборки.

В этой теме рассмотрим основные понятия комбинаторики: перестановки, сочетания и размещения. Выясним их суть и формулы, по которым можно найти их количество.

Для работы нам понадобятся кое-какие вспомогательные сведения. Начнём с такого фундаментального математического понятия как множество. Подробно понятие множества было раскрыто в теме “Понятие множества. Способы задания множеств”.

Очень краткий рассказ про множества: показатьскрыть

Рассмотрим некое непустое конечное множество $U$, мощность которого равна $n$, $|U|=n$ (т.е. в множестве $U$ имеется $n$ элементов). Введём такое понятие, как выборка (некоторые авторы именуют её кортежем). Под выборкой объема $k$ из $n$ элементов (сокращённо $(n,k)$-выборкой) будем понимать набор элементов $(a_1, a_2,ldots, a_k)$, где $a_iin U$. Выборка называется упорядоченной, если в ней задан порядок следования элементов. Две упорядоченные выборки, различающиеся лишь порядком элементов, являются различными. Если порядок следования элементов выборки не является существенным, то выборку именуют неупорядоченной.

Заметьте, что в определении выборки ничего не сказано про повторения элементов. В отличие от элементов множеств, элементы выборки могут повторяться.

Для примера рассмотрим множество $U={a,b,c,d,e}$. Множество $U$ содержит 5 элементов, т.е. $|U|=5$. Выборка без повторений может быть такой: $(a,b,c)$. Данная выборка содержит 3 элемента, т.е. объём этой выборки равен 3. Иными словами, это $(5,3)$-выборка.

Выборка с повторениями может быть такой: $(a,a,a,a,a,c,c,d)$. Она содержит 8 элементов, т.е. объём её равен 8. Иными словами, это $(5,8)$-выборка.

Рассмотрим ещё две $(5,3)$-выборки: $(a,b,b)$ и $(b,a,b)$. Если мы полагаем наши выборки неупорядоченными, то выборка $(a,b,b)$ равна выборке $(b,a,b)$, т.е. $(a,b,b)=(b,a,b)$. Если мы полагаем наши выборки упорядоченными, то $(a,b,b)neq(b,a,b)$.

Рассмотрим ещё один пример, немного менее абстрактный 🙂 Предположим, в корзине лежат шесть конфет, причём все они различны. Если первой конфете поставить в соответствие цифру 1, второй конфете – цифру 2 и так далее, то с конфетами в корзине можно сопоставить такое множество: $U={1,2,3,4,5,6}$. Представьте, что мы наугад запускаем руку в корзинку с целью вытащить три конфеты. Вытащенные конфеты – это и есть выборка. Так как мы вытаскиваем 3 конфеты из 6, то получаем (6,3)-выборку. Порядок расположения конфет в ладони совершенно несущественен, поэтому эта выборка является неупорядоченной. Ну, и так как все конфеты различны, то выборка без повторений. Итак, в данной ситуации говорим о неупорядоченной (6,3)-выборке без повторений.

Теперь подойдём с иной стороны. Представим себе, что мы находимся на фабрике по производству конфет, и на этой фабрике производятся конфеты четырёх сортов. Множество $U$ в этой ситуации таково: $U={1,2,3,4 }$ (каждая цифра отвечает за свой сорт конфет). Теперь вообразим, что все конфеты ссыпаются в единый жёлоб, около которого мы и стоим. И, подставив ладони, из этого потока отбираем 20 конфет. Конфеты в горсти – это и есть выборка. Играет ли роль порядок расположения конфет в горсти? Естественно, нет, поэтому выборка неупорядоченная. Всего 4 сорта конфет, а мы отбираем двадцать штук из общего потока – повторения сортов неизбежны. При этом выборки могут быть самыми различными: у нас даже могут оказаться все конфеты одного сорта. Следовательно, в этой ситуации мы имеем дело с неупорядоченной (4,20)-выборкой с повторениями.

Рассмотрим ещё пару примеров. Пусть на кубиках написаны различные 7 букв: к, о, н, ф, е, т, а. Эти буквы образуют множество $U={к,о,н,ф,е,т,а}$. Допустим, из данных кубиков мы хотим составить “слова” из 5 букв. Буквы этих слов (к примеру, «конфе», «тенко» и так далее) образуют (7,5)-выборки: $(к,о,н,ф,е)$, $(т,е,н,к,о)$ и т.д. Очевидно, что порядок следования букв в такой выборке важен. Например, слова «нокфт» и «кфтон» различны (хотя состоят из одних и тех же букв), ибо в них не совпадает порядок букв. Повторений букв в таких «словах» нет, ибо в наличии только семь кубиков. Итак, набор букв каждого слова представляет собой упорядоченную (7,5)-выборку без повторений.

Еще один пример: мы составляем всевозможные восьмизначные числа из четырёх цифр 1, 5, 7, 8. Например, 11111111, 15518877, 88881111 и так далее. Множество $U$ таково: $U={1,5,7,8}$. Цифры каждого составленного числа образуют (4,8)-выборку. Порядок следования цифр в числе важен, т.е. выборка упорядоченная. Повторения допускаются, поэтому здесь мы имеем дело с упорядоченной (4,8)-выборкой с повторениями.

Размещения без повторений из $n$ элементов по $k$

Размещение без повторений из $n$ элементов по $k$ – упорядоченная $(n,k)$-выборка без повторений.

Так как элементы в рассматриваемой выборке повторяться не могут, то мы не можем отобрать в выборку больше элементов, чем есть в исходном множестве. Следовательно, для таких выборок верно неравенство: $n≥ k$. Количество размещений без повторений из $n$ элементов по $k$ определяется следующей формулой:

$$
begin{equation}
A_{n}^{k}=frac{n!}{(n-k)!}
end{equation}
$$

Что обозначает знак “!”? : показатьскрыть

Пример №1

Алфавит состоит из множества символов $E={+,*,0,1,f}$. Определим количество таких трёхсимвольных слов в этом алфавите, которые не содержат повторяющихся букв.

Решение

Под трёхсимвольными словами будем понимать выражения вида “+*0” или “0f1”. В множестве $E$ пять элементов, поэтому буквы трехсимвольных слов образуют (5,3)-выборки. Первый вопрос: эти выборки упорядочены или нет? Слова, которые отличаются лишь порядком букв, полагаются различными, поэтому порядок элементов в выборке важен. Значит, выборка является упорядоченной. Второй вопрос: допускаются повторения или нет? Ответ на этот вопрос даёт условие: слова не должны содержать повторяющихся букв. Подводим итоги: буквы каждого слова, удовлетворяющего условию задачи, образуют упорядоченную (5,3)-выборку без повторений. Иными словами, буквы каждого слова образуют размещение без повторений из 5 элементов по 3. Вот примеры таких размещений:

$$
(+,*,f), ; (*,+,f), ; (1,+,0)
$$

Нас же интересует общее количество этих размещений. Согласно формуле (1) количество размещений без повторений из 5 элементов по 3 будет таким:

$$
A_{5}^{3}=frac{5!}{(5-3)!}=frac{5!}{2!}=60.
$$

Т.е. можно составить 60 трёхсимвольных слов, буквы которых не будут повторяться.

Ответ: 60.

Размещения с повторениями из $n$ элементов по $k$

Размещение с повторениями из $n$ элементов по $k$ – упорядоченная $(n,k)$-выборка с повторениями.

Количество размещений с повторениями из $n$ элементов по $k$ определяется следующей формулой:

$$
begin{equation}
bar{A}_{n}^{k}=n^k
end{equation}
$$

Пример №2

Сколько пятизначных чисел можно составить из множества цифр ${5,7,2}$?

Решение

Из данного набора цифр можно составить пятизначные числа 55555, 75222 и так далее. Цифры каждого такого числа образуют (3,5)-выборку: $(5,5,5,5,5)$, $(7,5,2,2,2)$. Зададимся вопросом: что это за выборки? Во-первых, цифры в числах могут повторяться, поэтому мы имеем дело с выборками с повторениями. Во-вторых, порядок расположения цифр в числе важен. Например, 27755 и 77255 – разные числа. Следовательно, мы имеем дело с упорядоченными (3,5)-выборками с повторениями. Общее количество таких выборок (т.е. общее количество искомых пятизначных чисел) найдём с помощью формулы (2):

$$
bar{A}_{3}^{5}=3^5=243.
$$

Следовательно, из заданных цифр можно составить 243 пятизначных числа.

Ответ: 243.

Перестановки без повторений из $n$ элементов

Перестановка без повторений из $n$ элементов – упорядоченная $(n,n)$-выборка без повторений.

По сути, перестановка без повторений есть частный случай размещения без повторений, когда объём выборки равен мощности исходного множества. Количество перестановок без повторений из $n$ элементов определяется следующей формулой:

$$
begin{equation}
P_{n}=n!
end{equation}
$$

Эту формулу, кстати, легко получить, если учесть, что $P_n=A_{n}^{n}$. Тогда получим:

$$
P_n=A_{n}^{n}=frac{n!}{(n-n)!}=frac{n!}{0!}=frac{n!}{1}=n!
$$

Пример №3

В морозилке лежат пять порций мороженого от различных фирм. Сколькими способами можно выбрать порядок их съедения?

Решение

Пусть первому мороженому соответствует цифра 1, второму – цифра 2 и так далее. Мы получим множество $U={1,2,3,4,5}$, которое будет представлять содержимое морозилки. Порядок съедения может быть таким: $(2,1,3,5,4)$ или таким: $(5,4,3,1,2)$. Каждый подобный набор есть (5,5)-выборка. Она будет упорядоченной и без повторений. Иными словами, каждая такая выборка есть перестановка из 5 элементов исходного множества. Согласно формуле (3) общее количество этих перестановок таково:

$$
P_5=5!=120.
$$

Следовательно, существует 120 порядков выбора очередности съедения.

Ответ: 120.

Перестановки с повторениями

Перестановка с повторениями – упорядоченная $(n,k)$-выборка с повторениями, в которой элемент $a_1$ повторяется $k_1$ раз, $a_2$ повторяется $k_2$ раза так далее, до последнего элемента $a_r$, который повторяется $k_r$ раз. При этом $k_1+k_2+ldots+k_r=k$.

Общее количество перестановок с повторениями определяется формулой:

$$
begin{equation}
P_{k}(k_1,k_2,ldots,k_r)=frac{k!}{k_1!cdot k_2!cdot ldots cdot k_r!}
end{equation}
$$

Пример №4

Слова составляются на основе алфавита $U={a,b,d}$. Сколько различных слов из семи символов может быть составлено, если в этих словах буква “a” должна повторяться 2 раза; буква “b” – 1 раз, а буква “d” – 4 раза?

Решение

Вот примеры искомых слов: “aabdddd”, “daddabd” и так далее. Буквы каждого слова образуют (3,7)-выборку с повторениями: $(a,a,b,d,d,d,d)$, $(d,a,d,d,a,b,d)$ и т.д. Каждая такая выборка состоит из двух элементов “a”, одного элемента “b” и четырёх элементов “d”. Иными словами, $k_1=2$, $k_2=1$, $k_3=4$. Общее количество повторений всех символов, естественно, равно объёму выборки, т.е. $k=k_1+k_2+k_3=7$. Подставляя эти данные в формулу (4), будем иметь:

$$
P_7(2,1,4)=frac{7!}{2!cdot 1!cdot 4!}=105.
$$

Следовательно, общее количество искомых слов равно 105.

Ответ: 105.

Сочетания без повторений из $n$ элементов по $k$

Сочетание без повторений из $n$ элементов по $k$ – неупорядоченная $(n,k)$-выборка без повторений.

Общее количество сочетаний без повторений из $n$ элементов по $k$ определяется формулой:

$$
begin{equation}
C_{n}^{k}=frac{n!}{(n-k)!cdot k!}
end{equation}
$$

Пример №5

В корзине размещены карточки, на которых написаны целые числа от 1 до 10. Из корзины вынимают 4 карточки и суммируют числа, написанные на них. Сколько различных наборов карточек можно вытащить из корзины?

Решение

Итак, в данной задаче исходное множество таково: $U={1,2,3,4,5,6,7,8,9,10}$. Из этого множества мы выбираем четыре элемента (т.е., четыре карточки из корзины). Номера вытащенных элементов образуют (10,4)-выборку. Повторения в этой выборке не допускаются, так как номера всех карточек различны. Вопрос вот в чём: порядок выбора карточек играет роль или нет? Т.е., к примеру, равны ли выборки $(1,2,7,10)$ и $(10,2,1,7)$ или не равны? Тут нужно обратиться к условию задачи. Карточки вынимаются для того, чтобы потом найти сумму элементов. А это значит, что порядок карточек не важен, так как от перемены мест слагаемых сумма не изменится. Например, выборке $(1,2,7,10)$ и выборке $(10,2,1,7)$ будет соответствовать одно и то же число $1+2+7+10=10+2+1+7=20$. Вывод: из условия задачи следует, что мы имеем дело с неупорядоченными выборками. Т.е. нам нужно найти общее количество неупорядоченных (10,4)-выборок без повторений. Иными словами, нам нужно найти количество сочетаний из 10 элементов по 4. Используем для этого формулу (5):

$$
C_{10}^{4}=frac{10!}{(10-4)!cdot 4!}=frac{10!}{6!cdot 4!}=210.
$$

Следовательно, общее количество искомых наборов равно 210.

Ответ: 210.

Сочетания с повторениями из $n$ элементов по $k$

Сочетание с повторениями из $n$ элементов по $k$ – неупорядоченная $(n,k)$-выборка с повторениями.

Общее количество сочетаний с повторениями из $n$ элементов по $k$ определяется формулой:

$$
begin{equation}
bar{C}_{n}^{k}=frac{(n+k-1)!}{(n-1)!cdot k!}
end{equation}
$$

Пример №6

Представьте себе, что мы находимся на конфетном заводе, – прямо возле конвейера, по которому движутся конфеты четырёх сортов. Мы запускаем руки в этот поток и вытаскиваем двадцать штук. Сколько всего различных “конфетных комбинаций” может оказаться в горсти?

Решение

Если принять, что первому сорту соответствует число 1, второму сорту – число 2 и так далее, то исходное множество в нашей задаче таково: $U={1,2,3,4}$. Из этого множества мы выбираем 20 элементов (т.е., те самые 20 конфет с конвейера). Пригоршня конфет образует (4,20)-выборку. Естественно, повторения сортов будут. Вопрос в том, играет роль порядок расположения элементов в выборке или нет? Из условия задачи следует, что порядок расположения элементов роли не играет. Нам нет разницы, будут ли в горсти располагаться сначала 15 леденцов, а потом 4 шоколадных конфеты, или сначала 4 шоколадных конфеты, а уж потом 15 леденцов. Итак, мы имеем дело с неупорядоченной (4,20) выборкой с повторениями. Чтобы найти общее количество этих выборок используем формулу (6):

$$
bar{C}_{4}^{20}=frac{(4+20-1)!}{(4-1)!cdot 20!}=frac{23!}{3!cdot 20!}=1771.
$$

Следовательно, общее количество искомых комбинаций равно 1771.

Ответ: 1771.