Возьмем циркуль. Установим ножку циркуля с иглой в точку «O», а ножку циркуля с
карандашом будем вращать вокруг этой точки. Таким образом, мы получим замкнутую
линию. Такую замкнутую линию называют — окружность.
Рассмотрим более подробно окружность. Разберёмся, что называют центром,
радиусом и диаметром окружности.
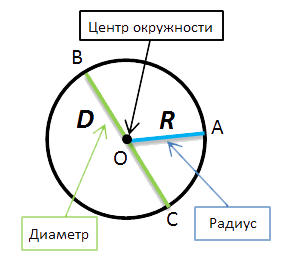
- (·)O — называется центром окружности.
- Отрезок, который соединяет
центр и любую точку окружности, называется радиусом окружности.
Радиус окружности обозначается буквой «R». На рисунке выше —
это отрезок «OA». - Отрезок, который соединяет
две точки окружности и проходит через её центр, называется
диаметром окружности.Диаметр окружности обозначается буквой «D».
На рисунке выше — это отрезок «BC».На рисунке также видно, что диаметр равен двум радиусам. Поэтому
справедливо выражение «D = 2R».
Число π и длина окружности
Прежде чем разобраться, как считается длина окружности, необходимо выяснить, что
такое число π (читается как «Пи»), которое
так часто упоминают на уроках.
В далекие времена математики Древней Греции внимательно изучали окружность
и пришли к выводу, что длина окружности и её диаметр взаимосвязаны.
Запомните!
Отношение длины окружности к её диаметру является одинаковым
для всех
окружностей и обозначается греческой буквой π
(«Пи»).
π ≈ 3,14…
Число «Пи» относится к числам, точное значение которых записать невозможно
ни с помощью обыкновенных дробей, ни с помощью десятичных дробей. Нам
для наших вычислений достаточно использовать значение π,
округленное до разряда сотых
π ≈ 3,14…
Теперь, зная, что такое число π, мы
можем записать формулу длины окружности.
Запомните!
Длина окружности
— это произведение числа π
и диаметра окружности.
Длина окружности обозначается буквой «С» (читается как «Це»).
C = πD
C = 2πR
, так как D = 2R
Как найти длину окружности
Чтобы закрепить полученные знания, решим задачу на окружности.
Разбор примера
Условие задачи:
Найдите длину окружности, радиус которой равен 24 см. Число
π
округлите до сотых.
Воспользуемся формулой длины окружности:
C = 2πR
≈ 2 · 3,14 · 24 ≈ 150,72 см
Разберем обратную задачу, когда мы знаем длину
окружности, а нас просят найти её диаметр.
Разбор примера
Условие задачи:
Определите диаметр окружности, если
её длина равна 56,52 дм.
(π ≈ 3,14).
Выразим из формулы длины окружности диаметр.
C = πD
D = С / π
D = 56,52 / 3,14 = 18 дм
Хорда и дуга окружности
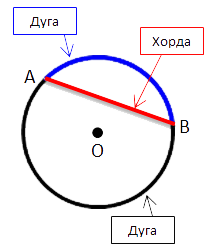
На рисунке ниже отметим на окружности две точки «A» и «B». Эти точки делят окружность
на две части, каждую из которых называют дугой.
Это синяя дуга «AB» и черная дуга «AB».
Точки «A» и «B» называют концами дуг.
Соединим точки «A» и «B» отрезком. Полученный отрезок называют
хордой.
Важно!
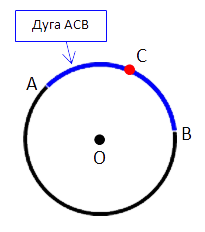
Точки «A» и «B» делят окружность на две дуги. Поэтому важно
понимать, какую дугу вы имеете в виду, когда пишите дуга «AB».
Для того чтобы избежать путаницы, часто вводят дополнительную точку на
нужной дуге и обращаются к ней по трем точкам.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
3 мая 2020 в 10:27
Владислав Заступневич
Профиль
Благодарили: 0
Сообщений: 1
Владислав Заступневич
Профиль
Благодарили: 0
Сообщений: 1
, Радиус одной окружности равен 12 см, а второй-36см.Чему равно отношения длины первой окружности к длине второй окружности?
0
Спасибо
Ответить
6 мая 2020 в 15:48
Ответ для Владислав Заступневич
Галина Федотова
Профиль
Благодарили: 0
Сообщений: 3
Галина Федотова
Профиль
Благодарили: 0
Сообщений: 3
С=2πR
если длину одной окружности разделить на дилну другой, то 2π сократится, следовательно длины будут относится так же как радиусы, то есть 12:36=
0
Спасибо
Ответить
22 сентября 2016 в 19:03
Вика Камалова
Профиль
Благодарили: 0
Сообщений: 2
Вика Камалова
Профиль
Благодарили: 0
Сообщений: 2
Помогите 2) чему равен деаметр если радиус равен а)12см б)10 децеметров
1) начертить окружность радиусом а)2 см пот буквой б)4см 5мм (начертиь!)
3)Чему равен радиус если деаметр равен а)6см б)9см в)12мСРОЧНО СЕГОДНЯ! ПРОШУ!!!
0
Спасибо
Ответить
23 сентября 2016 в 14:51
Ответ для Вика Камалова
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Радиус равен половине диаметра. Обратно диаметр равен двум радиусам. Подробнее здесь.
1) а) 12см · 2=24см б)10дм · 2 = 20дм
2) ответил в теме.
3) а) 6см: 2 = 3см б) 9см: 2 = 4см 5 мм в)12м: 2 = 6м
0
Спасибо
Ответить
22 сентября 2016 в 18:54
Вика Камалова
Профиль
Благодарили: 0
Сообщений: 2
Вика Камалова
Профиль
Благодарили: 0
Сообщений: 2
1)Начертить окружность радиусом а)2 см пот буквой б)4 см 5 мм
0
Спасибо
Ответить
23 сентября 2016 в 14:46
Ответ для Вика Камалова
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Радиус окружности это расстояние от центра до любой точки окружности. Подробнее можно посмотреть вот здесь. На линейке циркулем отмеряем необходимый радиус и чертим окружность.
0
Спасибо
Ответить
24 января 2016 в 13:45
Инна Шабрашина
Профиль
Благодарили: 0
Сообщений: 5
Инна Шабрашина
Профиль
Благодарили: 0
Сообщений: 5
Длина окружности и площадь круга.
Я не понимаю как найти площадь круга.
0
Спасибо
Ответить
19 сентября 2016 в 10:56
Ответ для Инна Шабрашина
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
0
Спасибо
Ответить
7 сентября 2015 в 21:08
Игорь Желтоновский
Профиль
Благодарили: 0
Сообщений: 1
Игорь Желтоновский
Профиль
Благодарили: 0
Сообщений: 1
радиус — 2,1 м.Найти длинну круга и его площадь(помогите плз)
0
Спасибо
Ответить
2 сентября 2016 в 15:18
Ответ для Игорь Желтоновский
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Длина окружности(l) вычисляется по формуле: l=2?r
Площадь круга(S) вычисляется по формуле: S=?r2
Подставляем значения и считаем, приняв ?=3,14
l=2 · 3,14 · 2,1 = 13,188
S = 3,14 · 2,12=13,8474
Более подробно можно прочитать здесь: math-prosto.ru/index.php?page=pages/circle/square_of_circle.php
0
Спасибо
Ответить
Загрузить PDF
Загрузить PDF
Пи (π) — одно из самых важных и интригующих чисел в математике. Эта константа, примерно равная 3,14, используется для вычисления длины окружности с учетом ее радиуса.[1]
Это также иррациональное число, то есть оно может быть вычислено до бесконечного числа знаков после запятой.[2]
Это не так-то просто сделать, но все-таки возможно.
-
1
Убедитесь, что вы используете идеальный круг. Этот метод не работает с эллипсами, овалами и чем-либо иным, этот метод подходит только для идеальной окружности. Окружность определяется как совокупность всех точек на плоскости, которые лежат на одинаковом расстоянии от одной центральной точки. Крышка банки — идеальный предмет для этого метода. Если вы хотите сделать наиболее точные вычисления, используйте карандаш с очень тонким грифелем.
-
2
Измерьте длину окружности настолько точно, насколько это возможно. Это нелегкая задача (вот почему Пи так важно).
- Оберните нитку вокруг крышки как можно плотнее. Отметьте точку совпадения начала и конца, а затем измерьте длину нитки с помощью линейки.
-
3
Измерьте диаметр окружности. Диаметр — длина отрезка, проходящего через центр окружности и любые две точки, лежащие на окружности.
-
4
Используйте формулу. Длина окружности вычисляется по формуле C= π*d = 2*π*r. Таким образом, Пи равно длине окружности, деленной на ее диаметр. Посчитайте Пи (с вашими значениями) на калькуляторе. Результат должен быть примерно равен 3,14.[3]
-
5
Чтобы уточнить расчеты, повторите эту процедуру с несколькими различными окружностями, а затем усредните результаты. Ваши измерения не будут совершенными для одной взятой окружности, но с учетом нескольких окружностей, они должны усредниться до точного значения Пи.
Реклама
-
1
Используйте ряд Лейбница. Математики нашли несколько различных бесконечных рядов, которые позволяют точно вычислить Пи до большого количества знаков после запятой. Некоторые из них настолько сложны, что требуются суперкомпьютеры для обработки. Однако одним из простейших рядов является ряд Лейбница. Хотя он и не самый эффективный, с каждой итерацией он будет давать более точное значение Пи; после 500 000 итераций ряд Лейбница даст точное значение Пи с десятью знаками после запятой.[4]
Here is the formula to apply.- π = (4/1) – (4/3) + (4/5) – (4/7) + (4/9) – (4/11) + (4/13) – (4/15) …
- Возьмите 4/1 и вычтите 4/3. Затем прибавьте 4/5. Затем вычтите 4/7. Продолжайте, чередуя сложение и вычитание дробей с 4 в числителе и каждым последующим нечетным числом в знаменателе. Чем больше раз вы это сделаете, тем более точное значение Пи вы получите.
-
2
Попробуйте ряд Нилаканта. Это еще один бесконечный ряд для вычисления Пи, который довольно легко понять. Этот ряд более сложный, чем ряд Лейбница, но он дает точное значение Пи гораздо быстрее.[5]
- π = 3 + 4/(2*3*4) – 4/(4*5*6) + 4/(6*7*8) – 4/(8*9*10) + 4/(10*11*12) – (4/(12*13*14) …
- Для этого ряда запишите число 3 и чередуйте сложение и вычитание дробей с числом 4 в числителе и произведением трех последовательных целых чисел, которые увеличиваются с каждой новой итерацией, в знаменателе. Каждое последующее произведение начинается с наибольшего числа, используемого в предыдущем произведении. Проделайте это всего несколько раз и вы получите довольно точное значение Пи.
Реклама
-
1
Проведите эксперимент. Оказывается, Пи можно найти, проведя интересный эксперимент под названием метод иглы Буффона,[6]
который стремится определить вероятность того, что случайно брошенные иглы приземлятся либо между нарисованными равноудаленными параллельными прямыми, либо пересекут ровно одну прямую. Если расстояние между прямыми равно длине иглы, то отношение числа бросков, когда игла пересекает прямую, к общему числу бросков стремится к 2/Пи. Также можете попробовать провести эксперимент с хот-догами (перейдите по ссылке в начале шага).- Ученые и математики не могут определить точный способ вычисления Пи, так как они не могут найти настолько тонкий предмет, чтобы вычисления были точными.[7]
- Ученые и математики не могут определить точный способ вычисления Пи, так как они не могут найти настолько тонкий предмет, чтобы вычисления были точными.[7]
-
1
Сначала выберите большое число. Чем больше это число, тем точнее будет результат.
-
2
Затем подставьте это число (обозначим его х) в формулу для расчета Пи: x * sin(180 / x)’. Чтобы этот метод сработал, калькулятор нужно включить в режиме «Градусы». Мы говорим, что в этом методе используется предел, так как результат ограничен числом Пи (то есть значение Пи является предельно возможным). Чем больше значение х, тем точнее вы рассчитаете Пи.
Реклама
-
1
Выберите любое число от -1 до 1. Функция y=arcsin(x) не имеет таких значений x, больших 1 и меньших -1, которым можно было бы сопоставить хоть какое-нибудь значение y (неважно — бесконечное или нет). Это означает, что функция y=arcsin(x) определена только на интервале от x=-1 до x=1 включительно и не определена при любых других x.
-
2
Подставьте свое число в следующую формулу и вы сможете вычислить число Пи.
- Пи = 2 * (Arcsin (SQRT (1 – х ^ 2))) + ABS (Arcsin (х)).
- Значение арксинуса будет представлено в радианах.
- Sqrt — это квадратный корень.
- Abs — это абсолютное значение числа
- х ^ 2 — в данном случае это х в квадрате.
Реклама
- Пи = 2 * (Arcsin (SQRT (1 – х ^ 2))) + ABS (Arcsin (х)).
Советы
- Расчет Пи — увлекательное и интересное занятие, но вычисление многих знаков после запятой не имеет большого смысла. Астрофизики утверждают, что значения Пи с 39 знаками после запятой достаточно для космологических расчетов, которые проводятся с точностью до размеров атома.
Реклама
Об этой статье
Эту страницу просматривали 240 931 раз.
Была ли эта статья полезной?
Число Пи
Даже если вы давно закончили школу и из всего курса математики помните только таблицу умножения, мы уверены: про число пи вы знаете. Скажете с ходу, чему оно равно? Помните, для чего нужно число пи и как его посчитать? Если нет, читайте наш урок
Представляете, мы живем в эпоху технологического прорыва, но до сих пор не можем точно рассчитать площадь съеденного круглого торта? Все потому, что в формуле вычисления площади круга используется число π.
От автомобильного колеса до орбиты спутника, от часового механизма до электромагнитных и звуковых волн. В любой научной области есть расчеты, и практически в любом расчете не обойтись без числа пи. Даже там, где, казалось бы, окружности нет места, например в статистике.
Что такое число пи
Число пи — это отношение длины окружности к ее диаметру. Обозначается оно буквой греческого алфавита π. Если записать это отношение математическими символами, то выглядит оно так: π = C/d, где C — это длина окружности, а d — диаметр окружности. То есть π — это результат деления длины окружности на ее диаметр. Но само по себе число пи не является каким-то параметром окружности. Это математическая постоянная, или константа (то есть неизменная), которая нужна для расчета определенных данных. Например, число пи необходимо, чтобы посчитать площадь круга.
Чему равно число пи

Число пи не имеет точного значения. Это легко проверить. Возьмите круг любого размера, разделите его окружность на диаметр — у вас получится десятичная дробь с множеством цифр после запятой. Математики называют такие числа иррациональными. Результат, который вы увидите, будет равен 3 целых и сколько-то десятых, сотых, тысячных — и далее насколько хватит дисплея калькулятора. У числа пи бесконечное количество знаков после запятой. Но для удобства в расчетах используют округленные значения.
Число π примерно равно 3,14, или, если точнее, 3,1415926535. Именно значение с десятью знаками после запятой принято использовать. Но все дело в округлении. Там, где не нужны максимально точные расчеты, за число пи часто берут 3. А вот для точных расчетов в науке ученые используют число пи с 38-ю знаками десятичного разложения (после запятой в десятичной дроби).
Итак:
π = 3,14 или π = 3,1415926535
Как посчитать число пи самостоятельно

Возьмите несколько круглых предметов разного размера, например тарелку, блюдце и крышку от кастрюли. Измерьте окружность каждого. Для этого используйте сантиметровую ленту. Или можно обернуть их по окружности ниткой или веревкой, а потом полученную длину нитки или веревки измерить линейкой. С помощью сантиметровой ленты или линейки измерьте и диаметр каждого предмета. Длина окружности и диаметры у каждого будут разные, ведь предметы разные по размеру.
Теперь для каждого предмета разделите его длину окружности на диаметр. Вы увидите, что во всех случаях, какого бы размера ни был круглый предмет, полученное значение будет 3 целых и далее десятые и сотые доли. Оно необязательно соответствует принятому значению в 3,14, но всегда будет около него.
Практическое применение числа пи
В школе нас учат использовать число пи для вычисления площади круга. Рассчитывается она по следующей формуле: S = πr², где S — площадь, π — число пи, r² — радиус в квадрате. Можно использовать эту формулу: S = d²/4*π, где d² — диаметр.
Зная число пи и диаметр, можно посчитать длину окружности. Для этого вспомним школьные уравнения. Если π = C/d, то C (длина окружности) высчитывается по формуле C = π*d.
Но применение числа пи в науке гораздо шире. Оно используется практически для любых расчетов в любой области, будь то архитектура, авиация и даже статистика. Например, число π нужно для расчета времени полета самолета и расстояния, которое он должен преодолеть. А в статистике с помощью числа пи рассчитывают значения ниже так называемой кривой нормального распределения. Это нужно для того чтобы, например, выяснить, как распределялись голоса респондентов при опросе.
S (площадь круга) = πr²
История числа пи
Считается, что первым обозначать число пи буквой греческого алфавита π (pi) стал британский математик Уильям Джонс в 1706 году, а популяризировал обозначение его швейцарский коллега Леонард Эйлер в 1737 году. Есть версия, что эта буква выбрана не случайно, а как начальная в греческом слове perijereia, что означает «окружность», «периферия».
Как и на многие явления, известные науке сегодня, на существование некой постоянной, с помощью которой можно посчитать площадь круга, обратили внимание еще в Древнем мире. Но ученые того времени приходили к разному мнению относительно значения этой постоянной: одни использовали значение 3,125, другие — 3,16, третьи — 3,139. Но всегда это значение было 3 с небольшим.
На точное вычисление числа пи ушли тысячелетия. Первым, кто определил более-менее приблизительное значение π, был древнегреческий ученый Архимед. По его расчетам пи равно 3,142857142857143. Как мы знаем сейчас, верными оказались только первые два десятичных числа.
Натуральные числа
Их разряды, классы и свойства
подробнее
Точнее оказались расчеты китайского математика 480-х годов нашей эры — 3,1415927. Именно это значение числа пи считалось самым верным до 1420-х годов, пока ученые не расширили этот ряд до 16 цифр после запятой, затем до 20-ти, 32-х и так далее.
В XX веке с приходом компьютерных систем и вычислительной техники дело пошло быстрее: теперь уже точные десятичные значения высчитывали машины. С помощью специальных алгоритмов математики во всем мире продолжают определять новые, более точные значения числа пи, устанавливая рекорды по количеству цифр десятичного разложения (после запятой в десятичной дроби).
Популярные вопросы и ответы
Отвечают Вячеслав Смольняков, учитель математики и информатики высшей квалификационной категории, эксперт ОГЭ и ЕГЭ Региональной предметной комиссии по математике и информатике; Ирина Ходакова, учитель математики.
Как округлить число пи?
Чтобы не запоминать число пи с большим количеством десятичных значений, его принято округлять, — говорит Вячеслав Смольняков. — В математике все округления проводятся по строгим правилам. Для округления значения числа пи применяют метод округления к ближайшему целому. Если перед округляемым числом стоит число 5 и большее, то число округляется в большую сторону. Например, 12,513. Другой пример: 12,5812,613.
Если перед округляемым числом стоит число менее 5, то число округляется в меньшую сторону. Например, 12,412. Или: 12,3412,312.
Итак, возьмем π — 3,1415. Округление начинают с последнего значения, в данном случае это 5. Значит, следующая за ним единица округляется до двух: 3,14153,142. Последнее число 2 меньше пяти, значит, последующее 4 остается неизменным: 3,1423,14. Вот мы и пришли к общепринятому значению числа пи.
По тому же принципу давайте продолжим округление до целого числа: 3,143,23. И вот у нас получилось значение числа пи 3.
Как запомнить число пи?
Чтобы запомнить значение числа π, — советует Ирина Ходакова, — используют один из самых популярных способов — запомнить фразу, в которой количество букв в каждом слове совпадает с цифрами числа π.
Например, «Что(3) я(1) знаю(4) о(1) круге(5)?»
Чтобы запомнить больше знаков числа π, пользуются различными приемами мнемотехники (совокупность приемов, облегчающих запоминание информации). Например, существует стихотворение С. Боброва «Волшебный двурог» для запоминания числа π, которое совсем не сложно выучить:
«Чтобы нам не ошибаться,
Надо правильно прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Ну и дальше надо знать,
Если мы вас спросим —
Это будет пять, три, пять,
Восемь, девять, восемь»
Где используется число пи?
Изначально число π было необходимо для применения в строительстве. Ведь порой из-за погрешности в значении числа π падали башни и рушились целые дворцы. Сейчас π используется в различных сферах нашей жизни.
Мы уже выяснили, что число π позволяет нам рассчитывать и создавать окружности. Если колеса на вашем автомобиле будут немного отличаться друг от друга, то поездки для вас станут как минимум не очень удобными. Но применение числа π этим не ограничивается. Например, без числа π нельзя было бы обеспечить качественную работу телевизоров, радио и телефонов, так как инженеры используют π для расчета и оптимизации звуковых волн. Также π играет важную роль в расчете времени и расстояния путешествия на самолете, так как на большие расстояния самолеты летят по округлой дуге. Не было бы даже многих игр, таких как футбол, баскетбол, теннис, ведь мячи должны быть абсолютно круглыми.
У этого термина существуют и другие значения, см. Пи.
| Иррациональные числа ζ(3) — ρ — √2 — √3 — √5 — ln 2 — φ,Φ — ψ — α,δ — e — eπ и π |
|
| Система счисления | Оценка числа 
|
| Десятичная | 3,1415926535897932384626433832795… |
| Двоичная | 11,00100100001111110110… |
| Шестнадцатеричная | 3,243F6A8885A308D31319… |
| Шестидесятеричная | 3; 08 29 44 00 47 25 53 07 … |
| Рациональные приближения | 22⁄7, 179⁄57, 223⁄71, 333⁄106, 355⁄113, 103 993⁄33 102 (перечислено в порядке увеличения точности) |
| Непрерывная дробь | [3; 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, … ]
(Эта непрерывная дробь не периодическая. Записана в линейной нотации) |
| Тригонометрия |  радиан = 180° радиан = 180°
|
3,1415926535 8979323846 2643383279 5028841971 6939937510
5820974944 5923078164 0628620899 8628034825 3421170679
8214808651 3282306647 0938446095 5058223172 5359408128
4811174502 8410270193 8521105559 6446229489 5493038196
4428810975 6659334461 2847564823 3786783165 2712019091
4564856692 3460348610 4543266482 1339360726 0249141273
7245870066 0631558817 4881520920 9628292540 9171536436
7892590360 0113305305 4882046652 1384146951 9415116094
3305727036 5759591953 0921861173 8193261179 3105118548
0744623799 6274956735 1885752724 8912279381 8301194912
9833673362 4406566430 8602139494 6395224737 1907021798
6094370277 0539217176 2931767523 8467481846 7669405132
0005681271 4526356082 7785771342 7577896091 7363717872
1468440901 2249534301 4654958537 1050792279 6892589235
4201995611 2129021960 8640344181 5981362977 4771309960
5187072113 4999999837 2978049951 0597317328 1609631859
5024459455 3469083026 4252230825 3344685035 2619311881
7101000313 7838752886 5875332083 8142061717 7669147303
5982534904 2875546873 1159562863 8823537875 9375195778
1857780532 1712268066 1300192787 6611195909 2164201989
…
Число 
Если диаметр окружности равен единице, то длина окружности — это число «пи»

Свойства
Трансцендентность и иррациональность
Число 










В 1934 году Гельфонд доказал[5] трансцендентность числа 







Соотношения
Известно много формул для вычисления числа 
- Формула Виета для приближения числа π:
-
- Это первое известное явное представление
с бесконечным числом операций. Доказать его можно следующим образом. Применив тождество
рекурсивно и перейдя к пределу, получим
- Остаётся подставить
и воспользоваться формулой косинуса двойного угла:
- Формула Валлиса:
- Ряд Лейбница:
- Ряд с использованием двойного факториала:
- Формула, найденная Сринивасой Рамануджаном:
- Другие ряды:
-
(ряд обратных квадратов)
(следует из предыдущих формул)
- Следующие ряды позволяют вычислять знаки в шестнадцатеричной записи числа пи без вычисления предыдущих знаков:
- Кратные ряды:
- Пределы:
-
здесь
— простые числа
где
равно числу корней в выражении[8].
- Тождество Эйлера:
- Другие связи между константами:
-
- Формула, найденная Сринивасой Рамануджаном:
- Т. н. интеграл Пуассона или интеграл Гаусса:
-
где
— корень Бринга.
- Интегральный синус:
- Выражение через дилогарифм[9]:
- Через несобственный интеграл:
-
;
История
Впервые обозначением этого числа греческой буквой 
Исследование числа 

Геометрический период
То, что отношение длины окружности к диаметру одинаково для любой окружности, и то, что это отношение немногим более 3, было известно ещё древнеегипетским, вавилонским, древнеиндийским и древнегреческим геометрам, древнейшие приближения относятся к третьему тысячелетию до н. э.
В Древнем Вавилоне принимали 


Китайский философ и учёный Чжан Хэн во II веке предложил для числа 



Алгоритм Лю Хуэя для вычисления
Архимед, возможно, первым предложил математический способ вычисления 


Следующее приближение в европейской культуре связано с астрономом Клавдием Птолемеем (ок. 100 — ок. 170), который создал таблицу хорд с шагом в полградуса, что позволило ему получить для 


В Индии Ариабхата и Бхаскара I использовали приближение 3,1416. Варахамихира в VI веке пользуется в «Панча-сиддхантике» приближением 
Около 265 года н. э. математик Лю Хуэй из царства Вэй предоставил простой и точный итеративный алгоритм[en] для вычисления 

Позднее Лю Хуэй придумал быстрый метод вычисления 
В 480-х годах китайский математик Цзу Чунчжи продемонстрировал, что 


Классический период
До II тысячелетия было известно не более 10 цифр 


- Ряд Мадхавы — Лейбница
В 1400-х годах Мадхава из Сангамаграмы нашёл первый из таких рядов:
Этот результат известен как ряд Мадхавы — Лейбница, или ряд Грегори — Лейбница (после того, как он был заново обнаружен Джеймсом Грегори и Готфридом Лейбницем в XVII веке). Однако этот ряд сходится к 
Мадхава смог вычислить 

- Лудольфово число
Первым крупным европейским вкладом со времён Архимеда был вклад голландского математика Людольфа ван Цейлена, затратившего десять лет на вычисление числа 


Лудольфово число — приближённое значение для числа 
- Формула Виета для приближения π
Примерно в это же время в Европе начали развиваться методы анализа и определения бесконечных рядов. Первым таким представлением была формула Виета для приближения числа π:
,
найденная Франсуа Виетом в 1593 году.
- Формула Валлиса
Другим известным результатом стала формула Валлиса:
,
выведенная Джоном Валлисом в 1655 году.
Аналогичные произведения:
- Произведение, доказывающее родственную связь с числом e

Методы, основанные на тождествах
В Новое время для вычисления 
- Формулы Мэчина
Первый эффективный и современный способ нахождения числа 

Разложив арктангенс в ряд Тейлора
,
можно получить быстро сходящийся ряд, пригодный для вычисления числа 
Формулы такого типа, в настоящее время известные как формулы Мэчина[en], использовались для установки нескольких последовательных рекордов и остались наилучшими из известных методов для быстрого вычисления 


- Пи — трансцендентное число
Теоретические достижения в XVIII веке привели к постижению природы числа 



,
которое оказалось равно 

В 1945 году Картрайт упростила элементарное доказательство Шарля Эрмита иррациональности числа 
- Символ «
»
Считается, что книга Уильяма Джонса «Обозрение достижений математики» (Synopsis Palmoriorum Mathesios, 1706 год) первая ввела в использование греческую букву 

Эра компьютерных вычислений
История точности вычисления числа
Эпоха цифровой техники в XX веке привела к увеличению скорости появления вычислительных рекордов. Джон фон Нейман и другие использовали в 1949 году ЭНИАК для вычисления 2037 цифр 
Голландский математик Лёйтзен Брауэр в первой половине XX века привёл в качестве примера бессмысленной задачи поиск в десятичном разложении 

В начале XX века индийский математик Сриниваса Рамануджан обнаружил множество новых формул для 
.
Братьями Чудновскими в 1987 году найдена похожая на неё:
,
которая даёт примерно по 14 цифр на каждый член ряда. Чудновские использовали эту формулу для того, чтобы установить несколько рекордов в вычислении 
Эта формула используется в программах, вычисляющих 
В то время как последовательность обычно повышает точность на фиксированную величину с каждым следующим членом, существуют итеративные алгоритмы, которые на каждом шагу «умножают» количество правильных цифр, однако требуя высоких вычислительных затрат на каждом из таких шагов.
Прорыв в этом отношении был сделан в 1975 году, когда Ричард Брент и Юджин Саламин[en] независимо друг от друга открыли алгоритм Брента — Саламина[en], который, используя лишь арифметику, на каждом шагу удваивает количество известных знаков[21]. Алгоритм состоит из установки начальных значений
и итераций:
,
пока an и bn не станут достаточно близки.
Тогда оценка 
При использовании этой схемы 25 итераций достаточно для получения 45 миллионов десятичных знаков. Похожий алгоритм, увеличивающий на каждом шаге точность в четыре раза, был найден Джонатаном Боруэйном[en] Питером Боруэйном[en][22]. При помощи этих методов Ясумаса Канада и его группа, начиная с 1980 года, установили большинство рекордов вычисления 
Важным развитием недавнего времени стала формула Бэйли — Боруэйна — Плаффа, открытая в 1997 году Саймоном Плаффом[en] и названная по авторам статьи, в которой она впервые была опубликована[23].
Эта формула,
примечательна тем, что она позволяет извлечь любую конкретную шестнадцатеричную или двоичную цифру числа 

В 2006 году Саймон Плафф, используя алгоритм PSLQ, нашёл ряд красивых формул[25]. Пусть q = eπ, тогда
и другие вида
,
где q = eπ, k — нечётное число, и a, b, c — рациональные числа. Если k — вида 4m + 3, то эта формула имеет особенно простой вид:
для рационального p, у которого знаменатель — число, хорошо разложимое на множители, хотя строгое доказательство ещё не предоставлено.
В августе 2009 года учёные из японского университета Цукубы рассчитали последовательность из 2 576 980 377 524 десятичных разрядов[26].
19 октября 2011 года Александр Йи и Сигэру Кондо[ja] рассчитали последовательность с точностью в 10 триллионов цифр после запятой[27][28]. 28 декабря 2013 года они же рассчитали последовательность с точностью до 12,1 триллиона цифр после запятой[29].
14 марта 2019 года, когда отмечался неофициальный праздник числа пи, компания Google представила данное число с 31,4 триллиона знаков после запятой. Вычислить его с такой точностью сумела сотрудница Google в Японии Эмма Харука-Ивао[30].
В августе 2021 года швейцарские учёные Университета прикладных наук Граубюндена смогли вычислить число 

9 июня 2022 года команда Google под руководством Эммы Харука-Ивао рассчитала первые 100 триллионов знаков числа «пи» после запятой, потратив на это почти 158 дней[2][33].
Программа «Супер Пи[en]», фиксирующая время, за которое вычисляется заданное количество знаков (до 32 миллионов) числа Пи, может быть использована для тестирования производительности компьютеров.
Рациональные приближения
- Сравнение точности приближений
| Число | Округлённое значение | Точность (совпадения разрядов) |
 |
3,14159265… | |
 |
3,14285714… | 2 разряда после запятой |
 |
3,14166667… | 3 разряда после запятой |
 |
3,14159292… | 6 разрядов после запятой |
Открытые проблемы
| Цифра | Сколько раз появляется |
|---|---|
| 0 | 20 000 030 841 |
| 1 | 19 999 914 711 |
| 2 | 20 000 013 697 |
| 3 | 20 000 069 393 |
| 4 | 19 999 921 691 |
| 5 | 19 999 917 053 |
| 6 | 19 999 881 515 |
| 7 | 19 999 967 594 |
| 8 | 20 000 291 044 |
| 9 | 19 999 869 180 |
Однако строгое доказательство отсутствует.
- Неизвестно, принадлежит ли
к кольцу периодов.
Метод иглы Бюффона
На разлинованную равноудалёнными прямыми плоскость произвольно бросается игла, длина которой равна расстоянию между соседними прямыми, так что при каждом бросании игла либо не пересекает прямые, либо пересекает ровно одну. Можно доказать, что отношение числа пересечений иглы с какой-нибудь линией к общему числу бросков стремится к 
Мнемонические правила и рекорды запоминания
Стихотворения для запоминания 8—11 знаков числа 
|
|
Запоминанию может помогать соблюдение стихотворного размера:
Три, четырнадцать, пятнадцать, девять два, шесть пять, три пять
Восемь девять, семь и девять, три два, три восемь, сорок шесть
Два шесть четыре, три три восемь, три два семь девять, пять ноль два
Восемь восемь и четыре, девятнадцать, семь, один
Существуют стихи, в которых первые цифры числа 
|
|
Подобные стихи существовали и в дореформенной орфографии, поэтому во всех словах, заканчивающихся на согласную, в конце стоит «ъ».
Например, следующее стихотворение, сочинённое преподавателем Нижегородской гимназии Шенроком[43]:
Кто и шутя и скоро пожелаетъ
Пи узнать число, ужъ знаетъ.
Мировой рекорд по запоминанию знаков числа 

В России рекорд по запоминанию был установлен в 2019 году Денисом Бабушкиным (13 202 знака)[49].
В культуре
- В штате Индиана (США) в 1897 году была предпринята попытка принять Законопроект о числе пи, устанавливающий его значение равным 3,2[50]. Данный билль не стал законом благодаря своевременному вмешательству профессора Университета Пердью, присутствовавшего в законодательном собрании штата во время рассмотрения данного закона;
- Существует художественный фильм, названный в честь числа Пи;
- Неофициальный праздник «День числа пи» ежегодно отмечается 14 марта, которое в американском формате дат (месяц/день) записывается как 3,14, что соответствует приближённому значению числа
. Считается[51], что праздник придумал в 1987 году физик из Сан-Франциско Ларри Шоу, обративший внимание на то, что 14 марта ровно в 01:59 дата и время совпадают с первыми разрядами числа Пи = 3,14159;
- Американская прогрессив-метал-группа After The Burial записала песню Pi — The Mercury God of Infinity, в которой партия ритм-гитары и бас-бочки основана на высших разрядах десятичной дроби числа
.
- Франсуа Араго в «Общепонятной астрономии» писал[52]:
Посмотрим, с какою точностью возможно, пользуясь цифрами Пи (числа Пи), вычислить длину окружности, радиус которой равен среднему расстоянию Земли от Солнца (150 000 000 км). Если для Пи взять 18 цифр, то ошибка на одну единицу в последней цифре повлечет за собой в длине вычисляемой окружности погрешность в 0,0003 миллиметра; это гораздо меньше толщины волоса.
Мы взяли 18 цифр Пи. Легко представить себе, какую невообразимо малую погрешность сделали бы, при огромности вычисляемой окружности, если бы воспользовались для Пи всеми известными его цифрами. Из сказанного ясно, как заблуждаются те, которые думают, будто науки изменили бы свой вид, и их применения много выиграли бы от нахождения точного Пи, если бы оно существовало.
Итак, даже для астрономии‚ — науки, прибегающей к наиболее точным вычислениям‚ — не требуется вполне точного решения…
См. также
- Точка Фейнмана
- Число τ
- e (число)
Примечания
- Комментарии
- Источники
- ↑ PI. Дата обращения: 13 сентября 2010. Архивировано 3 сентября 2010 года.
- ↑ 1 2 Павел Котов. Сотрудница Google Cloud рассчитала число Пи до 100-триллионного знака после запятой — это новый рекорд. 3DNews Daily Digital Digest (9 июня 2022). Дата обращения: 10 июня 2022. Архивировано 10 июня 2022 года.
- ↑ Lambert, Johann Heinrich. Mémoire sur quelques propriétés remarquables des quantités transcendentes circulaires et logarithmiques, С. 265–322.
- ↑ Доказательство Клейна приложено к работе «Вопросы элементарной и высшей математики», ч. 1, вышедшей в Гёттингене в 1908 году.
- ↑ Weisstein, Eric W. Постоянная Гельфонда (англ.) на сайте Wolfram MathWorld.
- ↑ 1 2 Weisstein, Eric W. Иррациональное число (англ.) на сайте Wolfram MathWorld.
- ↑ Модулярные функции и вопросы трансцендентности
- ↑ Ромер П. Новое выражение для π // В.О.Ф.Э.М.. — 1890. — № 97. — С. 2—4.
- ↑ Weisstein, Eric W. Pi Squared (англ.) на сайте Wolfram MathWorld.
- ↑ Гнездовский Ю. Ю.. Введение // Справочник по тригонометрии. — Экоперспектива, 2006. — С. 3. — ISBN 985-469-141-1.
- ↑ 1 2 Вездесущее число «пи», 2007, с. 10—11.
- ↑ Кымпан, 1971.
- ↑ E. M. Bruins. Quelques textes mathématiques de la Mission de Suse Архивная копия от 3 марта 2016 на Wayback Machine, 1950.
- ↑ Стройк Д. Я. Краткий очерк истории математики = Abriss der Geschichte der Mathematik / Пер. с нем.; Гл. ред. физ.-мат. литературы. — 4-е изд., испр. — М.: Наука, 1984. — С. 47—48. — 285 с. — ISBN 5-02-014329-4.
- ↑ Вездесущее число «пи», 2007, с. 29.
- ↑ Кымпан, 1971, с. 81.
- ↑ Pi: A Source Book. Дата обращения: 19 ноября 2021. Архивировано 19 ноября 2021 года.
- ↑ Исаак Ньютон. Математические работы (в переводе и переработке Мордухай-Болтовского) / Мордухай-Болтовской (также перевод и комментарии). — Москва, Ленинград: Главное изд-во технико-теоретической литературы, 1937.
- ↑ Arndt, Jörg; Haenel, Christoph. Pi Unleashed (англ.). — Springer-Verlag, 2006. — P. 194–196. — 270 p. — ISBN 978-3-540-66572-4.
- ↑ Хоакин Наварро, 2014, с. 11..
- ↑ Brent, Richard (1975), Traub, J F, ed., Multiple-precision zero-finding methods and the complexity of elementary function evaluation, Analytic Computational Complexity (New York: Academic Press): 151–176, <http://wwwmaths.anu.edu.au/~brent/pub/pub028.html> Архивная копия от 23 июля 2008 на Wayback Machine (англ.)
- ↑ Jonathan M Borwein. Pi: A Source Book. — Springer, 2004. — ISBN 0387205713. (англ.)
- ↑ 1 2 David H. Bailey, Peter B. Borwein, Simon Plouffe. On the Rapid Computation of Various Polylogarithmic Constants // Mathematics of Computation. — 1997. — Т. 66, вып. 218. — С. 903—913. (англ.)
- ↑ Fabrice Bellard. A new formula to compute the nth binary digit of pi (англ.). Дата обращения: 11 января 2010. Архивировано 21 августа 2011 года.
- ↑ Simon Plouffe. Indentities inspired by Ramanujan’s Notebooks (part 2) (англ.) (недоступная ссылка — история). Дата обращения: 11 января 2010. Архивировано 21 августа 2011 года.
- ↑ Установлен новый рекорд точности вычисления числа π. Дата обращения: 20 августа 2009. Архивировано из оригинала 22 августа 2009 года.
- ↑ Определено 10 триллионов цифр десятичного разложения для π. Дата обращения: 4 октября 2019. Архивировано из оригинала 25 июля 2018 года.
- ↑ Round 2… 10 Trillion Digits of Pi. Дата обращения: 22 октября 2011. Архивировано 1 октября 2018 года.
- ↑ Pi – 12.1 Trillion Digits. www.numberworld.org. Дата обращения: 29 октября 2019. Архивировано 1 октября 2018 года.
- ↑ Значение числа «пи» вычислили до 31,4 трлн знаков после запятой. www.mk.ru. Дата обращения: 14 марта 2019. Архивировано 14 марта 2019 года.
- ↑ Swiss researchers declare new record for exact pi figure (англ.). phys.org (17 августа 2021). Дата обращения: 17 августа 2021. Архивировано 17 августа 2021 года.
- ↑ World record attempt by UAS Grisons (англ.). fhgr.ch (17 августа 2021). Дата обращения: 17 августа 2021. Архивировано 17 августа 2021 года.
- ↑ Роман Кильдюшкин. Google установила мировой рекорд по вычислению числа Пи Google рассчитала число Пи до 100 триллионов знаков после запятой. Газета.ru (9 июня 2022). Дата обращения: 10 июня 2022. Архивировано 10 июня 2022 года.
- ↑ Weisstein, Eric W. Мера иррациональности (англ.) на сайте Wolfram MathWorld.
- ↑ Doron Zeilberger, Wadim Zudilin. The Irrationality Measure of Pi is at most 7.103205334137. arxiv.org (2019). Архивировано 17 октября 2020 года.
- ↑ Weisstein, Eric W. Pi (англ.) на сайте Wolfram MathWorld.
- ↑ Some unsolved problems in number theory. Дата обращения: 27 сентября 2010. Архивировано 19 июля 2010 года.
- ↑ Weisstein, Eric W. Трансцендентное число (англ.) на сайте Wolfram MathWorld.
- ↑ An introduction to irrationality and transcendence methods. Дата обращения: 27 сентября 2010. Архивировано 17 мая 2013 года.
- ↑ Вездесущее число «пи», 2007, с. 67—69.
- ↑ Обман или заблуждение? Архивная копия от 30 января 2012 на Wayback Machine // Квант. — 1983. — № 5.
- ↑ Гальперин Г. А. Биллиардная динамическая система для числа пи Архивная копия от 13 июня 2014 на Wayback Machine.
- ↑ «Элементарная геометрия» Киселёва стр. 225
- ↑ 21-Year-Old Memorises 70,000 Pi Digits, Sets Guinness Record. Дата обращения: 3 апреля 2016. Архивировано 18 апреля 2016 года.
- ↑ Chinese student breaks Guiness record by reciting 67,890 digits of pi. Дата обращения: 26 сентября 2010. Архивировано 7 мая 2011 года.
- ↑ Interview with Mr. Chao Lu. Дата обращения: 26 сентября 2010. Архивировано 24 сентября 2010 года.
- ↑ How can anyone remember 100,000 numbers? — The Japan Times, 17.12.2006.
- ↑ Pi World Ranking List. Дата обращения: 26 сентября 2010. Архивировано 30 сентября 2010 года.
- ↑ Юлия Сталина. «Помогли мысли о Джонни Деппе»: школьник из Екатеринбурга запомнил 13202 знака числа Пи. KP.RU (28 октября 2019). Дата обращения: 10 июня 2022. Архивировано 15 мая 2022 года.
- ↑ The Indiana Pi Bill, 1897 Архивная копия от 17 июня 2016 на Wayback Machine (англ.)
- ↑ Статья в Los Angeles Times «Желаете кусочек
»? (название обыгрывает сходство в написании числа
и слова pie (англ. пирог)) Архивная копия от 19 февраля 2009 на Wayback Machine (недоступная ссылка с 22-05-2013 [3650 дней] — история, копия) (англ.).
- ↑ Цитируется со страниц 16-17 книги: Перельман Я. И. Квадратура круга. — Л.: Дом занимательной науки, 1941.
Литература
- Жуков А. В. О числе π. — М.: МЦМНО, 2002. — 32 с. — ISBN 5-94057-030-5.
- Жуков А. В. Вездесущее число «пи». — 2-е изд. — М.: Издательство ЛКИ, 2007. — 216 с. — ISBN 978-5-382-00174-6.
- Кымпан, Флорика. История числа пи. — М.: Наука, 1971. — 217 с.
- Наварро, Хоакин. Секреты числа
Почему неразрешима задача о квадратуре круга. — М.: Де Агостини, 2014. — 143 с. — (Мир математики: в 45 томах, том 7). — ISBN 978-5-9774-0629-1.
- Перельман Я. И. Квадратура круга. — Л.: Дом занимательной науки, 1941. Переиздание: ЁЁ Медиа, ISBN 978-5-458-62773-3.
- Шумихин С., Шумихина А. Число Пи. История длиною в 4000 лет. — М.: Эксмо, 2011. — 192 с. — (Тайны мироздания). — ISBN 978-5-699-51331-4. — ISBN 5-4574041-9-6. — ISBN 978-5-4574041-9-9.
- David H. Bailey, Jonathan M. Borwein. Pi: The Next Generation A Sourcebook on the Recent History of Pi and Its Computation. — Springer, 2016. — 507 с. — ISBN 978-3-319-32375-6.
- Arndt, Jörg; Haenel, Christoph. Pi Unleashed (англ.). — Springer-Verlag, 2006. — P. 194–196. — 270 p. — ISBN 978-3-540-66572-4.
Ссылки
- pi.delivery Архивная копия от 10 ноября 2020 на Wayback Machine 50 трлн знаков числа пи (мировой рекорд).
- Weisstein, Eric W. Pi Formulas (англ.) на сайте Wolfram MathWorld.
- Различные представления числа Пи Архивная копия от 12 августа 2011 на Wayback Machine на WolframAlpha (англ.)
- https://functions.wolfram.com/Constants/Pi/ Архивная копия от 12 января 2021 на Wayback Machine
- последовательность A000796 в OEIS
- 22,4 трлн знаков числа пи Архивная копия от 10 ноября 2020 на Wayback Machine (англ.)
Download Article
Download Article
Pi (π) is one of the most important and fascinating numbers in mathematics. Roughly 3.14, it is a constant that is used to calculate the circumference of a circle from that circle’s radius or diameter.[1]
It is also an irrational number, which means that it can be calculated to an infinite number of decimal places without ever slipping into a repeating pattern.[2]
This makes it difficult, but not impossible, to calculate precisely.
-
1
Make sure you are using a perfect circle. This method won’t work with ellipses, ovals, or anything but a real circle. A circle is defined as all the points on a plane that are an equal distance from a single center point. The lids of jars are good household objects to use for this exercise. You should be able to calculate pi roughly because in order to get exact results of pi, you will need to have a very thin lead (or whatever you are using). Even the sharpest pencil graphite could be huge to have exact results.[3]
-
2
Measure the circumference of a circle as accurately as you can. The circumference is the length that goes around the entire edge of the circle. Since the circumference is round, it can be difficult to measure (that’s why pi is so important).[4]
- Lay a string over the circle as closely as you can. Mark the string off where it circles back around, and then measure the string length with a ruler.
Advertisement
-
3
Measure the diameter of the circle. The diameter runs from one side of the circle to the other through the circle’s center point.[5]
-
4
Use the formula. The circumference of a circle is found with the formula C=πd=2πr. Thus, pi equals a circle’s circumference divided by its diameter. Plug your numbers into a calculator: the result should be roughly 3.14.[6]
-
5
Repeat this process with several different circles, and then average the results. This will give you more accurate results. Your measurements might not be perfect on any given circle, but over time they should average out to a pretty accurate calculation of pi.
Advertisement
-
1
Use the Gregory-Leibniz series. Mathematicians have found several different mathematical series that, if carried out infinitely, will accurately calculate pi to a great number of decimal places. Some of these are so complex they require supercomputers to process them. One of the simplest, however, is the Gregory-Leibniz series.[7]
Though not very efficient, it will get closer and closer to pi with every iteration, accurately producing pi to five decimal places with 500,000 iterations. Here is the formula to apply.- π=(4/1)-(4/3)+(4/5)-(4/7)+(4/9)-(4/11)+(4/13)-(4/15) ⋯
- Take 4 and subtract 4 divided by 3. Then add 4 divided by 5. Then subtract 4 divided by 7. Continue alternating between adding and subtracting fractions with a numerator of 4 and a denominator of each subsequent odd number. The more times you do this, the closer you will get to pi.
-
2
Try the Nilakantha series. This is another infinite series to calculate pi that is fairly easy to understand. While somewhat more complicated, it converges on pi much quicker than the Leibniz formula.[8]
- π=3+4/(2·3·4)-4/(4·5·6)+4/(6·7·8)-4/(8·9·10)+4/(10·11·12)-4/(12·13·14) ⋯
- For this formula, take three and start alternating between adding and subtracting fractions with numerators of 4 and denominators that are the product of three consecutive integers which increase with every new iteration. Each subsequent fraction begins its set of integers with the highest one used in the previous fraction. Carry this out even a few times and the results get fairly close to pi.
Advertisement
-
1
Try this experiment to calculate pi by throwing hotdogs. Pi, it turns out, also has a place in an interesting thought experiment called Buffon’s Needle Problem,[9]
which seeks to determine the likelihood that randomly tossed uniform elongated objects will land either between or crossing a series of parallel lines on the floor. It turns out that if the distance between the lines is the same as the length of the tossed objects, the number of times the objects land across the lines out of a large number of throws can be used to calculate pi. Check out the above wikiHow article link for a fun breakdown of this experiment using thrown food.- Scientists and mathematicians have not figured out a way to calculate pi exactly, since they have not been able to find a material so thin that it will work to find exact calculations.[10]
- Scientists and mathematicians have not figured out a way to calculate pi exactly, since they have not been able to find a material so thin that it will work to find exact calculations.[10]
-
1
Pick a large number. The bigger the number, the more accurate your calculation will be.
-
2
Plug your number, which we’ll call x, into this formula to calculate pi: x * sin(180 / x). For this to work, make sure your calculator is set to Degrees. The reason this is called a Limit is because the result of it is ‘limited’ to pi. As you increase your number x, the result will get closer and closer to the value of pi.
Advertisement
-
1
Pick any number between -1 and 1. This is because the Arcsin function is undefined for arguments greater than 1 or less than -1.[11]
-
2
Plug your number into the following formula, and the result will be roughly equal to pi.[12]
- π={arcsin[√(1 – x²)]+ abs[arcsin x]}·2.
- Arcsin refers to the inverse sine in radians
- Sqrt is short for square root
- Abs is short for absolute value
- x^2 refers to an exponent, in this case, x squared.
- π={arcsin[√(1 – x²)]+ abs[arcsin x]}·2.
Advertisement
Add New Question
-
Question
Is twenty two over seven equal to pi?
It is not precisely equal to pi. While it does look like pi at first (3.14285…), pi is 3.14159…
It cannot be equal to pi because 3.14285 ends up repeating. Pi is an irrational number, meaning it goes on forever and does not repeat. Remember that irrational numbers are defined as “not being able to be written as a ratio between two numbers.” 22/7 is a ratio of two numbers, so it cannot be exactly equal to pi. -
Question
How can I figure out pi as a fraction?
You can’t. Pi cannot be a fraction because it is irrational. This means that it cannot be expressed as a ratio of two rational numbers. Pi is sometimes expressed as the fraction 22/7, but that is just an approximation.
-
Question
What does the word irrational mean?
An irrational number is a number that cannot be expressed as a ratio of whole numbers (i.e., as a fraction). The root of the word ‘irrational’ is ‘ratio’, and the prefix ‘ir’ means ‘not’. The word can have different meanings outside of math.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
Calculating pi can be fun and challenging, but doing so too deeply has diminishing returns. Astrophysicists say they only need to use pi to 39 decimal places in order to do cosmological calculations that are accurate to the size of an atom.
Thanks for submitting a tip for review!
Advertisement
References
About This Article
Article SummaryX
Pi is roughly 3.14, but it’s actually an infinite number that never slips into a repeating pattern. If you want to calculate pi, first measure the circumference of a circle by wrapping a piece of string around the edge of it and then measuring the length of the string. Then, measure the diameter of the circle, which is the distance between one side and the other that runs through the center. Once you’ve got the circumference and diameter, plug them into the formula π=c/d, where “π” is pi, “c” is circumference, and “d” is diameter. Just divide the circumference by the diameter to calculate pi! To learn how to calculate pi using a limit or sine function, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,337,637 times.










































![pi =8sum limits _{k=1}^{infty }sum limits _{m=1}^{infty }{frac {1}{(4m-2)^{2k}}}=4sum limits _{k=1}^{infty }sum limits _{m=1}^{infty }{frac {m^{2}-k^{2}}{(m^{2}+k^{2})^{2}}}={sqrt[{4,,}]{360sum limits _{k=1}^{infty }sum limits _{m=1}^{k}{frac {1}{m(k+1)^{3}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/637f3bd1f1f43c56cd7c73ea811a470a11734006)
![pi =lim limits _{mrightarrow infty }{frac {(m!)^{4},{2}^{4m}}{left[(2m)!right]^{2},m}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7a427496d43d36660b1a338b6e4cc6e8a6f0c2e)




















































