Математика
5 класс
Урок № 67
Нахождение части целого и целого по его части
Перечень рассматриваемых вопросов
– нахождение целого по его части;
– нахождение части целого;
– моделирование условий задачи с помощью рисунка.
Тезаурус
Произведение двух дробей – это дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей этих дробей.
Частное дробей – это дробь, которая при умножении на делитель даёт делимое.
Обязательная литература
- Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5 класс. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Мы уже рассмотрели, как выполняют умножение и деление дробей. Сегодня с помощью этих действий мы будем решать задачи.
Рассмотрим две задачи.

Теперь определим, какие условия в задачах одинаковы, а какие различаются.
Общее:
- в задачах одинаковые числовые данные;
- за целое принята длина всей ленты.
Разное:
- в первой задаче целое известно (длина ленты – 18 м);
- во второй задаче целое нужно найти.
Значит, в первой задаче нужно найти часть отрезанной ленты, то есть часть от целого; а во второй задаче нужно найти всю длину ленты, то есть целое по его части.
Подобные задачи решаются в соответствие с известными правилами.
- Чтобы найти часть от целого, надо целое (соответствующее ему число) умножить на дробь, соответствующую этой части.
- Чтобы найти целое по его части, надо часть (соответствующее этой части число) разделить на соответствующую дробь.
Если вы затрудняетесь определить тип задачи, обратите внимание на союз «что» и указательное местоимение «это». Они встречаются в задачах на нахождение целого по его части.

Решение.
Смоделируем условие задачи с помощью рисунка.

После этого мы увидим, что длина целой ленты известна, а длину части следует вычислить. Значит, мы будем находить часть от целого. Используем для этого соответствующее правило. Чтобы найти часть числа, нужно число умножить на дробь. Получим:

Решение.
Опять смоделируем условие задачи с помощью рисунка.

Таким образом, мы увидим, что длина целой ленты неизвестна, а длина части указана в условии. Значит, нам надо вычислить целое по его части. Для этого мы используем подходящее правило. Чтобы найти целое, нужно число, соответствующее части, разделить на дробь.
Получится:

Итак, сегодня на уроке мы научились:
-
- моделировать условие задачи с помощью рисунка;
- устанавливать соответствие между математическим выражением и его текстовым описанием;
- решать задачи на нахождение части целого и целого по его части.
Рассмотрим старинную индийскую задачу XII века.
Из множества лотосов были подарены: богу Шиве – треть всех цветов, богу Вишну – пятая часть, а Солнцу – шестая, четвёртую долю получила богиня Бхавани, а остальные шесть частей – уважаемый учитель. Сколько было всего лотосов?
Сегодня мы с вами научимся решать такие задачи с применением действий умножения и деления, изученных ранее.
Решение.
Смоделируем условие задачи с помощью рисунка.

Общее количество лотосов обозначим за единицу. Также укажем части (лотосы), которые распределялись между всеми, кто указан в задании.
Известно, что часть, доставшаяся учителю, равна шести лотосам. Значит, если мы будем знать, какая это доля от общего количества лотосов, то придём ко второму типу задачи – вычислению целого по его части.
Итак, найдём, какая часть от общего количества цветков досталась учителю.
Для этого вычислим сначала, сколько составляют все остальные части. Сложим все дроби, соответствующие частям, приведя их к общему знаменателю 60.


Ответ: 120 цветков.
Тренировочные задания
№ 1. Какие части изображены на рисунках?




Правильные ответы:

№ 2. Подставьте в текст нужные слова:
При решении задач на ___ сначала нужно определить ___ задачи, а потом применить соответствующее правило.
Типы задач:
- нахождение ___ от целого;
- нахождение целого по его ___.
Варианты слов для подстановки в текст: части; тип; целого.
Правильный ответ: при решении задач на части сначала нужно определить тип задачи, а потом применить соответствующее правило.
Типы задач:
- нахождение части от целого;
- нахождение целого по его части.
Полоску разделили на (10) равных частей и (7) частей закрасили. Длина закрашенной части — (7) см. Как найти длину всей полоски?

Имеем, что длина части —
710
полоски — составляет (7) см. Найдём, сколько сантиметров составляет длина
110
части.
Очевидно, что она будет меньше в (7) раз:
Теперь найдём длину целого — всей полоски (десяти десятых):
Длину всей полоски можно найти более простым способом:
Чтобы найти число по его части, выраженной дробью, надо разделить эту часть на числитель и умножить на знаменатель дроби.
Пример:
если
47
отрезка составляют (16) см, то длина всего отрезка:
Если
25
арбуза весит (4) кг, то весь арбуз весит:
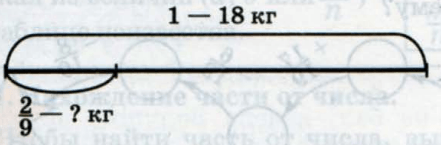
Составь задачу по схеме и придумай к ней две обратные задачи:
Как найти:
а) часть числа;
б) число по его части;
в) часть, которую одно число составляет от другого?

reshalka.com
ГДЗ учебник по математике 4 класс Петерсон. 6 урок. Правильные и неправильные части величин. Номер №6
Решение
В мешке было 18 кг картофеля. За день мама израсходовала
2
9
часть картофеля. Сколько кг картофеля израсходовала мама?
Решение:
18 : 9 * 2 = 2 * 2 = 4 (кг) − израсходовала мама.
Ответ: 4 кг.
Обратная задача 1.
За день мама израсходовала
2
9
часть картофеля, что составляет 4 кг. Сколько всего было картофеля?
Решение:
4 : 2 * 9 = 2 * 9 = 18 (кг) − картофеля было всего.
Ответ: 18 кг.
Обратная задача 2.
В мешке было 18 кг картофеля. За день мама израсходовала 4 кг. Какую часть составляет масса израсходованного картофеля?
Решение:
4
:
18
=
4
18
=
2
9
(картофеля) − израсходовала мама.
Ответ:
2
9
всего картофеля.
а) Чтобы найти часть от числа, выраженную дробью, надо это число разделить на знаменатель и умножить на числитель.
б) Чтобы найти число по его части, выраженной дробью, надо эту часть разделить на числитель и умножить на знаменатель.
в) Чтобы выразить дробью часть, которую одно число составляет от другого, надо первое число разделить на второе.
Содержание:
- § 1 Нахождение числа по его доле
- § 2 Нахождение числа по его части
- § 3 Решение задачи по теме урока
- § 4 Краткие итоги урока
§ 1 Нахождение числа по его доле
Рассмотрим такую задачу. Конфеты разложили в 6 пакетов. Каждый пакет весит 250 грамм. Сколько грамм весят все конфеты?
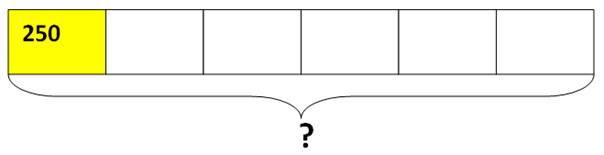
Из условия задачи известно, что целое разделили на 6 равных долей. Одна доля 1/6 весит 250 грамм. Чтобы найти вес всех конфет, необходимо вес 250 одной доли умножить на количество долей 6:
250 · 6 = 1500 грамм весят все конфеты.
Можем сделать вывод:
Чтобы найти неизвестное число А, можно его долю B =1/n умножить на n:A = B · n.
§ 2 Нахождение числа по его части
Рассмотрим еще одну задачу. Конфеты разложили в 7 пакетов. 3/7 всех конфет весят 390 грамм. Сколько грамм весят все конфеты?
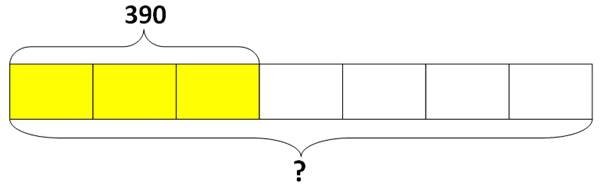
Из условия задачи известно, что целое разделили на 7 равных долей. 3 доли весят 390 грамм. 3/7 = 390. Для того чтобы найти вес всех конфет, необходимо в первую очередь найти вес одной доли 390 : 3, а затем умножить вес одной доли на количество всех долей 390 : 3 · 7. Или 390 разделить на 3 числитель дроби 3/7 и умножить на ее знаменатель 7,
390 : 3 · 7 = 910 грамм весят все конфеты.
Можно сделать вывод:
Чтобы найти число А по его части B =m/n, можно эту часть В разделить на числитель m и умножить на знаменатель n:A = B : m · n.
§ 3 Решение задачи по теме урока
Опираясь на полученные знания, решим задачу.

Задача:
Масса яблок составляет 25% от массы яблочного пирога и равна 225 грамм. Чему равна масса всего пирога?
Решение:
25% = 25/100 = 225 грамм,
100% (весь пирог) = неизвестное число = ? грамм.
Значит, по правилу A = B : m · n масса всего пирога равна
225 : 25 · 100 = 900 грамм.
§ 4 Краткие итоги урока
Подведем итоги нашего урока:
– Для того чтобы найти неизвестное число А, можно его долю B =1/n умножить на n:A = B · n.
– Для того чтобы найти число А по его части B = m/n, можно эту часть В разделить на числитель m и умножить на знаменатель n:A = B : m · n.
Список использованной литературы:
- Петерсон Л.Г. Математика. 4 класс. Часть 1. / Л.Г. Петерсон. – М.: Ювента, 2014. – 96 с.: ил.
- Математика. 4 класс. Методические рекомендации к учебнику математики «Учусь учиться» для 4 класса. / Л.Г. Петерсон . – М.: Ювента, 2014. – 280 с.: ил.
- Зак С.М. Все задания к учебнику математики для 4 класса Л.Г. Петерсон и комплекту самостоятельных и контрольных работ. ФГОС. – М.: ЮНВЕС, 2014.
- CD-ROM. Математика. 4 класс. Сценарии уроков к учебнику к 1 части Петерсон Л.Г. – М.: Ювент, 2013.
