Как найти число по его дополнительному коду

Лабораторная
работа 2

СЛОЖЕНИЕ И
ВЫЧИТАНИЕ ЦЕЛЫХ ЧИСЕЛ

1. Цель работы

Исследование
особенностей операций сложения и
вычитания целых чисел (знаковых и
беззнаковых) в ЭВМ

1. Дополнительный
   код

2.2.1
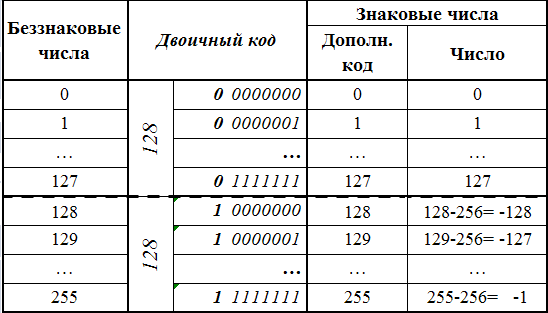
В ПК делается различие между целыми
числами без знака и знаковыми [7]. В
таблице 2.1 представлена схема формирования
чисел типа байт.

Таблица
2.1 – Схема формирования байтовых чисел

Целые числа со
знаком записываются в дополнительном
коде по правилу:

X
, если 0 ≤ X ≤ 2 ^k-1
– 1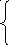

2^k
– | X | , если -2 ^k-1≤
X ≤ -1, ( 1 )

Доп
(x) =

где
k – общее количество разрядов,

отведенных
под число X

Если
k = 8 (байт), то правило конкретизируется:

X
, если 0 ≤ X ≤ 127

(
2 )

Доп
(x) =

256
– | X | , если -128 ≤ X ≤ -1

Левый бит
дополнительного кода играет роль
знакового: для
неотрицательных чисел он равен 0, для
отрицательных 1.

ПРИМЕРЫ

1. Дополнительным
   кодом числа –6
   является:

байт
FAh (= 256 – 6 = 250 ₍₁₀₎
= FA ₍₁₆₎)

слово
FFFA ₍₁₆₎

двойное
слово FFFFFFFA ₍₁₆₎.

1. Дополнительным
   кодом числа +98
   является:

байт
98 ₍₁₀₎
= 62 ₍₁₆₎

слово
0062 ₍₁₆₎

2.2.2
Для перевода числа из дополнительного
кода в обычное
представление необходимо сравнить
дополнительный код доп (X)
с величиной наибольшего неотрицательного
числа рассматриваемого размера (типа),
равного ( 2^k-1 – 1):

если
доп (X) 
2 ^k-1
– 1, то X = доп (X);

(
3 )

если
доп (X) > 2
^k-1 – 1, то
|X| = 2 ^k
– доп (X), а X отрицательно.

В
приведенных формулах |X| –
модуль (абсолютная величина) числа, а
k – общее
количество разрядов в ячейках, отведенных
под число X.

Если
k = 8 (байт), то чтобы получить число по
его дополнительному коду нужно сравнить
дополнительный код доп (X) с числом 127:

если
доп (X) 
127, то X = доп (X);

(
4 )

если
доп (X) > 127 то |X| =256 – доп (X), а X –
отрицательно.

ПРИМЕР

Дополнительный
код числа размером байт равен 3.
Определить величину числа.

Так
как 3 
127, то X = доп (Х) = 3.

ПРИМЕР

Дополнительный
код числа размером байт равен 253.
Определить величину числа.

Так
как 253 > 127, значит число отрицательное,
а его модуль определяют по формуле: |X|
= 256 – доп (Х) = 256 – 253 = 3

Таким
образом, X = – 3.

1. Беззнаковые
   целые числа

1. Сложение

Беззнаковые числа
складываются по правилам сложения
двоичных чисел. Однако возникает
проблема: что делать, если сумма получится
очень большой – такой, что она не умещается
в отведенную ячейку? Например, при
сложении байтовых чисел 250 и 10 получится
число 260 (=100000100
– 9 разрядов), которое не “влезает”
в ячейку размером в байт.

В
этом случае ошибка не фиксируется, левая
единица (единица переноса) отбрасывается,
и в качестве ответа выдается искаженная
сумма (в рассматриваемом примере ответом
будет байт 0000 0100, т. е. число 4). При этом
во флаг переноса CF записывается 1. Это
сигнал о том, что получилась неправильная
сумма (если переноса не было, то в CF
записывается 0).

Отбрасывание
1 в разряде номер 8 (девятая единица по
счету справа) равноценно вычитанию
числа 1 0000 0000 (= 2⁸
= 256).

ПРИМЕР

Сложить
беззнаковые числа 18 и 200 ( тип – байт
).

Сумма
18 + 200 = 218 <=
255, следовательно, сумма «помещается»
в байт, результат верен в математическом
смысле и флаг CF = 0 .

ПРИМЕР

Сложить
беззнаковые числа 58 и 200 (тип – байт ).

Сумма
чисел (58 +
200 = 258) больше 255 , то есть, байта «не
хватает» для ее размещения, следовательно,
бит номер 8 «теряется», что равноценно
вычитанию из суммы числа 256. Сумма будет
фиксирована как

(58
+ 200) – 256 = 2.

Так
как с точки зрения математики получен
неправильный результат, флаг CF = 1 (был
перенос).

2.3.2
Вычитание

Объявляя,
что та или иная операция выполняется с
данными определенного типа, понимают,
что и операнды, и результат являются
данными этого типа.

При
вычитании беззнаковых чисел возможно
появление следующей проблемы: если
уменьшаемое меньше вычитаемого,
получается отрицательная разность,
естественно, не принадлежащая области
беззнаковых чисел. Правило вычитания
учитывает эту возможность и корректирует
ее следующим образом.

Если
выполняется вычитание Х – У и при этом:

1. Х
   ≥ У, выполняется обычное вычитание;

2. Х
   < У, тогда числу Х дается “заем”
   единицы, то есть к числу Х прибавляется
   величина 2^k
   , (при K = 8 – байт – прибавляется число
   1 0000 0000 ₍₂₎
   = 2⁸
   = 256) и только после этого производится
   вычитание. Полученное таким образом
   число и объявляется разностью. Факт
   произведенного “заема” фиксируется
   тем, что во флаг переноса CF записывается
   1.

ПРИМЕР

Определить
разность 1-2 (размер – байт, числа
беззнаковые).

Так
как 1 < 2 , то выполняется «заем» и только
после этого производится вычитание:
( 1 + 256 ) – 2 =
255.

Число
255 объявляется результатом вычитания
1-2. При этом ошибка не фиксируется, но
во флаг переноса CF заносится 1, что
сигнализирует о неправильном результате.

2.4 Знаковые целые
числа

2.4.1 Сложение и
вычитание знаковых чисел

Сложение и вычитание
знаковых чисел, представленных их
дополнительными кодами – беззнаковыми
числами, производится по соответствующим
алгоритмам для беззнаковых чисел. В
таком виде их складывают или вычитают,
а полученный результат затем рассматривают
как дополнительный код знакового ответа.

Если
результат операции со знаковыми числами
не верен в математическом смысле, то
флаг переполнения OF получает значение
1, и значение 0 – если результат правильный.

ПРИМЕР

Сложить
байтовые числа +3
и (–1).

Получаем
дополнительные коды чисел, это
соответственно 3 и
( 256 – 1) = 255.

Складываем
коды по правилам для беззнаковых чисел.

Сумма
кодов 3 + 255
больше 255, то есть результат не вмещается
в байт. Следовательно, бит номер 8
«теряется», а это приводит к уменьшению
суммы на 256. За результат сложения кодов
принимается число
( 3 +
255 ) – 256 = 2. Факт того, что был перенос
фиксируется флагом CF = 1 (коды – числа
беззнаковые!!! ).

Полученная
величина 2 рассматривается как
дополнительный код результата. В
соответствии с п.2.2.2 искомая сумма равна
+2.

Результат
правильный, следовательно, флаг OF
равен 0.

ПРИМЕР

Сложить
байтовые числа ( -3 ) и +1.

Дополнительные
коды этих чисел: ( 256 – 3 ) =253 и 1.

Складываем
дополнительные коды как беззнаковые
числа:
253 +1
= 254. Полученная сумма меньше 255 (ей
«хватает» байта), значит флаг CF
равен 0.

Рассматривая
полученную величину как дополнительный
код ответа, определяем соответствующее
ему число: так как 254 > 127, то, в соответствии
с п. 2.2.2, искомое число отрицательно, а
его абсолютная величина рассчитывается
по формуле: 256 – 254 = 2, таким образом, число
равно -2.

Результат
правильный, следовательно, флаг OF
равен 0.

2.4.2 Возможные
проблемы

Напомним,
что при размере ячеек в 8 бит в дополнительном
коде представляются только числа от
-128 до +127.

Рассмотрим,
к примеру, сложение
знаковых байтовых чисел +127
и +2. Их
дополнительные коды – беззнаковые числа
127 и 2, сумма кодов равна 129 – это код
результата. Определяем знаковое число
по его дополнительному коду. Так как
129 > 127, то модуль числа равен 256 – 129 =
127, а само число -127. Таким образом, при
сложении двух положительных чисел
получено отрицательное число!

Это
произошло потому, что при представлении
чисел в дополнительном коде левый разряд
является знаковым, а на размещение
самого числа (на так называемую мантиссу
числа) отводятся,
в случае байта, оставшиеся 7 правых
разрядов. Самое большое число, которое
можно разместить на семи позициях, это
1111111₍₂₎,
то есть, 2⁷
– 1 = 127 ₍₁₀₎.
В примере получился ответ 129, в двоичном
представлении
это 1000 000l _(2).
Восьмиразрядной
мантиссе числа не хватило отведенных
7 разрядов, она “залезла” в знаковый
разряд, изменив его на противоположный.

Такое
«налезание» мантиссы ( цифровой части)
числа на знаковый разряд называют
“переполнением мантиссы“.

Переполнение
мантиссы фиксируется во флаге
переполнения OF: он
получает значение 1, если было переполнение
(результат неправильный), и значение 0
– в противном случае (результат
правильный).

Переполнение
мантиссы возможно и при вычитании.
Например, требуется вычислить (+127
) – (-2 ).

Определяем
дополнительные коды:

доп
(+127) = 127

доп
(-2) = 256 – 2 = 254

Так
как уменьшаемое 127 меньше вычитаемого
254, выполняется заем:

(127
+ 256 ) – 254 =
129,

при
этом флаг CF = 1 (коды – беззнаковые числа).

Устанавливаем
число по его коду. Так как 129 > 127, то
модуль числа равен 256 – 129 = 127, а само
число -127.

Это
число и выдается как результат вычитания,
хотя истинной разностью является число
+129. Настоящая
разность оказалась вне диапазона
представимых знаковых чисел. Факт
переполнения мантиссы фиксируется во
флаге OF , равном 1.

2.5 Замечание о
флагах

Поскольку
сложение и вычитание беззнаковых и
знаковых чисел производятся по одним
и тем же алгоритмам, особенности этих
операций для обоих классов чисел
одновременно фиксируются флагами CF и
OF.

При
работе с беззнаковыми числами
представляет интерес флаг CF
(был ли перенос
или заем) и безразличен флаг
OF. Для знаковых
чисел информативен флаг OF
(было ли переполнение мантиссы) и не
представляет интереса флаг CF.

2.6 Задания для
самостоятельной работы

Вычислить
выражения, указать значения флагов CF
и OF. Принять, что числа имеют размер
байт.

1. (-5)
   + 5

2. (-5)
   – (-5)

3. (-5)
   – 10

4. 5
   – (-10)

5. 5
   + (-10)

6. 125
   + 202

7. 125
   – 202

8. 100
   + 100 (беззнаковые числа)

9. 100
   + 100 (знаковые числа)

10. 120
    – 100 (беззнаковые числа)

11. 120
    – 100 (знаковые числа)

18

Соседние файлы в папке МУ_ЭВМ+ПУ_ч1

• #

  28.05.2015157 б21.~lock.1-МУ_ЭВМ+ПУ-сист_сч.docx#

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Получение числа по его дополнительному коду

а) Если в коде старший бит числа равен 0, то есть число положительное. Такое число переводим в десятичную систему счисления в соответствии с правилами позиционной системы исчисления;

б) Если в коде старший бит числа равен 1, то число отрицательное, тогда:

1) инвертируем число;

3) переводим в десятичную систему счисления в соответствии с правилами позиционной системы исчисления;

4) записываем со знаком «-».

Использование дополнительного кода позволяет заменить операцию вычитания на операцию сложения.

Пример 11

Пример 12

Провести следующие вычисления в двоичной форме: 25₁₀ – 35₁₀ = — 10₁₀

= 1101 1100₂ инверсия модуля числа — 35₁₀

1101 1101₂ дополнительный код числа — 35₁₀

Проверка: 0000 1010₂ = 0·2 7 + 0·2 6 + 0·2 5 + 0·2 4 + 1·2 3 + 0·2 2 + 1·2 1 + 0·2 0 = 10₁₀

Пример 13

Провести следующие вычисления в шестнадцатеричной форме: 44₁₀ – 59₁₀ = — 15₁₀

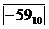= С4₁₆ инверсия модуля числа — 59₁₀

С5₁₆ дополнительный код числа — 59₁₀

С
+	С	дополнительный код числа — 3510
	F	старший разряд 1
Е	инверсия результата
+	+ 1
	F	результат вычитания

Проверка: 0F₁₆ = 0·16 1 + 15·16 0 = 15₁₀

Представление вещественных чисел

Для практических вычислений формат с плавающей запятой не используется – это формат представления чисел в памяти ЭВМ, не удобна.

Вещественное число N можно представить в системе счисления с основанием k в виде полинома:

,

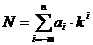
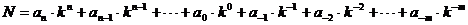здесь дробная часть любого вещественного числа содержит ∞ число членов.

Перевод вещественных положительных чисел из 10-ной системы счисления в систему с основанием Р

1) целая часть переводится как в случае с целыми числами;

2) дробная часть умножается на Р, целая часть результата запоминается и отбрасывается.

3) вновь полученная дробная часть умножается на Р и т.д.

4) Процедура продолжается до тех пор, пока дробная часть не станет равной нулю (или в пределе стремится к нулю, т.к. дробь в пределе является бесконечной);

5) полученный код отделяем от целой части запятой.

Пример 14

Перевести число 10,1₁₀ в двоичный вид

1. целая часть числа 10₁₀ = 1010₂

2. дробная часть числа 0,1

N п/п	запоминаем
0,1	×	0,2
0,2	×	0,41
0,4	×	0,8
0,8	×	1,6
0,6	×	1,2
0,2	×	0,4
0,4	×	0,8
0,8	×	1,6
0,6	×	1,2
0,2	×	0,4

Проверка: 10,0001100110₂ = 1·2 3 + 0·2 2 + 1·2 1 + 0·2 0 + 0·2 -1 + 0·2 -2 + 0·2 -3 + 1·2 -4 + 1·2 -5 +

0·2 -6 + 0·2 -7 + 1·2 -8 + 1·2 -9 + 0·2 -10 = 10,099609…

Видно, что результат и исходное число в дробной части отличаются.

Вычислим погрешность для дробной части нашего случая с числом двоичных разрядов после запятой 10

N_{исходное} – N_{получившееся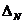} = абсолютная погрешность

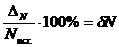относительная погрешность в процентах.

В нашем случае для 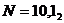: 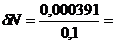0,391%.

Расчеты целесообразно вести до разумных пределов по погрешности или до ограничения разрядной сеткой.

Пример 15

Переведем число 973,232₁₀ в шестнадцатеричный код

N п/п	запоминаем
0,232	×	3,712
0,712	×	11,392	В
0,392	×	6,272
0,272	×	4,352

Ограничим число разрядов после запятой. Перевести число 3CD,3B₁₆ в десятичный код:

3CD,3B₁₆ = 3·16 2 + 12·16 1 + 13·16 0 + 3·16 -1 + 11·16 -2 = 973,23047₁₀

Погрешность 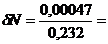0,202 %

Сложение дробной части вещественного числа в любой системе исчисления осуществляется традиционным образом, т.е. как и децимальной. При этом перенос в целую часть числа особенностей не имеет.

Пример 16

Сложить числа 0,5₁₀ + 0,625₁₀ = 1,125₁₀ в двоичной форме

0,
+	0,
	1,

Проверка: 1,001₂ = 1·2 0 + 0·2 -1 + 0·2 -2 + 1·2 -3 = 1,125₁₀

Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Источник

Дополнительный код (представление числа)

Дополнительный код (англ. two’s complement , иногда twos-complement) — наиболее распространённый способ представления отрицательных целых чисел в компьютерах. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел, чем упрощает архитектуру ЭВМ. Дополнительный код отрицательного числа можно получить инвертированием модуля двоичного числа (первое дополнение) и прибавлением к инверсии единицы (второе дополнение), либо вычитанием числа из нуля.

Дополнительный код (дополнение до 2) двоичного числа получается добавлением 1 к младшему значащему разряду его дополнения до 1. [1]

Дополнение до 2 двоичного числа определяется как величина полученная вычитанием числа из наибольшей степени двух (из 2 N для N-битного дополнения до 2).

Содержание

Представление отрицательного числа в дополнительном коде

При записи числа в дополнительном коде старший разряд является знаковым. Если его значение равно 0, то в остальных разрядах записано положительное двоичное число, совпадающее с прямым кодом. Если число, записанное в прямом коде, отрицательное, то все разряды числа инвертируются, а к результату прибавляется 1. К получившемуся числу дописывается старший (знаковый) разряд, равный 1.

Двоичное 8-ми разрядное число со знаком в дополнительном коде может представлять любое целое в диапазоне от −128 до +127. Если старший разряд равен нулю, то наибольшее целое число, которое может быть записано в оставшихся 7 разрядах равно , что равно 127.

Десятичное представление	Код двоичного представления (8 бит)
прямой	обратный	дополнительный
127	01111111	01111111	01111111
1	00000001	00000001	00000001
0	00000000	00000000	00000000
-0	10000000	11111111	—
-1	10000001	11111110	11111111
-2	10000010	11111101	11111110
-3	10000011	11111100	11111101
-4	10000100	11111011	11111100
-5	10000101	11111010	11111011
-6	10000110	11111001	11111010
-7	10000111	11111000	11111001
-8	10001000	11110111	11111000
-9	10001001	11110110	11110111
-10	10001010	11110101	11110110
-11	10001011	11110100	11110101
-127	11111111	10000000	10000001
-128	—	—	10000000

Дополнительный код для десятичных чисел

Тот же принцип можно использовать и в компьютерном представлении десятичных чисел: для каждого разряда цифра X заменяется на 9−X, и к получившемуся числу добавляется 1. Например, при использовании четырёхзначных чисел −0081 заменяется на 9919 (9919+0081=0000, пятый разряд выбрасывается).

При применении той же идеи к привычной 10-ричной системе счисления получится (например, для гипотетического процессора использующего 10-ричную систему счисления):

10-ричная система счисления («обычная» запись)	10-ричная система счисления, дополнительный код
.	.
13	0013
12	0012
11	0011
10	0010
9	0009
8	0008
.	.
2	0002
1	0001
0	0000
-1	9999
-2	9998
-3	9997
-4	9996
.	.
-9	9991
-10	9990
-11	9989
-12	9988
.	.

Преобразование в дополнительный код

Преобразование числа из прямого кода в дополнительный осуществляется по следующему алгоритму.

1. Если число, записанное в прямом коде, положительное, то к нему дописывается старший (знаковый) разряд, равный 0, и на этом преобразование заканчивается;
2. Если число, записанное в прямом коде, отрицательное, то все разряды числа инвертируются, а к результату прибавляется 1. К получившемуся числу дописывается старший (знаковый) разряд, равный 1.

Пример. Преобразуем отрицательное число −5, записанное в прямом коде, в дополнительный. Прямой код числа −5, взятого по модулю:

Инвертируем все разряды числа, получая таким образом обратный код:

Добавим к результату 1

Допишем слева знаковый единичный разряд

Для обратного преобразования используется тот же алгоритм. А именно:

Инвертируем все разряды числа, получая таким образом обратный код:

Добавим к результату 1 и проверим, сложив с дополнительным кодом

p-адические числа

В системе p-адических чисел изменение знака числа осуществляется преобразованием числа в его дополнительный код. Например, если используется 5-ричная система счисления, то число, противоположное 1000. (1) равно 4444. (−1).

Источник

Дополнительный код (представление числа)

Материал из Seo Wiki — Поисковая Оптимизация и Программирование

Дополнительный код (англ. two’s complement , иногда twos-complement) — наиболее распространённый способ представления отрицательных целых чисел в компьютерах. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел, чем упрощает архитектуру ЭВМ. Дополнительный код отрицательного числа можно получить инвертированием модуля двоичного числа (первое дополнение) и прибавлением к инверсии единицы (второе дополнение). Либо вычитанием числа из нуля.

Дополнительный код (дополнение до 2) двоичного числа получается добавлением 1 к младшему значащему разряду его дополнения до 1. [1]

Дополнение до 2 двоичного числа определяется как величина полученная вычитанием числа из наибольшей степени двух (из 2 N для N-битного дополнения до 2). [2]

Содержание

Представление числа в дополнительном коде

При записи числа в дополнительном коде старший разряд является знаковым. Если его значение равно 0, то в остальных разрядах записано положительное двоичное число, совпадающее с прямым кодом. Если же знаковый разряд равен 1, то в остальных разрядах записано отрицательное двоичное число, преобразованное в дополнительный код. Для получения значения, которое противоположно по знаку, все разряды, включая знаковый, инвертируются, а затем к результату добавляется единица.

Двоичное 8-ми разрядное число со знаком в дополнительном коде может представлять любое целое в диапазоне от −128 до +127. Если старший разряд равен нулю, то наибольшее целое число, которое может быть записано в оставшихся 7 разрядах равно 2^7-1 , что равно 127.

Десятичное представление	Код двоичного представления (8 бит)
прямой	дополнительный
127	01111111	01111111
1	00000001	00000001
0	00000000	00000000
-0	10000000	———
-1	10000001	11111111
-2	10000010	11111110
-3	10000011	11111101
-4	10000100	11111100
-5	10000101	11111011
-6	10000110	11111010
-7	10000111	11111001
-8	10001000	11111000
-9	10001001	11110111
-10	10001010	11110110
-11	10001011	11110101
-127	11111111	10000001
-128	———	10000000

При применении той же идеи к привычной 10-ричной системе счисления получится (например, для гипотетического процессора использующего 10-ричную систему счисления):

10-ричная система счисления («обычная» запись)	10-ричная система счисления, дополнительный код
.	.
13	0013
12	0012
11	0011
10	0010
9	0009
8	0008
.	.
2	0002
1	0001
0	0000
-1	9999
-2	9998
-3	9997
-4	9996
.	.
-9	9991
-10	9990
-11	9989
-12	9988
.	.

Преобразование дополнительного кода

Преобразование числа из прямого кода в дополнительный осуществляется по следующему алгоритму.

1. Если число, записанное в прямом коде, положительное, то к нему дописывается старший (знаковый) разряд, равный 0, и на этом преобразование заканчивается;
2. Если число, записанное в прямом коде, отрицательное, то все разряды числа инвертируются, а к результату прибавляется 1. К получившемуся числу дописывается старший (знаковый) разряд, равный 1.

Пример. Преобразуем отрицательное число −5, записанное в прямом коде, в дополнительный. Прямой код числа −5, взятого по модулю:

Инвертируем все разряды числа, получая таким образом обратный код:

Добавим к результату 1

Допишем слева знаковый единичный разряд

Для обратного преобразования используется тот же алгоритм. А именно:

Инвертируем все разряды числа, получая таким образом обратный код:

Добавим к результату 1 и проверим, сложив с дополнительным кодом

Дополнительный код для десятичных чисел

Тот же принцип можно использовать и в компьютерном представлении десятичных чисел: для каждого разряда цифра X заменяется на 9−X, и к получившемуся числу добавляется 1. Например, при использовании четырёхзначных чисел −0081 заменяется на 9919 (9919+0081=0000, пятый разряд выбрасывается).

Источник

Двоичное число: прямой, обратный и дополнительный коды

Прямой код двоичного числа
Обратный код двоичного числа
Дополнительный код двоичного числа

Прямой, обратный и дополнительный коды двоичного числа – способы представления двоичных чисел с фиксированной запятой в компьютерной (микроконтроллерной) арифметике, предназначенные для записи отрицательных и неотрицательных чисел

Мы знаем, что десятичное число можно представить в двоичном виде. К примеру, десятичное число 100 в двоичном виде будет равно 1100100, или в восьмибитном представлении 0110 0100. А как представить отрицательное десятичное число в двоичном виде и произвести с ним арифметические операции? Для этого и предназначены разные способы представления чисел в двоичном коде.
Сразу отмечу, что положительные числа в двоичном коде вне зависимости от способа представления (прямой, обратный или дополнительный коды) имеют одинаковый вид.

---

Прямой код

Прямой код – способ представления двоичных чисел с фиксированной запятой. Главным образом используется для записи неотрицательных чисел

Прямой код используется в двух вариантах.
В первом (основной) – для записи только неотрицательных чисел:

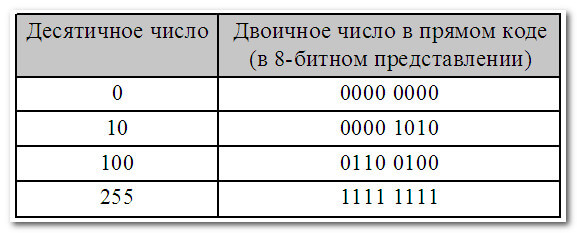В этом варианте (для восьмибитного двоичного числа) мы можем записать максимальное число 255 (всего чисел 256 – от 0 до 255)

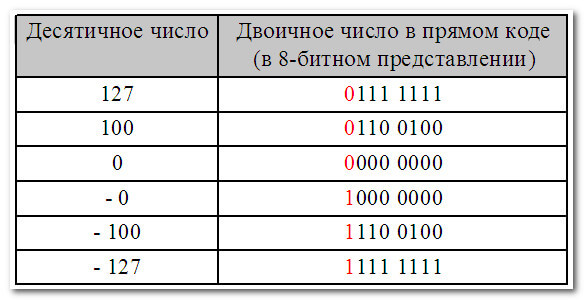
Второй вариант – для записи как положительных, так и отрицательных чисел.
В этом случае старший бит (в нашем случае – восьмой) объявляется знаковым разрядом (знаковым битом).
При этом, если:
– знаковый разряд равен 0, то число положительное
– знаковый разряд равен 1, то число отрицательное

В этом случае диапазон десятичных чисел, которые можно записать в прямом коде составляет от – 127 до +127:

Подводя итоги вопроса, не влезая в его дебри, скажу одно:
Прямой код используется главным образом для представления неотрицательных чисел.
 Использование прямого кода для представления отрицательных чисел является неэффективным – очень сложно реализовать арифметические операции и, кроме того, в прямом коде два представления нуля – положительный ноль и отрицательный ноль (чего не бывает):

---

Обратный код

Обратный код – метод вычислительной математики, позволяющий вычесть одно число из другого, используя только операцию сложения.
Обратный двоичный код положительного числа состоит из одноразрядного кода знака (битового знака) – двоичной цифры 0, за которым следует значение числа.
Обратный двоичный код отрицательного числа состоит из одноразрядного кода знака (битового знака) – двоичной цифры 1, за которым следует инвертированное значение положительного числа.

Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).
Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.

При 8-битном двоичном числе – знаковый бит (как и в прямом коде) старший (8-й)

Диапазон десятичных чисел, который можно записать в обратном коде от -127 до + 127

Арифметические операции с отрицательными числами в обратном коде:

(Арифметические операции с двоичными числами)

1-й пример (для положительного результата)
Дано два числа:
100 = 0110 0100
-25 = – 0001 1001
Необходимо их сложить:
100 + (-25) = 100 – 25 = 75

1-й этап
Переводим число -25 в двоичное число в обратном коде:
25 = 0001 1001
-25= 1110 0110
и складываем два числа:
0110 0100 (100) + 1110 0110 (-25) = 1 0100 1010, отбрасываем старшую 1 (у нас получился лишний 9-й разряд – переполнение), = 0100 1010
2-й этап
Отброшенную в результате старшую единицу прибавляем к результату:
0100 1010 + 1 = 0100 1011 (знаковый бит =0, значит число положительное), что равно 75 в десятичной системе

2-й пример (для отрицательного результата)
Дано два числа:
5 = 0000 0101
-10 = – 0000 1010
Необходимо их сложить:
5 + (-10) = 5 – 10 = -5

1-й этап
Переводим число -10 в двоичное число в обратном коде:
10 = 0000 1010
-10= 1111 0101
и складываем два числа:
0000 0101 (5) + 1111 0101 (-10) = 1111 1010 (знаковый бит =1, значит число отрицательное)

2-й этап
Раз результат получился отрицательный, значит число представлено в обратном коде.
Переводим результат в прямой код (путем инвертирования значения, знаковый бит не трогаем):
1111 1010 —-> 1000 0101
Проверяем:
1000 0101 = – 0000 0101 = -5

---

Обратный код решает проблему сложения и вычитания чисел с различными знаками, но и имеет свои недостатки:
– арифметические операции проводятся в два этапа
– как и в прямом коде два представления нуля – положительный и отрицательный

---

Дополнительный код

Дополнительный код – наиболее распространенный способ представления отрицательных чисел. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел.

В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).

Диапазон десятичных чисел которые можно записать в дополнительном коде от -128 до +127. Запись положительных двоичных чисел в дополнительном коде та-же, что и в прямом и обратном кодах.

Дополнительный код отрицательного числа можно получить двумя способами
1-й способ:
– инвертируем значение отрицательного числа, записанного в прямом коде (знаковый бит не трогаем)
– к полученной инверсии прибавляем 1
Пример:
Дано десятичное число -10
Переводим в прямой код:
10 = 0000 1010 —-> -10 = 1000 1010
Инвертируем значение (получаем обратный код):
1000 1010 —-> 1111 0101
К полученной инверсии прибавляем 1:
1111 0101 + 1 = 1111 0110 – десятичное число -10 в дополнительном коде

2-й способ:
Вычитание числа из нуля
Дано десятичное число 10, необходимо получить отрицательное число (-10) в дополнительном двоичном коде
Переводим 10 в двоичное число:
10 = 0000 1010
Вычитаем из нуля:
0 – 0000 1010 = 1111 0110 – десятичное число -10 в дополнительном коде

Арифметические операции с отрицательными числами в дополнительном коде

Дано: необходимо сложить два числа -10 и 5
-10 + 5 = -5
Решение:
5 = 0000 0101
-10 = 1111 0110 (в дополнительном коде)
Складываем:
1111 0110 + 0000 0101 = 1111 1011, что соответствует числу -5 в дополнительном коде

Как мы видим на этом примере – дополнительный код отрицательного двоичного числа наиболее подходит для выполнения арифметических операций сложения и вычитания отрицательных чисел.

---

Вывод:
1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода
2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода

---

Предыдущие статьи:
1. Микроконтроллеры – первый шаг
2. Системы счисления: десятичная, двоичная и шестнадцатиричная
3. Логические операции, логические выражения, логические элементы
4. Битовые операции

---

(39 голосов, оценка: 4,69 из 5)

Загрузка…

---